Abstract
The aim of this study was to investigate pharmacodynamic (PD) interactions in mice infected with Mycobacterium tuberculosis using population pharmacokinetics (PKs), the Multistate Tuberculosis Pharmacometric (MTP) model, and the General Pharmacodynamic Interaction (GPDI) model. Rifampicin, isoniazid, ethambutol, or pyrazinamide were administered in monotherapy for 4 weeks. Rifampicin and isoniazid showed effects in monotherapy, whereas the animals became moribund after 7 days with ethambutol or pyrazinamide alone. No PD interactions were observed against fast‐multiplying bacteria. Interactions between rifampicin and isoniazid on killing slow and non‐multiplying bacteria were identified, which led to an increase of 0.86 log10 colony‐forming unit (CFU)/lungs at 28 days after treatment compared to expected additivity (i.e., antagonism). An interaction between rifampicin and ethambutol on killing non‐multiplying bacteria was quantified, which led to a decrease of 2.84 log10 CFU/lungs at 28 days after treatment (i.e., synergism). These results show the value of pharmacometrics to quantitatively assess PD interactions in preclinical tuberculosis drug development.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ There is limited knowledge on the PD interactions between standard TB drugs due to a lack of a quantitative framework for their assessment.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ It addressed how to quantitatively assess drug‐drug PD interactions between two drugs in more than two‐drug combination therapies using sparse mice data.
WHAT THIS STUDY ADDS TO OUR KNOWLEDGE
☑ The application of the MTP model together with the GPDI model in TB‐infected BALB/c mice could describe untreated mice or mice treated with rifampicin, isoniazid, ethambutol, and pyrazinamide mono therapy, as well as an assessment of antagonistic interactions (less than expected additivity) between rifampicin and isoniazid and synergistic interactions (more than expected additivity) between rifampicin and ethambutol in combination therapies using a model‐based approach.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ Even with sparse animal data, PK‐PD relationships with PD interactions using the MTP‐GPDI model could be assessed, which provides information for phase II and phase III trials for translational development of novel combination therapies in TB drug development.
In 2015, approximately 1.8 million people died from Mycobacterium tuberculosis (M. tuberculosis) and 10.4 million new cases were reported worldwide.1 No regimen has yet proven to be superior to the standard regimen for drug‐susceptible tuberculosis (TB), which consists of a 2‐month initial phase of rifampicin, isoniazid, pyrazinamide, and ethambutol followed by a 4‐month continuation phase of rifampicin and isoniazid. Due to the development of drug resistance, long treatment periods cause a high risk of low patient adherence as well as disease relapse in patients. New drugs or combinations are highly needed to overcome these obstacles. Potential pharmacodynamic (PD) drug‐drug interactions (i.e., a lower (antagonism) or higher effect (synergism) compared to expected additivity, such as adding each drug effect in monotherapy), present a difficulty arising from combination therapies. The PD interactions are difficult to assess in a clinical setting, especially in the field of antitubercular drug development in which regimens contain two or more drugs. Hence, preclinical systems have to fill this knowledge gap, but evaluation of PD interactions has been methodologically challenging.2
The General Pharmacodynamic Interaction (GPDI) model provides a model‐based assessment of PD interactions given as fractional changes of PD parameters of monotherapy effects, which was originally developed and presented by Wicha et al.3 In contrast to other approaches, the GPDI model is applicable for more than two potentially interacting drugs, which is of key importance in TB drug development. A key feature of the GPDI approach is that interactions are quantified on the level of PD parameters and not on the pure effect level. Thereby, the GPDI approach is capable, in addition to determine pure synergistic or antagonistic interactions, to detect asymmetric interactions (i.e., in which both synergism and antagonism occur between two drugs over a concentration range or study time period). In addition, an advantage of the GPDI model compared with other traditional approaches is that it can estimate the interaction between an inactive perpetrator and an active victim drug. Moreover, the GPDI approach can be parameterized in different complexity and, hence, be used for both sparse and rich data.
The Multistate Tuberculosis Pharmacometric (MTP) model, predicting the change in bacterial numbers of fast, slow, and non‐multiplying bacteria, with and without drug effects, is a semimechanistic pharmacokinetic (PK) and PD model for studying antitubercular drug effects and was developed using in vitro data.4 The MTP model has successfully been used to describe rifampicin efficacy in an acute C57BL/6 mouse model using differences in colony‐forming units (CFUs) over time,5 and has also been applied to clinical data in order to estimate the drug efficacy of human early bacterial activity and to perform clinical trial simulations.6
The aim of this work was to use the MTP model approach to describe the drug effects of rifampicin, isoniazid, ethambutol, and pyrazinamide in the monotherapy in a BALB/c mouse model using biomarker CFU data. In addition, we aimed to link the MTP model to the GPDI model in order to assess PD interactions in combination therapies.
MATERIALS AND METHODS
Chemicals
Ethambutol and pyrazinamide were obtained from Sigma‐Aldrich (Zwijndrecht, The Netherlands) and isoniazid was obtained from the hospital pharmacy (Rotterdam, The Netherlands). Compounds were dissolved in distilled water. Rifampicin was obtained from Sanofi‐Aventis (Gouda, The Netherlands), dissolved in the supplemented dissolvent, and further diluted in water.
Animals
Specified pathogen‐free female BALB/c mice (13–15 weeks old, weighing 20–25 g) were obtained from Charles River (Les Oncins, France). Experimental protocols adhered to the rules specified in the Dutch Animal Experimentation Act and were in concordance with the European Union (EU) animal directive 2010/63/EU. The Institutional Animal Care and Use Committee of the Erasmus Medical Center approved the present protocols (117‐12‐08 and 117‐12‐13).
Mice were infected, as previously described.7 In brief, mice under anesthesia were infected through intratracheal instillation of a suspension (40 µL) containing 9.5 × 104 CFU of the Beijing VN 2002‐1585 genotype strain, followed by proper inhalation to ensure the formation of a bilateral TB infection.8
Anti‐TB treatment
In this study, the doses were chosen based on the human‐equivalent dose of each antitubercular compound. There were three dose levels chosen for each drug, 0.5 × human‐equivalent dose, 1 × human‐equivalent dose, and 2 × human‐equivalent dose. All treatments started 14 days after infection. Monotherapy of rifampicin at dose levels at 5, 10, and 20 mg/kg (R5, R10, and R20, respectively), isoniazid at 12.5, 25, and 50 mg/kg (H12.5, H25, and H50, respectively), ethambutol at 50, 100, and 200 mg/kg (E50, E100, and E200, respectively) or pyrazinamide at 75, 150, and 300 mg/kg (Z75, Z150, and Z300, respectively) were orally administered daily for 5 days per week via oral gavage, lasting for 4 weeks.8 The CFU counts were assessed in monotherapy after 1, 2, and 4 weeks of treatment with isoniazid or rifampicin, using 9 mice per time point, including 3 mice per dose level. The CFU counts were only obtained from 6 mice after 1 week of treatment with pyrazinamide and ethambutol, because the mice did not survive beyond 1 week with treatments of pyrazinamide or ethambutol. Fixed doses were used in combination therapies, including R10, H25, E100, and Z150. Combination therapies (R10H25, R10H25Z150, and R10H25Z150E100) lasted up to 24 weeks. The CFU counts were assessed in drug combinations after 1, 2, 4, 8, 12, and 24 weeks of treatment with 3 mice at each occasion. Bacterial natural growth (i.e., no treatment), was collected at 1, 3, 7, 14, and 21 days after infection.
Population pharmacokinetic study and modeling
The PK information was obtained from TB‐infected mice and was used for assessing PD in monotherapy. One blood sample per mouse was drawn from infected mice (n = 49) after 4 weeks of treatment with rifampicin (R5, R10, or R20), isoniazid (H12.5, H25, or H50), and after 1 week of treatment with ethambutol (E50, E100, or E200) or pyrazinamide (Z75, Z150, or Z300) at 1, 4, and 8 hours after dose with 3 mice per time point. Mice receiving Z75 in monotherapy only contributed CFU data and not PK data. The PK sampling was different for mice treated with pyrazinamide or ethambutol, as the treatment results in no survival beyond 1 week with treatments. Drug plasma samples from infected mice were frozen at −80°C and processed by protein precipitation with organic solvents plus filtration. Samples were then analyzed by ultraperformance liquid chromatography tandem mass‐spectrometry for quantification of each drug at GlaxoSmithKline. To support the population pharmacokinetic (PopPK) model development for rifampicin, drug concentrations from the sparsely sampled TB‐infected mice were combined with a second PK study in healthy mice (n = 18).8 Healthy mice were administered R10 or R160 for 5 days a week for 3 weeks and the PK was obtained at 0.08, 0.25, 0.5, 0.75, 1.5, 3, and 6 hours after the last dose (one sample per mouse). Rifampicin, quantified in plasma samples from healthy mice, was measured by protein precipitation, followed by high‐performance liquid chromatography with ultraviolet detection.9
All plasma concentrations of each drug were pooled and modeled simultaneously. One and two compartment distribution models with first‐order absorption and elimination were evaluated. Because of lack of data in the absorption phase, the absorption rate constant (ka) of isoniazid, ethambutol, and pyrazinamide was fixed to values from a previous study.10 Differences in PK between healthy and infected mice were evaluated. Similarly, concentration‐dependencies or time‐dependencies in all PK parameters were evaluated. Because only one sample was taken from each mouse, interindividual variability in PK was not quantified. A PopPK parameter approach was used as input and linked to the MTP model.11
Evaluation of drug effects in monotherapy
The MTP model, consisting of fast‐multiplying (F), slow‐multiplying (S), and non‐multiplying (N) bacteria was used for the PD modeling of CFU data from each drug. The differential equation system for F (Eq. (1)), S (Eq. (2)), and N (Eq. (3)) was as follows:
| (1) |
| (2) |
| (3) |
where kG is the growth rate of F, kFS, kSF, kFN, kSN, and kNS are transfer rates between each bacterial state and F, S, and N represent fast, slow, and non‐multiplying bacteria, respecitvely.
Initially, only CFU data without treatment were evaluated. The first‐order transfer rates from S to F (kSF), from S to N (kSN), from N to S (kNS), and from F to N (kFN) were fixed according to the original in vitro study.4 The transfer of F to S (kFS) increased linearly with time in the MTP model applied to in vitro data and was re‐evaluated using maximum effect (Emax) and linear functions with respect to time in this study. A re‐estimation of kFS as well as the other transfer rates, one at a time, was compared to fixing the parameter to the in vitro estimates.4 Gompertz, Emax, and linear growth functions were evaluated to describe the growth rate (kG) of F in this mouse model.
All parameters associated with natural growth (kG, kFS, kSF, kFN, kSN, and kNS) were fixed during the estimation of drug effects. The effect of each drug was first evaluated using only monotherapy data. The effects of monotherapy were evaluated as inhibition of the growth of F, and/or stimulation of the death on each of the three bacterial states using an on/off effect, a linear function (Eq. (4)), an ordinary Emax function (Eq. (5)), or a sigmoidal Emax function (Eq. (6)).
| (4) |
| (5) |
| (6) |
where Cdrug represents drug concentration; k is the kill rate for each drug in monotherapy; Emax is the maximal achievable drug effect for each drug; EC50 is the drug concentration at 50% of Emax for each drug; is a sigmoidicity parameter, and Edrug expresses the drug effect in monotherapy. In the following step, all identified drug effects from monotherapy were combined and evaluated for statistical significance (P < 0.05). A final backward evaluation step (P < 0.01) was also done where the effect functions were reduced to their simpler forms to identify the best model for each drug in monotherapy.
Evaluation of pharmacodynamic interactions
During the evaluation of PD interactions, data from combination regimens were pooled with data from natural growth and data from monotherapy. The MTP model parameters (kG, kFS, kSF, kFN, kSN, and kNS) and parameters of the monotherapy final exposure‐response relationships were fixed during the PD interaction assessment. If no drug effect was identified using only monotherapy, a re‐evaluation using the combination dataset was done with a similar modeling strategy as for monotherapy data. This step was required due to the different treatment lengths. The PD interactions were assessed at each effect site, including inhibition of the growth of F, and/or stimulation of the death of F, S, or N.
The Bliss Independence (BI)12 (i.e., EAB = EA + EB‐EA × EB) was used as an additivity criterion for the GPDI model,3 as the Loewe Additivity13 cannot handle differences in Emax. As BI was derived from probability theory, all effects were scaled between 0 and 1 relative to the highest Emax for BI calculation and then rescaled by the highest Emax, as described by Wicha et al.14 For slope models, the BI was simplified to EAB = EA + EB due to the minor contribution of EA·EB at concentrations well below the EC50 when linear models are identified. Hence, the drug effects of two drugs A and B can be expressed as in Eq. (7) and Eq. (8). In three and four‐drug combinations, interaction parameters identified in previous combinations were fixed. In the final MTP‐GPDI model, all parameters were estimated simultaneously.
| (7) |
| (8) |
where INTAB and INTBA characterize the maximum fractional change of the respective PD parameters. An estimated value of zero of INTAB or INTBA suggested no interaction. A positive value suggested decreased drug potency, whereas a value between −1 and 0 suggested increased drug potency caused by interaction between the two drugs. EC50INT,AB and EC50INT,BA represent the interaction potencies. HINT,A and HINT,B represent the interaction sigmoidicities.
Due to the fact that few exposure levels were included in the combination therapy data in this study, a joint was estimated (INTAB = INTBA) and EC50INT was set to a very low value of 1 × 10−8, which reduced the Emax function to an on/off effect, which was used in evaluating the PD interaction. Equation (9) shows an example of a reduced GPDI model for the evaluation of a joint effect of drugs A and B when the exposure‐response relationship was defined using a slope model, and on/off interaction with a joint interaction term INTAB:
| (9) |
where kA and kB are linear effects of drug A and drug B identified in monotherapy.
Model evaluation and selection
All modeling was done using the software NONMEM version 7.3 (Icon Development Solutions (http://www.iconplc.com/technology/products/nonmem), Ellicott City, MD) using the first‐order conditional estimation method.15 Model evaluation and selection were based on the objective function value (OFV) with a decrease of 3.84 considered statistically significant (P < 0.05, χ2 distribution) for nested models and one degree of freedom. In addition, goodness‐of‐fit plots, parameter precision, predictive performance assessed using visual predictive check (VPC),16 prediction‐corrected visual predictive checks (pcVPC),17 and scientific plausibility were used for model selection. In both pcVPC and VPC, 1,000 replicates were simulated based on the model and fifth, median, and 95th percentiles were used in conjunction with the corresponding data to assess model performance using Perl‐speaks‐NONMEM (PsN) version 4.2.0 (http://psn.sourceforge.net), Department of Pharmaceutical Biosciences, Uppsala University, Sweden).16 The R package Xpose version 4.4.1 (http://xpose.sourceforge.net), Department of Pharmaceutical Biosciences, Uppsala University, Sweden) was used for visualization of results and data management.16 The run record was produced with Pirana software version 2.7 (Pirana Software and Consulting (http://www.pirana-software.com), San Francisco, CA).18 The M3 method in NONMEM was used to handle data below the lower limit of quantification (LLOQ),19 which was 10 CFU/lungs for PD data (5.7% of the dataset) and 10 ng/mL, 100 ng/mL, 10 ng/mL, and 60 ng/mL of rifampicin (8.9%), isoniazid (27.8%), ethambutol (0%), and pyrazinamide PK data (0%), respectively. Proportional, combined proportional, and additive error models for PK data and an additive error model on log scale for PD data were evaluated to describe residual unexplained variability.
RESULTS
Population pharmacokinetic models
The final PopPK models of rifampicin, isoniazid, and pyrazinamide were one‐compartment models, whereas a two‐compartment model described the ethambutol data well. All data were well‐described using the final PopPK models (Figure 1) and all PK parameters are shown in Table 1. The pcVPCs of the final PopPK models are available as Supplementary Material S1.
Figure 1.
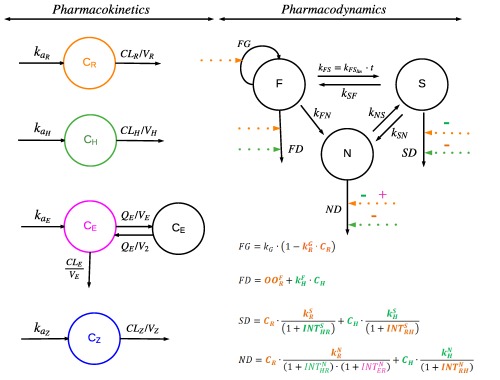
Schematic illustration of the final population pharmacokinetic (PK) models and the final Multistate Tuberculosis Pharmacometric model consisting of fast (F), slow (S), and non‐multiplying (N) bacterial states linked to the General Pharmacodynamic Interaction model. The bacterial system was described with a growth rate of F ( ), a time‐dependent linear rate parameter describing transfer rate from fast to slow‐multiplying bacteria (kFS), first‐order transfer rate from slow to fast‐multiplying state (kSF), first‐order transfer rate from fast to non‐multiplying state (kFN), first‐order transfer rate from slow to non‐multiplying state (kSN), and first‐order transfer rate from non to slow‐multiplying state (kNS). The final PK models of rifampicin (R; in orange), isoniazid (H; in green), ethambutol (E; in purple) and pyrazinamide (Z; in blue) are shown where the absorption rate constant (ka), clearance (CL), volume of distribution of the central and peripheral compartment (V and V2) and intercompartmental clearance (Q) are specified for different drugs with subscription. The monotherapy drug effects are shown as dashed lines for rifampicin (in orange), isoniazid (in green), ethambutol (in purple), and pyrazinamide (in blue) affecting the inhibition of the growth of fast‐multiplying bacteria (FG) and stimulation of the death of fast‐multiplying bacteria (FD), slow‐multiplying bacteria (SD), or non‐multiplying bacteria (ND). The is the linear rifampicin‐induced inhibition of fast‐multiplying bacteria growth rate in monotherapy. The is the rifampicin‐induced on/off stimulation of fast‐multiplying bacteria death rate in monotherapy. The and are rifampicin‐induced second‐order slow and non‐multiplying bacteria death rates, respectively, in monotherapy. The , , and are isoniazid‐induced second‐order fast, slow, and non‐multiplying bacteria death rates, respectively, in monotherapy. The pharmacodynamic (PD) interactions of rifampicin (R; in orange), isoniazid (H; in green), ethambutol (E; in purple) and pyrazinamide (Z; in blue) are shown as + (synergism) or – (antagonism) on the respective dashed drug effect line. and are the PD interactions on stimulation of the death of slow and non‐multiplying bacteria, respectively, observed between rifampicin and isoniazid in the combination. The is the PD interaction on stimulation of the death of non‐multiplying bacteria, observed between rifampicin and ethambutol in the combination.
Table 1.
Final population pharmacokinetic parameter estimates for rifampicin, isoniazid, ethambutol, and pyrazinamide in mice
| Parameters | Rifampicin | Isoniazid | Ethambutol | Pyrazinamide | ||||
|---|---|---|---|---|---|---|---|---|
| Typical value | RSE, % | Typical value | RSE, % | Typical value | RSE, % | Typical value | RSE, % | |
| ka (h−1) | 6.23 | 21.0 | 12.6 FIXa | ‐ | 0.87 FIXa | ‐ | 2.84 FIXa | ‐ |
| CL/F (mL·h−1·kg−1) | 234 | 22.4 | 612b | 5.4 | 3,400 | 11.0 | 273.71 | 15.9 |
| V/F (mL·kg−1) | 706 | 32.4 | 811 | 8.0 | 1,500 | 22.3 | 525.1 | 22.1 |
| Q/F (mL·h−1·kg−1) | ‐ | ‐ | ‐ | ‐ | 2,530 | 42.7 | ‐ | ‐ |
| V2/F (mL·kg−1) | ‐ | ‐ | ‐ | ‐ | 4,690 | 27.3 | ‐ | ‐ |
| Vhighest dose/F (mL·kg−1) | 1,700 | 11.6 | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ |
| CLhighest dose/F (mL·h−1·kg−1) | 94.6 | 6.3 | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ |
| Slopeʂ | ‐ | ‐ | 7.50E‐03 | 16.8 | ‐ | ‐ | ‐ | ‐ |
| CL/F (mL·h−1·kg−1) | 54.9 | 35.3 | ‐ | ‐ | ‐ | ‐ | ‐ | ‐ |
| Proportional residual error | 0.0419 | 13.0 | 0.0174 | 23.1 | 0.135 | 12.0 | 0.264 | 13.2 |
| Additive residual error | 7.77 | 35.0 | 0.232 | 25.0 | 0.0239 | 38.1 | ||
CL/F, apparent clearance; CLhighest dose/F, apparent clearance at the highest dose level of 160 mg/kg of rifampicin; CL/F, apparent clearance of rifampicin in healthy mice; ka, absorption rate constant; V/F, apparent volume of distribution in the central compartment; Vhighest dose/F, apparent volume of distribution at the highest dose of 160 mg/kg of rifampicin; V2/F, apparent volume of distribution in the peripheral compartment; Q/F, apparent intercompartmental clearance; RSE, relative standard error reported on the approximate SD scale.
ka fixed according to Chen et al.10; bCL/Fisoniazid for the lowest dose; CL/Fisoniazid, CL/Flowest dose·(1 – Slopeʂ (Dose – Doselowest dose)).
The final PopPK model for rifampicin included a separate apparent clearance (CL/F) in TB‐infected mice receiving 4 weeks of rifampicin treatment, which was 3 times higher than CL/F in healthy mice treated for 3 weeks. In addition, the CL/F at R160 was 2.5 times lower than for mice that received lower doses of rifampicin. Apparent volume of distribution of the central compartment (V/F) after R160 was 1,700 mL·kg−1, which was larger than V/F at other dose levels (706 mL·kg−1). Isoniazid CL/F decreased from 612 mL·h−1·kg−1 at lowest dose of 12.5 mg/kg to 440 mL·h−1·kg−1. Isoniazid V/F was estimated to 811 mL·kg−1. Apparent clearance (CL/F) of ethambutol was estimated to 3,400 mL·h−1·kg−1. Ethambutol V/F and apparent volume of distribution of the peripheral compartment (V2/F) were estimated to 1,500 and 4,690 mL·kg−1, respectively. Pyrazinamide PK was linear with respect to dose with CL/F estimated to 273 mL·h−1·kg−1 and V/F to 525 mL·kg−1.
Multistate tuberculosis pharmacometric model
The final model structure of the MTP model describing changes in CFU over time after treatment with rifampicin, isoniazid, pyrazinamide, or ethambutol is shown in Figure 1. The data supported estimation of initial bacterial numbers of fast‐multiplying (F0) and slow‐multiplying (S0) bacteria, but no inoculum of non‐multiplying bacteria, which was, therefore, set to zero in the final model. Re‐estimating the transfer rate from F to S (kFS) as a linear function with time produced a decrease in OFV of 22 points compared to fixing the parameter to the in vitro estimate.4 Re‐estimation of the other transfer rates between the states did not provide a reduction in OFV and was, therefore, fixed to in vitro estimates.4 An exponential growth function was used to describe the natural growth rate of F (kG).
Exposure‐response relationships for mono drug therapy
The final MTP model included rifampicin mono drug effects on inhibition of the growth of F, and stimulation of the death of F, S, and N, as well as isoniazid mono drug exposure‐response relationships as linear death rates of both F and S. Isoniazid effect on stimulation of the death of N was identified in R10H25Z150 using a linear function, which was not identifiable in isoniazid monotherapy and R10H25 combination. All equations of mono drug effects are shown in Figure 1.
Due to a lack of longitudinal CFU data on ethambutol and pyrazinamide during monotherapy, the mono drug effects of these drugs could not be quantified.
General pharmacodynamic interaction model
The GPDI model was linked to the MTP model for the evaluation of PD interactions using combination therapies. Rifampicin and isoniazid decreased their respective potencies on jointly killing S ( ) and N ( ). and were estimated to 4.49 and 0.32, respectively, which can be interpreted as a 4.49‐fold or 0.32‐fold decrease in the efficacy slope of rifampicin and isoniazid, respectively (Supplementary Material S2). This potency shift leads to 0.86 log10 CFU/lungs higher CFU at 28 days after treatment compared to the expected additivity of the two drugs based on monotherapy alone (i.e., PD antagonism was observed on the biomarker level (Figure 2)). Figure 3 illustrates simulations from the final MTP‐GPDI model and revealed that antagonistic interactions between rifampicin and isoniazid were more relevant in the lower dose range of rifampicin and higher dose range of isoniazid at 28 days after treatment.
Figure 2.
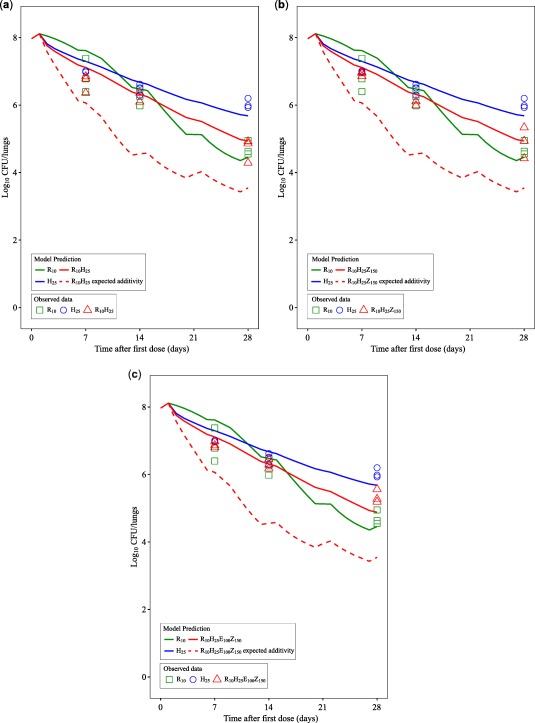
Predicted change from baseline of log10 colony‐forming unit (CFU)/lungs after mono and combination therapies based on the final Multistate Tuberculosis Pharmacometric‐General Pharmacodynamic Interaction model (solid lines) compared to model‐predicted expected additivity (dotted lines) after 10 mg/kg rifampicin monotherapy (R10), 25 mg/kg isoniazid monotherapy (H25), combination therapy of 10 mg/kg rifampicin and 25 mg/kg isoniazid (R10H25), combination therapy of 10 mg/kg rifampicin, 25 mg/kg isoniazid, and 150 mg/kg pyrazinamide (R10H25Z150), combination therapy of 10 mg/kg rifampicin, 25 mg/kg isoniazid, 150 mg/kg pyrazinamide, and 100 mg/kg ethambutol (R10H25 Z150E100). Observed data are given as symbols. The data did not support any drug effect from pyrazinamide or ethambutol in monotherapy. The fluctuations in response are due to drug treatments in 5 of 7 days per week.
Figure 3.
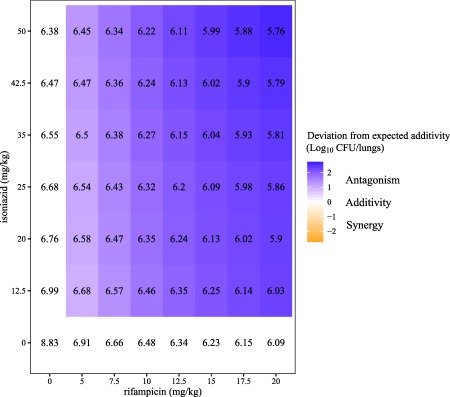
Predicted log10 colony‐forming unit (CFU)/lungs in numbers and log10 CFU/lungs deviation from expected additivity (in shaded areas) for rifampicin and isoniazid in different combinations at 28 days after treatment. White areas in the figure show expected additivity, whereas blue shaded areas show higher log10 CFU/lungs (antagonism) than expected additivity, and orange shaded areas show lower log10 CFU/lungs (synergism) than expected additivity.
Rifampicin and ethambutol increased their potencies ( = −0.15), as estimated by the GPDI model (Supplementary Material S2). The data did not support any PD interaction between ethambutol and pyrazinamide. These PD interactions led to 2.84 log10 CFU/lungs lower CFU compared to expected additivity between four drugs. PD parameters are shown in Table 2. An additive residual error on log scale was used in the final MTP‐GPDI model to describe the residual variability using log transformation of both sides.
Table 2.
Pharmacodynamic parameter estimates of the final Multistate Tuberculosis Pharmacometric‐General Pharmacodynamic Interaction model
| Parameter | Description | Typical value | RSE, % | |
|---|---|---|---|---|
| The MTP model | ||||
| F0 (lungs−1) | Initial fast‐multiplying bacterial number | 20,100 | 59.2 | |
| S0 (lungs−1) | Initial slow‐multiplying bacterial number | 119,000 | 31.0 | |
| kG (h−1) | Growth rate of the fast‐multiplying bacteria | 0.034 | 10.0 | |
| (h−2) | Time‐dependent transfer rate from fast‐multiplying to slow‐multiplying bacterial state | 6.65 10−5 | 20.3 | |
| kSF (h−1) | First‐order transfer rate from slow to fast‐multiplying bacterial state | 6.03 10−4 FIXa | ||
| kFN (h−1) | First‐order transfer rate from fast to non‐multiplying bacterial state | 3.74 10−8 FIXa | ||
| kSN (h−1) | First‐order transfer rate from slow to non‐multiplying bacterial state | 7.73 10−3 FIXa | ||
| kNS (h−1) | First‐order transfer rate from non to slow‐multiplying bacterial state | 5.11 10−5 FIXa | ||
|
|
Linear rifampicin‐induced inhibition of fast‐multiplying bacteria growth rate | 0.0022 | 29.2 | |
| (h−1) | Rifampicin‐induced on/off stimulation of fast‐multiplying bacteria death rate | 0.019 | 4.2 | |
| (mL·h−1·µg−1) | Rifampicin‐induced second‐order slow‐multiplying bacteria death rate | 0.0137 | 15.8 | |
| (mL·h−1·µg−1) | Rifampicin‐induced second‐order non‐multiplying bacteria death rate | 0.0033 | 8.0 | |
| (mL·h−1·µg−1) | Isoniazid‐induced second‐order fast‐multiplying bacteria death rate | 0.055 | 15.6 | |
| (mL·h−1·µg−1) | Isoniazid‐induced second‐order slow‐multiplying bacteria death rate | 0.00047 | 53.6 | |
| (mL·h−1·µg−1) | Isoniazid‐induced second‐order non‐multiplying bacteria death rate | 0.0012 | 5.0 | |
| The GPDI model | ||||
|
|
Interaction between rifampicin and isoniazid on stimulation of the death of slow‐multiplying bacteria | 4.49 | 28.1 | |
|
|
Interaction between rifampicin and isoniazid on stimulation of the death of non‐multiplying bacteria | 0.32 | 38.0 | |
|
|
Interaction between rifampicin and ethambutol on stimulation of the death slow‐multiplying bacteria | −0.15 | 57.7 | |
| σ2 | Additive residual variability on log scale (variance) | 1.23 | 16.7 | |
E, ethambutol; F, fast‐multiplying bacteria; H, isoniazid; N, non‐multiplying bacteria; R, rifampicin; RSE, relative standard error reported on the approximate standard deviation scale; S, slow‐multiplying bacteria.
Fixed to estimates from application of the MTP model in vitro by Clewe et al.4 2016.
The differential equation system for F (Eq. (10)), S (Eq. (11)), and N (Eq. (12)) for the final MTP‐GPDI model was as follows:
| (10) |
| (11) |
| (12) |
where FG and FD are the inhibition of the growth and stimulation of the death of F, and SD and ND are the stimulation of the death of S and N. Detailed equations of FG, FD, SD, and ND are shown in Figure 1. The VPCs for no treatment, monotherapies, and combination therapies based on the final models are shown in Figure 4. The final model code is available in the Supplementary Material S3.
Figure 4.
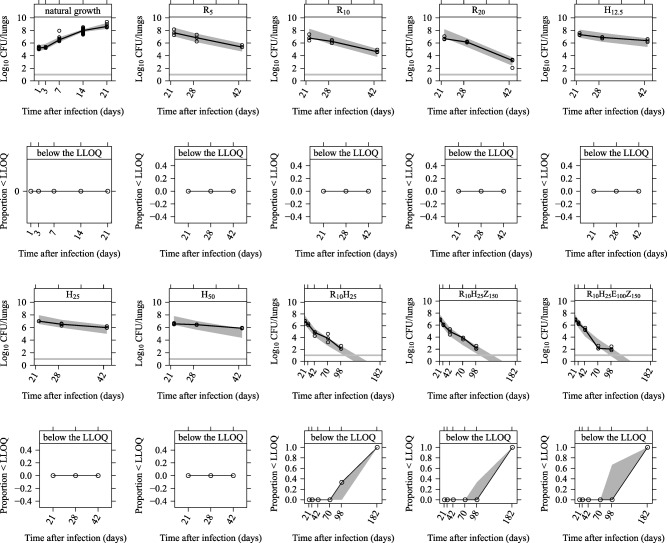
Visual Predictive Check of the final Multistate Tuberculosis Pharmacometric model linked to the General Pharmacodynamic Interaction model applied to colony forming unit (CFU) data from a tuberculosis‐infected experimental mouse model without treatment (natural growth) and with different drug treatments. Data above the lower limit of quantification (LLOQ) are shown in plots in the first and third rows, and the horizontal lines represent the LLOQ in plots in the first and third rows. The solid lines are the medians of the observations and open circles are the observations. Light gray shaded areas represent 95% confidence intervals for the medians. Data below the LLOQ are shown in plots in the second and fourth rows where the solid lines are the medians of the LLOQ data. Light gray shaded areas represent 95% confidence intervals for the medians of the LLOQ data. R5, R10, and R20 represent 5, 10, and 20 mg/kg of rifampicin monotherapy. H12.5, H25, and H50 represent 12.5, 25, and 50 mg/kg of isoniazid monotherapy. R10H25, R10H25Z150, and R10H25Z150E100 are different combinations using 10 mg/kg of rifampicin, 25 mg/kg of isoniazid, 150 mg/kg of pyrazinamide, and 100 mg/kg of ethambutol.
DISCUSSION
In this study, we describe the application of the MTP model together with the GPDI model using a BALB/c mouse model in order to describe untreated mice or mice treated with rifampicin, isoniazid, ethambutol, and pyrazinamide. The major focus of the work was the assessment of PD interactions using a model‐based approach, which could be applied to both mono and combination therapies of antitubercular drugs and the biomarker CFU data.
To go beyond simple dose‐response characterization, we included PK information to characterize the (joint) exposure‐response relationship of the antitubercular drugs studied. To our knowledge, for the first time, our modeling approach quantified that rifampicin CL/F in TB‐infected mice treated for 4 weeks is three times higher than in healthy mice treated for 3 weeks. This difference is potentially due primarily to different disease status, but auto‐induction of rifampicin may also contribute to some degree. The mechanism of action on dose‐dependent V/F of rifampicin and isoniazid is unknown.
Exposure‐response relationships were characterized in monotherapies by the MTP model. We fixed the transfer rate between each bacterial state according to an earlier in vitro study,4 except kFS, which was re‐estimated as a linear function of time. This provided a significant drop in OFV whereas re‐estimation of the other rate constants was not significant. The CFU data in this study did not contain enough information about transfer from the other bacterial states, which was evident in the in vitro data. It has been demonstrated that the decline in CFU after 60 days of in vitro incubation is not due to bacterial death. Instead, it is due to the fact that the bacilli entered into persistent stage in vitro and in vivo, which can only be woken up by resuscitation‐promoting factors.20 Natural growth rate (kG) of F was described by an exponential function, due to lack of plateau information on the bacterial burden. A similar approach to using (fixing) in vitro information about transfer between bacterial states was used in a previous study in the acute C57BL/6 mouse model,5 and in the other study as well.21 To treat drug‐susceptible TB, ethambutol is the last drug added in the combination of rifampicin, isoniazid, and pyrazinamide. The major role of ethambutol is to prevent drug resistance in the combination therapy.22 Pyrazinamide is effective to the bacterial subpopulation in acid pH conditions in the lesions.23 However, there is no lesion in BALB/c mouse model.24 Therefore, no effects of ethambutol and pyrazinamide were observed in monotherapy in this study.
Pharmacological synergism and antagonism are usually defined as greater or less than additive effect (additivity) of combined drugs. Loewe Additivity and BI are two major competing definitions of additivity. Empirical parametric interaction approaches, for instance, by using a power function25 or the Greco model,26 have been used to quantify how PD interactions lead to differences from additivity. However, results from these models are more difficult to interpret, as their interaction parameters have no quantitative meaning and only assess monodimensional symmetric interaction with single interaction parameter, limited to two drugs in combination and a single underlying additivity criterion.
This study quantified, we believe for the first time, the observed in vivo PD interactions in combination therapies by using the GPDI model.3 Both BI and Loewe Additivity are compatible with the GPDI model, which makes the GPDI model approach more flexible than previously described approaches. As our studies emphasize, the GPDI model based on BI is not limited to the two drugs in combination therapies. A property of the GPDI approach is that asymmetric interactions can be quantified (i.e., a different effect of drug A on drug B and vice versa), as shown in Supplementary Material S4. In our study, asymmetric interactions were not characterized, due to the single‐dose level of each drug in the combination therapy, which led to the assumption of an on/off effect only estimating INTAB, instead of an Emax function, which represents a limitation of our study originating from the sparse experimental data. Scalability of the GPDI approach to different levels of complexity (i.e., using the full four‐parameter model or a reduced single parameter model) is a key advantage of this approach over the conventional approaches. Moreover, interaction parameters are interpretable in the GPDI approach as fractional changes of the PD parameter (i.e., change of the slope in the present study). The PD interactions on the death rate of S ( ) and N ( ) between rifampicin and isoniazid were identified and presented in Figure 2 in solid and dashed red lines, illustrating prediction from the final MTP‐GPDI model with quantified, observed interaction and model‐predicted expected additivity based on the monotherapies. In R10H25Z150, isoniazid was shown to stimulate the death rate of N as well, which was not identified in monotherapy. There are some implications to consider when interpreting isoniazid effect on the N bacterial state. Due to the different length of the exposure‐response experiments (i.e., 4‐week mono drug treatments vs. 24‐week combination treatments), the composition of the bacterial burden was quite different, with a much higher number of N bacteria in the 24‐week experiment compared to the 4‐week experiment. However, isoniazid effect on the N bacterial state was not identified in R10H25 either, but solely in the presence of pyrazinamide in the triple combination, even though there was no pyrazinamide effect identified from monotherapy. Still, because of the lack of data on isoniazid mono effects at later time points, we could not clearly distinguish whether pyrazinamide triggered the isoniazid effect on N bacterial state or if this effect was an effect of isoniazid alone. This aspect of our work underscores the importance of defining the same setting of experiments for drug efficacy evaluation in monotherapy and in assessing PD interactions in combinations. In the report from Grosset et al.,27 the combination of isoniazid and rifampin was bactericidal to a similar magnitude as the combination of isoniazid, rifampicin, and pyrazinamide, but both of those two combinations were less effective than the one combining rifampin and pyrazinamide. They concluded that there was antagonism between isoniazid and the combination of rifampicin and pyrazinamide in mice. Later studies by Almeida et al.28 reported that the antagonism between isoniazid and the combination of rifampin and pyrazinamide was dependent on the dose of isoniazid. Increasing the dose of isoniazid alone resulted in a better antimicrobial effect. Conversely, increasing the dose of isoniazid in the combination of rifampicin and pyrazinamide resulted in a lower antimicrobial effect. Our model‐based approach matches these observations, but surpasses these results by providing quantitative measures to describe PD interactions (i.e., our model predicted a 0.86 log10 CFU/lungs higher bacterial load, compared to an expected additivity in R10H25). An antagonistic interaction (less effect than expected additivity) between isoniazid and rifampicin was found in this work (Figure 2 a and Figure 3) which is an agreement with clinical early bacterial activity data from day 0–14, as reported by Jindani et al.29 A synergistic interaction on N state bacteria was identified between rifampicin and ethambutol in this work. This interaction was only quantifiable by using the GPDI approach, which can capture interactions between active and inactive drugs, as interactions are quantified as shift of a PD parameter and not on the effect level. However, mono effects and interactions arising from ethambutol could not formally be differentiated using the data, because there was no longitudinal CFU data from mice receiving ethambutol alone, as these mice became moribund due to a lack of early ethambutol mono effects. This implies that, in future studies, higher doses of ethambutol should be studied to establish a complete exposure‐response relationship also in monotherapy. This would allow evaluating longer monotherapy time‐courses to clearly distinguish between mono and combinatory effects of ethambutol at later time points of therapy.
Using the MTP model together with the GPDI model, this study provides estimates of single drug effects together with a quantitative model‐based evaluation framework for PD interactions among antitubercular drugs in TB drug development.
Conflict of Interest
GlaxoSmithKline contributed financially to the conduct of the experimental work. The authors F.O., L.A., and V.S. are employees of GlaxoSmithKline. No conflicts of interest are associated with U.S.H.S., J.E.M.dS., G.J.dK., S.G.W., or C.C.
Author Contributions
U.S., C.C., S.W., G.J.dK., F.O., L.A., V.S., and J.E.M.dS. wrote the manuscript.
Supporting information
Supplementary Material S1 Prediction‐corrected visual predictive checks based on final (a) rifampicin, (b) isoniazid, (c) ethambutol, and (d) pyrazinamide population pharmacokinetic models in mice and drug plasma concentrations after different oral (PO) administration. The black circles are the prediction‐corrected observed plasma concentrations. The black solid line is the median of the prediction‐corrected observed data. The dark grey shaded area represents the simulation‐based 95% confidence interval for the median.
Supplementary Material S2 Model‐predicted exposure‐response relationships for (a) rifampicin and (b) isoniazid drug effects on fast (F), slow (S), or non‐multiplying (N) bacteria in monotherapy and in combinations (rifampicin, RIF; isoniazid, INH, ethambutol, EMB, and pyrazinamide, PZA). In Supplementary Figure S2a, the red line and the grey line are overlapping.
Supplementary Material S3 NONMEM model code for the combined pharmacokinetic (PK) models, the Multistate Tuberculosis Pharmacometric model and the General Pharmacodynamic Interaction model applied to mouse data.
Supplementary Material S4 Model‐predicted exposure‐response relationships for (a) symmetric antagonistic interaction and (b) symmetric synergistic interaction and (c) asymmetric interactions between drug A and drug B Emax effects on stimulation death rate of fast‐multiplying bacteria using Multistate Tuberculosis Pharmacometric model and the General Pharmacodynamic Interaction model approach.
Acknowledgments
The work was supported by the Swedish Research Council, the Innovative Medicines Initiative Joint Undertaking (www.imi.europa.eu) under grant agreement number 115337, which includes financial contributions from the European Union's Seventh Framework Programme (FP7/2007–2013), EFPIA companies, and the Chinese Scholarship Council.
References
- 1. World Health Organization . Global tuberculosis report 2016. (World Health Organization, Geneva, Switzerland, 2016). <http://www.who.int/tb/publications/global_report/en/>.
- 2. Foucquier, J. & Guedj, M. Analysis of drug combinations: current methodological landscape. Pharmacol. Res. Perspect. 3, e00149 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Wicha, S.G. , Chen, C. , Clewe, O. & Simonsson, U.S. A general pharmacodynamic interaction (GPDI) model based on the Bliss Independence criterion. PAGE Meeting, Lisbon, Abstract 5946 (2016). [Google Scholar]
- 4. Clewe, O. , Aulin, L. , Hu, Y. , Coates, A.R. & Simonsson, U.S. A multistate tuberculosis pharmacometric model: a framework for studying anti‐tubercular drug effects in vitro. J. Antimicrob. Chemother. 71, 964–974 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Chen, C. et al The multistate tuberculosis pharmacometric model: a semi‐mechanistic pharmacokinetic‐pharmacodynamic model for studying drug effects in an acute tuberculosis mouse model. J. Pharmacokinet. Pharmacodyn. 44, 133–141 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Svensson, R.J. & Simonsson, U. Application of the multistate tuberculosis pharmacometric model in patients with rifampicin‐treated pulmonary tuberculosis. CPT Pharmacometrics Syst. Pharmacol. 5, 264–273 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. de Steenwinkel, J.E. et al Drug susceptibility of mycobacterium tuberculosis Beijing genotype and association with MDR TB. Emerg. Infect. Dis. 18, 660–663 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. de Steenwinkel, J.E. et al Optimization of the rifampin dosage to improve the therapeutic efficacy in tuberculosis treatment using a murine model. Am . J. Respir. Crit. Care Med. 187, 1127–1134 (2013). [DOI] [PubMed] [Google Scholar]
- 9. Ruslami, R. , Nijland, H.M. , Alisjahbana, B. , Parwati, I. , van Crevel, R. & Aarnoutse, R.E. Pharmacokinetics and tolerability of a higher rifampin dose versus the standard dose in pulmonary tuberculosis patients. Antimicrob. Agents Chemother. 51, 2546–2551 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Chen, C. , Ortega, F. , Alameda, L. , Ferrer, S. & Simonsson, U.S. Population pharmacokinetics, optimised design and sample size determination for rifampicin, isoniazid, ethambutol and pyrazinamide in the mouse. Eur. J. Pharm. Sci. 93, 319–333 (2016). [DOI] [PubMed] [Google Scholar]
- 11. Zhang, L. , Beal, S.L. & Sheiner, L.B. Simultaneous vs. sequential analysis for population PK/PD data I: best‐case performance. J. Pharmacokinet. Pharmacodyn. 30, 387–404 (2003). [DOI] [PubMed] [Google Scholar]
- 12. Bliss, C.I. The toxicity of poisons applied jointly. Ann. Appl. Biol. 26, 585–615 (1939). [Google Scholar]
- 13. Loewe, S. The problem of synergism and antagonism of combined drugs. Arzneimittelforschung 3, 285–290 (1953). [PubMed] [Google Scholar]
- 14. Wicha, S.G. , Kees, M.G. , Kuss, J. & Kloft, C. Pharmacodynamic and response surface analysis of linezolid or vancomycin combined with meropenem against Staphylococcus aureus. Pharm. Res. 32, 2410–2418 (2015). [DOI] [PubMed] [Google Scholar]
- 15. Beal, S.L. , Sheiner, L.B. , Boeckmann, A.J. & Bauer, R.J. NONMEM User's Guides (1989–2009). (2009). [Google Scholar]
- 16. Keizer, R.J. , Karlsson, M.O. & Hooker, A. Modeling and simulation workbench for NONMEM: tutorial on Pirana, PsN, and Xpose. CPT Pharmacometrics Syst. Pharmacol. 2, e50 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Bergstrand, M. , Hooker, A.C. , Wallin, J.E. & Karlsson, M.O. Prediction‐corrected visual predictive checks for diagnosing nonlinear mixed‐effects models. AAPS J. 13, 143–151 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Keizer, R.J. , van Benten, M. , Beijnen, J.H. , Schellens, J.H. & Huitema, A.D. Piraña and PCluster: a modeling environment and cluster infrastructure for NONMEM. Comput. Methods Programs Biomed. 101, 72–79 (2011). [DOI] [PubMed] [Google Scholar]
- 19. Beal, S.L. Ways to fit a PK model with some data below the quantification limit. J. Pharmacokinet. Pharmacodyn. 28, 481–504 (2001). [DOI] [PubMed] [Google Scholar]
- 20. Hu, Y. , Liu, A. , Ortega‐Muro, F. , Alameda‐Martin, L. , Mitchison, D. & Coates A. High‐dose rifampicin kills persisters, shortens treatment duration, and reduces relapse rate in vitro and in vivo. Front. Microbiol. 6, 641 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Katsube, T. , Yamano, Y. & Yano, Y. Pharmacokinetic‐pharmacodynamic modeling and simulation for in vivo bactericidal effect in murine infection model. J. Pharm. Sci. 97, 1606–1614 (2008). [DOI] [PubMed] [Google Scholar]
- 22. Srivastava, S. , Musuka, S. , Sherman, C. , Meek, C. , Leff, R. & Gumbo, T. Efflux‐pump‐derived multiple drug resistance to ethambutol monotherapy in Mycobacterium tuberculosis and the pharmacokinetics and pharmacodynamics of ethambutol. J. Infect. Dis. 201, 1225–1231 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Mitchison, D.A. The action of antituberculosis drugs in short‐course chemotherapy. Tubercle 66, 219–225 (1985). [DOI] [PubMed] [Google Scholar]
- 24. Harper, J. et al Mouse model of necrotic tuberculosis granulomas develops hypoxic lesions. J. Infect. Dis. 205, 595–602 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25. Mohamed, A.F. , Kristoffersson, A.N. , Karvanen, M. , Nielsen, E.I. , Cars, O. & Friberg, L.E. Dynamic interaction of colistin and meropenem on a WT and a resistant strain of Pseudomonas aeruginosa as quantified in a PK/PD model. J. Antimicrob. Chemother. 71, 1279–1290 (2016). [DOI] [PubMed] [Google Scholar]
- 26. Greco, W.R. , Park, H.S. & Rustum, Y.M. Application of a new approach for the quantitation of drug synergism to the combination of cis‐diamminedichloroplatinum and 1‐beta‐D‐arabinofuranosylcytosine. Cancer Res. 50, 5318–5327 (1990). [PubMed] [Google Scholar]
- 27. Grosset, J. , Truffot‐Pernot, C. , Lacroix, C. & Ji, B. Antagonism between isoniazid and the combination pyrazinamide‐rifampin against tuberculosis infection in mice. Antimicrob. Agents Chemother. 36, 548–551 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Almeida, D. et al Paradoxical effect of isoniazid on the activity of rifampin‐pyrazinamide combination in a mouse model of tuberculosis. Antimicrob. Agents Chemother. 53, 4178–4184 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Jindani, A. , Doré, C.J. & Mitchison, D.A. Bactericidal and sterilizing activities of antituberculosis drugs during the first 14 days. Am. J. Respir. Crit. Care Med. 167, 1348–1354 (2003). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Material S1 Prediction‐corrected visual predictive checks based on final (a) rifampicin, (b) isoniazid, (c) ethambutol, and (d) pyrazinamide population pharmacokinetic models in mice and drug plasma concentrations after different oral (PO) administration. The black circles are the prediction‐corrected observed plasma concentrations. The black solid line is the median of the prediction‐corrected observed data. The dark grey shaded area represents the simulation‐based 95% confidence interval for the median.
Supplementary Material S2 Model‐predicted exposure‐response relationships for (a) rifampicin and (b) isoniazid drug effects on fast (F), slow (S), or non‐multiplying (N) bacteria in monotherapy and in combinations (rifampicin, RIF; isoniazid, INH, ethambutol, EMB, and pyrazinamide, PZA). In Supplementary Figure S2a, the red line and the grey line are overlapping.
Supplementary Material S3 NONMEM model code for the combined pharmacokinetic (PK) models, the Multistate Tuberculosis Pharmacometric model and the General Pharmacodynamic Interaction model applied to mouse data.
Supplementary Material S4 Model‐predicted exposure‐response relationships for (a) symmetric antagonistic interaction and (b) symmetric synergistic interaction and (c) asymmetric interactions between drug A and drug B Emax effects on stimulation death rate of fast‐multiplying bacteria using Multistate Tuberculosis Pharmacometric model and the General Pharmacodynamic Interaction model approach.


