Ion pair particles at the air–water interface

Significance

According to our Born–Oppenheimer molecular dynamics simulations, the ion pair particle formation from the hydrogen-bonded complex between methanesulfonic acid (HMSA) and ammonia/amines on the water droplet surface is observed within a few femtoseconds of the simulation time. This suggests a mechanism for the gas to particle conversion at the air–water interface. These results may help in understanding the aerosol particle formation in the remote marine atmosphere, particularly in polar regions, where the concentration of HMSA in the smallest particles was similar to that of nonsea salt sulfate and the mechanism of the particle formation remains unclear.

Abstract

Although the role of methanesulfonic acid (HMSA) in particle formation in the gas phase has been extensively studied, the details of the HMSA-induced ion pair particle formation at the air–water interface are yet to be examined. In this work, we have performed Born–Oppenheimer molecular dynamics simulations and density functional theory calculations to investigate the ion pair particle formation from HMSA and (R₁)(R₂)NH (for NH₃, R₁ = R₂ = H; for CH₃NH₂, R₁ = H and R₂ = CH₃; and for CH₃NH₂, R₁ = R₂ = CH₃) at the air–water interface. The results show that, at the air–water interface, HMSA deprotonates within a few picoseconds and results in the formation of methanesulfonate ion (MSA⁻)⋅⋅H₃O⁺ ion pair. However, this ion pair decomposes immediately, explaining why HMSA and water alone are not sufficient for forming stable particles in atmosphere. Interestingly, the particle formation from the gas-phase hydrogen-bonded complexes of HMSA with (R₁)(R₂)NH on the water droplet is observed with a few femtoseconds, suggesting a mechanism for the gas to particle conversion in aqueous environments. The reaction involves a direct proton transfer between HMSA and (R₁)(R₂)NH, and the resulting MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ complex is bound by one to four interfacial water molecules. The mechanistic insights gained from this study may serve as useful leads for understanding about the ion pair particle formation from other precursors in forested and polluted urban environments.

Aerosols are small particle suspensions in air that could be directly emitted into the atmosphere from primary sources or be formed in the atmosphere through nucleation of gas-phase species. Atmospheric aerosols influence the weather, climate, atmospheric chemistry and air quality, ecosystem, and public health (1). They cool the atmosphere by directly scattering a fraction of the incoming solar radiation back to space. By acting as cloud condensation nuclei (CCN) and ice nuclei, aerosols play a key role in controlling cloud formation, development, and precipitation on local, regional, and global scales (2, 3). Despite their impact on human health, urban visibility, and global climate, the exact formation pathways for atmospheric particles remain elusive (4).

New particle formation (NPF) from gas to particle conversion represents a significant source of atmospheric particles (4). NPF has been observed in a variety of environments ranging from urban centers to remote areas, including forests, grasslands, coastal sites, and the atmospheres of the sub-Arctic and Antarctica (4). Localized events of formation of high concentrations of atmospheric particles, such as those in urban and industrial plumes (5, 6) and in coastal marine locations (7), have also been observed. The NPF event accounts for ∼50% of the global aerosol production in the troposphere (8). A detailed knowledge of the potential nucleating precursors driving NPF and the underlying nucleation mechanisms is, therefore, crucial for better understanding the aerosol nucleation and growth processes that impact global climate and human health.

The most intensely studied NPF system is the nucleation of sulfuric acid (H₂SO₄), since sulfate represents an important component of the nucleation mode aerosols (9). However, binary H₂SO₄ nucleation has been recognized as incapable of explaining atmospheric nucleation events, and several alternative mechanisms have been proposed, including ternary nucleation of H₂SO₄ with ammonia (NH₃)/amines and water, ion-induced nucleation, and nucleation involving iodine species (4). NH₃ and amines are emitted from a wide range of sources, including biological processes in the ocean, animal husbandry, agricultural fertilizers, biomass burning, and industrial emissions (10). Although amines typically have concentrations one to three orders of magnitude lower than that of NH₃ in the atmosphere (10), laboratory experiments show that amines are more effective than NH₃ in enhancing the particle formation from H₂SO₄ (11–13).

While ternary nucleation of H₂SO₄, amines/NH₃, and water is recognized as a key contributor toward NPF (14, 15), increasing evidence suggests an appreciable contribution from methanesulfonic acid (HMSA; CH₃SO₃H), amines, and water under certain conditions (16–21). HMSA is formed from the oxidation of organosulfur compounds that originate from biological processes, biomass burning, industrial operations, and agricultural activities (22, 23). Over oceans and in coastal regions, gaseous HMSA is present in concentrations of ∼10–50% of the gaseous H₂SO₄ concentration (24), although HMSA/H₂SO₄ ratios of up to 250% have been reported (25). Similarly, in submicrometer aerosol particles, HMSA is detected in concentrations of 5–30% of the sulfate concentrations (26, 27), although HMSA/SO₄²⁻ ratios of ∼100% have been reported in aerosols smaller than 0.2 μm (16). HMSA is commonly detected in atmospheric particles (16, 27), and particulate methanesulfonate, dimethylamine, and CCN activity are found to be highly correlated (16). Several field studies have detected enhanced HMSA concentrations in small particles when NH₃ or amines are present (16, 27), supporting a role for HMSA and amines in NPF. The NPF from HMSA and amines is also believed to be important in the remote marine atmosphere (28, 29).

Despite being tightly linked to the aerosol growth, several fundamental questions pertaining to the formation mechanism of particulate HMSA are yet to be fully resolved. For example, it is not clear whether HMSA contributes to the aerosol formation or mainly enters the aerosol particle during growth. Although experiments indicate that water shows a significant enhancement effect on the particle formation and growth from HMSA (4, 16–21), the exact role of water remains elusive [i.e., it is far from clear whether water promotes proton transfer between HMSA and NH₃/amine or provides a conducive environment for stabilizing the methanesulfonate ion (MSA⁻)⋅⋅NH₄⁺/aminium ion pair]. The mechanistic nature of this multicomponent atmospheric reaction has yet to be fully established (i.e., the precise role of different channels HMSA-H₂O + NH₃/amine, HMSA + NH₃/amine-H₂O, and HMSA-NH₃/amine + H₂O to the overall NPF remains an open question). Although the role of HMSA in the NPF in gas phase has been extensively studied (18–21, 30–33), the molecular-level mechanism of the HMSA-based ion pair particle formation on the water surfaces in atmosphere is yet to be explored.

Herein, we use Born–Oppenheimer molecular dynamics (BOMD) simulations to examine the ion pair particle formation between HMSA and (R₁)(R₂)NH [for NH₃, R₁ = R₂ = H; for CH₃NH₂, R₁ = H and R₂ = CH₃; and for (CH₃)₂NH, R₁ = R₂ = CH₃] on the water droplet surface. The role of aqueous surfaces, such as clouds, fog, thin films, water microdroplets, or aqueous sea salt particles, in atmospheric and environmental processes is being increasingly recognized (33, 34). Many chemical reactions at the aqueous surface proceed faster and sometimes along different mechanisms than in the bulk water or gas phase (33, 34). Studying HMSA-based ion pair particle formation at the aqueous surface using BOMD simulations would allow unique insights into the dynamics, structures, nucleation timescales, and role of proton transfer and other possible chemical processes in the nucleation or stabilization of atmospheric clusters.

Results and Discussion

Dynamics Behavior of HMSA at the Air–Water Interface.

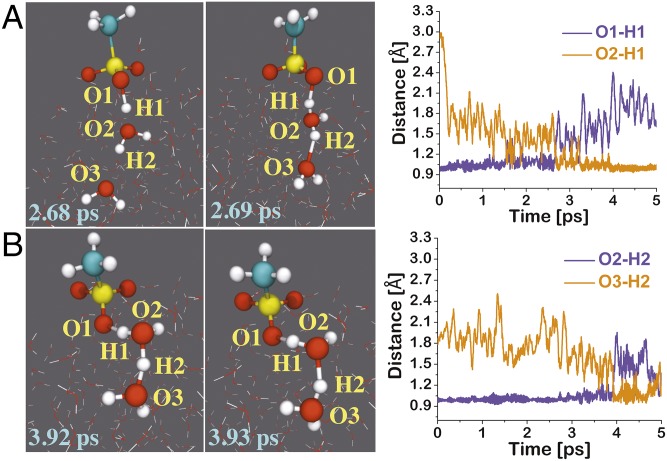
We first analyzed the dynamics behavior of HMSA at the air–water interface. The BOMD simulations suggest that HMSA deprotonates within a few picoseconds, resulting in the formation of MSA⁻ and interfacial H₃O⁺ ion (Fig. 1 and Movie S1). This is consistent with the strong acidic nature of HMSA (pK_a = −1.92) (35). At 2.68 ps, the transition state-like complex is formed, in which the hydroxyl proton of HMSA is situated between the hydroxyl oxygen and one of the interfacial water molecules (Fig. 1A). In this complex, the O1-H1 bond is 1.24 Å long, and the O2-H1 bond is 1.27 Å long. This complex converts into MSA⁻ and H₃O⁺ at 2.69 ps. The O1-H1 and O2-H1 bonds are now 1.48 and 1.04 Å long, respectively. This fully supports the formation of an MSA⁻⋅⋅H₃O⁺ ion pair. However, this ion pair remained stable only for a little over 1 ps, as H₃O⁺ loses its proton to the other interfacial water molecule. For this proton transfer, the transition state-like complex is formed at 3.92 ps (Fig. 1B), in which H2 is exactly localized in the middle of O2 and O3 (i.e., O2-H2 = O3-H2 = 1.24 Å). At 3.93 ps, the proton transfer is complete as evidenced by the time evolution profiles of the O2-H2 and O3-H2 bonds. In previous experimental studies (36, 37), the NPF from HMSA and water could not be observed. Our BOMD simulations provide a mechanistic explanation of why water alone is not sufficient for forming a particle with HMSA at the air–water interface. The simulations indicate that the H₃O⁺ ion in the MSA⁻⋅⋅H₃O⁺ ion pair would give up its proton to the water droplet within a few picoseconds; as a result, the MSA⁻⋅⋅H₃O⁺ ion pair would decompose on the water surface.

Fig. 1.

(Left) Snapshot structures taken from the BOMD simulations of HMSA adsorbed on a water droplet of 191 water molecules, which illustrate the formation of deprotonated HMSA (A) and the interfacial proton transfer between hydronium ion and one of the droplet water molecules (B). (Right) Time evolution of key bond distances O1-H1, O2-H1, O2-H2, and O3-H2 involved in both reactions.

Fig. S1 shows the distance between the center of mass (COM) of MSA⁻ and that of the water droplet vs. the simulation time. The MSA⁻ remain preferentially adsorbed on the water surface during the simulated timescale of 15 ps. This is because of hydrogen bonding between the oxygens of MSA⁻ and interfacial water molecules. To better understand the hydration structure of MSA⁻ at the air–water interface, we next calculated the average number of hydrogen bonds formed by the MSA⁻ oxygens with the interfacial water molecules. Our model specified a hydrogen bond between an MSA⁻ oxygen and H₂O if the O⋅⋅H distance was <2.5 Å and the ∠O⋅⋅H-O hydrogen bond angle was >150°. The results show that the MSA⁻ ion forms hydrogen bonds with 2.3 water molecules at the air–water interface. We also calculated the probability distributions for the angles involving the oxygens and sulfur of MSA⁻ and the COM of the water droplet (Fig. S2). Here, ∠θ₁, θ₂, and θ₃ are the angles centered at the MSA⁻ oxygens (i.e., θ₁ = ∠COM.O1.S, θ₂ = ∠COM.O2.S, and θ₃ = ∠COM.O3.S), where O1, O2, and O3 are the MSA oxygens and COM indicates the COM of the water droplet. All angles were found localized between 40° and 110°, indicative of the interfacial inclination of the MSA oxygens. The hydrophobicity of MSA⁻ methyl group also accounts toward its interfacial locus on the water droplet. The θ angle, which is centered at sulfur of MSA⁻ and also involves carbon of MSA⁻ and COM (θ = ∠COM.S.C), is a good measure of the hydrophobicity effect. The probability distribution for the θ angle is concentrated between 130° and 175°. This suggests that the methyl group of MSA⁻ remains projected away from the water surface over the simulated timescale of 15 ps and counts toward the interfacial preference of MSA⁻ ion.

Mechanism of MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ Particle Formation at the Air–Water Interface.

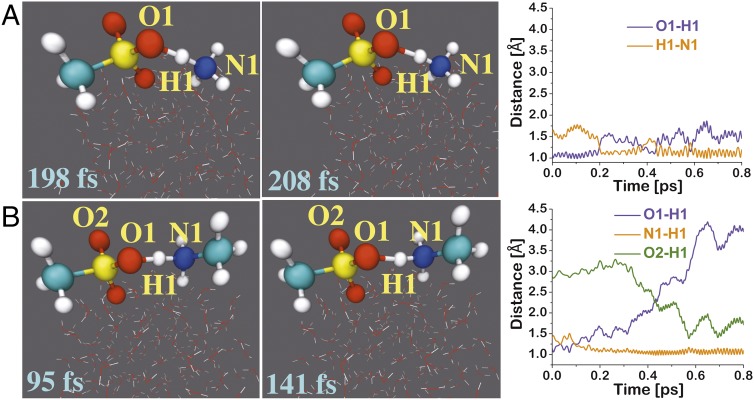
For investigating the ion pair formation at the air–water interface, we performed BOMD simulations starting from the hydrogen-bonded and nonhydrogen-bonded complexes between HMSA and (R₁)(R₂)NH (Fig. S3). However, only the former starting configurations resulted in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ ion pairs, suggesting that the hydrogen-bonded complexes between HMSA and (R₁)(R₂)NH in the gas phase must be formed for the ion pair formation to occur at the air–water interface. The HMSA⋅⋅(R₁)(R₂)NH → MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ reaction on the water surface involves a direct proton transfer between HMSA and (R₁)(R₂)NH and occurs within a few femtoseconds of the BOMD simulations (Fig. 2 and Movies S2 and S3). The ability of interfacial water molecules to stabilize the ion pairs is mainly responsible for the femtosecond formation of the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particles on the water surface. The reaction of HMSA with (CH₃)₂NH is so swift that the MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pair is instantaneously formed on the optimization of the hydrogen-bonded complex adsorbed on the water surface (Figs. S4 and S5 and Movie S4). Even in the gas phase-optimized complex between HMSA and (CH₃)₂NH, the hydroxyl proton of HMSA is found localized on (CH₃)₂NH [i.e., MSA⁻⋅⋅(CH₃)₂NH₂⁺] (Fig. S6). This is consistent with previous experimental studies (11–13), suggesting that substituted amines are more efficient toward the NPF events. However, it is important to note here that substituted amines are not always more efficient [i.e., in a recent study (20), CH₃NH₂ was found to be more efficient than trimethylamine in forming particles with HMSA].

Fig. 2.

(Left) Snapshot structures taken from the BOMD simulations for the reaction of HMSA with NH₃ and methylamine (CH₃NH₂), which illustrate the formation of MSA⁻⋅⋅NH₄⁺ (A) and MSA⁻⋅⋅CH₃NH₃⁺ (B) ion pairs on the water droplet. (Right) Time evolution of key bond distances O1-H1, O2-H1, and H1-N1 involved in the ion pair-forming reactions.

For the HMSA-NH₃ reaction on the water surface, the transition state-like complex is formed at 198 fs, in which the O1-H1 bond of HMSA is stretched to 1.25 Å and the H1-N1 bond is shrunk to 1.28 Å (Fig. 2A). This complex reflects a proton transfer between the hydroxyl oxygen of HMSA and nitrogen of NH₃. At 208 fs, this activated complex transforms into an MSA⁻⋅⋅NH₄⁺ ion pair. At this point, the H1-N1 bond (1.09 Å) is fully developed, whereas the O1-H1 bond (1.46 Å) is now changed from being a pure covalent bond to a hydrogen bond between O1 and H1 atoms of the ion pair. After few rounds of reversible proton transfer, the MSA⁻⋅⋅NH₄⁺ ion pair on the water surface remains stable beyond 500 fs. We have performed additional simulations on the MSA⁻⋅⋅NH₄⁺ ion pair inside the center of the water droplet. The ion pair is retained inside the droplet, implying that, after the particle goes into the bulk, it will stay there. However, since HMSA at the surface is very reactive, it will react immediately with amines or other precursors. The transition state-like complex for the MSA⁻⋅⋅CH₃NH₃⁺-forming reaction occurs on 95 fs, in which both of the O1-H1 and H1-N1 bonds are 1.25 Å long (Fig. 2B). The HMSA⋅⋅CH₃NH₂ → MSA⁻⋅⋅CH₃NH₃⁺ conversion is complete at 141 fs when the H1-N1 bond is 1.11 Å long and the O1-H1 bond is 1.46 Å long. Unlike the MSA⁻⋅⋅NH₄⁺ ion pair, the oxygens in the MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pairs undergo rotation around the C–S axis; as a result, the O2 oxygen of MSA⁻ forms a hydrogen bond with H1 in the ion pairs (Fig. 2B and Fig. S5). Despite this oxygen rotation, the MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pairs are retained at the air–water interface.

Dynamics Behavior of the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ Particle at the Air–Water Interface.

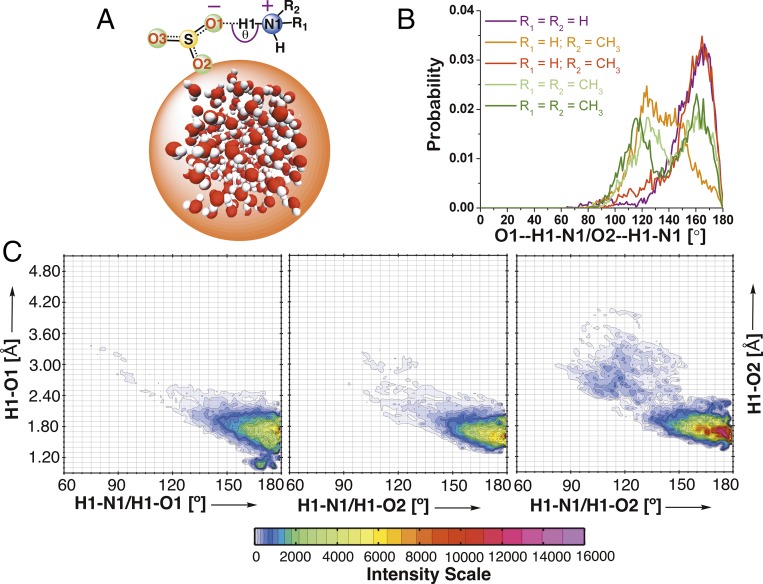
To analyze the locus of the ion pairs on the water droplet, we calculated the distance between the COM of the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ ion pairs and that of the water droplet over the simulated time of 15 ps. The results suggest that the ion pairs are preferentially localized at the interface (Fig. S7). The surface preference of the ion pairs is caused by a stabilizing intraparticle O1/O2⋅⋅H1-N1 hydrogen bond, their hydrogen bonding interactions with the interfacial water molecules, and the hydrophobicity of a methyl group. The probability distribution of the ∠O1⋅⋅H1-N1 bond angle in MSA⁻⋅⋅NH₄⁺ is mainly localized in the range of 150° ≤ θ ≤ 180° (Fig. 3B). The ∠O1⋅⋅H1-N1 bond angle in the MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pairs has relatively broad probability distribution of 110° ≤ θ ≤ 180°. Interestingly, the O1⋅⋅H1-N1 hydrogen bond in the HMSA⋅⋅(R₁)(R₂)NH reactions is broken after the formation of MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pairs, and simultaneously, the O2⋅⋅H1-N1 hydrogen bond is formed. The probability distribution of the ∠O2⋅⋅H1-N1 hydrogen bond angle in the MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pairs has a major peak in the 160°–180° range. This also explains why the ∠O1⋅⋅H1-N1 bond angle in the MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pairs has broad probability distribution.

Fig. 3.

(A) Schematics showing the intraparticle ∠O1⋅⋅H1-N1 hydrogen bond angle in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ ion pair particle. (B) Angular probability distribution of ∠O1⋅⋅H1-N1 in MSA⁻⋅⋅NH₄⁺ (R₁ = R₂ = H; magenta) and those of ∠O1⋅⋅H1-N1 and ∠O2⋅⋅H1-N1 in MSA⁻⋅⋅CH₃NH₃⁺ (R₁ = H and R₂ = CH₃; orange and red) and MSA⁻⋅⋅ (CH₃)₂NH₂⁺ (R₁ = CH₃ and R₂ = CH₃; green and olive) ion pairs. (C) CDF. The RDF between O1/O2 and H1 atoms of HMSA and an angular distribution function between the H1-N1 and the H1-O1/O2 vectors in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particle are plotted. Note that, for the MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅ (CH₃)₂NH₂⁺, the angular distribution functions between H1-N1 and the H1-O2 are plotted.

We next calculated the combined distribution functions (CDFs) by combining a radial distribution function (RDF) between the H1 and O1/O2 atoms of HMSA and an angular distribution function between the H1-N1 and H1-O1/O2 vectors in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particles. These histograms of higher dimensionality provide useful information into the intraparticle O1/O2⋅⋅H1-N1 hydrogen bond in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particles on the water droplet surface. As shown in Fig. 3C, for angles θ > 150°, the O1⋅⋅H1-N1 hydrogen bond in the MSA⁻⋅⋅NH₄⁺ ion pair and the O2⋅⋅H1-N1 hydrogen bond in MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pairs are mainly localized in the 1.60- to 2.20-Å range. This corresponds to the configuration where there is a tight and near-linear hydrogen bond between MSA⁻ and (R₁)(R₂)NH₂⁺ fragments of the ion pairs. Using CDFs, we could define hydrogen bonding criteria in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particle. The standard approach when defining a hydrogen bond criterion is often to take the first minimum of the RDF as a distance cutoff (0 ≤ r ≤ 4.50 Å) and an angle interval of, for example, 130° ≤ θ ≤ 180°. However, the careful analysis of CDFs suggests that the intraparticle hydrogen bond in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particle is quite strong and could be better characterized using a criterion with 0 ≤ O1/O2⋅⋅H1-N1 ≤ 2.20 Å and 150° ≤ θ ≤ 180°.

We also analyzed the CDFs generated by combining the two RDFs representing the O1/O2⋅⋅H1-N1 hydrogen bond. The first RDF observes the distance between the O1/O2 and H1 atoms of the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particle, and the second RDF observes the distance between the H1 and N1 atoms of the particle. As indicated by the peak at H1-N1 = 1.05 Å/H1-O1/O2 = 1.60–2.00 Å shown in Fig. S8, the MSA⁻ and (R₁)(R₂)NH₂⁺ fragments of the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particles are tightly bound through a hydrogen bond between O1/O2 and H1 atoms. For the MSA⁻⋅⋅NH₄⁺ particle, the H1-O1 bond distance at the peak is 1.80 Å, whereas for the MSA⁻⋅⋅CH₃NH₂⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ particles, the H1-O2 bonds at the peak are 1.60 and 1.65 Å long, respectively. Overall, the O1/O2⋅⋅H1-N1 bond distance is frequently observed in the range 1.40–2.20 Å, whereas the H1-N1 bond is frequently observed in the ∼1.00–1.20 Å.

To gain deeper insights into the nature of interfacial hydrogen bonding of the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ ion pairs, we next calculated the average number of hydrogen bonds formed by these particles with the interfacial water molecules. Our model specified a hydrogen bond between a sulfate oxygen and H₂O if the O⋅⋅H-O or O⋅⋅H-N distance was <2.5 Å and the ∠O⋅⋅H-O or ∠O⋅⋅H-N hydrogen bond angle was >150°. The results suggest that the MSA⁻⋅⋅NH₄⁺ particle forms an average number of 4.1 hydrogen bonds, whereas the MSA⁻⋅⋅CH₃NH₃⁺ and MSA⁻⋅⋅(CH₃)₂NH₂⁺ particles form 3.5 and 0.7 hydrogen bonds with the surface water molecules, respectively (Table 1). These results are consistent with the extent of hydrophobicity in the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ ion pair particles. The MSA⁻ oxygens of the MSA⁻⋅⋅NH₄⁺ and MSA⁻⋅⋅CH₃NH₃⁺ particles form relatively larger numbers of hydrogen bonds than the ammonium or aminium protons. For the MSA⁻⋅⋅NH₄⁺ particle, the oxygen atoms form an average number of 2.2 hydrogen bonds with the hydrogens of the surface water molecules, whereas the ammonium protons form 1.9 hydrogen bonds with the oxygens of surface water molecules. For the MSA⁻⋅⋅CH₃NH₃⁺ particle, the oxygens form 2.5 hydrogen bonds, whereas the aminium protons form one hydrogen bond with the surface waters. For the MSA⁻⋅⋅(CH₃)₂NH₂⁺ particle, the oxygens do not form any hydrogen bond with the water molecules, whereas the aminium protons form nearly one hydrogen bond with the surface waters. This hydration structure analysis reveals that the composition of an ion pair depends on the nature of gaseous precursors.

Table 1.

Calculated average number of hydrogen bonds between MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ (for NH₃, R₁ = R₂ = H; for CH₃NH₂, R₁ = H and R₂ = CH₃; and for CH₃NH₂, R₁ = R₂ = CH₃) and interfacial water molecules

MSA−⋅⋅(R1)(R2)NH2+	Average no. of hydrogen bonds
	Total	(R1)(R2)NH2+ bound	MSA− bound
R1 = R2 = H	4.1	1.9	2.2
R1 = H, R2 = CH3	3.5	1.0	2.5
R1 = R2 = CH3	0.7	0.7	0

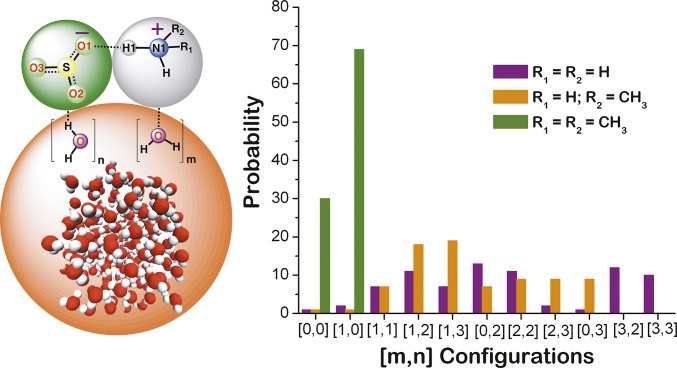
To deeply understand the hydration shell of the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particle at the air–water interface, we next identified the key [m,n] configurations and calculated their probabilities. Here, m and n are the numbers of interfacial water molecules bound to the (R₁)(R₂)NH₂⁺ and MSA⁻, respectively. As shown in Table 1, a relatively larger number of interfacial water molecules binds to the MSA⁻⋅⋅NH₄⁺ particle. This is also reflected in the probability distribution of [m,n] configurations (Fig. 4 and Table S1). For the MSA⁻⋅⋅NH₄⁺ particle, the [2,2] and [3,2] are the two most dominant configurations, with probabilities of 13 and 12%, respectively. The [1,2] and [2,3] are the next two most probable configurations, with each having a probability of 11%. The [3,3] configuration with a 10% probability is another notable configuration for the MSA⁻⋅⋅NH₄⁺ particle at the air–water interface. For both the MSA⁻⋅⋅CH₃NH₃⁺ and the MSA⁻⋅⋅(CH₃)₂NH₂⁺ particles, the configurations with smaller numbers of interfacial water molecules are the most probable ones. For the MSA⁻⋅⋅CH₃NH₃⁺ particle, the [1,2] and [1,3] are the two most dominant configurations, with probabilities of 18 and 19%, respectively. The [2,0], [2,3], and [3,0] are the other notable configurations, with each accounting for 9%. For the MSA⁻⋅⋅(CH₃)₂NH₂⁺ particle, the [1,0] configuration is the most dominant one, with a probability of 69%. An appreciable fraction of 30% of the MSA⁻⋅⋅(CH₃)₂NH₂⁺ particle remains nonhydrogen-bonded with the surface water molecules.

Fig. 4.

(Left) Schematic showing the [m,n] interfacial waters forming hydrogen bonds with ammonium or aminium protons and oxygens of MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ [for NH₃, R₁ = R₂ = H; for CH₃NH₂, R₁ = H and R₂ = CH₃; and for (CH₃)₂NH, R₁ = R₂ = CH₃], where m and n are the numbers of interfacial water molecules bound to (R₁)(R₂)NH₂⁺ and MSA⁻, respectively. (Right) Histograms of probabilities of different [m,n] configurations for the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particles (for NH₃, purple; for CH₃NH₂, orange; and for CH₃NH₂, olive).

Gas-Phase Quantum Chemical Calculations.

Considering that our BOMD simulations suggest that the hydrogen-bonded complexes between HMSA and (R₁)(R₂)NH in the gas phase must be formed for the ion pair formation to be observed on the water droplet surface, we next investigated the properties of these complexes in the absence and presence of one water molecule. The calculated equilibrium geometries and binding energies of HMSA⋅⋅(R₁)(R₂)NH complexes with and without one water molecule are given in Fig. S9. CH₃NH₂ and (CH₃)₂NH form tighter complexes with HMSA than NH₃. The binary HMSA⋅⋅CH₃NH₂ and HMSA⋅⋅(CH₃)₂NH complexes are 3.2 and 4.3 kcal/mol, respectively, more stable than HMSA⋅⋅NH₃. Note that the hydroxyl proton in HMSA⋅⋅(CH₃)₂NH is localized on the amine nitrogen [i.e., MSA⁻⋅⋅(CH₃)₂NH₂⁺]. This is consistent with the strong acidic nature of HMSA and relatively higher reactivity of (CH₃)₂NH compared with CH₃NH₂ and NH₃. The ternary complexes of HMSA, (R₁)(R₂)NH, and H₂O are at least 9.3 kcal/mol more stable relative to HMSA⋅⋅(R₁)(R₂)NH and H₂O. Interestingly, the hydroxyl proton in ternary HMSA⋅⋅(R₁)(R₂)NH⋅⋅H₂O complexes is transferred on the nitrogen of (R₁)(R₂)NH. This suggests that the HMSA-based ion pair formation in the gas phase could occur in the presence of a single water molecule. The ability of a water molecule to stabilize the charged MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ ion pairs via hydrogen bonding is the main driving force for inducing the instantaneous proton transfer between HMSA and (R₁)(R₂)NH.

We next calculated the equilibrium constants (K_eq) for the formation of binary HMSA⋅⋅(R₁)(R₂)NH complexes using the following equation:

$$\begin{array}{l}{\text{K}}_{\text{eq}}=\frac{\left[\text{HMSA}\cdot \cdot \left({\text{R}}_1\right)\left({\text{R}}_2\right)\text{NH}\right]}{\left[\text{HMSA}\right]\cdot \left[\left({\text{R}}_1\right)\left({\text{R}}_2\right)\text{NH}\right]}\\ \left[\text{HMSA}\cdot \cdot \left({\text{R}}_1\right)\left({\text{R}}_2\right)\text{NH}\right]=\left[\text{HMSA}\right]\cdot \left[\left({\text{R}}_1\right)\left({\text{R}}_2\right)\text{NH}\right]\cdot {\text{K}}_{\text{eq}},\end{array}$$

where the various Qs denote the partition functions of free HMSA and (R₁)(R₂)NH and the hydrogen-bonded HMSA⋅⋅(R₁)(R₂)NH complex (red color: HMSA oxygens; blue color: amine nitrogen). The E_C − E_R represents the binding energy of the HMSA⋅⋅(R₁)(R₂)NH complex.

The calculated K_eq for these hydrogen-bonded complexes in the atmospherically relevant temperature range of 200–300 K is given in Table S2. The K_eq values have been evaluated from the relative energies and partition functions calculated at the M06-2X/aug-cc-pVTZ level of theory. The HMSA⋅⋅CH₃NH₂ and HMSA⋅⋅(CH₃)₂NH complexes have at least four orders of magnitude larger K_eq values than HMSA⋅⋅NH₃ complex at all temperatures considered. This is in line with the trends in their binding energies. The temperature has a noticeable effect on the calculated K_eq for the hydrogen-bonded complexes. By lowering the temperature from 300 to 200 K, the calculated K_eq was enhanced by an order of magnitude.

An important issue for atmospheric purposes is to estimate the atmospheric concentration of HMSA⋅⋅(R₁)(R₂)NH complexes, which could be done using the following equation:

$$\begin{array}{l}\text{HMSA}+\left({\text{R}}_1\right)\left({\text{R}}_2\right)\text{NH}\stackrel{{\text{K}}_{\text{eq}}}{\rightleftarrows }\text{HMSA}\cdot \cdot \left({\text{R}}_1\right)\left({\text{R}}_2\right)\text{NH}\\ {\text{K}}_{\text{eq}}=\frac{{\text{Q}}_{\text{complex}}}{{\text{Q}}_{\text{HMSA}}{\text{Q}}_{\left({\text{R}}_1\right)\left({\text{R}}_2\right)\text{NH}}}{\text{e}}^{\frac{-\left({\text{E}}_{\text{c}}-{\text{E}}_{\text{R}}\right)}{\text{RT}}}.\end{array}$$

The atmospheric concentrations of HMSA are about 10⁵–10⁷ molecules per 1 cm³ (24, 38). We have used the average of these two estimates as the gas-phase concentration of HMSA, which is 10⁶ molecules per 1 cm³. The gas-phase concentrations of NH₃ (18 ppbV), CH₃NH₂ (2.5 ppbV), and (CH₃)₂NH (2.5 ppbV) are taken from a recent study by Finlayson-Pitts and coworkers (20). At 298 K and 1 atm, the concentrations of NH₃, CH₃NH₂, and (CH₃)₂NH translate into 4.4 × 10¹¹, 6.2 × 10¹⁰, and 6.2 × 10¹⁰ molecules per 1 cm³, respectively. Using these concentrations of gaseous precursors and the calculated K_eq for the HMSA⋅⋅(R₁)(R₂)NH complexes, their atmospheric concentrations at various temperatures were calculated and are provided in Table S2. The Cartesian coordinates of all key species are given in Table S3. Although CH₃NH₂ and (CH₃)₂NH are an order of magnitude less abundant than NH₃ in air (20), their HMSA complexes are expected to be one to three orders of magnitude more abundant than the HMSA⋅⋅NH₃ complex. For example, at 300 K, the concentration of HMSA⋅⋅CH₃NH₂ is 6.8 × 10⁴ molecules per 1 cm³, which is two orders of magnitude higher than that of HMSA⋅⋅NH₃ (i.e., 2.7 × 10² molecules per 1 cm³). Below 250 K, the HMSA⋅⋅CH₃NH₂ complex is three orders of magnitude more abundant than the HMSA⋅⋅NH₃ complex. At 200 K, the concentration of the HMSA⋅⋅CH₃NH₂ complex is 8.1 × 10¹⁰ molecules per 1 cm³, whereas that of the HMSA⋅⋅NH₃ complex is 3.3 × 10⁷ molecules per 1 cm³. The HMSA⋅⋅(CH₃)₂NH complex was calculated to be more abundant than HMSA⋅⋅NH₃ but relatively less abundant than the HMSA⋅⋅CH₃NH₂ complex at all temperatures. At 200 K, the HMSA⋅⋅(CH₃)₂NH complex (2.6 × 10⁹ molecules per 1 cm³) was two orders of magnitude more abundant than the HMSA⋅⋅NH₃ complex. This may further explain why substituted amines, which are relatively less abundant, are so efficient in forming new particles in air (11–13).

Conclusions

In summary, our BOMD simulations provide mechanistic insights into the ion pair particle formation from HMSA and (R₁)(R₂)NH at the air–water interface. The results suggest that the particle formation from the hydrogen-bonded complex of HMSA and (R₁)(R₂)NH on the water surface involves a proton transfer between HMSA and (R₁)(R₂)NH and occurs within a few femtoseconds of the simulated time. This mechanism for the gas to particle conversion should be relevant over oceans and in coastal regions. Interestingly, the formation of the MSA⁻⋅⋅(CH₃)₂NH₂⁺ ion pair is instantaneously observed on optimization of the multicomponent system, suggesting that the reactivity of a particular amine also plays a key role in the particle formation. At the air–water interface, the MSA⁻⋅⋅(R₁)(R₂)NH₂⁺ particles are tied to one to four water molecules, where the number of water molecules depends on the nature of R₁ and R₂. The insights from these simulations may help in better understanding the particle formation from other precursors, such as organic acids and inorganic acids, in aqueous atmospheric environments.

Computational Details

The BOMD simulations were carried out based on a density functional theory (DFT) method implemented in the CP2K (39) code. The droplet system containing 191 water molecules and 1 HMSA (CH₃SO₃H) molecule with and without 1 (R₁)(R₂)NH [for NH₃, R₁ = R₂ = H; for CH₃NH₂ or methylamine, R₁ = H and R₂ = CH₃; and for (CH₃)₂NH or dimethylamine, R₁ = R₂ = CH₃] molecule was examined via BOMD simulations. For studying the droplet systems involving NH₃ or an amine, we used two different starting configurations, namely hydrogen-bonded and nonhydrogen-bonded complex, between HMSA and (R₁)(R₂)NH adsorbed on the water droplet. The dimension of the simulation box is x = 35, y = 35, and z = 35 Å, which is large enough to neglect interactions between adjacent periodic images of water droplet. The BOMD simulations were carried out in the constant volume and temperature ensemble with the Nose–Hoover chain method for controlling the temperature (300 K) of the system. The integration step was set as 1 fs, which had been proven to achieve sufficient energy conservation for the water system. Additional simulation details are in Supporting Information. The DFT calculations were also carried out to investigate the properties of the gas-phase hydrogen-bonded complexes of HMSA with one (R₁)(R₂)NH molecule in the absence and presence of one water molecule. All quantum mechanical calculations reported in this work were performed using Gaussian09 (40) software at the standard temperature (298.15 K) and pressure (1 atm). Additional method details are in Supporting Information.