Incremental heating of Bishop Tuff sanidine reveals preeruptive radiogenic Ar and rapid remobilization from cold storage

Significance

Recent improvements in analytical and microsampling techniques for multiple geochronometers have resulted in datasets with unprecedented temporal and spatial resolution. These advances are accompanied by the discovery of crystal- and outcrop-scale complexities previously obscured by low analytical precision. Single-crystal incremental heating resolves subtle, intracrystal isotopic heterogeneity, allowing for more-accurate ⁴⁰Ar/³⁹Ar eruption ages. The eruption ages of widespread volcanic ash deposits are critical for calibrating the geologic timescale, and thus their accuracy has substantial implications for the geologic, biologic, and global climate records. Complex distribution of ⁴⁰Ar/³⁹Ar dates in the deposits of supervolcanic eruptions requires rethinking the magmatic processes and their effect on the ⁴⁰Ar/³⁹Ar system, specifically the extent of cooling and remobilization during the decades to centuries preceding these events.

Abstract

Accurate and precise ages of large silicic eruptions are critical to calibrating the geologic timescale and gauging the tempo of changes in climate, biologic evolution, and magmatic processes throughout Earth history. The conventional approach to dating these eruptive products using the ⁴⁰Ar/³⁹Ar method is to fuse dozens of individual feldspar crystals. However, dispersion of fusion dates is common and interpretation is complicated by increasingly precise data obtained via multicollector mass spectrometry. Incremental heating of 49 individual Bishop Tuff (BT) sanidine crystals produces ⁴⁰Ar/³⁹Ar dates with reduced dispersion, yet we find a 16-ky range of plateau dates that is not attributable to excess Ar. We interpret this dispersion to reflect cooling of the magma reservoir margins below ∼475 °C, accumulation of radiogenic Ar, and rapid preeruption remobilization. Accordingly, these data elucidate the recycling of subsolidus material into voluminous rhyolite magma reservoirs and the effect of preeruptive magmatic processes on the ⁴⁰Ar/³⁹Ar system. The youngest sanidine dates, likely the most representative of the BT eruption age, yield a weighted mean of 764.8 ± 0.3/0.6 ka (2σ analytical/full uncertainty) indicating eruption only ∼7 ky following the Matuyama−Brunhes magnetic polarity reversal. Single-crystal incremental heating provides leverage with which to interpret complex populations of ⁴⁰Ar/³⁹Ar sanidine and U-Pb zircon dates and a substantially improved capability to resolve the timing and causal relationship of events in the geologic record.

Accurate, high-precision geochronology of volcanic ash deposits is essential to determine the timing of magnetic, tectonic, biologic, and climate events and the rates of surficial and deep Earth processes. It is indispensable for establishing causal relationships between physical and biologic processes that occur over only centuries to millennia (1). Moreover, the crystallization histories revealed by high-precision zircon and sanidine dates establish a tempo for the dynamics of crustal magmatism and triggering of large, caldera-forming eruptions (2, 3). Voluminous ash fall deposits from explosive silicic eruptions are also important chronostratigraphic markers. Their wide dispersal allows for intercalibration among radioisotopic, geomagnetic, and astrochronologic timescales and correlation of the marine and terrestrial records (1, 4, 5).

The ⁴⁰Ar/³⁹Ar method is among the most commonly employed techniques to determine the eruption ages of these deposits, typically by fusing dozens of individual sanidine crystals. We use the term “date” when referring to time calculated using the radiogenic parent–daughter ratios measured in a single crystal. An “age” refers to the geologic significance of a date, or group of dates, and as in this study may require interpretation of large sets of dates from a common rock or deposit (6). Owing to rapid diffusion of Ar at magmatic temperatures, ⁴⁰Ar/³⁹Ar dates are commonly interpreted as eruption ages without the ambiguity of protracted crystallization intervals recorded by U-Pb dates of accessory phases (1). However, dispersion of the nominal dates produced by sanidine fusion analysis is common and typically attributed to xenocrysts, nonradiogenic Ar, or Ar loss. Filtering and pooling many low-precision dates may yield a statistically valid weighted mean age (7, 8). However, the increased sensitivity of multicollector noble gas mass spectrometers relative to older, single-collector instruments now yields dates that are nearly an order of magnitude more precise. These high-precision dates reveal intracrystal and intercrystal heterogeneities that require interpretation and complicate the assignment of an eruption age (9–11). However, the relative contributions of the sources of these perturbations and their implications for magma dynamics are not commonly explored.

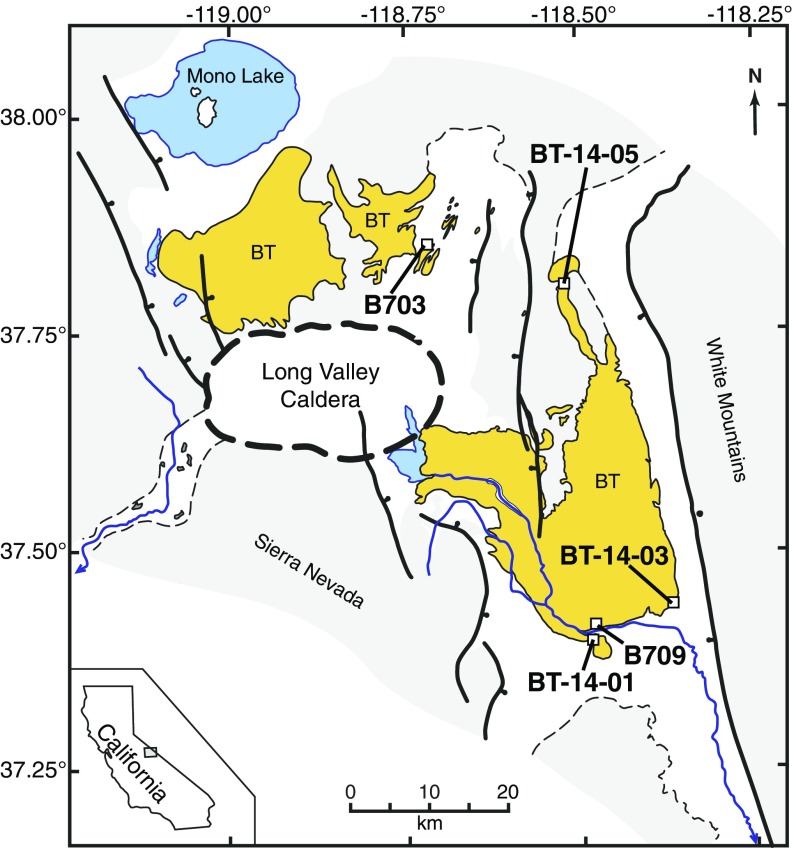
This enhanced analytical resolution also allows for the incremental heating of single young sanidine crystals that can reduce the overall dispersion of the dataset and discriminate between subpopulations of dates that are convoluted by low-precision techniques (10–14). We applied an incremental heating multicollector mass spectrometry (IH-MCMS) procedure (11) (see Supporting Information for details) to dating single sanidine from the Bishop Tuff (BT), an extensively studied middle Pleistocene rhyolitic fall and ignimbrite deposit erupted from Long Valley Caldera, CA (Fig. 1). The proximity of the normally magnetized BT to the Matuyama−Brunhes magnetic polarity reversal makes it an important middle Pleistocene stratigraphic marker in the western United States (15), and models of its magmatic evolution have shaped the current understanding of the dynamics of voluminous silicic magma systems (16).

Fig. 1.

Simplified map of Long Valley showing the BT (orange) and sample locations. Adapted from ref. 16.

The ⁴⁰Ar/³⁹Ar age of the BT eruption has recently been controversial due to proposed ages, 776.4 ka to 780.0 ka (17, 18), that are older than the youngest zircon dates (19, 20). Subsequent isotope dilution thermal ionization mass spectrometry (ID-TIMS) and laser ablation inductively coupled plasma mass spectrometry (LA-ICP-MS) studies of BT zircon show that the geologic uncertainties of the initial zircon U-series disequilibrium are not sufficient to produce this discordance between the ⁴⁰Ar/³⁹Ar and U-Pb systems (21, 22). The older ⁴⁰Ar/³⁹Ar ages for the BT are calculated relative to the age of the Alder Creek sanidine standard (ACs) proposed by Renne et al. (17). Several recent studies suggest the age of the ACs is >1% younger than previous estimates (11, 23, 24), thereby bringing all recent ⁴⁰Ar/³⁹Ar and U-Pb BT ages into agreement.

However, all BT ⁴⁰Ar/³⁹Ar single-crystal fusion datasets exhibit a significant range, 40 ky to 420 ky, between the oldest and youngest dates (7, 8, 18). We present high-precision IH-MCMS dates to better characterize the BT sanidine population and thereby improve the accuracy and precision of the eruption age. Moreover, these data provide leverage with which to investigate the source and geologic significance of scattered ⁴⁰Ar/³⁹Ar sanidine dates that require a reassessment of analytical and statistical procedures typically employed in ⁴⁰Ar/³⁹Ar geochronology.

Sanidine Incremental Heating Dates

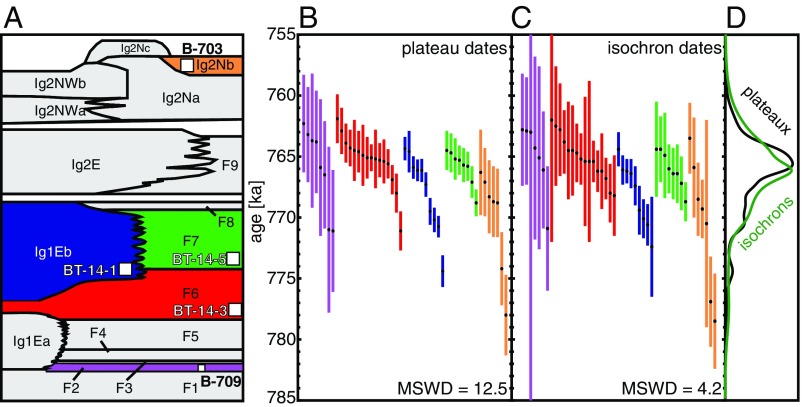
IH-MCMS measurements yield plateau dates for 49 of 51 crystals, with all but 8 comprising >70% of the ³⁹Ar released. Only one isochron intercept is distinguishable from the atmospheric ⁴⁰Ar/³⁶Ar ratio at the 95% confidence level; however, it and all other crystals produced equivalent plateau and isochron dates, and thus we favor the more precise plateau calculations. Plateau dates range from 761.9 ka to 778.0 ka with a median 2σ analytical uncertainty of 1.7 ka (Fig. 2); analytical uncertainties reported throughout this paper include the uncertainty of the J parameter. Median uncertainties of individual steps produced by incremental heating of multicrystal aliquots and single-collector mass spectrometry (7) are nearly double those now achievable by IH-MCMS analysis of a single sanidine (Fig. 3A).

Fig. 2.

(A) Simplified stratigraphy of the BT showing the stratigraphic location of the dated samples. Adapted from ref. 16. (B and C) The (B) plateau and (C) isochron dates produced by single sanidine incremental heating, which are equivalent for all crystals. A weighted mean calculated from all of either the plateau or isochron dates yields a high MSWD, indicating neither is a geologically meaningful age for the Bishop Tuff. Error bars are 2σ analytical uncertainties. (D) Probability density curves for the plateau and isochron dates illustrating that the populations are highly similar.

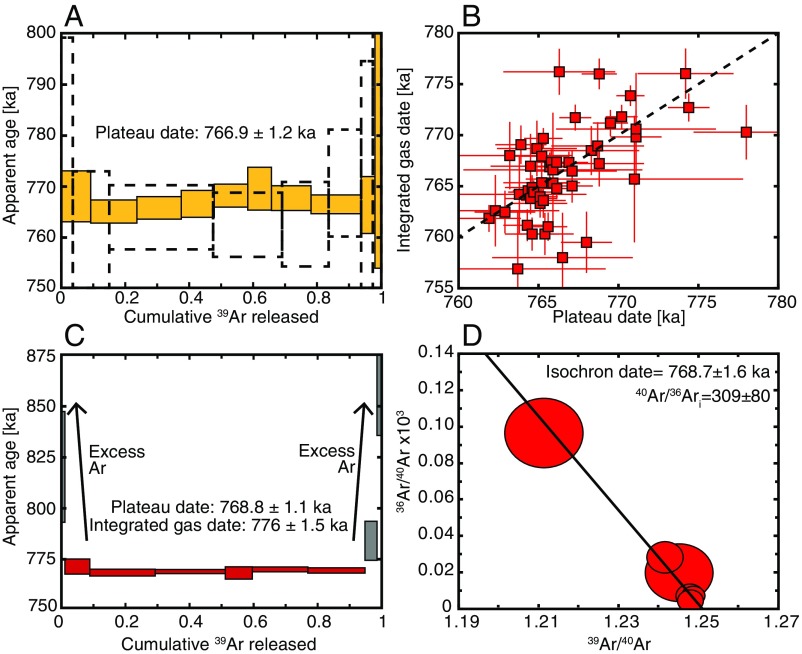
Fig. 3.

(A) An unperturbed incremental heating spectra comprising 100% of the released ³⁹Ar. The dashed outlined plateau is a single-collector, multicrystal incremental heating experiment from Mark et al. (7) highlighting the nearly twofold greater resolution achievable per heating step by the Noblesse multicollector mass spectrometer. (B) Comparison of the integrated gas and incremental heating plateau dates. The two dates are not within 2σ analytical uncertainty for 17 of 49 crystals, illustrating the effect of compromised crystal domains excluded from the plateau age calculations. (C) Example of a concave-up age spectra reflecting contributions of excess Ar to the low and high temperature steps (gray boxes) that produce apparent ages older than the plateau (red boxes). The discordance of the plateau and integrated gas ages illustrates the potential bias to fusion analyses that can be excluded by IH-MCMS. (D) Isochron plot for the plateau steps plotted in C. The intercept within uncertainty of the atmospheric ⁴⁰Ar/³⁶Ar ratio and isochron date indistinguishable from the plateau date indicates that the excess Ar apparent in C does not affect the plateau steps.

The smaller crystals of fall unit F2 compared with the other samples (0.5 mm to 1 mm vs. >1 mm) did not produce a significantly different age population, indicating there is no systematic variation of sanidine ⁴⁰Ar/³⁹Ar age with crystal size. Similarly, despite the well-documented compositional and thermal zoning of the BT magma reservoir (16), there is no stratigraphic gradient in sanidine incremental heating dates (Fig. 2). Each sample contains a coeval population of dates at ca. 765 ka; however, crystals that yield older plateau dates are more abundant in the ignimbrites than in the fall units.

Sources of Age Dispersion

The 16-ky spread in the IH-MCMS plateau dates exceeds that predicted by the analytical uncertainties. A weighted mean of all 49 plateau dates has a mean square weighted deviation (MSWD; i.e., reduced χ² statistic) of 12.5. However, this 16-ky dispersion is 2.5 to 25 times less than that of recent, “high-precision” single-crystal fusion datasets (7, 8, 18). Moreover, the youngest 70% of the plateau dates comprise a range of only 5.4 ky, indicating most of the 16 ky spread is produced by a subordinate crystal population.

The accuracy of a ⁴⁰Ar/³⁹Ar eruption age depends on isolating the radiogenic ⁴⁰Ar (⁴⁰Ar*) component, derived from the in situ radioactive decay of ⁴⁰K, produced since the eruption. Sanidine crystals also contain trapped Ar comprising atmospheric Ar (Ar_atm) and excess ⁴⁰Ar (⁴⁰Ar_xs). Excess ⁴⁰Ar is derived from neither in situ radioactive decay nor the atmosphere (25) and may be hosted in melt or mineral inclusions or the sanidine crystal itself. The ⁴⁰Ar_xs may originate from within mantle magma sources or incorporation of melts from ancient wall rock into a magma system (25, 26). The Ar_atm component is routinely corrected for, based on the ³⁶Ar abundance. However, the ⁴⁰Ar* content of a crystal may be perturbed by the presence of ⁴⁰Ar_xs or Ar loss.

The more precise age spectra achieved by IH-MCMS resolves and allows for the exclusion of these compromised intracrystal domains. For example, Fig. 3C illustrates how this approach identifies sanidine domains which likely contain a small amount of ⁴⁰Ar_xs. An integrated gas date (the mean of the dates produced by each heating step, weighted by the proportion of ³⁹Ar released; the result is equivalent to a crystal fusion date) including these steps is 9 ky older than the plateau date. This approach reveals that the integrated gas dates of 17 of 49 crystals are either older or younger than the plateau dates (Fig. 3B). The IH-MCMS procedure therefore eliminates age bias that reflects subtle quantities of either ⁴⁰Ar_xs or loss of Ar that would affect dates produced by crystal fusion analysis.

These coupled improvements in analytical precision and aggregate dispersion counterintuitively result in greater relative scatter, i.e., a higher MSWD, of the incremental heating data compared with the lower-precision fusion datasets. This does not imply the introduction of an analytical artifact by the IH-MCMS procedure, but rather that the less precise crystal fusion analyses are unable to resolve the isotopic heterogeneity either within individual crystals or in the aggregate population analyzed. Additionally, 10 sanidine crystals yield plateaux comprising 100% of the released ³⁹Ar and isochrons with atmospheric y-axis intercepts. The plateau dates of these crystals range from 763.8 ± 4.2 to 771.1 ± 1.6 ka, a spread that cannot be attributed to ambiguity about which steps should be included in the plateau or isochron calculation.

Whereas IH-MCMS can identify some compromised crystal domains, plateau dates that predate the eruption age require the presence of ⁴⁰Ar_xs or ⁴⁰Ar* accumulated before eruption. Biotite that contains these Ar components can produce spurious ages up to 10⁵ y older than eruption (27); however, both are thought to be minor in sanidine due to its low closure temperature for Ar diffusion and low affinity for Ar during crystallization (25, 26). The precision of the IH-MCMS dates offer the opportunity to evaluate the relative importance of these sources of bias and the potential impact of magmatic processes on the ⁴⁰Ar/³⁹Ar system. The occurrence of a continuous distribution of older sanidine dates throughout the BT reflects a pervasive source in the BT magma reservoir able to produce a differential effect for various sanidine crystals rather than mixing between two distinct populations. To explain this population of dates, we first consider the potential presence of ⁴⁰Ar_xs, then the magmatic processes required for sanidine to retain ⁴⁰Ar* produced by preeruption decay.

Contribution of Excess Ar to Plateau Dates

Excess ⁴⁰Ar is among the most pervasive sources of inaccuracy in the ⁴⁰Ar/³⁹Ar method (27, 28), and is clear in a number of BT sanidines. Discordant low- and high-temperature heating steps yield ages significantly older than the plateau; this concave-up geometry is a classic indicator of the presence of ⁴⁰Ar_xs (25) (Fig. 3C). Inverse isochron analysis is typically employed to assess the presence of ⁴⁰Ar_xs in the plateau steps and calculate a date that is free from its effects (Fig. 3D). The y intercept of the isochron is an estimate of the isotopic composition of the trapped component. An isochron intercept indicating a ⁴⁰Ar/³⁶Ar ratio within uncertainty of the atmospheric ratio of 298.56 ± 0.31 (29) indicates the crystal does not contain resolvable ⁴⁰Ar_xs. However, sanidine commonly contains little Ar_atm, and the y intercept of the isochrons for some crystals are imprecisely constrained owing to clustering of the data near the x axis (Fig. 3D). Thus, the imprecise estimate of the trapped ⁴⁰Ar/³⁶Ar ratio can potentially mask the presence of small amounts of ⁴⁰Ar_xs that could bias a plateau date.

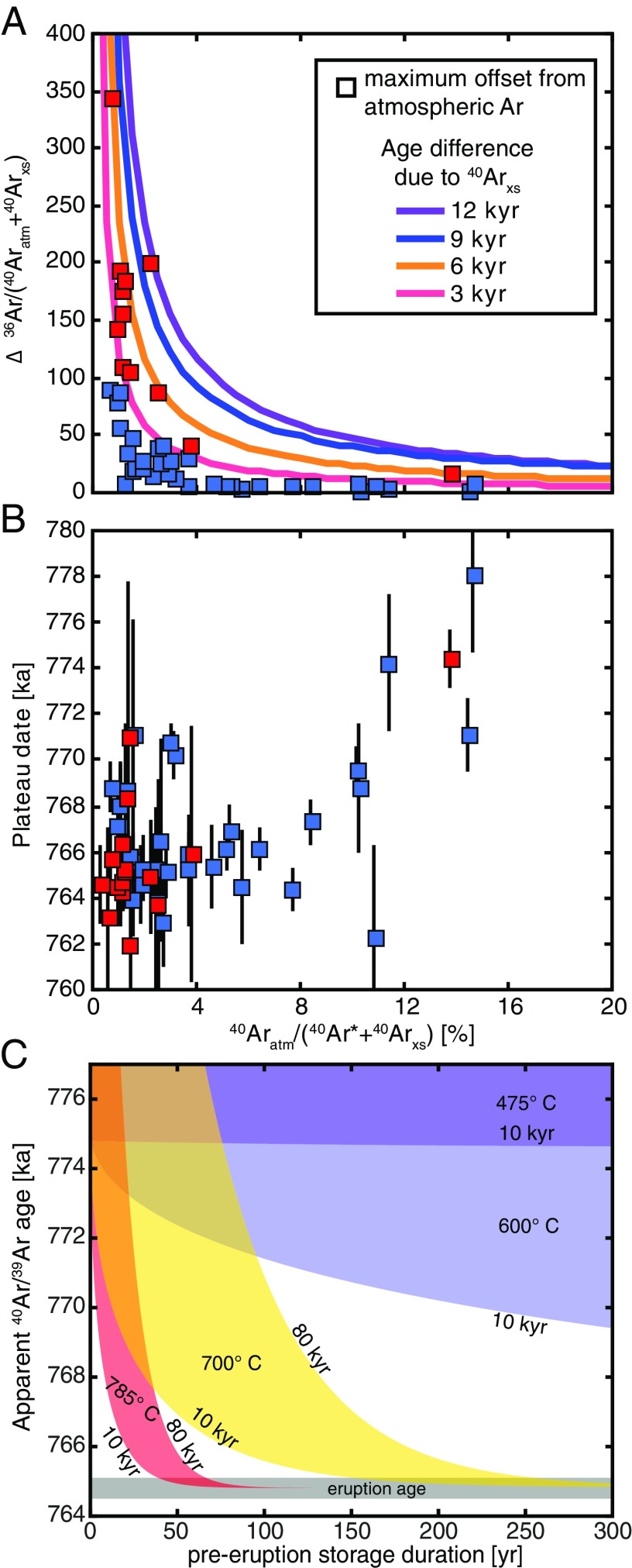
To evaluate the sensitivity of the BT isochrons to ⁴⁰Ar_xs, we calculated the expected isochron intercept for sanidine containing 0.5 to 20% Ar_atm and ⁴⁰Ar_xs sufficient to produce a 3- to 12-ky increase in the apparent age (see Supporting Information for details). The ³⁹Ar-weighted mean of the percent Ar_atm of the plateau steps and the upper bound of the isochron intercept 2σ uncertainty envelope for each crystal are then compared with these models to estimate the maximum potential age offset due to Ar_xs that is not resolvable by the isochron calculation (Fig. 4A). Most isochrons are sufficiently precise to resolve ⁴⁰Ar_xs that could produce an age difference of 3 ky or less. The less precise isochron intercepts could allow for potential age offsets of up to 12 ky. However, these crystals did not preferentially produce older plateau dates (Fig. 4). Thus, unresolvable ⁴⁰Ar_xs may affect a minority of crystals, but it is not the primary source of dispersion.

Fig. 4.

(A) Sensitivity of the isochron intercepts to ⁴⁰Ar_xs in BT sanidine. The squares are the maximum potential deviation from the atmospheric ⁴⁰Ar/³⁶Ar ratio [Δ ³⁶Ar/(⁴⁰Ar_atm + ⁴⁰Ar_xs)] of the trapped Ar component of each crystal, i.e., the upper bound of the 95% confidence interval of the isochron intercept, plotted against the ³⁹Ar-weighted average fraction of Ar_atm of the plateau steps; red squares indicate isochron intercepts insufficiently precise to resolve a ⁴⁰Ar_xs component that would produce a 3-ky difference in apparent age. Curves show the expected isochron intercepts of crystals containing ⁴⁰Ar_xs that would produce age differences of 3 ky to 12 ky. (B) Plateau date (with 2σ analytical uncertainties) vs. % Ar_atm for BT sanidines. Older plateau dates are not associated with imprecise isochron intercepts, indicating unresolved ⁴⁰Ar_xs is not their source. (C) Results of the Ar diffusion numerical model using the diffusion parameters of Wartho et al. (53). The y axis shows the apparent age that would be measured today for a crystal initially containing 10 ky to 85 ky of accumulated ⁴⁰Ar* following an interval of storage at 475 °C to 785 °C. Whereas crystals residing at less than 475 °C would accumulate ⁴⁰Ar*, the temperatures recorded by BT mineral thermometry would reset the apparent sanidine age in no more than a few centuries.

Accumulation of ⁴⁰Ar* in Cold Storage

Large, long-lived intermediate to silicic volcanic systems have complex thermal histories involving protracted periods of magma accumulation and crystallization punctuated by magma recharge events that produce prograde temperature excursions, magma mixing, and melting of previously emplaced magma batches (16, 30–33). The BT is an archetypal example of the progressive extraction of rhyolite melt from a highly crystalline magma mush (16). Ion probe dating of zircon indicates the BT magma body accumulated over ca. 80 ky (20, 21, 34), during which time no eruptions occurred within Long Valley (35). The precaldera Glass Mountain rhyolites erupted in Long Valley between ∼2.2 and 0.84 Ma (20, 36), yet crystals inherited from this earlier magmatic episode or the wall rock are rare in the BT. Accordingly, the dominant sanidine population of the BT crystallized from the growing BT magma body (16, 20, 37, 38). Crystals that yield preeruption ages were most likely segregated along the magma reservoir margins, cooled sufficiently to retain ⁴⁰Ar* produced by in situ decay, and remobilized before the BT eruption.

The ⁴⁰Ar* produced before and after eruption should be distributed similarly within a sanidine crystal and, in contrast to trapped Ar, are not associated with ³⁶Ar. Consequently, sufficiently precise isochron calculations will detect ⁴⁰Ar_xs, but are unable to distinguish preeruptive and posteruptive ⁴⁰Ar*. We use a model of simultaneous ⁴⁰Ar volume diffusion and ⁴⁰K decay to place specific constraints on the temperature history and timescales of sanidine remobilization required to retain preeruptive ⁴⁰Ar*. The model assumes an initial concentration of ⁴⁰Ar* produced by 10 to 80 ky of in situ decay and calculates the effect of storage at temperatures of 425 °C to 785 °C (see Supporting Information for details). Production of ⁴⁰Ar* outpaces diffusive loss at temperatures less than 475 °C. Crystals stored at 600 °C could retain preeruption ages for several millennia; however, residence at temperatures of >700 °C, consistent with the BT mineral thermometry (16, 39, 40), would reset sanidine in no more than several centuries (Fig. 4C). Thus, for preeruption in situ decay to yield the tail of older ages, sanidine must cool to subsolidus temperatures, then be rapidly remobilized before eruption.

Whereas ion probe dating indicates 80 ky of zircon crystallization, the range of sanidine dates is conspicuously similar to the shorter duration (14 to 33 ky) recorded by the more precise ID-TIMS zircon dates (19, 21). The contrast between the ion probe and ID-TIMS dates likely results primarily from the bias of the ID-TIMS method toward the volumetrically dominant, later crystallized material (1, 21) and the ID-TIMS studies not including zircons from the later erupted ignimbrite units in which the oldest zircons are found (20). Thus, the ID-TIMS dates likely capture a later period of crystallization that was pervasive in the magma reservoir, but not the earlier crystallization history recorded by the greater spatial and stratigraphic resolution of the ion probe dates (1, 20, 21). Remobilization of sanidine from the magma reservoir margins would favor the most recently crystallized material, consistent with the similarity of the sanidine and ID-TIMS zircon age populations.

Physical evidence for incorporating this subsolidus rind is not widespread. The BT is overall crystal-poor, <25% phenocrysts, and sanidine is found as isolated crystals rather than in clots or with adhering quartz as might be expected if it was remobilized following cooling below the solidus (16). On the other hand, older sanidine is more common in the crystal-rich ignimbrites than in crystal-poor fall deposits, indicating that remobilized material, further disaggregated by pyroclastic flow, could contribute to this distinction in crystallinity despite the lack of crystal-scale textural evidence for this process. Overgrowths on zircon, sanidine, and quartz crystals record the remelting of crystal mush at the base of the magma system and the intrusion of the resulting hotter, less evolved rhyolite into the main BT magma body (20, 40, 41). Trace element diffusion timescales and zircon crystallization ages indicate this intrusive episode may have occurred over 10 ky but was most vigorous during the final 500 y before eruption (20, 40). The similar timescales of sanidine remobilization and crystal residence following this magma recharge event suggest the processes could be linked. However, the stratigraphic distribution of crystal overgrowths shows the intruding magma was restricted to the lower reaches of the reservoir (20, 40), in contrast to the older ⁴⁰Ar/³⁹Ar plateau dates produced by crystals throughout the BT stratigraphy (Fig. 2). Increasing pressure within the BT magma body in response to magma recharge could promote fracturing, disaggregation along grain boundaries, and incorporation of the subsolidus, crystalline reservoir margins (42, 43). Thus, the well-documented incursion into the lower BT magma body leading up to its eruption could also have catalyzed the reintroduction of crystals held in cold storage throughout the reservoir margins (e.g., refs. 30 and 33).

Single-crystal incremental heating of sanidine has not yet been widely applied, but existing data share features with the BT dates. Fusion analysis of sanidine from the Huckleberry Ridge Tuff (HRT) and Mesa Falls Tuff (MFT) produced ranges of 43 ky to 443 ky (2, 10, 44) and 50 ky (13), respectively. Incremental heating dates are significantly less dispersed in both cases; however, the MFT sanidine yields a uniform population of dates that is interpreted as the eruption age (13), whereas HRT sanidine possesses a 22-ky range, including 4 of 17 dates older than the eruption (10). Sanidine incremental heating yields dates up to 19 ky older than the 930 CE (Common Era) Millennium eruption of Tianchi Volcano, China, similar to the range of ²³⁸U−²³⁰Th zircon dates (12, 45). Sanidine dates of Middle Holocene trachyte and comendite Tianchi lavas yield a similar, several-kiloyear spread (12).

These examples illustrate the capability of IH-MCMS to resolve intracrystal and age population complexities not accessible by crystal fusion analysis. The similarity of the range of ⁴⁰Ar/³⁹Ar and zircon dates and the contribution of magma rejuvenation and recycling to the Yellowstone rhyolite (31, 46) suggest magmatic perturbations of ⁴⁰Ar/³⁹Ar systematics may be underappreciated. Moreover, IH-MCMS is a promising tool for probing the thermochemical evolution of long-lived silicic systems that can be combined with in situ compositional measurements and thermal modeling.

Eruption Age of the BT and Implications for ⁴⁰Ar/³⁹Ar Geochronology

IH-MCMS analysis identifies crystal domains compromised by Ar loss, the primary source of spuriously young crystal fusion dates, to be excluded from age calculations. Consequently, preeruption ⁴⁰Ar* accumulation, and possibly ⁴⁰Ar_xs, are the most substantial sources of age bias, and thus the youngest dates of the BT population are likely most representative of the eruption age. Typically applied data filtering methods that assume the mean or median of the aggregate population is the best estimate of the eruption age are inappropriate for the IH-MCMS dataset; accordingly, we propose an alternative set of criterion for calculating an eruption age from IH-MCMS data. The youngest group of sanidine plateau dates in all five BT subunits is defined as that for which the difference between the weighted mean of the youngest group and the next oldest date is greater than zero with 95% confidence. This group comprises 25 of the 49 dates and yields an inverse variance-weighted mean age of 764.8 ± 0.3/0.6 ka (analytical/full 2σ uncertainties; MSWD = 1.1; Fig. 5). The statistical coherence of the youngest population indicates either that these crystals contain minimal preeruptive ⁴⁰Ar* or that more than half of the sanidine population fortuitously retained similar amounts. We prefer the former explanation and interpret the weighted mean as the eruption age; however, the presence of small amounts of preeruptive ⁴⁰Ar* cannot be strictly ruled out, in which case this age would be an upper bound.

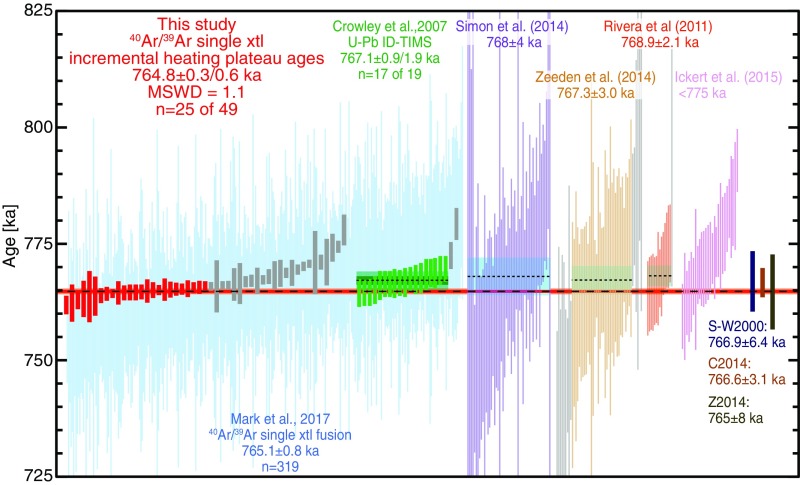
Fig. 5.

Comparison of our preferred eruption age, 764.8 ± 0.3/0.6 ka (2σ; analytical/full uncertainties), with the weighted mean eruption age (light blue fields showing 2σ analytical uncertainties) produced by ⁴⁰Ar/³⁹Ar single and multicrystal fusion analysis (7, 8, 15, 18, 47), zircon ages produced by U-Pb ID-TIMS (19, 21) and SIMS (20), and an astronomically tuned age (8). Dates of individual crystals are plotted with 2σ analytical uncertainties; those excluded from the weighted mean calculation are light gray. The two-tone fields show the analytical and full uncertainties for the weighted mean of the BT IH-MCMS dates and the U-Pb ID-TIMS zircon dates of Crowley et al. (19). All ⁴⁰Ar/³⁹Ar data are recalculated using an ACs age of 1.1864 Ma (11, 23) and the decay constants of Min et al. (48). C2014, Chamberlain et al. (20); S-W2000, Sarna-Wojcicki et al. (15); and Z2014, Zeeden et al. (8).

The IH-MCMS age is equivalent within 2σ analytical uncertainty to the eruption ages derived from ⁴⁰Ar/³⁹Ar single crystal fusion analyses of 765.1 ± 0.8 ka (7), 768 ± 4 ka (18), 767.3 ± 3.0 ka (8), and 766.9 ± 6.4 ka (15), and is younger than a multicrystal fusion age of 768.9 ± 2.1 ka (47)—all calculated relative to an ACs age of 1.1864 Ma (11, 23) and the decay constants of ref. 48 (Fig. 5). Our preferred age is consistent with the youngest BT ID-TIMS U-Pb zircon dates (19, 21), the mean of 167 ion probe zircon rim analyses (20), and the astronomical age proposed by Zeeden et al. (8). The Matuyama−Brunhes geomagnetic polarity reversal has been dated using astrochronologic and U-Pb zircon methods in globally distributed marine sediments at 773 ka to 772 ka (49–52). Our IH-MCMS age of 764.8 ± 0.6 ka indicates that the eruption of the normally magnetized BT took place only 7 ky to 8 ky later.

Whereas comparison of the BT datasets indicates fusion analysis can produce accurate estimates of eruption age despite geologic complexities, their accuracy is dependent on a fortuitous balance of crystals biased older or younger by Ar loss, ⁴⁰Ar_xs, or preeruption ⁴⁰Ar* accumulation. However, there is no method to test whether this criterion has been met. Moreover, to achieve an acceptable MSWD, several of the typically sized (n ≈ 50) fusion datasets (8, 18) required data filtering based on a median or mean without any indication that these values are representative of the eruption age, and only the unusually large dataset (n = 314) of Mark et al. (7) approaches the precision of the IH-MCMS age. In contrast, the BT incremental heating results demonstrate the capability to explicitly identify and address geologic complexities that are masked by less precise crystal fusion dates. This technique can recognize crystals compromised by ⁴⁰Ar_xs, Ar loss, melt and mineral inclusions, or petrologic processes and thus permits a more robust assessment of which dates are most representative of the eruption. Pooling large sets of relatively imprecise ⁴⁰Ar/³⁹Ar dates is a problematic approach to high-precision geochronology because it retains these sources of bias. Whereas rapid acquisition of single-crystal fusion dates remains useful for a variety of geologic problems, we recommend that single sanidine incremental heating be considered “best practice” for those studies that require the highest precision and accuracy.