Myoanatomy of the velvet worm leg revealed by laboratory-based nanofocus X-ray source tomography

Significance

X-ray computed tomography (CT) imaging has become popular for investigating, nondestructively and three-dimensionally, both external and internal structures of various specimens. However, the limited resolution of conventional laboratory-based CT systems (≥500 nm) still hampers the detailed visualization of features on the low nanometer level. We present a laboratory CT device and data processing pipeline to routinely and efficiently generate high-resolution 3D data (≈100 nm) without requiring synchrotron radiation facilities. Our setup is especially relevant for conducting detailed analysis of very small biological samples, as demonstrated for a walking appendage of a velvet worm. Comparative analyses of our CT data with those obtained from other popular imaging methods highlight the advantages and future applicability of the nanoCT setup.

Abstract

X-ray computed tomography (CT) is a powerful noninvasive technique for investigating the inner structure of objects and organisms. However, the resolution of laboratory CT systems is typically limited to the micrometer range. In this paper, we present a table-top nanoCT system in conjunction with standard processing tools that is able to routinely reach resolutions down to 100 nm without using X-ray optics. We demonstrate its potential for biological investigations by imaging a walking appendage of Euperipatoides rowelli, a representative of Onychophora—an invertebrate group pivotal for understanding animal evolution. Comparative analyses proved that the nanoCT can depict the external morphology of the limb with an image quality similar to scanning electron microscopy, while simultaneously visualizing internal muscular structures at higher resolutions than confocal laser scanning microscopy. The obtained nanoCT data revealed hitherto unknown aspects of the onychophoran limb musculature, enabling the 3D reconstruction of individual muscle fibers, which was previously impossible using any laboratory-based imaging technique.

X-ray computed tomography (CT) (1) imaging allows the noninvasive visualization and 3D reconstruction of internal structures of an object or organism based on the distribution of its attenuation coefficient. Therefore, the method became very popular in different fields such as medical diagnostics, industrial testing, and scientific research. Over the years, the increasing demand for higher resolutions in X-ray CT created an emerging research field known as X-ray microCT imaging ($\mathrm{\mu }$CT).

So far, exploring CT imaging at resolutions as high as a few nanometers required highly brilliant X-rays, which could only be generated by synchrotron facilities (2–4). Differently, CT devices designed for laboratories were limited to resolutions on a micrometer scale for several years, mainly due to limitations associated with the spot size of the X-ray sources available. More recently, this resolution constraint has been overcome by different approaches. Commercially available table-top devices using rotating anode generators at 8 keV combined with X-ray optics can acquire CT data at resolutions below 100 nm (5–7). Likewise, similar X-ray spot sizes can be created by pointing a highly focused electron beam at a suitable metal target, for example by using a scanning electron microscope (8, 9) or an electron probe microanalyzer (10). While these devices can achieve 2D resolutions below 100 nm (11, 12), CT imaging at comparable resolutions has not yet been demonstrated with such a system.

For conventional X-ray sources, however, the limited resolution was improved by developing X-ray tubes with advanced electron optics and thin transmission targets: the so-called nanofocus tubes. So far, commercially available nanoCT devices based on transmission tubes (6, 13–15) as well as custom-built setups (16) have remained limited to resolutions around 400 nm (16). In this paper we introduce a table-top nanoCT system that combines a prototype nanofocus source and a single-photon counting detector. The system is based on the principle of geometrical magnification and is able to perform CT scans at higher resolutions (≈100 nm) than any other CT system based on the same principle. Compared with devices using X-ray optics (5–7), our nanoCT offers several advantages, such as shorter acquisition times, lower costs, a larger field of view (FOV), and a more flexible energy range.

Their high resolving power combined with their ability to provide 3D information in a nondestructive manner renders nanoCT systems very attractive for many fields, in particular for biological sciences. There, the nanoCT system will allow one to generate a wealth of new data from samples that have remained poorly investigated thus far because of their rarity and/or small size together with the destructive nature of the methods required to investigate them.

To demonstrate the potential applications of the nanoCT for biological investigations, we studied a representative of Onychophora, or velvet worms—a small group of terrestrial invertebrates pivotal for understanding animal evolution (17). Despite their relevance, there are still many gaps in our knowledge of these animals. A recent discussion regarding the evolution of their locomotory system, for example, has brought them back into the scientific spotlight (18). In particular, researchers try to understand the evolution of the limb musculature from their ancestors—marine Cambrian animals called lobopodians—to exclusively terrestrial modern onychophorans (18). Nevertheless, it is still difficult to draw any major conclusions about this issue, as the complex limb musculature of extant onychophorans remains poorly understood.

In this study we scanned an onychophoran limb using the nanoCT setup and explored its external and internal anatomy in detail. The onychophoran limb has previously been investigated, to a certain extent, by widely available imaging methods such as light microscopy, histology, SEM, and confocal laser scanning microscopy (CLSM) (e.g., refs. 19–21). Therefore, we also generated corresponding SEM and CLSM data and performed a comparative study to assess the reliability and usefulness of the nanoCT technique for studying complex biological samples.

Results

Resolution of the NanoCT.

The 2D resolution of the nanoCT setup has been tested by acquiring images of a standard resolution test pattern (JIMA RT RC-04), in which the width of the dark lines and bright spaces is exactly 200 nm (Fig. 1 A–C). The background-corrected projection image initially obtained shows identifiable lines and spaces but the edges are not well-defined and the image is noisy (Fig. 1A). This situation could be substantially improved by subsequently applying different image processing operations to the original image. Using a Gaussian filter and a Richardson–Lucy deconvolution (22–24) clearly enhances the definition of the lines and spaces, although the overall image still exhibits a substantial amount of noise, evidenced by its granulated appearance (Fig. 1B). This image noise can be further improved by applying a dictionary denoising algorithm (25, 26), which reduces the noise distribution while preserving the edges of the structures. The result is an image with a lower noise level and sharper edges (Fig. 1C) compared with the unprocessed image.

Fig. 1.

Resolution of the nanoCT setup. (A–C) Projection images of a resolution pattern with 200-nm lines and spaces. (D and F) Transversal CT slices through the center of a silicon sphere (diameter ≈30 $\mathrm{\mu }$m) with 98-nm voxel size. (E and G) Analysis of the edge profiles corresponding to the orange lines through the border of the sphere and the surrounding air. Error functions with a free width parameter (blue lines) were fitted to the data points of the respective edge (orange dots). The 10% MTF measure of the corresponding MTF and the rmse of the regression are given in the lower box in each plot. (A) The background was corrected with a flat-field image; no further processing steps were applied. (B) A 2D Gaussian filter followed by Richardson–Lucy deconvolution were used to process the background corrected image in A. (C) Dictionary denoising applied to the image in B. The training image for the dictionary creation was the image shown in A. (D and E) FBP reconstruction without preprocessing of the projection images. (F and G) Richardson–Lucy deconvolution applied to the projection images before FBP reconstruction.

To assess the resolution of our setup for 3D imaging we analyzed nanoCT data of a highly refracting glass microsphere (diameter ≈30 $\mathrm{\mu }$m; Corpuscular Inc.) imaged with an effective voxel size of 98 nm (Fig. 1 D and F). When reconstructing the unprocessed projections with a filtered backprojection (FBP), a transversal CT slice through the center region of the sample (Fig. 1D) revealed that the sample was not perfectly round and featured some imperfections. We fitted a Gaussian error function to the profile of the border between the sphere and the surrounding air in a single slice in the center of the sphere. The corresponding modulation transfer function (MTF) was derived in form of a Gaussian function and the 10% MTF value was chosen as a measure for the resolution (Fig. 1 E and G). To estimate the goodness of the fit of the edge profile, we also calculated the root-mean-square error (rmse) of the regression, which describes the deviation of the original data points from the fit function. Analyzing the marked edge profile (Fig. 1E) demonstrated that the raw FBP data show a very high in-plane resolution (10% MTF = 4,767 line pairs (lp) per mm; resolution ≈105 nm). By applying a Richardson–Lucy deconvolution to the projections before FBP reconstruction (Fig. 1F), the resolving power could be further improved (10% MTF = 5,102 lp/mm; resolution ≈100 nm). Unfortunately, the noise was also amplified by this processing step, consequently leading to a decreased goodness of the fit (Fig. 1G). A detailed description of the analysis steps and supplementary results are presented in Supporting Information.

Optimization for Biological Samples: Onychophoran Limb as an Example.

An ∼350-$\mathrm{\mu }$m-long walking appendage of the onychophoran species Euperipatoides rowelli (Fig. 2A) was imaged using the nanoCT setup. When reconstructing nanoCT data from unprocessed projection images the resulting contrast modality is a combination of the conventional attenuation contrast and phase effects caused by Fresnel diffraction. Analysis of different processing steps applied to nanoCT data of the onychophoran limb (Fig. S2) showed that the soft-tissue contrast and the image sharpness could be optimized by using a combination of deconvolution and Paganin’s single-distance phase-retrieval algorithm (27). This processing approach was used for the onychophoran limb data presented in this paper and is described in detail in Materials and Methods section and Supporting Information.

Fig. 2.

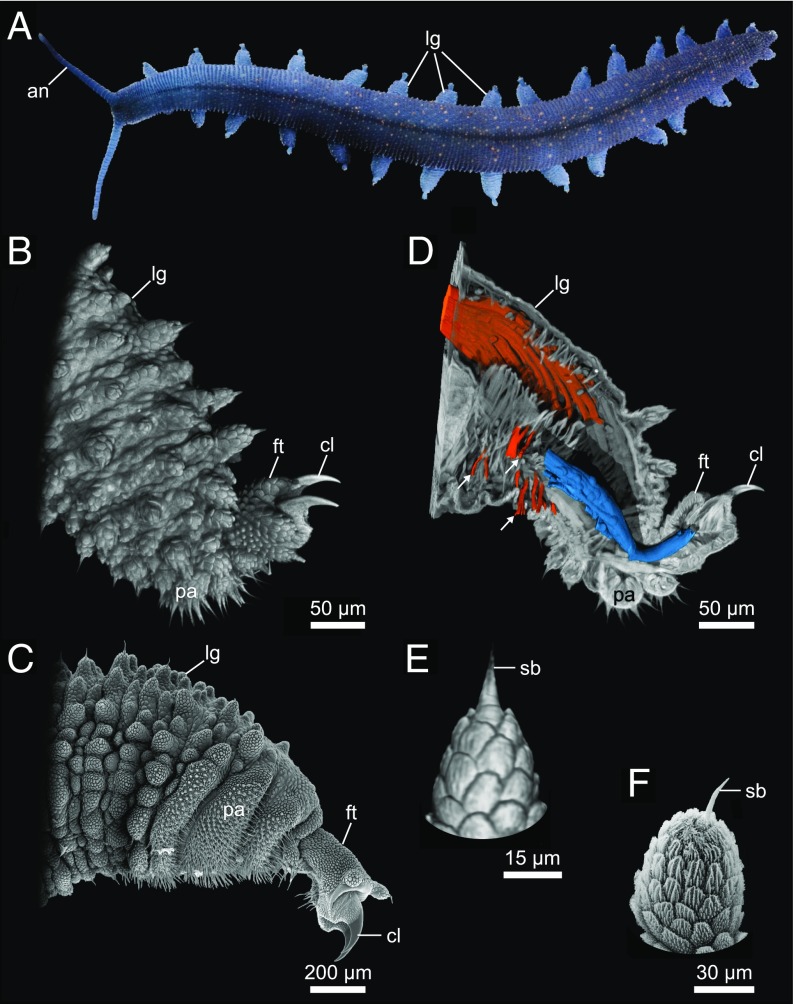
The onychophoran limb anatomy. Photograph (A), nanoCT volume renderings (B, D, and E), and scanning electron micrographs (C and F) of the onychophoran species E. rowelli. Note that the detail visibility obtained in the volume rendering of nanoCT data from a newborn specimen (B and E) is comparable to that from scanning electron microscopy of an adult specimen (C and F). (A) Overview of a 5-cm-long living specimen walking. Note the repeated arrangement of the legs along the anteroposterior body axis. (B and C) External anatomy of the leg. (D) Digital sagittal section through the same leg as in B showing the leg musculature. The claw retractor muscle is segmented in blue and the leg remotor in orange. Note that this technique allows us to reconstruct single muscle fibers in detail (arrows). (E and F) Detail of a primary papilla of the leg. an, antenna; cl, claw; ft, foot; lg, leg; pa, spinous pad; sb, sensorial bristle.

Fig. S2.

Processing of nanoCT data from an onychophoran limb. Virtual horizontal section through the ventral region of the onychophoran leg (A–D) and details of a mechanoreceptor of the spinous pad (E–H) in E. rowelli. The magnified region shown in E–H is marked by the orange rectangle in A. Note that single muscle/nerve fibers can be seen in the acquired images. The reconstructed voxel size is 269 nm. (A and E) FBP reconstruction without preprocessing of the projection images. (B and F) Statistical iterative reconstruction without preprocessing of the projection images. (C and G) Phase retrieval applied to projection images before FBP reconstruction. (D and H) Richardson–Lucy deconvolution and subsequent phase-retrieval processing of projection images before FBP reconstruction. cr, claw retractor muscle; ld, anterior leg depressor muscle; pa, spinous pad; pd, posterior leg depressor muscle; sb, sensorial bristle of the spinous pad.

Comparison with SEM Data.

To assess the usefulness of the nanoCT device for investigating the external morphology of biological samples we reconstructed the limb anatomy of the onychophoran E. rowelli based on nanoCT data and compared it with corresponding SEM images obtained from the same species. Given that the limbs in adult onychophorans are larger than the FOV of the setup at the desired voxel sizes of approximately 400 nm, the limb selected for nanoCT imaging was substantially smaller than the sample analyzed using SEM (see scale bars in Fig. 2 B and C) and a complete nanoCT reconstruction of this structure could only be achieved by combining several separate volumes.

Despite the smaller size of the sample, the resolution of our nanoCT data clearly allows detailed 3D volume reconstructions (Fig. 2 B and E) comparable to SEM images (Fig. 2 C and F). All structures associated with the onychophoran limb, including dermal papillae, ventral spinous pads, and a terminal foot equipped with a pair of claws (Fig. 2C), can be clearly identified in our 3D volume rendering (Fig. 2B). The numerous microscales covering the foot and dermal papillae could be also clearly visualized, as well as the fine sensorial bristles on the spinous pads (cf. Fig. 2 B, C, E, and F). Nevertheless, the fine texture of single scales, which is evident in SEM images, could not be retrieved with the same level of detail in our nanoCT data (Fig. 2 E and F).

Comparison with CLSM Data.

While the usefulness of SEM techniques is limited to the examination of external features, the nanoCT data further provide relevant insights into the internal structure of the E. rowelli limb, particularly regarding the complex and poorly understood musculature of the leg, foot, and claws (Figs. 2D and 3 D–F and Movie S1). To demonstrate the potential of the nanoCT setup for exploring these internal features, we compared our data with corresponding CLSM images obtained from vibratome sections of legs specifically labeled with phalloidin rhodamine for muscular visualization (Fig. 3 A–F). As for the SEM, the CLSM images were obtained from legs substantially larger than the leg used for the nanoCT analyses. Nevertheless, our findings show that the nanoCT dataset is able to reproduce the results of the CLSM analyses with similar or higher level of detail (Fig. 3 A–F).

Fig. 3.

Myoanatomy of the onychophoran leg. Confocal laser scanning micrographs from vibratome sections labeled for f-actin in Principapillatus hitoyensis (A) and E. rowelli (B and C) compared with the corresponding nanoCT images in E. rowelli (D–F). Proximal is up in A and D and left in B, C, E, and F. Arrows point to the circular musculature of the foot. Note that the single 3D dataset acquired with the nanoCT allows a direct comparison with the CLSM data obtained from several vibratome sections in different perspectives. (A and D) Leg in horizontal section. (B and E) Leg in sagittal section. (C and F) Foot in median sagittal section. cr, claw retractor muscle; df, distal foot papilla; fr, foot retractor muscle; ft, foot; ld, anterior leg depressor muscle; lp, leg promotor muscle; pa, spinous pad.

Our analyses revealed hitherto unclear details of the leg and foot musculature. The foot shows prominent circular muscle fibers that, despite being single-layered, form a dense musculature in the dorsolateral region of the foot (arrows in Fig. 3 A–F). The precise anatomical position, attachment sites, and the orientation of muscle fibers in more conspicuous muscles are also revealed by our nanoCT data. This holds true for the claw retractor, leg depressor, leg promotor, and foot retractor muscles (Fig. 3 B, C, E, and F). While all these anatomical details could be observed in both nanoCT and CLSM datasets, the nanoCT data allowed the reconstruction and segmentation of individual muscles in 3D, such as the claw retractor (blue in Fig. 2D), or single muscle fibers that compose them (arrows in Fig. 2D and Movie S1). By contrast, we were unable to perform the same reconstruction based on the CLSM data because of the intrinsic limitations of this method, such as the necessity of sectioning the limb before scanning and the nonisotropic voxel size obtained in different scans.

Discussion

In the present work we introduce a nanoCT setup that, besides being a device suitable for any laboratory, can perform high-resolution scans within short acquisition times. Our nanoCT system can achieve in-plane resolutions down to 100 nm in CT images, which is the highest resolving power demonstrated thus far for a laboratory CT setup without X-ray optics. The capacity of our nanotube to create smaller X-ray spots than comparable devices is the main factor behind the superior resolution of our setup. The images of the resolution pattern show that we can clearly visualize 200-nm structures in two dimensions. Furthermore, we demonstrate that processing our data with deconvolution and dictionary denoising techniques can considerably improve the visibility of the 200-nm lines. Unfortunately, a smaller source-to-sample distance could not be tested due to the shape of the resolution pattern housing. Therefore, we were unable to overcome the limitations posed by Fresnel diffraction effects and resolve structures below 200 nm, even though our nanofocus source can create X-ray spots that allow features smaller than this to be visualized in projection images (28).

Nevertheless, the resolution achieved in projection images does not necessarily reflect that of the CT data obtained with the same setup. In addition to the image quality of each projection image, various factors affect the resolution of the resulting CT slices, namely the tomographic acquisition parameters, the reconstruction and processing of the projections, and technical conditions such as the mechanical stability of the setup and the X-ray spot stability. The results obtained from edge analysis of the sphere clearly show that our system is stable enough to perform CT scans with resolutions down to 100 nm in the transversal plane. Deconvolution with a suitable point spread function (PSF) increased the effective resolution of our CT data considerably, which was also demonstrated with the velvet worm data. Due to technical constraints we were unable to reliably determine the resolution along the rotation axis with the presented sample. Nevertheless, when taking into account the isotropic resolution of the presented projection image and the fact that the positional drifts of our setup are randomly distributed in all directions, we conclude that the nanoCT is capable of achieving resolutions in the direction of the rotation axis comparable to those in the transversal plane.

In comparison with other nanoCT setups with nanofocus sources and conventional CCD or flat panel detectors our approach with a single-photon counting detector presents additional benefits. First, the absence of readout and dark-current noise in our detector greatly increases the data quality when imaging with low photon statistics. Consequently, the acquisition time per projection image can still be relatively short, even for the very low photon flux characteristic of X-ray spots in the nanometer range. Second, the direct conversion principle of our camera and its very sharp PSF with an FWHM of one detector pixel does not suffer from the usual decrease in resolution caused by signal spread in scintillation detectors. In summary, the single-photon counting detector can produce sharper and less-noisy images than conventional integrating X-ray cameras and its superiority is particularly pronounced for imaging techniques with relatively small numbers of detected photons, as is the case for laboratory-based nanoCT imaging.

Compared with quasi-monochromatic CT imaging systems using Fresnel zone plates (5–7), our nanoCT offers several advantages, for example an infinite depth of focus that allows a larger and more adaptable FOV. Moreover, the full polychromatic spectrum of the source, which reaches up to 60 kVp, broadens the bandwidth available for potential applications to include more strongly absorbing samples that cannot be penetrated by X-rays with energies below 10 keV. Furthermore, shorter acquisition times are possible for comparable voxel sizes, reducing the overall acquisition times for full CT datasets and, consequently, favoring an effective workflow in research groups with multiple users.

The small X-ray spot of the source and the sharp system PSF introduce phase effects, such as edge enhancement, into the raw contrast of the nanoCT setup. Those effects can be exploited by applying phase-retrieval techniques that strongly enhance the soft-tissue contrast within the sample. The feasibility of phase-contrast imaging combined with the still relatively low effective energy of the X-ray tube spectrum (20 keV at 60 kVp) render the nanoCT particularly suitable for examining biological and medical samples.

In this study we demonstrate the potential of the nanoCT setup for biological samples by investigating a representative of Onychophora, or velvet worms. This choice was motivated by the evolutionary importance of these animals (17) as well as the many gaps in our knowledge of their musculature and locomotory system (18, 20, 21). Furthermore, the size of their limbs allows comparative analyses between the nanoCT device and other imaging techniques popular in the biological sciences (e.g., SEM and CLSM). Since the latter are the foremost techniques applied in onychophoran research (e.g., refs. 21 and 29), the results presented here also contribute relevant information to the field.

Indeed, our comparative analyses revealed a set of previously obscure features of the onychophoran limbs, mainly associated with the foot and leg musculature. The putative presence of circular muscles in the onychophoran foot, although mentioned twice in the literature (20, 30), remained uncertain, as these structures had not been demonstrated. Our data confirm the existence of these muscles and reveal details of their position, arrangement, and size. Given their characteristics, the circular muscles of the foot are most likely responsible for the protraction of the onychophoran claws. It has been previously suggested that the claws in these animals are protracted by the hydrostatic action of the hemolymph on an eversible sac situated dorsal to the claws (20, 21), but the muscles involved in this process remained unknown. It is reasonable to assume, however, that when the circular muscles of the foot contract they increase the hydrostatic pressure within the foot and pump the haemolymph into the eversible sac, which everts and externally protracts the claws.

Our data further suggest that the function of the so-called foot retractor muscle might have been misinterpreted in a recent study, in which the authors assumed that this muscle is responsible for elevating the foot (21). The size, position, and attachment sites of this muscle revealed in this study instead indicate that the foot retractor most likely plays the role of a protractor. This is in line with previous studies (19, 31), which propose an antagonistic relationship between the foot retractor and the prominent claw retractor muscles. In other words, while the claw retractor is responsible for contracting the claws and elevating the foot, the foot retractor may be responsible for depressing the foot back to the ground. It is important to highlight, however, that the functional morphology of most onychophoran muscles remains unexplored and the nomenclature hitherto used will require a thorough revision once the function of these muscles has been clarified. Further investigating the onychophoran myoanatomy will eventually shed light on the open question regarding the evolution of their locomotory system from a marine ancestor (18).

The present study used a nanoCT device to investigate the onychophoran limb anatomy. On the one hand, we demonstrated that this method is able to retrieve data that are congruent with commonly used methods, such as CLSM and SEM. On the other hand, the comparison of these different techniques suggests that the nanoCT setup presents advantages that could open new doors for investigating biological samples. First, the sample preparation that precedes the imaging proved to be less expensive and time-consuming for nanoCT than for SEM and CLSM, in particular for the latter, which requires sectioning techniques and expensive fluorescent markers for specific labeling of the target structure/tissue. Second, the nanoCT dataset generated from a single onychophoran limb provided high-resolution details of both its internal and external anatomy, whereas investigating the corresponding internal and external features requires both CLSM and SEM analyses, respectively. Moreover, investigating the complete anatomy of the onychophoran limb by CLSM or SEM demands numerous samples to be sectioned or mounted onto stubs from different perspectives, whereas a nanoCT scan of a single sample can be digitally rotated and analyzed from different points of view.

It should be noted that morphological analyses using CLSM and SEM also have advantages over the nanoCT approach. SEM proved to be more powerful for resolving morphological details of very small structures, such as the scales on the dermal papillae. The possibility of using specific markers/antibodies in CLSM analyses to reveal particular tissue/cell types is a clear advantage of this method, since comparable tissue-specific labeling is not yet possible using nanoCT scans. Nevertheless, CLSM analyses commonly require the sectioning of samples a priori, as body pigmentation and sample thickness hampers the penetration of the scanning laser into the tissue. Sectioning inevitably introduces morphological artifacts that are undesirable when attempting to reconstruct the anatomy of an organism. In contrast, nanoCT imaging does not have these limitations and samples can be scanned as a whole without artifacts. The nondestructive nature of nanoCT analysis also renders it a powerful tool to analyze rare materials placed in scientific collections, which are only allowed to be analyzed using limited noninvasive methods such as light microscopy.

Finally, the nanoCT technique applied in this study enabled us to perform detailed interactive 3D reconstructions of the onychophoran limb (Movie S1) not possible with the other methods used. This is because SEM images correspond to a single plane and CLSM data typically have nonisotropic resolutions, that is, the voxel sides have unequal sizes, thus limiting the available 3D information about samples and hampering the virtual selection of arbitrary planes in the acquired data set. By contrast, nanoCT imaging provides isotropic volume data with higher resolutions and smaller voxel sizes. Consequently, it offers us the possibility to visualize arbitrary planes and volumes within the acquired sample, for example the virtual slices presented above that are compared with CLSM images of vibratome sections, and the volume rendering of the entire structure. Furthermore, the high resolution of the nanoCT data allows us to segment and track individual muscle fibers even within the most complex muscles (Movie S1), which is currently impossible with any other laboratory-based nondestructive imaging technique. Although this was previously possible in synchrotron facilities, the nanoCT setup presented here extends this possibility to laboratory environments, allowing high-resolution data and detailed 3D reconstructions to be obtained without requiring external facilities.

Materials and Methods

NanoCT: Experimental Setup and Acquisition.

The lens-free nanoCT setup consists of a nanofocus X-ray source, a rotation stage, and a single-photon counting detector and is described in more detail in Supporting Information (Fig. S1). The acceleration voltage of all presented measurements was 60 kV, which corresponds to a mean energy of 20 keV. The acquisition time for the projection images of the resolution pattern was 600 s. The source-to-sample distance was 0.57 mm and the source-to-detector distance was 1,680 mm, leading to an effective pixel size of 58 nm. All presented CT data were acquired with 1,599 projections distributed over 360°. Flat fields (i.e., images of the illumination of each possible detector position without the sample in the beam) were acquired before the measurement and each projection was normalized by a flat field to achieve an isotropic background intensity. The CT dataset of the silicon sphere was acquired with an exposure time of 5 s per projection and a total acquisition time of 4 h. The source-to-rotation-axis distance was 0.4 mm, and the source-to-detector distance was 700 mm, resulting in an effective voxel size of 98 nm. For the velvet worm data of the entire limb, 10 datasets were acquired and subsequently combined to the volume data presented in this article. These datasets were all acquired with the same acquisition parameters, namely, 2-s exposure time per projection, a source-to-rotation-axis distance of 0.94 mm, and a source-to-detector distance of 400 mm. The effective voxel size was 404 nm.

Fig. S1.

The nanoCT setup. Renderings of the setup components (A and B) and photograph of the nanofocus source (C). The entire system (A) is mounted on an optical table that is damped to minimize the influence of external vibrations. The sample rotation stage is mounted as an overhead construction. The detector and rotation stages are both motorized to move precisely in the x, y, and z directions with travel ranges up to 1.50 m. (Inset) The active area of the photon-counting detector. High-precision piezo stages and a goniometer head are mounted on the rotation table (B) to precisely align the sample relative to the rotation axis. The nanofocus X-ray tube (C) is composed of a thin tungsten target and can generate the small and stable X-ray spots required for CT imaging with resolutions in the nanometer range.

NanoCT: Processing and Reconstruction.

For the deconvolution procedure, a Richardson–Lucy algorithm (22–24) was applied. Using a blurred input image and a suitable 2D PSF the method sharpens the resulting image by iteratively calculating the most probable pixel values. The applied dictionary denoising algorithm (25, 26) uses a training image to create a dictionary of small patches with the typical structures and features of the training image. The final image is compiled from the image patches that are individually modeled as linear combinations of a small number of dictionary patches. For phase retrieval, the single-distance phase-retrieval algorithm developed by Paganin was applied (27). For CT reconstruction, an FBP algorithm was used to reconstruct the volume data. The individual processing steps are further described in Supporting Information. The volume renderings in Fig. 2 B, D, and E and in Movie S1 were generated with VGStudio MAX 2.1 (Volume Graphics GmbH). The highlighted structures were segmented using Amira 6.0.1 (FEI Visualization Sciences Group) and VGStudio MAX 2.1.

Specimens.

Two species of Onychophora were collected from typical microhabitats, such as leaf litter and rotten logs. The specimens of the peripatid species P. hitoyensis (32) and the peripatopsid species E. rowelli (33) were obtained and kept as described elsewhere (32, 34, 35). The living specimens were photographed with a Nikon D7000 camera before the experiments.

SEM.

The specimens were fixed, preserved, and prepared for SEM as previously described (32, 36). Samples were examined using a field emission scanning electron microscope Hitachi S4000 (Hitachi High-Technologies Europe GmbH). The terminology for their morphological features was reproduced from refs. 20, 32, and 37.

Vibratome Sectioning and CLSM.

Specimens of E. rowelli and P. hitoyensis were cut into small pieces, fixed, embedded, and vibratome-sectioned following Oliveira and Mayer (21). Vibratome sections were labeled for f-actin using phalloidin rhodamine (Invitrogen) as described previously (38). The labeled sections were mounted on glass slides in Vectashield Mounting Medium (Vector Laboratories) and analyzed with the confocal laser-scanning microscope Zeiss LSM 510 META (Carl Zeiss MicroImaging GmbH).

NanoCT Sample Preparation.

Before sample preparation for nanoCT imaging the newborn specimens of E. rowelli had been stored in 4% formaldehyde in distilled water for several weeks. Selected specimens were washed several times in PBS and cut into smaller pieces containing one leg and a small part of the body wall. The separated legs were postfixed overnight in 1% osmium tetroxide (Science Services GmbH) in PBS, dehydrated in an ethanol series, dried in a critical-point dryer as previously described (32), and mounted onto sample holders for the nanoCT.

SI Materials and Methods

NanoCT: Experimental Setup and Acquisition.

The prototype X-ray tube (Excillum AB) (Fig. S1C) is composed of a thin tungsten transmission target on a diamond layer with integrated water cooling (28). The design of the head of the source allows the object to be positioned very close to the focal spot and consequently enables high magnification factors to be achieved. The spot size can be fully controlled by software and goes down to about 200–300 nm FWHM in its current state. The position, size, and intensity of the source spot are sufficiently stable for high-resolution CT imaging over several hours. The X-ray camera is a PILATUS 300K-W 20-Hz detector system with a 1-mm-thick silicon sensor. The image area consists of 1,475 × 195 square pixels with a side length of 172 $\mathrm{\mu }$m (Fig. S1A, Inset). The detection principle is based on direct conversion without scintillation processes and the PSF of the detector has an FWHM of one pixel. Furthermore, the detector is operated in single-photon counting mode, that is, it only counts X-ray photons above a certain threshold energy, which can be selected continuously between 2.7 keV and 18 keV. This allows signal acquisition without readout or dark-current noise (39–41). In all presented data the threshold of our detector was set to 2.7 keV. The camera is motorized and can be translated along all three Cartesian axes with micrometer precision. The entire sample stage is mounted as an overhead construction and the sample is rotated with a high-precision air-bearing rotary stage. Additional stages are mounted on the rotation stage to correct for displacements of the sample relative to the rotation axis (Fig. S1B). A manual goniometer head is used to compensate for angular deviations, and high-precision piezo stages are installed to correct sample offsets. The FOV of the setup depends on the required voxel size. For a single scan the FOV is approximately 1,400 voxels in the horizontal direction and 190 voxels in the vertical direction. The FOV can be extended in the vertical direction by acquiring multiple scans at different vertical positions of the sample and combining them to a larger volume. Consequently, for a full-FOV CT measurement, there is a trade-off between resolution and sample size in the direction perpendicular to the rotation axis. However, the setup also allows for high-resolution local tomography measurements of larger samples. Due to constraints of the setup geometry the sample is limited to a diameter of 1.8 mm for a voxel size of 100 nm.

NanoCT: Processing and Reconstruction.

For the deconvolution procedure, a Richardson–Lucy algorithm (22–24) was applied. Using a blurred input image and a suitable 2D PSF, the method sharpens the resulting image by iteratively calculating the most probable pixel values. The model used for the PSF in all presented results was a rotationally symmetric Gaussian function, as the measurement errors of our device that cause the blurring are isotropically distributed in all directions. The width of the PSF was estimated individually for each measurement by considering the relevant acquisition parameters, such as the X-ray spot size, the geometrical parameters, and the detector PSF. For the projection image of the resolution pattern 20 iterations were used with the SD of the Gaussian function being $\sigma$ = 2 pixels. As the processing with the Richardson–Lucy algorithm also amplifies the noise in the resulting data, the initial image of the pattern was smoothed with a rotationally symmetric Gaussian ($\sigma$ = 1 pixels) before deconvolution. For the presented CT slices of the sphere the projections were processed using 10 iterations with $\sigma$ = 1 pixels before reconstruction. The projections of the entire limb were processed using 10 iterations with $\sigma$ = 1 pixels, whereas 10 iterations with $\sigma$ = 2 pixels were applied to the projections of the horizontal portion of the ventral limb.

The presented dictionary denoising algorithm (25, 26) uses a training image to create a dictionary of small patches with the typical structures and features of the training image, the so-called dictionary patches. The actual input image is also divided into small overlapping patches (i.e., the image patches). The algorithm models each image patch individually as a linear combination of a small number $n$ of dictionary patches, with $n\ll N$, where $N$ denotes the number of pixels in an image patch. The final image is then compiled from the individually processed image patches. Since the noise in the image patches, contrary to structures and features, cannot be sparsely represented by dictionary patches, the resulting data are less noisy. To apply dictionary denoising to the data of the resolution pattern the dictionary patches were created from the initial background-corrected image, whereas the input image was processed with a Gaussian filter and the deconvolution algorithm beforehand.

For phase retrieval, Paganin’s single-distance phase-retrieval algorithm (27) was applied to the projection images before reconstruction. This method exploits the fact that there is a direct relationship between the intensity and the phase of a monochromatic X-ray beam at the exit surface of a sufficiently weakly scattering object composed of a single material (42). The algorithm basically requires three input parameters, namely the wavelength $\lambda$ of the monochromatic beam, the ratio $r$ between the real part $\delta$ and the imaginary part $\beta$ of the refractive index of the single material, and the effective propagation distance $Z_{eff}$. While the algorithm provides quantitative results when the stated requirements on setup and sample are fulfilled, it can also be used to improve the image quality of polychromatic data from samples composed of different materials (42, 43). For the presented results, the wavelength $\lambda$ was calculated from the mean energy (20 keV) of the effective spectrum of our setup at 60 kV. We optimized the ratio $r$ for the case of the velvet worm limb, finding that a value of $r=200$ provides the best results. This ratio was used for the phase retrieval in all presented velvet worm data. The effective propagation $Z_{eff}$ was calculated from the source-to-rotation-axis distance and the source-to-detector distance of the respective measurement.

For reconstruction of the entire velvet worm limb and the sphere an FBP algorithm was applied. For iteratively reconstructed data of the horizontal portion of the ventral limb, an edge-preserving statistical iterative reconstruction (SIR) algorithm (44, 45) was used with a Huber function (46) as the regularization term. The Huber threshold, which defines the border between quadratic and linear penalties, was calculated from the background noise in the corresponding FBP data.

Data Analysis of the Resolution Measurement in 3D.

To retrieve a characteristic resolution measure from the edge profile measurements of the sphere data the following steps were applied. The first derivative of the Gaussian error function, namely the line spread function, was calculated. Subsequently, the absolute of the Fourier transform of the line spread function, namely the MTF, was computed. The spatial frequency $f_{10}$ at which the MTF falls below 10% was used to define the resolving power of the system. A characteristic length $l_0$ describing the maximum resolution is given by $l_0=1/(2f_{10})$. When the value of the MTF is still above 10% for the Nyquist frequency of the system, the measure is no longer well-defined and $f_{10}$ is substituted by the Nyquist frequency (i.e., the characteristic length is equal to the sampling distance of the system). This was the case for all presented results of the sphere data processed with the Richardson–Lucy algorithm.

Optimization of Velvet Worm Data.

To analyze the contrast and image sharpness of the nanoCT data from the velvet worm we imaged the ventrodistal region of the onychophoran limb. The data were acquired with an exposure time of 4 s, a source-to-rotation-axis distance of 0.94 mm, and a source-to-detector distance of 600 mm, resulting in an effective voxel size of 269 nm. The data revealed that this structure features a complex musculature filling most parts of its cavity (Fig. S2A). A virtual horizontal section through the ventral limb portion revealed three prominent muscles: the anterior and posterior leg depressor muscles, which run parallel to the anterior and posterior border of the leg, respectively, and the claw retractor muscle, which appears displaced anteriorly inside the leg (Fig. S2A). In addition to these muscles, a mass of oblique muscle fibers belonging to additional leg muscles (e.g., the anteroposterior septal muscle) is observed crossing the anteroposterior axis of the limb. Our nanoCT data further demonstrate that the mechanoreceptors covering the spinous pads are filled with a dense tissue, which possibly includes nerve fibers, epidermal cells, and a collagenous extracellular matrix (Fig. S2 E–H).

When reconstructing nanoCT data from projection images that are not further processed the resulting contrast modality is a combination of the conventional attenuation contrast and phase effects caused by Fresnel diffraction. Those effects can be exploited to improve the contrast in weakly absorbing samples by applying so-called phase-retrieval techniques (47). Even though the structures discussed above are distinguishable in the raw contrast data reconstructed with an FBP algorithm (Fig. S2 A and E) the images notably present a very pronounced level of noise. This situation could be improved by using an SIR algorithm (Fig. S2 B and F), which further allowed for an easier comparison between attenuation and phase data. A phase-retrieval algorithm applied to the projection images followed by reconstruction with a standard FBP algorithm diminished the noise, improved the contrast within the sample, and reduced the edge-enhancement effect that may negatively influence subsequent segmentation techniques (Fig. S2 C and G). However, fine structures such as thin muscle fibers became less evident due to the blurring effect resulting from the suppression of high spatial frequencies in the image by the phase-retrieval algorithm. This could be avoided by applying a deconvolution algorithm to the projections before phase retrieval and FBP reconstruction (Fig. S2 D and H). This approach substantially improved the image sharpness compared with the data processed only with the phase-retrieval algorithm, while still providing enhanced soft-tissue contrast and less edge enhancement compared with the attenuation images.

Acquisition and Data Analysis of the Contrast-to-Noise Ratio Measurement.

The analysis of the contrast-to-noise ratio (CNR) measurement included the following steps. We acquired four projection images of the resolution pattern at 60 kV with a source-to-sample distance of 0.57 mm and a source-to-detector distance of 1,680 mm, resulting in an effective pixel size of 58 nm. The acquisition times were 50, 120, 240, and 600 s, respectively. The images were normalized with a corresponding flat-field image. The mean value of the normalized transmission $M$ and the SD of the mean value $\sigma$ for two specific regions of each image were calculated. Subsequently, the following formula was applied to determine the corresponding CNR values:

$$CNR=\frac{\left|M_i-M_j\right|}{\sqrt{{\sigma }_i^2+{\sigma }_j^2}}.$$ [S1]

Since the X-ray camera of the nanoCT is a single-photon counting detector without dark-current and readout noise, the noise distribution was expected to follow Poisson statistics. Therefore, we fitted a square-root function (blue curve in Fig. S3E) to the determined CNR values (orange dots in Fig. S3E). From the found fit function we determined a scaling factor $k$ that is proportional to the photon flux per pixel for the applied acquisition parameters. According to the considerations above, the CNR value for a given relative contrast value $C_{rel}=(T_i-T_j)/T_i$ with $T_i\ge T_j$ can be estimated by

$$CNR(T_i,T_j,t)=k\frac{T_i-T_j}{\sqrt{T_i+T_j}}\sqrt{t},$$ [S2]

where $T_i$ and $T_j$ are the normalized transmission values for the respective attenuating structures, $t$ is the exposure time, and $k$ is the scaling factor. The exposure-time-dependent CNR functions for the relative contrast values of 20% and 30% (turquoise and pink curve in Fig. S3E) were calculated using Eq. S2.

Fig. S3.

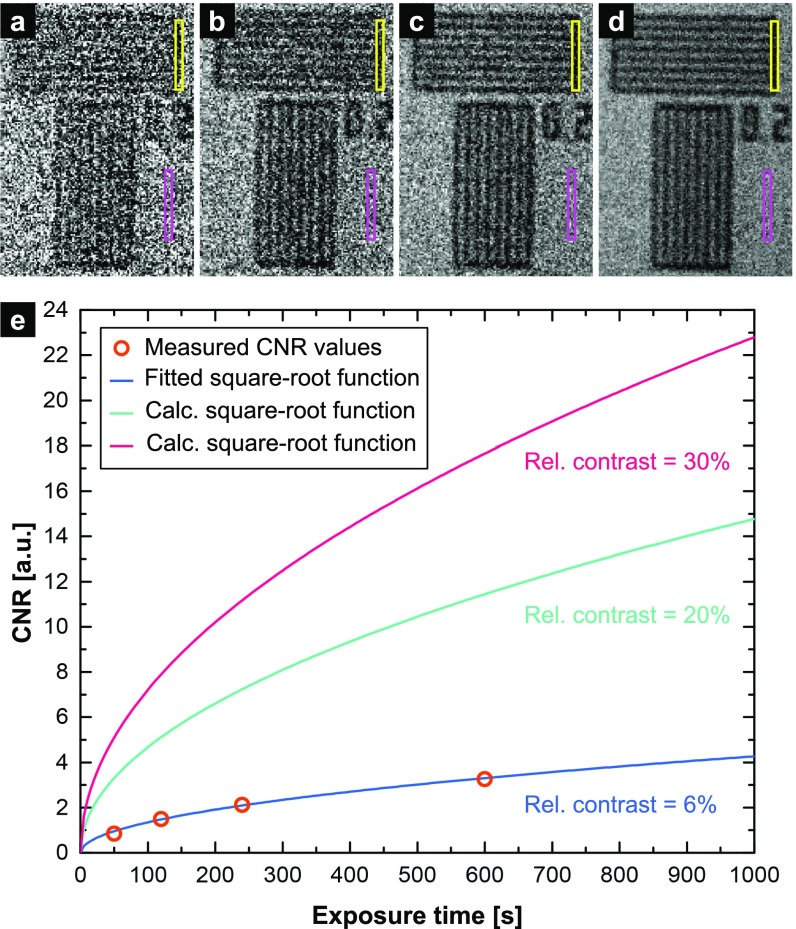
CNR as a function of exposure time. (A–D) Projection images of a resolution pattern with 200-nm lines and spaces acquired with exposure times of 50 s (A), 120 s (B), 240 s (C), and 600 s (D). The background of the images was corrected with a corresponding flat-field image, and no further processing steps were applied. The regions used for the calculation of the CNRs are indicated by the yellow and purple rectangles. (E) Diagram showing the CNR as a function of exposure time. A square-root function (blue curve) was fitted to the CNR values calculated from the regions in the resolution pattern images (orange dots). The relative contrast between the analyzed regions is 6%. The turquoise and pink curves represent exposure-time-dependent CNR functions for a relative contrast of 20% and 30%.

SI Results

Resolution of the NanoCT in 3D.

To substantiate the results of the 3D resolution measurement of the highly refracting glass microsphere we performed the edge profile analysis in $x$ and $y$ direction for 10 transversal slices close to the center of the sphere. In Table S1 the averaged values of the 10% MTF measure and the rmse of the regressions are displayed for the CT data of the unprocessed projections (FBP) as well as for the reconstructions of the projections processed with the Richardson–Lucy algorithm (RL & FBP). The results confirm that we can reach a 3D resolution of ∼100 nm with the presented nanoCT device.

Table S1.

Supporting results from the edge profile analysis of the 3D resolution measurement

Edge	Dataset	Average 10% MTF	Average rmse
Horizontal edge	FBP	4292	0.083
	RL & FBP	5102	0.136
Vertical edge	FBP	4238	0.077
	RL & FBP	5102	0.129

Average values of the 10% MTF measure and the rmse of the fitted edge profiles calculated from 10 transversal slices from the central region of the sphere.

CNR as a Function of Exposure Time.

To analyze the CNR of nanoCT data in dependence on the exposure time the CNR has been determined for flat-field corrected projection images of the resolution pattern acquired with varying exposure times (Fig. S3 A–D). The CNR values were calculated for the regions indicated by the yellow and purple rectangles in Fig. S3 A–D. Since the X-ray camera of the nanoCT is a single-photon counting detector without dark-current and readout noise, we expected the noise distribution to follow Poisson statistics. Therefore, we fitted a square-root function (blue curve in Fig. S3E) to the found CNR values (orange dots in Fig. S3E), which represents the exposure-time dependence of the determined CNR values very well. From the fit function we determined a scaling factor that is proportional to the photon flux per pixel for the applied acquisition parameters (e.g., the photon flux of the source, the air absorption for the used source-to-detector distance, and the detector efficiency for the respective X-ray spectrum). Note that the relative contrast between the background and the absorbing tungsten bars of the pattern is approximately 6%. To illustrate the exposure-time-dependent CNR progression for more strongly attenuating sample structures we calculated the CNR as a function of exposure time for a contrast of 20% (turquoise curve in Fig. S3E) and 30% (pink curve in Fig. S3E) relative to the background.

From the dose-fractionation theorem (48) it is given that the total dose required to achieve statistical significance for each voxel of a computed 3D reconstruction is the same as that required to obtain a single 2D image of the pixel at the same level of statistical significance. Consequently, the presented values for the exposure time required for achieving a particular CNR in a projection image are equal to the total exposure time required for a CT measurement. Note that the demonstrated results are valid for the maximum source-to-detector distance of our setup. Thus, for shorter source-to-detector distances the scaling factor for the square-root function is considerably higher, and the same CNR values can be reached with lower exposure times.