Limiting (zero-load) speed of the rotary motor of Escherichia coli is independent of the number of torque-generating units

Significance

Rotation of the bacterial flagellar motor is driven by multiple torque-generating units. The duty ratio of the units, defined as the fraction of time that a unit engages with the rotor, characterizes the torque-generating dynamics of the motor. Our data showed that the limiting speed of the motor is independent of the number of torque-generating units for the flagellar motor in Escherichia coli, demonstrating conclusively that the units have a duty ratio close to 1.

Abstract

Rotation of the bacterial flagellar motor is driven by multiple torque-generating units (stator elements). The torque-generating dynamics can be understood in terms of the “duty ratio” of the stator elements, that is, the fraction of time a stator element engages with the rotor during its mechanochemical cycle. The dependence of the limiting speed (zero-load speed) of the motor on the number of stator elements is the determining test of the duty ratio, which has been controversial experimentally and theoretically over the past decade. Here, we developed a method combining laser dark-field microscopy and optical trapping to resolve this controversy. We found that the zero-load speed is independent of the number of stator elements for the bacterial flagellar motor in Escherichia coli, demonstrating that these elements have a duty ratio close to 1.

Rotation of the bacterial flagellar motor in Escherichia coli is powered by a transmembrane proton flux (1) and driven by up to 11 torque-generating units (stators; for convenience, we refer to a torque-generating unit or to a stator element as a stator) working independent of one another (2, 3), each composed of four copies of the protein MotA and two copies of MotB (4). Protons flow through two channels, formed by the MotA and MotB proteins in each stator, driving conformational changes that exert forces on the periphery of the rotor (5). The duty ratio of the stators (D), defined as the fraction of time for which a stator engages with the rotor, characterizes the torque-generating dynamics of the rotary motor (6). The motor works against a viscous load and behaves differently at high or low loads (7). When the load is high, most of the mechanochemical cycle of a stator is spent on mechanically rotating the rotor and each stator has time to reach thermodynamic equilibrium; thus, the motor speed is proportional to the number of stators whether D is large or small. When the load is near zero, steps other than the mechanical rotation of the rotor, such as rates of proton translocation, are rate-limiting and any stator bound to the rotor limits its speed. Thus, the speed is proportional to the number of stators when D is very small and independent of the number of stators when D is 1. Therefore, the dependence of the zero-load speed on the number of stators is a crucial test of the duty ratio of the stators (6).

An early attempt at measuring this dependence was published by Ryu et al. (6) in 2000, when the torque-speed curves for motors with different numbers of stators ranging from one to five were measured. As it was impossible to directly measure the zero-load speeds in that study, the curves were extrapolated to zero load, predicting the zero-load speed to be nearly independent of the number of stators. However, there were substantial uncertainties due to the long-range extrapolation from the lowest load used in the study to zero load. Subsequently, a model of the motor dynamics was proposed by Xing et al. (8), which predicted that the zero-load speed decreases with the number of stators due to interference among stators. A method of directly measuring the zero-load speed was then developed by Yuan and Berg (9), and the zero-load speed was observed to jump from zero to a maximum value in a single step as stators were incorporated into the motor in a “resurrection” experiment, demonstrating that the zero-load speed is independent of the number of stators. The model proposed by Xing et al. was modified by incorporating the effect of compliance between each stator and the rigid framework of the cell wall, thereby reproducing the independence of zero-load speed on the number of stators (9, 10). An elegant model on the dynamics of the motor with multiple stators proposed by Meacci and Tu (11) also reproduced this independence. Recent experiments showed that the number of stators in the motor is load-dependent, with a very small number of stators engaged with the motor near zero load in a steady state (12, 13). This raised the question of whether the behavior in the resurrection experiment at zero load was observed only for motors with one or two stators. A recent study on the torque-speed curves for a chimeric sodium-driven motor hinted that the zero-load speed increases with the number of stators (14). A subsequent model suggesting low duty ratios for the stators was put forward, which reproduced the increase (15).

Results

To determine the dependence of zero-load speed on the number of stators for a flagellar motor in E. coli, the number of stators has to be measured. This is difficult with fluorescence labeling of stators as their number is small for motors at zero load, and the signal-to-background ratio is poor. We developed a method that combines laser dark-field microscopy and optical trapping to determine the number of stators for motors at zero load (Fig. 1), where a laser dark-field technique was used to measure the motor speed at zero load with nano-gold bead labeling of the motor hook, and the optical trap was used to hold and stick a 1-μm-sized latex bead to the gold bead to increase the motor load abruptly. Details of the setup are presented in Materials and Methods. Gold beads with a diameter of 100 nm were attached to the hook of the flagellar motors of an E. coli strain that lacks flagellar filaments. The zero-load speed of the motor was measured with laser dark-field microscopy by collecting the scattered light from the gold beads (9). A polystyrene latex bead with a diameter of 1 μm was held in the optical trap, and a cell with gold bead attached to the motor hook was brought up to the latex bead. The optical trap was turned off immediately when the latex bead touched and stuck to the gold bead. Rotation of the latex bead was observed continuously with bright-field microscopy. When the latex bead was attached, the load condition for the motor changed from zero load to high load. As the steady-state number of stators is larger for motors at high loads than for those at low loads (12, 13), more stators started to be incorporated into the motor after the latex bead was attached to the gold bead, and the motor speed measured from the rotation of the latex bead showed typical resurrection behavior at high load: stepwise increase of the motor speed in near-equal size (12). A typical example of the measurements with the number of stators started at two is shown in Fig. 2. The corresponding video recording is shown in Movie S1, along with more examples, with the number of stators starting at one to five (SI Appendix, Figs. S1–S22). The time between sticking the latex bead and the first measurement of the bead rotational speed was estimated to be less than 1 s, which is much less than the typical time it takes for the number of stators to change after the latex bead is attached (∼10 s, indicated by the stepwise changes in speed). From the initial speed immediately after the latex bead was attached and the step size per stator in the speed increment, we can determine the number of stators in the motor before the latex bead is attached (when the motor is at zero load). Different motors over a population of bacteria may have different numbers of stators at zero load. Therefore, the dependence of the zero-load speed on the number of stators can be determined from measurements performed on a population of motors. We would like to emphasize that the number of stators we measured are those that are docked and generate torque on the rotor during their mechanochemical cycle, not including those that might be close by but are resting and doing nothing.

Fig. 1.

Setup: a schematic diagram of the optical setup combining laser dark-field microscopy and optical trapping. Details about the setup are presented in Materials and Methods. CMOS, complementary metal-oxide semiconductor; DM, dichroic mirror; M, mirror.

Fig. 2.

Example of measurement showing the motor speed as a function of time. The motor speed at zero load was measured for ∼15 s, and a 1-μm-diameter latex bead was attached to the motor at a time of about 20 s, increasing the motor load abruptly. Subsequently, the motor speed increased stepwise (with the initial number of stators being two). The blue lines are the average speeds found by the step-finding algorithm. The red line is the average zero-load speed.

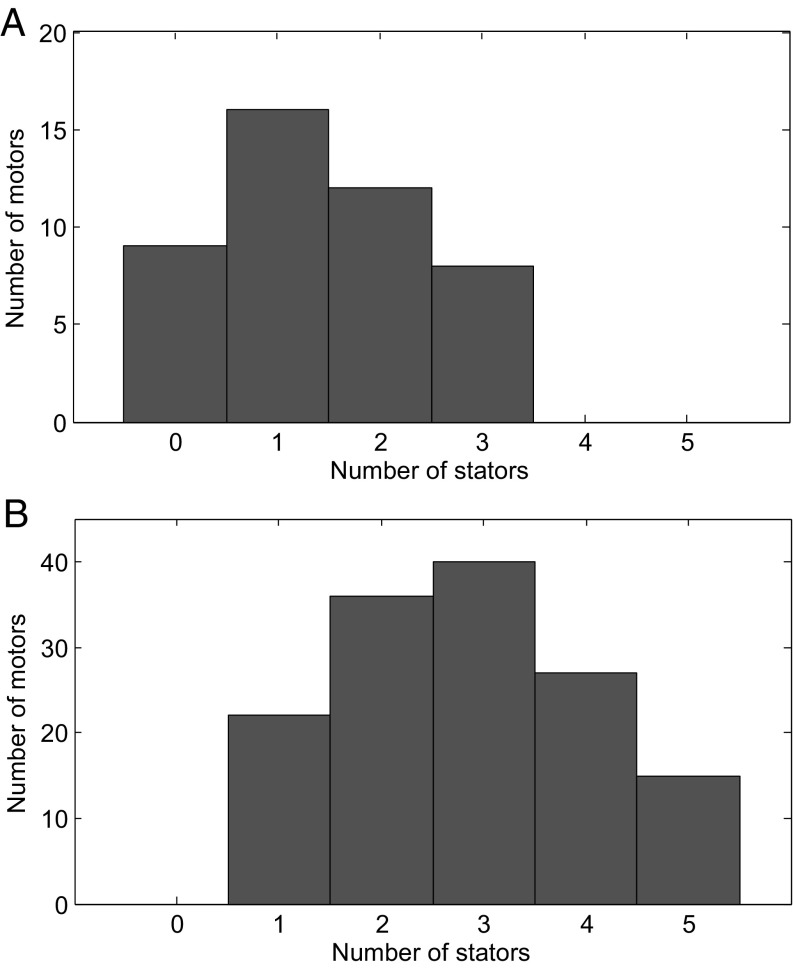
We first used the bead-addition technique to measure the steady-state number of stators for a population of wild-type E. coli motors at zero load. The distribution of the number of stators is shown in Fig. 3A. Of 36 motors observed, we found 16 of the motors with one stator engaged, 12 with two stators engaged, and 8 with three stators engaged. It is difficult to directly use the bead-addition technique to determine the number of motors with zero stators; instead, we observed the rotation of a population of wild-type motors with a 100-nm gold bead attached to the hook, finding 78 motors that rotated and 19 motors that did not rotate but exhibited normal Brownian diffusion. An example of the trajectory of a motor undergoing rotational Brownian diffusion, along with the mean-square angular displacement showing its linear dependence on time, is presented in SI Appendix, Fig. S23. Normalizing to the number of rotating motors (n = 36) we measured with the bead-addition technique, we rescaled the number of motors with zero stators to nine (19/78 × 36 = 9), to plot along with the result from the bead-addition technique in Fig. 3A. To get some information on the kinetics of stators coming on and off the motor, we monitored the zero-load speed of some motors for a longer time. We concentrated on those that showed speed fluctuations between zero and maximum speed (∼300 Hz), probably due to stators coming on and off the motor when the number of stators is mostly zero and one. The distributions of the zero-speed and maximum-speed intervals are shown in SI Appendix, Fig. S24. The distributions are nearly exponential, exhibiting the randomness of stators coming on and off the motor.

Fig. 3.

Distributions of the number of stators for the wild-type cells (A) and cells with overexpressed stator proteins (B). The number of motors with zero, one, two, and three stators are 9, 16, 12, and 8, respectively for the wild-type cells. The number of motors with one, two, three, four, and five stators are 22, 36, 40, 27, and 15, respectively, for the cells with overexpressed stator proteins.

From Fig. 3A, we concluded that motors at zero load with wild-type-level expression of stator proteins typically operate with a small number of stators. To obtain more measurements on motors with a higher number of stators, we introduced into the wild-type E. coli strain a plasmid that expresses the stator proteins (MotA and MotB) under an arabinose-inducible promoter (16). We overexpressed the stator proteins and performed measurements with the combined laser dark-field and optical trapping setup. Most of the motors have a steady-state number of stators less than six at zero load. The distribution of the number of stators for motors with overexpressed stator proteins is shown in Fig. 3B. Clearly, overexpressing the stator proteins increased the number of stators in the motor. Motors in the E. coli strain with a higher level of expression of the stator proteins showed similar zero-load speed and speed increment per stator at high load as the wild-type strain. The dependence of the zero-load speed on the number of stators is shown in Fig. 4 from measurements on 140 motors. The number of motors measured for each stator number are 22, 36, 40, 27, and 15 for one to five stators, respectively. Clearly, the zero-load speed is independent of the number of stators. We also calculated the average zero-load speeds for the 36 wild-type motors and the 140 motors with overexpressed stator proteins we observed before attaching the 1-μm latex bead. They were 284 ± 28 Hz and 286 ± 39 Hz (mean ± SD) for the wild-type and stator protein overexpressed motors, respectively, which provided indirect evidence that the zero-load speed is independent of the number of stators.

Fig. 4.

Zero-load motor speed as a function of the number of stators. The number of motors measured for each stator number are 22, 36, 40, 27, and 15 for one to five stators, respectively. Error bars are the SEM.

We considered a general argument for the motor dynamics at zero load. A stator at zero load works as fast as possible, as fast as protons can reach and bind to the critical aspartate residue and as fast as the changes in conformation that result from this binding and subsequent unbinding can occur (5). In other words, it works at its kinetic limit, reaching a minimum cycle time for the mechanochemical cycle. Additional stators work no faster. Thus, the motor does not speed up with the number of stators engaged with the rotor; that is, the instantaneous speed ω when N (≥1) stators are engaged is independent of N. Because the motor is rotating in a low Reynolds number environment, inertia can be neglected. The instantaneous speed is zero when no stator is engaged and ω when at least one stator is engaged. Stators are working independent of one another. For motors with N stators at zero load, and with a stator duty ratio of D, the motor net speed Ω is the sum of all possible cases with one, two, ..., or N stators engaged, with the same instantaneous speed ω for each case:

$$\mathrm{\Omega }={\displaystyle \sum _{\text{i}=1}^{\text{N}}{C}_{\text{N}}^{\text{i}}{D}^{\text{i}}{\left(1-D\right)}^{\text{N}-\text{i}}\omega }=\left[1-{\left(1-D\right)}^{\text{N}}\right]\omega ,$$

where C_Nⁱ is the binomial coefficient denoting the number of ways to pick i stators out of N stators to engage with the rotor, and C_NⁱDⁱ(1 − D)^N−i is the probability of i stators engaged with the rotor. Details of the derivation are provided in SI Appendix. Therefore, the zero-load speed is proportional to the fraction of time that at least one stator is engaged with the rotor (i.e., 1 minus the fraction of time that none of the N stators are engaged). We fit the data in Fig. 4 with the above equation. The fitted curve is shown in Fig. 5 (solid line), with a fitted value for D equal to 1.00 ± 0.05 and a fitted value for ω equal to 286 ± 6 Hz. Therefore, the duty ratio for the stators in the flagellar motor of E. coli is very high: D ≥ 0.95. Fig. 5 also shows the dependence of zero-load speed on the number of stators for different values of D using the above equation (dashed lines from top to bottom: D = 0.9, D = 0.7, and D = 0.5, respectively).

Fig. 5.

Dependence of zero-load speed on the number of stators. The data in Fig. 4 were fitted using the equation (1 − (1 − D)^N)ω, with D and ω as two fitting parameters. The result of fitting (solid line) for D is 1.00 ± 0.05, and for ω, it is 286 ± 6 Hz. The dashed curves show the dependence using the same equation with different values of D: 0.9, 0.7, and 0.5, respectively, from top to bottom.

Summary and Discussion

In summary, we developed a technique that combines laser dark-field microscopy and optical trapping, and showed conclusively the independence of zero-load speed on the number of stators, thus demonstrating a stator duty ratio close to 1 for the flagellar motor in E. coli. A recent study on the torque-speed curves for a chimeric sodium-driven motor hinted that the zero-load speed increases with the number of stators (14). One possibility is that the kinetics of the chimeric motor are different from the proton-driven motor in E. coli. Another possibility is that driving the rotation of a 100-nm gold sphere is not a near-zero load condition for the chimeric motor. A study comparing the torque-speed curves for the chimeric motor and the E. coli wild-type motor showed that the stall torques for the two motors are comparable but that the extrapolated zero-load speeds differ by more than threefold (about 1,000 Hz for the chimeric motor and 300 Hz for the E. coli motor) (17). Kinetic steps other than mechanical rotation of the rotor are more than threefold faster in the chimeric motor than in the E. coli motor, so it is possible that the mechanical rotation of the rotor still occupies a nonnegligible fraction of the mechanochemical cycle for the chimeric motor driving the rotation of a 100-nm gold sphere, which makes the cycle time for each stator dependent on the number of stators bound to the rotor (i.e., the speed depends on the number of stators).

We argued that the instantaneous motor speed ω when N stators are engaged does not increase with N, as each stator works at its kinetic limit. Our measurements actually not only showed that the duty ratio is high but also demonstrated that ω will not increase by the engaging of more stator units: Assuming that ω increases with N, the motor net speed Ω will increase with N no matter what the duty ratio is, which is in contradiction to our measurements. It was proposed in a model of the motor mechanism that ω may decrease with N due to interference among stators (8), but the compliance in the stator (especially the compliance in the linkage between the stator and the cell wall) was neglected in the model. By taking into account this compliance, the model was updated, suggesting ω is independent of N (9, 10).

The duty ratio was normally defined as the fraction of time for which a stator is bound to the rotor (6). In light of a recent model proposed by Oster and coworkers (18), where an electrosteric power-stroke mechanism for torque generation was suggested, we defined the duty ratio as the fraction of time for which a stator engages with the rotor. It was argued previously that the duty ratio must be close to 1 for motors under high load (1), by considering a tethered cell driven by a motor with a single stator: The cell would not spin due to unwinding of the tether if the duty ratio was not close to 1. A recent model accommodated this requirement (15), proposing that the duty ratio is high for motors under high load but low for motors under low load, thereby predicting that the zero-load speed would increase with the number of stators. Our measurements here showed that the zero-load speed is independent of the number of stators, thereby demonstrating that the duty ratio is also close to 1 for motors near zero load in E. coli.

Materials and Methods

Strains and Plasmids.

JY27 (ΔfliC cheY), a derivative of E. coli K12 strain RP437, was used for measurements on wild-type motors. JY27 transformed with the plasmid pJY7 was used for measurements on motors with overexpressed stator proteins. pJY7 expresses wild-type MotA and MotB under the control of an arabinose-inducible promoter in the vector pBAD33 (19).

Optics.

A schematic of the setup combining laser dark-field microscopy and optical trapping is shown in Fig. 1. Lights from two lasers (1,064 nm for optical trapping and 633 nm for laser dark-field microscopy) were introduced into a Nikon Ti-U inverted microscope through the rear port. The optical trap was constructed with a 1,064-nm fiber laser (AFL-1064-33-B-FA; Amonics), the light from which was expanded to a parallel beam with diameter of about 3.5 mm and focused to a diffraction-limited spot with an oil-immersion objective lens (OL; Nikon Plan Apo vc 100×/1.40 oil). The laser dark field was formed as follows: Light from a 633-nm He-Ne laser (10 mW; Thorlabs) was attenuated threefold and expanded into a parallel light beam about 7 mm in diameter, combined into the 1,064 nm light path with a dichroic mirror (ZT670-rdc; Chroma), reflected by a 50/50 beam splitter (BS; 21014; Chroma), and focused at the back focal plane of the OL using a plano convex lens (focal length = 400 mm; Thorlabs). The BS is 50/50 for 633-nm light, but 100% reflective for 1,064-nm light. The sample was illuminated with 633-nm light parallel to the optical axis. Background 633-nm light reflected by the sample was focused and blocked by a 1.5-mm-diameter beam block located in a plane conjugate to the objective back focal plane. Scattered 633-nm light from the gold sphere was collected using the same objective as for illumination, and after passing the 50/50 BS and the beam block, the ring of scattered light was imaged onto a high-speed complementary metal-oxide semiconductor camera (EoSens CL MC1362; Mikrotron). The light for bright-field microscopy was provided by a tungsten lamp illuminating the sample from right in Fig. 1.

Experimental Procedure.

Cells were grown at 33 °C in T-broth with the appropriate antibiotic (170 μg/mL chloramphenicol) and the inducer (100 μg/mL arabinose) to an OD₆₀₀ between 0.45 and 0.50, and were harvested by washing twice with motility medium (10 mM potassium phosphate, 0.1 mM EDTA, 10 mM lactate, and 70 mM NaCl at pH 7.0). Gold spheres 100 nm in diameter (15711; Ted Pella, Inc.) were attached to hooks of the washed cells with antihook antibody, following a procedure described previously (9).

A flow chamber was constructed by drilling two 0.75-mm-diameter holes through a glass slide which formed the inlet and outlet of the chamber, and a glass coverslip coated with poly-l-lysine (0.01%, P4707; Sigma) was then put over the slide using double-sided sticky tape (about 100 μm thick) cut in a ring shape as the spacer. The boundary of the chamber was sealed additionally with Apiezon vacuum grease. Labeled cells were stuck to the coverslip, and unstuck cells were washed away by flow of motility medium (100 μL⋅min⁻¹) using a syringe pump (Pump-22; Harvard Apparatus). The laser dark field was then turned on, and a gold sphere with a stable rotational trajectory was identified. A solution of 1.0-μm-diameter polystyrene latex beads (no. 07310; Polysciences) diluted to 0.0027% (wt/vol) in motility medium was drawn slowly into the flow chamber using the pump (50 μL⋅min⁻¹). The shutter for the 1,064-nm laser (200 mW) was then opened to capture a latex bead, and the light from 1,064-nm laser was attenuated 10-fold immediately after the capture to avoid possible damage to the cells. The rotation of the gold sphere identified earlier was measured for about 20 s, and the sample stage was then translated so that the antibody-coated gold sphere was moved close to and stuck to the captured latex bead (due to passive adsorption). The two lights for laser dark-field microscopy and optical trapping were immediately shut off, and the rotation of the latex bead was observed for several minutes with bright-field microscopy.

Data Analysis.

Data analysis was carried out using custom scripts in MATLAB (MathWorks). The fitting shown in Fig. 5 was performed using a nonlinear least squares method with the Levenberg–Marquardt algorithm in MATLAB. To obtain accurate motor speed, elliptical orbits of the beads were converted to circular orbits under the assumption that an elliptical orbit represents the projection of a circular orbit onto the focal plane of the microscope. The speed traces of the latex beads showed stepwise increments identical to those occurring in typical resurrection experiments with induced expression of stator proteins. Determination of the length and position of each segment of the speed step was carried out using a step-finding algorithm described previously (12). The step-finding algorithm was applied to the speed trace after the latex bead was attached. The number of stators in the first segment was determined by dividing the mean value of speed in this segment by the mean speed increment per stator in the subsequent steps. Including the slight effect of nonlinearity in the dependence of motor speed at high load on the number of stators did not change the results. The step sizes of speed increment per stator are fairly constant for each motor, with variations among different motors. The histogram of step sizes for all of the motors is presented in SI Appendix, Fig. S25.