Depolarization signatures map gold nanorods within biological tissue

Abstract

Owing to their electromagnetic properties, tunability and biocompatibility, gold nanorods (GNRs) are being investigated as multifunctional probes for a range of biomedical applications. However, detection beyond the reach of traditional fluorescence and two-photon approaches and quantitation of their concentration in biological tissue remain challenging tasks in microscopy. Here we show how the size and aspect ratio that impart GNRs with their plasmonic properties also make them a source of entropy. We report on how depolarization can be exploited as a strategy to visualize GNR diffusion and distribution in biologically relevant scenarios ex vivo, in vitro and in vivo. We identify a deterministic relation between depolarization and nanoparticle concentration. As a result, some of the most stringent experimental conditions can be relaxed, and susceptibility to artefacts is reduced, enabling microscopic and macroscopic applications.

Gold nanorods (GNRs) have demonstrated broad capabilities in science and medicine^1–15. Their ability to confine resonant photons with rapid dephasing yields optical properties for applications as molecular rulers^11–13, single molecule detection^14,15 and multifunctional probes for photo-activated drug delivery and cell injury in cancer therapy^3–8. Two photon processes^9,10 and dark field microscopy^16,17 allow single GNR detection, while nanoparticle distances less than 70 nm have been monitored based on frequency shifts from plasmon coupling effects¹¹. Such imaging methods redefine our understanding on a nanoscopic scale but the quantitation and comprehensive visualization of GNR distribution in biological samples, 3D tissues and in vivo remain challenging. Visualizing GNRs without the stringent requirement of thin and transparent samples or limitations from high photon densities and small fields of view would help to facilitate their diagnostic and therapeutic uses.

Due to GNRs having a high aspect ratio and a size much smaller than optical wavelengths, they permit electrons to move and oscillate more readily in response to incident radiation along their longitudinal axis. The resulting differential scattering cross-section makes each GNR an effective diattenuator (Figure 1a). Numerical analysis of scattering by single GNRs confirms a strongly polarization dependent scattering cross-section in the vicinity of their longitudinal resonance wavelength (Supplementary Figure S1a). Further experimental validation reports a high diattenuation coefficient of 0.75 near the longitudinal resonance of 10 × 81 nm sized GNRs (Supplementary Figure S1b). Uncontrolled and randomly orientated GNRs thus introduce a stochastic variation of states within an ensemble of particles, making GNRs a source of entropy and decoherence. Generally, this is an unwanted complication in the context of coherent imaging, and significant effort has sought to reduce its impact^18,19. Interestingly, probing polarization entropy provides information about a system that can be described by classical depolarization²⁰.

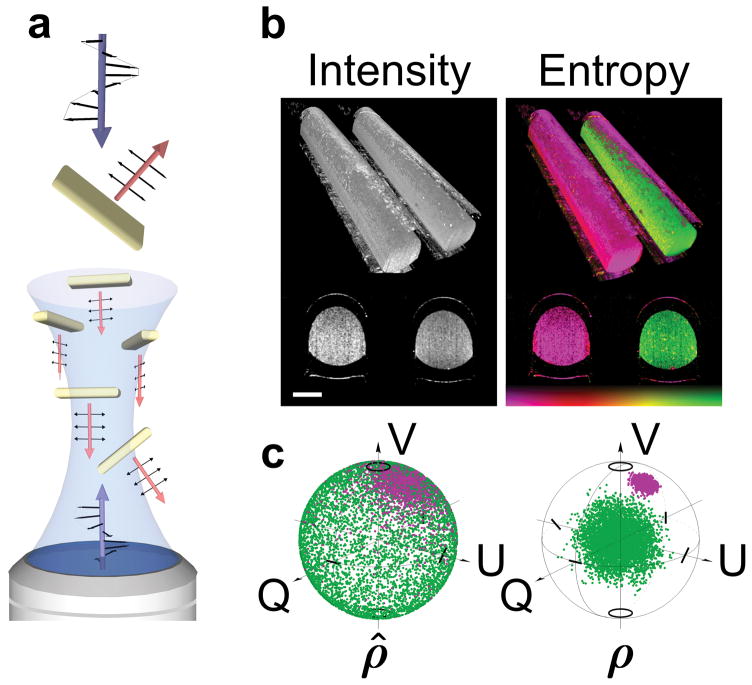
Figure 1. Gold nanorod diattenuation and entropy.

a, Schematic of the diattenuation of a single GNR and decoherence from an ensemble of GNRs. b, Rendered visualization of a volumetric image of two capillaries filled with GNRs (right capillary) and a non-depolarizing solution (intralipid, left capillary). High GNR entropy offers a signature to identify nanoparticle location. Scale bars, 500 μm. c, Poincaré spheres showing coherently detected pure states, ρ̂, and reconstructed mixed states using a density operator, ρ, for GNRs (green) and intralipid (purple). Colour bar represents entropy, 0 – 1.

Depolarization of light by anisotropic nanoparticles has been investigated in detail^21–24 but without exploring its use as a definitive GNR signature. Depolarization is an instantaneous process, allows fast acquisition and does not suffer from photobleaching, quenching or autofluorescence. Measuring depolarization does not require a pulsed laser or additional light sources and photon densities within safety limits of the human eye are sufficient. Depolarization from GNRs is readily tunable to longer wavelengths (beyond fluorescence and two-photon wavelengths) where scattering is significantly reduced and penetration depth enhanced.

Multiple scattering is a competing source of decoherence. To selectively detect GNR depolarization, we employ coherently gated detection to filter ballistic photons from a multiply scattered background^25–27 (Methods). Coherent systems detect the coherent superposition of the scattering contributions, always resulting in pure states ρ̂_s = |Ψ_s〉〈Ψ_s|. We probe the entropy of states from an ensemble (incoherent sum) of pure states of spatially varying coherence volumes (voxels), effectively rendering the imaging system partially coherent. The result is a mixed state, formally described by a density operator ρ = Σ_sp_s|Ψ_s〉〈Ψ_s|, where p_s is the occurrence of each pure state. This complex Hermitian matrix is equivalent to the coherency matrix and connects GNR entropy with depolarization by the eigenvalues of ρ (Supplementary Information). Figure 1b illustrates polarization entropy and provides an example of the signature obtained from GNRs. Figure 1c displays coherently detected pure states, ρ̂, and reconstructed mixed states, ρ, for GNRs (green) and a non-depolarizing target (purple).

Experimental observations emphasize a strong dependency of depolarization, Δ, on the input state (Figure 2a). Whereas Δ remains equally low for all linear states (blue points), it increases dramatically when converging to a circular state (red points), which is explained by the diattenuating property of GNRs. A probing linear state may align with either the long or short axis of the particle, resulting in the preservation or loss of these states, respectively. A circular state probes the GNRs with both linear bases concurrently, ensuring an alteration of the input state and equal scattering amplitude at any azimuthal particle orientation, thus leading to increased entropy. Maximum detection sensitivity is therefore realized with a circular polarization state. Moreover, any variation of the probing state during propagation inside the sample would result in a bias and underestimation of depolarization.

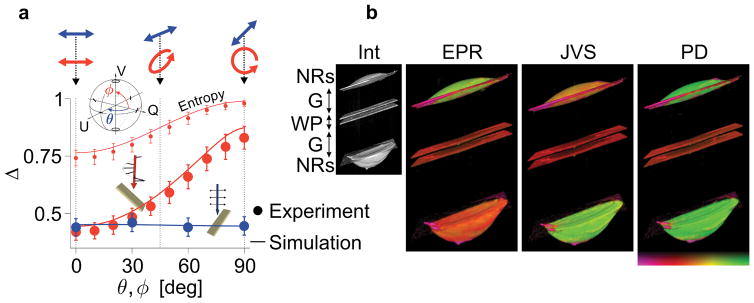
Figure 2. Definitive depolarization from gold nanorods.

a, Experimental and simulated depolarization (Δ) from GNRs for different input states. The inset illustrates the variation of input states on the Poincaré sphere. The polarization states were varied from linear horizontal to linear 45-deg polarization (θ, blue points) and from linear horizontal to circular polarization (ϕ, red points). Entropy is shown only for ϕ (red data set) for comparison. Error bars indicate standard deviation. b, Rendered visualization of volumetric images of a birefringent target made of a wave-plate (WP) and two drops of GNR solution (2 × 0.5 μL, 0.4 nM) at the front and back side of the plate. The small image shows the intensity-based image (Int). Three attempts at measuring definitive depolarization, using a single circular input state (EPR, Methods), Jones vector synthesis (JVS, Methods) and polar decomposition (PD, Supplementary Section II). Definitive depolarization and maximum detection sensitivity is only local for EPR and JVS. Polar decomposition offers maximum contrast and sensitivity, independent on the input state and object orientation, even for birefringent targets and at any depth location. Image dimension, 1.5 × 1.5 × 3 mm. Colour bar represents depolarization, 0 – 1.

This is illustrated in Figure 2b with a birefringent target consisting of GNR solution in front of and behind a wave-plate. Using a circular probing state results in high depolarization from superficial GNRs, but low depolarization from the GNRs behind the wave-plate, which rotates the polarization state of the probing light (EPR in Figure 2b, Methods). Many biological tissues exhibit birefringence, including muscle, collagen, and myelin, emphasizing the need for a definitive measure of depolarization, independent of the probing state. With an incident set of orthogonal states it is possible to retrospectively synthesize an optimum state and find maximum depolarization from GNRs (JVS in Figure 2b, Methods). The solution is expected to correspond to circular polarization behind the wave-plate, and accordingly compromises the depolarization of the superficial GNRs. To obtain definitive depolarization from GNRs, irrespective of birefringence and probing state, we extend the density matrix formalism and construct the Müller matrix corresponding to the mixed states ρ. We use polar decomposition²⁸ and eigenvalue decomposition to extract the principal depolarization factors and find the optimum state corresponding to strongest GNR depolarization independent of sample location (Supplementary Information). Indeed, this approach yields maximized and equal (i.e. definitive) depolarization from GNRs at the front and back interface of the wave-plate (PD in Figure 2b).

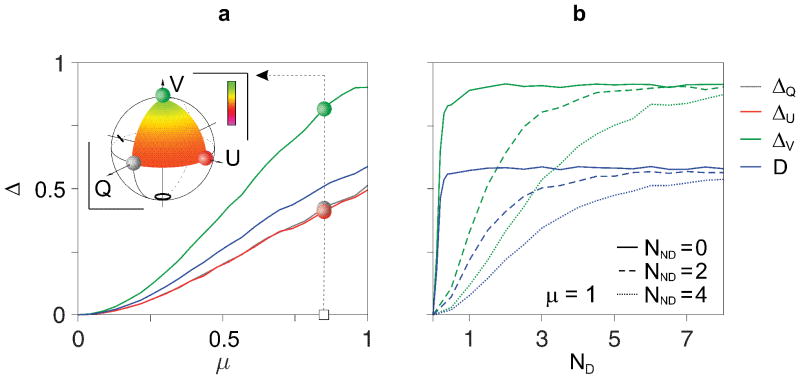
In Figure 3 we present numerical simulations of mixed states computed from coherent particle backscatter signals, confirming the dependency of depolarization on input states and that maximum depolarization is found in the case of circular polarization (Δ_V in Figure 3a). Depolarization quickly increases with diattenuation (Figure 3a) and plateaus for approximately 2 independently oriented particles per coherence volume (N_D) (Figure 3b). Importantly, the presence of polarization-maintaining scatterers (having density N_ND) results in a more traceable mapping of depolarization to GNR concentration.

Figure 3. Depolarization characteristics of diattenuating gold nanorods.

Numerical simulations show depolarization of mixed states consisting of coherently detected scatter signals. a, Depolarization increases with increasing diattenuation, μ, and yields a dependency on the input states. Δ_Q, Δ_U, Δ_V represent depolarization for horizontal, 45-deg and circular input polarization, respectively, while depolarization power (D) corresponds to the average of principle depolarization factors. The inset shows depolarization for a continuum of probing states on the Poincaré sphere for μ = 0.85. Colour bar represents depolarization, 0 – 1. b, Simulated depolarization for mixtures of depolarizing scatterers, N_D, and non-depolarizing scatterers, N_ND. Depolarization reaches a maximum for approximately 2 scatterers per volume. Non-depolarizing scattering biases the depolarization from GNRs and restores sensitivity (dynamic range) to higher GNR concentrations, preventing a premature depolarization maximum.

In practice, GNR aggregation may impair independent nanoparticle orientation. Although GNR aggregation alters depolarization properties, experiments confirmed that significant aggregation still provides a clear depolarization signal (Supplementary Figure S3). This suggests that depolarization, which depends on the GNR differential cross-section, may be more robust to GNR aggregation than techniques that rely on a specific surface plasmon resonance.

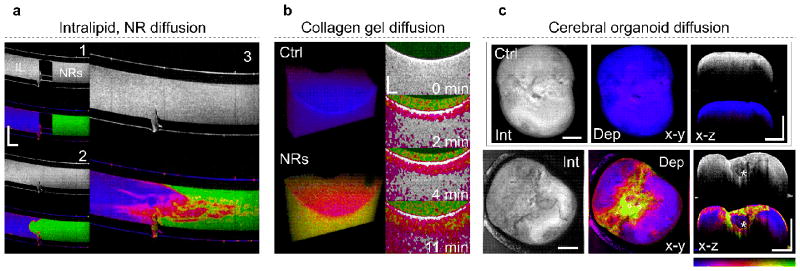
To demonstrate the benefit of definitive depolarization as a GNR signature we conducted a series of clinically and biologically relevant experiments. Techniques that quantify diffusion can give valuable insight into the viscoelastic properties of a medium. Figure 3a shows the mixing of nonpolar bonding intralipid (left) and polar bonding phosphate-buffered saline solution with GNRs (right) in a capillary. Depolarization clearly details intermediate stages of mixing that are indistinguishable by scatting intensity. Figure 4b utilizes collagen gel as a model for GNR transport into 3D biological environments. Depolarization reveals GNR gradients in real-time as they passively diffuse into the collagen over time. In another experiment, we evaluated definitive depolarization of GNRs in cerebral organoids, which simulate micro-anatomy and create cellular models of human disease²⁹. Depolarization from GNRs, passivated with polyethylene glycol (PEG-GNR) to ensure biocompatibility, reveals region-specific PEG-GNR accumulation that highlights tissue microarchitecture. Figure 4c displays distinct regions of increased PEG-GNR penetration, pointing to low cell density, that surround a denser core (white asterisk). Definitive depolarization from GNRs offers a promising tool to visualize heterogeneity and density of micromorphology, and may offer a new avenue to optimize the growing process and subsequent application of refractive index matching and tissue clearing³⁰ (Figure 4c).

Figure 4. Gold nanorod diffusion.

a, Depth resolved slices (x–z) of intensity and depolarization showing diffusion of GNRs suspended in saline (right) with intralipid (left). While the intensity image exhibits a uniform grey level, depolarization allows the assessment of different mixing stages. b, Three-dimensional view and depth resolved slices (x–z) showing PEG-GNRs in collagen gel. The three-dimensional views depict the depolarization of collagen gel (15 % collagen) without (control) and mixed with PEG-GNRs. The depth resolved slices (x–z) illustrate diffusion of PEG-GNRs into the collagen gel sample over a time span of 11 minutes, at 87 μm per minute. The images display intensity overlaid with depolarization. Depolarization < 0.2 was disregarded, corresponding to regions with no GNR diffusion. c, Volumetric projections (x–y) and depth resolved slices (x–z) of cerebral organoids in vitro after incubation with 18 nM PEG-GNRs for 1 hour. Exogenous contrast by GNRs highlights regions of varying tissue density and heterogeneity. Colour bar represents depolarization, 0 – 1. Scale bars, 1 mm (a,c), 500 μm (b). Supplementary Figure S8, Supplementary Media 1,2.

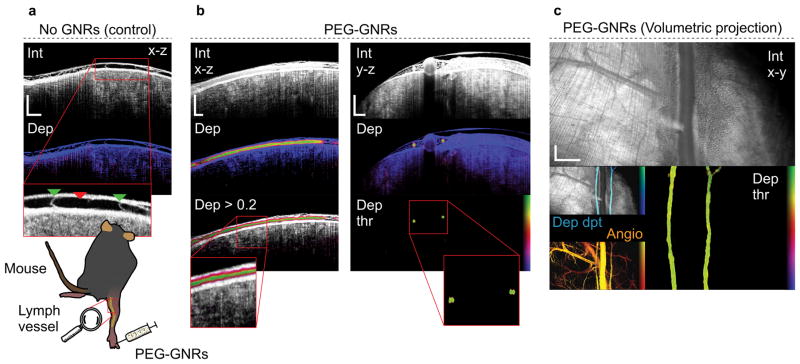
To validate depolarization from GNRs under more realistic biological conditions, we imaged passive accumulation of GNRs in the lymphatics of the hind limb of mice in vivo. Without exogenous contrast, assessment of the lymphatic system has proven extremely challenging using intensity as lymph yields signals near the noise floor of the instrument. Careful alignment reveals the lymph vessel as a region void of appreciable signal (Figure 5a). A magnified view emphasizes the vessel (red triangle) and vessel valves (green triangle). The depolarization signature clearly outlines the lymphatic vasculature after GNR injection into the foot improving their visualization (Figure 5b,c). Imaging lymphatic vessels and lymph nodes in vivo using antibody conjugated GNRs may enable new studies of disease progression. Figure 5c demonstrates projections over all depths, presenting morphological and functional details of entire volumes. Angiography confirms the location of the lymphatics (Angio in Figure 5c), albeit being sensitive to motion, it also highlights blood vessels (Supplementary Figure S9). Moreover, the GNR uptake in inguinal lymph nodes was investigated (Supplementary Figure S10). Sentinel lymph nodes are the first draining nodes that are reached by metastatic cancer cells. An exogenous depolarization signature from cancer cell conjugated GNRs could generate new multifunctional probes and may delineate morphological structures that are not recognizable with intrinsic backscattering. Indeed, GNR imaging in inguinal lymph nodes demonstrated depolarizing areas in the subcapsular sinus, 72 hours postinjection.

Figure 5. Gold nanorod transport in mouse lymphatic vessel (in vivo).

a, Control measurement showing depth resolved view (x–z) of intensity and depolarization. The lymph vessel (red triangle) and vessel valves (green triangles) are highlighted in the magnified view. b,c, Mouse lymphatic vessel after injecting 10 μL of 36 nM PEG-GNRs into the foot. Imaging was performed 2 minutes postinjection. b, Depth-resolved views (x–z and y–z) showing intensity and depolarization. The lymphatic vessel is outlined in the depolarization view. c, Volumetric projections (x–y) over all depths showing intensity (Int), depolarization > 0.3 (Dep thr), intensity overlaid with depth-encoded depolarization (Dep dpt) and angiography (Angio). Depth-encoded depolarization (Dep dpt) displays superficial regions as bright blue and deeper regions of depolarization as dark blue. Depth span, 1.2 mm. Angiography (Angio) is displayed for comparison. The angiogram (Angio) contrasts moving scatterers (flow) from a static background. Superficial vessels are presented in yellow and deeper vessels are presented in red. Depth span, 1.5 mm. Scale bars, 500 μm (a,b), 1 mm (c). Supplementary Media 3.

When GNRs are injected into biological tissue, susceptibility to polarization-maintaining scattering becomes relevant. Non-depolarized scattering prevents an early saturation of the depolarization with increasing GNR concentration, defining a nonlinear dependency between depolarization and GNR concentration (Figure 3b). This is confirmed experimentally by utilizing GNRs mixed with non-perturbing scatterers, i.e. intralipid (IL) (Figure 6a). Depolarization decreases and intensity increases with growing polarization-maintaining scattering. The contribution of the GNR backscattering to total intensity becomes negligible with increasing IL concentration. However, the combined effect of polarization-maintaining scattering and GNRs renders the system sensitive to low GNR concentrations that would fail to generate sufficient backscatter intensity otherwise (green curve). We identified an analytic model that explains the observed depolarization dependency on both depolarizing and polarization-maintaining scattering and that enabled us to recover GNR concentration (Figure 6b, Supplementary Information).

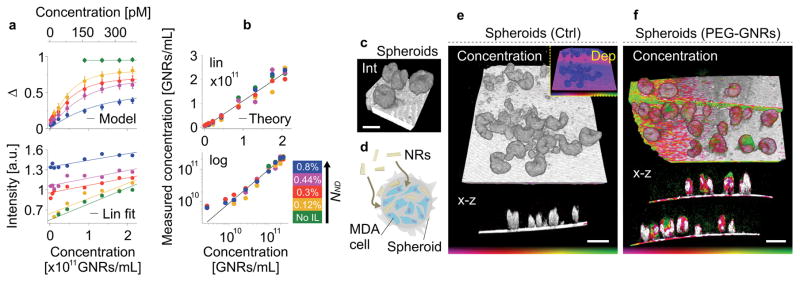
Figure 6. Gold nanorod penetration and concentration in metastatic spheroids (in vitro).

a, Experimental depolarization and normalized backscattering intensity for various GNR mixtures. The dependency of depolarization on GNR concentration increases with increasing non-depolarizing scattering (IL). The depolarization measurements are fitted using the analytical model (Supplementary Section IV). b, Reconstructed GNR concentration for different set concentrations using the analytical approach, taking into account depolarizing and backscattering intensity (i.e. depolarizing and non-depolarizing scatterers) (Supplementary Section IV). c, Three-dimensional intensity image of cancer cell spheroids made of a MDA-MB-435 cancer cell line. d, Schematic of 10 × 80 nm PEG-GNRs entering a spheroid and accumulating in the interstitial spaces. e, Control measurement showing the intensity overlaid with reconstructed GNR concentration of cancer cell spheroids in a three-dimensional and depth-resolved (x–z) view, respectively. The inset displays depolarization. f, Three-dimensional and depth-resolved (x–z) views showing the reconstructed GNR concentration after 12 hours of incubation with 1 nM PEG-GNRs. Due to the GNR size, particle penetration is limited and mostly unnoticeable, presenting a mean concentration of 2.4 × 10¹⁰ GNRs/mL (40 pM) in the penetrated regions. Colour bar represents depolarization, 0 – 1 (e, inset) and GNR concentration, 9 × 10⁹ - 6 × 10¹⁰ GNRs/mL (15 – 100 pM) (e,f). Scale bar, 250 μm (c), 500 μm (e,f).

We compared the depolarization measurements with two-photon luminescence (TPL) microscopy and confocal detection of fluorescently labelled GNRs for a wide range of GNR concentrations (Supplementary Figure S4a,b). The detection dynamic range and detection limit of depolarization are comparable with those of fluorescence and TPL, albeit without being subject to experimental inaccuracies in the preparation of fluorescently labelled GNRs or photobleaching. We determined qualitative and quantitative detection limits of 2.4 × 10⁹ GNR/mL (4 pM) and 9 × 10⁹ GNRs/mL (15 pM), respectively. Furthermore, fluorescent GNRs were added to PFA-fixed cerebral organoids, demonstrating enhanced imaging depth and imaging speed for a coherently gated depolarization signature compared to confocal fluorescence detection (Supplementary Figure S4c–g). Because the fluorescence and TPL signals are directly proportional to concentration (GNRs, fluorophores) and excitation power, they are affected by scattering and absorption. They exponentially decrease with depth, even if the GNR concentration remains constant. Unlike fluorescence and TPL, depolarization provides a metric that is largely independent of optical power, attenuation and hence depth (Supplementary Figure S5).

We applied the analytical approach in vitro to investigate PEG-GNR penetration and concentration in cancer cell spheroids. Spheroids are routinely used to screen the transport and biological interactions of nanomaterials in 3D cellular environments³¹ (Figure 6c–f). PEG-GNR accumulation occurred predominantly at the spheroid surface with localized permeable regions showing an average concentration of 2.4 × 10¹⁰ GNRs/mL (40 pM). Penetration and concentration inside spheroids was limited, consistent with previous findings demonstrating the restricted penetration of nanoparticles > 70 nm in MDA-MB-435 cell spheroids and tumors³¹.

Diattenuating GNRs are a source of entropy, a phenomenon that we exploit as an imaging signature. A key to our approach is describing the statistics of pure states from spatially varying coherence volumes by the density matrix of a mixed state and using polar decomposition of corresponding Müller matrices for an unambiguous (definitive) measurement of depolarization. Our findings provide experimental evidence of definitive depolarization as a contrast mechanism to visualize GNR distribution, diffusion and concentration in biological specimens and in mice in vivo. GNR depolarization offers comprehensive imaging over large fields of view and at imaging depths up to 2 mm, exceeding the limitations of conventional fluorescence and TPL microscopy. This offers new avenues for GNRs as carriers or therapeutic agents. Antibody conjugated GNRs could serve as imaging labels for coherent imaging with molecular specificity. Unlike confocal or two-photon microscopy, coherent imaging can be readily implemented into minimally invasive, flexible catheters. This extends GNR depolarization to tubular and deeper lying organs, offering new opportunities for imaging the urinary and gastrointestinal tracts, the lung, or the vasculature in vivo^32,33. In cerebral organoids, the GNR depolarization signature likely reflects growth and reorganization of different cell types. Visualizing heterogeneity in cancer cell spheroids may ultimately correlate with clonal outgrowths. The ability to observe the subcapsular sinus, for example, has strong research and clinical importance as it is the most likely location where the earliest manifestations of metastatic carcinoma in a lymph node might be found, as well as the site of arrival of antigen critical to stimulating immune responses.

METHODS

Experimental set-up

The experimental set-up is illustrated in Supplementary Figure S7. Optical frequency domain imaging (OFDI), also known as coherent optical frequency domain reflectometry (C-OFDR) in fibre optics, utilized a custom-built frequency-swept external cavity laser in a Littman-Metcalf configuration^25–27. Light emitted from the laser had a linewidth of 34 GHz and was swept at a repetition rate of 50 kHz over a bandwidth of 20 THz at the fibre zero dispersion wavelength of 1.3 μm. An interferometer directed light to an object of interest through one path, while providing a local oscillator through the other. Light was split into orthogonal polarization states by a polarizing beam splitter. The linearly polarized basis vectors were frequency shifted by ± 25 MHz, respectively, before being recombined using another polarizing beam splitter, while the local oscillator was shifted by 50 MHz using acousto-optic modulators (AOM). This resulted in a heterodyne measurement at two beat frequencies (f₁ = 25 MHz, f₂ = 75 MHz) carrying the weakly backscattered signal for the two incident principle states. The depth information had a frequency range depending on the optical path difference of a scatterer, centred about f_1,2. The output was projected on two orthogonal polarization channels. Using the relative phase enabled retrieval of the Jones vector corresponding to the scattered field. Moreover, the linearly independent illumination states (linear basis) cast the Jones matrix for all depths from a single wavelength sweep. A depth-resolved cross-sectional image was acquired in 20 ms, while a volumetric measurement took 20 s. The lateral resolution was 22 μm and the axial resolution was 6 μm in tissue. The propagation of states from the frequency multiplexing unit to the object and output is described by Ψ(z) = CB^TO(z)^TO(z)BAI, where I is the identity matrix corresponding to the linearly polarized basis of two orthogonal states. A is a fiber transformation matrix from the multiplexing unit to the fibre coupler, B is the Jones matrix from the fibre coupler to the object, O is the transformation through an object to a depth z and C describes a transformation from the fibre coupler to the output. The columns of the measurement matrix Ψ provide two pure states, |Ψ_1,2〉. Single-mode fibre was assumed free of diattenuation and polarization mode dispersion (< 0.5-radians across the 20 THz bandwidth). The matrices A, B and C thus describe general unitary transformations without polarizing or depolarizing behaviour and any statistical variation of pure states in Ψ is solely caused by O. For a detailed description of definitive depolarization measurements see Supplementary Information.

Diattenuation measurements

Diattenuation and diattenuation variance were calculated from the eigenvalues, v_1,2, of the diagonalized measurement matrix Ψ as μ(z) = (|v₁|² − |v₂|²)/(|v₁|² + |v₂|²). Please refer to Supplementary Information for more details.

Angiography

Angiography was used comparison³⁴. We analysed time-varying speckle to separate flow from a static background. Intensity measurements at the same object coordinates, temporally separated by one cross-sectional tomogram (1024 wavelength scans), were compared to evaluate speckle variance as $I_{SV}=\frac{1}{N}{\sum }_{i=1}^N{\left(I_i-\frac{1}{N}{\sum }_{i=1}^N{I}_i\right)}^2$, where N is the number of time varying intensity measurements, I.

Retardation measurements

The local Jones matrix was obtained from two cumulative Jones matrices separated by a depth increment dz, with Ψ(z + dz) = CB^TO(z)^Tm(dz)^Tm(dz)O(z)BAI. The matrix transformation governed by dz is thus Ψ(z + dz)Ψ(z)⁻¹ = Qm(dz)^Tm(dz)Q⁻¹, where Q = CB^TO(z)^T. This is a similarity transformation by Q with members in SU(2) for biological tissue that merely map rotations in SO(3) (rotations in a Poincaré sphere), thus Q has no impact on the retardation of the local Jones matrix. Local retardation, δ, was calculated from the phase difference between eigenvalues, v_1,2, of the measurement matrix Ψ(z + dz)Ψ(z)⁻¹ after matrix diagonalization, δ = arg(v₁) – arg(v₂).

Numerical simulation of depolarization from nanorods

Our experimental observations of diattenuation-mediated decoherence from nanoparticles were modelled with a uniform distribution of random scatterers in the frequency-domain. An ensemble of scatterers was given a diattenuation coefficient, μ, at uniformly distributed, linear diattenuation axes. The model was probed with a linearly polarized basis as was the case in our experimental configuration. The simulation takes into account a vertical cross-section, ignoring the second lateral dimension. The simulated sample, covering an ensemble of distributed diattenuating scatterers, spanned 500 μm in the lateral and axial directions, with a resolution of 8 μm in both dimensions after two-dimensional Fourier transform.

$$\left[\begin{array}{cc}{\psi }_{1x}& {\psi }_{2x}\\ {\psi }_{1y}& {\psi }_{2y}\end{array}\right]=\int {\int }_{-\infty }^{\infty }\left(\sum _{n=1}^{N_{ND}}{e}^{i2\pi x_n\stackrel{\sim }{x}}{e}^{i2z_{n}k}\mathit{I}+\sum _{n=1}^{N_D}{e}^{i2\pi x_n\stackrel{\sim }{x}}{e}^{i2z_{n}k}{\mathit{P}}_{\gamma }\left[\begin{array}{cc}1+\mu & 0\\ 0& 1-\mu \end{array}\right]{\mathit{P}}_{\gamma }^{-1}\mathit{I}\right)e^{i2(\pi x\stackrel{\sim }{x}+zk)}d\stackrel{\sim }{x}dk$$ (1)

The first term on the right hand side of Equation 1 represents an ensemble of N_ND non-diattenuating scatterers and the second term represents N_D diattenuating scatterers, all uniformly distributed in spatial frequency x̃ (lateral location) and fringe modulation frequency of optical path length 2z_n along a wave vector k. For convenience, the unit for the number of particles was normalized to source coherence length, δz. P_γ is a rotation matrix considering a diattenuation axis orientation γ and I is the identity matrix representing a linearly polarized basis of two incident states. The model assumes a constant average scattering cross section for the diattenuating, N_D, and non-diattenuating, N_ND, particles equally. The columns of the output of Equation 1 yield two pure states, |Ψ_1,2〉, that have some probability distribution for diattenuating scatterers and are deterministic for non-diattenuating scatterers. Diattenuation and diattenuation variance was extracted from the eigenvalues, v_1,2, of the diagonalizable output matrix in Equation 1 as μ = (|v₁|² − |v₂|²)/(|v₁|² + |v₂|²). Mixed states were described by a distribution of pure states from either |Ψ₁〉 or |Ψ₂〉, where entropy and depolarization was obtained from the eigenvalues of the density operator ρ. Alternatively, depolarization was calculated in SO(3,1). Moreover, the Jones matrix given by the output of Equation 1 can be represented by a Müller-Jones matrix. Similar to the coherency matrix that conveniently describes an ensemble of pure states, a statistical ensemble of spatially varying Müller-Jones matrices leads to a general Müller matrix. It is used to calculate depolarization power, D, as an unambiguous measure of depolarization for comparison. Please refer to Supplementary Information for more details.

Eigenpolarization referencing (EPR)

A circular state at the object is desirable as it yields highest entropy from GNRs. After propagation in a single-mode fibre, the polarization state at the fibre output (at the object) is unknown due to fibre birefringence³⁵. The polarization state can be referenced remotely to the eigenvectors (eigenpolarization) of a birefringent medium. The concept of EPR is shown in Supplementary Figure S7. Before illuminating the object, a small portion of the radiation was mixed with the local oscillator (blue circle), while another small portion was phase shifted by a quarter-wave plate (QWP1) before mixing with the local oscillator at a slightly different optical path length (red triangle). Using a polarization controller, we selected the polarization state at the fibre tip so that both states were the same on the Poincaré sphere, thus referencing the polarization state to the optic axis (eigenstate) of the wave plate. Any linear state could be obtained with 90-deg ambiguity in Jones space by adjusting the fast optic axis of QWP1 (Figure 2a). Circular polarization was obtained by inserting a second quarter-wave plate (QWP2) with a relative orientation at 45-deg with respect to QWP1 (Figure 2b, EPR). Any elliptical state could be obtained by adjusting the fast optic axis of QWP2 between a differential adjustment of 0-deg and 45-deg (Figure 2a).

Jones vector synthesis (JVS)

The experimental configuration provided two polarization states orthogonal in Jones space, |Ψ_1,2〉. This offered a set of linearly independent basis vectors that uniquely expressed other states as a linear combination in the vector space. We applied this property to numerically express an optimized state at the object, e.g. horizontal |Ψ₁〉, vertical |Ψ₂〉, 45-deg |Ψ₁〉 ± |Ψ₂〉 and circular polarization |Ψ₁〉 ± i|Ψ₂〉, where the orientation of |Ψ₁〉 was used as a reference frame for convenience. A general form of an optimum state can be written as |Ψ_opt〉 = κ|Ψ₁〉 + |Ψ₂〉e^iφ, where 0 ≤ κ ≤ 1 is a scaling factor and 0 ≤ φ ≤ π/2 describes a phase delay.

Nanorod preparation

We used gold nanorods (GNRs) with a surface plasmon resonance (SPR) at 1200 nm (A12-10-1200) or 1064 nm (A12-10-1064) (Nanopartz Inc.). The GNRs had an aspect ratio of 8.1 (10 × 81 nm) and 6.7 (10 × 67 nm), respectively (Supplementary Figure S6). The GNR solution was warmed to room temperature to dissolve CTAB crystals and a working volume was collected then centrifuged for 10 min at 5000g. The GNRs were resuspended in a wash solution (0.01% sodium citrate tribasic + 0.01% Tween-20) at half the original volume. Thiol-terminated methoxy polyethylene glycol 5 kDa (PEG) was added from a stock solution to achieve a final concentration of 1 mM and incubated for 1h at 60°C. During this incubation the thiol groups formed a gold-sulfur semi-covalent bond and covered the GNR surface with a self-assembled monolayer. The prepared solutions were cooled to room temperature, centrifuged and washed three times to remove unbound PEG. PEG-coated GNRs were resuspended in phosphate-buffered saline (PBS) then added to appropriate cell culture medium during experiments with collagen, spheroids and organoids. PEG-GNRs were resuspended in PBS for dilution. PBS is transparent at a wavelength of 1.3 μm and showed no depolarization or scattering. The measured GNR depolarization was the same for CTAB-GNRs (Supplementary Figure S6b, aspect ratio 8.1) and PEG-GNRs (Supplementary Figure S3d, CTL), indicating that neither CTAB nor PEG influence depolarization. 10 × 81 nm GNRs were used for all experiments expect for lymph node experiments that used 10 × 67 nm GNRs.

Gold nanorod aggregates

GNR aggregates were generated by addition of NaCl to thrice washed GNRs. At high enough concentrations, Cl⁻ anions can neutralize positive charges of remaining CTAB on the GNR surface. Van der Waals attractive forces causes GNR aggregation over time. After exposure to 1M NaCl for 15 min, methyl-terminated SH-PEG-5k was added to stabilize aggregates at an excess of 20 molecules per nm². Samples were then analysed by spectrometry or microscopy. (Supplementary Information)

Fluorescent gold nanorods

GNRs were washed by centrifugation (5,000g for 15 min) in wash buffer (0.01% sodium citrate + 0.05% Tween-20) then functionalized with a molar excess of thiolated PEG molecules (20 per nm²). For fluorescent GNRs, we used a proportion of 85% methyl-terminated SH-PEG-5k and 15% amine-terminated SH-PEG-5k. GNRs were incubated with PEG in wash buffer at RT overnight, then washed three times at 10,000g for 10 min. Fluorescent GNRs were then resuspended in 200 mM sodium bicarbonate buffer (pH 8.3) and reacted with an excess of amine-reactive AlexaFluor594-NHS ester (10,000 fluorophores per nm²). Fluorescent GNRs were washed 3 times by centrifugation and resuspended in a final volume of PBS. (Supplementary Information)

Spheroid preparation

Spheroids were prepared using the MDA-MB-435 cancer metastatic cell line. Cells were cultured in DMEM media supplemented with 10% fetal-bovine serum (FBS) and penicillin-streptomycin (Life Technologies). Cells were grown in monolayers and collected by exposure to 0.05% trypsin solution (Life Technologies). Round-bottom, 96-well plates were coated with a solution of 2.5% Poly 2-hydroxyethyl methacrylate (Sigma) in 95% ethanol for 24h at 37°C. 10,000 cells were seeded in each well and centrifuged at 500g for 10 min at 4°C. The cells formed a pellet at the bottom of the round-bottom wells and were left to grow for 3–7 days. During this culture period, the cells produced some extracellular matrix and formed cell-cell interactions leading to the formation of 3D spheroids with a diameter of approximately 300 μm. The cell spheroids were collected, left to settle at the bottom of a conical plastic tube and resuspended in culture medium. The spheroids were incubated with 1 nM PEG-GNRs for 12 hours before imaging.

Organoid preparation

Cerebral organoids were made from stem cells following a previously described protocol²⁹. Organoids were cultured for 50 days then fixed in 4% PFA overnight at 4°C, washed with PBS 3 times then exposed to PEG-GNR for 1 hour. Organoids were incubated with 18 nM PEG-GNRs for 1 hour prior to imaging.

Animal preparation

Experiments were conducted in the hind limb of 10 weeks old C3H male mice (26–36 g). Mice were anesthetized using a Ketamine/Xylazine 10 mg/1 mg per kg body weight and the surgical procedure was performed according to Liao et al.³⁶. Tissue was hydrated using physiological saline. Mice were euthanized at the conclusion of the experiments. 10 μL of 36 nM PEG-GNRs were injected into the foot and in vivo imaging of lymph vessels was performed approximately 2 minutes postinjection. For the lymph node experiments, 15 μL of 35 nM PEG-GNRs were injected into the foot. The same GNR volume and GNR concentration was injected into the foot close to the same location after 24 hours and 48 hours. Imaging of excised lymph nodes was performed 72 hours after the first injection. The animal protocol was reviewed and approved by the Institutional Animal Care and Use Committee of the Massachusetts General Hospital.

Fluorescence and confocal detection

Fluorescently labelled GNRs were detected using an inverted confocal microscope (Olympus FV1000). AlexaFluor594 was excited at a wavelength of 559 nm and an incident power of 4.5 mW through a 10× (0.4 NA) objective lens. A 40× (0.8 NA) objective lens with 13 mW incident power was also used for comparison. Tissue imaging was performed using the 10x lens. Fluorescence emission was detected using a 180 μm pinhole and photomultiplier tube after bandpass filtering from 590 nm to 630 nm to reject the excitation light. (Supplementary Information)

Two-photon luminescence detection

Two-photon (2P) luminescence was detected from GNRs with a surface plasmon resonance (SPR) at 1060 nm and a size of 10 × 67 nm. A pulsed laser (Ti:sapphire, MaiTai HP DeepSee-OL, Spectral physics) with a pulse width of < 100 fs and a repetition rate of 80 MHz, at a wavelength of 1000 nm was used. The samples was illuminated through a water immersion lens of 40x magnification (0.8 NA) in an inverted microscope setting with an average power of 1 mW (125 W peak power, 0.01 nJ energy). The two-photon luminescent signal was bandpass filtered from 630 nm to 700 nm to reject the excitation light and detected by a photomultiplier tube. (Supplementary Information)

The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.