Detecting population–environmental interactions with mismatched time series data

Abstract

Time series analysis is an essential method for decomposing the influences of density and exogenous factors such as weather and climate on population regulation. However, there has been little work focused on understanding how well commonly collected data can reconstruct the effects of environmental factors on population dynamics. We show that, analogous to similar scale issues in spatial data analysis, coarsely sampled temporal data can fail to detect covariate effects when interactions occur on timescales that are fast relative to the survey period. We propose a method for modeling mismatched time series data that couples high-resolution environmental data to low-resolution abundance data. We illustrate our approach with simulations and by applying it to Florida’s southern Snail kite population. Our simulation results show that our method can reliably detect linear environmental effects and that detecting nonlinear effects requires high-resolution covariate data even when the population turnover rate is slow. In the Snail kite analysis, our approach performed among the best in a suite of previously used environmental covariates explaining Snail kite dynamics and was able to detect a potential phenological shift in the environmental dependence of Snail kites. Our work provides a statistical framework for reliably detecting population–environment interactions from coarsely surveyed time series. An important implication of this work is that the low predictability of animal population growth by weather variables found in previous studies may be due, in part, to how these data are utilized as covariates.

Introduction

Determining how population fluctuations are driven by density-independent and density-dependent processes is a fundamental goal of ecology (Davidson and Andrewartha 1948, Saether et al. 2005). Time series analysis is an appealing approach for linking fluctuations in population size to variation in environmental variables (e.g. Perkins and Jager 2011). Despite its attraction, recent work using time series models to search for macroecological patterns in population–environment interactions has had limited success (Knape and de Valpine 2010, Herrando-Pérez et al. 2014), finding that environmental variables often have a weak statistical signature in abundance time series. Several potential reasons might underlie these results besides a weak coupling between populations and their environment. The difficulties in these analyses involve choosing biologically relevant covariates (van de Pol et al. 2016), decomposing measurement and process error (Knape and de Valpine 2011), and the filtering of nonlinear environmental interactions through structured populations (van de Pol et al. 2011, Ferguson et al. 2016).

Several studies have shown that the timescale of an analysis can affect estimates of ecological interactions. Hallett et al. (2004) demonstrated that extreme winter weather conditions could cause immediate or delayed mortality in Soay sheep (Ovis aries) populations that could only be attributed to weather if surveys of sheep occurred within several weeks of a climatic event. In another example, Keitt and Fischer (2006) showed that the timescale of analysis could affect the sign of species-pair correlations. Most population data sets are collected annually; these data rarely have the resolution to explore effects occurring at fine temporal scales. Factors that might generate population variation but operate sub-annually include seasonal mortality (Wang and Getz 2007), harvesting of resources (Kokko and Lindström 1998), and resource competition (O’Regan et al. 2012). It is not currently clear whether interactions that occur on these faster time scales can be detected in annually surveyed populations.

Standard time series methods (e.g., autoregressive models) assume that response and covariate data are collected at the same frequency (Shumway and Stoffer 2006), thus ignoring the potential for mismatches in sampling frequency between the response and covariate. Using standard time series methods with finely measured covariates requires somehow summarizing this fine-scale data on the same interval as the population response. The coarsening of this high-resolution environmental data often occurs through the construction of summary statistics (e.g., daily temperatures become yearly averages). It is not currently clear what effects coarsening may have on the detection of population–environment interactions.

Although population surveys are costly and time -consuming, environmental data, such as temperature and precipitation, can often be collected automatically at high temporal resolutions (Collins et al. 2015). There has been little research on whether this high-resolution temporal data can be used to improve the detection of population–environment interactions. Spatial analyses, in contrast, have long been able to utilize mismatches by exploiting the spatial relationships among multiple data sets collected at different spatial resolutions. For example, Jager et al. (1990) used observed correlations between stream chemistry at headwater tributary sites and elevation data to predicted the chemistry of unsampled headwater tributary sites. Despite the widespread attention to scale issues in spatial analyses, we have little understanding of how to exploit high-resolution temporal information.

Here, we addressed three objectives: first, we developed a modeling approach to link environmental data collected at fine (e.g., daily) temporal scales to population data collected at coarser (e.g., yearly) scales. Second, we determined the consequences of averaging covariates on the wrong timescale. Third, we show how to detect nonlinear environmental interactions with coarsely sampled abundances. We address these questions using simulations and through the application of our modeling approach to a long-term time series on an endangered raptor, the Snail kite (Rostrhamus sociabilis). Our results show that a coherent statistical framework for modeling mismatched time series can lead to more accurate inferences about the role environmental factors have on population dynamics.

Models and Methods

Our strategy for modeling mismatched time series was to define a microscopic process (sensu Hastings 2011) that describes a population–environment interaction that could be solved over the period of the more finely measured covariate. We show that this yields a discrete population model defined on the period of the covariate measurements that can be scaled up to the period of the response measurements. The resulting model describes dynamics of the current population in terms of past measurements of both the fine-scale environmental data and coarse-scale population data.

We first used a simulation study to explore how coarsened environmental covariates affect the explanatory power of linear time series models. We assumed that populations follow the linear dynamics of a Gompertz model with reproduction driven by an environmental covariate. To test the robustness of our approach, we also applied it to a more realistic scenario of nonlinear population growth using an ectothermic model of thermal performance. Finally, we illustrated our approach with an analysis of Florida’s southern population of Snail kites.

Linear dynamics: The Gompertz model

We develop our approach using the Gompertz growth model driven by an exogenous forcing term

$$\frac{\mathrm{d}X}{\mathrm{d}t}=\mathrm{\alpha }-\mathrm{\beta }X(t)+\mathrm{\delta }E(t).$$ (1)

Here X is the log-population size (X(t) = ln(N(t)), α/β is the stationary mean when E(t) = 0. The intrinsic reproductive rate, α, is defined as the number of offspring produced in a population with a single reproductive individual. Finally, E(t) is an exogenous variable that modifies the intrinsic reproductive rate with an effect size of δ. In this derivation, we will assume that E(t) is measured daily, N(t) is measured only once per year, and the population growth over the course of a single day is small. Since the daily growth is small, we can use the Euler approximation with daily step sizes to get a discrete map of the daily abundance

$$X(t+\mathrm{\Delta })=X(t)+\mathrm{\Delta }(\mathrm{\alpha }-\mathrm{\beta }X(t)+\mathrm{\delta }E(t)).$$ (2)

Here, Δ is the fine-scale measurement period; we will use Δ = 1 for a daily time step throughout this manuscript. The finely measured covariate, E(t), will then be measured 365 times between each measurement of the population state, X(t). In order to fit this model to data, we will rewrite it in terms of the coarsely sampled time series so that X(t) is a function of the previously observed population, here denoted as X(0), and the past daily environmental states. We can do this by iterating Eq. 2 to get a general relationship between X(0) and the population on day t. This gives

$$X(t)=a+bX(0)+d\sum _{i=0}^{t-1}E(t-i-1){(1-\mathrm{\Delta }\mathrm{\beta })}^i.$$ (3)

The discrete form of the Gompertz model has new parameters defined at the coarse timescale that are analogous to the continuous time model parameters: b = (1 − Δβ)^t, $a=\frac{\mathrm{\alpha }}{\mathrm{\beta }}(1-b)$, and d = Δδ. If the time step is quite fine relative to the rate parameter β, then this geometric sum can be approximated by exponential decay, exp[−Δβ].

Eq. 3 shows that influence of past the environmental states is determined by β, the strength of density dependence. In the case of exponential growth (β = 0), the impact of the environment over the sample period is the sum of all the previous environmental states, statistically equivalent to using the yearly average as a covariate. As the value of β increases, environmental states in the past have less of an influence on the population than more recent environmental states because the population has had sufficient time to respond to past environmental perturbations (Fig. 1). Thus, β is the rate that the current population becomes uncorrelated with past environments. Over the period 1/Δβ we can use the exponential approximation of the geometric sum in Eq. 3 to determine that the effect of the environmental covariate will decay to approximately 1−exp[−1] = 64% of the original effect size.

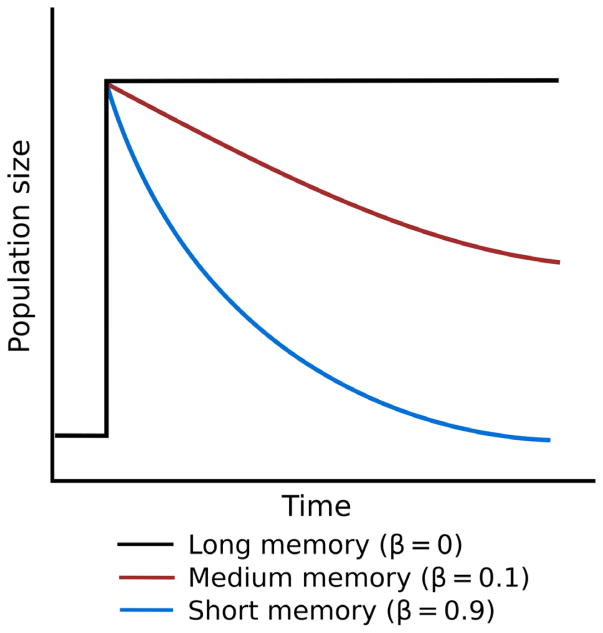
Fig. 1.

Conceptual illustration showing the effect of a sudden environmental perturbation on three populations. In the case of a population with long memory, the response to a perturbation is slow, while a population with short memory responds quickly. [Color figure can be viewed at wileyonlinelibrary.com]

Analogous to an organism’s ability to recall information, the time scale 1/Δβ determines how well the current population state “remembers” past environments. This ecological memory (sensu Padisak 1992, Ogle et al. 2015) predicts that populations with high β (short memory) will quickly lose information about the environment and populations with low β (long memory) will retain information about past environments over a longer period. We illustrate this effect in Fig. 1. In our model, the ecological memory is equivalent to the characteristic return time of the population from a small perturbation (e.g., Wissel 1984).

Our derivation assumed linear population dynamics and a linear response to environmental fluctuations. We will examine the robustness of these assumptions in later sections although our derivation also suggests a general strategy for integrating fine-scale covariate data with coarse-scale response data. The first step in this general approach is to build a model on the time scale of the finely sampled covariate, for example, by integrating or approximating a differential equation as in Eq. 2. The second step is to iterate this model up to the survey period to obtain a relationship like Eq. 2. The linear Gompertz model with daily steps can be solved analytically over both the fine and coarse period. However, for other models, this may not be possible but both steps can be performed numerically for more complex models.

Simulation analysis

We conducted a simulation analysis to determine how standard time series methods capture dynamics when generating data from the Gompertz model with daily exogenous drivers (Eq. 3). For these simulations, we fixed the carrying capacity of the population, α/β = 1, and varied the reproductive period, 1/α, over 64 values from 7 d up to 730 d (2 yr) with equally spaced values on the log-scale of this interval. All populations were initialized at the carrying capacity, X(0) = 1. The daily environmental state, E(t), was drawn from a normal distribution with mean 0 and standard deviation of 1 and we set the environmental effect size as d = 1 in Eq. 3. We fit three models to each simulated data set to determine how averaging the environment over different timescales affects the inference. Our fitted models were of the form

$$X(y+1)=a+bX(y)+\mathrm{d}f({\mathbf{E}}_y)+\mathrm{\epsilon }(y)$$ (4)

where X(y) is the log population abundance in year y, and f(E_y) is a yearly summary statistic of the past environmental states throughout the year. E_y denotes an ordered vector of daily environmental states measured in year y. The final term, ε(y), is the regression error term, assumed here to be drawn from a normal distribution with mean 0 and unknown variance.

Our first fitted model included density dependence but no environmental covariates (d = 0, denoted as “density dependence only”). The second fitted model included density dependence and the effect of the average yearly environment between population censuses, $f({\mathbf{E}}_y)=\frac{1}{365}{\sum }_{i=1}^{365}{E}_y(i)$, (denoted as “yearly average environment”). The third fitted model included density dependence and the weighted geometric sum of the yearly environment, $f({\mathbf{E}}_y)={\sum }_{i=1}^{365}{E}_y(365-i){(1-\mathrm{\beta })}^{i-1}$, where the environmental memory parameter, β, is the decay rate of past environmental states on the current population abundance. Note that this last model explicitly accounts for the ecological memory, whereas the previous ones do not. Although the value of the decay rate of the environmental effect in the Gompertz model is determined by the strength of density dependence, b = (1 − β)^t, we treated 1−β in the weighted geometric sum as a free parameter to illustrate the general case where β is not dependent on b. This could occur when density dependence and the environmental covariate operate on multiple life history stages such that the overall strength of density dependence and the environmental memory parameter, β, cannot be expressed as a simple relationship.

We estimated the memory parameter, β, by profiling over values of 1/β from 7 up to 730, where values are incremented by step sizes of 1 and the maximum likelihood is calculated at each value. Optimization was done using the linear model function, lmin R (R Core Team, 2015), and we assessed the goodness of fit for each model using the coefficient of determination, R². For each value of the reproductive period we simulated 10,000 samples to remove the effects of sampling variation on estimates of R². We provide code to reproduce this analysis in Data S1.

Nonlinear dynamics: Ectotherm simulations

We used another set of simulations to test the impact of nonlinearities in both the population growth rate and the response to environmental fluctuations on the weighted geometric covariate approach defined in Eq. 3. Population time series were simulated using previously studied models of ectotherm thermal performance (Deutsch et al. 2008) coupled with empirical temperature data. This model describes performance, P(T), as a function of temperature that rises gradually from a critical thermal minimum (CT_min) to the optimal temperature, T_opt, then declines rapidly to the critical thermal maximum, CT_max

$$P(T)=\{\begin{array}{ll}exp\left[-{\left(\frac{T-T_{\text{opt}}}{2{\mathrm{\sigma }}_{\mathrm{p}}}\right)}^2\right]\hfill & \text{for}T\le T_{\text{opt}},\hfill \\ 1-{\left(\frac{T-T_{\text{opt}}}{T_{\text{opt}}-{\text{CT}}_{max}}\right)}^2\hfill & \text{for}T>T_{\text{opt}}\hfill \\ 0\hfill & \text{for}T<{\text{CT}}_{\text{min}}\text{or}T>{\text{CT}}_{max}\hfill \end{array}$$ (5)

The spread of the Gaussian curve below T_opt is determined by the scale parameter, σ_p. We assumed that CT_min = T_opt − 4σ_p following Deutsch et al. (2008). We only considered thermal performance in fecundity, although mortality could also be temperature dependent. This performance curve has been qualitatively linked to the thermal dependence of a single enzyme’s catalytic reaction (Amarasekare and Savage 2012).

We simulated population dynamics from the logistic model with a temperature-dependent birthrate. Our modified logistic model is

$$\frac{\mathrm{d}N(t)}{\mathrm{d}t}=rP(T(t))N(t)-\mathrm{\mu }N{(t)}^2$$ (6)

where P(T(t)) is given by Eq. 5 and T(t) is the temperature at time t. The per-capita vital rates are given by r, the intrinsic reproductive rate, and μ, defined as the mortality rate when N(t) = 1 otherwise the mortality rate is μN(t).

Deutsch et al. (2008) estimated parameter values of Eq. 5 for 38 terrestrial insect species, occurring over a latitudinal range from about 40° south to about 50° north. We used these parameters to simulate plausibly realistic temperature-dependent population dynamics by coupling Eq. 6 to empirical temperature data for each insect population. Surface temperature data were downloaded from the location nearest to the latitude and longitude of each species as reported in Deutsch et al. (2008). These data were available at a resolution of 2.5°. We used daily air temperatures (taken at midnight) from the NCEP/NCAR Reanalysis data set (Kalnay et al. 1996) for 22 yr, from 1990 to 2011. We used the RNCEP package (Kemp et al. 2012) to download and process the temperature data. Unlike the linear simulations in the previous section, thes temperature data have strong seasonal autocorrelation.

To generate plausible dynamics from Eqs. 5 and 6 we simulated dynamics during a period of the year that was likely to have plausible growing conditions for each population. We defined this growing season using a two-step process. First, we used the location of each population reported in Deutsch et al. (2008) to determine the growing year; second, we used the physiological response to daily temperatures to define the growing season within each growing year. The growing year for populations in the southern hemisphere was assumed to start on 1 July and end on 30 June. For northern hemisphere populations, the growing year was assumed to start on 1 January and end on 31 December. To keep the length of simulated time series the same for northern and southern populations, we excluded 2011 temperature data in simulations of northern populations. Each population’s growing season was defined as the period of the year when the average thermal tolerance was greater than 10% of the maximum value. We calculated the average tolerance as E_y[P(T_y(t))], where the subscript y denotes the growing year that is averaged over and the argument t denotes the day within the year. Thus, we end up with 365 values of average thermal performance for each population. We defined the start of the growing season as the first day of the year that was greater than 10% of the maximum possible thermal performance. The last day of the growing season for a population (defined as t = m) was the last day of the year that thermal performance was on average greater than 10% of the maximum. In Stethorus punctillum, the average thermal tolerance was never greater than 10%; thus we removed this population from further analysis.

We simulated populations by plugging in the local daily temperature data from the first day of the growing season (t = 1) to the last day (t = m) each year into Eq. 6, which was discretized using the Euler method with daily time steps. As in the previous section, we simulated dynamics on a range of time scales, from individuals with a lifetime of one week (1/μ = 7) to a lifetime of two years (1/μ = 730). We varied 1/μ on this interval with 64 values equally spaced on the logarithm of this range. To approximate stationary population dynamics, all populations were initialized to N₁(t = 1) = 1. For each value of μ we found the value of r that determined the population size at the end of the last year as N₂₂(t = m) = 1 using the optimize function in R. We assumed that the initial population on the first day of the growing season of a new year is equal to the population size at the end of the previous year’s growing season. Once the value of r was determined, we simulated a new data set and censused the population once per year at the end of the growing season, N_y(t = m), to generate a time series that would be similar to those obtained from empirical sampling. This process led to time series with 22 observations (including the initial value of N₁(t = 1) = 1) for each of the 37 insect species and each of the 64 values of μ.

We fit a set of discrete time series models defined by Eq. 4 to each simulated data set. We assumed that the growing season daily temperatures, T_y(t), were known, but the population’s thermal performance function, P(T_y(t)), was unknown. We tested the same suite of environmental covariates as in the Gompertz model simulation: the density dependence model, the weighted geometric temperature, and the yearly average temperature. We also fit two niche models that included both linear and quadratic terms of the environment. In the weighted niche model our quadratic term was the square of the daily temperature, ${\sum }_{i=1}^{365}{(1-\mathrm{\beta })}^{i-1}{T}_y{(365-i)}^2$. In the second model, denoted the naive weighted niche, we squared the linear predictor to get the quadratic term as is commonly done using standard time series methods, ${\left({\sum }_{i=1}^{365}{(1-\mathrm{\beta })}^{i-1}{T}_y(365-i)\right)}^2$. We fit the parameter β by profiling 1/β over values of 7 to 730. We summarized the goodness of fit using the coefficient of determination (R²) and calculated the Bayesian information criterion (BIC) values to determine which model was the most parsimonious description of the data. We used BIC rather than the more common Akaike’s information criterion (AIC) because of BIC’s stronger penalty term that reduces the chance of overfitting these models.

Application to Snail kites

Florida’s federally endangered Snail kite population declined dramatically between 1997 and 2008. Range-wide population estimates then increased significantly between 2010 and 2016 (Reichert et al. 2016). However, Snail kite abundance has continued to decline in the southern portion of its range, a region of wetlands designated as “critical habitat”. Here we explored the potential of geometric weighted covariates to modeling this population. Our analyses used abundance estimates for the southern population of Florida Snail kites as these estimates account for age-related and spatial sources of heterogeneity in detection (Reichert et al. 2016). Reichert et al. (2016) found that the southern Snail kite population underwent a rapid change in age structure between 2007 and 2010 that resulted in a population dominated by senescent individuals. Thus, we included abundances from 1997 to 2007 into our primary analysis based on a changepoint analysis (Appendix S1), which showed that dynamics significantly differed pre- and post-2007.

Snail kite vital rates are driven by the hydrology of their environment in several ways. Observed increases in mortality have been linked to wetland drying events (Martin et al. 2008, Reichert et al. 2010), flooding events have been associated with increases in juvenile survival (Bennetts et al. 2002), and prolonged high water events have had potentially detrimental effects on nesting and foraging habitat (Mooij et al. 2002, 2007). Nearly all wetlands used by Florida’s Snail kites for foraging and nesting are actively managed. Therefore, understanding the mechanisms that drive correlations between water levels and population growth is a high priority (U.S. Fish and Wildlife Service, 2010).

We tested the ability of a suite of previously used environmental covariates to predict population growth rates (Reichert et al. 2011). We used daily water levels from Water Conservation Area 3A to construct predictor variables as this wetland has been previously linked to Snail kite population dynamics (Martin et al. 2008). There were several missing values in this data set (approximately 2% missing) that were imputed by fitting a loess model to daily water levels. The environmental covariates we tested were the yearly mean water level (MEAN), the annual recession rate calculated as the water level on 1 January minus the minimum water level and divided by the number of days it took to reach this minimum (REC), the annual maximum water level (MAX), the annual minimum water level (MIN), the standard deviation in the annual water level (SD), and the proportion of days each year above the yearly mean water level (DAM). Each of these predictors was calculated for three different lags. For lag 0, each covariate is calculated for the year of the current population (y + 1), for lag 1, each covariate is calculated over the past year (y), and for lag 2, each covariate is calculated at y−1.

To compare the ability of our approach to detect environmental signals against previously used methods we compared the fit of the annual statistics (MEAN, REC, MAX, MIN, DAM) to the weighted geometric covariate (WEIGHT) at lag 0, 1, and 2. The short time series limited degrees of freedom we had to work with, therefore we applied the constraint to the WEIGHT covariate that β = 1 − b, where b is an estimated parameter, rather than treating β as a free parameter independent of b. This constraint arises from the derivation of the Gompertz model with an environmental covariate (Eq. 3). Instead of using the calendar year to construct the WEIGHT covariate, we set the last day of the survey year to be the last day of the sampling season, 31 June (Reichert et al. 2016). Thus, for the lag 0 model, the weighted statistic is ${\sum }_{i=1+\mathrm{\varphi }}^{365+\mathrm{\varphi }}{E}_y(365-(i-\mathrm{\varphi })){(1-\mathrm{\beta })}^{(i-\mathrm{\varphi })-1}$ where we chose the first day of the year (i = 1) to correspond to the day after the final day of surveys from the previous year, 1 July (ϕ = 184). As discussed in the following paragraph, the timing parameter ϕ, can be treated as an estimated parameter as well. BIC values for all fitted models were compared to determine the most parsimonious model. Code to reproduce this analysis is provided in Data S1.

Finally, we conducted an analysis exploring the link between the documented demographic change (Reichert et al. 2016) and water levels. For this analysis, we used a breakpoint model and let the population growth rate, strength of density dependence, and the environmental model vary before and after the changepoint in 2007 (Appendix S2). We estimated the timing parameters ϕ_pre (before changepoint) and ϕ_post (after changepoint) by profiling the likelihood over parameter values that ranged from 1 to 730 with step sizes of 7 d. For each combination of values for ϕ_pre and ϕ_post, we estimated the maximum likelihood. We report the relative likelihood, defined as the ratio between the likelihood evaluated at (ϕ_pre, ϕ_post) and the maximum likelihood. This model contains many parameters (8) for the available years of data (16) so we considered it purely as an exploratory exercise to inform future work in the system.

Results

Linear dynamics: The Gompertz model

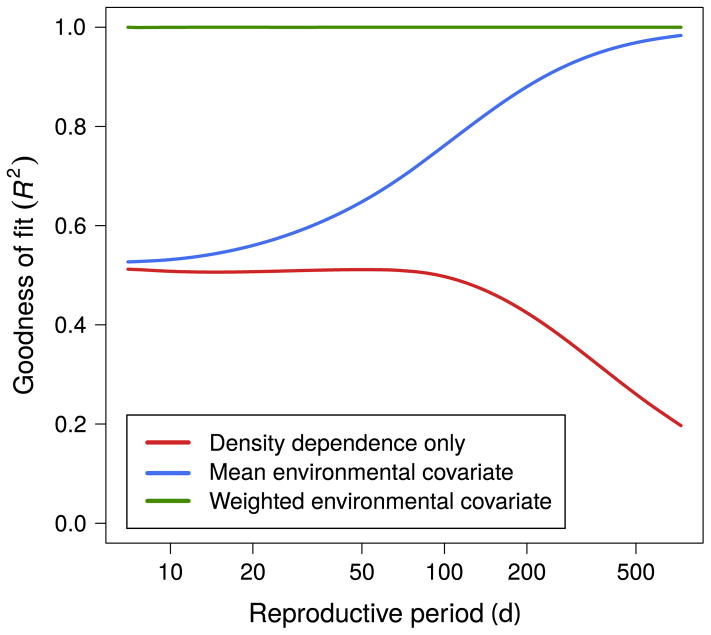
Our Gompertz model simulation analysis showed that even when the correct environmental data are measured, performance can be highly sensitive to the period over which these data are averaged. The “density dependence only” model displayed a decrease in the goodness of fit as reproductive period increased (Fig. 2). This effect arises because we fixed the equilibrium value in the Gompertz equation leading to a decrease in the strength of population regulation as the reproductive period is increased. The annual mean covariate resulted in accurate predictions for reproductive periods greater than about 365 d (R² >0.9). Longer reproductive periods than this were well approximated by the annual mean because for these values the geometric decay is slow enough to be approximately constant over the past year. For fast reproductive periods (7–50 d) the annual predictor was not much better than the density dependence model. As expected from the design of the simulation study, using the weighted covariate led to nearly perfect fits for all simulated lifetimes.

Fig. 2.

Goodness of fit (R²) of different population models. Data was generated using the Gompertz model (Eq. 3). The mean environmental covariate uses the yearly mean of the daily environmental covariate; the weighted environmental covariate uses the weighted geometric sum of the daily environmental covariate. [Color figure can be viewed at wileyonlinelibrary. com]

Nonlinear dynamics: Ectotherm simulations

The results of the nonlinear ectotherm simulations had several similarities with the results from the linear Gompertz model simulations.

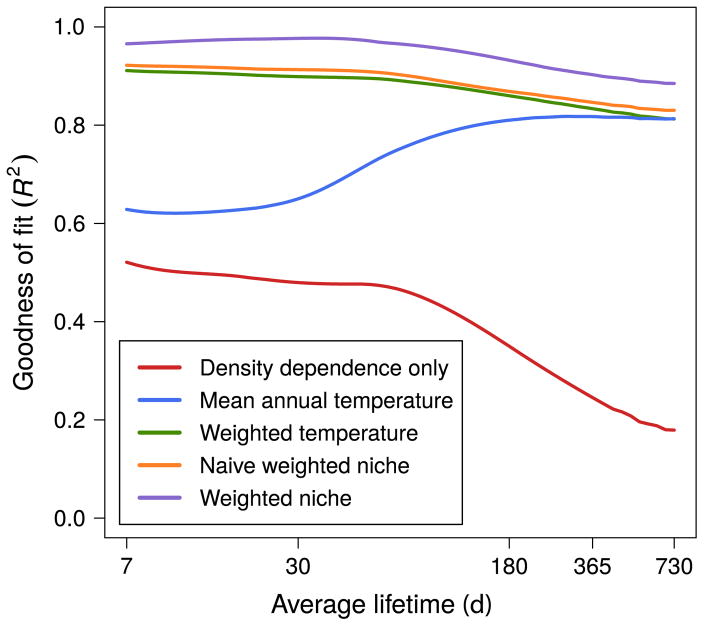
As in the Gompertz model, environmental covariates averaged over ecologically significant periods performed better than covariates averaged over the sampling period. However, unlike the Gompertz model, we found that the explanatory ability of all covariates decreased at longer lifetimes (Fig. 3). This effect arose because individuals with longer lifetimes are more likely to have experienced extreme environmental conditions, therefore the thermal performance curve is no longer well modeled with a linear approximation.

Fig. 3.

Average goodness of fit (R²) of 37 different ectotherm species using different environmental summary statistics. The mean environmental covariate uses the yearly mean of the daily environmental covariate, the weighted environmental covariate uses the weighted geometric sum of the daily environmental covariate. The naive weighted niche covariate uses the square of the annual weighted covariate while the weighted niche covariate uses the weighted geometric sum of the square of the daily environmental covariate. [Color figure can be viewed at wileyonlinelibrary.com]

We found that the goodness of fit for the naive weighted niche model (the yearly squared covariate) explained about the same amount of variation as the model with the linear covariate suggesting that it did not adequately capture the nonlinear response to environmental fluctuations (Fig. 3). However, the weighted niche model (daily squared covariate) performed well over all lifetimes although there was still a decrease in performance at longer lifetimes. We note that if the actual underlying physiological response to the environment is known (e.g., Eq. 5), then we can recover near-perfect model fits using the weighted geometric covariate.

Finally, we found that the geometric weighted niche model was always ranked as the most parsimonious model when applying BIC to the fitted model set. This result suggests that even with a relatively limited time series, high-resolution environmental data can be used to accurately detect the nonlinear response of populations to environmental fluctuations.

Application to Snail kites

Based on our changepoint analysis (Appendix S1) we included population surveys from 1997 to 2007 in the assessment of the impacts of water levels on Snail kite dynamics. Our model selection analysis found that the best overall environmental covariate was the annual minimum water level with no time lag (MIN, lag 0). Parameter estimates from this model were â = 2.05 (1.22), b̂ = 0.70 (0.17), and d̂ = 0.27 (0.08). The annual standard deviation (lag 0) performed nearly as well (ΔBIC = 0.5) while the weighted geometric sum of daily water levels (WEIGHT, lag 1) was within the commonly used cutoff used to determine the set of best models (ΔBIC ≤ 2; Table 1). In this geometric decay model, we estimated â = 2.14 (1.30), b̂ = 0.69 (0.03), and the effect of the standardized geometric weighted covariate was d̂ = 0.25 (0.01). This estimate of b̂ equals a decay rate in the geometric weighted covariate of Δβ = 0.37, roughly corresponding to a memory of past water levels over the previous four months.

Table 1.

Daily Bayesian information criterion (ΔBIC) values for a suite of covariates constructed from yearly summary statistics of daily water levels.

Covariate	WEIGHT	MEAN	REC	MAX	MIN	SD	DAM
Lag 2	8.4	8.4	8.4	9.1	9.1	8.9	8.2
Lag 1	1.7	5.6	9.1	8.5	8.5	8.9	2.2
Lag 0	8.2	9.0	7.9	8.6	0.0	0.5	9.0

Notes: Values in boldface type denote with ΔBIC ≤ 2. Lag denotes how far back in years from the response population abundance that the covariate is calculated. WEIGHT is the weighted geometric water levels, MEAN is the yearly mean water level, REC is the recession rate, MAX is the yearly maximum water level, MIN is the yearly minimum water level, SD is the yearly standard deviation in daily water levels, and DAM is the yearly days that water level is above the median. For a model with density dependence and no environmental covariate we found ΔBIC = 6.8.

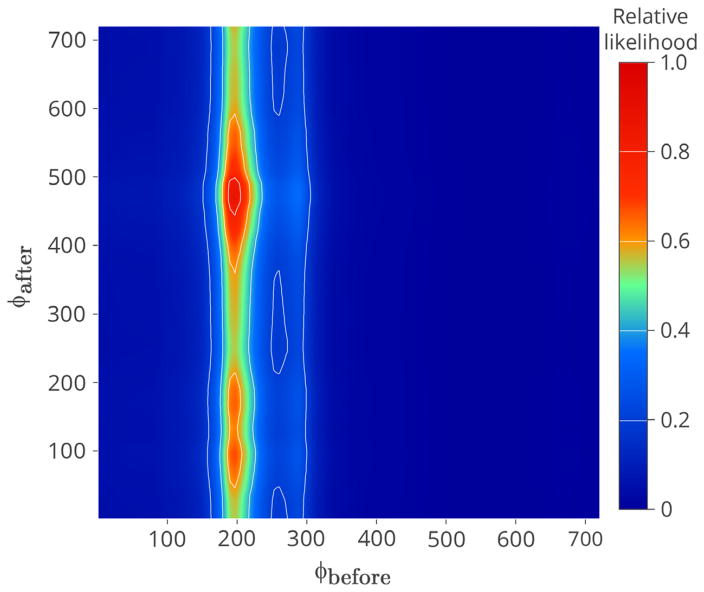
Our exploratory analysis of the southern population of Snail kites found evidence that a shift in the interaction between the population and their environment may have occurred in 2007. Up to 2007, we found that Snail kite dynamics were driven by water levels in the previous survey year, ϕ̂_pre = 197 (15 July of the past year). After 2007 we found evidence that the dependency may have changed to the current survey year with the best estimate corresponding to ϕ̂_post = 470, (14 April of the current year) (Figure 4). However, we note that post-2007 results must be treated as preliminary because only 6 yr of data were available for this period.

Fig. 4.

Relative likelihood, scaled so that the maximum is 1, for the timing parameters (ϕ_before and ϕ_after) in the geometric weighted covariate. [Color figure can be viewed at wileyonline library.com]

Discussion

We found the rate that populations become decorrelated with past environments is a natural time scale to describe population–environment interactions. Sometimes called the ecological memory, this timescale is determined by the population’s vital rates. Decorrelation between the population and environment is due to the population returning to equilibrium after an environmental perturbation. We can account for this effect by using a geometric sum of past environmental states. We were able to show that this leads to the reliable detection of both linear and nonlinear environmental covariates independent of the vital rates and population survey frequency.

Standard time series models assume that the covariate and response variables are measured on the same time-scale (Shumway and Stoffer 2006). Here we showed that averaging environmental covariates over incorrect time-scales leads to weaker than expected covariate effects. We also showed detecting nonlinear covariates will often require fine-scaled environmental data. Thus, standard methods may often provide poor inferences about covariate effects in ecological systems. We developed an approach to correct this problem that led to the reliable detection of covariate effects in simulations.

Our simulations indicated that when the ecological memory was greater than the sampling period, we can reliably detect linear, but not nonlinear, effects. However, using fine-scale environmental data and calculating the nonlinearity on the fine timescale using the weighted covariate approach did allow us to detect nonlinear effects. Jensen’s inequality shows that we cannot expect that calculating a nonlinear niche effect on the coarse scale to be comparable to a nonlinear effect of on the fine scale. In mathematical terms this is expressed as ${\left({\displaystyle \sum _i}{x}_i\right)}^2\ne {\displaystyle \sum _i}{x}_i^2$ for the environmental covariate x. For a covariate calculated at the coarse timescale to be statistically equivalent to a covariate calculated on the fine timescale, there must exist a one-to-one transformation between these different functions. Our simulation results show that this transformation does not exist in general; thus, high-resolution environmental information may be crucial for the detection of nonlinear environmental effects.

Other work on mismatched time series in ecology has focused on using weighted splines to smooth fine-scaled covariate data (Teller et al. 2016), their exponential smoother is the continuous equivalent of our geometric weighted covariate. In econometrics, models for mismatched data are more common. “Mixed data sampling” regression has been well-developed over the course of the last decade (Ghysels et al. 2004) yielding methods for estimating and choosing appropriate smoothing functions in data-rich settings. Our approach to this problem focused on understanding the processes that generate mismatched temporal data sets in population ecology. As shown here, determining how these processes are linked to the covariate smoothing function leads to constraints that allow our method to be applied in data-limited applications. Working from this perspective also revealed a fundamental insight about detecting nonlinear effects in time series models.

We illustrated the utility of geometric weighted covariates on a Snail kite population in south Florida. The model performed well against a suite of previously developed environmental variables but was not the best competing hypothesis (Table 1). Previous work has identified a positive effect of yearly minimum water level on Snail kite population growth (Beissinger 1995, Cattau et al. 2014) consistent with our best model describing population growth increasing with the annual minimum water level. Snail kites are known to have a multifaceted relationship with their abiotic environment that is linked to both foraging and nesting success (Mooij et al. 2002, Martin et al. 2008, Zweig and Kitchens 2008) and our analysis suggests that growth of the southern Snail kite population may also be related to the daily water levels during the wet season. Consistent with previous work we found that the degree and timing of low water levels during the breeding season on Snail kite population growth before 2007. These effects may be related to the effects of drying events on snail populations (Darby et al. 2008).

Our analysis revealed a fundamental limitation of the Snail kite data set, the ecological memory estimated by our model identified a window of about four months in which we can detect the effects of environmental fluctuations. This result suggests that short-term environmental dependencies that occur outside this window are not detectable using these data and would require more frequent surveys of the Snail kite population. An additional consideration is that long-term memory processes may be occurring simultaneously with the short-term memory processes that we detected. Ogle et al. (2015) utilized a flexible concept of ecological memory to model the temporal history of population and ecosystem processes over multiple timescales. These multiscale processes can arise due to the environment affecting both reproductive (short-term) and adult survival (long-term) rates. The ecological memory framework of Ogle et al. (2015) is quite flexible due to making minimal parametric assumptions similar; however, this comes at the cost of being of highly data intensive. Combining the insights of Ogle’s multiscale framework with our model could allow Snail kite managers to decompose the short-term and long-term contributions of water levels on population dynamics, an important goal given that drawdowns are necessary for the long-term management of these wetlands.

Our analysis of Florida’s southern Snail kites comparing dynamics before and after 2007 is based on limited data. Therefore, we must treat these results as speculative. However, our analysis revealed a potential shift occurring in this population. Before 2007, growth was dependent on water levels from the previous breeding season in a manner consistent with past work (Beissinger 1995, Cattau et al. 2014), while after 2007, there was a potential shift to dependence on water levels during the current breeding season. Such a change in timing may be due to a recent shift in the Snail kite’s primary food resource. Historically, Snail kites forage almost exclusively on the native freshwater apple snail Pomacea paludosa (Reichert et al. 2015) with a lifespan of 1 to 1.5 yr and whose local densities are closely tied to the previous year’s hydrology (Darby et al. 2008). However, recently (circa 2006) Snail kites have increasingly become reliant on a highly invasive apple snail (Pomacea maculata) that lives longer, reproduces multiple times throughout the year, grows faster, and is more drought tolerant than P. paludosa, and are likely more closely tied to short-term hydrological periods (Cattau et al. 2016). While our analysis was not able to resolve the temporal dependence of Snail kites on seasonal water levels post-2007, we were able to generate a new hypothesis for managers working to identify specific hydrologic targets since the invasion of P. maculata.

Understanding the role of scale in temporal ecological data has lagged behind developments in the study of spatial scale (Wolkovich et al. 2014). Work over the last 30 yr in spatial ecology has led to the recognition that ecological processes operate at distinct spatial scales and that the artificial aggregation of data at the incorrect scale can result in biased estimators through the well-studied modifiable areal unit problem (Gotway et al. 2002, Fortin and Dale 2005). Here we showed that similar effects can arise due to improperly accounting for scale in temporal models. Reliably detecting the effects of environmental drivers of population fluctuations with time series requires the correct identification of the underlying ecological time scales and models that capture dynamics on those scales. Current theory has provided little guidance on how temporal scale might drive statistical inferences or on best modeling practices when data are collected at different frequencies. Here we have worked toward a better understanding of how standard methods can fail to detect the effects of environmental covariates and an improved a modeling framework that utilizes high-resolution environmental data to estimate these effects. We expect that these models coupled with high-resolution environmental data will provide significant insight into role of density-independent processes on population regulation.