Regulation and Plasticity of Catalysis in Enzymes: Insights from Analysis of Mechanochemical Coupling in Myosin

Abstract

The mechanism of ATP hydrolysis in the myosin motor domain is analyzed using a combination of DFTB3/CHARMM simulations and enhanced sampling techniques. The motor domain is modeled in the pre-powerstroke state, in the post-rigor state, and a hybrid model based on the post-rigor state with a closed nucleotide-binding pocket. The ATP hydrolysis activity is found to depend on the positioning of nearby water molecules, and a network of polar residues facilitates proton transfer and charge redistribution during hydrolysis. Comparison of the observed hydrolysis pathways and the corresponding free energy profiles leads to detailed models for the mechanism of ATP hydrolysis in the pre-powerstroke state and proposes factors that regulate the hydrolysis activity in different conformational states. In the pre-powerstroke state, the scissile P_γ-O_3β bond breaks early in the reaction. Proton transfer from the lytic water to the γ-phosphate through active site residues is an important part of the kinetic bottleneck; several hydrolysis pathways that feature distinct proton transfer routes are found to have similar free energy barriers, suggesting a significant degree of plasticity in the hydrolysis mechanism. Comparison of hydrolysis in the pre-powerstroke state and the closed post-rigor model suggests that optimization of residues beyond the active site for electrostatic stabilization and pre-organization is likely important to enzyme design.

Graphical Abstract

Introduction

Design of highly efficient catalysts is one of the grand challenges of modern science. Guided by different theoretical and computational analyses, many successful examples of catalyst design have been reported, with applications in electrocatalysts,¹ inorganic materials,² nanoporous metal-organic-frameworks³ and artificial enzymes.^4,5 It remains difficult to achieve a consistently high degree of catalytic proficiency, especially for structurally flexible systems. The design process requires not only a deep understanding of the physicochemical properties of the active site (e.g., flexibility and hydration)⁶ but also of the allosteric coupling throughout the system; multiple studies show that even mutations that are remote from the active site make significant contributions to catalysis.^7–9 Consequently, despite ongoing progress, most designed enzymes have a rather low level of catalytic activity, and need to be further refined through rounds of directed evolution.^4,5,10,11

Further progress in the design of efficient catalysts will require a precise understanding of how the immediate coordination shell of active site and nearby residues and water molecules affect catalytic efficiency. This issue goes beyond artificial enzymes. For example, in the design of nano/mesoporous materials, an open question is whether the catalysis can be fine-tuned by adjusting the polarity and solvation properties of intrazeolite void environments.¹²

With these considerations in mind, in this study we focus on ATP hydrolysis in the Myosin II molecular motor. Myosins are remarkable biomolecular machines that utilize the chemical energy of ATP hydrolysis to perform diverse biological functions, such as cellular transport, signaling and muscle contraction.^13,14 In normal myosin function, ATP hydrolysis is tightly coupled to the conformational state of the motor domain. The underpinnings of this “mechanochemical coupling” in ATPases have been studied by both experiment^15–20 and computations^21–38 for several systems, but the mechanism is not completely understood.

Myosin II (henceforth referred to as myosin) is chosen for this study because its functional cycle³⁹ is well-characterized, and because several high-resolution Xray structures are available. We investigate ATP hydrolysis in the pre-powerstroke(PPS)⁴⁰ and in the post-rigor(PR)⁴¹ states of the motor domain.

The PR state binds ATP tightly but is incapable of ATP hydrolysis.^18,42 In the PPS state Switch II motif (SwII) in the active site (Fig. 1) moves to interact with the Switch I motif (SwI), forming a salt-bridge between Arg238 in SwI and Glu459 in SwII (the numbering of residues follows myosin II from D. discoideum), and a hydrogen bond between the backbone amide of Gly457 of SwII and the γ-phosphate of ATP. As a result of these changes, ATP is hydrolyzed efficiently in the PPS state, (in fact, the X-ray structure⁴⁰ contains the hydrolysis transition state analog ${\text{ADP}·\text{VO}}_4^{-}$ in the active site).

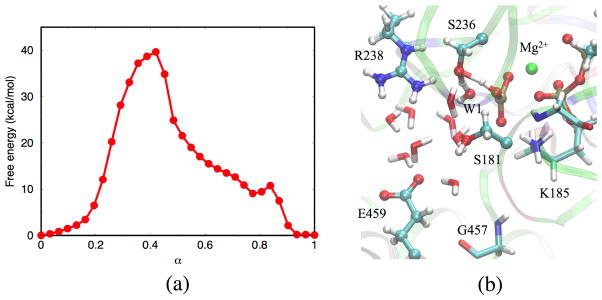
Figure 1.

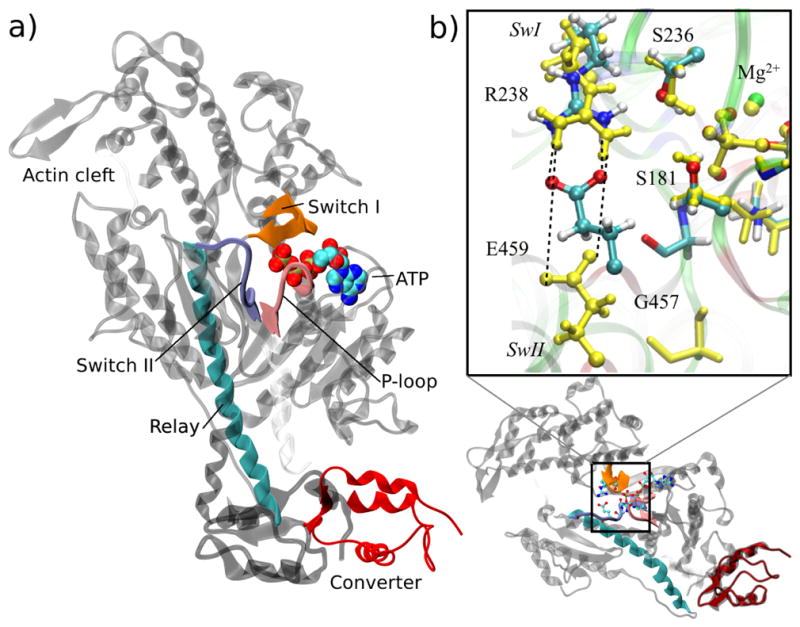
Structural transition between the post-rigor (PR) and pre-powerstroke (PPS) state of the myosin motor domain. (a) Overview of the myosin motor. The main structural elements involved in the mechanochemical coupling between ATP hydrolysis and mechanical motion are shown for the PPS conformation in color ribbon; these are Switch I, Switch II and P-loop in the nucleotide binding site, and the Relay helix connected to the Converter; the rest of myosin is drawn in light gray; ATP is drawn as color spheres. The displacements of the converter and the Relay in the transition to the PR structure are indicated in dark gray. (b) Expanded view of the nucleotide pocket centered on the QM region. Local transition in the active site largely involves the displacement of the SwII motif, leading to the break of the salt-bridge between Glu459 and Arg238 as well as displacement of Gly457 away from the γ-phosphate of ATP in PR (shown in yellow). Switch I and P-loop remain largely intact between the PR and PPS states.

Representative X-ray structures for the PR and PPS states^18,40,41 have additional differences that span different scales (Fig. 1). The most striking structural change is that the C-terminal converter undergoes a (60°) rotation⁴³ (Fig. 1a). The converter rotation in the PR→PPS transition ‘primes’ the converter for the subsequent power stroke, which is triggered by interactions with actin, and is accompanied by the sequential release of hydrolysis products, phosphate and ADP. The power stroke is the main motion responsible for muscle contraction.¹⁸ The communication between the nucleotide pocket and the converter is facilitated by a “Relay helix”^18,19 (Fig. 1b), which adopts a locally unwound or “kinked” conformation in the PPS state. The Relay immediately follows SwII in sequence, and thus translates the ‘chemical’ signals of ATP binding and hydrolysis in the active site into mechanical motions of the converter.

In this study, we focus on identifying the main features of the PPS conformation that facilitate ATP hydrolysis. Previously, the importance of aligning the lytic water molecule in a “near-in-line-attack” configuration has been emphasized.⁴⁴ Active site water molecules in PR and PPS states feature different average positions⁴⁵ and dynamics.³² However, the free energy penalty associated with aligning the lytic water molecule at room temperature was estimated through classical molecular dynamics to be only 2–3 kcal/mol.³³ This corresponds to a hydrolysis rate difference of ~30–150 fold according to transition state theory, and is unlikely to be a major factor considering that ATPase activity is associated only with the pre-powerstroke states.^18,45

Previous studies focused on polar interactions involving the γ-phosphate to activate hydrolysis. Applying minimum energy path (MEP) analysis and QM/MM calculations to myosin, Li et al.³² and Kiani et al.^29,46 highlighted the importance of γ-phosphate stabilization by polar interactions unique to the PPS active site, e.g., via the aforementioned Gly457 backbone amide. This is similar to discussions in the study of F₁-ATPase^30,47 and GTPases,^35,36,48,49 for which the role of an “Arginine finger” in activating hydrolysis in specific conformational states has been established. For example, in combined DFT/MM and experimental IR study of GTPase activity in ras and ras-GAP, Gerwert and co-workers⁵⁰ noted the importance of electrostatic stabilization of the γ-phosphate, including a change of relative orientation of the β- and γ-phosphates that promotes further polarization of the scissile P_γ-O_3β bond.^48,51 However, a calculation to characterize the explicit contribution of this effect to the GTP hydrolysis barrier was not performed.

During the hydrolysis reaction, one proton of the lytic water is transferred to a nearby base, which can be either a protein side chain or the γ-phosphate of the ATP (or GTP). Therefore, proton transfer is an important aspect of the hydrolysis reaction, and motifs that facilitate such transfers are likely to be part of the regulatory mechanism. In myosin, the highly conserved SwII residue Glu459 establishes a water-mediated interaction with the γ-phosphate only in the PPS state, and is therefore likely to play a crucial role in the hydrolysis reaction. Consistently, mutation of either Arg238 or Glu459 leads to significant decrease in the ATPase activity, while swapping the position of the two residues preserves normal hydrolysis activity.^52,53 It is unclear whether Glu459 is involved explicitly by serving as a general base, or merely provides stabilization for the proton transfer. The former scenario was observed in a QM/MM-MEP study of myosin by Grigorenko et al.,⁵⁴ and was also proposed for several other NTPases including F₁-ATPase,^30,47 kinesin³¹ and actin⁵⁵ based on QM/MM and free energy simulations.

In contrast, Kiani and co-workers²⁹ found that the energy barrier for the pathway in which Glu459 is explicitly protonated is higher than in mechanisms in which it is involved indirectly. However, the barriers were computed along a path of minimum energy (rather than minimum free energy), and therefore exclude contributions due to the fluctuations in the local protein environment and the hydrogen bonding network.^56–58 Consistently, an earlier study from our group³⁴ showed that, for the hydrolysis-competent PPS state, the computed MEP barriers were substantially higher (~12 kcal/mol) than the experimental measurements, which could be explained by a lack of entropic compensation. At minimum, a thermodynamically rigorous computation of the hydrolysis rate should involve an average over water and protein configurations sampled from the canonical ensemble, which would include realistic enthalpic and entropic corrections to the barrier energies.

To understand the influence of water molecules beyond the immediate coordination shell of the γ-phosphate on the catalysis rate, Yang et al.³⁴ performed ATP hydrolysis calculations starting from several different snapshots obtained from molecular dynamics simulations of a model myosin structure in which the active site adopts the structure of PPS while the rest in the PR conformation. The barriers along the MEPs were found to be highly variable (>10 kcal/mol). The differences were mainly due to the higher mobility of water molecules in the active site, which prevented them from being persistently engaged in the stabilization of the hydrolysis transition state. These observations underscored the importance of sampling over multiple configurations of water molecules in the active site that follow the canonical distribution.

The above discussion makes clear that free energy simulations of ATP hydrolysis are needed. In the current study, we perform DFTB3/CHARMM^59–62 free energy simulations of ATP hydrolysis with the myosin head modeled in different conformational states. The DFTB3/CHARMM approach was parameterized recently for phosphoryl transfer reactions (the 3OB/OPhyd variant),⁶¹ and found to provide a semi-quantitative description of phosphoryl transfer transition states in alkaline phosphatase, including trends in the transition state structure⁶³ for a series of substrates, and also primary and secondary kinetic isotope effects.⁶⁴ Therefore, we expect that the approach is able to capture key trends in ATP hydrolysis in different conformational states of myosin. The computational efficiency of DFTB3 makes it possible to conduct much more thorough conformational sampling (by a factor of ~100) than previous DFT/MM studies.^31,55 The DFTB3/CHARMM method is combined with the metadynamics⁶⁵ and the string method in collective variables^66,67 to compute minimum free energy pathways. The string method was used previously in classical MD simulations compute transition pathways of converter rearrangement in myosin VI;^67,68 a variant of the method was also used in DFT/MM simulations to study the mechanism of phosphoryl transfers in Ribonuclease H.⁶⁹ Here, the unique combination of DFTB3/CHARMM with metadynamics and the string method (see Computational Methods) allows us to identify multiple hydrolysis reaction pathways; comparison of energetics of these pathways provides further insights into factors that regulate the hydrolysis activity.

In the following, we first summarize the computational methodology and system setup. Next, we present optimized reaction pathways and corresponding free energy profiles for ATP hydrolysis in the different conformational states of myosin; these include the PPS and PR states based on the corresponding X-ray structures, as well as the closed PR model similar to that constructed in Ref. 34. The results are discussed first in the context of myosin, and then in the broader context of catalytic activity regulation in enzymes. We end with a concluding discussion.

Computational Methods

Basic QM/MM setup

The enzyme model is constructed based on high-resolution X-ray structures of the myosin motor domain from D. discoideum. Three systems are studied: PPS with ATP bound (PDB code 1VOM⁴⁰) at 1.9 Å resolution, PR with ATP bound (PDB code 1FMW ⁴¹) at 2.15 Å resolution, and the closed PR model with ATP bound (see below). QM/MM calculations are carried out to obtain the reaction pathways of ATP hydrolysis and the corresponding free energy profiles. The QM region includes the tri-phosphate and part of the ribose group of ATP (C5O, H5O and H5”), Ser181, Ser236, Glu459, Arg238, the full coordination shell of the Mg²⁺ ion and any water molecules that potentially participate in the reaction. Only side chain atoms of protein residues are included in the QM region, and link atoms are introduced to saturate the valence of the QM boundary atoms using the DIV scheme.⁷⁰ The QM regions are identical in all simulations except for the water molecules, because the PR structure has a significantly more open active site and therefore more active site water molecules (Fig. 1b); PPS and closed PR simulations include 3 QM waters and PR simulations contain 9 water molecules in the QM region. To ensure that the QM water molecules are always inside the active-site pocket in the post-rigor state simulations, the Flexible Inner Region Ensemble Separator (FIRES)⁷¹ restraining potential is imposed. ATP is assumed to be fully deprotonated, and all titratable sidechains are kept in their standard protonation states, using estimates of pK_a values from Poisson-Boltzmann (PB) calculations.⁷²

Because of the considerable computational cost associated with QM/MM free energy calculations (with more than 80 QM atoms), our approach is to use generalized solvent boundary potential (GSBP)^73,74 in a DFTB3/MM framework.⁵⁹ For metalloenzyme applications, recent DFTB3 developments have led to encouraging results in predicting structural and semi-quantitative energetic properties,^75–77 including trends in phosphoryl transfer transition state properties in alkaline phosphatase.^63,64 Nevertheless, we perform calibration for DFTB3/3OB-OPhyd⁶¹ using B3LYP calculations for both model and enzyme systems (see Supporting Information); although there remain quantitative errors in DFTB3/3OB-OPhyd, the results support the general trends observed in the DFTB3/CHARMM simulations since the errors are systematic. In the GSBP setup, the system is partitioned into a 24 Å spherical inner region centered at the Mg²⁺ ion, with the remaining portion of the system in the outer region. Newtonian equations-of-motion are solved for the MD region (within 20 Å), and Langevin equations-of-motion are solved for the buffer region (20–24Å) with a temperature bath of 300 K.⁷⁸ Protein atoms in the buffer region are harmonically constrained with force constants determined from the crystallographic B-factors.⁷⁸ Protein atoms in the MM region are described by the all-atom CHARMM22 force field⁷⁹ (including the CMAP correction⁸⁰) and water molecules are described with the TIP3P model.⁸¹ All water molecules in the inner region are subject to a weak GEO type of restraining potential to keep them inside the inner sphere. The static field due to outer-region atoms, ${\varphi }_s^{(io)}$, is evaluated with the linear PB equations. The reaction field matrix M is evaluated with 625 spherical harmonics. In the PB calculations, the protein dielectric constant is set to 1, the water dielectric constant is set to 80, and the salt concentration is set to 0. To be consistent with the GSBP protocol, the extended electrostatic model⁸² is used to treat the electrostatic interactions among inner region atoms where interactions beyond 12 Å are calculated with multipolar expansions. Our previous studies^83,84 indicated that the GSBP protocol is reliable for a site well shielded from the bulk solvent. Prior to the free energy simulations, we run QM/MM simulations to equilibrate the structures for 500 ps with a time step of 0.5 fs.

A Closed PR Structural Model

The closed PR model is a conformation in which SwII is displaced to form a closed active site starting from the PR crystal structure. The model was constructed by Yang et al.³⁴ to investigate the contribution to the ATP hydrolysis activity of residues beyond the immediate coordination shell of the γ-phosphate. Starting from the PR X-ray structure, a RMSD restraint is applied to selected atoms in the active site (backbone atoms of SwI res. 232–238, SwII res. 454–459 and P-loop res. 179–186 and side chain atoms of res. 238, 459, and 461) to drive their positions to the PPS conformation. The force constant is 500 kcal·mol⁻¹·Å⁻² and the target RMSD is 0.5 Å with respect to the PPS structure. The model is equilibrated with 500 ps before the QM/MM free energy simulations. As discussed in the Supporting Information, the active site of the closed PR model remains close to that of the PPS state; we observed, however, that SwII is slightly more flexible, and the salt-bridge between Glu459 and Arg238 sidechains has a minor tendency to deviate from planarity.

Metadynamics

We explore ATP hydrolysis mechanisms in myosin using a combination of metadynamics^65,85 simulations and the string method in collective variables.⁶⁶ Metadynamics is performed using the PLUMED⁸⁶ package interfaced to CHARMM.⁸⁷ The collective variables (CVs) for metadynamics are the anti-symmetric stretch involving the lytic water and the scissile P-O bond (i.e., ${\mathrm{P}}_{\gamma }{\mathrm{O}}_{3\beta }^{\text{ATP}}-{\mathrm{P}}_{\gamma }{\mathrm{O}}^{\mathrm{W}1}$) and the ζ coordinate⁸⁸ that describes proton transfers in the active site. The proton donor, acceptor, and other residues that potentially participate in the proton transfer for various pathways are summarized in the Supporting Information. For each pathway, SHAKE⁸⁹ is applied to bonds involving hydrogens that do not participate in proton transfer. The well-tempered metadynamics method⁹⁰ is utilized with a bias factor of 20~30 depending on the estimated barrier height. Gaussian potentials are placed every 50 fs; the Gaussian height is initially set to 0.1 kcal/mol, and the Gaussian width for the anti-symmetrical stretch and ζ coordinate are set to 0.1 Å and 0.05, respectively. The simulations are performed for 2 ns for each mechanism, and recrossing events between two free energy minima are observed two to three times for each pathway before the simulation is terminated.

The use of the ζ CV is advantageous because neither the identity nor the number of the groups that facilitate the proton transfer need to be specified prior to the simulation.⁸⁸ However, a disadvantage is that the ζ CV cannot not separate distinct proton transfer pathways, e.g., different configurations that correspond to physically distinct pathways can be mapped to the same value of ζ, which also implies that ζ is not generally a kinetically meaningful quantity. To overcome this limitation, metadynamics is used here only to explore the ensemble of configurations sampled by various proton transfer pathways. These configurations are subsequently used to generate initial pathways for free energy simulations using string method, discussed below. Therefore, the metadynamics simulations do not have be completely converged for the purpose of our work.

String Method

The String Method in Collective Variables computes a minimum free energy path (MFEP) that connects local minima on the free energy surface defined in the space of the chosen CVs by

$$W(\overrightarrow{\widehat{\xi }})=-{\beta }^{-1}log\left[Z^{-1}\int e^{-\beta U(\mathbf{X})}\prod _{i=1}^n\delta ({\widehat{\xi }}_i-{\xi }_i(\mathbf{X}))d\mathbf{X}\right],$$ (1)

where ζ⃗(X) = (ζ₁(X), ζ₂(X), ···, ζ_n(X)) are the CV chosen to describe the reaction, and Z is the configuration integral. The MFEP on this surface is a curve (or ‘string’) defined by the condition that the projection of the mean force perpendicular to the path vanishes, i.e.,

$${\left[\mathbf{M}(\overrightarrow{\widehat{\xi }})·\nabla W(\overrightarrow{\widehat{\xi }})\right]}^{\perp }=0,$$ (2)

where ${\mathbf{M}}_{i,j}={\langle {\nabla }_X^{\ast }\overrightarrow{{\xi }_i}·{\nabla }_X^{\ast }\overrightarrow{{\xi }_j}\rangle }_{\overrightarrow{\xi }=\overrightarrow{\widehat{\xi }}}$ is the metric tensor asociated with the transformation to the space of collective variables, and X^* are mass-weighted coordinates. The significance of the MFEP for describing transition pathways comes from the fact that, under certain conditions, it lies near the center of a tube which contains the most likely reaction pathways.⁶⁶ We note that, because the MFEP is one-dimensional, the computational cost of computing the MFEP is generally insensitive to the number of the CVs.

In practice, the string is discretized into a set of N equidistant images ${\overrightarrow{\widehat{\xi }}}_i$, with i ∈ [1 . . . N], and to each point a separate simulation system is assigned. Starting from an initial condition for the string, the images ${\overrightarrow{\widehat{\xi }}}_i^m$ are updated iteratively until a discretized version condition Eq. 2 is satisfied. A straightforward iterative method is to first advance the string using steepest descent:

$${\overrightarrow{\widehat{\xi }}}_i^{\ast }={\overrightarrow{\widehat{\xi }}}_i^m-\frac{\mathrm{\Delta }t}{\gamma }\mathbf{M}({\overrightarrow{\widehat{\xi }}}_i^m)\nabla W({\overrightarrow{\widehat{\xi }}}_i^m),$$ (3)

followed by an an interpolation step that enforces equal distances between adjacent images. M and ∇W in Eq. 3 are computed from simulations with harmonic restraints $k\times {[\overrightarrow{\xi }(\mathbf{X})-{\overrightarrow{\widehat{\xi }}}_i]}^2$, and the parameters Δt and γ are adjusted empirically to accelerate convergence to the MFEP. The free energy profile is the integral along the converged path

$$\mathrm{\Delta }W(\alpha )=W(\overrightarrow{\xi }(\alpha ))-W(\overrightarrow{\xi }(0))={\int }_0^{\alpha }\sum _{i=1}^n\frac{d{\xi }_i({\alpha }^{\prime })}{d{\alpha }^{\prime }}\frac{\partial W(\overrightarrow{\xi }({\alpha }^{\prime }))}{\partial {\xi }_i}d{\alpha }^{\prime },$$ (4)

in which α is used to parametrize the string curve. Further implementation details can be found in Ref.⁶⁷

In the present study, 32 string images are used for each reaction pathway; the initial guess of the string images is constructed from the approximate reaction path obtained in metadynamics simulations using the ${\mathrm{O}}^{\mathrm{W}1}-{\mathrm{P}}_{\gamma }-{\mathrm{O}}_{3\beta }^{\text{ATP}}$ anti-symmetric stretch and ζ as the collective variables as described above, while the CV set used to span each string involves 13–19 active site distances, depending on the reaction pathway, as summarized in the Supporting Information. The values employed for the harmonic force constant and friction in the string method are k = 400 kcal·mol⁻¹·A⁻² and γ = 20 ps⁻¹ (determined by trial and error). 1.5 ns MD simulation at 300 K with a time step of 0.5 fs is performed for each string image. For the last 500 ps, image centers are fixed and free energy gradients are calculated and stored for data analysis. String evolution and reparametrization are performed every 0.5 ps. Due to a substantial degree of sampling for each image, Hamiltonian exchange⁶⁹ was not used in the string simulations. As discussed below, the fact that different mechanistic pathways lead to very similar reaction free energies supports adequate convergence of string simulations.

Average Electrostatic Potential Analysis

For each image of interest (see Sect. “ATP hydrolysis in the closed post-rigor model”), which corresponds to either the reactant or a transition state in the hydrolysis reaction, 2,000 configurations are taken from the corresponding trajectories during the final stage of string simulations. In the Poisson-Boltzmann (PB) calculations, the protein interior is assigned a dielectric constant of 1, and all explicit water molecules are retained and considered part of the solute (thus are assigned a dielectric constant of 1); the implicit bulk solvent has a dielectric constant of 80. As in the GSBP calculations, PB calculations are carried out with a smooth dielectric boundary. Charges on all atoms in the QM region and all water molecules are turned off, and the average electrostatic potential at the grid points within the van der Waals surface of the sites of interest are recorded.

Results

Reactant and Product Structures in the Pre-powerstroke State

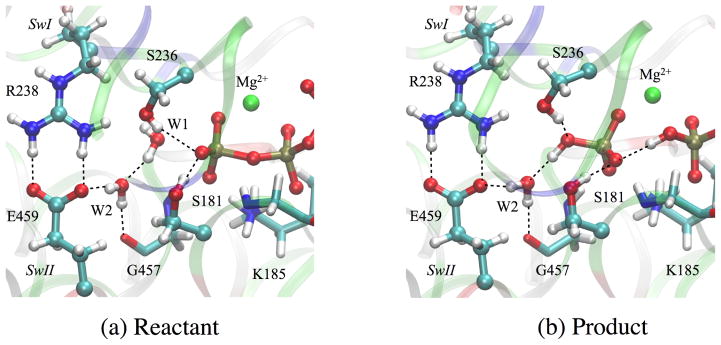
The first issue concerns the definition of reactant and product states in the ATP hydrolysis reaction, which are depicted in Fig. 2. In the reactant state (Fig. 2a), water molecules W1 and W2 form a hydrogen-bonding network that connects the γ-phosphate of ATP and Glu459. In the presence of such a network, the lytic water W1 adopts a favorable position to conduct an in-line nucleophilic attack. ${\mathrm{O}}^{\mathrm{W}1}-{\mathrm{P}}_{\gamma }^{\text{ATP}}$ distance is stable during the MD simulations around 3.2 Å, and the ${\mathrm{O}}^{\mathrm{W}1}-{\mathrm{P}}_{\gamma }^{\text{ATP}}-{\mathrm{O}}_{3\beta }^{\text{ATP}}$ angle fluctuates around 170°. The active site undergoes very minor structural changes when the ATP molecule is hydrolyzed to ADP·Pi in the product state (compare Figs. 2a and b). The inorganic γ-phosphate retains the H-bond to the W2 water and makes a H-bond to the β-phosphate group of the ADP. In the present calculations, the proton between the β- and the γ-phosphate is bonded to the β-phosphate rather than the γ-phosphate. However, the species $\text{ADP}·{\mathrm{H}}_2{\text{PO}}_4^{-}$ and $\text{ADPH}·{\text{HPO}}_4^{2-}$ may be too close in energy (e.g., ~2–3 kcal/mol as found in Ref.²⁹), to be distinguished reliably by DFTB3, which has limited accuracy predicting proton affinity in phosphate species.^59,61 However, the precise location of the proton is not expected to have a significant effect on the reaction mechanisms described below, since the geometries of the two possible end structures are very close.

Figure 2.

The reactant and product states of ATP hydrolysis in myosin simulated by DFTB3/CHARMM (a) Reactant ATP. (b) Product ADP·P_i. Ligands of Mg²⁺ are omitted for clarity. Key hydrogen bonds are highlighted with dotted lines. Note that these structures do not represent energy-optimized stationary points but rather selected structures in the trajectory.

The positions of the other catalytically relevant residues, Lys185, Ser236, Ser181, Gly457 and P-loop backbones remain almost identical between the reactant and the product (the RMSD of residues listed above is 0.36 Å between the average reactant/product structures). Moreover, the salt bridge between the SwI and SwII regions remains intact; the coordination shell of Mg²⁺ in the product also remains the same as in the reactant.⁶² The similarity between reactant and product structures is consistent with the reversibility of ATP hydrolysis in myosin.^91,92

Reaction Pathways in the Pre-powerstroke State

We have observed several distinct reaction pathways for ATP hydrolysis in the pre-powerstroke state. A common feature among these pathways is that the P_γ-O_3β bond breaks before the bond between P_γ and the lytic water (W1) is completely formed. This indicates that the reaction is concerted in nature with a loose transition state, since the metaphosphate species does not correspond to a stable intermediate.⁹³ The lytic water readily associates with the metaphosphate-like species, and the free energy barrier is associated mainly with the transfer of the proton from the lytic water that ends up on one of the dissociation products (either the inorganic phosphate or ADP); the proton transfer can be mediated by different polar groups in the active site, leading to distinct pathways with different free energy profiles. We note that the different pathways show similar free energy differences for the overall hydrolysis reaction, indicating that the computed free energy profiles are converged. In the following, several reaction pathways are discussed in the order of their thermodynamic significance.

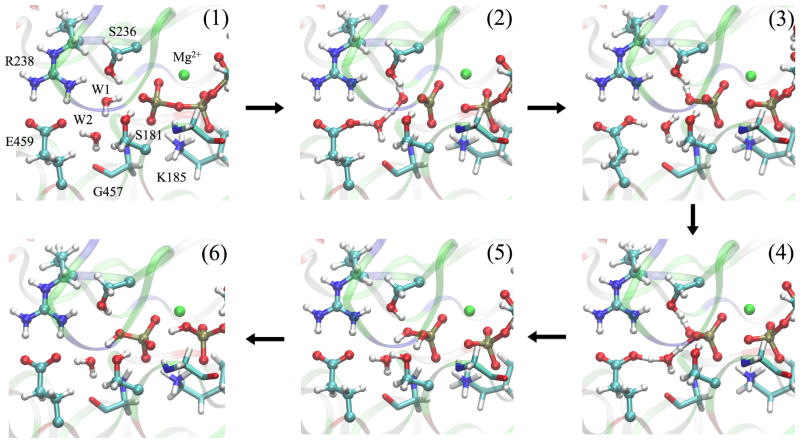
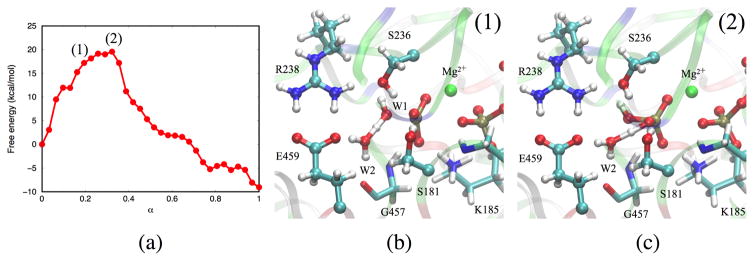
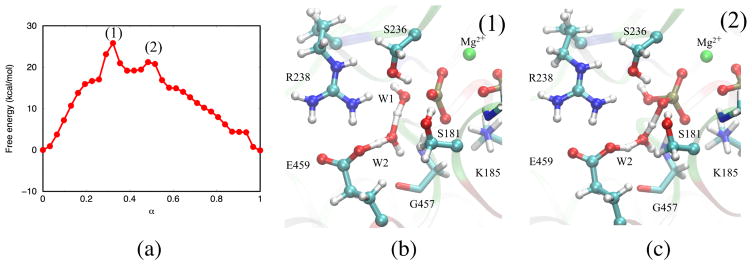
The pathway with lowest free energy profile involves Glu459 and W2 directly in the proton transfers; we refer to this pathway as the W2-E459 mechanism. Representative structures along the MFEP are illustrated in Fig. 3. Immediately following the P_γ-O_3β bond cleavage, proton transfer from the lytic water to the carboxylate of Glu459 proceeds through the mediating water molecule W2 (Fig. 3(2)), leading to a high-energy meta-stable intermediate state (Fig. 3(3)). During the same transition, W1 becomes a OH⁻ and covalently bonds to P_γ, leading to the formation of inorganic phosphate. Next, a proton is transferred from the carboxylic acid of Glu459 to the inorganic phosphate via the same mediating water molecule W2 (Fig. 3(4)), generating the doubly protonated inorganic phosphate (Fig. 3(5)). The proton is subsequently transfered to atom O_3β of ADP, yielding the final hydrolysis products (Fig. 3(6)).

Figure 3.

Representative structures along the MFEP obtained for the W2-E459 mechanism. The structures are numbered according to the locations identified in Fig. 5.

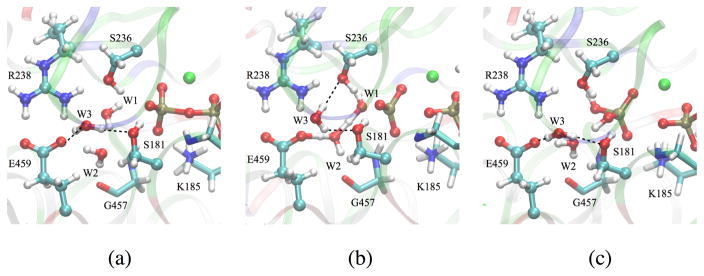
We note that the H-bond network in the active site is not optimal prior to the first proton transfer, because another active site water molecule W3 donates a H-bond to the Glu459 side chain (Fig. 4a). Therefore, a rearrangement of H-bond network is required to facilitate the reaction: W3 breaks its H-bond with Glu459 and rotates to become H-bonded to Ser236 (Fig. 4b). After Glu459 delivers the proton to the γ-phosphate, the H-bond between W3 and Glu459 is restored (Fig. 4c). We note that such H-bond reorganization is difficult to take into account using only a ‘zero-temperature’ minimum-energy path (MEP) analysis, because at least some thermal activation may be required to overcome barriers to W3 rotation, which is orthogonal to the (reaction) coordinate of the proton transfer. This may explain why the W2-E459 pathway was found to have higher barriers in the study of Kiani and Fischer²⁹.

Figure 4.

Rearrangement of a hydrogen-bond involving water W3 in the W2-E459 mechanism (see dotted lines).

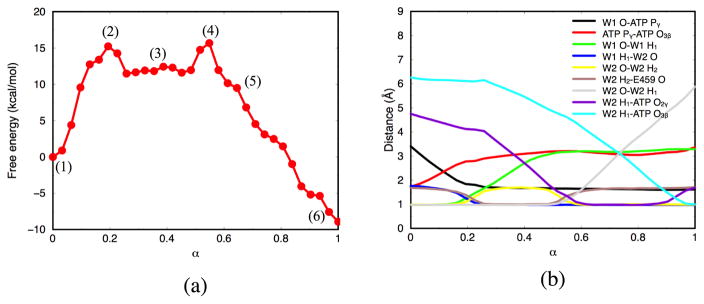
The free energy profile is depicted in Fig. 5a. The first barrier (~15–16 kcal/mol) corresponds to the proton transfer between the lytic water to the side chain of Glu459, while the second barrier is for the proton transfer from Glu459 to the inorganic phosphate and is of similar height; the relatively flat plateau between the two peaks lies ~12 kcal/mol above the reactant and corresponds to the metastable state in which the carboxylate of Glu459 is protonated. Fig. 5b shows the changes in several key bond distances along the MFEP. In the beginning of the reaction, $\mathrm{d}({\mathrm{O}}^{\mathrm{W}1}-{\mathrm{P}}_{\gamma }^{\text{ATP}})$ decreases and $\mathrm{d}({\mathrm{P}}_{\gamma }^{\text{ATP}}-{\mathrm{O}}_{3\beta }^{\text{ATP}})$ increases. Dissociation of the P_γ – O_3β bond is closely correlated with the distance of the new P – O bond with W1. Subsequently, changes in $\mathrm{d}({\mathrm{O}}^{\mathrm{W}1}-{\mathrm{H}}_1^{\mathrm{W}1}),\mathrm{d}({\mathrm{H}}_1^{\mathrm{W}1}-{\mathrm{O}}^{\mathrm{W}2}),\mathrm{d}({\mathrm{O}}^{\mathrm{W}2}-{\mathrm{H}}_2^{\mathrm{W}2}),\mathrm{d}({\mathrm{H}}_2^{\mathrm{W}2}-{\mathrm{O}}^{\mathrm{E}459})$ are synchronous, indicating a concerted proton transfer process.

Figure 5.

(a) Free energy profile along the MFEP obtained from W2-E459 mechanism. Each dot corresponds to an image along the string. (b) Values of the important distances along the MFEP.

Our simulations predict an activation free energy of 15–16 kcal/mol. Experimentally obtained ATPase rate constants^94–96 range from 1 to 100 s⁻¹, which correspond to free energy barriers in the range of 15–17 kcal/mol (converted based on transition state theory and a prefactor of kT/h at room temperature). Therefore, the computed and experimental barrier heights are in good agreement, although single point B3LYP calculations along MEP indicate that the DFTB3 barrier appears systematically too low by at least 2–3 kcal/mol (see Supporting Information). For the exothermicity, the DFTB3/CHARMM value is about 10 kcal/mol. Using the difference between DFTB3 and B3LYP/aug-cc-pVTZ for the exothermicity of a model hydrolysis reaction, which was 9 kcal/mol (see Supporting Information), the corrected value is range of 1~2 kcal/mol, which is in rough agreement with the experimental finding that ATP hydrolysis in the pre-powerstroke state is nearly thermoneutral.^42,94 The relatively small free energy difference reflects that force generation in myosin is driven by the binding to actin, and by the concomitant release of hydrolysis products; the actual hydrolysis step mainly functions to move the system forward into the next stages of the functional cycle.^21,33,97

A pathway that does not explicitly protonate Glu459 involves a proton transfer through the species $\mathrm{W}1\to \mathrm{W}2\to {\mathrm{P}}_{\gamma }{\mathrm{O}}_3^{-}$, and is named here the W2 mechanism. W2 transiently becomes a H₃O⁺ hydronium (Fig. 6b), stabilized by the negatively charged Glu459 sidechain; tilting of the hydronium allows it to transfer a proton back to ${\mathrm{P}}_{\gamma }{\mathrm{O}}_3^{-}$ (Fig. 6c). This pathway has a barrier of 19 kcal/mol (Fig. 6a), which is somewhat higher than the W2-E459 mechanism. The competition between the W2 mechanism and the W2-E459 mechanism can be traced back to the pK_b difference between Glu459 and W2 water in the enzyme environment. Single point calculations of potential energy barriers at the B3LYP level (see Supporting Information) are consistent with the observation that the W2 mechanism is less favorable than the W2-E459 pathway.

Figure 6.

(a) Free energy profile along the MFEP obtained from the W2 mechanism. Each point corresponds to an image along the string. (b) Proton transfer from W1 to W2. (c) Proton transfer from H₃O⁺ to ${\text{HP}}_{\gamma }{\mathrm{O}}_4^{2-}$. Note that these structures do not represent energy-optimized stationary points but selected structures in the specific string image.

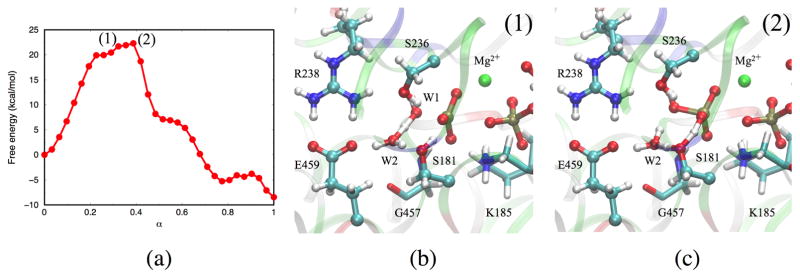
Another route to transfer a proton from W1 to ${\mathrm{P}}_{\gamma }{\mathrm{O}}_3^{-}$ involves the intervening water W2 and Ser181: $\mathrm{W}1\to \mathrm{W}2\to \text{Ser}181\to {\mathrm{P}}_{\gamma }{\mathrm{O}}_3^{-}$. This W2-S181 mechanism was found to be the most probable by the B3LYP/MM MEP studies by Kiani et al.²⁹ The pathway requires W2 to first break an H-bond with the carbonyl group in Gly457, and to form a new H-bond with the side chain of Ser181. The next event of the reaction is similar to the W2 mechanism: formation of a “metaphosphate” and proton transfer occurs from W1 to W2; the proton is further transferred to the hydroxyl oxygen of Ser181, then to the inorganic phosphate, and finally to ADP. The most important intermediates are shown in Fig. 7b–c, and the overall free energy barrier is 22 kcal/mol. The higher free energy barrier compared to the W2-E459 mechanism is likely due to the extra penalty for the initial rearrangement of H-bond network associated with the W2 water. However, single-point energy calculations using QM/MM with B3LYP suggest that the barrier energies for W2-E459 are underestimated with DFTB3/CHARMM (see Supporting Information), and therefore the W2-S181 and W2-E459 should be considered competitive.

Figure 7.

(a) Free energy profile along the MFEP obtained from the W2-S181 mechanism. Each dot corresponds to an image along the string. (b) Proton transfer from W1 to W2. (c) Concerted proton transfer from H₃O⁺ to S181 and from S181 to ${\text{HP}}_{\gamma }{\mathrm{O}}_4^{2-}$. Note that these structures do not represent energy-optimized stationary points but selected structures in the MD trajectories.

Additional reaction pathways in the pre-powerstroke state

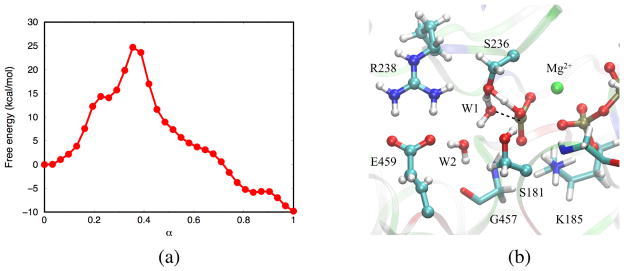
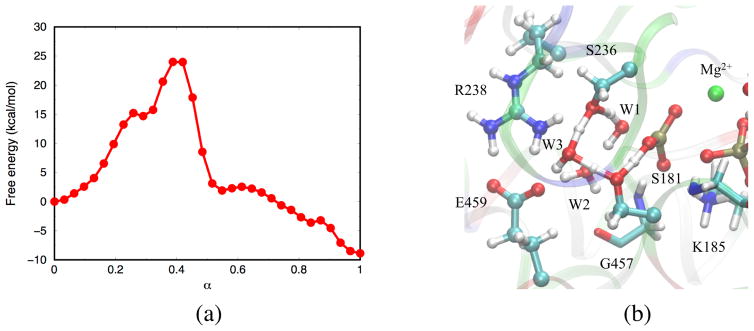
Highly conserved active site serine residues such as Ser236 and Ser181 were proposed^32,34 to serve as proton relays during the hydrolysis process, allowing better stereochemistry for the proton transfers.^44,98 In the S236 mechanism, for example, the lytic water W1 first transfers one of its protons to Ser236, which in turn transfers its hydroxyl proton to the γ-phosphate through a six-membered H-bond ring (Fig. 8b). The rate-limiting barrier along the free energy profile (Fig. 8a) is 25 kcal/mol. Alternatively, a “cycling” pathway, referred to as the S236-W3-S181 mechanism, is also observed; proton transfer occurs along the path $\mathrm{W}1\to \text{Ser}236\to \mathrm{W}3\to \mathrm{S}181\to {\mathrm{P}}_{\gamma }{\mathrm{O}}_3^{-}$ (Fig. 9b). During this transition, P_γ··· O^W1–H^W1 ··· O^S236–H^S236 ··· O^W3–H^W3 ··· O^S181–H^S181 ··· O-P_γ switches to P_γ–O^W1 ··· H^W1–O^S236 ··· H^S236–O^W3 ··· H^W3–O^S181 ··· H^S181–O–P_γ. This process involves a barrier of 24 kcal/mol (Fig. 9a). In the above two mechanisms, the barriers are higher than in the other mechanisms because the center of excess charge in the proton wire lies further away from W2 and Glu459 (see further discussions below).

Figure 8.

(a) Free energy profile along the MFEP obtained from the S236 mechanism. Each dot corresponds to an image along the string. (b) Transition structure in which W1 transfers one of its protons to Ser236, which in turn transfers its hydroxyl proton to the γ-phosphate.

Figure 9.

(a) Free energy profile along the MFEP obtained from the S236-W3-S181 mechanism. (b) Transition structure in which proton transfers along the proton wire $\mathrm{W}1\to \text{Ser}236\to \mathrm{W}3\to \mathrm{S}181\to {\mathrm{P}}_{\gamma }{\mathrm{O}}_3^{-}$.

ATP Hydrolysis in the Post-rigor State

In the PR state of myosin, SwII moves away from the active site and the salt bridge between Glu459 and Arg238 is broken (Fig. 1b). This has at least two consequences to the hydrolysis activity. First, both Glu459 and Gly457 are further away from ATP, and the backbone amide of Gly457 can no longer make an H-bond to the γ-phosphate. This implies that Glu459 is too far away from the reaction site to participate in the proton transfer. Second, the active site is more accessible to bulk water; water molecules in the active site exhibit significantly larger motions.³² Because of these motions, there are no water molecules that can maintain stable contacts with the lytic water. Therefore below we only discuss the S236 mechanism.

In the transition state of the S236 pathway in PR, similar to the situation in PPS (Fig. 8b), the lytic water proton is shared between the donor O^W1 and the acceptor O^S236, while the hydroxyl proton in Ser236 is transferred to the γ-phosphate oxygen (Fig. 10b). The free energy profiles (compare Fig. 8a and 10a), however, are rather different. The hydrolysis reaction is substantially less exothermic in the post-rigor state and the barrier is ~ 40 kcal/mol, which is nearly 25 kcal/mol above the lowest free energy barrier in PPS and ~15 kcal/mol higher than the same S236 pathway in PPS; in fact, it is about 5–10 kcal/mol above the barrier for uncatalyzed ATP hydrolysis in aqueous solution.⁹⁹ Such a high barrier is qualitatively consistent with the lack of hydrolysis activity in PR, an important feature that avoids futile hydrolysis in the functional cycle of myosin.^18,42

Figure 10.

(a) Free energy profile along the MFEP obtained from the S236 mechanism in the PR state. Each dot corresponds to an image along the string. (b) Transition structure in which proton transfers between W1 and S236, and S236 and γ-phosphate.

ATP hydrolysis in the closed post-rigor model

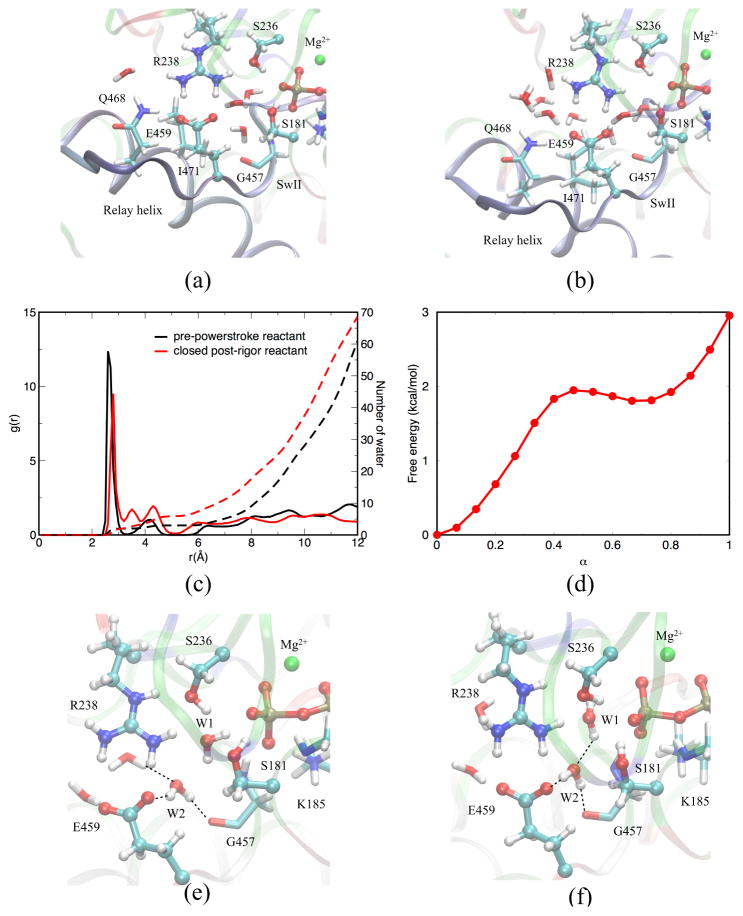
An important question is the extent to which ATPase activity is influenced by groups beyond the immediate coordination shell of the γ-phosphate. To address this question, we study the hydrolysis reaction in the closed PR structural model,³⁴ in which the immediate environment of the γ-phosphate resembles that in PPS, while the rest adopts the PR conformation.

As shown in the Supporting Information, most structural features of the active site in the closed PR model indeed remain close to those in PPS in MD simulations. Therefore, we focus on the W2-E459 mechanism, which is found to be most favorable in PPS. The approximate transition states (shown in Fig. 11b, c) are similar to the ones for PPS (see Fig. 3(2,4)). However, somewhat surprisingly, the free energy barrier is substantially higher in the closed PR model, by about 9 kcal/mol, and the reaction is also notably less exothermic by approximately the same amount (compare Fig. 11a and 5a). The latter observation supports that hydrolysis is less favorable in the closer PR model, regardless of the reaction mechanism.

Figure 11.

(a) Free energy profile for the W2-E459 mechanism in the closed post-rigor structural model. (b) Proton transfer from W1 to the carboxylate group in E459 via W2. (c) Proton transfer from -COOH in E459 to ${\mathrm{H}}_{\gamma }{\text{PO}}_4^{2-}$ through W2. The structures are taken from MD simulation trajectories.

The differences are due in part to distinct water structures in the closed post-rigor model compared to the PPS state. Even though the active site in the model has been closed (Fig. 12a,b), it still is more accessible by the solvent than in the PPS structure (Fig. 12c). This is essentially because residues in the N-terminus of the relay helix, which is immediately C-terminal to SwII, remain in the PR state.

Figure 12.

Comparison of water distribution around carboxylate oxygen of Glu459 (the one closer to water W1) in (a) PPS and (b) closed PR structures. The radial distribution function and its integrated values are shown in (c). (d) Free energy profile for water reorganization in the hybrid PR model state. (e) Initial state of water orientation. (f) W1 and W2 reorient their dipoles before hydrolysis.

W2 is located somewhat further away from the γ-phosphate and receives more stabilization from bulk water (see Fig. 12c). As a result, the hydrogen bonds involving W2 need to reorganize prior to hydrolysis via the W2-E459 mechanism; e.g., the distance between O^W2 and P_γ changes from 5.7 Å to 4.5Å during this transition. To estimate the free energy cost associated with the reorganization step, we conducted separate string calculations for the transition between structures shown in Fig. 12e and f. As shown in Fig. 12d, the free energy change is ~3 kcal/mol, similar to our previous finding.³³

To understand the origin for the remaining ~6 kcal/mol difference in the hydrolysis barriers in the pre-powerstroke and closed post-rigor states, we analyze electrostatic potentials in the active site using Poisson-Boltzmann calculations. Since the barriers in the W2-E459 pathway mainly involve proton transfers among W1, W2 and E459, we focus on the electrostatic potential differences on the relevant oxygen atoms (Table 1). To explicitly evaluate contributions from the protein environment, charges of QM atoms and all water molecules are set to zero; including water contributions does not alter the qualitative trends.

Table 1.

The average electrostatic potential difference (Δϕin kcal·mol⁻¹·e⁻¹) between sites of interest due to the protein environment (excluding QM atoms and water molecules) in the reactant and transition state configurations for the pre-powerstroke and closed post-rigor structures

Structural model	Reactive configuration	Residues excluded	(ΔϕW1;W2 (OW1 - OW2)	(ΔϕW2;E459 (OW2 - OGlu459)
pre-powerstroke	Reactantb	None	25.2 (1.7a)	9.1 (1.3)
pre-powerstroke	TS1c	None	24.8 (2.2)	9.9 (2.6)
pre-powerstroke	Reactant	G457	7.6 (1.7)	17.8 (1.3)
pre-powerstroke	TS1	G457	6.7 (2.3)	17.4 (2.6)
pre-powerstroke	Reactant	S456	18.9 (1.7)	−1.4 (1.1)
pre-powerstroke	TS1	S456	20.2 (2.1)	−0.8 (2.6)
pre-powerstroke	Reactant	≤ 5 Å of OW1	−12.1 (1.7)	9.2 (1.3)
pre-powerstroke	TS1	≤ 5 Å of OW1	−12.8 (2.1)	7.7 (2.5)
“closed” post-rigor	Reactantd	None	25.6 (1.4)	2.8 (1.5)
“closed” post-rigor	TS1e	None	12.6 (2.9)	4.7 (2.6)
“closed” post-rigor	Reactant	G457	6.9 (1.2)	11.1 (1.4)
“closed” post-rigor	TS1	G457	−2.3 (2.8)	7.8 (2.6)
“closed” post-rigor	Reactant	S456	20.5 (1.4)	−6.6 (1.4)
“closed” post-rigor	TS1	S456	11.4 (2.3)	5.2 (2.1)
“closed” post-rigor	Reactant	≤ 5 Å of OW1	1.3 (0.9)	10.0 (1.3)
“closed” post-rigor	TS1	≤ 5 Å of OW1	−0.6 (1.3)	11.4 (1.0)

^aThe values in parentheses are statistical errors calculated from block average;

^bImage 3 of the string in the pre-powerstroke state;

^cImage 6 of the string in the pre-powerstroke state;

^dImage 7 of the string in the “closed” post-rigor structural model (i.e., active site water reorientations described in Fig. 12 has been completed);

^eImage 10 of the string in the “closed” post-rigor structural model;

The electrostatic potential differences summarized in Table 1 reflect the degree to which the protein environment favors the proton transfer between sites. In PPS, the electrostatic potential difference between O^W1 and O^W2 (Δϕ_W1;W2) is ~25 kcal·mol⁻¹·e⁻¹ in both reactant and TS1. The equality of the potential suggests that the protein environment is preorganized for the proton transfer between W1 and W2; e.g., significant dipolar reorganization is not needed to reach the transition state from the reactants. Similar trend is found for the difference between O^W2 and O^E459 (Δϕ_W2;E459). In the closed PR model, Δϕ_W1;W2 is also ~25 kcal·mol⁻¹·e⁻¹ in the reactant configuration (following the completion of the water reorganization shown in Fig. 12e–f); however, the value drops substantially to ~13 kcal·mol⁻¹·e⁻¹ in TS1. For Δϕ_W2;E459, the TS1 value in the closed PR model is also smaller by 50% compared to PPS. Therefore, compared to PPS, the transferring proton in the closed PR structure experiences a smaller electrostatic driving force going from W1 to W2 (and from W2 to E459) in the transition state; moreover, the large difference in Δϕ_W1;W2 between the reactant and TS1 in the closed PR model indicates that the protein environment undergoes more significant dipolar reorganization compared to PPS. These two factors (less electrostatic driving force and larger reorganization) combine to yield a higher barrier in the closed post-rigor model compared to the pre-power stroke state.

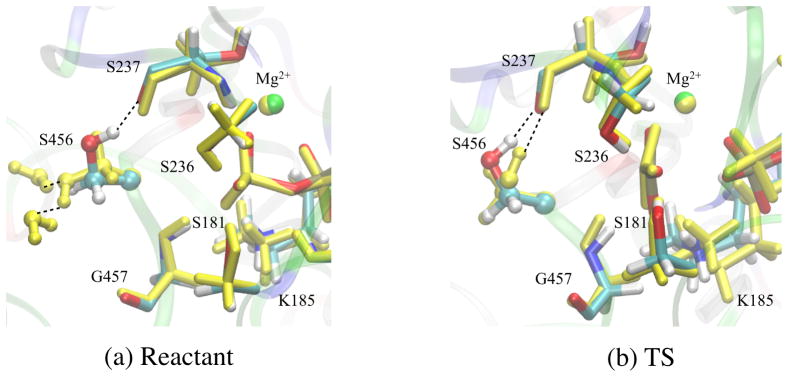
In an attempt to identify residues that dictate the drop in driving force and increase in reorganization in the closed PR model, perturbative analysis is conducted in which the partial charges of specific residues are set to zero and Δϕ values are re-evaluated. In light of the discussion above, we focus on the value of $\mathrm{\Delta }{\varphi }_{W1;W2}^{TS1}$ and the value of ΔΔϕ_W1,W2 between reactant and TS1. As shown in Table 1, when the contributions from residues within 5 Å from O^W1 are excluded, ΔΔϕ_W1,W2 is near zero for both closed PR and PPS structures, and $\mathrm{\Delta }{\varphi }_{W1;W2}^{TS1}$ is in fact more unfavorable (i.e., more negative) in the PPS state. These observations suggest that the larger electrostatic reorganization and lower electrostatic driving force for the closed PR model are dictated by nearby residues (≤ 5 Å from W1). Further, the perturbation results reveal major contributions from Gly457 and Ser456. In PPS, removing Gly457 and Ser456 contributions decreases $\mathrm{\Delta }{\varphi }_{W1;W2}^{TS1}$ by ~18 and ~4 kcal·mol⁻¹·e⁻¹, respectively; the corresponding effects on ΔΔϕ_W1,W2 are small and close to be ±1 kcal·mol⁻¹·e⁻¹. In the closed PR model, removing Gly457 and Ser456 contributions decreases $\mathrm{\Delta }{\varphi }_{W1;W2}^{TS1}$ by ~15 and ~ 1 kcal·mol⁻¹·e⁻¹, respectively; the corresponding effects on ΔΔϕ_W1,W2 are ~ 4 kcal·mol⁻¹·e⁻¹. Therefore, compared to in PPS, Gly457 and Ser456 contribute less to the electrostatic driving force and more to the electrostatic reorganization in the closed PR structural model. Analysis of conformations sampled in different MD simulations suggests that, at least for Ser456, the difference arises from different orientations of the side chain atoms in the PPS vs. closed PR structures due to differences in the local solvation environment (see Fig. 13).

Figure 13.

Superposition of average positions of several active site residues in the (a) reactant and (b) TS windows in the PPS and closed PR (yellow) simulations. The most visible difference is that Ser456 adopts different orientations in the reactant state window due to differences in the solvation environment.

Discussion

Mechanism of ATP hydrolysis in the pre-powerstroke state of myosin

The mechanism of ATP/GTP hyrdolysis in various molecular motors, GTPases and actin has been discussed extensively in recent years. For a number of insightful and recent review articles, see Refs.^{36,38,100,101} In this study, we performed free energy simulations of ATP hydrolysis in different conformation of myosin II using a combination of QM/MM and enhanced sampling methods.

The hydrolysis pathways characterized here are broadly consistent with previous studies of related systems,¹⁰² and in particular, with the recent analysis of Kiani and Fischer²⁹ who found that P_γ-O_3β bond cleavage is facile and occurs early during the reaction. Proton transfer is found to be an important part of the rate-limiting transition state, as also found for other molecular motors, e.g., kinesin³¹ and F₁-ATPase^30,47 using kinetic isotope effect measurements.³⁰ (To the authors’ knowledge, similar kinetic isotope effect experiments in myosin have not been performed.) However, we note that the metaphosphate species was found to form a metastable intermediate prior to proton transfers in several previous computational studies of molecular motors,^29–31 while the P_γ-O_3β bond cleavage and lytic water O-H bond cleavage were found to be largely concerted in the current work. In the study of kinesin,³¹ however, some metadynamics trajectories also showed nearly concerted P_γ-O_3β and lytic water O-H bond cleavages; the barrier for the proton transfer following the metaphosphate was found small in the case of F₁-ATPase.³⁰ Therefore, to fully resolve the competition between concerted and asynchronous mechanisms,¹⁰¹ additional studies that employ a more accurate potential function than the current DFTB3/3OB-OPhyd (see discussion in SI) with adequate sampling is required.

Other differences from previous studies involve identity of the general base, and whether the number of water molecules involved in mediating proton transfer is important to the hydrolysis barrier. Although glutamate has been suggested to be a viable base for ATP hydrolysis in several systems,^30,31,55 Glu459 in myosin forms a salt-bridge with Arg238 in the PPS state; this interaction is expected to lower the pK_a of Glu459, making it a weaker base. Nevertheless, the present QM/MM simulations indicate that the W2-E459 pathway is likely; in fact, DFTB3/CHARMM free energy simulations predict that the W2-E459 pathway has the lowest free energy barrier; however, single point energy calculations using higher-level B3LYP/CHARMM, performed along minimized structures from DFTB3/CHARMM reaction paths (see Supporting Information), indicate that the W2-E459 and W2-S181 pathways are both equally likely. (Free energy simulations using B3LYP/MM are currently computationally prohibitive for large systems). The free energy profile in Fig. 5 indicates that, although protonating Glu459 is indeed energetically costly, the formation of the hydroxide as a strong nucleophile ensures that the energetics of the intermediate species (3) to be in an acceptable range.

Rearrangements in hydrogen bonding networks (Fig. 4) also facilitate changes in the protonation of Glu459 in the W2-E459 pathway; such rearrangements can be missed in an MEP type of analysis, which could explain the finding of a higher energy barrier for the W2-E459 pathway in MEP studies;²⁹ further, since Glu459 is expected to have a low pK_a due to interaction with the positivey-charged Arg238, the deprotonation of Glu459 is unlikely to involve a high barrier.

We note that experiments are unlikely to shed light on the relative importance of the pathways involving Glu459 or Ser181 as the base; for example, both W2-E459 and W2-S181 pathways involve the transfer of multiple protons transition state, and it is unclear whether proton inventory experiments¹⁰³ would be able to distinguish between the two mechanisms.

It is noteworthy that the reaction barrier cannot be estimated on the basis of the number of water involved in mediating the proton transfer. For example, both W2-S181 and S236 pathways involve one water and one hydroxyl as proton relay groups, yet the free energy barrier for W2-S181 is notably lower (compare Figs. 7 and 8). The S236-W3-S181 has a significantly longer proton relay pathway, yet its free energy barrier is close to that for the S236 pathway (compare Figs. 8 and 9). As discussed further below, the free energy barrier is more sensitive to the proximity of the excess charge in the proton transfer transition state to the stabilizing charge group, e.g., Glu459 in the present case.

Factors that regulate ATPase activity in myosin

Several possible factors that influence ATPase activity have been previously discussed, e.g., orientation of the lytic water along the in-line attack trajectory,⁴⁴ polarization of the γphosphate via nearby polar/charged interactions,^29,32,104 β-γ-phosphate orientation,⁴⁸ length of water wire that bridges the general base and the γ-phosphate,⁵⁵ and stability of hydrogen bonding network in the active site, which may rely on the interaction network surrounding the active site and therefore structural state of distal regions.³⁴ These factors are discussed in turn below in light of the present results.

Calculation of the free energy cost for the water reorganization in the closed post-rigor model (Fig. 12d) using the present DFTB3/CHARMM simulations is in accord with the previous classical MD results of 2–3 kcal/mol. This number is modest compared with the difference in the hydrolysis free energy barriers between the PPS and PS states of >15kcal/mol; i.e. water reorganization is insuffucient to explain differences in the hydrolysis rates corresponding to different structures or pathways.

On the role of γ-phosphate polarization by nearby polar residues, our analysis of Δϕ_W1,W2 (Table 1) supports the importance of Gly457 backbone amide as proposed by several previous studies.^29,32,104 The free energy barrier for the S236 pathway is higher by ~15 kcal/mol in the PR vs. the PPS state (see Figs. 10 and 8), and underscores the importance of electrostatic polarization of the γ-phosphate; however, the contribution probably comes from residues besides Gly457, such as water-mediated interactions with Glu459. Other polar interactions that involve SwI and the P-loop,^29,32,104 e.g., residues Ser181, Lys185 and Asn234, are also important to the polarization of ATP; however, they are similar the PPS and PR states.

Gerwert and co-workers observed that when Mg²⁺·GTP binds to Ras or Ras·GAP, the β-γ-phosphate moiety changes its orientation from staggered to eclipsed.⁴⁸ This conformational change could potentially contribute to the polarization of the scissile bond. In the PR and PPS states of myosin, the β-γ-phosphate orientation remains similar with a O_1γ-P_γ-P_β-O_1β dihedral angle close to −25° in both states; the eclipsed conformation is stabilized because Mg²⁺ is coordinated to β and γ-phosphate in both cases. Therefore, change of β-γ-phosphate orientation is unlikely to be significant in regulating the ATPase activity in myosin. Time-resolved infrared spectroscopic studies could provide additional information on how ATP is polarized in the different conformational states of the myosin motor domain, as was done for the analysis of GTP hydrolysis in Ras/Rab systems.^48,49

We highlight, however, that although analysis of vibrational spectra and charge transfer effects in the ground state structures are informative, it is important to evaluate the contribution of these factors to catalysis by explicitly computing the transition states and comparing barrier heights.¹⁰⁵

It is instructive to understand why the different reaction pathways considered here have substantially different barrier heights. In a study of ATP hydrolysis in actin,⁵⁵ McCullagh et al. found that the hydrolysis barrier in G-actin is substantially higher than in F-actin, in agreement with experimental observations; analyses of active site properties such as water wire length and water dynamics led them to propose that “The reduction in barrier height is thus attributed, at least in part, to the favorable proton transport environment seen in the F-actin nucleotide binding pocket ”. As discussed before, comparison of the present pathways in the PPS state indicates that, in myosin, the length of the proton transfer wire per se does not correlate with lower barriers. Instead, the free energy barrier is lowered when the excess charge in the transition state is stabilized by charged residues in the active site. This occurs in the three lowest-barrier pathways: W2-E459, W2 and W2-S181, whereby the hydronium-like species in the transition state are directly stabilized by the carboxylate of Glu459. In the two highest-barrier pathways, S236 and S236-W3-S181, the hydronium-like species are further away from Glu459 and receive less stabilization. This behavior can be captured by a simple gas-phase cluster model (see Supporting Information), which also shows that the effect is adequately reproduced when the carboxylate is described by a MM model, and thus suggests that electrostatic polarization is more important than charge transfer. Finally, as discussed above, the importance of Glu459 electrostatic polarization is also reflected by the much higher barrier for the S236 pathway in PR than in PPS.

A comparison of hydrolysis free energy profiles for the PPS and closed PR model provides insights on the influence of residues beyond the immediate coordination shell of the γ-phosphate. Despite the general similarity in the active site protein structures (see Supporting Information), hydrolysis in the closed PR model is substantially less (~9 kcal/mol) exothermic, and has a higher barrier than in PPS (compare Figs. 11a and 5a). A modest part (2–3 kcal/mol) of this difference comes from water reorganization (Fig. 12d), while the rest is mainly due to residues in close proximity (≤ 5 Å) of the γ-phosphate; compared to in PPS, these nearby residues (e.g., Ser456 and Gly457) in the closed PR model provide a smaller electrostatic driving force, and undergo more significant dipolar reorganization for the proton transfers during hydrolysis. Evidently, efficient hydrolysis explicitly requires precise positioning of only the nearby residues, which control both electrostatic driving force (stabilization) and reorganization contributions.

This observation does not rule out the importance of residues further away. As discussed in Refs. 27,34, maintaining a stable and precise positioning of active site residues relies on structural organizations of distal regions; in the particular case of myosin, this includes the N-terminus of the relay helix and relay loops. Without the structural support of these motifs, the active site would fluctuate between the open and closed configurations with a rather flat free energy profile;³³ mutations to evaluate the contribution of these distal residues on the ATPase activity were proposed.³⁴

Broader Implications: geometry, electrostatics and plasticity in catalysis

It is instructive to discuss the present results in the broader context of enzyme catalysis and enzyme design in general. In their study of ketosteroid isomerase, Boxer and co-workers^106,107 observed a strong correlation between catalytic efficiency and the magnitude of electric field in the active site, as measured through the Stark effect, underscoring the importance of electrostatics in catalysis. On the other hand, Herschlag and co-workers,¹⁰⁸ argue that the electrostatics will not be an effective driver of catalysis unless key polar residues are positioned correctly in the active site. In the case of the design enzyme for Kemp elimination,¹⁰⁹ Mayo and co-workers showed that the low level of catalytic power could be enhanced 6×10⁸ fold with directed evolution; comparison of the crystal structures for the low- and high-activity enzymes suggested that the low activity was due to suboptimal orientation of the substrate, which weakened the stabilization of the transition state for proton abstraction.

In the case of ATP hydrolysis in myosin, we have shown here that the positioning of water molecules and nearby polar/charged groups (Gly457, Glu459) is important; e.g., disruption of the water network contributes to an amount of 2–3 kcal/mol in free energy barrier. Displacement of SwII from the active site, as in the the PR state, weakens stabilizing electrostatic interactions from Gly457 and Glu459, and leads to a much higher hydrolysis barrier. Further, simulations using the closed PR model structure show a substantially higher hydrolysis barrier, compared to simulations that use the PPS structure. This was somewhat surprising, because in the model structure the active site was modified to be in a very similar conformation to that of the PPS state. We therefore conclude that residues beyond the active site also have a significant effect on the catalysis rate. Analysis of electrostatic potentials in the active site further suggests that proper positioning of residues in the active site is important for both enhancement of electrostatic driving force and minimization of dipolar reorganization (or maximization of pre-organization). Therefore, it is fruitful to consider both electrostatic stabilization and pre-organization effects in catalyst design.^110–112

Another interesting feature observed in myosin is the existence of multiple hydrolysis with similar free energy barriers in the pre-powerstroke state; the barriers for the five pathways found span a range of about 10 kcal/mol, which is not much larger than the level of accuracy associated with the semiempirical QM/MM approach adopted here (see Supporting Information). Together with the discussion of catalytic promiscuity in enzymes,^63,113–116 the existence of multiple competitive pathways makes clear that enzyme catalysis can be much more plastic in nature than the traditional “one-enzyme-one-mechanism” postulate. It will be interesting to systematically explore whether multiple competitive pathways coexist in other enzymes and if so, the implication to biological function and evolution of enzymes.¹¹⁷ For instance, the existence of multiple electron transfer pathways and inference among them has been highlighted,^118,119 and multiple polar groups may mediate proton transfers.^120–123 Does this mean the existence of multiple pathways is mostly limited to enzymes that catalyze electron and proton transfer reactions? Is the existence of multiple pathways an accidental feature or actually taken advantage of by evolution, since one may argue that the existence of multiple pathways improves robustness of catalysis and thus perhaps the evolvability of the enzyme. With progress in automated reaction pathway exploration methods^124,125 and integration with exploding amount of enzyme structure data,¹²⁶ these questions can be tackled in the near future.

Concluding Remarks

One of the major hallmarks of natural enzymes is that their activities are tightly regulated. This feature is particularly important to enzymes involved in energy and signal transductions, for which a tight regulation of the chemical event (e.g., NTP hydrolysis) is key to the efficiency of energy transduction^{21,24,33,97,127} and timing of signal transduction.¹²⁸ Therefore, understanding how catalytic activities in enzymes are modulated by structural and dynamical properties of the active site and its surrounding is essential to the elucidation of mechanism for these fascinating systems. On the practical side, such understanding is valuable to the design of effective catalysts.^4,5,12

By combining QM/MM simulations with metadynamics and the string method, we have analyzed in detail the mechanism of ATP hydrolysis activity in the myosin domain. Focusing mainly on the hydrolysis-competent PPS state, we identified multiple reaction pathways of ATP hydrolysis and computed the associated free energy profiles. The scissile bond in the γ-phosphate of ATP breaks early in the reaction; proton transfer from the lytic water to the γ-phosphate through active site residues is an important part of the kinetic bottleneck of the hydrolysis. Different hydrolysis pathways with similar free energy barriers are found, indicating plasticity in the hydrolysis mechanism.

To understand the factors that determine the catalytic efficiency, we also analyzed hydrolysis pathways in PR (in which hydrolysis is disfavored), and in a hybrid model that has active site features of the PPS state, with the overall conformation of the PR state. The results suggest that the ATPase activity depends directly on the positioning of nearby water molecules to conduct efficient in-line attack, but also, indirectly, on residues beyond the active site. From the functional perspective of avoiding futile hydrolysis, the apparent sensitivity of ATPase activity to the positioning of active site motifs is clearly essential, provided that structural transitions in the active site and distal regions are highly co-operative in nature.⁹⁷ In the more general context, the results suggest that optimization of residues beyond the active site for electrostatic stabilization and pre-organization is likely important to enzyme design.

Finally, from a technical point of view, the efficiency of DFTB3/MM simulations enables a unique combination of metadynamics and string simulations for exploring complex reaction mechanisms in an almost automated fashion. Further integration with progress in automated reaction pathway exploration methods^124,125 will be worthwhile. On the other hand, we note that DFTB3 still has considerable errors in the energetics of reactions such as phosphoryl transfers, thus continuing efforts in understanding the origin of these errors and developing physically motivated improvements remain important.¹²⁹ Another possible avenue is to use the DFTB3/MM optimized pathway as initial guess to DFT/MM based minimum free energy path calculations^130,131 to obtain more reliable energetics. Efforts along these lines will be reported in future work.