Substrate and Transition State Binding in Alkaline Phosphatase Analyzed by Computation of Oxygen Isotope Effects

Abstract

Enzymes are powerful catalysts and a thorough understanding of the sources of their catalytic power will facilitate many medical and industrial applications. Here we have studied the catalytic mechanism of alkaline phosphatase (AP), which is one of the most catalytically proficient enzymes known. We have used quantum mechanics calculations and hybrid quantum mechanics/molecular mechanics (QM/MM) simulations to model a variety of isotope effects relevant to the reaction of AP. We have calculated equilibrium isotope effects (EIEs), binding isotope effects (BIEs), and kinetic isotope effects (KIEs) for a range of phosphate mono- and diester substrates. The results agree well with experimental values, but the model for the reaction’s transition state (TS) differs from the original interpretation of those experiments. Our model indicates that isotope effects on binding make important contributions to measured KIEs on V/K, which complicated interpretation of the measured values. Our results provide a detailed interpretation of the measured isotope effects and make predictions that can test the proposed model. The model indicates that the substrate is deformed in the ground state (GS) of the reaction and partially resembles the TS. The highly preorganized active site preferentially binds conformations that resemble the TS and not the GS, which induces the substrate to adapt to the enzyme, rather than the other way around—as with classic “induced fit” models. The preferential stabilization of the TS over the GS is what lowers the barrier to the chemical step.

Graphical Abstract

Introduction

Enzymatic phosphoryl transfer is ubiquitous in biology and it is the central reaction in processes ranging from transcription to protein regulation to ion pumping.^1,2 A compelling hypothesis as to why phosphoryl transfer evolved to play such a central role in biology is that phosphate esters are quite stable in biological conditions, yet enzymes are capable of cleaving phosphate ester bonds with astounding proficiency.^1–3 The notable catalytic proficiency of phosphoryl transferases makes them well suited to serve as models for understanding the fundamental principles of enzyme catalysis. A comprehensive understanding of enzyme catalysis promises important breakthroughs in drug design⁴ and enzyme design.⁵ One of the best examples of a model for studying phosphoryl transfer is alkaline phosphatase (AP),⁶ which boasts a catalytic proficiency ((k_cat/K_M)/k_uncat) of up to 10^27.3,7 In addition to its tremendous catalytic activity in hydrolyzing its native substrates, phosphate monoesters, AP exhibits promiscuous activity toward a wide range of substrate classes, which allows for many tests of its catalytic mechanism and the active site motifs that contribute to catalysis.^8–15

The catalytic mechanism of AP is common to many phosphoryl (and sulfuryl) transferases,^{1,2,6,16–18} where the substrate phosphorylates an enzymatic nucleophile (S102) and releases an alkoxide leaving group (LG). Subsequently, the phosphorylated enzyme intermediate is hydrolyzed to release inorganic phosphate and regenerate the apo enzyme. While much work has gone into experimentally probing the physical mechanism of the first phosphorylation step,^8–13 the interpretation of many experimental probes of this reaction is far from straightforward.^19,20 Mechanisms of phosphoryl transfers can be classified into three categories.^6,17 “Associative” mechanisms are stepwise addition-elimination reactions where nucleophilic attack precedes cleavage of the bond to the leaving group (LG) and those reactions form a true phosphorane intermediate. “Dissociative” mechanisms are stepwise elimination-addition reactions (S_N1-like) where the bond to the LG cleaves prior to nucleophilic attack, forming a metaphosphate intermediate. In concerted mechanisms (S_N2-like), bond cleavage and nucleophilic attack occur in a single kinetic step and there is no intermediate. Concerted phosphoryl transfer can be further classified according to the path the reactants take across the reaction’s free energy surface. Concerted reactions that are “tight” or “loose” are analogous to associative and dissociative reactions, respectively, with the major difference being that instead of a phosphorane or metaphosphate intermediate, the concerted reactions have phosphorane-like or metaphosphate-like TSs (Figure 1). “Synchronous” reactions, on the other hand, have roughly simultaneous cleavage of the bond to the LG and formation of the bond to the nucleophile, so overall bonding to the central P is relatively constant during the reaction.

Figure 1.

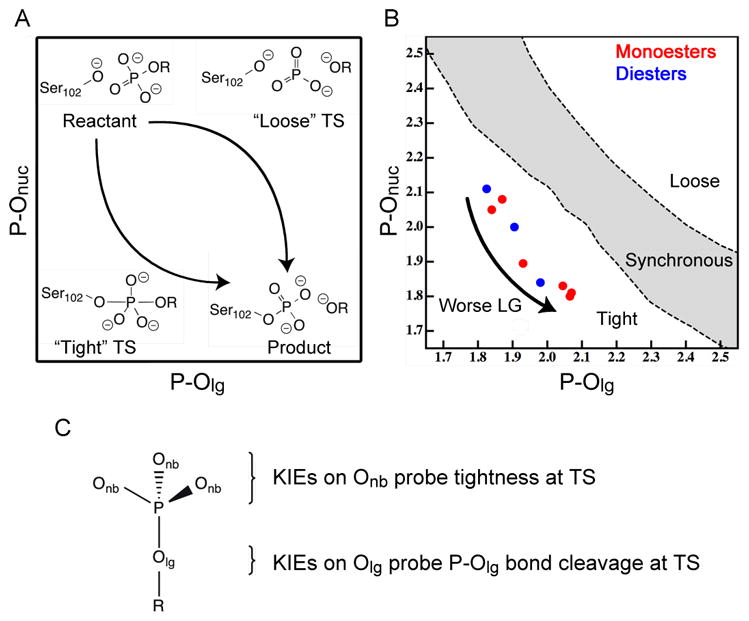
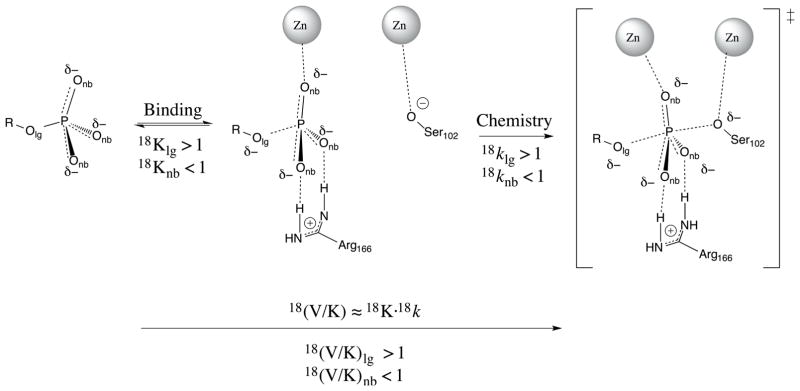
The TS of concerted phosphoryl transfer in AP can be probed with KIEs. (A) The schematic shows that a phosphate ester substrate phosphorylates S102. The phosphorylation step can occur through pathways that range from a tight pathway, with a phosphorane-like TS, to a loose pathway, with a metaphosphate-like TS. (B) Calculated positions of TSs for hydrolysis of phosphate monoesters and diesters from ref. ²⁰. The demarcations of the tightness are based on Wiberg Bond Order (WBO) for the P-O_lg and P-O_nuc bonds. (C) KIEs depend on both the tightness of the TS and the extent of cleavage of the P-O_lg bond at the TS.²¹ Note that while all of the substrates have TSs with similar levels of tightness, the length of the P-O_lg bond at the TS differs substantially among different substrates. Interpretation of experimental KIEs has been further complicated by strong interactions with two active site Zn²⁺ ions in AP.¹²

Experimental probes of transition state (TS) structure, such as free energy relationships (FERs)^8–11,13,19 and kinetic isotope effects (KIEs)^12,22 offer insight into these pathways but these experiments do not always offer a unique and obvious mechanistic interpretation.^23–25 In our recent work,²⁰ we found that a model where LG ability affected TS structure was supported by the observation of curved FERs in AP, changes in KIEs for good vs. poor LGs, and changes in catalytic proficiency across the range of LGs. One of the outcomes of that work, as well as the previous computational work on the reaction in solution,^23–25 was to realize that substrates with different LGs can have markedly different TSs—and indeed use different mechanistic pathways²⁵—which complicates the use of FERs as a means of probing the TS of any given substrate.

While FERs have limitations in probing TS structure due to the perturbation they effect on that structure, KIEs use a much more subtle perturbation, isotopic substitution, that is unlikely to influence TS structure for phosphoryl transfer. (Although isotopic substitution sometimes affects TS structure for hydrogen transfer due to tunneling effects.²⁶) The measurement of KIEs in AP is unlikely to alter the TS being probed, but the interpretation of KIEs for this system is still not straightforward. KIEs are the ratio of rates for substrates that differ only in isotopic substitution and KIEs in phosphoryl transfers are typically interpreted based on a series of guidelines²¹ developed by comparison of KIEs and FERs for relatively simple reactions in solution.²⁷ These guidelines indicate correlations between TS structure and the values of ¹⁸O KIEs on both the LG oxygen (O_lg) and the non-bridging phosphoryl group oxygens (O_nb), shown in Figure 1. The primary (1°) KIE on O_lg indicates the extent of P-O_lg cleavage at the TS, where larger magnitude indicates more cleavage. The secondary (2°) KIE on O_nb reports on the tightness of the TS, where a loose TS typically has an inverse KIE (KIE<1) and a tight TS typically has a normal KIE (>1).

While these guidelines have served for many years, interpretation of many experimental results—particularly those for AP—has been quite challenging. Futhermore, computational work^28–30 has demonstrated the difficulty in reproducing experimental KIEs from microscopic models of reactions and TSs. Even for non-enzymatic phosphoryl transfers, TS structures and the resulting KIEs are sensitive to solvation and protonation states.³⁰ Additionally, catalytic metal ions, such as the active site di-Zn²⁺ in AP, complicate matters even more. An aqueous Zn²⁺-catalyzed phosphoryl transfer, for example, was found to be extremely sensitive to the particular binding mode(s) of Zn^2+.29 Another phosphoryl transfer was found to have a change in mechanism across a series of closely related reactants, thus complicating the computation of KIEs.^25,28 Others have highlighted the sensitivity of simulations of AP to the size of the QM region.³¹ The sensitivity of computational models to so many parameters highlights the fact that KIEs are a sensitive probe of reactivity, challenging to model correctly, and potentially equally challenging to interpret experimentally. Part of the difficulty may stem from an expectation that KIEs on O_lg and O_nb will generally be correlated. Some analyses^6,21 implicitly or explicitly assume that a tight pathway necessarily has little cleavage of the P-O_lg bond at the TS, while that bond is necessarily broken at the TS of a loose reaction. These analyses, however, ignore the position of the TS along the reaction coordinate (e.g., early or late TS) and unnecessarily link the tightness of a TS and the extent of P-O_lg cleavage. There are other challenges, though, that may be somewhat unique to AP, but must be overcome in order to obtain a complete understanding of catalysis by AP.

A particular challenge with interpretation of experimental KIEs in AP (Table 1) is that the measured KIEs did not fit with expectations from the classic guidelines for KIEs in phosphoryl transfers.¹² For example, those guidelines suggest that a loose TS typically has a relatively large KIE on O_lg and a corresponding inverse KIE on O_nb. In AP, however, the substrate p-nitrophenyl phosphate (pNPP) exhibited a ¹⁸(V/K)_lg that was significantly smaller than expected for a loose TS, despite the inverse ¹⁸(V/K)_nb (Table 1).¹² Furthermore, ¹⁸(V/K)_lg for an alkyl phosphate (m-nitrobenzyl phosphate, mNBP) was significantly larger than that for pNPP, even in the R166S mutant where the chemical step is fully exposed for both substrates. Still, the two substrates had similar values of ¹⁸(V/K)_nb. These results were difficult to interpret, particularly in the context of previously measured FERs that were interpreted to indicate that the enzyme does not alter TS structure vs. that in the uncatalyzed reaction.¹³ The authors offered two hypotheses to explain the KIEs in AP: 1) strong interactions between the substrate and the active site moieties (particularly the di-Zn²⁺ moiety) diminished the KIEs (on both O_lg and O_nb) in the enzyme relative to those in solution and 2) KIEs on O_lg are innately larger for alkyl phosphates than aryl phosphates, even for the same extent of P-O_lg cleavage at the TS.

Table 1.

Experimentally measured KIEs for phosphoryl transfer.

Enzymatica	8(V/K)lg	18(V/K)nb
pNPP/WT	1.0003(4)	0.9982(1)
mNBP/WT	1.0072(7)	0.9988(4)
pNPP/R166S	1.0091(6)	0.9925(11)
mNBP/R166S	1.0199(13)	0.9933(4)
Uncatalyzedb	18klg	18knb
pNPP monoanion	1.0087(3)	1.0184(5)
pNPP dianion	1.0189(5)	0.9994(5)

^aFrom ref. ¹².

^bFrom ref. ²⁷.

Here we explore these possibilities using a variety of computational methods ranging from quantum mechanics calculations of small molecules and active site models to hybrid Quantum Mechanics/Molecular Mechanics (QM/MM) simulations of the enzyme. In addition to KIEs on k_chem and V/K, we calculate equilibrium isotope effects (EIEs), which serve as an approximate upper limit for the corresponding KIEs on O_lg, and we also calculate binding isotope effects (BIEs) which allow us to distinguish between different models for the magnitude and direction (normal or inverse) of KIEs on V/K. Our results support the hypothesis that interactions with the active site diminish some KIEs relative to those in solution, but we find that this does not apply to KIEs on O_lg. We also find that the differences in magnitude of the KIEs on O_lg indicate real differences in TS structures. Furthermore, our calculations of BIEs indicate that the substrate is deformed toward a TS-like conformation in the ground state (GS) of the reaction. GS destabilization has been proposed previously as a means of catalysis in AP^7,32 and here we provide additional detail on the GS interactions that affect the reaction. Altogether, our results are consistent with experimental results for AP, but our model deviates somewhat from the previous interpretations of those results. After describing our results and how the model informs notions of catalysis in AP, we propose experiments that can further test our model.

Methods

Active Site Model

QM calculations of an active site model of wild-type (wt) AP mirrored those conducted in previous studies of this enzyme.^20,33 The model contained the active site Zn²⁺ ions and their coordinating ligands (including both the substrate and the nucleophile), and the sidechain of R166 (Figure 2). The starting geometry came from the crystal structure of E. coli AP with phosphate bound in the active site (PDB: 1ED8).³⁴ The phosphate in the active site was converted to the relevant substrate manually and hydrogens were added to the crystal structure using the HBUILD module of CHARMM.³⁵ Enzymatic sidechains in the model were truncated at their β-carbons, which were converted to methyl groups and held fixed during optimizations. Ground state (GS) and TS geometries were found using both density functional theory^36,37 (DFT) at the B3LYP/6-31+G* level as well as using DFTB3.^{33,38– 41} DFT calculations were done using Gaussian 09⁴² and DFTB3 calculations were in CHARMM.³⁵ Additionally, reactant and product geometries were calculated using a variety of DFT methods and DFTB3 in order to calculate EIEs, BIEs, and KIEs on V/K.

Figure 2.

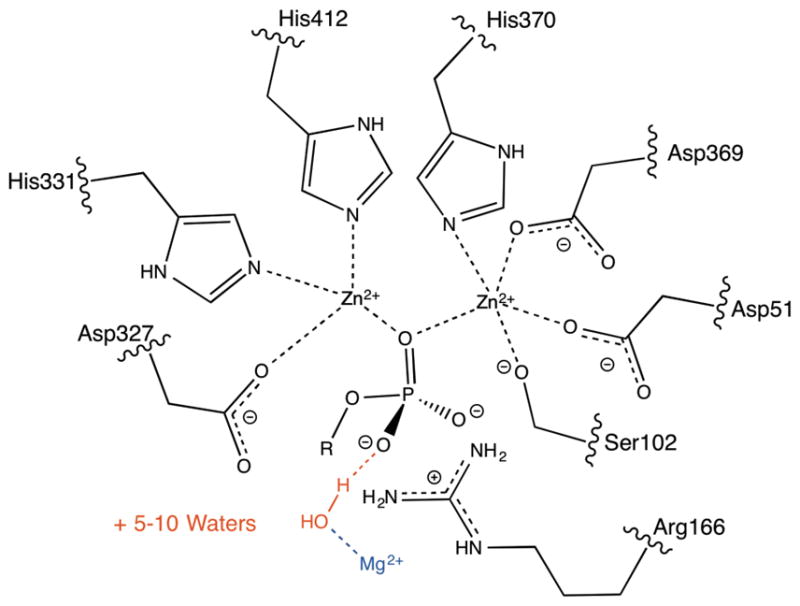
The residues included in the active site model, which was also the QM region for the QM/MM PI-FEP simulations. Only the residues in black were in the active site model. The Mg²⁺ is shown for reference, but was not included in the QM region. In the R166S mutant, S166 was not included in the QM region because prior work showed that including it had negligible effects.²⁰

QM/MM Model

All simulations were done using CHARMM³⁵ according to protocols developed previously in our lab.^20,43–45 The initial setup for the system started from the same crystal structure as the active site model. The protonation states of titratable amino acids were chosen based on hydrogen bonding contacts apparent in the crystal structure. The nucleophilic serine (S102) was deprotonated and disulfide bridges were formed between C168–C178 and C286–C336. The system was overlaid with a 25 Å spherical water droplet centered on one of the zinc ions. Non-crystallographic waters within 2.5 Å of crystallographic atoms were deleted. The R166 mutation was performed in silico, and otherwise that enzyme was treated identically to the WT.

The simulation scheme followed general procedures developed for this enzyme previously^20,43–45 using the generalized solvent boundary potential (GSBP) framework.^46,47 The system was partitioned into 3 regions: the active site was treated with quantum mechanics at the DFTB3 level.^{33,38–40,48} This region consisted of the same atoms as the active site model but with the addition of 5–10 water molecules (ca. 120 atoms, depending on substrate). QM link atoms, using the DIV scheme,⁴⁹ were placed between the α and β carbons of QM residues and a FIRES potential⁵⁰ centered on the P atom of the substrate held the QM waters in the active site. Non-QM atoms within a 27 Å sphere surrounding the active site (ca. 7650 atoms) were treated with the CHARMM36 force field.^51,52 Outside of the 27 Å sphere, all atoms (ca. 8450 atoms) were frozen and this region was treated with the GSBP. The inner sphere was primarily treated with classical Newtonian dynamics, but a buffer region 4 Å from the edge of the sphere was treated with Langevin dynamics. NOE potentials were added to compensate for overpolarization of the QM region by nearby MM atoms, as the boundary between the QM and MM regions needs to be treated with care.⁵³ This included a restraint on the C-O bond of Asp51, and a restraint on the H-bond between the side chain of Asp330 and the backbone of Ser347.⁴⁵ Potentials of mean force (PMFs) along the reaction coordinate (ξ, defined as the difference in length of the breaking and forming P-O bonds) were calculated at 298 K using adaptive umbrella sampling. In most cases, additional biasing was used to sample along the tightness coordinate (defined as the sum of P-O_lg and P-O_nuc). PMFs were calculated using the weighted histogram analysis method⁵⁴ from at least 300 ps of sampling in each window. Most windows included at least 1 ns of sampling.

Calculation of KIEs

We calculated EIEs based on vibrational frequencies in the reactant and product states according to the Bigeleisen equation^55,56 using the program ISOEFF:⁵⁷ This was also the method we used to calculate KIEs and BIEs in the active site model at the B3LYP level. We note that the active site model was constrained by freezing the β-carbons during optimizations, and therefore harmonic vibrational analysis is, in principle, inappropriate. Previous scrutiny of this sort of method, though, found that harmonic vibrational analysis at non-stationary points does not introduce major artifacts into KIE calculations, even when the restrained atoms are directly involved in the reaction.⁵⁸ Another analysis suggested that including all degrees of freedom in the KIE calculation, in contrast to the standard method where rotations and translations are omitted, results in more reliable KIEs for “cut-off” models.⁵⁹ We found that for our model the differences are negligible when we include all degrees of freedom in the calculation (Table S1). It appears that the external rotational and vibrational modes are isotopically insensitive in our model. A difference between our results and those of ref. ⁵⁹ is that our Hessian matrix included all of the atoms that were included in the optimization. The nuances described by ref. ⁵⁹ are apparently more important when the Hessian is calculated only for a small subset of the atoms that were optimized.

We calculated DFTB3 isotope effects in the active site model and DFTB3/MM isotope effects in the full enzyme model using a path-integral free energy perturbation (PI-FEP) method⁶⁰ using similar procedures to refs. ^20,61. PI simulations were done in four states: the unbound substrate and product in solution, an umbrella window in the reactant region (the Michaelis complex), and an umbrella window at the TS for each substrate. In both the Michaelis complex and the TS, the force constant for the umbrella potential was 215 kcal/mol• Ų Simulations in solution mirrored those in the enzyme: the substrate (or product) was dissolved in a 20 Å spherical water droplet whose boundaries were treated with the same GSBP protocol. The substrate and the first solvation shell surrounding the phosphate moiety (or oxide moiety, in product) were treated with DFTB3 and all other waters were treated classically.⁶² The QM waters were held near the phosphate (or oxide) using a FIRES potential⁵⁰ and the P (or O) atom was constrained harmonically to remain in the center of the sphere.

For each PI-FEP simulation, the atom whose mass was changing (i.e., O_lg for 1° isotope effects, O_nb for 2° isotope effects) and any atoms covalently bound to that atom were all quantized and treated as strings of 16 quasi-particles each. In each of 20,000 classical configurations per simulation (representing 200 ps of sampling) we performed 10 Monte Carlo sampling steps of the quasi-particle configurations, for a total of 200,000 quantum configurations. For the active site model, since the classical structure is stationary (i.e., no MD sampling, just the optimized structures), sampling of quasi-particles converged after 100,000 quantum configurations.

Results and Discussion

EIEs Guide the Interpretation of KIEs

We initially explored the EIEs for phosphate ester hydrolysis for two reasons. First, they serve as a simple benchmark to gauge the accuracy of DFTB3 at calculating isotope effects. Second, EIEs on O_lg can serve as an upper limit for the value of KIEs on that atom.²¹ That is, since the KIE measures the extent of P-O_lg bond cleavage at the TS, the maximum value it can reach is the EIE, where the bond is completely cleaved. Measured KIEs, then, can indicate the extent of bond cleavage at the TS in proportion to the upper limit set by the EIE.⁶³ We calculated EIEs for a range of both phosphate mono- and diesters using a variety of methods and the results are presented in Table 2. An important trend appears from these results: worse LGs have larger EIEs. The reason for this is a strengthening of the P-O_lg bond for worse LGs, as manifested by shorter bond lengths and higher stretching frequencies. This is true for all of the methods and in the gas phase, implicit solvent, and using explicit solvent. We refer to this trend as a difference in “innate KIEs” for different LGs (as opposed to “intrinsic KIEs”, which refer to KIEs on a single isotopically sensitive step⁶⁴). That is, for a given TS structure (i.e., a given P-O_lg bond length at the TS) the trend in innate KIEs indicates that worse LGs will have larger KIEs on O_lg. Importantly, DFTB3 captures this trend quite accurately, in terms of reproducing the results of higher-level DFT methods. The direct comparison between methods in the gas phase indicates that DFTB3 is quantitatively reliable and the DFTB3/MM simulations indicate that the trend is clearly manifested in the simulations with explicit solvent. We note that we previously estimated the EIE of ethyl phosphate (EtOP) to be somewhat smaller;²⁰ the discrepancy is in our use of different implicit solvent models. The PCM model⁶⁵ used in Table 2 gives results that are generally consistent with the gas phase trends and that model was successful at reproducing experimental KIEs in a related phosphoryl transfer.²⁸ We previously used the SMD model,⁶⁶ which shows important differences from the trends in the gas phase calculations and in the PCM calculations (Table S2).

Table 2.

EIEs for phosphate mono- and diesters.^a

		Gas Phase				PCM/UFF radiib			Explicit Solvent
Substrate	LG pKa	B3LYP	M06	PBE	DFTB3	B3LYP	M06	PBE	DFTB3/MM
Monoesters
m-nitrophenyl phosphate (mNPP)	8.4	1.008	1.009	1.004	1.011	1.016	1.018	1.012	1.014
phenyl phosphate (PhOP)	10.0	1.009	1.010	1.007	1.019	1.019	1.019	1.014	1.014
p-aminophenyl phosphate (pAPP)	10.3	1.011	1.011	1.008	1.019	1.019	1.022	1.014	1.018
propargyl phosphate (PrAP)	13.6	1.021	1.024	1.016	1.030	1.034	1.035	1.027	1.021
m-nitrobenzyl phosphate (mNBP)	14.9	1.025	1.031	1.028	1.025	1.034	1.037	1.028	1.023
ethyl phosphate (EtOP)	16.0	1.023	1.025	1.017	1.026	1.035	1.038	1.030	1.023
Diesters
methyl-p-nitrophenyl phosphate (mpNPP)	7.2	1.015	1.017	1.012	1.016	1.014	1.019	1.014	1.008
methyl-m-nitrophenyl phosphate (mmNPP)	8.4	1.018	1.020	1.014	1.015	1.023	1.025	1.018	1.012
methyl-phenyl phosphate (mPhOP)	10.0	1.019	1.022	1.011	1.019	1.025	1.028	1.020	1.017

^aAll DFT calculations used the 6-31+G* basis set. Tests using larger basis sets indicated negligible differences.

^bThe implicit solvent⁶⁵ has not been parameterized for DFTB3. An implicit solvent for DFTB-based methods is available,⁶⁷ but it is not yet parameterized for DFTB3.

Capturing this trend is important because one of the principle hypotheses used to interpret the measured KIEs in AP was that EIEs for alkyl LGs are significantly larger than those for aryl LGs.¹² Our results support that hypothesis, although our EIEs do not span as large of a range as was proposed originally (1.03–1.06). Estimates of the EIE are challenging because the product alkoxide gets protonated following bond cleavage. Estimates can be made, however, based on the maximum observed KIEs for similar reactions or from measurements of vibrational frequencies using FTIR. KIEs of 1.06 were observed, for example, in the hydrolysis of alkyl esters,⁶⁸ but our results suggest that extrapolating from one kind of reaction to another is not straightforward: the LG is not all that matters in determining the EIEs, as demonstrated by the differences between mono- and diesters for the same LG (e.g., for PhOP vs. mPhOP). Others have approximated the EIEs by assuming that loss of the P-O_lg stretching mode, as measured by FTIR, is the only contribution to the EIE (and KIE).⁶³ If one approximates that this stretching frequency is the sole contributor to the isotope effect, one can calculate the isotopic ratio of partition functions for that mode and obtain an approximation of the isotope effect.⁶⁹ A difficulty with this is that many vibrational modes may contribute to observed isotope effects. We also note there may be some discrepancy about which IR absorption band corresponds to the P-O_lg stretch. Some sources^70,71 indicate that a band around 1200 cm⁻¹ corresponds to that stretch, but our calculations indicate that the frequency of that mode is much lower (e.g. 656 cm⁻¹ for PhOP and 681 cm⁻¹ for EtOP in implicit solvent at the B3LYP level). The band near 1200 cm⁻¹ in aryl phosphates appears to be the C-O_lg stretch (1275 cm⁻¹ for PhOP), which decreases in frequency for alkyl phosphates (e.g. 1080 cm⁻¹ for EtOP). The P-O_lg and C-O_lg stretching modes are not coupled due to the difference in mass between C and P. In any case, multiple modes make important contributions to the EIE. The C-O_lg stretch, for example, increases in frequency to 1365 cm⁻¹ in the product state, thus diminishing the calculated EIEs. Since the limits set by EIEs play such an important role in guiding interpretation of KIEs for phosphoryl transfers, direct measurements of EIEs would be very helpful. Nevertheless, the fact that multiple DFT methods yield similar results, and that DFTB3 captures the trends and magnitudes of the DFT, gives us confidence in the ability of DFTB3 to accurately model isotope effects for phosphate ester hydrolysis.

Isotope effects in an active site model

We recently²⁰ explored TS structure for the first phosphorylation step in an active site model of WT AP using DFT at the B3LYP level as well as DFTB3. We found that TS structure in the active site model does not depend strongly on the nature of the LG (Figure 3 and Table 3). Here we have tested whether these TSs reproduce the experimentally measured KIEs. Our results for 1° KIEs on both V/K and k_chem, as well as BIEs, are listed in Table 3 (See Supporting Information for definition of V/K for this reaction). For the full range of phosphate monoesters, both DFT and DFTB3 result in early TSs where the bond to the LG has yet to break and that to the nucleophile has yet to form; the value of the reaction coordinate (ξ) at the TS is insensitive to LG ability. The tightness at the TS, however, appears to have some sensitivity to LG ability, where worse LGs have tighter TSs, which resembles results for phosphate ester hydrolysis in solution.²³ The implications of these geometries for the KIEs are intriguing. Both DFT and DFTB3 indicate that ¹⁸k_chem is relatively small and insensitive to LG ability; this may be a compensation effect between the tightening of the TS for worse LGs and an increase in innate KIEs for worse LGs. Intriguingly, there is a notable inverse BIE on O_lg, despite the fact that O_lg does not interact directly with any active site atoms in the Michaelis complex. In some sense this result lends plausibility to the first hypothesis above, that interactions with active site moieties decrease the magnitude of observed KIEs in AP. On the other hand, the active site model calls into question the second hypothesis above: despite the similarity in extent of O_lg cleavage among the various LGs, the calculated KIEs do not follow the trend in the innate KIEs. We do not dwell on the implications of these results for the active site model, though, because the active site model does not reproduce the experimentally observed ¹⁸(V/K)_lg; for all LGs the calculated value is significantly smaller in magnitude than the observed values. The discrepancies in KIEs indicate the active site model does not adequately reflect the enzymatic reaction and the full enzymatic environment is necessary to model the reaction. This may be due to the lack of flexibility in the active site model, where β carbons of all the active site residues were frozen during optimizations. Still, the similarity of trends (or lack thereof) between DFT and DFTB3 adds confidence to our use of DFTB3 for study of the full enzyme model.

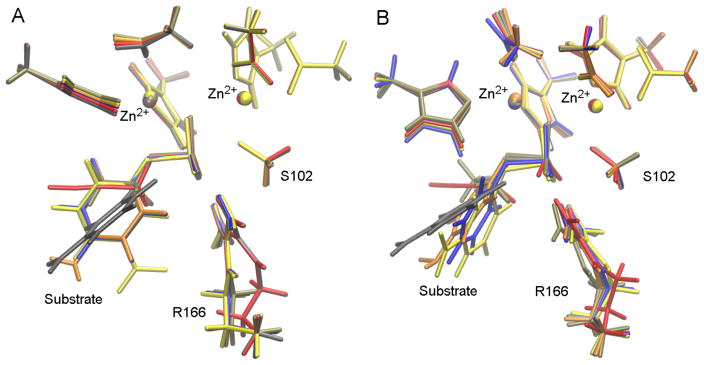
Figure 3.

Overlay of TS geometries in the active site model using DFTB3 (A) and DFT (B). In both cases, TS structure is very similar for all the substrates studied. All TSs are early in the reaction coordinate, with little cleavage of the P-O_lg bond (cf. Table 3).

Table 3.

TS geometries and 1° KIEs in an active site model of WT AP.

		ξ (Å)		R(P-Olg)		R(P-Onuc)		18kchem		BIE	18(V/K)lg
Substrate	LG pKa	B3LYP	DFTB3	B3LYP	DFTB3	B3LYP	DFTB3	B3LYP	DFTB3	B3LYPb	B3LYPb
mNPP	8.4	−0.46	−0.35	1.89	1.89	2.35	2.23	1.010	NDa	0.995	1.004
PhOP	10.0	−0.49	−0.35	1.83	1.83	2.32	2.18	1.009	1.004	0.995	1.004
pAPP	10.3	−0.54	−0.35	1.82	1.82	2.36	2.17	1.007	1.004	0.994	1.001
PrAP	13.6	−0.48	−0.34	1.80	1.79	2.28	2.13	1.010	1.003	0.994	1.003
mNBP	14.9	−0.50	−0.36	1.80	1.80	2.30	2.15	1.007	NDa	0.994	1.000
EtOP	16.0	−0.46	−0.33	1.80	1.78	2.26	2.11	1.010	1.002	0.994	1.004

^aNot Determined because for these substrates the GS structures in the active site model suffer from slow convergence of the SCF using DFTB3, which made calculating KIEs prohibitively expensive. The SCF convergence does not suffer the same problems in QM/MM calculations of the enzyme.

^bSince an implicit solvent model is not yet parameterized for DFTB3,⁶⁷ we could not make a direct comparison between the BIEs and ¹⁸(V/K)_lg, which relied on implicit solvent for the B3LYP calculations.

As mentioned above, standard interpretations of 2° KIEs on the non-bridging phosphoryl oxygens (O_nb) indicate that they report on the tightness of the TS. As with ¹⁸(V/K)_lg, our calculations of ¹⁸(V/K)_nb (Table 4) are somewhat smaller (i.e., more inverse) than those observed experimentally, indicating some deficiency in the active site model. Still, our calculated 2° ¹⁸k_chem is close to unity for both DFT and DFTB3 indicating reasonably good agreement between the methods. DFTB3 gives slightly normal KIEs, while DFT gives slightly inverse KIEs, but the large magnitude of the BIEs indicates that 2° ¹⁸k_chem does not make an important contribution to ¹⁸(V/K)_nb in the active site model. The large inverse 2° BIE results from the strong interactions with active site moieties, which in the case of all three O_nb are direct interactions (Figure 3). The 2° BIE is insensitive to LG, which is not surprising since there is little change in structure of the Michaelis complex as a function of LG. There is, however, a trend in the tightness of the TS as a function of LG, where worse LGs have a tighter TS. Based on the suggestions of ref. ²¹ one would expect an accompanying increase in both ¹⁸k_chem and ¹⁸(V/K)_nb. What we observe, however, is that both ¹⁸k_chem and ¹⁸(V/K)_nb are invariant as a function of tightness. ¹⁸k_chem is near unity for the monoester substrates, which would be expected for a synchronous TS. Unfortunately, there is little guidance available as to how sensitive KIEs ought to be to the changes in tightness our model yields. Ref. ²¹ notes that KIEs on O_nb will involve some cancellation of effects from loosening of stretching modes at the TS vs. tightening of bending modes. Additionally, ref. ¹² proposed that interactions with the di-Zn²⁺ would diminish KIEs. We hesitate to read too much into the active site model since it does not reproduce the experimental KIEs, but these two effects may explain why the contributions from k_chem are insignificant to the observed ¹⁸(V/K)_nb. If so, this suggests that KIEs on O_nb may offer little guidance as to the tightness of the TS for this particular reaction. Instead, they may primarily report on binding effects.

Table 4.

TS tightness and 2° KIEs on O_nb in the active site model.

Substrate		Tightness (Å)		18kchem		Binding	18(V/K)nb
	LG pKa	DFT	DFTB3	DFT	DFTB3	DFT	DFT
mNPP	8.4	4.24	4.12	1.001	NDa	0.974	0.975
PhOP	10.0	4.15	4.01	0.998	1.003	0.977	0.975
pAPP	10.3	4.18	3.99	0.998	1.003	0.975	0.973
PrAP	13.6	4.08	3.92	0.999	1.004	0.976	0.975
mNBP	14.9	4.10	3.95	1.001	NDa	0.970	0.972
EtOP	16.0	4.06	3.89	0.994	1.002	0.974	0.969

^aNot determined. See note to Table 3.

Based on the calculated KIEs, the active site model has clear deficiencies in modeling the reaction of AP. Nonetheless, the active site model has helped to calibrate our intuitions on what factors may contribute to KIEs in AP, and perhaps other phosphoryl and sulfuryl transfers. Additionally, the active site model has assessed the relative accuracy of our semi-empirical method, DFTB3, in reproducing nuclear quantum effects. Importantly, DFTB3/PI-FEP simulations reproduce the trends and (to an extent) magnitudes of higher-level DFT for both 1° and 2° isotope effects. We now turn our attention to DFTB3/MM/PI-FEP simulations of isotope effects in the full enzymatic environment in order to provide a detailed understanding of how observed KIEs for the AP reaction relate to TS structure.

QM/MM simulations of the full enzyme

One of the central findings of our recent studies of AP²⁰ is that the TS structure is sensitive to LG ability, where the extent of P-O_lg bonding at the TS for poor LGs is substantially less than that for good LGs. This result was similar to findings from another study⁷² of TS structure in AP. Here we find that this trend in TS structure translates into substantial differences in the magnitude of 1° KIEs for both monoesters and diesters (Table 5). For both classes, substrates with worse LGs have larger ¹⁸(V/K)_lg. The magnitude of change for diesters is particularly pronounced, where the size of the KIE increases by an order of magnitude over a change in LG ability of just a few pH units. We note that two of our calculated KIEs, those for EtOP/R166S and WT/mPhOP, actually exceed the calculated EIEs for those substrates. Studies of hydrogen transfer typically take KIEs in excess of the relevant limits set by EIEs as evidence of nuclear tunneling effects.⁷³ The PI-FEP method includes all nuclear quantum effects and has been used to understand tunneling effects,^74,75 but we do not take the size of the KIEs here as evidence of tunneling for the following reason. We expect tunneling effects for this reaction to be exceedingly small due to the large mass of the atoms involved. The reduced mass of an O-P stretch is an order of magnitude larger than that of a C-H stretch; its nuclear wavefunction is relatively localized. Instead, we interpret the observation of KIEs in excess of relevant EIEs as an indication of the relative error in the calculations (the statistical uncertainty is on the order of 10⁻⁴). Thus, the fact that the KIEs for poor LGs are within error of the EIEs for those LGs is consistent with the P-O_lg bond being nearly completely broken at the TS for those substrates.

Table 5.

1° KIEs in AP from QM/MM simulations.

Substrate/Enzyme	LG pKa	R(P-Olg)	18(V/K)lg	18kchem	BIE
Monoesters
mNPP/wt	8.4	1.87	1.010	1.004	1.008
PhOP/wt	10.0	1.87	1.008	1.004	1.004
PhOP/R166S	10.0	1.77	1.004	1.001	1.004
pAPP/wt	10.3	1.94	1.012	1.007	1.004
PrAP/wt	13.6	2.05	1.019	1.016	1.004
mNBP/wt	14.9	2.07	1.023	1.017	1.006
mNBP/R166S	14.9	2.12	1.028	1.022	1.006
EtOP/wt	16.0	2.08	1.023	1.017	1.007
EtOP/R166S	16.0	2.09	1.026	1.017	1.008
Diesters
mpNPP/wt	7.2	1.82	1.002	0.997	1.005
mmNPP/wt	8.4	1.87	1.002	1.000	1.002
mPhOP/wt	10.0	1.98	1.020	1.011	1.009

Experimental measurements of KIEs in AP¹² are quantitatively consistent with our calculations for substrates matched on LG ability (~LG pK_a). The measurements observed a smaller KIE for a monoester with a good LG (pNPP, LG pK_a=7.2, ¹⁸(V/K)_lg=1.009) than for one with a poor LG (mNBP, LG pK_a=14.9, ¹⁸(V/K)_lg=1.020). Those KIEs were originally interpreted in a way that sought consistency with previous interpretations of FERs,^8,10,11,13 indicating that the TS for all substrates had substantial P-O_lg cleavage. The reason offered for the large difference in KIE for pNPP vs. mNBP was that KIEs for alkyl substrates are innately larger than those for aryl substrates. Our calculations of EIEs are somewhat consistent with this notion (Table 2), but they do not reflect the scale of differences proposed by ref. ¹². Additionally, our analysis of the active site model, where TS structure is independent of LG ability, indicates that the differences in magnitude of the EIEs do not necessarily translate into differences in magnitude of the KIEs. Instead, our simulations find that the root of the difference in KIEs is in differences in TS structure for good versus poor LGs, where poor LGs have substantially more cleavage of the P-O_lg bond at the TS. We point out that pNPP did not actually fit on the same FER that was used to support the conclusion that the KIEs for pNPP and mNBP represented the same TS; the rate for pNPP deviated from the FER by a factor of 100.¹²

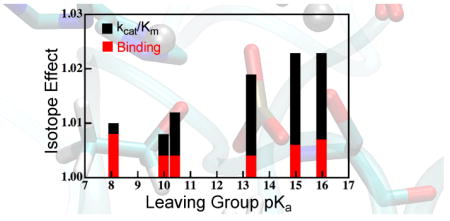
An additional hypothesis that ref. ¹² proposed to explain the KIEs in the context of a TS with substantial cleavage of the P-O_lg bond is that strong interactions with the active site Zn²⁺ ions diminish the observed KIEs relative to their typical values. We can test this possibility in the QM/MM model by examining the substrate with the worst LG ability (EtOP), which has the largest extent of P-O_lg cleavage at the TS, and the closest interactions with the active site Zn²⁺ ion.²⁰ If the interactions with the Zn²⁺ ion diminish 1° KIEs relative to their innate values, the KIEs for EtOP would be significantly smaller than the corresponding EIE. According to our calculations, though, this is not the case. For both WT and R166S, EtOP shows a ¹⁸(V/K)_lg near in magnitude to its EIE. Furthermore, a portion of the values for ¹⁸(V/K)_lg appear to come from normal BIEs (Figure 4), which contradicts the hypothesis that interactions with the active site diminish the observed values of ¹⁸(V/K)_lg. The observation of normal BIEs for this reaction is quite intriguing and suggests that merely binding to the active site already deforms the substrate toward a TS-like configuration. The discrepancy in the direction of BIEs between the active site model and the full enzyme model highlight the necessity of including the full environment in reproducing catalytically important properties. Similar deformations in the GSs of closely related reactions have been observed by vibrational spectroscopy^76–78 and we discuss this phenomenon more below in the context of models of catalysis.

Figure 4.

¹⁸(V/K)_lg increases as a function of LG pK_a due to the increased extent of P-O_lg bond cleavage at the TS for worse LGs. Intriguingly, GS interactions make significant contributions to the value of ¹⁸(V/K)_lg as indicated by the normal (>1) BIEs. The normal BIEs indicate that interaction with the active site of AP in the Michaelis complex deforms the P-O_lg bond toward a TS-like configuration.

2° KIEs in the QM/MM model

Measurements of 2° KIEs in AP found them to be significantly inverse and therefore they supported a model where the TS for phosphoryl transfer was loose.¹² The measured ¹⁸(V/K)_nb were actually substantially smaller (i.e., more inverse) than standard guidelines predict for a loose TS.²¹ This bolstered the hypothesis that interactions with Zn²⁺ decrease KIEs for the AP reaction. We have calculated KIEs on non-bridging oxygens for monoesters in both the WT and R166S (Table 6) and they are largely consistent with the measured values. We obtain inverse ¹⁸(V/K)_nb, which is normally expected for a loose TS,²¹ but based on bond order analyses (Figure 1) the TSs for the AP reaction are tight. Despite the difference in TS structure in our model, the fact that our tight TSs yield inverse ¹⁸(V/K)_nb is consistent with the hypothesis that interactions with Zn²⁺ decrease the 2° KIEs relative to those of a hypothetical uncatalyzed reaction with an identical TS structure. To further understand these KIEs, we dissected the ¹⁸(V/K)_nb into contributions from binding (BIE) and the chemical step (k_chem) and what we found is that even k_chem exhibits inverse KIEs, in contrast to expectations for a tight TS. Interactions with active site moieties do diminish the 2° KIEs in this reaction, including effects on both binding and the chemical step.

Table 6.

2° KIEs on the non-bridging phosphoryl oxygens.

Substrate/Enzyme	LG pK	Tightness (Å)	18(V/K)nb	BIE	18kchem
Monoesters
PhOP/WT	10.0	3.91	0.991	0.996	0.995
PhOP/R166S	10.0	3.84	0.986	0.994	0.992
mNBP/WT	14.9	3.88	0.990	0.997	0.992
mNBP/R166S	14.9	3.94	0.997	0.997	1.000
EtOP/WT	16.0	3.89	0.990	0.995	0.994
EtOP/R166S	16.0	3.91	0.993	0.992	1.001
Diesters
mpNPP/WT	7.2	3.94	0.992	0.992	1.000
mPhOP/WT	10.0	3.83	0.991	0.992	0.998

One note of intrigue in the experimental results was that the values of ¹⁸(V/K)_nb were significantly smaller (more inverse) for R166S than for WT (Table 1), even for mNBP, where the chemical step is exposed in WT. Our results do not reproduce this effect: ¹⁸(V/K)_nb is slightly smaller in R166S for PhOP, but slightly larger for mNBP and EtOP; the differences are likely within the error in the calculations. Unfortunately, the original experimental study did not fully address the difference in ¹⁸(V/K)_nb in the mutant, so it is difficult to understand where our model’s shortcomings might be. Part of the difference between WT and R166S, of course, stems from the fact that chemistry is not fully rate-limiting for WT, as evidenced by the negligible ¹⁸(V/K)_lg for pNPP in WT,²⁷ as well as little LG-dependence of rate, and viscosity effects.⁸ For the WT, monoesters with good LGs are rate-limited by binding;¹⁴ the measured value of ¹⁸(V/K)_nb for pNPP in WT, therefore, is best interpreted as an isotope effect on binding. ¹⁸O BIEs of this magnitude have been observed in other enzymes⁷⁹ and our calculated BIEs on O_nb are consistent with the measured value. ¹⁸(V/K)_lg for mNBP in WT, though, is at least partially exposed (significantly larger than unity), and viscosity effects indicate it is rate-limited by the chemical step. Nonetheless, ¹⁸(V/K)_nb is roughly equal for pNPP and mNBP—if anything, ¹⁸(V/K)_nb is less inverse for mNBP. This suggest that ¹⁸(V/K)_nb reports primarily on binding; exposure of the chemical step in WT does not increase the magnitude of ¹⁸(V/K)_nb meaning that ¹⁸k_chem for the non-bridging oxygens must be near unity. What really convolutes interpretation of ¹⁸(V/K)_nb, though, is the fact that the values in R166S are substantially smaller (more inverse) than the values in WT. If ¹⁸(V/K)_nb reports primarily on binding, one would expect less of an effect in R166S, where an arginine that forms a salt bridge with two out of the three oxygens in question is missing and replaced by water. One might consider, then, whether this is indicative of a change in TS structure for the mutant: there could be a large inverse contribution to ¹⁸(V/K)_nb from the chemical step in the mutant. A large inverse ¹⁸k_chem on the non-bridging oxygens would typically indicate a loose TS where P-O_lg bond cleavage is complete at the TS. A model where the TS is substantially looser for R166S vs. WT would be consistent with the substantially larger ¹⁸(V/K)_lg for mNBP in R166S. It would not, however, be consistent with FERs, which indicated that if anything, the TS for R166S has less P-O_lg bond cleavage than that for WT (β_lg=−0.66 ± 0.1 in R166S and β_lg=−0.85 ± 0.1 in WT). An alternative explanation is that in contrast to standard expectations, a more inverse ¹⁸(V/K)_nb is actually an indication of a tighter TS, but this contradicts the larger value of ¹⁸(V/K)_lg in R166S. We thus lack a plausible model that would completely explain the measured values of ¹⁸(V/K)_nb in R166S and our simulations offer no help. More work will be necessary to understand the subtle factors that influence ¹⁸(V/K)_nb for this reaction and others.

Binding and Catalysis

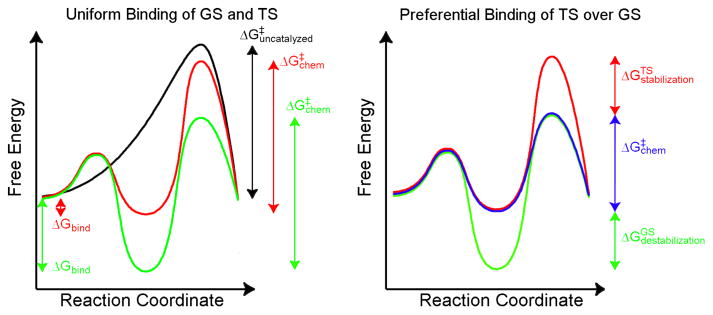
One of the central questions of enzyme catalysis—and indeed all forms of catalysis—is how a catalyst lowers the activation barrier for the chemical step.⁸⁰ That is, how does a substrate bind to a catalyst in such a way that it binds more strongly in the TS than in the GS? A survey of the available literature on enzyme catalysis^81–85 suggests that this preferential binding comes from a combination of interactions that provide specific stabilization of the TS along with interactions that provide specific destabilization of the GS. While most studies focus on the TS, recent studies of AP have highlighted a role for GS destabilization in this reaction,^7,32 One can understand these effects by comparing the catalyzed reaction to a reference reaction where the catalyst is less effective at lowering the barrier. The choice of an appropriate reference reaction can be difficult, though. At times one can evaluate the role of a specific residue (e.g. R166 in AP¹⁴) and use a mutant as a reference to understand catalysis relative to that mutant by measuring rates and binding constants in both cases. In terms of absolute catalysis relative to the reaction in solution, though, the choice to refer to a catalytic effect as TS stabilization or GS destabilization is often a philosophical matter. To assess absolute catalytic effects, one must imagine a reference reaction where the substrate binds uniformly in the GS and TS (Figure 5). The reference reaction one chooses, though, is generally entirely hypothetical—no such reaction with uniform binding exists in reality—and thus one is free to choose a hypothetical reaction that implies one model or the other or some combination of the two. The distinguishing feature between various models is merely how strongly the substrate is bound in the hypothetical reference reaction. A strongly binding reference reaction leads one to conclude that the primary source of catalysis is GS destabilization, while a weakly binding reference reaction leads to a conclusion of TS stabilization. Since the choice of a reference reaction is largely arbitrary, the choice of how to classify any given interaction that lowers the barrier for the chemical step is largely arbitrary. That is, the catalyst’s preferential binding of the TS over the GS cannot easily be attributed to either its interactions with the TS or its interactions with the GS.

Figure 5.

TS stabilization versus GS destabilization as sources of catalysis. To understand the origins of catalysis, it is useful to compare the uncatalyzed and catalyzed reactions with alternative scenarios where binding of the substrate is not preferential for the TS. On the left are two situations of uniform binding, where the GS and the TS bind equally to a hypothetical catalyst. In the example given by the red curve, the substrate binds more weakly to the catalyst than in the green curve. Since binding is uniform, though, the strength of binding does not affect ΔG^‡ for the chemical step; for both strong and weak binding, ΔG^‡ for the chemical step is equal to that for the uncatalyzed reaction. On the right is a situation (blue) where the substrate binds preferentially to the catalyst in the TS over the GS and thus lowers the activation barrier for the chemical step. Depending on which hypothetical reaction one uses as a reference, the barrier height is lowered by the value of ΔG_{stabilization} of the TS or by ΔG_{destabilization} of the GS (both of which are equal). The question of whether to refer to this phenomenon as TS stabilization or GS destabilization is a question of the reference reaction of uniform binding one chooses. If one prefers a reference that binds weakly (red), then the catalytic phenomenon is TS stabilization. If one uses the strongly binding reference (green), then the catalytic phenomenon is GS destabilization. One could also use a reference with intermediate binding that would imply that a combination of TS stabilization and GS destabilization is at work. Since the choice of reference is largely arbitrary, one cannot easily assign catalytic effects to the TS or the GS.

Thus, while it is intuitively tempting to classify the phenomenon highlighted by the BIEs on O_lg as GS destabilization, we prefer to state merely that the substrate is deformed in the GS and partially resembles the TS. The normal (>1) 1° BIEs for O_lg indicate that O_lg is more delocalized in the Michaelis complex than it is in the unbound substrate, consistent with a weakening of the P-O_lg bond in the Michaelis complex. Previous studies of binding effects in AP and a closely related phosphatase suggested a role for GS destabilization in lowering the barrier for the chemical step.³² Those results showed that the charge repulsion between the anionic nucleophile and the substrate destabilize the Michaelis complex relative to complexes lacking anionic nucleophiles. That model is consistent with the effect we observe. In particular, negative charge repulsion between the nucleophile and the phosphoryl moiety would favor depletion of negative charge in the phosphoryl group in the GS. One mechanism to accomplish this is to shift electron density away from the phosphoryl group by polarizing and weakening the P-O_lg bond, thus moving negative charge onto O_lg (Figure 6 and Table S3). Deformations like this are present in the GSs of similar enzymes^76,78,86 and this may be a general phenomenon.

Figure 6.

Observed KIEs on V/K result from contributions of both binding and chemistry (See Supporting Information for derivation of rate equations). GS interactions between the non-bridging oxygens and active site moieties yield inverse BIEs on O_nb. BIEs on O_lg indicate that the substrate is deformed in the GS such that the P-O_lg bond is weakened and is beginning to resemble the TS. The various positions of the TS for various substrates yield different extents of P-O_lg bond cleavage in the TS, which results in different magnitudes of ¹⁸k_lg for different substrates. ¹⁸k_nb is near unity (or slightly inverse), consistent with the tight TSs obtained in our simulations.

The phenomenon of deformed GS structures is reminiscent of near attack conformers,⁸⁷ and adds a level of nuance to classic “induced fit” models found in textbooks. In such models, flexible enzymes are thought to adapt to the properties of the substrate in order for the substrate to bind tightly. An overly flexible enzyme, though, might easily adapt to both the GS and TS, providing uniform stability to the GS and TS and not serving as a good catalyst (cf. Figure 5). An enzyme that is highly preorganized for the TS, however, could potentially provide more preferential binding of the TS over the GS. That is, a preorganized enzyme that has evolved to be complementary to the TS will not adapt to the geometry and electronic properties of the GS. Instead, the enzyme’s unwavering preference for the TS could lead to deformation of the substrate in the GS to partially resemble the TS. In this situation, then, it is not the enzyme that adapts to the shape and charge distribution of the substrate, but the substrate that adapts to the physicochemical features of the enzyme. The enzymology literature of course contains a number of notable, well-studied examples where the enzyme undergoes substantial structural changes upon binding a substrate and at other steps along the reaction coordinate.^88,89 Furthermore, motions on various timescales are believed to be directly coupled to the chemical transformation in many enzymes.^90,91 Nonetheless, AP is one of the most catalytically proficient enzymes known^3,92 and it appears to be highly preorganized for the TS; crystal structures with a variety of ligands—both covalently and non-covalently bound, representing GS and TS analogs, as well as intermediates, and products—are all strikingly similar to the structure of the apo enzyme.^34,93–97 This suggests that while conformational flexibility may serve a purpose in many enzymes, it is not required to achieve catalytic proficiency.

Experimental Tests and Predictions

We find it gratifying that our DFTB3/MM model accurately reproduces trends and magnitudes in ¹⁸(V/K)_lg and reproduces the direction (normal or inverse) and approximate magnitudes of ¹⁸(V/K)_nb while providing a plausible explanation for non-linear FERs and other catalytic intrigues.²⁰ Since the present model differs from other models that were proposed to interpret those experimental results, one may wonder at this point if there are additional tests that can distinguish between our model and that proposed previously. For that we first turn our attention to ¹⁸(V/K)_lg for diesters, where even for aryl LGs we predict substantial differences in the magnitude of the KIEs. Since our calculated KIEs for the best LGs (p-nitrophenoxide and m-nitrophenoxide) are near unity, indicating little (if any) P-O_lg bond cleavage at the TS, very little of the difference in magnitude versus the phenoxide LG can be attributed to differences in innate KIEs. We urge experimental enzymologists to measure KIEs for diesters in AP.

An additional test that we concede will be significantly more challenging is to measure KIEs on O_nuc. The fact that O_nuc is part of the catalyst would likely preclude the use of competitive KIE measurements and therefore make it difficult to obtain measurements with the necessary precision. Nonetheless, we suggest this as a challenge to the experimental community because we expect substantial differences in KIEs on O_nuc for different substrates (essentially the opposite trend observed in KIEs on O_lg). Additionally, the combination of KIEs on O_lg and on O_nuc would provide more easily interpretable information on the tightness at the TS, because it would give information on both the P-O_lg and the P-O_nuc bonds at the TS. Thus, measuring ¹⁸(V/K)_nuc would go a long way toward distinguishing between the present model and that proposed by ref. ¹². Another challenging but potentially rewarding test would be to measure BIEs for substrate analogues. Such measurements could help to further articulate the role of GS deformation in this reaction, thereby furthering our understanding of the catalytic power of AP.

Conclusions

We have provided an extensive analysis of isotope effects in AP that sheds light on the catalytic mechanism of this reaction, and ought to provide guidance for understanding related enzymes involved in both phosphoryl and sulfuryl transfers. We find that a model of the reaction where the structure of the TS is tight, but the extent of P-O_lg cleavage at the TS depends heavily on LG ability accurately reproduces the trends and magnitudes of the measured KIEs in AP. The model indicates that substantial portions of the observed KIEs on V/K stem from contributions from binding. The O_lg atom experiences a significant loosening of its vibrational environment upon binding, while O_nb atoms experience a significant tightening of their vibrational environment. The results provide a detailed picture of the enzyme’s reaction pathway, which helps to articulate recent findings on “GS destabilization”^7,32 as a means of understanding the immense catalytic power of AP. The enzyme is preorganized to bind the TS and when the substrate binds, it is deformed toward a TS-like conformation.

The fact that our model reliably reproduces both 1° and 2° KIEs is satisfying given the difficulty in calculating KIEs for phosphoryl transfers.^28–30 Others found, for example, that phosphoryl transfer KIEs are highly sensitive to the mode of interaction with Zn²⁺ ions²⁹ and without any specific parameterization of Zn-interactions, our model reproduces trends and magnitudes of KIEs for a range of substrates. In addition to reproducing the KIEs for AP, we have provided calculations of EIEs, which can serve as a guide for interpreting KIEs in other phosphoryl transfers. In the past, approximations of those EIEs have guided interpretations of KIEs and the importance of having accurate guides cannot be overstated. In the end, our calculations provide mixed support for the hypothesis about EIEs originally proposed to explain AP’s KIEs. The upper limits of KIEs on O_lg set by EIEs are larger for worse LGs, but the range is not as large as previously thought and the difference in innate KIEs alone cannot explain the difference in KIEs for different substrates in AP. The TS structures are different for good vs. poor LGs. Our model also supports the hypothesis that KIEs on O_nb are diminished in AP due to interactions with the active site Zn²⁺ ions. Inverse BIEs contribute to the observed ¹⁸(V/K)_nb, but even ¹⁸k_nb is inverse, despite the fact that tight TSs typically have normal ¹⁸k_nb.

Our model does, however, contain a discrepancy in the calculated magnitude of the 2° KIEs in R166S vs. WT. Unfortunately, we are unable to propose a model to explain this discrepancy. The many subtle factors that contribute to isotope effects in an enzyme active site must be properly balanced in order to achieve a thoroughly predictive model of enzyme catalysis. Isotope effects are one of the most potentially useful probes of reactivity available. They inflict a very minor perturbation on the reaction yet they are very sensitive to structural and environmental properties along the reaction coordinate. Their sensitivity to interactions within enzyme active sites complicates their interpretation and necessitates finding agreement between microscopic computational models and experimental observations. The method we have used, based on DFTB3/MM/PI-FEP simulations, makes an important step forward in providing a microscopic basis for the observed KIEs. Furthermore, the qualitative and semi-quantitative agreement with experiment instills confidence in using DFTB3/MM simulations to understand phosphoryl transfer in enzymes where experimental benchmarks are not as readily available as for AP. There is a wide variety of phosphoryl transferases—as well as closely related sulfuryl transferases—and computational study has the potential to uncover the principles underlying catalysis and substrate specificity of these enzymes.