Leaving Group Ability Observably Affects Transition State Structure in a Single Enzyme Active Site

Abstract

A reaction’s transition state (TS) structure plays a critical role in determining reactivity and has important implications for the design of catalysts, drugs, and other applications. Here we explore TS structure in the enzyme alkaline phosphatase using hybrid Quantum Mechanics/Molecular Mechanics simulations. We find that minor perturbations to the substrate have major effects on TS structure and the way the enzyme stabilizes the TS. Substrates with good leaving groups (LGs) have little cleavage of the phosphorus-LG bond at the TS while substrates with poor LGs have substantial cleavage of that bond. The results predict non-linear free energy relationships for a single rate-determining step, and substantial differences in kinetic isotope effects for different substrates; both trends were observed in previous experimental studies, although the original interpretations differed from the present model. Moreover, due to different degrees of phosphorous-LG bond cleavage at the TS for different substrates, the LG is stabilized by different interactions at the TS: while a poor LG is directly stabilized by an active site zinc ion, a good LG is mainly stabilized by active site water molecules. Our results demonstrate the considerable plasticity of TS structure and stabilization in enzymes. Furthermore, perturbations to reactivity that probe TS structure experimentally (i.e., substituent effects) may substantially perturb the TS they aim to probe, thus classical experimental approaches such as free energy relations should be interpreted with care.

Graphical abstract

Introduction

Chemical reactivity is largely determined by the structure and energetics of the transition state (TS) of a given reaction, thus it is vital to thoroughly understand the nature of TSs. Good models for the nature of TSs have allowed for accurate predictions of reactivity in organic chemistry,¹ the design of TS analogue inhibitors of enzymes as drugs,² and even the de novo design of enzymes.³ Inherent in most models of TS structure is the expectation that small changes to reactants (e.g., different substituents) will have negligible effects on TS structure.^4,5 The supposed reliability of this assumption has facilitated the apparent success of classic experimental probes of TS structure, such as free energy relationships⁵ (FERs) and kinetic isotope effects (KIEs). Similarly, the catalytic roles of active site residues are assumed to be identical for closely related substrates. In the present exploration of TS structure in an enzymatic phosphoryl transfer, however, we find that these assumptions may not rest on very firm ground.

Enzymatic catalysis of phosphoryl transfer is a ubiquitous biological process, which offers a window into the general mechanisms by which enzymes catalyze reactions.^6,7 An excellent model enzyme for understanding catalysis of phosphoryl transfer is alkaline phosphatase (AP).⁸ AP catalyzes the hydrolysis of phosphate monoesters, its native substrates, in addition to exhibiting promiscuous activity toward phosphate diesters,^9,10 phosphorylated pyridines,¹¹ phosphorothioates,¹² and even sulfonic esters.¹³ AP’s promiscuity allows for a variety of tests of the mechanism and source(s) of catalytic power of this enzyme. The chemical mechanism of hydrolysis by AP is similar to phosphoryl transfer in many enzymes:¹⁴ the substrate phosphorylates an enzymatic nucleophile (S102), and this phosphorylated-enzyme intermediate is subsequently hydrolyzed to release inorganic phosphate. Important questions remain about how AP and other phosphoryl transferases catalyze the first phosphorylation step.

Phosphoryl transfers are generally classified to occur through three characteristic pathways:^8,15 (1) “Associative” reactions are stepwise addition-elimination mechanisms with a true pentavalent phosphorane intermediate. (2) “Dissociative” reactions are stepwise elimination-addition mechanisms (S_N1-like) with a true metaphosphate intermediate. (3) Concerted reactions occur in a single step (S_N2-like) and have no intermediate. Concerted reactions are further classified by their pathways in an analogous way, but for concerted pathways, they are referred to as “tight”, “loose”, or “synchronous”. Tight pathways involve formation of the bond to the nucleophile earlier in the reaction coordinate than cleavage of the bond to the leaving group (LG). Tight reactions are characterized by a phosphorane-like TS; a tight reaction pathway is geometrically similar to an associative reaction pathway, but the free energy surface of a tight reaction contains just a single saddle point along that pathway. Likewise, a “loose” pathway resembles a dissociative pathway geometrically, but the free energy surface contains a single saddle point constituting a metaphosphate-like TS. Synchronous pathways, then, involve roughly simultaneous bond cleavage and bond formation during the single step. Hydrolysis of phosphate esters tends to be concerted,^8,14 and thus our discussion will generally be limited to questions of tight, synchronous, or loose pathways and their associated TSs. Studies of uncatalyzed phosphoryl transfer in solution indicated that the tight and loose pathways pose similar free energy barriers,^16,17 suggesting that an enzyme catalyzing this reaction could have evolved to stabilize a TS along either one of those pathways. The possibility that reaction pathways for phosphoryl transferases must be determined on a case-by-case basis is daunting, so there is a need to discover underlying principles that select for one pathway over the other. This requires an explicit probe of TS structure in an enzyme active site using multiple types of substrates.

AP is an excellent system in this context. Its open active site and accompanying promiscuity have allowed for classic experimental probes of TS structure, including measurements of FERs^10,12,18,19 and KIEs²⁰ using a broad range of substrates. Interpretation of such measurements, however, has not been straightforward. Some data points do not fit with expectations from simple models of TS structure and were therefore excluded from fits.^10,12,19 After excluding those points, the best fit to the data was a model where monoesters go through a loose TS, while diesters go through a more synchronous TS;¹⁰ in other words, the TSs in the AP active site resemble those in solution. The suggestion that native substrates use a loose pathway, though, raises questions about the role of an active site arginine, R166, which provides a 10⁴-fold rate enhancement.²¹ R166 H-bonds to the non-bridging phosphoryl oxygens in crystal structures of product²² and TS analogue complexes.²³ If the TS is indeed loose, one would expect negative charge on those oxygens to decrease (i.e., become less negative) at the TS (Figure 1), meaning that interactions with the positively charged arginine could be anti-catalytic. The difficulties in interpreting experimental probes motivated us to examine TS structure in AP using hybrid Quantum Mechanics/Molecular Mechanics (QM/MM) simulations with the additional goal of demonstrating the reliability of using computations in the future to understand enzymes that are less susceptible to experimental probes.

Figure 1.

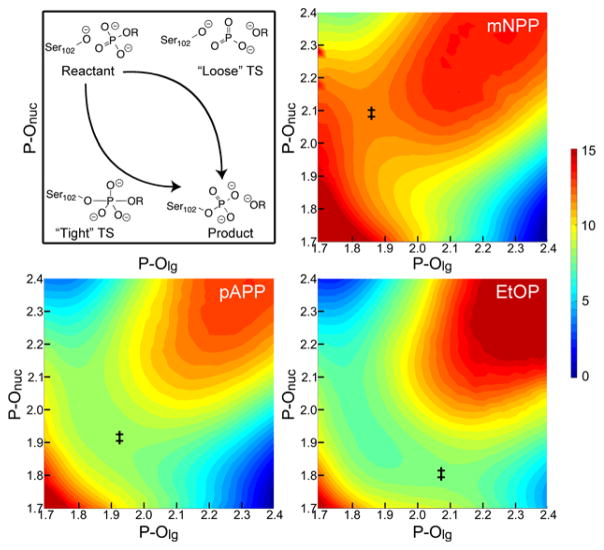
Schematic of possible reaction pathways for concerted phosphoryl transfer (top left) and corresponding calculated potentials of mean force (PMFs) for hydrolysis of phosphate monoesters in WT AP. Phosphoryl transfer pathways vary as functions of the lengths of the breaking and forming P-O bonds (P-O_lg and P-O_nuc, respectively) and can occur through “tight” or “loose” pathways, or somewhere in between (“synchronous”). A tight TS (‡), where the bond to the nucleophile forms before the bond to the LG cleaves, is expected to have significant negative charge accumulation on the phosphoryl group. A loose TS, where the bond to the LG cleaves before the bond to the nucleophile forms, is expected to have a significant decrease in negative charge on the phosphoryl group (i.e., it becomes less negative). Based on an analysis of bond order in these reactions (Table 1, Table S5, and Figure S7), phosphate monoesters follow a slightly tight pathway, but the position of the TS along that pathway changes as a function of LG ability. Bond lengths are in Å and free energies are in kcal/mol. PMFs for additional monoesters, as well as diesters, are available in Figures S8 and S13.

We have conducted atomistic simulations of the hydrolysis of a series of substrates by wild-type (WT) E. coli AP. The simulations indicate that relatively small changes to the substrate can produce substantial changes to TS structure. The model that arises differs from the interpretations originally provided for the most relevant experimental results. In the following, we first describe our computational methods and the most important results, which lead to a model that makes testable predictions. In some cases, these predictions will be for experiments that have already been published, but rather than using the historical interpretations of those experiments as a guide, we ask whether the experimental results per se support or refute our model. We find that rigorous tests of TS structure and stability thoroughly support the model. We also propose future experimental tests and detailed predictions for their outcomes.

Methods

Computational Calibration and Benchmarks

Due to the large number of substrates studied and the large degree of solvent accessibility to the AP active site, we adopted the latest version of the self-consistent charge density functional tight binding model,²⁴ DFTB3.²⁵ The model has been carefully parameterized for zinc and phosphate hydrolysis, thus it represents a promising balance of computational accuracy and efficiency. We conducted additional benchmark calculations (Text S1) using a series of solution and active-site models to further support its applicability to the AP system, especially concerning the capture of trends in TS variation for substrates with different LGs.

QM/MM Simulations

All simulations were done using CHARMM.²⁶ The initial setup for the system started from a crystal structure of WT E. coli AP with bound phosphate (PDB: 1ED8).²² This structure contains all 898 residues of the homodimer, as well as the three active site metals in each subunit, at 1.75 Å resolution. The phosphate in the active site was converted to the relevant substrate manually and hydrogens were added to the crystal structure using the HBUILD module of CHARMM. The protonation states of titratable amino acids were chosen based on hydrogen bonding contacts apparent in the crystal structure. The nucleophilic serine (S102) was deprotonated and disulfide bridges were formed between C168-C178 and C286-C336. The system was overlaid with a 25 Å spherical water droplet centered on one of the zinc ions. Non-crystallographic waters within 2.5 Å of crystallographic atoms were deleted. The R166 mutation was performed in silico, and otherwise that enzyme was treated identically to the WT.

The simulation scheme followed general procedures developed for this enzyme previously in our lab.^27,28 Briefly, the system was partitioned into 3 regions: the active site was treated with quantum mechanics at the DFTB3 level.^{24,25,29–31} This region consisted of the atoms in Figure S2 (ca. 120 atoms, depending on substrate). QM link atoms, using the DIV scheme, were placed between the alpha and beta carbons of QM residues and a FIRES potential³² centered on the P atom of the substrate held the QM waters in the active site. Non-QM atoms within a 27 Å sphere surrounding the active site (ca. 7650 atoms) were treated with the CHARMM36 force field.^33,34 Outside of the 27 Å sphere, all atoms (ca. 8450 atoms) were frozen and this region was treated with the generalized solvent boundary potential (GSBP).³⁵ The inner sphere was primarily treated with classical Newtonian dynamics, but a buffer region 4 Å from the edge of the sphere was treated with Langevin dynamics. NOE potentials were added to compensate for overpolarization of the QM region by nearby MM atoms, as the boundary between the QM and MM regions needs to be treated with care.³⁶ This included a restraint on the C-O bond of Asp51, and a restraint on the H-bond between the side chain of Asp330 and the backbone of Ser347. These residues are near the QM-MM boundary and initial simulations found that inaccuracy in those interactions lead to distortions of active site geometry that are unlikely to be physically realistic, given the similarity of crystal structures with various ligands, as well as the apo form.^22,23

After a short geometry optimization, the system was heated from 48 K and equilibrated at 298 K over the course of 150 ps. During heating and equilibration, NOE restraints were placed on the substrate to prevent the phosphorylation reaction and to keep the substrate bound in the active site. Those NOE restraints were removed after the initial equilibration. Potentials of mean force (PMFs) along the reaction coordinate (ξ, defined as the difference in length of the breaking and forming P-O bonds) were calculated using adaptive umbrella sampling. A biasing potential roughly equal to the opposite of the PMF and harmonic potentials with force constants of 20 kcal/mol•Å² centered at points every 0.25 Å along the reaction coordinate ensured thorough sampling. Simulations in each window were initiated from trajectories equilibrated for at least 15 ps in the neighboring window. Simulations were further equilibrated in each window for at least 50 ps prior to acquiring data for analysis. In most cases, additional biasing and harmonic potentials were used to sample along the tightness coordinate (defined as the sum of P-O_lg and P-O_nuc). 1D and 2D PMFs were calculated using the weighted histogram analysis method³⁷ from at least 300 ps of sampling in each window. Most windows included at least 1 ns of sampling.

KIEs were calculated using a path-integral free energy perturbation (PI-FEP) method³⁸ using similar procedures to ref. ³⁹. Since experimental measurements of KIEs are on V/K, we used the unbound substrate in solution as the ground state (GS). Simulations of the GS mirrored those of the TS: the substrate was dissolved in a 20 Å spherical water droplet whose boundaries were treated with the same GSBP protocol. The substrate and 10–15 waters surrounding the phosphate moiety were treated with DFTB3 and all other waters were treated classically. The QM waters were held near the phosphate using a FIRES potential and the P atom was constrained harmonically to remain in the center of the sphere. We calculated the KIE on O_lg, so that atom, as well as the two atoms it is directly bonded to (C and P) were all quantized and treated as strings of 16 quasi-particles each. In each of 20,000 classical configurations in the GS and TS (representing 200 ps of sampling each) we did 10 Monte Carlo sampling steps of the quasi-particle configurations, for a total of 200,000 quantum configurations.

Results and Discussion

We have used DFTB3/MM^25,29 simulations to calculate 2D PMFs for the first chemical step of WT AP hydrolysis with a series of phosphate monoesters (Figures 1 and S8); for calibration and benchmark of the methodology, see SI. Our calculations did not require any assumptions as to stepwise/concerted, tight/loose, etc., but we had to define reactant and product states for the reaction and in particular, protonation states of the species involved. Assessing protonation mechanism in uncatalyzed phosphate hydrolysis is quite difficult,⁴⁰ but the active site of AP simplifies matters. The active site cations (2 Zn²⁺, Mg²⁺, and Arg) stabilize negative charge enough that the pK_a of S102 is less than 5 in the apo enzyme.⁴¹ Thus it seemed very likely that the nucleophile is deprotonated in the reactant and the LG is deprotonated in the product of the phosphoryl transfer step. We explored the pathways between these preordained end states and found that in general, the reaction follows a slightly tight pathway, where nucleophilic attack precedes cleavage of the bond to the LG, but overall bond order to P only increases marginally (depending on how bond order is determined; see Figure S7 and Table S5). A notable trend appears in the position of the TS for the series of monoesters (Table 1). Worse LGs, characterized by a higher pK_a for the conjugate acid of the LG, have TSs that are later (more product-like) in the reaction coordinate. By altering the LG ability in going across the series from m-nitrophenyl phosphate (mNPP) to ethyl phosphate (EtOP), the reaction becomes less exergonic, and is actually endergonic for EtOP. This change in thermodynamics results in a shift in the location of the TS from mNPP (LG pK_a=8.4, ξ=−0.219 Å) to EtOP (pK_a=16.0, ξ =+0.265 Å). A potential concern in determining the precise location of the TSs is that the reactions with poor LGs have flat regions in vicinity of the TS in the PMFs. Despite this, the calculated positions of TSs fit a very consistent trend (Table 1). Furthermore, PMFs in the R166S mutant had much more curvature in the TS region, but the precise location of the TS in the mutant was very similar (Figures S9 and S15). These results, coupled with the fact that experiments show that the mutation does not alter the TS¹⁸ give us confidence in the calculated locations of the TS. Thus, the differences we see in the positions of the TS seem to be real and lead to important differences in structural features of the TS, which are illustrated in Figure 2. While one could expect such changes from Hammond’s Postulate,⁴² which relates the position of the TS to the thermodynamics of the reaction, substituent dependent changes in TS structure are expected to be negligible by most classic models,^4,5 thus the observed magnitude of changes here is intriguing.

Table 1.

Calculated TS geometries,^a bond orders, and KIEs.

Substrate	LG pKa	ξb	P-Olg		P-Onuc		Tightness		18(V/K)lg
			Length	WBOc	Length	WBOc	Length	WBOc
Monoestersd
m-nitrophenyl phosphate (mNPP)	8.4	−0.22	1.87	0.75	2.09	0.47	3.96	1.22	1.010
phenyl phosphate (PhOP)	10.0	−0.18	1.87	0.69	2.05	0.47	3.91	1.16	1.008
p-aminophenyl phosphate (pAPP)	10.3	0.03	1.94	0.60	1.91	0.65	3.85	1.26	1.012
propargyl phosphate (PrAP)	13.6	0.22	2.05	0.49	1.83	0.79	3.89	1.29	1.019
m-nitrobenzyl phosphate (mNBP)	14.9	0.26	2.07	0.46	1.81	0.77	3.88	1.22	1.023
ethyl phosphate (EtOP)	16.0	0.27	2.08	0.43	1.81	0.78	3.89	1.21	1.024
Diesters
methyl-p-nitrophenyl phosphate (mpNPP)	7.2	−0.30	1.82	0.70	2.11	0.53	3.94	1.22	NDe
methyl-m-nitrophenyl phosphate (mmNPP)	8.4	−0.16	1.87	0.59	2.02	0.58	3.89	1.22	ND
methyl-phenyl phosphate (mPhOP)	10.0	0.14	1.98	0.48	1.84	0.80	3.83	1.28	ND

^aBond lengths are averages during at least 400 ps trajectories constrained to the listed value of ξ using a harmonic force constant of 215 kcal/mol•Å<EESUP>2</EESUP>.

^bReaction coordinate at the TS, determined from the calculated PMFs.

^cWiberg bond order, given as a fraction of the bond order in the reactant or product for P-O_lg and P-O_nuc, respectively. The values were calculated at the B3LYP/6-31+G*/LANL2DZ level for the QM region of the simulations. Each value is the average of 10 snapshots from simulations of the TS separated by 50 ps. See SI for other methods of calculating bond order.

^dInitial studies using p-nitrophenyl phosphate (pNPP) indicated the potential presence of computational artifacts (see Text S2), so we did not pursue extensive studies of that substrate, despite its frequent use in experimental and theoretical work.

^eNot determined.

Figure 2.

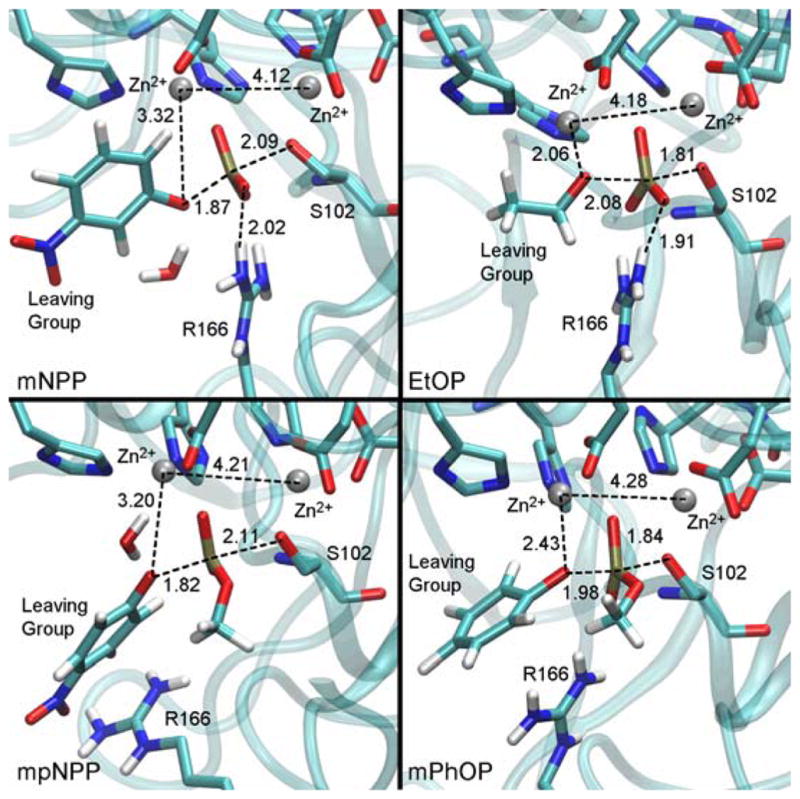
Representative snapshots from the TS region for some of the substrates studied here. Distances are in Å and are averages during at least 400 ps trajectories with the reaction coordinate constrained to the TS value using a harmonic force constant of 215 kcal/mol·Å². The orientation of the methyl substituent in the diesters was chosen in accordance with the results from ref. ⁴³, and simulations were long enough to ensure adequate sampling of rotational conformers (Figure S10). Water molecules in the active site stabilize good LGs where close ligation by Zn²⁺ is not possible (Figure S11). Corresponding structures for the other substrates studied here are available in Figure S12. Note that additional PMF calculations ensured that different binding modes of the LG to the zinc ion are not due to limited sampling. While simulations were not long enough to completely sample the conformational space available to the bulkier LGs, those rings do not interact directly with the enzyme and are unlikely to affect TS structure.

Most notably, Table 1 and Figure 2 show differences in the extent of bonding to the LG and the nucleophile at the TS. An analysis of the Wiberg Bond Order (WBO) of the P-O_lg bond allowed us to quantify the extent of bond breaking/formation at each TS. In the reaction of mNPP, the P-O_lg bond order has decreased only 25% relative to the reactant, while in the reaction of EtOP, the bond is nearly 60% broken. The P-O_nuc bond follows the opposite trend, where the TS for mNPP has significantly less bonding to the nucleophile than does the TS for EtOP. Meanwhile, the tightness of the TS⁸ is very much preserved across this range of LGs and represents an increase in bonding to the P, indicating a tight TS (Table 1). We note that caution should be used when interpreting the bond order calculations as there are different ways for assigning bond order. Natural Bond Order (NBO) is apparently far more sensitive to the changes in structure we observe here (see Figure S7 and Table S5). Nonetheless, the differences in TS structure for these substrates lead to differences in how the reacting atoms interact with the active site at the TS. At the TS of EtOP, where the P-O_lg bond is mostly broken, O_lg interacts closely with one of the Zn²⁺ ions. At the TS of mNPP, on the other hand, O_lg does not interact very closely with the Zn²⁺; instead, the LG is stabilized by active site water molecules (Figure S11) for two reasons. First, there is little cleavage of the P-O_lg bond at the TS of mNPP, and thus there is less need for stabilization of O_lg by the Zn²⁺. Additionally, the coordination around the Zn²⁺ appears not to permit ligation by both the non-bridging oxygen and O_lg when they are so close together. Zn²⁺ tends to have tetrahedral coordination and adding a fifth ligand in the form of O_lg is unfavorable for substrates with early TSs. Once the P-O_lg bond is more broken, though, as it is at the TS for worse LGs, the Zn²⁺ accommodates O_lg ligation since the non-bridging oxygen is more symmetrically coordinated with both zinc ions. We note that in contrast to another series of simulations of AP catalysis,^44,45 our simulations show no evidence of major elongation in the Zn-Zn distance relative to the crystal structure.

The structures in Figure 2 indicate that R166 interacts closely with the phosphoryl oxygens and possibly stabilizes negative charge accumulation there, which is expected for tight pathways. To test the role of R166, we have examined changes in charge distributions along the reaction coordinate (Figure 3). Calculations of Mulliken charges indicate that the non-bridging phosphoryl oxygens (O2 and O4) do become more negatively charged near the TS. H-bonds to R166 are present in both the reactant and the TS, but the accumulation of negative charge on those oxygens near the TS allows R166 to provide specific stabilization of the TS vs. the reactant.

Figure 3.

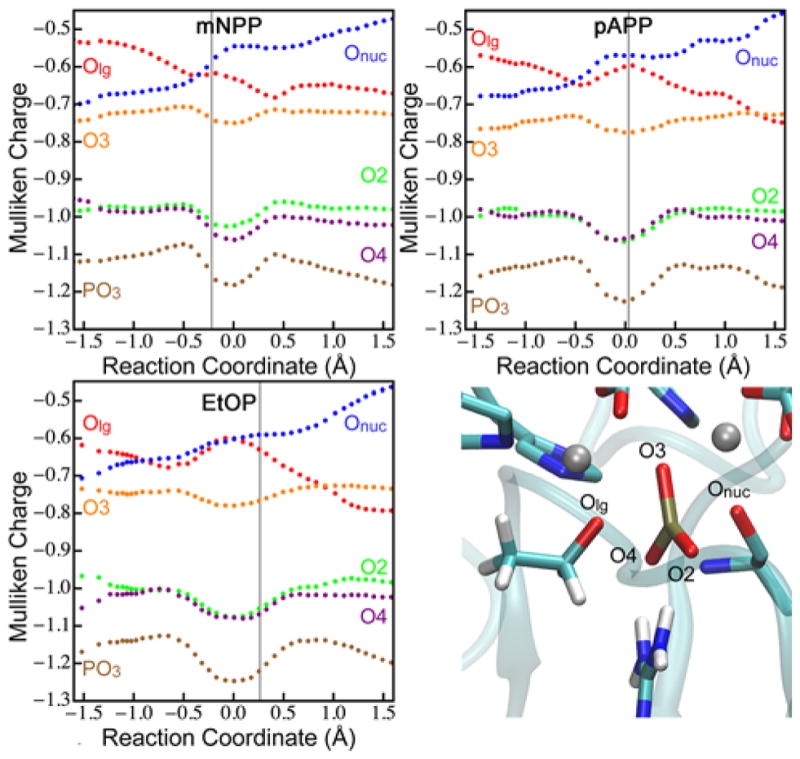
Changes in DFTB3 Mulliken charges during the reactions of monoesters. Each point represents the average of 1000 frames from multiple trajectories, binned according to reaction coordinate. Oxygens are labeled in the lower right; PO₃ (the phosphoryl group) is the sum of the charges on P, O2, O3, and O4. The vertical line indicates the position of the TS for each substrate. The trends of the Mulliken charges are confirmed by calculations of natural atomic charges using B3LYP (Table S6). DFTB3 Mulliken charges for diesters are available in Figure S14.

In addition to hydrolyzing monoesters, AP is known to hydrolyze phosphate diesters,^9,10 which have altered structure and charge of the phosphate moiety. The most conspicuous observation from computed TS structures (Figure 2) is the large distances from the R166 sidechain to the substrate. The steric hindrance from the methyl substituent apparently precludes interaction with R166 at the TS, regardless of charges on the phosphoryl oxygens (Figure S14). Computed PMFs (Figure S13) indicate that reactions of the diesters follow slightly tight pathways, similar to the pathways of monoesters. Importantly, we also observe a shift in the position of the TS for the diesters, where worse LGs have later TSs, though the shift from early to late TS occurs at a LG with lower pK_a for diesters than monoesters (Table 1).

Experimental Support and Tests

The model that emerges from our simulations provides a number of testable predictions. The importance of making testable predictions in a computational analysis has been constantly highlighted in the experimental enzymology literature. The approach we have taken in this study is to first make predictions based on the mechanistic model that has emerged from our analysis, and then evaluate the model based on published experimental data that are relevant to the predictions; any predictions that have not been tested experimentally in the literature will serve as additional blind tests that can be used to further evaluate our mechanistic model. To facilitate such experimental studies in the future, we summarize the key predictions from our study in Table 2. For completeness and recognizing the complexity of enzyme catalysis, we also include possible alternate experimental results and corresponding interpretations. We hope such a summary of explicit predictions will become standard in computational studies and help to stimulate rigorous interactions between computational and experimental communities. In the following, we discuss the most intriguing predictions from Table 2.

Table 2.

Experimental Tests^a of the Proposed Model

Aspect of Model	Measurement	Prediction	Alternate Resultsb	Interpretation of alternate results
Worse LGs have more P-Olg cleavage at TS	Rate vs. LG pKa	Steep slope for poor LGs and shallow slope for good LGs	Constant slope for all LGs	The extent of P-Olg cleavage at the TS is not a function of LG ability
Worse LGs have more P-Olg cleavage at TS	18(V/K)lg for range of LGs	Large KIEs for poor LGs and small KIEs for good LGsc	Equal KIEs for all LGs	The extent of P-Olg cleavage at the TS is not a function of LG ability
Moderate LGs have the most negative charge on the PO3-group at the TS	Catalytic proficiency vs. LG pKa in monoestersd and diesters	Enzyme is most proficient for monoester LGs with pKa around 10–11 and diester LGs with pKa around 8–9	Catalytic proficiency as a function of LG is constant	Charge buildup at the TS is not a function of LG ability
Moderate LGs have the most negative charge on the PO3-group at the TS	Rate vs. LG pKa in R166S vs. WTc for monoesters	Effect of mutation is greatest for monoester LGs with pKa around 10–11.	R166S has a constant effect on rate	LG does not affect charge distribution on the PO3 group at the TS.
For very good or very poor LGs, monoesters and diesters have similar TSs	18(V/K)lg for monoesters vs. diesters	Poor LGs have large KIEs and good LGs have small KIEs for both classes	KIEs for diesters are always smaller than for monoesters	Diesters use a tighter reaction pathway than monoesters
The shift from early to late TS occurs at a higher LG pKa for monoesters than diesters	18(V/K)lg for monoesters vs. diesters with moderate LGs	18(V/K)lg is larger for diesters than monoesters with LG pKa ~9–10	18(V/K)lg is the same for mono- and diesters in that region	For the same LG, the position of the TS does not change for mono- vs. diesters
The shift from early to late TS occurs at a higher LG pKa for monoesters than diesters	Rate vs. LG pKa for monoesters and diesters	The change in slope of the FER occurs at higher LG pKa for monoesters than diesterse	The change in slope occurs at the same LG pKa	For the same LG, the position of the TS does not change for mono- vs. diesters

^aSince a number of these experiments have already been published and are known to support the model, those ones are listed in italics. The remaining tests are predictions that have not been measured yet.

^bOne could of course imagine a very long list of possible results for any given experiment, but here we provide only the most obvious results that would indicate rejection of the model.

^cQuantitative predictions are available in Table 1.

^dSince the chemical step is not rate-limiting for the good LGs in WT,²⁰ another mutant may be necessary to compare the rates with and without R166. For example, the E322A mutation impedes the chemical step and shows no cooperativity with R166,⁴⁶ so the best comparison may be E322A vs. E322A/R166S double mutant.

^eThis prediction assumes that curved FERs have been measured (as they have).^18,19,21

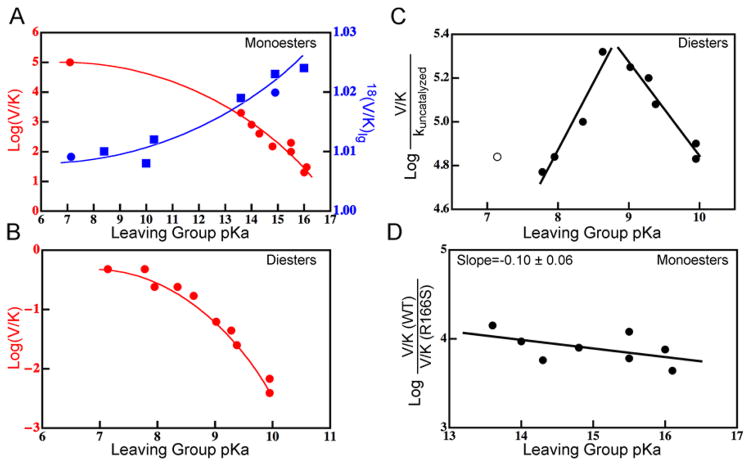
Since free energies of activation may be similar for tight and loose pathways,^16,17 predictions of activation barriers do not provide rigorous tests of TS structure. One of the most sensitive tests of TS structure is the measurement of KIEs. KIEs are the ratio of rates between substrates that differ only in isotopic substitution and ref. ⁴⁷ describes their use in phosphoryl transfers. We have calculated ¹⁸O KIEs on V/K for O_lg using a PI-FEP method,³⁸ which has successfully reproduced ¹⁸O KIEs in enzymes.³⁹ We find surprisingly large changes in the magnitude of KIEs for different substrates (difference of a factor of 3). Worse LGs have much larger ¹⁸(V/K)_lg, which is consistent with the greater extent of P-O_lg bond cleavage observed for worse LGs. The equilibrium isotope effect (EIE, see Text S1) on O_lg serves as an upper limit for the magnitude of the KIE^20,47 so to contextualize the extent of bond cleavage represented by our calculated KIEs, we calculated the EIE for EtOP. The value we obtained was 1.022, which is similar to the KIEs for poor LGs, indicating that those substrates have near complete cleavage of the P-O_lg bond at the TS, while substrates with good LGs have mostly formed bonds at the TS. Promisingly, measured ¹⁸(V/K)_lg values for two monoesters²⁰ are consistent with the trend and magnitudes we have calculated (Figure 4A); measurement of additional KIEs would serve as an important test of our model.

Figure 4.

Experimental support for the computational model. A) Monoesters show curved FERs^18,20,21 (red) along with differences in KIEs for different substrates. Calculated and measured^20,18(V/K)_lg are shown in blue squares and circles, respectively. B) Diesters show curved FERs.¹⁰ C) The catalytic proficiency for diesters reaches a maximum for LGs with TSs that are most symmetric (ξ=0). Good LGs (pK_a<8.75) and poor LGs (pK_a>8.75) are fitted separately. The p-nitrophenyl LG (open circle) was omitted from the fit because it deviates from linearity in the FER in solution and therefore does not fit the trend in catalytic proficiency. We discuss the reason for this deviation in the main text. Data are from ref. ¹⁰. D) The catalytic effect of R166 for monoesters is greatest for good alkyl LGs where the TS is most symmetric. Data are from refs. ^18,19. Since the chemical step is not rate-limiting on V/K for aryl monoesters in WT,¹⁹ the experiments in panel A were done in the R166S mutant (the exposed KIEs confirm that chemistry is rate-limiting in the mutant); those in panels B and C were also done in the R166S mutant for consistency. To ensure that the mutation does not change the nature of the TS,¹⁸ we calculated PMFs for some representative substrates in the mutant and found no changes in the position of the TS vs. WT (Figures S9 and S15). The curves in panels A and B are not fits to any model; they are merely meant to guide the eye to trends in the data.

Another classic test of TS structure is an FER, which compares a kinetic property with an equilibrium property (in our case, rate as a function of LG pK_a), and for the AP reaction FERs test the extent of P-O_lg cleavage at the TS.^5,8,14 Experimental rate measurements for AP are generally limited to V/K because product inhibition precludes the use of saturating concentrations of substrate,²¹ but direct calculations of V/K are beyond the scope of the present work. Still, the geometric features of the TSs found here allow for qualitative predictions about FERs for this enzyme. Specifically, since the extent of P-O_lg cleavage at the TS changes as a function of LG pK_a, our model predicts a changing slope to the FER. For both mono- and diesters, the model predicts a steep slope of V/K vs. pK_a for poor LGs and a shallow slope for good LGs. This is a surprising prediction because simplistic models of reactivity do not predict curved FERs for a single rate-determining step,⁴⁸ and standard analyses of FERs implicitly assume a static TS even though fundamental models of reactivity predict changes to TS structure across a series.⁵ This approach has generally seemed reasonable given that most FERs appear linear over a broad range of substrates. This is not to say that curved FERs have never been observed for a single rate-determining step;^49–52 a potential problem, though, is that curved FERs are often overlooked. Available measurements of FERs for both monoesters and diesters in AP, for example, confirm our model’s prediction: they both exhibit a large degree of negative curvature (Figure 4). Yet at the time these measurements were published, they were interpreted as representing true linear FERs.^10,18 As we discuss below, there are other examples where curvature has been overlooked. Measurements of monoesters with LGs in the range of 8<pK_a<13 would serve as an additional test of our model’s predicted curvature in that FER, as would additional measurements of diesters with pK_a<7 or pK_a>10.

Intriguingly, the changing structure of the TS as a function of LG, coupled with the non-monotonic changes in charge accumulation in the phosphoryl group (Figure 3), predict non-monotonic changes in catalytic effects. LGs with the most symmetric TSs (ξ=0.0, ca. LG pK_a=10–11 for monoesters and LG pK_a=8–9 for diesters, see Table 1) will have the greatest negative charge accumulation on the phosphoryl group at the TS. Since the Zn²⁺ ions and R166 stabilize negative charge at the TS, TSs with the greatest charge accumulation will be most stabilized by those moieties. This behavior can be observed if one calculates the catalytic proficiency (V/K vs. k_uncatalyzed) of AP for diester hydrolysis based on data from ref. ¹⁰ (Figure 4C). The proficiency reaches a maximum at LG pK_a=8.5–9.0. We note that the best LG for which data are available, p-nitrophenoxide (pK_a=7.2), deviates slightly from the trend of the other LGs. This is because that LG deviated from the (otherwise linear) FER in solution.¹⁰ As discussed below, we believe this is indicative of a shift in TS structure for good LGs in the reaction in solution^16,53 and the trend in catalytic proficiency breaks down when the trend in intrinsic reactivity (i.e., uncatalyzed) breaks down. Nonetheless, equivalent measurements of catalytic proficiency with monoesters would be useful in further testing the predicted catalytic effects.

Since the catalytic proficiency was measured in R166S AP, the measurements highlight the ability of the Zn²⁺ ions, not R166, to stabilize negative charge at the TS for diesters. Our model actually predicts that R166 will have minimal catalytic effects for diesters, due to steric hindrance by the methyl substituent (Figure 2). Measurements show that indeed, R166S mutation has negligible effects on the rate of diester hydrolysis.⁹ For monoesters, however, our model predicts similar non-monotonic catalytic effects stemming from both the Zn²⁺ ions and R166. This predicted effect has been partially tested, as rates have been measured for alkyl LGs in both the WT¹⁹ and the R166S mutant.¹⁸ The measurements were originally interpreted in terms of β_lg for WT and R166S, but the data show that the effect of mutating R166 is more severe for alkyl phosphates with better LGs (i.e., more symmetric TSs, Figure 4D). Additional measurements of the effect of R166 mutation for a series of aryl phosphates are necessary to test the prediction that for those substrates, mutation will be more severe for worse LGs. This experiment will also distinguish between the present model and one where the difference in β_lg for WT and R166S is due to more P-O_lg cleavage at the TS for WT; our calculations (Figures S9 and S15) indicate little difference between the TS structures in WT and R166S.

Broader Implications

If a change in TS structure is a simple consequence of changing reaction thermodynamics, why are curved FERs seldom^49–52 reported for a single rate-determining step? York and coworkers recently studied a phosphoryl transfer that involves a change in TS structure across the series of LGs, but that effect owed to a change in rate-determining step.⁵⁴ An active site model of AP, on the other hand, did find a similar shift in TS structure to ours for the two substrates they examined.⁵⁵ Williams noted that in principle, all FERs should be curved,⁵ but an analysis by Jencks indicated that the effects of changing substituent on TS structure will generally be difficult to observe.⁴ Thus, a standard analysis of FERs calculates an effective charge at the TS based on the slope of the FER.⁵ Our finding that TS structure and accompanying bond order can change substantially for a single rate-determining step is therefore quite surprising. The results in Figure 3 indicate that the notion of extracting a single effective charge at the TS for a series of substrates is misguided; each substrate is likely to have a different charge at the TS, although in AP some of those differences are attenuated by partial charge transfer to the Zn²⁺ ions.

Part of the reason that this sort of analysis is so routine may be because non-linearity is often overlooked. For example, FERs of phosphate monoester⁵⁶ and diester¹⁰ hydrolysis in solution are generally linear in the range of LGs examined, but the LG with lowest pK_a shows a conspicuous deviation from linearity in the diesters. Computational analyses of those reactions^16,53 indicated that the TS structure did change somewhat as a function of LG (though not the P-O_lg bond length) and cautioned that experimental FERs may not have unique interpretations. Based on our model, the steep slopes of those FERs in the range measured suggest that the P-O_lg bond is mostly broken for all LGs; they do not cross the threshold from early TS to late TS or from a formed P-O_lg bond to a broken one as the enzymatic reaction features. It is that transition, namely from a mostly formed P-O_lg at the TS to a mostly broken one, that is necessary to observe a curved FER for a single rate-determining step. A simple model based on a generalized LEPS potential⁵⁷ (see Text S3 for details) indicates that highly endergonic reactions do not deviate from linearity, but that thermoneutral or exergonic reactions may deviate from linearity, depending on the tightness of the reaction pathway. A close analysis of published FERs hints that there are many examples of such reactions, but the curvature was misinterpreted as indicative of a change in rate-determining step, a change in mechanism, or other effects. Based on analyses indicating that curvature due to changing TS is difficult to observe^4,5 this possibility is generally ignored, even when other sources for deviation are ruled out. The supporting information of ref. ¹⁰, for example, discusses a series of reactions, including hydrolyses of acetates, benzoates, phosphorothioates, and others, where FERs deviate from linearity. Those deviations, however, were attributed to “resonance effects” that are present for good aryl LGs—not poor ones—and only in some reactions. In other cases (see ref. ¹⁹ and refs. within that study), deviations from linearity for good alkyl LGs have been ignored with no proposal for the source of the deviation; the authors ruled out changes in rate-determining step or mechanism. In light of the current study, reexamination of the many classes of reactions with deviations from linear FERs would be prudent. While tests for changes in mechanism and rate-determining step are still vital, possible changes in TS structure cannot be ignored so readily.

Conclusions

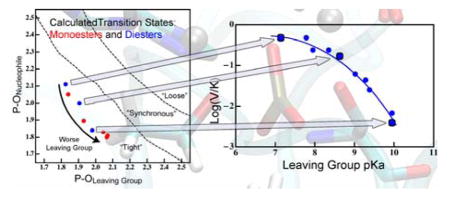
Our study of a broad set of substrates in AP provides a picture that differs in important ways from classic models of reactivity.^4,5 We have observed that rather modest changes in the reactivity of a substrate can have significant, conspicuously observable effects on the nature of a TS without changing the chemical mechanism or rate-determining step. The fact that AP catalyzes the hydrolysis of the whole range of LGs largely bolsters previous notions about catalytic promiscuity in AP ^9,28,58,59 and similar systems,^60,61 namely that the enzyme is capable of stabilizing TSs with a variety of structures and that it does so by different means. Nonetheless, our results indicate significant departures from the previously proposed reaction pathways taken by AP’s phosphate ester substrates.^{10,12,18–20} We conclude that the pathways for both mono- and diesters are slightly tight, but that substrates with poor LGs have significant P-O_lg cleavage at the TS. Figure S7 presents a summary of the TS structures found in this work, as well as the geometry of a crystal structure with the TS analogue vanadate.²³ The TS analogue apparently mimics a tight, slightly late TS, somewhat similar to the TS of monoesters with moderate to poor LGs. Thus, much of the intuition that has arisen from the crystal structure about the roles of active site residues in catalysis appears to be valid, despite the fact that kinetic experiments were interpreted to suggest a looser TS.^10,18–20

We have shown that the experimental results^{10,12,18–20} provide stronger support to our model than to the original interpretations of those experiments. In particular, rather than dismissing measurements of LGs with low pK_as as outliers,^10,12,19 we interpret curved FERs and differences in the magnitude of KIEs as the result of changes in TS structure as a function of reaction thermodynamics. Thus, a change in slope to an FER cannot be taken as evidence of a stepwise mechanism; the deviations from linearity caused by changes in TS structure are not nearly as negligible as classic models described.^4,5 This result ought to provide enzymologists and organic chemists with a new perspective on how to interpret FERs; the result highlights the need to examine a wide range of substituents for such purposes and cautions against extrapolating results from one substrate to another. Such extrapolation is common in model systems like alcohol dehydrogenase where most experimental probes of TS structure use benzyl alcohol in order to expose the chemical step, but the native substrate is ethanol.⁶² Extrapolation between substrates could lead to inaccuracies in our understanding of underlying mechanisms.

We have shown that standard experimental tests may not always make obvious distinctions between models of TS structure that differ substantially (e.g. loose vs. tight), which corroborates previous computational analyses.^16,53 Furthermore, the experimental tests themselves may alter the TS in the process of probing it. Interpretation of substituent effects typically focuses on the ability of a substituent to stabilize a static TS, but our computational model indicates that the substituent can substantially alter the TS and the way it is stabilized by the enzyme. Similarly, others have found that isotopic substitution in KIE measurements can change the structure of the TS.⁶³ Interpretations of experiments must bear in mind that the experiment itself can alter the property being measured. Such alterations, however, occur in predictable ways; as discussed here, experimental data need only be interpreted with full knowledge of those alterations.

Finally, the differences we propose versus previous models of AP catalysis should also concern those who hope to use knowledge of enzymatic TS structures for applications in drug or enzyme design. Those developing effective TS analogue inhibitors as drugs or those developing enzymes to catalyze new reactions require precise knowledge of the TS they wish to mimic² or stabilize,³ respectively. It has been known that slight changes in enzyme structure can induce important changes in TS structure;² we now add to that the fact that slight changes in substrate structure can make important changes in TS structure.