Copper Oxidation/Reduction in Water and Protein: Studies with DFTB3/MM and VALBOND Molecular Dynamics Simulations

Abstract

We apply two recently developed computational methods, DFTB3 and VALBOND, to study copper oxidation/reduction processes in solution and protein. The properties of interest include the coordination structure of copper in different oxidation states in water or in a protein (plastocyanin) active site, the reduction potential of the copper ion in different environments, and the environmental response to copper oxidation. The DFTB3/MM and VALBOND simulation results are compared to DFT/MM simulations and experimental results whenever possible. For a solvated copper ion, DFTB3/MM results are generally close to B3LYP/MM with a medium basis, including both solvation structure and reduction potential for Cu(II); for Cu(I), however, DFTB3/MM finds a two-water coordination, similar to previous Born-Oppenheimer molecular dynamics simulations using BLYP and HSE, while B3LYP/MM leads to a tetrahedron coordination. For a tetra-ammonia copper complex in solution, VALBOND and DFTB3/MM are consistent in terms of both structural and dynamical properties of solvent near copper for both oxidation states. For copper reduction in plastocyanin, DFTB3/MM simulations capture the key properties of the active site, and the computed reduction potential and reorganization energy are in fair agreement with experiment, especially when periodic boundary condition is used. Overall, the study supports the value of VALBOND and DFTB3(/MM) to the analysis of fundamental copper redox chemistry in water and protein, and the results also help highlight areas where further improvements in these methods are desirable.

Graphical abstract

1 Introduction

Copper is an important metal ion in biology.^1–4 Due to its redox activity, it is involved in many electron transfer proteins and serves as the catalytic co-factor in many enzymes. On the other hand, uncontrolled copper distribution may lead to the generation of undesirable reactive oxygen species or aggregation/misfolding of peptides/proteins,^5–8 resulting in serious diseases. Therefore, it is important to develop effective computational models for copper in different redox states to aid experimental investigation of copper biochemistry.

For condensed phase computations, a full quantum mechanical description remains prohibitively expensive. Therefore, hybrid quantum mechanical/molecular mechanical (QM/MM) methods^9–14 or pure MM models are most applicable. QM/MM models are more general and can be used to probe both chemical reactions and structural properties. To allow adequate sampling, which is essential to most condensed phase applications, an approximate QM method has to be used. In this regard, we have recently reported the parameterization of a density functional tight binding^15,16 (DFTB3¹⁷) model for copper.¹⁸ By including orbital angular momentum dependence of the Hubbard parameter and its charge derivative, we were able to describe the structural properties of both oxidation states in generally good agreement with “first principle” density functional theory (DFT) methods such as B3LYP^19–21 and B97-1,²² which were shown to give adequate description for copper complexes of biological relevance (see discussion in Ref. 18 in relation to previous work^23–25). We note that the DFTB3 model in the current form has PBE²⁶ as its “parent functional”, which was shown¹⁸ to be less accurate than B3LYP and B97-1 for copper. Thus, although some of the intrinsic limitations of the PBE functional were alleviated during the parameterization process, the energetic properties of copper compounds, such as ligand binding energies and proton affinities, are described only at a semi-quantitative level with the first generation of the DFTB3 model. For example, the binding energies for a series of biologically relevant charge-neutral molecules have a mean absolute deviation (MAD) of 3.1 and 4.7 kcal/mol for Cu(I) and Cu(II) compounds, respectively, in comparison to B3LYP/aug-cc-pVTZ; the errors are substantially larger for charged ligands, likely reflecting the use of a minimal basis in DFTB3. Nevertheless, the performance of DFTB3 is substantially better than other semi-empirical methods, such as PM6,²⁷ which is fairly useful for geometries but much less applicable for energetics. Moreover, single point B3LYP calculations at DFTB3 structures lead to substantially improved energetics for all ligand types, highlighting the good quality of DFTB3 structures.

In our previous work,¹⁸ the DFTB3 method was tested only against DFT and, in some cases, CCSD(T) methods for gas phase molecules. The computational efficiency of DFTB3 over DFT and ab initio methods makes it an attractive QM approach in QM/MM applications. Therefore, in the current study, we further explore the applicability of DFTB3 by studying several condensed phase problems, which involve both solution (Fig. 1a–b) and protein (Fig. 1c) systems. We focus on redox processes in water and protein to investigate whether DFTB3 is able to provide a balanced treatment for the two redox states of copper in condensed phase environments. The properties of interest include structural/coordination environment of the copper ion, especially response(s) to oxidation/reduction, redox potential and reorganization energy.

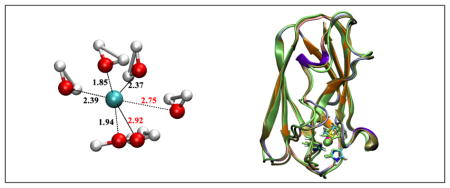
Figure 1.

The three systems studied here: (a) copper reduction in water; (b) oxidation of [Cu(I)(NH₃)₄]⁺ in water; (c) copper reduction in a blue copper protein, plastocyanin. In (a–c), the minimal QM region is highlighted with a different representation compared to the solvent or the rest of the protein. In (c), 3₁₀ helices are colored violet, extended β sheet regions are colored orange, bridge β sheet regions are colored lime green, turns are colored ice-blue, and coils are colored pink. The figures are generated using VMD.³⁹

At the MM level, force field development is not straightforward due to the open-shell nature of Cu(II) and charge transfer effects associated with metal-ligand interactions. Nevertheless, several models have been developed in recent years and met different degrees of success.^28–30 It is difficult to study chemistry or absolute redox potential with MM models, although they can be used to study structural/coordination properties of the copper ion in different redox states. In this study, we focus on the VALBOND model, which was originally proposed by Landis and co-workers to treat large amplitude angular motions of transition metal ligands.^31–33 The model has been recently implemented in CHARMM by Meuwly and co-workers,³⁴ who showed promising applications in several organometallic systems. ^35,36 Here we develop the VALBOND model for copper and compare its performance to DFTB3/MM for [Cu(NH₃)₄]^+/2+ in water (Fig. 1b). We are particularly interested in probing the time-dependence of the solvent response to the oxidation of copper ion, a process that can potentially be probed with modern solution X-ray experiments. ^37,38 Comparison of VALBOND and DFTB3/MM also helps better refine the VALBOND model, which is computationally even more efficient than DFTB3/MM, for certain protein applications in the future.

In the following, we first describe the computational methodologies (QM/MM and VALBOND) used to study the three condensed phase systems. DFTB3/MM is applied to all three, while VALBOND simulations focus on [Cu(NH₃)₄]^+/2+ in water; in selected cases, as validation, DFT/MM simulations are also carried out. Next, we present results of QM/MM and VALBOND simulations; comparison to experiment is made whenever possible, and the discussion helps highlight the applicability and limitations of the current generation of DFTB3(/MM) and VALBOND models. Finally, we end with a few concluding remarks.

2 Methods

2.1 Aqueous copper ion simulations with QM/MM models

The copper ion in water is described with QM/MM simulations in which the copper ion and closest water molecules are treated at the QM level, while the remaining water is treated with MM. In most cases, the QM water partition includes only the closest 6 water molecules, although calculations with a larger QM region (~21 water) are also carried out for comparison; as shown in the Supporting Information, the first solvation shell properties are not very sensitive to the QM region size while the second solvation shell properties do exhibit a modest level of dependence, especially for Cu(I). The MM region includes a droplet of 16 Å radius subject to the stochastic boundary condition.⁴⁰ In most simulations, the MM water is TIP3P,⁴¹ although a polarizable water model based on Drude oscillator is also tested (see below). To avoid the exchange of QM and MM water molecules, the Flexible Inner Region Ensemble Separator (FIRES) potential⁴² is applied; previous studies⁴³ and larger QM region studies in the Supporting Information indicate that the FIRES approach gives satisfactory results for structural properties of the copper ion, especially when the QM region does not deviate significantly from spherical symmetry. Equilibrium simulations are carried out for solvated Cu(I) and Cu(II) ions using the mixed Newtonian/Langevin dynamics protocol;⁴⁰ in addition, reduction potential is also computed (see Sect.2.1.3). All calculations are carried out using CHARMM;^44,45 DFT/MM calculations are done with the Gaussian09/CHARMM interface.⁴⁶

2.1.1 The QM method

As mentioned in the Introduction, the main goal is to test our recent parameterization of the DFTB3 model for copper. The parameterization was done in the framework of the 3OB set⁴⁷ and calculations for Cu(II) containing systems are done with the spin-polarised formulation of DFTB.^48,49 The orbital angular momentum dependence of the Hubbard parameter and its charge derivative is considered only for copper. For comparison, DFT/MM calculations are also carried out in which DFT is either B3LYP, BLYP or MPWB1K.⁵⁰ Based on gas-phase model systems studied previously¹⁸ and here (see below), the B3LYP approach generally gives satisfactory results in comparison to high quality ab initio calculations such as CCSD(T) with a large (aug-cc-pVTZ⁵¹) basis set. BLYP is also tested here because it is the functional used in many previous CPMD/BOMD simulations of solvated copper ions (see below). MPWB1K, a meta-GGA functional, is tested because a recent study⁵² found it to work well for several copper complexes. To obtain longer DFT/MM simulations, a small basis that contains the Hay-Wadt effective core potential (Lanl2dz⁵³) for copper and 6-31G(d) for other elements is used; gas phase calculations for copper-water complexes (see Tables 1,2 and Supporting Information) indicate that this basis set leads to good geometries in comparison to calculations using aug-cc-pVTZ.

Table 1.

Calculated binding energy for water to [Cu(H₂O)₅]²⁺ to form [Cu(H₂O)₆]^2+a

Method	Binding Energy (kcal/mol)
B3LYP/aug-cc-pVTZ	−19.9
BLYP/aug-cc-pVTZ	−16.8
B3LYP/lanl2dz/6-31G(d)	−25.7
BLYP/lanl2dz/6-31G(d)	−21.2
DFTB3	−21.2
CCSD(T)/aug-cc-pVTZ	−23.8

^aOptimized at the respective level, except for CCSD(T), for which B3LYP/aug-cc-pVTZ structures are used.

Table 2.

Selected geometrical properties of [Cu(I/II)(H₂O)_n]^+/2+ optimized by various methods in the gas phase^a

Methodb	rCuO	rCuO′	rCuO″	rCuO‴	∠OCuO′
[Cu(II)(H2O)5]2+
B3LYP/aug-cc-pVTZ	1.98	2.02	2.19
B97-1/aug-cc-pVTZ	1.98	2.02	2.20
B3LYP/Lanl2dz/6-31G(d)	1.99	2.04	2.16
BLYP/Lanl2dz/6-31G(d)	2.04	2.05	2.26
DFTB3	2.01	2.04	2.22
[Cu(II)(H2O)6]2+
B3LYP/aug-cc-pVTZ	2.02	2.31	–	–	90.0/180.0
B97-1/aug-cc-pVTZ	2.02	2.31	–	–	90.0/180.0
B3LYP/Lanl2dz/6-31G(d)	2.03	2.25	–	–	90.0/180.0
BLYP/Lanl2dz/6-31G(d)	2.05	2.28	–	–	90.0/180.0
DFTB3	2.03	2.34	–	–	90.0/180.0
[Cu(I)(H2O)2]+
B3LYP/aug-cc-pVTZ	1.91	–	–	–	180.0
B97-1/aug-cc-pVTZ	1.92	–	–	–	180.0
B3LYP/Lanl2dz/6-31G(d)	1.92	–	–	–	180.0
BLYP/Lanl2dz/6-31G(d)	1.92	–	–	–	180.0
DFTB3	1.89	–	–	–	180.0
CCSD(T)	1.90	–	–	–	180.0
[Cu(I)(H2O)4]+c
B3LYP/aug-cc-pVTZ	2.04	2.11	2.20	2.23	135.2
B97-1/aug-cc-pVTZ	2.04	2.11	2.22	2.26	138.8
B3LYP/Lanl2dz/6-31G(d)	2.03	2.12	2.17	2.23	135.4
BLYP/Lanl2dz/6-31G(d)	2.01	2.05	2.31	2.31	153.1
DFTB3	1.92	1.91	2.43	2.51	173.5

^aOptimized at the respective levels; distances in Å, angles in degrees. Also see Fig. 4 for the labels of relevant distances and angles.

^bFor results with additional basis sets, see Supporting Information.

^cResults included here are for the tetrahedron structure; for discussion of the alternative two-coordinated structure (see Fig. 4c), see Supporting Information.

2.1.2 MM method

In most simulations, the TIP3P model is used to describe the MM water. In previous QM/MM studies of metal ion solvation,^42,43 a polarizable water model based on Drude oscillator (SWM4-NDP⁵⁴) was recommended, thus we have also carried out simulations with DFTB3/SWM4-NDP. As shown in the Supporting Information, DFTB3/TIP3P and DFTB3/SWM4-NDP simulations generally give rather similar solvent distribution near the copper ion, except for minor differences in the angular distribution of water, especially those in the second solvation shell.

For interaction among MM molecules, the extended electrostatic model is used for consistency with the QM/MM interactions⁵⁵ (see Supporting Information for a discussion of MM cutoff schemes in reduction potential calculations). van der Waals interactions are switched off beyond 12 Å using the VSWITCH scheme.⁵⁶ All water molecules are kept rigid using the SHAKE algorithm⁵⁷ during molecular dynamics simulations.

2.1.3 Reduction potential calculation

The reduction potential of copper (Cu(II)/Cu(I)) is computed using a dual-topology-single-coordinate (DTSC) approach.⁵⁸ In DTSC, the system is propagated with a hybrid potential function that is a combination of potentials of the two end states (Cu(II), Cu(I)) through a coupling parameter λ,

$$U(\lambda )=(1-\lambda )U_{Cu(II)}+\lambda U_{Cu(I)}=U_{Cu(II)}+\lambda (U_{Cu(I)}-U_{Cu(II)}).$$ (1)

The reduction free energy is then given by thermodynamic integration as,

$$\mathrm{\Delta }F={\int }_0^1\frac{\partial F(\lambda )}{\partial \lambda }\mathrm{d}\lambda ={\int }_0^1{\langle \frac{\partial U(\lambda )}{\partial \lambda }\rangle }_{\lambda }\mathrm{d}\lambda ={\int }_0^1{\langle (U_{Cu(I)}-U_{Cu(II)})\rangle }_{\lambda }\mathrm{d}\lambda ,$$ (2)

where (U_Cu(I) − U_Cu(II)) = ΔU is referred to as the energy gap below. Eleven λ windows are used for DFTB3/MM, with each window sampled for ~500 ps. For comparison, B3LYP/MM calculations are also carried out but with only the end states (λ = 0, 1, sampled for 280 ps for Cu²⁺ and 120 ps for Cu⁺); reduction free energy is then estimated using a linear response model.

In the water droplet set up using the stochastic boundary condition, the system is surrounded by vacuum. Therefore, a Born model⁵⁹ is used to estimate the missing bulk solvation free energy contribution. This simply includes the corresponding “ion solvation term”,

$$\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}=-\frac{Q_{\mathit{tot}}^2}{2R}(1-\frac{1}{{\epsilon }_W}),$$ (3)

where Q_tot = 2 for Cu(II) and Q_tot = 1 for Cu(I), and R = 16 Å, ε_W = 78. The reduction free energy is given by,

$$\mathrm{\Delta }{F}_{\mathit{red}}=-\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}(Cu(II))+\mathrm{\Delta }{F}_{\mathit{droplet}}+\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}(Cu(I))=\mathrm{\Delta }{F}_{\mathit{droplet}}+\mathrm{\Delta }\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}.$$ (4)

Here ΔF_droplet is the reduction free energy computed (using Eq. 2) with the water droplet, and $\mathrm{\Delta }\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}$ is a numerical constant:

$$\mathrm{\Delta }\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}=-\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}(Cu(II))+\mathrm{\Delta }{F}_{\mathit{slv}}^{\mathit{Born}}(Cu(I))=+30.70\mathit{kcal}/\mathit{mol}.$$ (5)

For comparison with the water droplet model using stochastic boundary condition, we have also computed the reduction potential at the DFTB3/MM level with the GSBP (Generalized Solvent Boundary Potential)^55,60 and PBC (Periodic Boundary Condition) setups. In GSBP, the entire water droplet is treated as the inner region and the outer region is described as a dielectric continuum (ε_W = 78); spherical harmonics up to order 20 (i.e., 400 basis functions) are used to expand the reaction field matrix. In the PBC simulations, the metal ion is first solvated by a 32 Å cube of water molecules and then equilibrated with the NPT ensemble; the final box length is 29.8 Å. Ewald summation is applied to QM/MM electrostatics⁶¹ and Particle-Mesh-Ewald⁶² is used for MM-MM electrostatics with a grid size of ~ 1 Å.

2.2 Copper-ammonia solution simulations

2.2.1 VALBOND in CHARMM

We first briefly review the VALBOND module recently introduced to CHARMM. In the VALBOND force field, based on valence bond theory, hybrid orbital strength functions are used to describe the energetics of distorted bond angles.^31–33,63 The additional force field term not only describes the energetics around the energy minimum but also for very large angle distortions and helps to model hypervalent molecules and transition metal complexes.^34,64

Non-hypervalent molecules

For molecules involving sp^mdⁿ hybridization with an angle θ between the hybrid orbitals, the bending energy is E(θ) = k(S^max − S(θ)). Here, k, S^max and S are scaling factor (force constant), maximum strength function and strength function respectively. For sp^mdⁿ hybrids the explicit expressions are $S^{\mathit{max}}=\sqrt{\frac{1}{1+m+n}}(1+\sqrt{3m}+\sqrt{5n}),S(\theta )=S^{\mathit{max}}\sqrt{1-\frac{1-\sqrt{1-{\mathrm{\Delta }}^2}}{2}}$, and $\mathrm{\Delta }=\frac{1}{1+m+n}[1+mcos\theta +\frac{n}{2}(3{cos}^2\theta -1)]$ is the non-orthogonality integral. For [Cu(I)(NH₃)₄]⁺ investigated in the present work, an sp³ hybridization is used to describe its tetrahedral geometry, similar to Ni(CO)₄. In this case, the maximum strength function evaluates to $S^{max}=\sqrt{\frac{1}{1+3+0}}(1+\sqrt{3\times 3}+\sqrt{5\times 0})=2.0$.

Hypervalent molecules

Hypervalent molecules contain atoms having more than eight electrons in their valence shell. Excess electrons in hypervalent molecules are accommodated in 3c-4e⁻ bonds. Thus, for hypervalent molecules one has to take care of the resonance structures and this can be accomplished by a weighting factor c_j called mixing coefficients. Hence, the total energy is a weighted sum E_t = Σ_j c_jE_j over all j resonance structures. The mixing coefficients c_j are determined from³¹ $c_j=\frac{{\displaystyle \prod _{i=1}^{\mathit{hype}}}{cos}^2{\theta }_i}{{\displaystyle \sum _{j=1}^{\mathit{con}\mathit{fig}}}{\displaystyle \prod _{i=1}^{\mathit{hype}}}{cos}^2{\theta }_j}$, where hype and config are the number of hypervalent angles and number of resonance configurations respectively. The square-planar arrangement for [Cu(II)(NH₃)₄]²⁺ involves an sd¹ (hypervalent) hybridization with S^max = 2.29 and six resonance configurations are retained in the simulations.

2.2.2 Simulation setups for Copper-ammonia in water

The system consists of a solvated [Cu(I)(NH₃)₄]⁺ or [Cu(II)(NH₃)₄]²⁺ complex, immersed in 1,728 TIP3P⁴¹ water molecules in a periodic cubic box of side length 37.25 Å (see Fig. 1b). All simulations are carried out using CHARMM⁴⁴ with provisions for the VALBOND³⁴ force field to describe the metal complex.^31–33 All bonds involving hydrogen atoms are constrained by applying SHAKE.⁶⁵ The remaining parameters for the ammonia ligand are taken from the CHARMM force field.⁶⁶

The system is prepared for simulations by minimization and subsequent heating to 300 K. This is followed by an NVT equilibration simulation at 300 K for 10 ns using a Verlet integrator⁶⁷ with a time step of 1 fs using a Nosé-Hoover thermostat⁶⁸ for temperature control.

For comparison, hybrid QM/MM simulations are performed using DFTB3¹⁷ and the 3OB parameterization for ONCH⁴⁷ and copper¹⁸ is used. The metal complex is described by DFTB3 whereas the water molecules are treated by TIP3P. An NVT simulation is carried out at 300 K using the Verlet algorithm with a time step of 0.1 fs for 5 ns. The SCF convergence criterion used for this is 10⁻⁸ hartree. The van der Waals radii for the Cu(I) and Cu(II) ions are σ_Cu = 1.40 and 0.87 Å, respectively. ^69,70 Furthermore, simulations with the seven water molecules closest to the Cu atom included in the QM part are carried out. To avoid the exchange of QM and MM water molecules the FIRES potential is applied.⁴²

Along with the DFTB3/MM simulations, a hybrid QM/MM simulation is also performed with B3LYP/MM using the Gaussian09/CHARMM interface.⁴⁶ The metal complex is treated with B3LYP and the same basis as for a copper ion in aqueous solution (Lanl2dz for Cu and 6-31G(d) for other QM atoms), and water with TIP3P. Since the calculation is computationally demanding, only ~100 ps of simulation is performed.

In addition to the equilibrium simulations, we have also carried out non-equilibrium simulations in which the oxidation from Cu(I) to Cu(II) is induced in silico by changing the force field parameters between the two oxidation states for VALBOND³⁴ simulation; in the QM/MM simulations the total charge and number of unpaired electrons is changed and the van der Waals parameters for the metal atoms are also updated. For the VALBOND³⁴ simulations, after 10 ns of NVT simulation, an NVE simulation is performed for 1 ns using starting coordinates and velocities obtained from the NVT simulation. From this 1 ns of NVE trajectory, coordinates and velocities at 100 frames separated by 10 ps are stored and used as initial conditions for the subsequent non-equilibrium simulations. For DFTB3/MM,¹⁷ subsequent to NVT simulation, an NVE simulation is performed for 100 ps, from which coordinates and velocities at 20 frames separated by 5 ps are selected to initiate the non-equilibrium trajectories.

2.3 Plastocyanin at pH 7

2.3.1 GSBP simulations

Starting from the crystal structure 5PCY,⁷¹ hydrogen atoms are added using HBUILD in CHARMM considering standard protonation states for all titratable residues at pH 7. Then the protein is solvated in a 20 Å sphere of water molecules centered at Cu (consistent with an inner region of radius 22 Å in the GSBP protocol^55,60). The protein is treated with the CHARMM22 force-field⁶⁶ while the modified TIP3P model is used for the water molecules. Newton’s equations-of-motion are solved for the Molecular Dynamics (MD) region (within 18 Å), and Langevin equations-of-motion are solved for the buffer region (18–22 Å) with a temperature bath of 300 K.⁴⁰ All water molecules in the inner region are subjected to a weak GEO (Geometrical) type restraining potential to keep them inside the inner sphere with the MMFP module of CHARMM. The GEO restraining potential is in the form of a quartic polynomial on each oxygen atom in water: k × Δ²(Δ² − V_P), where Δ = r − r_off; k is the restraining quartic force constant (0.5 kcal/(mol·Å⁴)), r is the distance of the oxygen from the center of the simulation sphere, r_off is the cutoff distance (22.0 – 1.5 = 20.5 Å) below which the GEO restraint is set to zero, V_P is an offset value taken to be 2.25 Ų. These parameters lead to a restraining potential on water that smoothly turns on at 20.5 Å, reaches a well at 21.5 Å with a depth of −0.625 kcal/mol, and then quickly rises to be repulsive beyond 22.0 Å. All protein atoms in the buffer region are harmonically restrained with force constants determined directly from the B-factors in the PDB file.⁴⁰ Langevin atoms are updated every 20 steps during the simulation to consistently treat protein groups and water molecules that may switch regions during the simulation. Non-bonded interactions within the inner sphere are treated with an extended electrostatics model,⁷² in which groups beyond 12 Å interact as multipoles and up to quadrupoles.

In the GSBP^55,60 set up, the static field due to outer region atoms, ${\varphi }_s^o$, and the reaction field matrix, M, are evaluated using Poisson-Boltzmann (PB) calculations using a focussing scheme that places a 52.8 Å cube of fine grid (0.4 Å) into a larger 158.4 Å cube of coarse grid (1.2 Å). The inner region charge density is expressed using the first 20th-order spherical harmonics with a total of 400 basis functions. The optimized radii of Roux and Nina⁷³ are adopted to define the solvent-solute dielectric boundary. Dielectric constant of 1.0 and 80.0 are used for protein and solvent, respectively.

For preliminary MM equilibration, Cu, His 37, His 87, Cys 84, Met 92, Pro 36, Asn 38 are kept fixed in space; a charge of +1 is assigned to Cu and CHARMM charges are used for the rest of the protein. Post a 500 ps equilibration (the final structure from which is also used to set up PBC simulations, vide infra), the final structure is used to set up DFTB3/MM simulations. The QM region includes Cu and the side-chains of His 37, His 87, Cys 84 and Met 92. Link atoms are added between the C_α and C_β atoms for His 37, His 87 and Cys 84; for Met 92, the link atom is added between the C_β and C_γ atoms. The DIV scheme is used for the treatment of MM-host interactions with the QM region.⁷⁴

Post separate minimizations for the Cu(I) and Cu(II) states, two independent 250 ps equilibration runs are carried out for each Cu oxidation state. Thermodynamic integration simulations are carried out to compute the reduction potential in the dual-topology-single-coordinate (DTSC-TI) framework⁵⁸ (Eq. 2). λ=0.0, 0.2 and 0.4 windows start with equilibrated Cu(II) structures and λ=0.6, 0.8 and 1.0 windows start with the equilibrated Cu(I) structures. The length of simulation for each λ window is typically about 1 ns; for statistics, see Supporting Information.

2.3.2 PBC simulations

Starting from MM/GSBP-equilibrated coordinates for the protein (vide supra), to which link atoms have been added corresponding to the same QM region as in GSBP simulations, the protein is solvated in a rhombic dodecahedron of edge length 68 Å. To neutralize the net charge of the protein, K⁺ and Cl⁻ ions are added, keeping the ionic concentration at 0.150 M. Electrostatics interactions between QM and MM atoms are treated using Ewald summation,⁶¹ while those among MM atoms are treated using particle-mesh-Ewald;⁶⁷ the grid size is about 1 Å in both cases. Van der Waals interactions are truncated at atom-atom distances of 12 Å using the SHIFT scheme.⁵⁶

Respective DFTB3/MM minimized structures for the Cu(I) and Cu(II) states are used to set up 200 ps heating/equilibration runs for each state. Two independent simulations are carried out for each state with a time-step of 1 fs and the Nosé-Hoover thermostat.⁶⁸ In the DTSC-TI framework, ~700 ps long simulations are carried out for the λ=0.0 (i.e., Cu(II)) and the λ=1.0 (i.e., Cu(I)) windows. The final structures from these simulations are used to initiate runs for the other λ windows: λ=0.2 and 0.4 windows start from the λ=0.0 structure while λ =0.6 and 0.8 windows start from the λ=1.0 structure. For additional simulation statistics, see Supporting Information.

3 Results and Discussion

3.1 Copper ions in aqueous solution

3.1.1 Solvation of copper ions in different oxidation states

The structural features of a solvated Cu(II) ion have been discussed extensively by previous experimental and computational studies. The debate focused on whether the first solvation shell consists of six water molecules in a Jahn-Teller distorted octahedron configuration or involves only five directly coordinated water molecules. Experimentally, numerous techniques that include neutron diffraction,^75–79 Extended X-Ray Absorption Fine Structure (EXAFS),^80–85 X-ray Absorption Near Edge Structure (XANES)⁸² and Large Angle X-ray diffraction (LAXS)⁸³ have been applied, and the results are not quite consistent with each other. This is partly because interpretation of EXAFS, XANES or LAXS data depends on a fitting procedure that requires a priori assumptions of the structure; neutron diffraction can measure the four closely bound Cu-O_eq distances but can not distinguish the Cu-O_ax and Cu-H bonds. With the second-difference isotopic substitution method and neutron diffraction,⁷⁹ g_CuO(r) and g_CuH(r) can be measured separately, but the g_CuO(r) plot is rather broad and the g_CuO(r) integration plot is not quite flat to indicate the predominant five-coordinated structure in solution.

The latest X-ray scattering study of Hodgson et al.⁸⁵ considered three models: square pyramidal, split axial and distorted Jahn-Teller; the first has a five-coordinated Cu(II) while the latter two have a six-coordinated Cu(II). With EXAFS analysis, the square pyramidal and split axial fit slightly better than the distorted Jahn-Teller, and the two axial water oxygen atoms differ by about 0.14 Å in terms of distances to Cu(II) in the split axial model. With a MXAN (Minuit X-ray Absorption Near edge structure) analysis, which considers Cu-H scattering explicitly, a better fit involves two distinct but structurally related non-centrosymmetric axially elongated square pyramidal Cu(II) ions; one involves a non-bonded (sixth) axial water at Cu-O ~ 3 Å, while the other is axially elongated square pyramidal without any trans-axial water ligand.

Using computations, different methods have been applied and include QM/MM molecular dynamics,^86–89 Car-Parrinello molecular dynamics (CPMD),^90–93 Born-Oppenheimer molecular dynamics (BOMD),^94,95 gas phase cluster analyses,^96–101 and classical molecular dynamics using a polarizable force field.²⁹ Again, different conclusions were reached. In the latest BOMD simulations⁹⁵ using BLYP^19,20 and HSE¹⁰² functionals, a five-coordinated Cu(II) was observed; with a ligand-field force field,²⁹ by contrast, a six-water first solvation shell was observed. We note that the use of BLYP functional in most CPMD/BOMD likely overemphasizes the importance of the five-water first solvation shell. As shown in Table 1, compared to hybrid DFT and CCSD(T) calculations, BLYP underestimates the binding affinity of the sixth water molecule by about 4 kcal/mol.

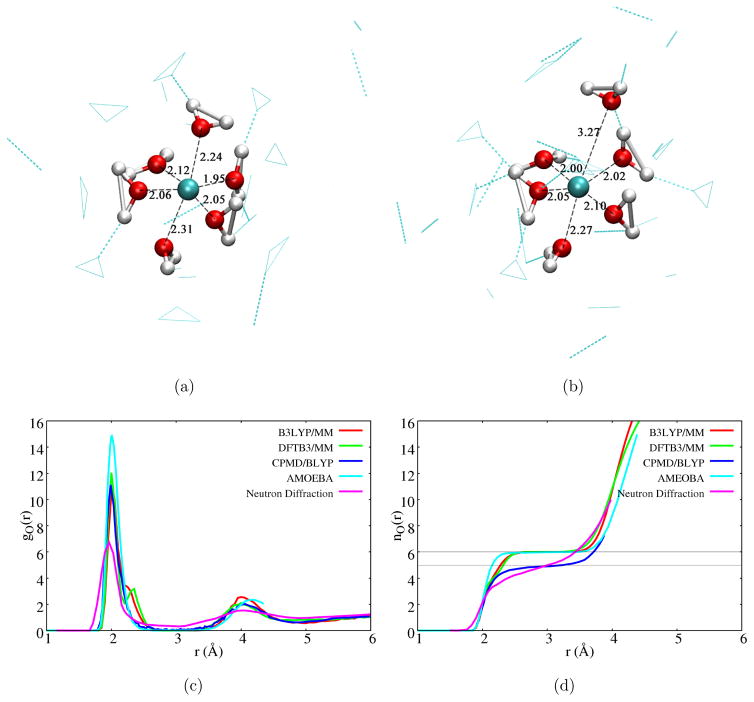
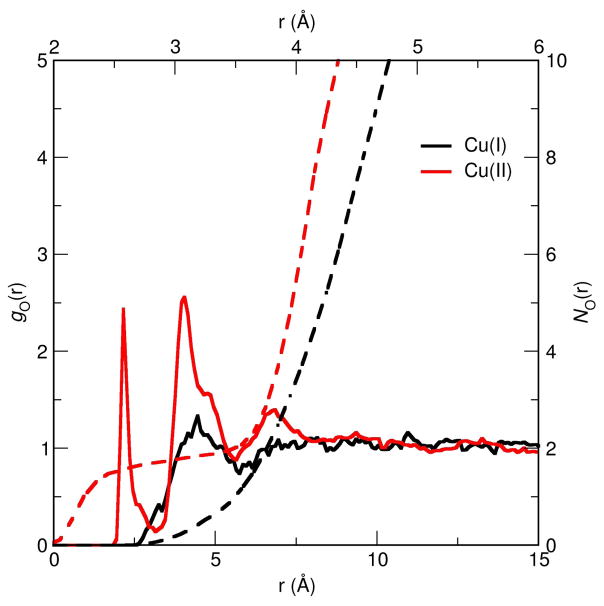
With the DFTB3/MM simulations, we capture both five- and six-coordinated structures (for snapshots, see Fig. 2a–b). The six-coordinated structure properly captures the expected Jahn-Teller distortion in which the axial Cu-O distances are longer than the equitorial values by about 0.2 Å. Indeed, due to Jahn-Teller distortion, the Cu-O radial distribution function has a major peak at Cu-O distance of 2.00 Å and a minor peak at 2.35 Å (Fig. 2c); these values are reasonably close to the distances of 1.95±0.02 Å for the equatorial and 2.23±0.11 Å for the closest axial ligand, respectively, from the latest MXAN analysis.⁸⁵ In the five-coordinated structure, the two axial ligands may have substantial Cu-O distance difference that approaches 1 Å. Nevertheless, the six-coordinated species is clearly more populated, as indicated by the integrated radial distribution function (Fig. 2d). Compared to the recent classical force field simulation,²⁹ which observed only six-coordinated first solvation shell, the integrated radial distribution function (Fig. 2d) rises more slowly as a function of Cu-O distance to the value of six. Interestingly, these features are also observed in B3LYP/MM simulations: the Cu-O radial distribution function has a shoulder at Cu-O distance of 2.25 Å, and the integrated radial distribution function well overlaps the DFTB3/MM data; results from MPWB1K/MM simulations also agree with the B3LYP/MM and DFTB3/MM data (see Supporting Information). The agreement between DFTB3/MM and B3LYP/MM results is consistent with the observation that DFTB3 and B3LYP give similar structural and energetic properties for Cu(II)-water clusters in the gas phase (see Tables 1 and 2). By contrast, BLYP based CPMD⁷⁹ and BOMD simulations,^94,95 as discussed above, led to five-coordinated first solvation shell; this is confirmed here by BLYP/MM simulations (see Supporting Information).

Figure 2.

Coordination environment of a Cu(II) ion in water. (a–b) Snapshots from DFTB3/MM simulations that illustrate the six- and five-coordinated species. (c–d) Cu-O radial distribution function and coordination number function from different simulations and neutron diffraction experiment.⁷⁹ The CPMD/BLYP results are taken from Ref. 79 and those from AMEOBA from Ref. 29.

For Cu(I), which is nominally a closed-shell ion, the situation is in fact also complex. The standard text-book description for Cu(I) has a coordination number of four,¹⁰³ although a concrete experimental characterization is complicated by the instability of Cu(I) toward disproportionation.¹⁰⁴ Indeed, in the gas phase, IR studies of $\text{Cu}{({\mathrm{H}}_2\mathrm{O})}_n^{+}$ clusters^105,106 pointed to a linear dihydrate structure similar to Cu⁺ diammine complex;¹⁰⁷ mass spectrometry study on water-Cu binding¹⁰⁸ also found that the binding energy of the third water and after dropped by a factor of two compared to the first two binding energies. The two-coordination configuration was supported by several theoretical calculations in the gas phase^96,97 and in CPMD/BOMD simulations for a solvated Cu(I).^90,94,95

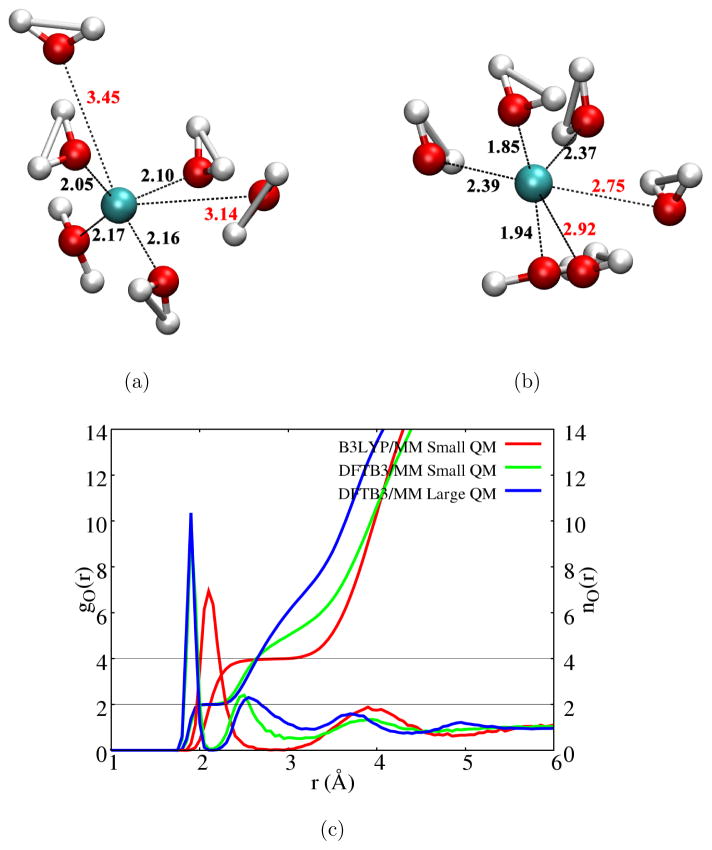
Snapshots from B3LYP/MM and DFTB3/MM simulations are shown in Figs. 3a–b, respectively. In the DFTB3/MM simulations, the first solvation shell is dictated by a two-water coordination configuration (Fig. 3b); this is most clearly illustrated by the integrated Cu-O radial distribution function (Fig. 3c). This feature is not altered by enlarging the QM region, although the second-solvation shell becomes broader in the large-QM region simulations (see additional discussion in Supporting Information regarding the impact of the DFTB model for water¹⁰⁹ and FIRES potential). The two-water coordination was also observed in previous BOMD simulations using either the BLYP^94,95 or HSE⁹⁵ functional. Interestingly, in B3LYP/MM simulations, the solvation structure is rather different and dictated by a distorted tetra-coordination configuration (illustrated by a snapshot in Fig. 3a), the Cu-O radial distribution function and the integrated coordination number function in Fig. 3c.

Figure 3.

Coordination environment of a Cu(I) ion in water. (a–b) Snapshots from B3LYP/MM and DFTB3/MM simulations; the former features a distorted tetrahedron coordination while the latter is dominated with a first solvation shell that contains two closely coordinated water. (c) Radial distribution function of water near Cu(I) and the integrated coordination number. See Supporting Information for additional discussion on the dependence of second-shell properties on the QM region size and FIRES potential.

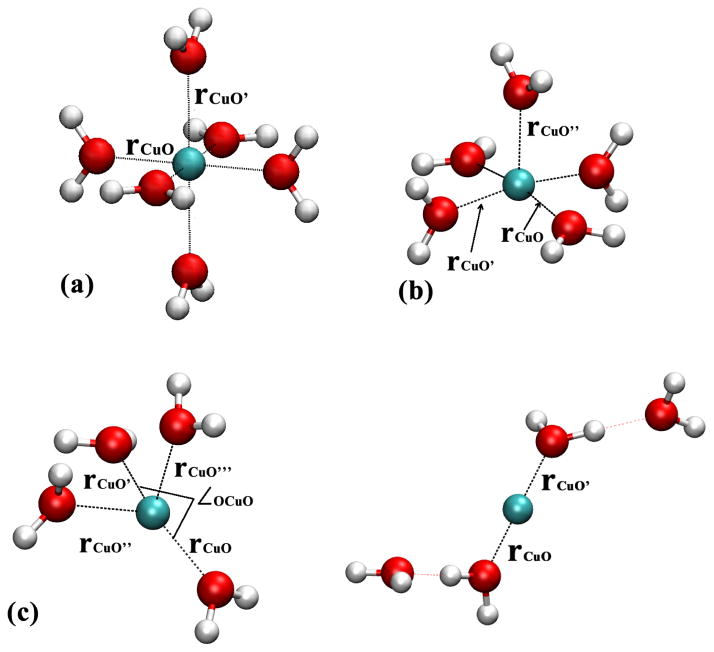
To understand the difference between DFTB3/MM and B3LYP/MM results, we study small Cu(I)/Cu(II)-water clusters in the gas phase. As shown in Table 2, DFTB3 and B3LYP give very similar results for Cu(II)-water complexes (Figs. 4a–b) and for [ $\text{Cu}(\mathrm{I}){({\mathrm{H}}_2\mathrm{O})}_2^{+}$]; the results are also very similar with a few other functionals and CCSD(T). For the [ $\text{Cu}(\mathrm{I}){({\mathrm{H}}_2\mathrm{O})}_4^{+}$] cluster, however, the situation becomes complex. With B3LYP and B97-1, a distorted tetrahedron configuration is locally stable in which two Cu-O distances are slightly (~0.1 Å) longer than the other two. With BLYP and PBE, however, the tetrahedron configuration is not locally stable and optimization leads to a linear structure in which Cu(I) is directly coordinated with only two water molecules (see Fig. 4c). With DFTB3, the tetrahedron-like structure is also locally stable although two Cu-water distances are substantially longer. At all levels, the linear structure stabilized by two hydrogen-bonded water is locally stable and represents the global minimum of [ $\text{Cu}(\mathrm{I}){({\mathrm{H}}_2\mathrm{O})}_4^{+}$]; the degree of energy stabilization relative to the tetrahedron-like structure, however, differs (see Supporting Information), which apparently leads to different Cu(I) solvation structure in the bulk.

Figure 4.

Cu(I)/Cu(II)-water gas phase models studied to compare different computational methods. (a) [Cu(II)(H₂O)₆]²⁺; (b) [Cu(II)(H₂O)₅]²⁺ (c) [Cu(I)(H₂O)₄]⁺. See Table 2 for optimized values of distances and angles; see Supporting Information for additional results, including the relative stability of the two types of [Cu(I)(H₂O)₄]⁺ configurations in (c).

3.1.2 Reduction potential

Computed reduction potentials and reorganization energies at different levels of theory are summarized in Table 3. At the DFTB3/MM level, the stochastic boundary condition (SBC) simulation with a Born solvation correction gives very similar results as GSBP. Reduction potential directly computed from free energy simulation using the periodic boundary condition (PBC) differs by about 7 kcal/mol from the SBC and GSBP values. As discussed in previous work,^110–113 this magnitude of difference is expected and due to the change of net charge in PBC simulations using Ewald summation. The PBC simulations also give a reorganization energy that is lower by 0.2 eV.

Table 3.

Reduction potential calculations for copper in solution and in plastocyanin at pH 7 from QM/MM simulations^a

Methodb	〈ΔU〉λ=0c	〈ΔU〉λ=0	Bornd	ΔFrede	ℰred (mV)	Λ (eV) f
Cu(II)→Cu(I) in water
B3LYP-SBC	−66.3 (0.2)	−215.1 (0.4)	+30.7	−110.0	330	3.22
DFTB3//B3LYP-SBC	−68.1 (0.2)	−215.7 (0.3)	+30.7	−111.2	382	3.20
B3LYP//DFTB3-SBC	−69.3 (0.1)	−212.0 (0.2)	+30.7	−110.0	330	3.09
DFTB3-SBC	−69.1 (0.2)	−222.5 (0.3)	+30.7	−115.1	551	3.33
DFTB3-GSBP	−40.8 (0.1)	−196.0 (0.2)	–	−114.5	525	3.37
DFTB3-PBCg	−52.4 (0.2)	−196.5 (0.3)	–	−122.4 (−114.7)	867 (525)	3.12
Exp.h	–	–	–	−106.1	159	–
Cu(II)→Cu(I) in plastocyanin
DFTB3-GSBP1i	−67.0 (0.2)	−121.2 (0.7)	–	−96.4 (−103.0)	−260 (27)	1.18
DFTB3-GSBP1i	−65.9 (0.3)	−123.4 (0.3)	–	−95.6 (−102.2)	−294 (−8)	1.25
DFTB3-PBC1g	−88.8 (0.6)	−145.8 (0.2)	–	−118.6 (−110.9)	703 (369)	1.24
DFTB3-PBC2g	−84.9 (0.4)	−150.5 (0.3)	–	−117.8 (−110.1)	668 (334)	1.42
Exp.h	–	–	–	−111.0	375	1.296

^aAll energies are in kcal/mol, except for the final reduction potential and reorganization energy, which are given in mV (relative to the standard hydrogen electrode) and eV, respectively.

^bThe QM level is indicated (B3LYP uses Lanl2dz for copper and 6-31G(d) for other elements), and MM is CHARMM22 force field for proteins and a modified TIP3P model for water. DFTB3//B3LYP indicates single point energy gap calculated at the DFTB3/MM level using B3LYP/MM trajectories. Three different boundary conditions are used: stochastic boundary condition (SBC), generalized solvent boundary potential (GSBP) and periodic boundary condition (PBC). Extended electrostatics are used for both SBC and GSBP, while Ewald is used for PBC (see text for details).

^cAlthough multiple λ windows are used, only the end point (λ = 0, 1) values are summarized here. See Supporting Information for additional data.

^dBorn correction is needed for the SBC simulations; a radius of 16 Å is used.

^eFollowing a linear propagation of statistical errors of free energy derivatives, the statistical error of computed ΔF_red is ~0.1–0.2 kcal/mol for copper reduction in water and ~0.2–0.5 kcal/mol for plastocyanin.

^fEstimated using a linear model, $\mathrm{\Lambda }=\frac{1}{2}({\langle \mathrm{\Delta }U\rangle }_{\lambda =0}-{\langle \mathrm{\Delta }U\rangle }_{\lambda =1})$.

^gNumbers in parentheses include a correction due to the net charge^110–113 in PBC free energy simulation; a value of 7.7 kcal/mol is taken from Ref. 113 for Na⁺ solvation; for plastocyanin, perturbative analysis indicates that ions in PBC simulations lower ΔF_red by about 9 kcal/mol.

^hMeasured reduction potential is taken from Ref.¹¹⁴ for copper reduction in water; values for plastocyanin are those summarized in Refs.^115,116

ⁱValues in parentheses include a smooth boundary correction for GSBP with an inner region charge of −8.75 using Poisson-Boltzmann calculations of 100 snapshots taken from the λ = 0/1 trajectories.¹¹²

The B3LYP/MM simulation gives a reduction free energy of about −110.0 kcal/mol, which is ~5 kcal/mol (~0.22 eV) higher than the DFTB3/MM simulations and ~4 kcal/mol (~0.17 eV) lower compared to experimental data. Considering the relatively small basis set in the B3LYP/MM simulations and the intrinsic error of B3LYP for copper reduction (see Supporting Information for a comparison between B3LYP and CCSD(T) for the oxidation/reduction energy of small copper-water clusters), this level of difference from the experimental value is expected; for comparison, the error in the computed reduction potential from BOMD simulations ranged from 0.15 to 1.26 eV when different functionals (BLYP, HSE) and pseudopotentials are used.⁹⁵

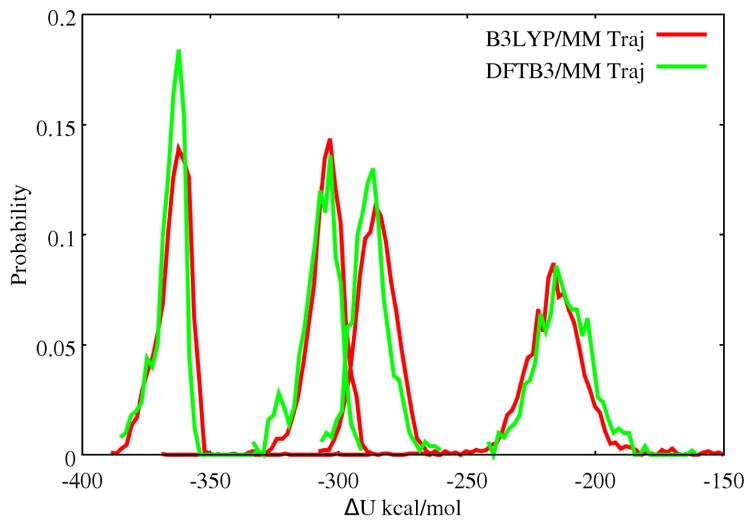
To better understand the difference between DFTB3 and B3LYP results, the energy gaps at the two end-states (λ = 0, 1) are recomputed by B3LYP/MM (DFTB3/MM) single point calculations at snapshots collected from DFTB3/MM (B3LYP/MM) trajectories. Interestingly, the results are all similar (within ~1 kcal/mol) to the B3LYP/MM simulation. This is somewhat unexpected because, as discussed above, although DFTB3/MM and B3LYP/MM give similar solvation environment for Cu(II) (Fig. 2), they appear to give fairly different descriptions for a solvated Cu(I) (Fig. 3). We then examine the distribution of the energy gap (always calculated at the B3LYP/MM level) for snapshots taken from the DFTB3/MM and B3LYP/MM trajectories for the Cu(I) state, with a specific number (2, 4, 6 or all) of water molecules closest to the copper ion included. As seen in Fig. 5, the distributions are remarkably similar when snapshots from B3LYP/MM and DFTB3/MM trajectories are used, regardless of the number of water molecules included. Therefore, we conclude that the energy gap is not highly sensitive to the precise distance and orientation of the nearby water molecules; rather, the mean energy gap appears to be most sensitive to the density of nearby water. This explains why B3LYP/MM and DFTB3/MM trajectories lead to fairly similar reduction potentials despite the notable differences in the solvation structure of Cu(I) as shown in Fig. 3.

Figure 5.

Energy gap distribution (calculated at the B3LYP/MM level) using snapshots taken from B3LYP/MM and DFTB3/MM Cu(I) trajectories. Plotted from left to right are the distributions of energy gap calculated by including two, four, six closest or all water molecules to the copper center.

Compared to the latest work of Sprik and co-workers⁹⁵ on BOMD calculations of Cu(II) reduction in water, the errors in the computed reduction potential from the current QM/MM simulations, as noted above, are similar in magnitude. There is striking difference, however, in the magnitude of the reorganization energy. Using a linear response model, our estimated reorganization energy is on the order of 3 eV (see Table 3), while the BOMD values are in the range of 2.0 eV;⁹⁵ we note that the deviation of free energy derivatives from a linear model is very modest (see Supporting Information). The origin of the difference is not quite clear; we note that our system size is substantially larger and the simulations are also much longer (the box size in Ref. 95 is 9.86 Å, and most λ windows were simulated for < 10 ps), although these differences are unlikely to lead to a difference of 1.0 eV in reorganization energy. The issue is worth investigating in the future by, for example, using Drude oscillator model for the MM water in QM/MM simulations (in Supporting Information, we show that this has only small effects on the solvation structure of copper ions in water). Moreover, the limitations in the description of bulk water by the DFT methods as discussed in Ref. 95 might also contribute.

3.2 Solvent response to copper oxidation in copper-ammonia complex

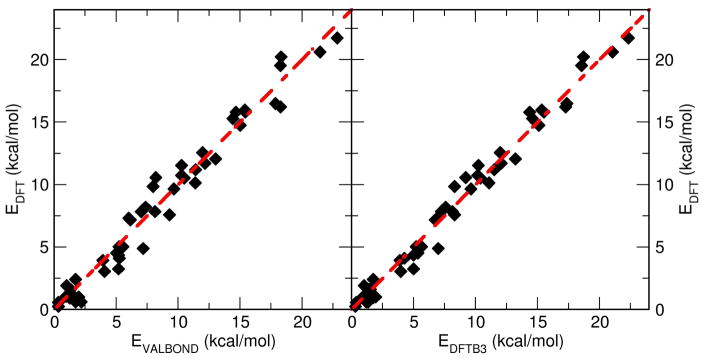
The VALBOND force field parametrization is first validated by comparing with ab initio data calculated at the B3LYP/6-31G(d,p) level of theory. From the MD simulations, the energies for 50 snapshots of the [Cu(II)(NH₃)₄(H₂O)₂]²⁺ complex, each separated by 5 ps, were computed using VALBOND, DFTB3 and ab initio methods. Fig. 6 shows a correlation plot for all three methods. Between VALBOND and DFT the RMSD_E (root mean square deviation) was 1.1 kcal/mol compared to 0.82 kcal/mol between DFTB3 and DFT. Furthermore, the structures were compared in a similar fashion by correlating all atom to atom distances for the energy optimized geometries from the three methods. The RMSD was found to be 0.29 Å between VALBOND and DFT, and 0.28 Å between DFTB3 and DFT. Hence, for structures and energetics, VALBOND and DFTB3 are in good agreement with DFT.

Figure 6.

Comparison of energies obtained from the VALBOND force field, DFTB3 and DFT calculations (B3LYP/6-31G(d,p)) for 50 snapshots of [Cu(II)(NH₃)₄(H₂O)₂]²⁺ taken from the MD simulations.

3.2.1 Equilibrium simulation

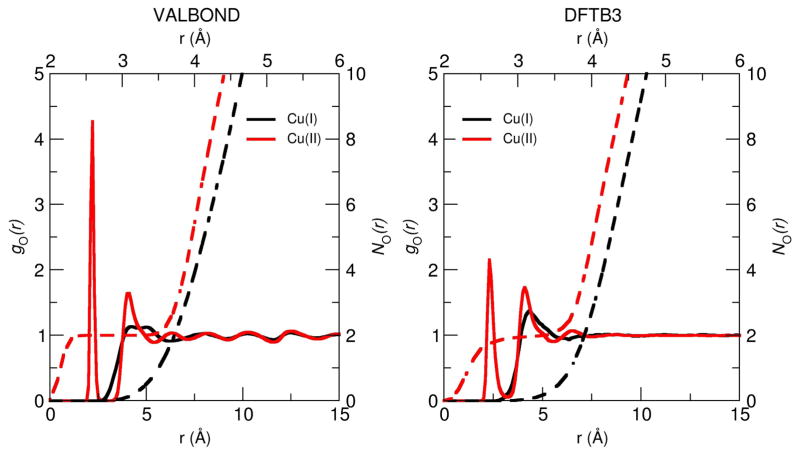
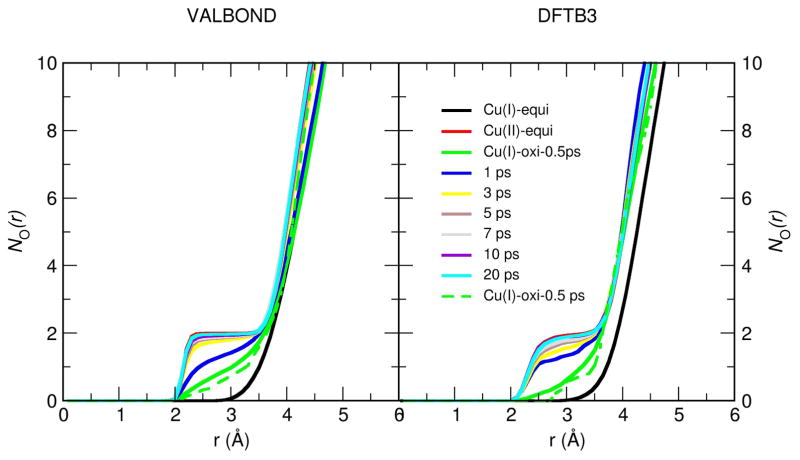
As shown in Fig. 7, VALBOND and DFTB3/MM give qualitatively similar g_O–Cu(r) although for VALBOND the coordination of water to Cu(II) appears to be stronger as suggested by the higher peak for the first solvation shell. However, the number of water molecules in the first shell, as determined from $N_O(r_s)=4\pi \rho {\int }_0^{r_s}{r}^{2}g(r)dr$ is identical and a value of two is given by both simulations. A similar conclusion can be drawn for Cu(I). Hence, from a structural perspective, the two methods yield comparable results, albeit at different computational speed.

Figure 7.

Radial distribution function (RDF) of the water oxygen with respect to the Cu ion obtained from the equilibrium simulation of 10 ns using VALBOND force field (left) and 5 ns using DFTB3/MM (right).

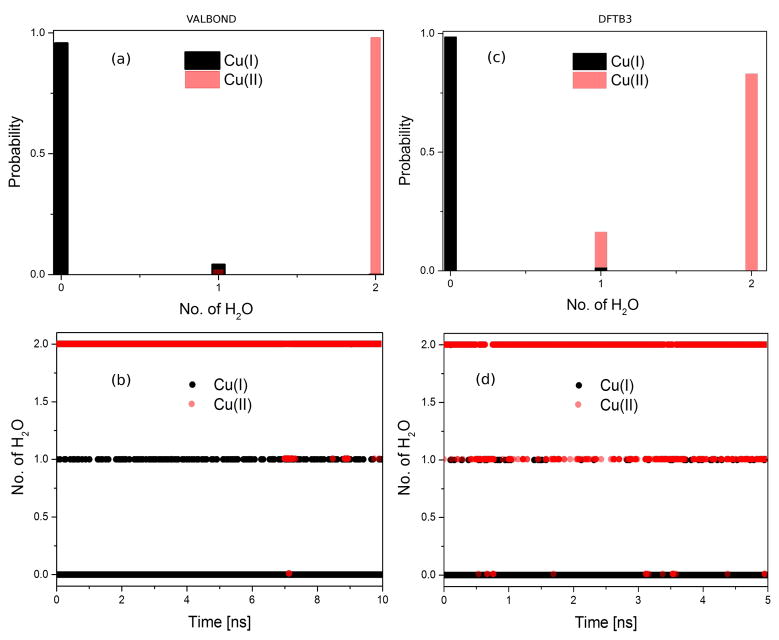
During equilibrium simulations, the number of water molecules within a given solvation shell is not constant as a function of time. For [Cu(I)(NH₃)₄]⁺ and [Cu(II)(NH³)⁴]²⁺, this is illustrated in Fig. 8. For Cu(I), an insignificant number of water molecules is expected at 3 Å due to the tetrahedral structure of the complex, as found in both VALBOND (Fig. 8a–b) and DFTB3/MM (Fig. 8c–d) simulations. By contrast, the square-planar structure of the Cu(II) complex allows up to two water molecules to coordinate axially. This is the dominant structure using both methods. However, the propensities are slightly different (Fig. 8a, c): close to 100 % for VALBOND and about 85 % for DFTB3/MM (see below). This is consistent with the observation that the g_O–Cu(r) pair distribution function is more strongly peaked for the VALBOND simulations and confirms that the copper-water interaction is stronger with VALBOND than with DFTB3/MM; including the first solvation shell of copper into the QM region in the DFTB3/MM simulations does not change the qualitative trends. Moreover, considering the dynamics of a larger water shell around the Cu(I) ion (see Supporting Information) reveals an overall similar occupation pattern for the two methods: the maximum occupation is shifted to slightly smaller numbers of water molecules in the DFTB3/MM simulations, further suggesting reduced interaction between the metal complex and the surrounding solvent.

Figure 8.

Distribution of water molecules around Cu(I)/Cu(II) ion at a distance of 3 Å obtained from the equilibrium simulation of (a–b) 10 ns using VALBOND and (c–d) 5 ns using DFTB3/MM.

In the B3LYP/MM simulation of the Cu(II) complex, also 1–2 water molecule(s) are observed to be coordinated to the metal ion, similar to DFTB3/MM simulations; the integrated radial distribution function appears to rise to 2 somewhat slower than DFTB3/MM (compare Figs. 7 and 9), thus the situation is similar to the discussion in the last section regarding the coordination number of a Cu(II) ion in water. In DFTB3/MM simulations, regardless of whether the first solvation shell is QM or MM, the single water coordination accounts for about 15% of the population (see Fig. 8b); by comparison, the value is about 22% in the B3LYP/MM simulations.

Figure 9.

Radial distribution function (RDF) of the water oxygen with respect to the Cu ion obtained from 90 ps of equilibrium B3LYP/MM simulation.

Regarding comparison to experiments, we note that Extended X-ray absoprtion fine structure (EXAFS) experiments suggested that the most stable average structure of the Cu(II) ammine complex in 4MpH-10 aqueous NH₃ can be represented as [Cu(II)(NH₃)_4.62(H₂O)_0.38(solv)]²⁺·6solv, where solv=H₂O, NH₃.¹¹⁷ Here “solv” in the first solvation shell is a localized but chemically unidentified (either H₂O or NH₃) solvent molecule at a distance of ≈3 Å due to to the charge-dipole interaction along the axial direction. Thus, our observation of two axial ligand (water) molecules coordinating Cu(II) qualitatively agree with EXAFS experimental results. Also, in the second shell (~ 4 Å from the metal center) 6 solvent molecules were inferred from the analysis¹¹⁷ which is again in good agreement with our coordination number analysis N_O–Cu(r) ≈ 5.5 based on the radial distribution function.

3.2.2 Non-equilibrium simulation

In state-of-the art time resolved X-ray experiments, structural changes and solvent responses upon switching the oxidation state at a metal center can be followed on the picoseconds time scale.^37,38 As a simple attempt to mimic such experiments, oxidation state change is induced by changing the force field parameters instantaneously from Cu(I) to Cu(II) in VALBOND simulations; in DFTB3/MM simulations, the total charge and number of unpaired electrons are changed (see Methods). Structural rearrangement of solvent molecules is monitored by computing time evolved radial distribution functions and coordination numbers of water oxygen with respect to the Cu ion.

Since the most pronounced difference in g_O–Cu(r) between Cu(I) and Cu(II) is the peak at ≈ 2.5 Å (see Fig. 7), we focus on the time-dependence of this region of the solvent distribution and show the time evolved N_O–Cu(r) in Fig. 10. The general behaviors are again similar in VALBOND and DFTB3/MM simulations. The structural response of the water shell after oxidation takes place within a few picoseconds. Somewhat larger changes occur between 0.5 ps to 1 ps in the DFTB3/MM simulations than with VALBOND, although in both cases the change of local solvation is essentially complete after 3 ps. The result from a single trajectory (dotted lines in Fig. 10) is fairly close to those averaged over many trajectories, indicating that the key features are not sensitive to the initial solvent structure. Taking all data in this section together, we see that VALBOND and DFTB3/MM are consistent in terms of equilibrium and dynamical properties of solvents near the metal complex.

Figure 10.

Running coordination number N_O–Cu(r) of water oxygen with respect to the Cu ion obtained from the non-equilibrium simulation at different time intervals using VALBOND force field (left panel) (averaged over 100 trajectories except the dotted green line which is only a single trajectory) and using DFTB3/MM (averaged over 20 trajectories except the dotted green line which is only a single trajectory) (right panel) along with the equilibrium N_O–Cu(r).

3.3 Reduction potential of plastocyanin at pH 7

Blue copper proteins have been widely studied as prototypical electron transfer proteins.^118–121 Several computational studies have also been conducted to analyze factors that dictate the reduction potential under different conditions.^{115,122–124} In this work, we focus on the degree to which DFTB3/MM is able to describe the structural and energetic properties of plastocyanin in different copper oxidation states. We leave a more systematic dissection of residual contributions, comparison to related blue copper proteins (e.g., rusticyanin) and the effect of pH^125,126 to future studies.

3.3.1 Structural properties

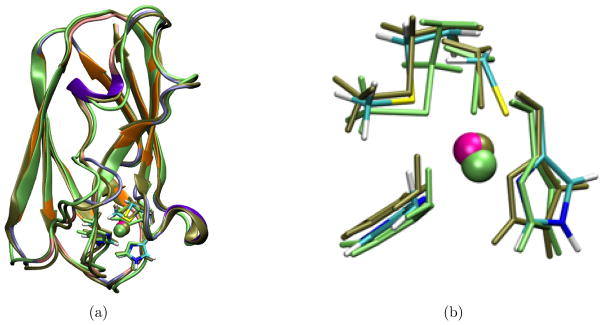
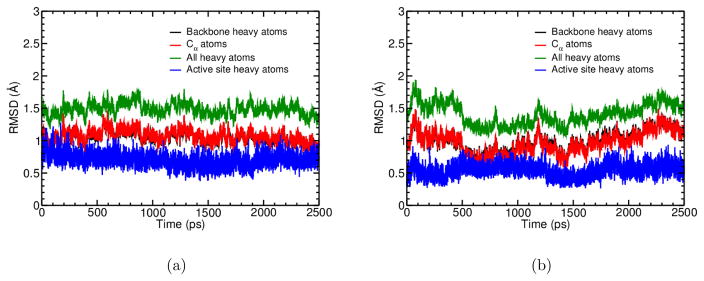
Overall, the protein remains structurally stable during the course of the simulations at the nanosecond timescale. This is illustrated visually by the overlap of crystal structure and the averaged protein structure from PBC simulations (Fig. 11a), and quantitatively by the RMSD values (~1.5 Å for all non-hydrogen atoms) relative to the starting crystal structure during the PBC simulations (Fig. 12a–b). In GSBP simulations, since part of the protein is fixed, even smaller changes in the overall protein structure are observed and therefore not shown.

Figure 11.

Overlay of the crystal structure (PDB ID 5PCY) of plastocyanin with representative structures from Cu(I) and Cu(II) PBC simulations. The crystal structure and the representative structures from simulations are aligned based on the backbone heavy atoms. The representative structures from the Cu(I) and Cu(II) PBC simulations are chosen such that they have the smallest backbone heavy atom RMSD relative to the average protein structures in the simulations. The active site in the crystal structure is colored by atom type and the cartoon representation for the protein is colored using the same scheme as in Fig. 1c. The representative structure from Cu(I) PBC simulation is colored lime green, and that from Cu(II) PBC simulation is colored tan. (a) Overlay of the entire structure. (b) Overlay of the active site region (copper is coordinated with His 37, His 87, Cys 84 and Met 92).

Figure 12.

RMSD for selected atoms during the PBC simulations for (a) Cu(I) and (b) Cu(II) states of plastocyanin.

Focusing now on the active site region, the general structural features are again well maintained for both copper oxidation states. This is again illustrated visually by the overlap of crystal structure and the averaged structures from PBC simulations (Fig. 11b), and quantitatively by the RMSD values (Fig. 12a–b), which are slightly higher for Cu(I) (~0.75 Å) than for Cu(II) (~0.5 Å) simulations. In a recent MM study using the AMOEBA force field,²⁹ two similar blue copper systems were simulated in their Cu(II) states, and somewhat lower RMSD values (~0.5–0.6 Å) were observed during also two nanoseconds of molecular dynamics.

Looking at the key distances between copper and its ligands (see Table 4), the overall agreement is satisfactory for most cases for both GSBP and PBC simulations, especially for the Cu(II) state. In the crystal structures, the most pronounced difference in the active site upon copper oxidation is that the two histidine residues (His 37, His 87) move closer to the copper ion by about 0.2 Å (Cu-Nδ distances). This is partially reproduced by the DFTB3/MM simulations in both GSBP and PBC setups: the Cu-Nδ(His 37) indeed shortens from ~2.15 Å (~2.05 Å) to ~1.96 Å in GSBP (PBC) simulations upon copper oxidation. The Cu-Nδ(His 87) distance, however, remains to be 1.95 Å in all simulations, independent of the redox state, and quite a bit shorter than the values in the crystal structures, especially for Cu(I). On the other hand, Met 92 in Cu(I) is further away from the copper ion in both GSBP and PBC simulations by about 0.2–0.3 Å relative to the crystal structure; the fluctuation of the Cu(I)-S distance, especially in the GSBP simulations (~0.3–0.4 Å), is also substantially larger than other copper-ligand distances (~0.05–0.1 Å). In PBC simulations for the Cu(I) state, Cu-S(Cys 84) also has higher fluctuations and, on average, deviates more from the crystal value compared to most other copper-ligand distances. Finally, although Cys 84 and His 87 are fairly close in the crystal structure (~4 Å), they become further apart in the Cu(I) simulations; the mean distance between S(Cys 84)-Nδ(His 87) falls in the range of 4.7–5.0 Å. By contrast, the hydrogen bond between Cys 84 and Asn 38 remains intact (see Table 4).

Table 4.

Key bond distances (in Å) during MD simulations of plastocyanin in comparison to available crystal structures

	Cu-ligand atom					Other
	Nδ(H37)	Nδ(H87)	Sγ(C84)	Sδ(M92)	O(P36)	Sγ (C84)-N(N38)	Sγ (C84)-N(H87)
Cu(I)
5PCYa	2.1	2.4	2.2	2.9	4.0	3.5	3.9
4PCYa	2.1	2.3	2.1	2.9	4.1	3.5	3.9
GSBP1b	2.15±0.11	1.95±0.05	2.26±0.06	3.25±0.45	3.98±0.25	3.55±0.17	4.92±0.30
GSBP2b	2.14±0.11	1.95±0.05	2.26±0.06	3.21±0.31	3.94±0.25	3.54±0.16	4.96±0.28
PBC1b	2.05±0.11	1.95±0.05	2.36±0.16	3.13±0.24	3.95±0.31	3.59±0.18	4.81±0.32
PBC2b	2.01±0.11	1.94±0.05	2.46±0.24	3.11±0.21	3.81±0.39	3.52±0.17	4.69±0.40
Cu(II)
1PLCa	1.9	2.1	2.1	2.8	3.9	3.5	4.2
GSBP1b	1.96±0.05	1.95±0.04	2.19±0.05	2.96±0.16	3.43±0.24	3.58±0.15	4.26±0.31
GSBP2b	1.96±0.05	1.95±0.04	2.19±0.05	2.96±0.16	3.47±0.24	3.58±0.15	4.35±0.35
PBC1b	1.96±0.05	1.95±0.04	2.20±0.05	2.98±0.17	3.46±0.25	3.59±0.16	4.48±0.35
PBC2b	1.96±0.05	1.95±0.04	2.20±0.05	2.95±0.16	3.43±0.26	3.57±0.15	4.31±0.34

^a5PCY [Cu(I)]: pH 7.0, resolution 1.8 Å; 4PCY [Cu(I)]: pH 7.8, resolution 2.15 Å; 1PLC [Cu(II)]: pH 6.0, resolution 1.33 Å.

^bGSBP1/2 indicates the two independent trajectories using GSBP; PBC1/2 indicates the two independent trajectories using PBC.

For the key angles between copper and its ligands (see Table 5), the agreement between crystal structures and simulations is overall satisfactory for Cu(II) for both GSBP and PBC calculations. For Cu(I), however, there are several notable deviations, such as S(Met 92)-Cu-S(Cys 84), S(Cys 84)-Cu-Nδ(His 87) and S(Cys 84)-Cu-Nδ(His 37); the deviations are consistent with the larger copper-ligand distance deviations for Cys 84 and Met 92 in Cu(I) simulations. In PBC simulations of Cu(I), the Nδ(His 87)-Cu-Nδ(His 37) angle is also fairly different from the crystal structure value; this is consistent with the observation that His 37 is pulled closer to Cu(I) in those simulations by almost 0.1 Å.

Table 5.

Key bond angles (in ∁) during MD simulations of plastocyanin in comparison to available crystal structures

	Nδ(H87)-Cu-Nδ(H37)	Nδ(H37)-Cu-Sδ(M92)	Sδ(M92)-Cu-Sγ (C84)	Sγ (C84)-Cu-Nδ(H87)	Sγ (C84)-Cu-Nδ(H37)	Sδ(M92)-Cu-Nδ(H87)
Cu(I)
5PCYa	99	88	113	110	136	106
4PCYa	92	90	114	112	141	102
GSBP1b	101.4±7.8	94.4±7.3	93.8±7.1	148.1±11.5	107.4±7.3	94.3±7.2
GSBP2b	102.5±8.2	94.2±7.3	94.2±7.2	147.9±11.2	106.6±6.7	93.6±7.3
PBC1b	113.9±15.7	91.3±7.9	91.6±7.1	133.1±17.2	109.5±7.5	100.5±8.2
PBC2b	123.3±20.1	92.0±8.4	93.1±8.6	124.6±21.3	109.0±7.5	97.3±9.4
Cu(II)
1PLCa	97	89	110	121	132	101
GSBP1b	102.7±5.8	85.5±6.3	98.5±6.3	128.5±11.1	123.9±10.2	104.3±6.6
GSBP2b	102.2±4.9	89.5±6.5	98.7±6.6	131.4±11.4	121.2±10.6	102.5±6.4
PBC1b	102.3±5.5	86.4±6.4	97.2±6.6	131.3±12.4	122.1±11.8	103.1±6.6
PBC2b	102.1±5.0	87.2±6.5	99.6±7.4	129.0±11.7	124.2±10.9	100.8±8.8

^a5PCY [Cu(I)]: pH 7.0, resolution 1.8 Å; 4PCY [Cu(I)]: pH 7.8, resolution 2.15 Å; 1PLC [Cu(II)]: pH 6.0, resolution 1.33 Å.

^bGSBP1/2 indicates the two independent trajectories using GSBP; PBC1/2 indicates the two independent trajectories using PBC

In short, the overall trends concerning the active site structural properties are: GSBP and PBC simulations are largely consistent with each other, except for the Cu(I)-His 37 distance, and that the Cu(II) state is generally better behaved (i.e., remains closer to the crystal structure) than the Cu(I) state, in which the copper-sulfur interactions appear to be underestimated by the current DFTB3 model. This is consistent with our previous finding¹⁸ that for the interaction between copper and charged ligands (e.g., deprotonated Cys sidechain), the current DFTB3 model still has considerable errors, due most likely to the use of minimal basis. Improvement of polarization using chemical potential equalization^127–129 (or a larger basis for the charged ligands) is likely to reduce the deviations observed here.

3.3.2 Solvation of active site

In addition to the copper-ligand geometry, another property of interest is the level of solvation of the active site. In previous PBE/AMBER simulation study,¹²⁴ for example, it was observed that the response of nearby water molecules to copper oxidation contributes 80% of the reorganization energy; this notion was also raised in previous experimental studies,¹³⁰ and is consistent with the small structural changes in the protein structure and active site geometry upon copper oxidation (see Tables 4–5).

In the current simulations, we also observe notable solvent responses. As shown in Fig. 13a–b, the hydration structure of the active site (as measured by the water radial distribution function around copper and Nε (His 87)) undergoes considerable change and the general trend is very consistent in independent GSBP and PBC simulations. The copper ion is not directly bound to any solvent; in the Cu(II) state, the more positively charged copper ion induces more structure in the nearby solvent, hence water molecules are further away from Cu(II) than from Cu(I). The oxidation also leads to a better hydration of His 87, a solvent-exposed ligand of the copper ion. These trends are qualitatively consistent with observations from a previous PBE/AMBER simulation,¹²⁴ which was much shorter in length (~ 8 ps); evidently, the solvent response occurs rapidly, as also witnessed in Sect.3.2.2.

Figure 13.

Water oxygen radial distribution function around (a) copper (b) Nε of His 87 from independent GSBP and PBC simulations.

3.3.3 Reduction potential and reorganization energy

The computed reduction potential and reorganization energy values are summarized in Table 3. As discussed in detail in Refs. 112,113, both GSBP and PBC reduction potential values need to be corrected for boundary condition artifacts; for GSBP, the correction is related to the smooth boundary approximation, and for PBC, the correction is related to Ewald summation for a system with a net charge. With these corrections included, the computed reduction potentials from GSBP and PBC still differ by about 8 kcal/mol. A perturbative analysis^131,132 of charge contributions to the free energy derivatives (i.e., computed energy gaps) indicates that the explicit ions included in the PBC simulations make a notable contribution of about 9 kcal/mol. Although this is likely an upper bound due to the perturbative nature of the analysis,^131,132 the comparison highlights that salt ions may have a considerable contribution to reduction potential, which is not unexpected for an electrostatically driven process. Moreover, as pointed out in Ref. 112, the more limited degree of structural response allowed in GSBP may also contribute to the difference from PBC simulations; considering the limited change in overall protein structure between the two oxidation states (Fig. 11) and similarity in active-site solvation from GSBP and PBC simulations (Fig. 13), we expect the magnitude of the effect to be small.

In terms of absolute values, the computed reduction potentials, especially those from PBC simulations, appear to be close to the experimental value. This agreement, however, is likely fortuitous because our previous analysis¹³³ indicated that higher-level correction for DFTB3 energetics is not negligible; we leave a more quantitative investigation of this issue to future studies. An encouraging observation is that the computed reorganization energy is also in close agreement with experimental measurement and substantially lower than that for copper reduction in solution. As discussed in previous experimental and theoretical analyses,^{119,120,122,124} the significant decrease in the reorganization energy, which is essential to the rapid electron transfer rate, is largely due to the shielding of the copper site from solvent and the relatively rigid nature of the protein scaffold.

4 Conclusions

Development of effective computational methodologies for transition metal ions in solution and biomolecules is an important yet challenging topic of research. In this study, we report our progress in this area by studying copper oxidation/reduction in water and protein using two methods developed in our groups: DFTB3 and VALBOND. Being an approximate density functional method, DFTB3 is more generally applicable and can be used to compute absolute reduction potentials. VALBOND is a molecular mechanical model and therefore needs to be parameterized for specific copper coordination and redox state; its advantage is computational efficiency and can be very effective at studying structural properties and non-equilibrium environmental responses to copper redox chemistry.

By comparing DFTB3/MM and VALBOND results to DFT/MM and available experimental data, we show that these two methodologies generally provide consistent and satisfactory descriptions of copper coordination in the condensed phase. For example, for a Cu(II) ion, DFTB3/MM and VALBOND capture the presence of both five- and six-coordinated species, as hinted by numerous experimental studies. The absolute reduction potentials and reorganization energies computed from DFTB3/MM simulations fall in the expected range spanned by experimental data. Therefore, we anticipate that the two computational methods are valuable tools for the analysis of copper redox chemistry in the condensed phase. Both methods allow routine sampling at the nanosecond scale, making them complementary to the much more expensive ab initio or DFT based QM/MM molecular dynamics simulations.

Our study also highlights a number of subtle issues worth further investigation. For example, although experimental studies favor a five-coordinated Cu(II) ion in water, VALBOND, DFTB3/MM and hybrid DFT/MM simulations carried out here point to six-coordinated species being more populated; the dominance of five-coordinated species in previous BLYP based simulations appears to be due to the underestimated binding affinity of the sixth water to Cu(II) by BLYP compared to hybrid DFT methods and CCSD(T) calculations. The coordination of Cu(I) in water also remains unclear: DFTB3/MM and previous BLYP simulations point to a two-water first solvation shell, while B3LYP/MM seems to favor a tetrahedron-like first solvation shell. Clearly, the competition between different coordination modes is subtle and deserves more thorough analysis from both computation and experiments. For plastocyanin, quantitative evaluation of the reduction potential using DFTB3/MM trajectories and higher-level energetics is worthwhile; moreover, improving the treatment of charged residues by DFTB3¹²⁹ appears essential to a better description of the Cu(I) state in DFTB3/MM simulations.