Development of the head, pinnae, and acoustical cues to sound location in a precocial species, the guinea pig (Cavia porcellus)

Abstract

The morphology of the head and pinna shape the spatial and frequency dependence of sound propagation that give rise to the acoustic cues to sound source location. During early development, the physical dimensions of the head and pinna increase rapidly. Thus, the binaural (interaural time and level differences, ITD and ILD) and monaural (spectral shape) cues are also hypothesized to change rapidly. Complex interactions between the size and shape of the head and pinna limit the accuracy of simple acoustical models (e.g. spherical) and necessitate empirical measurements. Here, we measured the cues to location in the developing guinea pig, a precocial species commonly used for studies of the auditory system. We measured directional transfer functions (DTFs) and the dimensions of the head and pinna in guinea pigs from birth (P0) through adulthood. Dimensions of the head and pinna increased by 87% and 48%, respectively, reaching adult values by ~8 weeks (P56). The monaural acoustic gain produced by the head and pinna increased with frequency and age, with maximum gains at higher frequencies (>8 kHz) reaching values of 10–21 dB for all ages. The center frequency of monaural spectral notches also decreased with age, from higher frequencies (~17 kHz) at P0 to lower frequencies (~12 kHz) in adults. In all animals, ILDs and ITDs were dependent on both frequency and spatial location. Over development, the maximum ILD magnitude increased from ~15 dB at P0 to ~30 dB in adults (at frequencies >8 kHz), while the maximum low frequency ITDs increased from ~185 µs at P0 to ~300 µs in adults. These results demonstrate that the changes in the acoustical cues are directly related to changes in head and pinna morphology.

1. INTRODUCTION

There are three main acoustic cues to sound location, each of which is generated by the spatial- and frequency-dependent filtering of propagating sound waves by the head, torso and external ears (or pinnae). The two binaural cues to sound location − interaural differences in time (ITD) and level (ILD) − arise due to the physical separation of the two ears by the head, and mediate localization of sound sources in azimuth (horizontal position) in mammals. The difference in time it takes for a sound to reach the two ears is the ITD, where the ear closer (ipsilateral) to the sound source receives the sound prior to the farther (contralateral) ear (Strutt, 1907; Kuhn, 1977a). ILDs are the differences in sound level (dB) between the two ears resulting jointly from the attenuation at the contralateral ear due to the “acoustic shadow” cast by the head and the amplification of the sound (due to the shape of the pinna) at the ipsilateral ear (Rayleigh, 1907; Stevens and Newman, 1936). The third major cue to sound source location, which are monaural spectral shape cues, arise from the direction-dependent acoustic filtering properties of the head, body, and pinna. They consist of spectral notches and peaks, whose magnitude and center frequency depend on elevation, and to a lesser extent, azimuth, of the sound source. These characteristic spectral features mediate localization of sounds in elevation, including discrimination of sounds in the frontal hemisphere from those in the rear (Musicant, 1985; Tollin and Yin, 2003).

In human and smaller mammals alike, the physical dimensions of the head and pinna are the primary determinants of the cues to sound location (Shaw, 1974; Tollin and Koka, 2009a, b). This poses a challenge to the auditory system, particularly during development for precocial mammals whose hearing onset occurs before birth (Clifton et al., 1988; Tollin and Koka, 2009a,b; Jones et al., 2011). Presumably, the neural representation of sound source location needs to remain plastic to accommodate the maturation of the acoustic cues to location. Such plasticity has been suggested by studies in the ferret where the time course of the growth of the head and pinna correlates with the duration of a “sensitive period” of auditory development (Carlile, 1991; Schnupp et al., 1998). Withington-Wray and colleagues (1990) also found that cells in the guinea pig superior colliculus, a multisensory midbrain nucleus, are broadly tuned to sound location at birth and improve spatial tuning with age. Similarly, in the barn owl (an altricial bird species) the growth of the head and facial ruff (a structure similar to the mammalian pinna) was shown to correspond to developmental changes in neural representation of sound position (Knudsen et al., 1984a). These studies suggest that there is a period of calibration where neural circuits adjust to the changing acoustic cues, driving the maturation of the auditory space map.

Guinea pigs are a common model for anatomical (Dong et al., 2010; Schofield et al., 2006), physiological (Koehler and Shore, 2013; Shackleton et al., 2009; Zohar et al., 2011), behavioral (Berger et al., 2013; Dehmel et al., 2012; Mulders et al., 2014) and developmental (Withington-Wray et al., 1990; Withington et al., 1994) studies of the auditory system. They are also popular models for studies of middle (Guan and Gan, 2011; Lee et al., 2014) and inner (Chen et al., 2014) ear mechanics likely because the guinea pig is audiometrically similar to humans in that they hear sounds over comparable ranges of frequencies (Heffner et al., 1971; Syka et al., 2000). Guinea pigs also share similar pinna features (Greene et al., 2014) as humans–unlike many other commonly used animal models (i.e., cat, chinchilla, bat) with upright, conical pinna, guinea pigs have more oval-shaped, “flattened” ears positioned on either side of the head. Finally, also like humans, guinea pigs are precocial with functional central and peripheral auditory systems at birth (Sedlácek, 1976). As a result, the guinea pig presents as a unique model for studies of auditory development, particularly for studies of sound localization.

Aside from measurements in the adult guinea pig (Carlile and Pettigrew, 1987; Greene et al., 2014; Sterbing, 2003), there has not been a systematic study of the monaural and binaural acoustic cues to location in the developing animal. In order to utilize the guinea pig as a model for auditory development, we must understand the sound localization cues available to the auditory system at different stages of development. In this study, we assessed the development of the head and pinna in the guinea pig (Cavia porcellus) along with the concurrent development of the acoustic cues to sound location.

2. METHODS

2.1 Animal preparation

All surgical and experimental procedures complied with the guidelines of the University of Colorado Anschutz Medical Campus Animal Care and Use Committees and the National Institutes of Health. Pigmented guinea pigs were obtained from an external vendor (Elm Hill Labs, Chelmsford, MA), as well as from an in-house breeding colony. Eleven (5 male, 5 female, 1 unknown due to young age) guinea pigs of different ages were used for acoustic measurements in this study, and 63 (34 male, 24 female, 5 unknown) were used for longitudinal measurements of the head and pinna. Prior to each set of acoustical measurements, selected animals were anesthetized with an intraperitoneal (IP) injection of ketamine hydrochloride (80 mg/kg) and xylazine hydrochloride (8 mg/kg), and euthanized with an intracardiac (IC) injection of sodium pentobarbital (100 mg/kg). Body weight, head diameter, and pinna length and width were then measured (see Figure 1A,B).

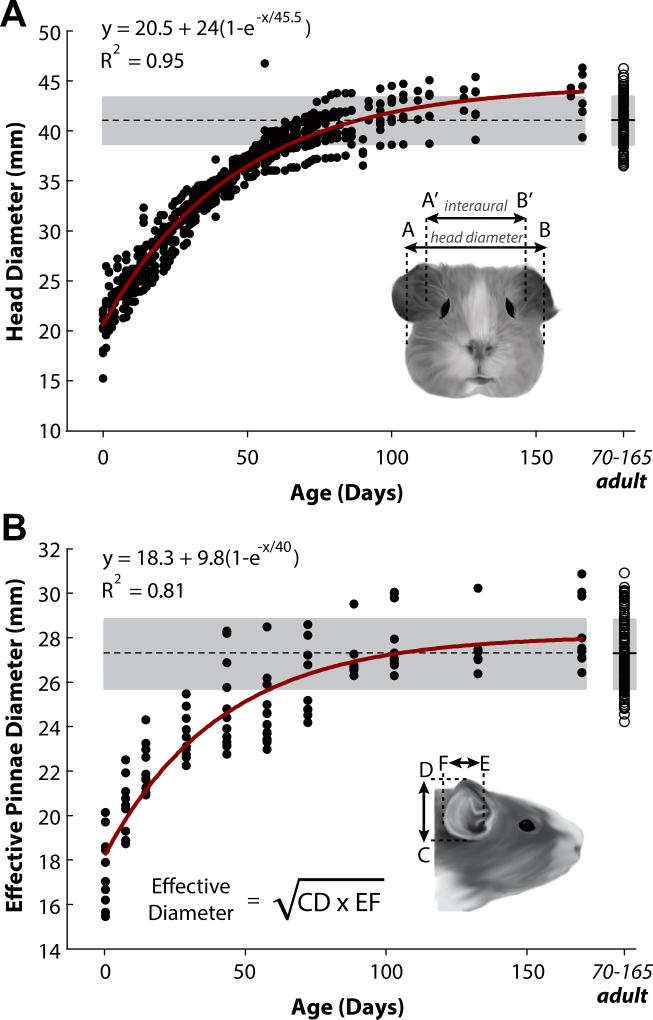
Figure 1.

Measurements of head and pinna dimensions in the developing guinea pig. A: Head diameter was measured as the widest part of the skull (between points AB; see inset) as well as from P0 through P165 in 50 animals. Measurements between the ear canals were also taken (interaural distance; A’B’). B: Effective pinna diameter was calculated by measuring pinna height (CD) and pinna width (EF; see inset for equation) in 20 animals. Data points in A and B indicate single animal measurements. The dashed line and gray area indicate the mean and associated standard deviation, respectively, for the adult animal population (>P70; data points compiled on far right). Dimensions of the head and pinna increased by factors of 2.4 and 1.56, respectively, reaching adult values by ~8 weeks (P56).

Experimental setup and procedures for acoustic measurements were similar to those described in previous publications (Koka et al. 2011, 2008; Tollin and Koka 2009a,b; Greene et al. 2014) and are only briefly described here. Measurements were made on recently euthanized, frozen subjects; care was taken to ensure that the animal was frozen in a natural, alert position. We chose this method as it allows for consistent access and placement of the microphone probe tubes near the tympanic membrane. Similar techniques have been used previously to measure the acoustic cues in anesthetized (Koka et al., 2011; Tollin and Koka, 2009a;b), frozen (Greene et al., 2014; Koka et al., 2008; Obrist et al., 1993; Wotton, 1995), formalin-fixed (Aytekin et al., 2004; Firzlaff and Schuller, 2003; Fuzessery, 1996), alcohol-fixed (Obrist et al., 1993), and freshly euthanized animals (Chen et al., 1995; Coles and Guppy, 1986; Harrison and Downey, 1970; Maki and Furukawa, 2005; Martin and Webster, 1987; Middlebrooks and Pettigrew, 1981; Moore and Irvine, 1979). These previous studies have found negligible effects between preparation conditions.

Following measurements of the head and pinna dimensions, a 50-mm-long flexible silicone probe tube (1.65 mm outer diameter) was inserted into the cartilaginous ear canal through a puncture at the posterior base of the pinna. The tip of the probe tube was positioned approximately 2 mm from the tympanic membrane at the boundary between the cartilaginous and bony ear canals (see Greene et al. 2014 for a more detailed description of probe placement). The final position of the probe tube was verified via otoscopic visualization and fixed in place with cyanoacrylate adhesive. The animal was then placed on a small acrylic platform in the center of the sound-attenuating chamber, with its interaural axis aligned to the center of an arc of loudspeakers. Care was taken to ensure the platform did not impede any signals from all speaker locations. The distal ends of the tubes were then connected to two microphones (Bruel and Kjaer, ¼” probe tube microphone Type-4182). Pinna positions were not altered or standardized across animals in order to conserve the natural orientation of the pinna, thus retaining some variability in ear positioning across the population. The contribution of the pinna was assessed by repeating the acoustical measurements after surgical removal. This involved a circular incision around the perimeter of the pinna, carried down through the lateral aspect of the cartilaginous portion of the ear canal resulting in an en bloc excision of the intact pinna. Otoscopic examination of the microphone probe-tube position in the ear canal before and after pinna removal ensured that the position was not altered during the surgical process.

2.2 Experimental setup

All experiments were conducted in a double-walled, sound-attenuating chamber (interior dimensions: ~3 × 3 × 3 m; IAC, Bronx, NY) lined with 4-inch thick reticulated wedge acoustic foam (Sonex Classic). Stimuli were presented using a polar coordinate system from 25 identical loudspeakers (Morel MDT-20) attached to a custom-built, semicircular arc with a radius of 1 m (Leong and Carlile, 1998; Middlebrooks and Pettigrew, 1981). The 25 loudspeakers were spaced in azimuth along the arc at 7.5° intervals, from +90° (left of the animal) to −90° (right of the animal). The axis of arc rotation was aligned with the interaural axis of the animal (i.e., through the ears). Directional transfer functions (DTFs) were recorded from a total of 775 different locations, covering azimuth (+90° to −90°) and elevation (−45° in the frontal hemisphere to +180°, exactly behind the animal).

The acoustic measurement stimuli consisted of 11th order maximum length sequences (MLS; Rife and Vanderkooy, 1989) repeated without interruption 128 times from each loudspeaker. The MLS stimuli were presented at full 24-bit resolution at a rate of 97656.25 Hz (Tucker-Davis Technologies, RP2.1, TDT, Alachua, FL). A single sequence of 11^th order MLS is comprised of 2047 samples (2¹¹-1) and is 20.96 ms in duration. The 256-tap digital finite impulse response filters were computed from loudspeaker output levels for tones from 0.1 to 30 kHz (0.1-kHz interval), providing a virtually flat acoustic response (± 2 dB) and maximum compensated output levels of ~95 dB SPL. The resulting acoustic waveforms were simultaneously recorded in the left and right ear canals using two probe tube microphones, amplified, collected using two analog to digital converter channels, and stored for off-line analysis. Measurements made previously in the lab (e.g., Lupo et al. 2011) demonstrated that the chamber is effectively anechoic for frequencies down to 250 Hz. An acoustic calibration measurement was also made in the absence of the animal to capture the spectral characteristics of the loudspeakers and microphones. These measurements were used to eliminate the spectral properties of the speakers and the varying microphone probe tube placement from the acoustic recordings (more details below).

2.3 Data processing and analysis

The impulse responses for each ear at each location were calculated by circular cross correlation of the original 11th order MLS stimulus and the in-ear recording from the probe tube microphone (Rife and Vanderkooy, 1989). The impulse responses were then truncated to 512 points (5.24 ms) by a Hanning window beginning 700 samples (7.17 ms) after the start of the stimulus presentation, thereby approximately centering maximum deflection of the impulse response. This windowing procedure removes the small-amplitude reflections from the wall opposing the active speaker (~ 2 m distance, approximately 5 ms delay) that may be contained in the original measurement. In other words, the time-windowing of recorded waveforms removed any contributions of reflections across frequency prior to analysis (discussed in detail in Koka et al. 2011).

Head related transfer functions (HRTFs) were derived by dividing the frequency response of the in-ear recording by that of the appropriate loudspeaker calibration measurement, thereby removing the frequency response of the loudspeaker and microphone from each in-ear measurement. The resulting function is referred to as the HRTF, and comprises the acoustic gain and delay introduced by the head and the pinna. However, the resulting HRTF can be highly dependent on the exact placement of the tip of the probe tube microphone in the ear canal relative to the tympanic membrane (Middlebrooks, 1989). To reduce the confounding effects of the probe tube placement in each ear canal, the HRTF recorded for each spatial location was divided by the geometrical mean of all the measured HRTFs across all measurement locations. The spectral features resulting from the exact placement of the probe tube microphone in the ear canal are expected to be similar for all measurement locations (i.e., they are not dependent on spatial location), so this “common” spectral feature is removed from the HRTFs, yielding directional transfer functions (DTFs, (Middlebrooks and Green, 1990). In essence, DTFs are the sound source direction-dependent components of HRTFs.

Amplitude spectra of the DTFs were calculated using a bank of band pass filters that simulate the effects of auditory peripheral filtering. The filter bank consisted of 500 Butterworth filters, with the center frequencies spaced at intervals of 0.0143 octaves spanning from 0.25–32 kHz. The 3 dB bandwidth of filters was held constant across all frequencies at 0.0571 octaves, and the upper and lower slopes of the filters fell off at ~105 dB/octave. These filters have properties similar to triangular band pass filters described elsewhere in the literature (Schnupp et al., 2003; Xu and Middlebrooks, 2000). We computed the 99^th percentile of the DTF gains for each subject and frequency as a more robust estimator of the sample maximum, which we defined here as the maximal DTF gain. We chose this method of estimation (as opposed to simply selecting the maximum gain value) as it avoided the selection of outliers in the data (Benichoux et al., 2016; Papadatos, 1995).

For spatial plotting purposes, the data were displayed as Aitov projections (Bugayevskiy and Snyder, 1995). In this projection, the animal’s nose was oriented at 0° azimuth and 0° elevation, as if the animal were looking at the reader. Unless stated otherwise, spatial plots gave frontal hemifield data (i.e. azimuth from +90° to −90° and elevation from −45° to +90°).

2.4 Binaural cues computation

ILDs were computed in frequency bands using the filter bank mentioned in Section 2.3. We defined ILD as the DTF gain in the left ear minus the DTF gain in the right ear, thus a positive ILD indicates that the sound intensity is higher at the left ear than for the right ear. ILDs for particular frequencies and locations were extracted from the ILD spectra. The ITD was computed using the phase spectrum of the DTFs in a manner similar to that described by Benichoux et al. (2016). Briefly, the ITD at any given frequency was computed as the difference in unwrapped phase (expressed in cycles) of the right versus left DTFs divided by the frequency.

3. RESULTS

Physical measurements of head and pinna dimensions were obtained from 63 guinea pigs, some of which were measured nearly every day starting within 24 hours of birth (postnatal day 0, P0) until well into maturity (>P70). We chose to begin measurements at birth as guinea pigs are a precocial species, where hearing onset begins prior to birth (Sedlácek, 1976). Measurements from 15 animals aged >P70 were selected to establish the adult distributions of head and pinna sizes. Acoustic measurements were obtained in 11 animals, 3 were adults and 8 were animals at different ages ranging from P0 to P42.

3.1 Development of head and pinna dimensions

Figure 1 shows linear measurements of head and effective pinna diameter as a function of age for 63 guinea pigs starting at birth (P0) through P165. Head diameter was taken at the widest part of the skull (between points A and B in Fig. 1A, inset) along the zygomatic arch (the bizygomatic breadth) of the temporal bone (Wysocki, 2005). Individual data points indicate single animal measurements. The dashed line and the gray area indicate the mean ± 1 standard deviation (SD) in the adult animal population (>P70). All measurements taken for >P70 were grouped and plotted on the far right of Figures 1A, B. The mean head diameter for the guinea pig population at birth (P0) was 21.85±2.9 mm and 40.91±2.1 mm for the adult population. To quantify the growth rate of the head dimensions, data were fit with a three-parameter exponential rise-to-maximum function of the form y = y₀ + Δy(1−e^−x/τ), where x is in days, y₀ is the dimension at birth (P0), Δy is the amount by which that dimension increases during development (thus y₀ + Δy is the asymptotic value at full development), and τ is the rate of growth (in days). Data were well-captured by this function (R² > 0.9; see Fig. 1A). We observed that full growth occured over a 46 day period (τ =45.5 days), during which the head diameter more than doubled from 20 mm (y₀ = 20 mm) to 44 mm (y₀ + Δy = 44 mm).

Interaural distance, defined as the linear distance between the entrances of each ear canal, was also measured (between A’ and B’ in Fig. 1A). The mean interaural distance was 24.02±0.9 mm for P0 animals (N=6) and 34.1±8.4 mm for the adult animals (N=17). These values were larger than those reported by Withington-Wray (1990; interaural distance of ~13 mm at birth increasing ~85% to ~24 mm in the adults). This discrepancy may be due to a difference in the anatomical location of the interaural axis measurement as it is not clear where the measurements were taken for that study. Disagreements in measurements could also arise from differences in the strains of animals used, the individual specimens, or housing and/or feeding practices. Despite this discrepancy, both data sets indicated that interaural distance asymptotes at ~P56. Across all ages, the interaural diameter for each animal was on average 16.68 ± 6.09% smaller than the head diameter measured at the widest part of the skull.

We also measured the dimensions of the pinna using the method of Coles and Guppy (1986), in order to account for both the height and width dimensions of the oval-shaped pinna (see inset of Fig.1B). The effective diameter, given by the square root of the product of pinna height and pinna width (the geometric mean of pinna height and width; see equation, inset of Fig.1B), was based on an equal areas approximation to a circular aperture (for more detail regarding this calculation, see Jones et al. 2011). The lengths and widths of the pinna (CD and EF, Figure 1B) in the guinea pig population were 19.30±1.9 mm and 15.74±1.8 mm respectively at birth and 30.47±2.4 mm (CD) and 24.44±0.9 mm (EF) at adulthood. Thus, the effective pinna diameter at P0 was 18.40±2.4 mm and 27.28±1.5 mm for the adult population. Pinna measurements were reported as averages of the left and right ear dimensions. A complete description of head and pinna dimensions (and body weight) for ages P0, P7, P14, P28, P42, P56, and >P70 can be found in Table 1.

Table 1.

Average head, pinna dimensions and associated weights in the developing guinea pig.

Age	Head Diameter, AB (mm)	Interaural Distance, A’B’ (mm)	Pinna Height, CD (mm)	Pinna Width, EF (mm)	Effective Pinna Diameter, ED (mm)	Weight (kg)
P0	21.85±2.9 (n=22)	24.02±0.91 (n=6)	19.3±1.9 (n=11)	15.74±1.76 (n=11)	18.4±2.4 (n=16)	0.09±0.03 (n=23)
P7	25.85±3.03 (n=18)	25.94±1.87 (n=3)	21.84±1.51 (n=13)	20.3±3.16 (n=13)	20.99±1.64 (n=13)	0.14±0.05 (n=18)
P14	27.14±2.56 (n=15)	27.4±2.3 (n=4)	24.25±1.19 (n=11)	20.20±1.06 (n=11)	21.78±0.98 (n=11)	0.19±0.06 (n=15)
P28	32.17±1.62 (n=19)	29.83±0.86 (n=3)	25.67±1.56 (n=11)	21.57±0.93 (n=11)	23.21±1.06 (n=15)	0.31±0.06 (n=23)
P42	34.83±1.29 (n=12)	30.85±0.48 (n=3)	27.54±3.21 (n=13)	22.33±1.18 (n=13)	23.54±1.34 (n=12)	0.4±0.05 (n=12)
P56	37.95±1.66 (n=17)	35.27±1.55 (n=4)	27.11±2.47 (n=14)	22.28±1.01 (n=14)	25.72±1.33 (n=11)	0.51±0.07 (n=20)
>P70	40.91±2.07 (n=16)	34.1±2.43 (n=17)	30.47±2.44 (n=13)	21.85±2.9 (n=22)	27.76±1.48 (n=10)	0.67±0.13 (n=20)

Values are listed as the average ± standard deviation.

Head and pinna dimensions were defined as “adult” once the measured dimensions fell within the adult range of values (shaded area, Fig. 1), which occurred at ~P56 for all measures (8 weeks after birth). We found that from P0 to the adult range, head diameter increased by 87% and the effective pinna diameter increased by 48%.

3.2 Development of monaural aspects of directional transfer functions

3.2.1 Spatial distributions of DTF amplitude gain

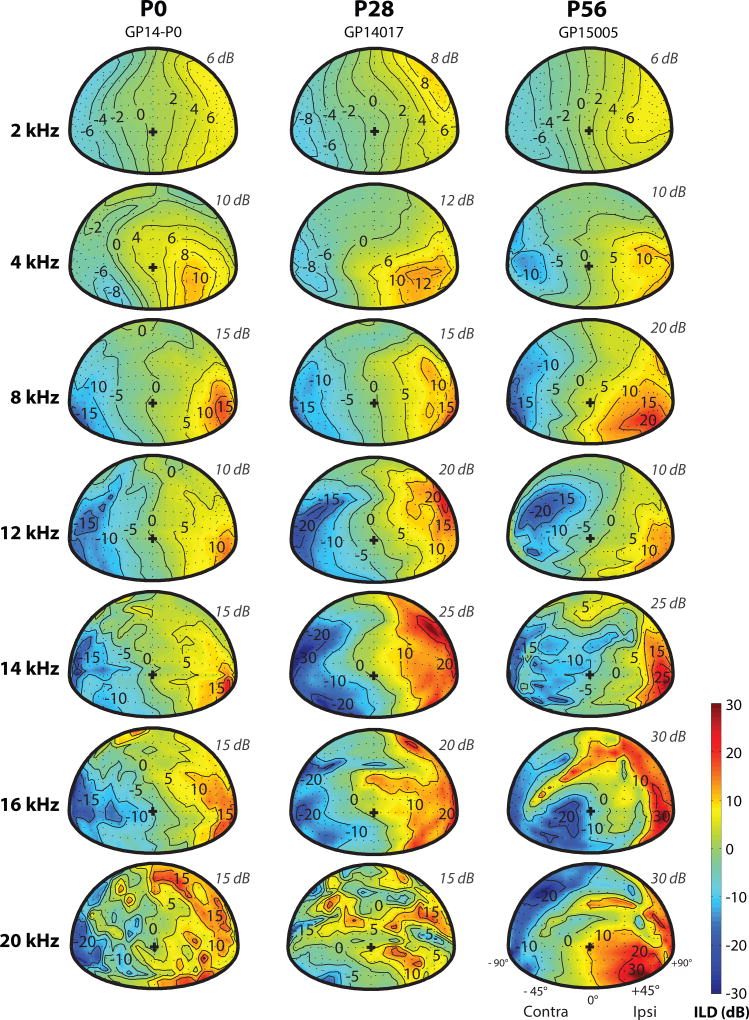
DTF gains varied with frequency and source direction across measurements taken at different ages. Figure 2A shows the spatial dependence of DTF gains for three representative animals (aged P0, P14, and P56), at six different frequencies, for sources in the frontal hemisphere. For reference, a schematic representation of the animal orientation is shown in Figure 2B. The gain plots are shown for the left ear for all animals, and a positive gain is depicted with a warmer color gradient (see color bar in 2A).

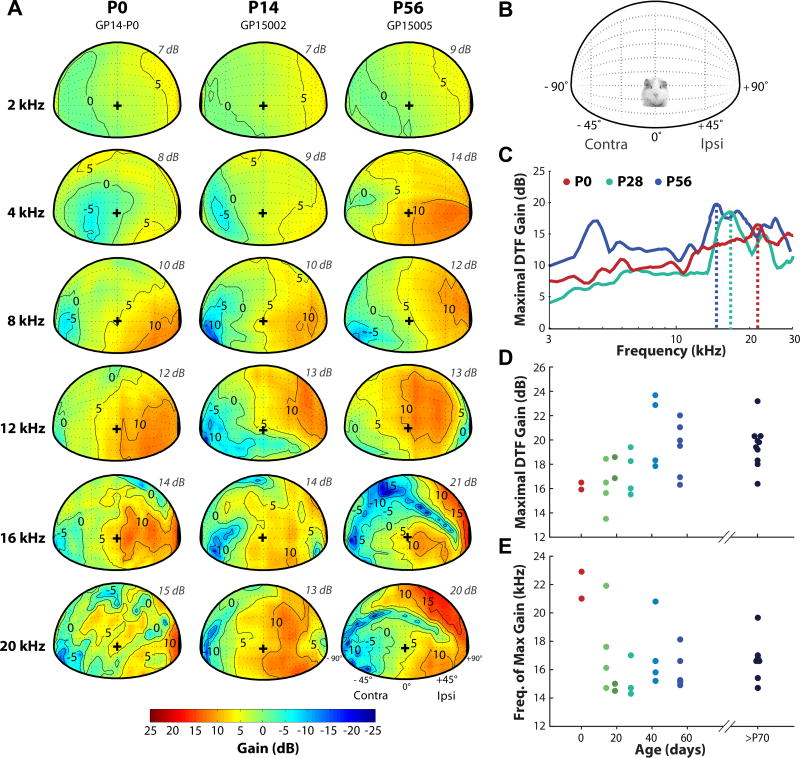
Figure 2.

Monaural DTF gain varies with frequency, source direction, and magnitude across animals at different ages. A: Spatial distribution of DTF gains for six frequencies for the left ear (+90° is ipsilateral) of three animals aged P0, P14, and P56 (adult). The maximum gain for each frequency shown (frequency listed on left side of every row) is given on the upper right side of each panel (italicized grey text). The contours are plotted at −5 dB intervals from the maximum gain. The color bar indicates the gain in decibels (dB), with the warmer colors indicating the positive gain with respect to the left ear. “+” indicates the origin 0°, 0°. B: Schematic representation of the speaker positions for the gain plots in (A). C: Maximal gain (dB) in the DTFs as a function of frequency for example animals aged P0 (red), P28 (green), and P56 (blue). Maximal gain is shown for both frontal and back hemispheres. The vertical dotted lines indicate the frequency at which the peak in acoustic gain (dB) occurs for each animal. D: Maximal gain as a function of age for all animals tested. Data from both left and right ears are shown. E: Frequency of peak maximal gain as a function of age. >P70 data in both E, F are from Greene et al., 2014.

The maximum DTF gain observed at each particular frequency is shown on the upper right side of each panel (Figure 2A, italicized grey text). The maximum DTF gain increased with frequency at each age, consistent with model predictions (Duda and Martens, 1998). At P0-P14, the maximum DTF gains were ~7–8 dB for frequencies up to 4 kHz and ~10–15 dB above 8 kHz. These gains increased with age for all frequency bands: at P56, the DTF gains are ~9–14 dB up to 4 kHz and ~12–21 dB above 8 kHz. The locations at which these maximum gains were observed also appeared to shift with age, with the area of highest gain shifting from below the origin (the position directly in front of the animal, 0°,0°; designated as “+” in Figure 2A) in the frontal hemisphere at P0-P14 to higher elevation (above the origin) at P56. This trend was most apparent at high frequencies (>8 kHz). In addition, a spectral notch originating in contralateral space appeared at age P14 (for frequencies 16 and 20 kHz), and formed a distinct, “diagonal” feature in the adult (P56) DTF.

Figure 2C represents the maximum DTF gain as a function of frequency for three example animals at P0, P28, and P56/adult (P0 and adult data are from Fig. 2A). Here, the maximum gains are depicted for both the front and back hemispheres, with elevations from −45° (below the origin) to +180° (directly behind the animal). In all animals, the maximum gain increased with frequency with the largest gains occurring above 10kHz. For the P56 example animal, there were two prominent peaks in the maximum acoustic gain: the first occurring at 4.8 kHz and the second occurring at ~15 kHz. This large peak in gain around 4–5 kHz was also observed in other adult data. Figures 2D,E show maximal gain and peak-gain frequency as a function of age in all animals tested. Data from older adult animals (>P70), from Greene et al., 2014, were included to validate the adult-like ranges of the P56 data. The magnitude of the maximal acoustic gain increased with age from ~16dB at P0 to ~20dB in adults, while the frequency at which the maximum gain appeared (represented by vertical dotted lines in Fig. 2C) decreased from ~22 kHz at P0 to ~ 16 kHz in adults. The shift in peak gain frequency with age was consistent with the increase in the linear dimensions of the head and pinna (see Fig. 1) and has been observed in other species (cat: Tollin and Koka, 2009a; chinchilla: Jones et al., 2011; (rat: Koka et al., 2008), although the trend observed here was not as prominent as observed in other species.

3.2.2 Acoustic Axis

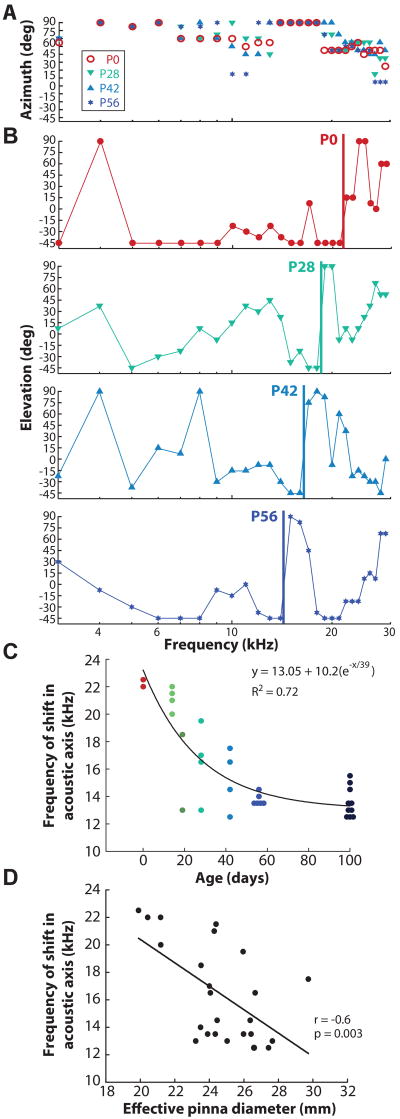
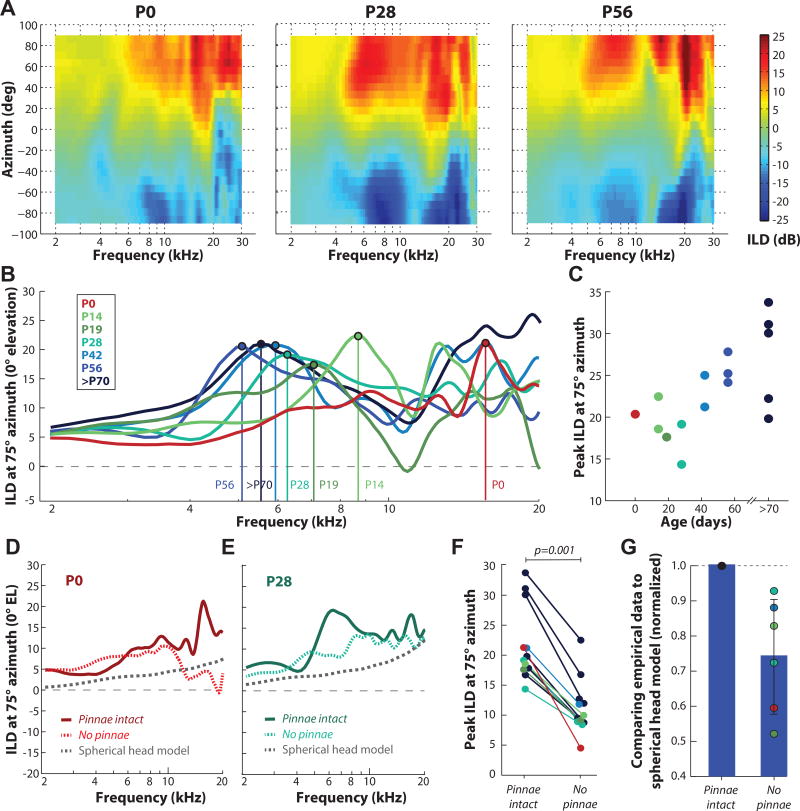
The spatial distribution of DTF gain was further quantified by calculating the acoustic axis, the direction of the maximum acoustic gain for a given frequency (Middlebrooks and Pettigrew, 1981; Phillips et al., 1982). Figure 3 shows the spatial location of the acoustic axis for azimuth (Fig. 3A) and elevation (Fig. 3B) as a function of frequency for four representative animals at different ages (P0, P28, P42, P56). The azimuth of the acoustic axis followed a similar pattern across all ages (Fig. 3A): with increasing frequency, the location of the axis shifted from lateral azimuthal locations towards the midline (0°) with additional abrupt shifts from midline to lateral locations at ~ 14 kHz. The elevation of the acoustic axis (Fig. 3B) also followed a distinct pattern across all ages shown: with increasing frequency, the acoustic axis first increased in elevation, then transitioned back down to lower elevations at ~12–15 kHz and abruptly returned to higher elevations at high frequencies (this is particularly evident in the P0, P28, and P56 panels). Vertical lines in Fig. 3B demarcate the lower frequency at which this abrupt transition occurred. Interestingly, the transition frequency appeared to systematically shift from higher to lower frequencies with increasing age (P0: 22kHz, P28: 18kHz, P42: 16kHz, P56: 14kHz).

Figure 3.

Spatial location of the acoustic axis for azimuth (A) and elevation (B) as a function of frequency for animals aged P0 (red), P28 (green), P42 (light blue), and P56 (blue). Vertical lines in (B) indicate frequencies at which discrete transitions occur in the location of the acoustic axes with changes in sound source elevation. C: The frequency of the discrete transitions in acoustic axes (with changes in elevation) as function of age for all animals. The black line is the fitted exponential decay function. D: Linear regression (black line) between the frequency of acoustic axis shift in elevation and the effective pinna diameter.

Figure 3C shows the frequency of the discrete transitions of the acoustic axes for elevation as a function of age for all animals tested. To quantify the decrease in frequency with age, a three-parameter exponential decay function was fit to the data of the form y = y₀ + Δy(e^−x/τ), where x is in days, y₀ is the frequency at birth (P0), Δy is the amount by which that frequency decreased during development, τ is the rate of decrease (kHz). We observed that the frequency decreased over a 39 day period, during which the frequency decreased by ~36% from P0. Notably, the duration of full pinna growth followed a very similar time course (40 days). In addition, the ratio of P0 to P56 frequency transition was ~1.57, which corresponded nicely with the increase in effective pinna diameter of 1.5x from P0 to P56. On the assumption that these frequency effects scaled inversely with the dimensions of the pinnae (i.e, increasingly larger pinnae affected increasingly lower frequencies). To test the relationship between the frequency shifts and the pinna, we show the linear regression between the frequency transition and the inverse of effective pinna diameter (Fig. 3D) and found that there was a significant correlation (r=−0.6, p=0.003). This suggests that the frequency of the transitions in the acoustic axes is due to the pinna, whose frequency was proportional to the inverse of its effective diameter. Altogether, our data suggest that the growth of the pinna was contributing to the shift in frequency of the acoustic axis in azimuth and elevation.

3.2.3 Broadband spectral notches

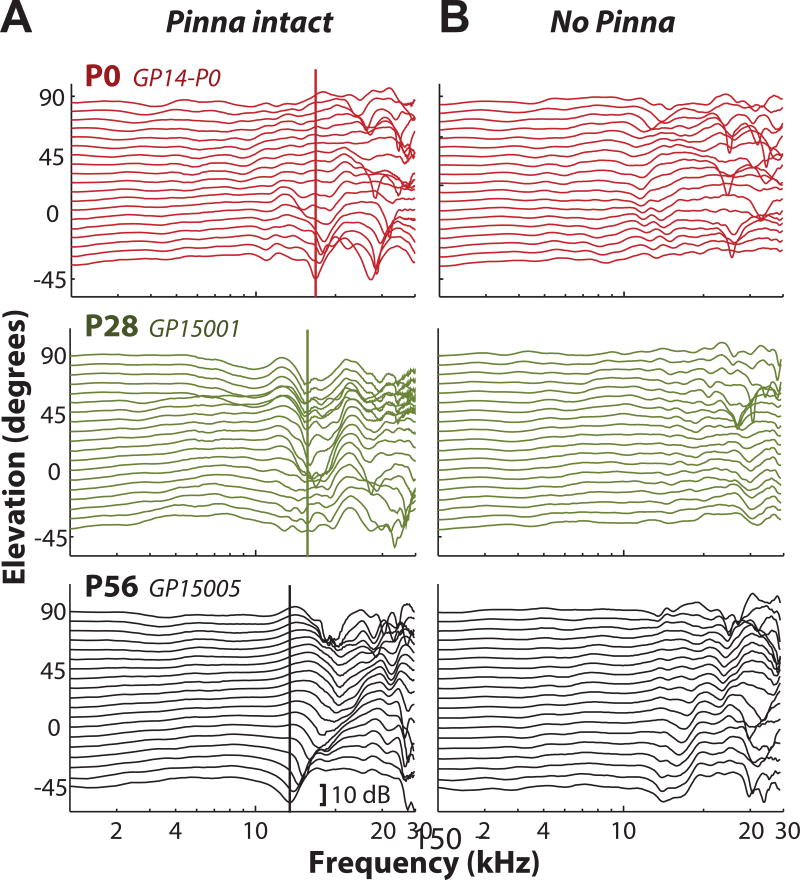
The center frequency of the lowest-frequency spectral notch (the first notch frequency, FNF) in the monaural DTF typically shifts with changes in sound source elevation (Rice et al., 1992). Figure 4A shows DTFs for the left ear of three animals at different ages (P0, P28, P56) for elevations ranging from −45° to +90° in 7.5° steps for 0° azimuth. The FNF (indicated by the vertical line) decreased from higher frequencies (~17 kHz) in animals aged P0 to lower frequencies (~12 kHz) in adult animals. The prominent spectral notches present in Figure 3A were largely eliminated following pinna removal for all animals (see Figure 4B). While some notch-like features were still present following pinna removal, the prominent and orderly nature of the notches was no longer present. This supports the hypothesis that the broadband spectral notches are largely generated by the pinna.

Figure 4.

Monaural broadband spectral notches shift systematically with age and are largely produced by the pinna. A: DTF gain as a function of frequency for locations varying in elevation ranging from −45° to +90° in 7.5° increments (at 0° azimuth) for animals aged P0 (red, top panel), P28 (green, middle panel), and P56 (adult; black, bottom panel). Vertical lines indicate the frequency of the first spectral notch (first notch frequency, FNF). B: The prominent spectral notches present in (A) are largely eliminated following pinna removal.

While there were some similarities in the general features of the DTFs from different guinea pigs, we observed variability in the monaural DTFs both within animals (e.g., differences in left/right DTFs) and across animals. We speculate that this may be due to the large variability in the morphology of the pinna, which we discuss further in the Discussion (Section 4.2.2).

3.3 Development of the interaural level difference (ILD) cues

3.3.1 Spatial distribution of ILDs

The spatial dependence of ILD cues (shown relative to the left ear; see Methods for details of calculation) for seven different frequencies are shown in Figure 5 for three representative animals aged P0 (left column), P28 (middle column), and P56 (right column). The maximum ILD for each animal at each frequency is also listed in the upper-right quadrant above each spatial plot. Similar to DTF gain (Figure 2), the ILD cue varied with frequency and source location. At all ages, ILDs in the frontal hemifield were small (<6 dB) and generally symmetric for frequencies below ~8 kHz. At higher frequencies, the ILDs were much larger (>20 dB for frequencies >8 kHz) and their frequency and spatial dependence more complex (e.g. at 20 kHz, bottom panels of Figure 5). In fact, the complex ILDs reflected the high frequency spectral notches present in monaural DTFs which depended on the pinna (see Figure 4). In general, the magnitude of the maximum ILD increased over development from ~15 dB at P0 to ~30 dB in adults (at frequencies >8 kHz).

Figure 5.

Frequency- and spatial-dependence of ILD at different ages. Spatial distributions of ILD are shown for seven frequencies in animals aged P0, P28, and P56 (adult). Each column shows data from a representative animal at each age, and each row shows data from a different frequency (2, 4, 8, 12, 14, 16, and 20 kHz). The maximum ILD for each frequency shown is depicted on the upper right side of each panel (italicized grey text). The color bar indicates the ILD magnitude in decibels (dB), with positive ILD (warmer colors) indicating higher sound level (dB) at the left ear vs. the right ear.

3.3.2 Spatial and frequency dependence of ILD along the horizontal plane

Figure 6A plots ILD as a joint function of frequency and location for sources along the frontal horizontal plane (+90°, left ear to −90°, right ear in 7.5° increments) for the same animals shown in Figure 5, aged P0 (left panel), P28 (middle panel), and P56/adult (right panel). ILDs were generally largest for lateral azimuths and at high (≥5 kHz) frequencies. We also observed a systematic shift of the ILD spectra at lateral locations (greater than 40° from midline) with increasing age. Figure 6B shows ILD spectra for one azimuth (75°) for animals of different ages (P0 through P100). This azimuth was selected as it produced, on average, the largest ILD magnitude for all animals. The vertical lines indicate the lowest-frequency peak in ILD and illustrate the systematic decrease in frequency from ~16 kHz at P0, ~8.7 kHz at P14, ~6.3 kHz at P28, to ~5–6 kHz at ages >P42. Figure 6C shows the peak ILD for 75° azimuth as a function of age across all animals tested. Peak ILD increased with age from 14–22 dB for ages P0-P28 to 20–35 dB for ages >P56.

Figure 6.

Development of ILD along the horizontal plane. A: ILD as function of azimuth and frequency (kHz) for animals aged P0 (left panel), P28 (middle panel), and P56/adult (right panel). Measurements are shown for 25 locations in azimuth (+90° to −90°) in 7.5° increments at 0° elevation. The color bar indicates the ILD magnitude in decibels (dB), with positive ILD (warmer colors) indicating higher sound level (dB) at the left ear vs. the right ear. B: ILD (dB) at 75° azimuth as a function of frequency for animals at all ages tested. Vertical lines indicate the peak in ILD spectra. Ages with the corresponding color remain consistent throughout the figure. C: Peak ILD at 75° azimuth as a function of age. >P70 data from Greene et al., 2014. D, E: ILD at 75° azimuth for the P0 and P28 animal shown in (A) with pinna intact (solid line) and following pinna removal (dotted line). Dotted grey line: predicted ILD using the spherical head model (Duda and Martens, 1998). F: Peak ILD with pinna intact and following pinna removal. G: Sum of differences comparison of the spherical head model to the empirically-measured ILDs (normalized to “pinna intact” condition).

3.3.3 Growth of the pinna contributes to ILD magnitude

Over the course of development, the sizes of the head and pinna were rapidly increasing (see Figure 1) and were contributing to the changing features of the ILD spectrum. It was not clear, however, which anatomical structure (head or pinna) was more important in generating the ILD cues for the developing guinea pig. To address this question, we first calculated ILDs for a rigid spherical model of the head (Duda and Martens, 1998) as a function of head size across postnatal age. This acoustic model predicts an increased attenuation for the sound reaching the ear contralateral to the source (i.e., an increased head shadow effect) as the size of the head increases. ILDs predicted by the spherical head model for head sizes at P0 (22.5 mm) and P28 (33.1 mm) are plotted in Figures 6D and 6E (dotted grey lines), respectively, along with empirical data for two representative animals at those time points. While the spherical prediction roughly captured the increase in maximal ILDs across frequency with increasing head size, particularly at mid-to-high frequencies, the spherical model systematically underestimated the empirical ILDs (compare dotted grey lines and solid red and blue lines). This result indicated that head size alone was not sufficient to account for the magnitude of measured ILDs. Although it should also be mentioned that while the spherical model closely predicted the ILD below ~5 kHz, it did not approximate ILD very well at higher frequencies. Next, we explored the possibility that the pinna also accounted for the discrepancy between the empirically measured and predicted ILDs.

To determine the contribution of the pinna to ILD, we repeated the DTF measurements following pinna removal in a subset of our animals (n=6). Dotted red and blue lines in Figures 6D and 6E show the ILD spectra after pinna removal for the two example P0 and P28 animals, respectively. The ILD magnitude was generally reduced after pinna removal, particularly at higher frequencies and at the “peak” ILD. For example, the peak ILD in the P0 animal was 21 dB at 16 kHz in the “pinna intact” condition. In the “no pinna” condition, the ILD at 16 kHz was reduced to 4.5 dB, and the overall peak was 10 dB at ~10 kHz. This reduction in ILD peak magnitude following pinna removal was observed in all animals tested (Figure 6F), and occurred mainly at higher frequencies (>5 kHz). On average, ILD magnitude (for 75° azimuth) was significantly reduced (by 52%) following pinna removal (paired-student’s t test: p=0.001). In all animals tested, ILDs shifted closer to the spherical head model predictions following pinna removal. To quantify the disparity between the model and empirical measurements with and without pinna, we summed the differences in ILD across frequency (e.g., the ILD spectrum) with pinna intact or removed (Figure 6G). The head size for each animal tested was used as the input to the Duda and Martens (1998) head model. The empirical data were then normalized to the “pinna intact” condition to observe the change in differences with the “no pinna” condition. The sum of across-frequency ILD differences in the “no pinna” condition was smaller in all cases (paired-student’s t test: p=0.01), indicating that the ILD spectra following pinna removal were indeed closer to the spherical predictions. Although the spherical head model does not fully account for measured ILDs with the pinna removed, the dramatic difference between the pinna intact and removed conditions suggested that the pinna were a major contributing feature to the magnitude of the acoustic ILDs, particularly for high frequencies.

3.4 Development of the interaural time difference (ITD) cues

3.4.1 ITD magnitude increases with age

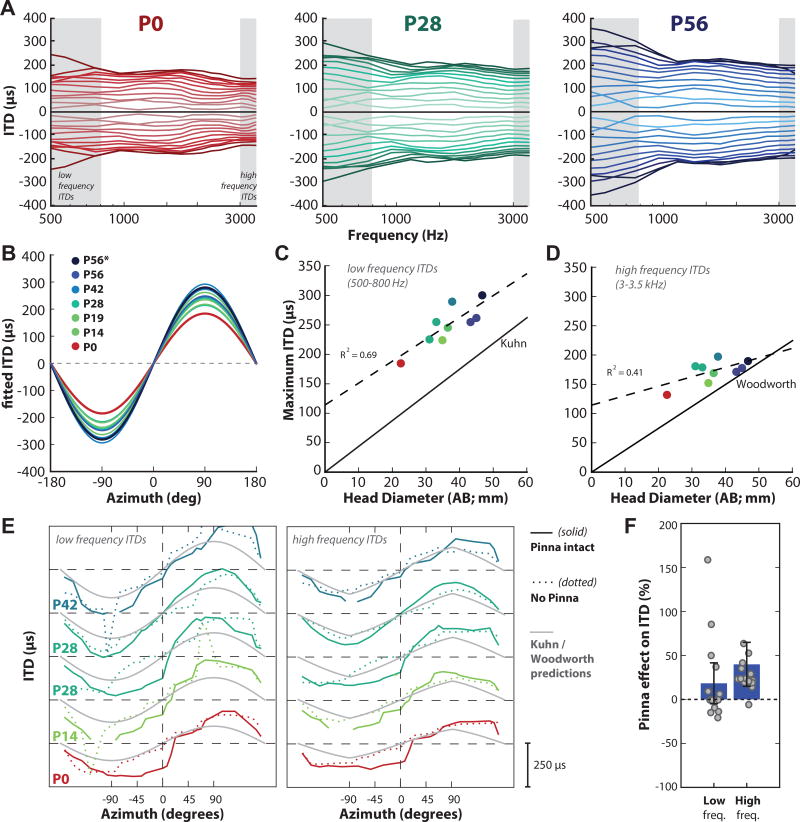
The frequency and spatial dependence of ITDs at different ages are shown in Figure 7. Figure 7A displays ITD as a function of frequency along the frontal horizontal plane for the same animals aged P0 (left panel), P28 (middle panel), and P56 (adult; right panel). Lines correspond to measurements taken from each of the 25 locations in azimuth relative to the left ear. Positive ITDs are the difference in arrival time for leftward speakers relative to rightward; ITDs are generally symmetric, thus ITDs for negative azimuthal locations were generated as the inverse of the positive azimuthal locations. Across all ages, the ITDs were largest at low frequencies (particularly below 1 kHz). Figure 7B plots the fitted ITD as a function of source azimuth along the horizontal plane (0° elevation) for animals of varying ages, from P0 through adulthood (colors in this and subsequent Fig. 7 panels match those in Fig. 7A). The fits were generated from the average ITD across the low frequency range (500–800 Hz; corresponds to shaded area in Figure 7A) at each azimuthal source location. The maximum ITDs for low frequencies increased with age, from ~185 µs at P0 to ~300 µs at P56.

Figure 7.

Frequency- and spatial-dependence of ITD at different ages. A: ITD (µs) vs frequency (Hz) for sound sources in the frontal plane for example animals aged P0 (left panel, red), P28 (middle panel, green) and P56/adult (right panel, blue). Each line corresponds to measurements taken from 25 locations in azimuth (+90° to −90°) in 7.5° increments. Gray bands indicate the low frequency range (500–800 Hz) and high frequency range (3–3.5 kHz) of ITDs used to compute low and high frequency ITDs, respectively. B: Fitted ITD as a function of source azimuth along the horizontal plane (0° elevation) for animals of varying ages, from P0 through adulthood (see legend). The asterisk (*) indicates the P56 animal shown in A (right panel). C, D: Maximum ITD as a function of age (n=11); colors correspond to the legend in (B). The dotted line indicates the linear regression of maximum ITD on head diameter for low frequency ITDs (C) and high frequency ITDs (D). The solid black line in (C) indicates the ITD prediction from the spherical head model of low frequency ITDs proposed by Kuhn (1977). The solid black line in (D) indicates the ITD prediction from the spherical head model of high frequency ITDs proposed by Woodworth (1938). E: Low frequency ITD (left panel) and high frequency ITD (right panel) as a function of azimuth for five animals. Solid lines indicate “pinna intact” condition, dotted lines indicate “no pinna” condition, and grey lines indicate the Kuhn (left panel) or Woodworth (right panel) ITD predictions. F: Pinna effect on the magnitude of low and high frequency ITDs. The effect is expressed in terms of percentage ([ITD_pinna/ITD_nopinna − 1]*100) averaged over all subjects from (E). Each grey data point is a different azimuthal position from 30° to 150° on either side (the small ITDs between ±29° were excluded). Error bars indicate standard deviation.

3.4.2 Increasing head diameter contributes to the developmental increase in ITD magnitude

The systematic increase in low frequency ITD magnitude with increasing animal age has previously been shown to result from the increase in the head diameter over development (cat: Tollin and Koka, 2009; chinchilla: Jones et al., 2011). Consistent with those observations, our data in the guinea pig also suggested that head size contributes to ITD magnitude for low frequencies. Figure 7C plots the maximum low frequency ITD as a function of head diameter. The head diameter increased from 22.5 mm from the P0 animal to 45 mm in the adults (averaged across the three P56-aged animals). Both maximum ITDs and head diameter systematically increased over development by a factor of ~1.5× and 2×, respectively. A linear regression of maximum ITD for low frequencies on head diameter was significant (dotted black line; R² = 0.69; p= 0.0016; y= 114 +3.7x; n=11). Figure 7C also represents the predicted maximum ITD based on the empirically measured head diameter and Kuhn’s spherical head model (1977) for low frequency ongoing ITDs (solid black line). Importantly, our empirically measured ITDs were much larger than Kuhn’s prediction (~36% larger), based on the empirical measurement of the head diameter.

We also computed the maximum high frequency ITD (µs; 3–3.5 kHz) as a function of head diameter (Figure 7D). The maximum ITDs for high frequencies were smaller than the ITDs computed for low frequencies, reflective of the frequency dependence of ITD for a given azimuth (Roth et al., 1980; Benichoux et al., 2016; Kuhn, 1977). A similar increase in ITDs with age was observed: the high frequency maximum ITDs increased with age from ~132 µs at P0 to ~181 µs at P56. A linear regression of maximum ITD for high frequencies on head diameter was not as strong as the low frequency ITDs, but was still significant (Figure 7D, dotted black line; R² = 0.41; p= 0.033; y= 114.4 +1.6x; n=11). Figure 7D includes the ITD prediction from the spherical head model of high frequency ITDs (solid black line) proposed by Woodworth (1938). The Woodworth model is valid for high frequencies as the wavelength of sound is small compared to the head radius; thus, the ITD is computed as the difference between the shortest path length to the two ears divided by the speed of sound (Benichoux et al., 2016). Similar to the discrepancy observed with low frequency ITDs, we also observed much larger empirically measured high frequency ITDs than expected per the animal’s head diameter (on average ~22% larger). However, this discrepancy decreased with head diameter: for larger head diameters, the Woodworth high frequency prediction was much closer to the empirical data (the slope of the fits converges at ~50mm). This was different from the low frequency ITDs, where the model underestimated the ITDs across all head sizes (the slope of the fits never converges).

3.4.3 The pinnae contribute to high frequency ITDs

Similar to previous reports in the cat (Tollin and Koka, 2009a; Benichoux et al., 2016), rat (Benichoux et al., 2016; Koka et al., 2008), chinchilla (Benichoux et al., 2016; Jones et al., 2011), monkey (Benichoux et al., 2016; Slee and Young, 2010) and adult guinea pig (Benichoux et al., 2016; Greene et al., 2014; Sterbing et al., 2003), our data showed that models of ITD based on head diameter generally underestimated the ITD at both low and high frequencies in small mammals. This discrepancy between model predictions and empirically measured ITDs suggests that other morphological features (besides head size) can affect temporal aspects of sound transmission into the guinea pig ear. One possibility is that the pinna increases ITD magnitudes in guinea pigs as in other species (Tollin and Koka, 2009a; Koka et al., 2008; Jones et al., 2011). This is notable as the pinna of the guinea pig is anatomically different from other species with upright, conical pinna. Given the pinna differences, it should not be assumed that they would contribute to, or augment, the ITDs in the same way as the pinna of other species like the chinchilla or the cat.

Other studies have looked at pinna contribution to ITDs for low frequencies (<2 kHz), and have consistently reported a reduction in ITD magnitude in the rat (~36%, Koka et al., 2008), chinchilla (~25%, Jones et al., 2011), and adult guinea pig (~23%, Greene et al., 2014). It has been suggested that these deviations of ITD from the spherical head model prediction is due to the presence of the pinna (e.g. Benichoux et al., 2016). Indeed, the pinna which generally extend away from the lateral aspect of the head, may contribute ITDs by increasing the effective acoustic diameter of the head. To test this hypothesis, we computed ITDs using the subject’s morphological head size (AB in Fig 1) and the Kuhn and Woodworth models (in low and high frequencies respectively, Fig 7E). When we compared the agreement of those spherical head model predictions and the measured ITDs before and after pinna removal, we observed that in low frequencies the Kuhn model did not fit either condition very well. This indicates that the discrepancy between the Kuhn prediction and the empirical ITDs may not be attributable to the pinna. With high frequencies on the other hand, the Woodworth model was a much better fit of the ITDs after pinna removal (Fig 7G), suggesting that much of the discrepancy between the Woodworth prediction and the measured ITDs is in fact attributable to the pinna. To test this observation further, we computed the change in ITD magnitude (in terms of percentage: [ITD_pinna/ITD_nopinna − 1]*100) averaged over all subjects from Fig 7E for low and high frequencies (Fig 7F). We excluded very small ITDs from the computation by limiting the range of azimuthal positions: each grey data point is a different position within 60° of ±90°; that is, positions from 30° to 150° on both sides. We found that the high frequency ITDs were significantly different between the pinna-intact and no-pinna conditions (Wilcoxon rank sum, Z = −1.0, p = 0.0008), while the low frequency ITDs were not (Wilcoxon rank sum, Z = 55, p = 0.78).

Taken together, our results suggest that the pinnae do not significantly contribute to low frequency ITDs, while they do seem to contribute to high frequency ITDs. This is consistent with the idea that the pinnae, because of their small size, only have an impact on the propagation of high frequency sound waves. The low frequency ITD inflation may be due to larger morphological factors, such as the body of the animal.

4. DISCUSSION

4.1 Head, pinna, and ear canal growth

4.1.1 Development of the head and pinna morphology

We studied the morphological development of the head and pinna in 63 guinea pigs (Cavia porcellus) from birth to adulthood. The head and the pinna increased in size substantially during the first ~8 weeks of life: the head diameter at the widest part of the skull (between the zygomatic arches; AB in Figure 1) increased by a factor of 2.4, and the interaural distance (distance between the opening of the two ear canals) increased by a factor of 1.4. The effective pinna diameter, which takes into account both the width and the height of the pinna, increased by a factor of 1.56. Aside from the interaural distance measurements reported in Withington-Wray et. al. (1990) this is to our knowledge the first joint assessment of head and pinna growth in the developing guinea pig.

4.1.2 Development ear canal and concha resonance and gain

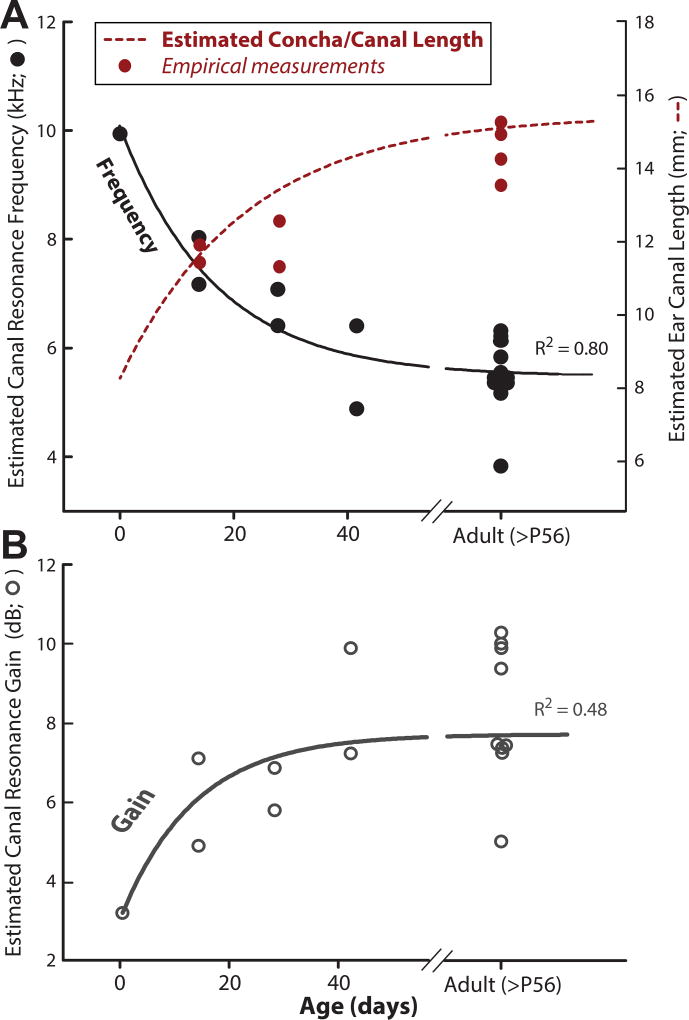
In addition to tracking anatomical development, we measured directional transfer functions (DTFs) in a subset of animals. By construction, DTF measurements do not include non-directional acoustic gains, such as that resulting from the resonance of the ear canal and concha (Rosowski et al., 1988; Tollin et al., 2009). By looking specifically at the non-directional components of the HRTF, we could estimate the resonance properties of the ear canal/concha in our subjects. It has been shown in humans (Keefe et al., 1993), cats (Olmstead and Villablanca, 1980; Tollin et al., 2009), and mice (Mikaelian and Ruben, 1965) that the length of the ear canal and concha increases over development, by e.g. lowering the frequency of the ear canal resonance (in the cat: Tollin et al., 2009)). To see if this is also the case for the guinea pig, we estimated the resonance frequency (Figure 8A) and resonance gain (Figure 8B) for all animals tested. As predicted, the canal resonance frequency decreased as a function of age, from ~10 kHz at P0 to ~5kHz at P56. An exponential decay function was fit to the data to quantify the developmental decrease (y=4.1+5.7e^−0.03x; R²=0.85; solid black line), which showed an increase in canal resonance gain with age from ~3 dB at P0 to ~8 dB at P56 (Figure 8B). An exponential rise-to-max function was fit to the data to quantify the developmental increase in resonance gain (y=3.1+4.5(1-e^−0.7x); R²=0.48). Altogether, this data suggests that the ear canal of the guinea pig is acoustically adult-like by ~P42.

Figure 8.

Estimated development of the resonance frequency, concha/ear canal length (A), and acoustic gain (B). The gain and resonance frequency were estimated from the nondirectional common components of the DTFs in 20 animals. A: Black solid line indicates the three-parameter exponential decay function relating the concha/canal resonance frequency to age (days). Red dotted line indicates the concha/canal length (in millimeters) estimated from the fitted resonance frequency function and assuming that the canal/concha can be modeled as a simple cylinder (see text). Red circles: empirical measurements of concha/canal length in 4 animals (2 canals per animal). B: The gray solid line indicates the three-parameter rise-to-max exponential function relating concha/canal resonance gain to age.

We can further estimate the length of the canal from the acoustical resonance by modeling it as a cylinder closed at one end by the tympanic membrane (Rosowski et al., 1988; Shaw, 1974; Tollin and Koka, 2009). In this model, the resonant wavelength is equal to 4x the length of the canal, or equivalently the ear canal length is equal to ¼ of the resonant wavelength. Using this equation, we estimated that the length of the ear canal and concha increased from ~6.5 mm at P0 and asymptotes to ~15 mm in adults (Figure 8A, red dotted line). Two physical measurements of canal length were taken to compare against the model: the distance between 1) the tympanic membrane (TM) to the tragus and 2) the TM to the lateral aspect of the concha. This was accomplished by placing a thin metal rod onto the umbo of the TM under microscopic examination, marking the two locations on the rod, and measuring the distance using a digital caliper. We found that the measurements of the canal including the concha were well described by the cylindrical model (see red circles on Fig. 8A). Deviations from the model may be accounted for by the slight horn-shape of the concha, similar to the tube and horn model described in Rosowski et al. (1988). In the guinea pig, the concave shape of the concha may act as a resonator, providing amplification between 4 and 10 kHz depending on the age of the animal. This is consistent with other measurements of ear canal and concha resonance in the adult guinea pig (Sinyor, 1973).

4.2 Monaural cues

4.2.1 Development of acoustic gain, the acoustic axis, and broadband spectral notches

We measured DTFs in animals at different ages and estimated the monaural acoustic features (e.g. DTF acoustic gain, acoustic axis, broadband spectral notches). The maximum monaural acoustic gain produced by the head and pinna increased with frequency and age. Across all ages, a gain of ~7–14 dB was observed at lower frequencies (2–4 kHz), while at higher frequencies (>8 kHz), the maximum gains reached values of 10–21 dB for both younger and adult animals (Figure 2A). The adult data agree with previous reports for the guinea pig (Carlile and Pettigrew, 1987; Greene et al., 2014).

There is a complex relationship between frequency and the elevation of maximal monaural gain, i.e., the acoustic axis (see Results section 3.2.2). The most notable feature of the frequency-elevation function was an abrupt transition to higher elevations at a particular frequency that systematically decreased with age (e.g., ~22 kHz at P0 to ~14 kHz at P56). This trend has also been reported in other species (cat: Musicant, 1985; wallaby: Coles and Guppy, 1986; ferret: Carlile, 1990; bat: Firzlaff and Schuller, 2003; chinchilla: Jones et al., 2011). Sterbing et al. (2003) reported similar frequency-dependent shifts in the acoustic axis in adult guinea pigs, similar to the ranges observed in our adult animals. Both our results and Sterbing et al. (2003) show that the acoustic axis is located at ~70–90° azimuth and 20–40° elevation for frequencies between 1–2 kHz, and high in the front (70–90° elevation) for frequencies ~13–15 kHz.

The center frequency of the lowest-frequency spectral notch decreased with age, from ~17 kHz at P0 to ~12 kHz in adults. This decrease in FNFs with age was likely due to the increase in the size of the pinna (Figure 1B), consistent with the hypothesis that a larger pinna interacts with sounds of longer wavelengths (lower frequencies, see Tollin and Koka, 2009a). In order to test this hypothesis empirically, pinna-removal surgery was performed and the acoustic measurements were repeated in 6 of the animals at different developmental ages (P0, P14, P28, P42). Consistent with our hypothesis, pinna removal substantially affected the broadband spectral notch feature from the DTFs across all ages (Figure 4B). Such a dependence of spectral notch characteristics on pinna shape has been demonstrated in other species, including the rat (Koka et al., 2008), bat (Wotton, 1995; Aytekin et al., 2004), cat (Musicant, 1985; Tollin and Koka, 2009), chinchilla (Jones et al., 2011), ferret (Parsons et al., 1999), and adult guinea pig (Greene et al., 2014).

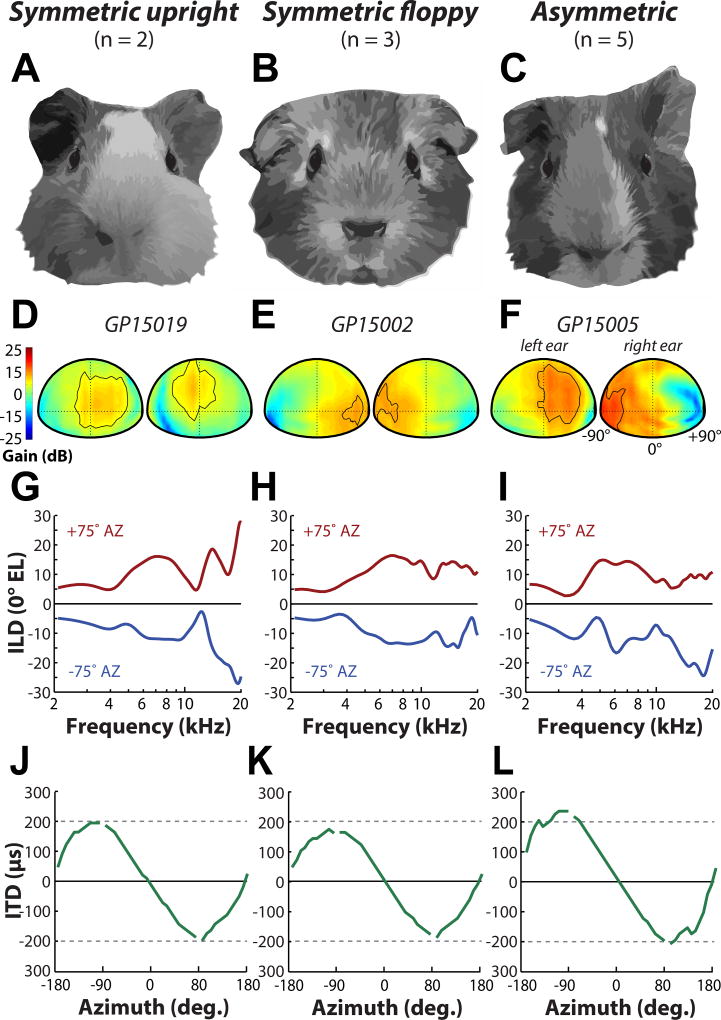
4.2.2 Pinna morphology as an explanation for across animal variability

While there were some similarities in the general features of the DTFs from different guinea pigs, we observed a large intra-individual (i.e., differences in left/right DTFs) and inter individual variability in the DTFs, consistent with previous reports (guinea pig: Carlile and Pettigrew, 1987, cats: Xu and Middlebrooks, 2000, humans: Hofman et al., 1998). We hypothesized that this variability is due to differences in the shape and orientation of the guinea pig external ears. Indeed, unlike humans and many other commonly-used animal models (i.e., cat, rat, chinchilla, bat) with largely homogenous and symmetrical pinna, the guinea pig often display variability in pinna morphology and orientation (e.g., upright vs “floppy”). The differences in pinna geometry between animals have been noted previously (Carlile and Pettigrew, 1987; Sterbing et al., 2003; Rauschecker, 1999). Here, we classified the pinna orientation based on two features: symmetry and “floppiness.” Figure 9 illustrates the three main categories we observed: symmetric upright (A), symmetric floppy (B), and asymmetric (C). Figure 9D–F shows monaural DTF gain plots for the left and right ears of three example animals with symmetric upright (D), symmetric floppy (E), or asymmetric (F) pinna at 12 kHz. Approximately half of our animals were observed to have asymmetric pinnae, and in those subjects the DTF gain for the left and right ears were asymmetric. Figure 9F shows a representative animal that has a floppy left ear and an upright right ear- the location of maximum gain for the left ear was closer to midline while the location of maximum gain for the right ear was much farther lateral. Conversely, DTF gain for the two symmetric pinna conditions (D,E) were nearly identical between the left and right ear DTF gain (see the contour line which contains the -5 dB area from maximum gain). In general, the maximum gain areas for upright pinnae were located ipsilateral to the leading ear near midline, and for floppy pinnae, the maximum gain areas were located at much more lateral locations.

Figure 9.

Variability in pinna orientation. Examples of three different guinea pig pinna morphological features: symmetric upright (A), symmetric floppy (B), and asymmetric (C). D–F: Spatial distribution of left and right ear DTF gains at 12 kHz for example animals with symmetric upright (D), symmetric floppy (E), and asymmetric (F) pinna. Contour line is plotted at -5 dB from the maximum DTF gain. G–I: ILD at +75° (red line) and −75° (blue line) azimuth as a function of frequency (at 0° elevation) for symmetric upright (G), symmetric floppy (H), and asymmetric (I) pinna. Examples shown are the same animals depicted in (D–F). J–L: Broadband ITD (µs) vs azimuth for example animals with symmetric upright (J), symmetric floppy (K), and asymmetric (L) pinna.

The process of domestication is known to introduce distinct changes in morphology, physiology, and behavior (Darwin, 1868; Jensen, 2006), and has been suggested that variability in pinna shape and orientation may reflect domestication. Indeed, the presumed ancestors of the domesticated guinea pig (Cavia porcellus; Rood, 1972), wild cavies (Cavia aperea, Cavia tschudii) have erect, consistently symmetric upright pinnae. The introduction of the wild cavy into artificial environments under human guidance likely shifted evolutionary selective pressures on certain traits. Strikingly, a similar shift from erect to floppy pinna in wild and domesticated counterparts has also been reported in cows, pigs, sheep, dogs, and rabbits (Trut et al., 2009). Charles Darwin even suggested that the “drooping” of the ears is due to the lack of ear muscle use, likely from the animals being “seldom much alarmed” (Darwin, 1859). In the case of the guinea pig, the evolutionary constraint on erect, homogenous orientation of the pinna was not strong, perhaps leading to the floppiness and variability in the present-day domesticated guinea pig.

4.3 Binaural cues

4.3.1 Interaural level differences (ILD)

Consistent with previous reports, measured ILDs were dependent on both frequency and spatial location: ILDs were small (<10dB) for frequencies below 4 kHz, and were much larger (>20dB) for frequencies greater than 8 kHz. Over development, the maximum ILD magnitude (generally occurring around ±75° azimuth at frequencies >8 kHz) increased from ~15 dB at P0 to ~30 dB in adults. We also observed a shift in the peak of the ILD magnitude from high to low frequencies over the course of development, as has been reported in the cat (Moore and Irvine, 1979; Tollin and Koka, 2009) and chinchilla (Jones et al., 2011). When we compared our results with the estimation of ILD using a spherical head model (Duda and Martens, 1998), we found that the model systematically underestimated the empirical ILDs suggesting that a sphere was a poor model for the head of a guinea pig. Similar discrepancies have been reported in the adult guinea pig (Greene et al., 2014) and other species (chinchilla: Koka et al., 2011; cat: Tollin and Koka, 2009a,b; rat: Koka et al., 2008). We suspected that this may be due to the acoustical contribution of the pinna, which is not accounted for by a spherical model. Consistent with this possibility, we found that ILD magnitude was significantly reduced by 52% when the pinna was surgically removed, even in young animals with small pinna dimensions. Other reports in small mammals such as the chinchilla (Jones et al., 2011), cat (Tollin and Koka, 2009), and rat (Koka et al., 2008) also describe the significant contribution of the pinna on high-frequency ILDs.

In many animals, ILDs were asymmetric in the left and right hemifields, which we sought to attribute to the potentially asymmetric orientation of the pinna (as defined above: e.g., one ear floppy and the other upright). To examine this effect in more detail, ILD as a function of frequency is plotted for animals with symmetric upright (Fig. 9G), symmetric floppy (Fig. 9H), and asymmetric (Fig. 9I) pinna orientations for +75° (red line) and −75° (blue line) azimuth. The ILD functions for the two symmetric conditions (Fig. 9G,H) appeared to be largely mirror-image between the two azimuthal locations, whereas the animal with asymmetric pinna displayed distinct differences (Fig. 9I). This supports the idea that the position of the pinna can influence ILDs as it did the monaural DTFs (see above). Changing the orientation of the pinna has been shown to alter ILDs in the rabbit (Kim et al., 2010) and cat (Young et al., 1996), although it should also be noted that these two species, unlike the guinea pig, have mobile pinna that the animal can rapidly orient towards a sound source (Populin and Yin, 1998; Tollin et al., 2010; Tollin et al., 2009).

4.3.2 Interaural time differences (ITD)

In all animals, the ITD cue depends mostly on frequency and sound source azimuth. The maximum ITDs for low frequencies (500–800 Hz) increased by a factor of 1.5, from ~185 µs at P0 to ~300 µs in adults. ITDs at larger frequencies were ~30% smaller, but also increased with age from ~132 µs at P0 to ~181 µs in adults. Our data suggests that head size is correlated with ITD magnitude, particularly for low frequencies. In fact, we report ITDs that are consistently larger than the predictions based on a spherical head model. The observed low frequency ongoing ITDs was~36% larger than the ITDs predicted by Kuhn’s formula for low frequency ITDs (1987), and the maximum ITDs for high frequencies (3–3.5 kHz) were larger than expected given the animal’s head diameter (~22% larger using the Woodworth prediction). Similar differences between predicted ongoing ITDs from spherical head models and empirical ITDs have been previously reported (cat, Roth et al. 1980; Tollin and Koka 2009a; monkey, Spezio et al. 2000; Slee and Young 2010; gerbil, Maki and Furukawa 2005; rat, Koka et al. 2008; rabbit, Kim et al. 2010; chinchilla, Jones et al., 2011; and adult guinea pig, Greene et al., 2014; Sterbing, 2003; also Benichoux et al., 2016).

This discrepancy between model predictions and empirically-measured ITDs suggests that other morphological features besides head size can affect the timing of sound transmission into the guinea pig ear. It has been previously shown in the cat (Tollin and Koka, 2009a), rat (Koka et al., 2008), and chinchilla (Jones et al., 2011), that the pinna can increase the magnitudes of ITDs. By repeating acoustic measurements following pinna removal, we also found that the pinna contributes to the inflation of ITDs with respect to the spherical head model predictions only for high frequency ITDs, consistent with the idea that the pinna only affects the acoustics of the head at high frequencies (due to its small size). The presence of the pinna does not account for the inflation of low frequency ITDs with respect to spherical head model predictions, indicating that other morphological features are at play, particularly since the sphere is not a good approximation of the guinea pig shape. Kim et al., (2010) found that shifting the position of the pinna in the rabbit can distinctly alter low frequency ITDs, suggesting that our subjects’ asymmetric pinna positions could also lead to ITD asymmetries. Indeed, when broadband ITDs are plotted as a function of azimuth for animals with symmetric upright (Fig. 9J), symmetric floppy (Fig. 9K), and asymmetric (Fig. 9L) pinna orientations, we observe a shift in the ITD magnitude for the asymmetric condition, but not for the two symmetric pinnae conditions. In summary, as with ILDs, we find that the position of the pinnae can also influence ITDs.

4.4 Implications for physiological and behavioral development

Guinea pigs are widely used as a model for the study of the auditory system. The acoustic results presented here are relevant to these studies as we provide a detailed analysis of the cues to sound location that would be expected in the developing guinea pig. Since the maturation of the auditory system is largely influenced by the development of the acoustic properties of the head and pinna, understanding how these cues change with age is essential when considering how the neural encoding of these cues, and ultimately the perception of these cues, are shaped over time.

Paper Highlights.

• Here, we measured the dimensions of the head, pinna, and cues to sound location in the developing guinea pig

• Head and pinna dimensions increased by 87% and 48%, respectively, reaching adult values by ~8 weeks (P56)

• The monaural acoustic gain produced by the head and pinna increased with frequency and age, with maximum gains at higher frequencies (>8 kHz) reaching values of 10–21 dB for all ages

• Over development, the maximum ILD magnitude increased from ~15 dB at P0 to ~30 dB in adults (at frequencies >8 kHz)

• The maximum low frequency ITDs increased from ~185 µs at P0 to ~300 µs in adults