Defining the factors that affect solute permeation of gap junction channels

Abstract

This review focuses on the biophysical properties and structure of the pore and vestibule of homotypic gap junction channels as they relate to channel permeability and selectivity. Gap junction channels are unique in their sole role to connect the cytoplasm of two adjacent cells. In general, these channels are considered to be poorly selective, possess open probabilities approximating unity, and exhibit mean open times ranging from milliseconds to seconds. These properties suggest that such channels can function as delivery pathways from cell to cell for solutes that are significantly larger than monovalent ions. We have taken quantitative data from published works concerning unitary conductance, ion flux, and permeability for homotypic connexin 43 (Cx43), Cx40, Cx26, Cx50, and Cx37, and performed a comparative analysis of conductance and/or ion/solute flux versus diffusion coefficient. The analysis of monovalent cation flux portrays the pore as equivalent to an aqueous space where hydrogen bonding and weak interactions with binding sites dominate. For larger solutes, size, shape and charge are also significant components in determining the permeation rate. This article is part of a Special Issue entitled: Gap Junction Proteins edited by Jean Claude Herve.

1. Introduction

Presently, there are at least 21 known human connexin genes [1]. For each connexin protein there is a documented homotypic gap junction channel form composed of 12 identical connexins where 6 identical connexins form a hemichannel in each cell of a cell pair. Heterotypic gap junction channels are formed by two non-identical hemichannels. Heteromeric channels are formed by hemichannels that are composed of more than one connexin type. For any two mutually compatible connexins there are, in theory, 196 gap junction channel types possible [2], either as a heteromeric or heterotypic form. In principle, it is therefore possible to have hundreds if not thousands of different channel types. The in vivo state of affairs for connexin expression and thus functionality is clearly complicated by the potential for multiple connexin expression [1,3,4], which is hampered by yet another factor, the rapid turnover rates of the connexin protein subunits [5].

To understand the biophysical properties of gap junction channels composed of connexins, researchers have used connexin deficient cell types transfected with DNA for a single connexin. This allows analysis of the physical properties that govern homotypic gap junction channel function. A number of groups have studied properties such as fluorescent probe and second messenger permeability as well as unitary conductance to better understand the molecular nature of gap junction permeability and selectivity [6,7]. In this review we will use data from a number of published works to elucidate some of the experimentally deduced properties of gap junction pore selectivity/permeability and discuss the possible underlying molecular mechanisms.

1.1. The anatomy of the pore

Each connexin is composed of 4 alpha-helices which are membrane spanning domains, 2 extracellular loops, one cytoplasmic loop, an N-terminus and a C-terminus [6,8–10]. Crystal structures of two homotypic gap junction channels composed of Cx26 or Cx43 have been determined to a resolution of 0.3–0.4 nm for Cx26 and 0.75 nm in the membrane plane and 2.1 nm in the vertical plane for Cx43. Both structures reveal a pore with a minimum of approximately 1.4 nm [11,12], a width bigger than the hydrated diameter of most permeant ions. To help define which domains of a connexin contribute to the lining of the pore, the substitution cysteine accessibility method (SCAM) has been employed extensively with Cx46 and to a lesser degree on Cx32 and Cx26 [13]. The combined studies strongly suggest that part of the N-terminus, the first transmembrane domain (TM1), and portions of the extracellular loops are significant contributors to the lining of the pore [8].

1.2. Channel properties apart from the pore itself that influence permeability

Two important measurements of all channels are their mean open and closed times. Mean open time (along with single channel conductance) determines the number of ions that will transit a channel from one compartment to another within a cell, from intracellular to extracellular space, or in the case of gap junction channels intercellularly. The mean open time of many channels is strongly influenced by voltage. Gap junction channels, also display voltage dependent behavior but atypically spend most of their time in the open state. For homotypic channels, voltage dependence is symmetrical such that when transjunctional voltage is 0 the channel remains open more often than closed. A number of studies have demonstrated voltage dependence and determined that mean open time declines with increased transjunctional voltage [14–17]. Since at 0 transjunctional voltage gap junctions are open more than 50% of the time, it is not surprising that Cx43 homotypic channels have a mean open time that exceeds their mean closed time, averaging 2.5 s in the open state versus 0.7 s in the closed state [18]. These values are 2–3 orders of magnitude longer in duration than K⁺, Na⁺, and Ca²⁺ channels. Such long open times of Cx43 might permit solutes of greater mass as large as 4–5 kD to traverse this gap junction channel, particularly, if they are long with a narrow radius implying a large aspect ratio [19].

Another potentially significant factor regarding permeability and selectivity is access to the pore. Depending on the sign of net fixed charge near the pore orifice, it can effectively repel or attract charged solutes creating the basis for charge selectivity [20].

2. A broad spectrum of permeant ions and solutes

Initial observations of single gap junction channels revealed unitary conductances of over one hundred picosiemens [21,22]. Subsequent identification of the connexin family [23] resulted in numerous studies where measurements of homotypic channels revealed that connexins were permeable to more than one monovalent ion and also allowed the transit of fluorescent probes [6,14,24–26], polypeptides [27], and oligonucleotides [19].

Initially, the observation that varied ions and solutes are able to transit from one cell to another via gap junctions resulted in the belief that the channels were non-selective, with the solute size and charge as the only rate limiting steps [6]. However, a number of studies, including that of Elfgang et al. [28], showed that specific homotypic and heterotypic gap junction channels displayed different apparent permeabilities to a number of fluorescent probes, leading to the suggestion that not all connexins function the same, especially for solutes in the size range of second messengers [26]. Data like that shown by Elfgang et al. and others [26,29,30] have led many to speculate: is there any evidence for cation or anion selectivity in gap junction channels?

2.1. Monovalent ions: are gap junction channels selective or simply non-discriminant conduits?

In the early 1960s when the search for ion selective microelectrodes began Eisenman predicted selectivity sequences based on binding to ion-selective glasses of different compositions [31]. He concluded that for the 5 alkali metal cations only 11 out of a possible 120 sequences are relevant to chemistry and biology [31]. Gap junction channels appear to possess conductive properties for monovalent cations most like Eisenman sequences I (Cs > Rb > K > Na > Li) or II (Rb > Cs > K > Na > Li) [31]. Table 1 gives the sequences for a number of connexins for which there is sufficient data on unitary conductances and where Cx43 and Cx40 are consistent with Eisenman sequences I and II. Both sequences represent a circumstance where solute binding to a site is weak based on electrostatic attraction and energy of hydration [32]. Cx37 and Cx50 are two examples that do not quite fit the simple conduit model for gap junction pores. Cx50 is an Eisenman I sequence but the slope of the regression coefficient is nearly twice that of Cx43 and Cx40, indicating that some additional solute-solvent or solute pore interactions might be occurring. Cx26 is consistent with an Eisenman I or II sequence but with only two data points it is not possible to assign a precise sequence. In the case of Cx37, the slope of the regression coefficient is intermediate to Cx50 and the others. Further, the best or closest Eisenman sequence for Cx37 is a series IV sequence yet another indicator that solutes are interacting with the pore walls and/or solvents to a greater extent than, for example, in Cx43.

Table 1.

Connexin permselectivity sequences for monovalent cations.

Cx43 Rb+ ≥ Cs+ > K+ > Na+ > TMA+ > Li+ > TEA+	[24]
Cx40 Cs+ > Rb+ > K+ > Na+ > Li+ > TMA+ > TEA+	[25]
Cx26 K+ > Na+	[33]
Cx37 K+ > Cs+ > Rb+ > Na+ > Li+ > TMA+	[34]
Cx50 Cs+ > K+ > Na+	[35,36]

Another way to view the single channel conductance data is to compare the unitary conductance for each homotypic channel to a measure of the same ion’s mobility in free solution. Fig. 1A is a plot of unitary conductances (normalized to Cs⁺) for Cx43, Cx40, Cx50, Cx37, and Cx26 homotypic channels on the ordinate versus their respective diffusion coefficients on the abscissa. If free diffusion was occurring with no selectivity, the fractional change in diffusion coefficient should match the decline in single channel conductance with change in permeant ion. This is true except Cx50. Fits of the data in Fig. 1A to a linear regression produced the following slopes: 0.5139 ± 0.06552/cm²s⁻¹ × 10⁻⁵ (Cx43), 0.5544 ± 0.02908/cm²s⁻¹ × 10⁻⁵ (Cx40), 0.724 ± 0.1496/cm²s⁻¹ × 10⁻⁵ (Cx37), 1.066 ± 0.2853/cm²s⁻¹ × 10⁻⁵ (Cx50), and 0.3956 ± 0.1019/cm²s⁻¹ × 10⁻⁵ (Cx26). Comparison of the slopes by analysis of covariance (Graph Pad Prism) revealed significant differences between Cx40 and Cx50 slopes (P = 0.0116). The differences between the slopes of other connexins were not significant. In fact for all but Cx50, the diffusion coefficient is decreased by roughly 0.5 and are non-significantly different than 0.5. Cx50 however, decreases twice the expected rate for free diffusion suggesting that there is weak selectivity based on any wall charges and hydrogen bonding which reduce the permeability of larger monovalent cations. The most likely factors that explain the large Cx50 unitary conductance and strong apparent selectivity are a shorter pore with a reduced diameter along the length of the pore and a fixed charge near the orifice of the channel [20].

Fig. 1.

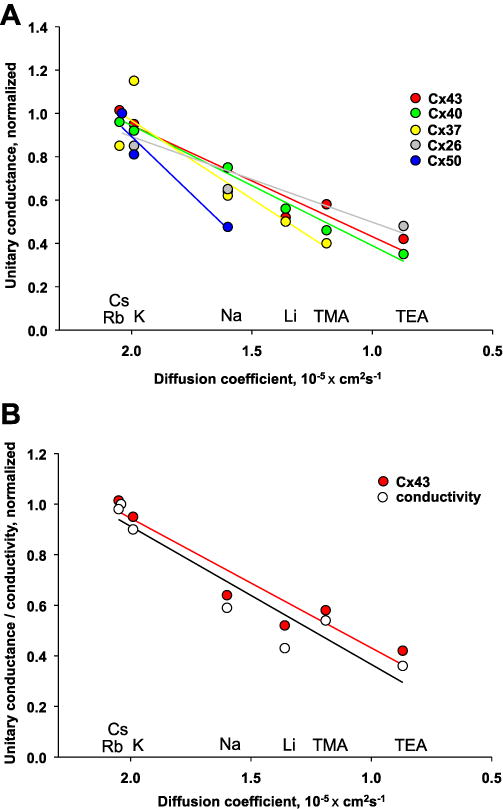
Comparison of connexin permeability to monovalent ions. (A) Plots showing normalized unitary conductances with various monovalent solutes, all relative to Cs, for Cx43 (Cs, Rb, K, Na, LI, TMA, TEA), Cx40 (Cs, Rb, K, Na, Li, TMA, TEA), Cx37 (Cs, Rb, K, Na, Li, TMA, TEA), Cx26 (Cs, K, Na, TEA), and Cx50 (Cs, K, Na) versus the solutes’ respective diffusion coefficients. The solid lines represent the data fit to a linear regression with the following R² values: 0.92 (Cx43), 0.99 (Cx40), 0.85 (Cx37), 0.88 (Cx26), and 0.93 (Cx50). (B) Plots of normalized equivalent solute conductivity (○) versus the respective diffusion coefficient along with normalized Cx43 conductance (●) for Cs, Rb, K, Na, Li, TMA, and TEA, all relative to Cs. See text for references on derivation of data and details.

Fig. 1B is a plot of the normalized equivalent conductivity for the same ions also plotted with the normalized data for Cx43. Analysis of the slopes exhibited a statistically similar relationship (P = 0.7712) for the two data sets: 0.506 ± 0.06732/cm²s⁻¹ × 10⁻⁵ (Cx43) and 0.538 ± 0.08307/cm²s⁻¹ × 10⁻⁵ (conductivity). The data shown in Fig. 1A and B are strong indicators that the pore is, in fact, functioning like an aqueous space for the respective monovalent cations. The only apparent relevant forces seem to be hydrogen bonding and weak electrostatic interactions. Further experimentation using mutant connexins in combination with rigorous quantitative analysis is a clear and necessary step to advancing our understanding of the permeability to monovalent cations.

Monovalent anion permeability has also been assessed for Cx43 and Cx40 [24,25]. Using asymmetric salt solutions to measure reversal potentials as a measure of relative selectivity, Beblo and Veenstra found that organic acids were more permeant than halides for Cx40 while Cx43 permeability to organic anions and halides was inversely proportional to mobility. The rationale put forth to explain why Cx40 appears to be more permeable to larger organic anions than halides was that organic anions tend to transit the channels whilst bound to K⁺ which renders the complex neutral.

Another ion, H⁺, has been shown to transit Cx43 gap junction channels as a complex with a “proton-porter” [37]. The carrier concept for many charged solutes might well be an essential mechanism for inter-cellular transport via gap junctions.

For a majority of the connexins discussed here, weak field strengths and hydrogen bonding of solutes, or complexes to the pore wall or solvents within the pore, are the simplest explanations [24,25,38]. A recent publication by Luo et al. presented a computational study of uncharged solute diffusion through a Cx26 channel structural model [39]. The simulations revealed that solute interactions with water and those moieties that compose the surface of the channels vary over the entire length of the pore and that both hydrogen bonding and K⁺ played essential roles in the permeation process. The conclusions drawn from the simulation are consistent with the experimental results referenced in this text [24,25,39,40] and lend important insights into the nature of gap junction channel permeability and selectivity.

2.2. Permeability to larger solutes: a comparative approach

A number of gap junction types are also permeable to larger, often charged, solutes with minor diameters as large as 1.0–1.1 nm including second messengers and small interfering RNAs [7,19,33,40–42]. Heterotypic and heteromeric channel forms also appear to possess similar permeability characteristics for fluorescent probes like Lucifer Yellow [2,26, 43,44].

Fig. 2 presents flux data for Cx43, Cx40, and Cx26 to specific solutes, including monovalent ions and larger solutes, normalized to K⁺ flux and plotted against the solutes’ respective diffusion coefficients. For the monovalent cations, diffusion coefficients were taken from Hille [38] and for the larger solutes diffusion coefficients were estimated according to the Stokes-Einstein equation. This equation considers spheres and demonstrates that the diffusion coefficient is inversely proportional to the radius [38]. If a particle is of the same density but larger radius, the volume, V is proportional to the cube of the radius, a³ of the sphere. Thus the diffusion equation is inversely proportional to the volume, V³ and thus mass, MW³. For the monovalent ions, unitary conductance was converted to ion flux using the method outlined in Valiunas et al. [26] and Kanaporis et al. [40]. Data for oligonucleotides permeation of Cx43 is derived from Valiunas et al. [19,41]. Linear regression analysis reveals R² values of 0.98 for Cx43 data, 0.99 for Cx40, and 0.98 for Cx26. Fits of the data in Fig. 2 to first order regression using a linear (rather than log₁₀) Y axis scale revealed the following slopes for monovalent ions and cAMP: 0.4733 ± 0.027/cm²s⁻¹ × 10⁻⁵ (Cx43), 0.5805 ± 0.02784/cm²s⁻¹ × 10⁻⁵ (Cx40), and 0.6174 ± 0.06167/cm²s⁻¹ × 10⁻⁵ (Cx26). Slope analysis revealed significant differences between Cx43 and Cx40 (P = 0.0171), as well as the slopes of Cx43 and Cx26 (P = 0.0289). The difference between the slopes of Cx40 and Cx26 were not significant (P = 0.5227). However, fits of the data that included larger solutes produced slightly different slopes (0.5382 ± 0.01876/cm²s⁻¹ × 10⁻⁵ (Cx43); 0.5736 ± 0.02149/cm²s⁻¹ × 10⁻⁵ (Cx40), and 0.6003 ± 0.04086/cm²s⁻¹ × 10⁻⁵ (Cx26)), which were statistically insignificant for all three connexins. The lack of significance with the addition of the estimated permeabilities of the morpholinos/siRNAs is presumed to be a result of some inaccuracy in determining the fluxes of these larger molecules. Analysis of smaller solutes and electrolytes along with the oligonucleotides indicates that the oligonucleotides may permeate the pore in a very different way than the charged solutes, such as cAMP or monovalent ions.

Fig. 2.

Summary of connexin permeability to ions, dyes, metabolites, morpholinos, and siRNA. Flux data of different solutes normalized to K⁺ flux plotted versus their respective diffusion coefficients for Cx43 (Cs, Rb, K, Na, Li, TMA, TEA, cAMP, LY, 12mer, 16mer, 24mer, 21 siRNA), Cx40 (Cs, Rb, K, Na, Li, TMA, TEA, cAMP, LY), and Cx26 (Cs, K, Na, cAMP, LY). The data has been plotted on a log scale to better depict lowered flux for larger solutes like morpholinos and siRNA. See text for references on derivation of data and details.

All three connexins allow the transit of cAMP, with Cx43 being the most permeable and Cx40 the least. Cyclic AMP has a net charge of zero but has hydroxyl groups and a phosphate group that suggests it is weakly negatively charged. The minor diameter of cAMP is 0.52 nm [33] and it is a hydrophilic molecule. Lucifer Yellow, with a minor diameter of 0.99 nm [40], is negatively charged and all three homotypic channels are permeable to it, although the permeability of Cx43 relative to K⁺ is 10 times greater than that of Cx40. With increasing size and/or negative charge, permeability declines for all three connexins. Clearly, size is ultimately a rate-limiting factor, given that if the minor diameter is larger than the pore diameter along any portion of the channel’s length, then that particular solute is rendered impermeant. In principle, a solute with a minor diameter that is smaller than the pore diameter should be permeable, but the charge of said solute can also affect permeation. The most likely area for solute charge to influence the permeability is near the orifice of the pore where access resistance in the form of fixed charges can potentially attract or repel a charged solute [20].

2.3. Permeability to very large rod shaped molecules MicroRNAs, siRNAs, and morpholinos

A number of studies have either directly or indirectly demonstrated the transit of siRNA/miRNAs through Cx43 [19,41,45–48]. To assess permeability fluorescently tagged morpholinos and siRNAs have been used to assess cell to cell transfer, both with and without the blocking of endo/exosomal traffic [19,41]. Data from these two studies is included in Fig. 2. Flux for oligomers (morpholinos) of 12, 16, and 24 base pairs as well as an siRNA of 21 base pairs is illustrated. The major diameters for the single stranded forms of the molecules ranges from ~6.0 to 11.0 nm, but in all cases the minor diameters of single strands are close to or equal to 1.1 nm. It should be noted that Valiunas et al. [19] also tested the permeability of a double stranded fluorescently tagged morpholino. Very little transfer occurred and that which did might have represented the movement of a small number of single stranded forms that had dissociated from their double stranded form. It is clear from Fig. 2 that the permeability of oligonucleotides is very small relative to monovalent ions, approximately 3 orders of magnitude less than for K⁺ ions in the case of Cx43. Fig. 3 examines permeability of Cx43 only. Fig. 3A is a linear plot of data in Fig. 2 for Cx43. It also demonstrates that LY and oligomers fall off expected value, while cAMP is much closer to expectation from the linear plot generated by monovalent data. Fig. 3B plots only the large molecules against the cube root of their molecular weight, $\sqrt[3]{\mathit{MW}}$, which as described above is inversely proportional to the diffusion coefficient based on the Stokes-Einstein relationship. The reasons for the large differences between these three molecules are unknown. However, two factors could play a role: 1) as the minor (median axial) diameter of the molecule approaches the pore diameter its permeation should drop, and 2) the longer the median length of the molecule the fewer orientations that will be permeant, thus, the aspect ratio (ratio of the major to the median axial diameter) of the molecule. The greater the deviation from a sphere, the fewer molecular orientations being able to enter the pore. For the molecules considered here the median axial diameters are: cAMP ~0.52 nm, LY ~0.99 nm and 24mer ~1.1 nm, while the major diameters are cAMP ~1.12 nm, LY ~1.22 nm and 24mer ~7.6 nm [19,40]. From the median axial diameters it is clear that cAMP has a major advantage over both of other molecules, while their length suggests that the 24mer has a distinct disadvantage. Despite the relatively low permeability, siRNA transfer via gap junctions has been shown to target specific proteins under in vitro conditions [41,46] more efficiently than extracellular (endo/ecocytotic/exosomal) delivery [41,46,48].

Fig. 3.

(A) Linear plot of different solutes flux data normalized to K⁺ versus respective diffusion coefficients for Cx43. The solid line represents monovalent data fit to a linear regression (R² = 0.978) and the dashed lines are the 95% confidence intervals. The flux data for the large solutes: 12mer, 16mer, 24mer, 21 siRNA were not fit to linear regression. (B) Normalized flux data for large solutes 12mer, 16mer, 24mer, 21 siRNA plotted on expanded scale versus cube root of their respective molecular weight (see text for details).

Interestingly, Falk et al. [49] suggested that formation of annular gap junction (AGJ) vesicles via internalization of gap junction plaque in cellular process could transfer large substances (not permeable to gap junctions) from cell to cell. Such substances, like regulatory proteins, or large microRNAs could be entrapped in the AGJ vesicle lumen, and requires AGJ degradation. In such a case perm selectivity of gap junction channels may be insignificant. However, it should be noted that for the permeability of the largest molecules discussed here their minor diameter is less than the pore radius at its narrowest point.

3. Conclusions

There are a number of factors that affect the transit of solutes through gap junction channels. Fig. 4 provides a simplified illustration of those factors. First is the cytoplasmic vestibule through which all permeable solutes must pass to gain access to the pore. In an equivalent circuit it represents access resistance. The vestibule might best be viewed as the site or sites that allow for charge and size discrimination either through binding or electrostatic interactions. Both Cx37 and Cx43 have been shown to possess fixed charge moieties within the vestibule. Both variation of ionic strength and voltage dependence can be used to assess the presence of fixed charges [20,50]. The second factor is the narrowest diameter along the length of a given pore, functioning as a size selectivity point. For example Cx26 has its narrowest diameter at the cytoplasmic mouth of the pore that opens into the cytoplasmic vestibule, which inherently determines solute transit [11]. A third factor within the pore that affects the transit of solutes is hydrogen bonding. Both experimental data and simulations suggest that solute permeation is highly dependent on the energy of hydration [24,39]. If energy of hydration is a dominating factor governing permeation of solutes, then the more hydrogen bonding there is, the lower the permeability. For solutes, both solute hydrogen bonding to the pore wall moieties and the solvent within the pore itself would then be one of the rate limiting steps for permeation. A fourth factor, also within the pore, is potential binding sites for solutes to interact with. Again, both experimental data and simulations suggest this a factor within the pore, albeit a lesser one than hydrogen bonding [24,39].

Fig. 4.

Schematic of a gap junction pore depicting the factors that affect solute transfer via gap junction channels.

Oligonucleotide permeability is clearly of great importance when considering that microRNAs/siRNAs could act as intercellular second messengers regulating gene expression. Oligonucleotides are only weakly positively charged molecules and more subject to hindered access due to their length than similarly charged smaller spheroid molecules. The oligonucleotide must, in essence, “line up” in order to gain access. Once so aligned, the oligonucleotide would most likely have a greater interaction with the pore wall via hydrogen bonding. Whether such interactions would promote or hinder transit is not clear from experimental data, but the simulation of Luo et al. [39] applied to an oligo-nucleotide might well lend valuable insight.

The physiological role of ionic flux through gap junctions in the heart was clearly demonstrated by Barr et al. [51] who used a sucrose gap method to increase the extracellular longitudinal resistance in a cardiac bundle. As the resistance increased, conduction slowed and then finally failed. A similar conclusion has been drawn concerning the vasculature with regard to endothelium-dependent smooth muscle hyperpolarization [52]. For second messengers, an in vivo demonstration has been more elusive as many of the second messengers, including cAMP, are not only permeable to gap junction channels [33] but can also affect connexin expression [1,53,54]. Despite this complication, determination of accurate permeability values for specific intercellular messengers like cAMP has been deemed essential to ultimately answering the question of physiological relevance [55,56]. The evidence for intercellular siRNA/micoRNA transit that is able to affect gene expression has been shown in vitro [19,41,45–48], but an in vivo demonstration has yet to be validated.

The permeability properties in the form of molecular interactions of solutes and the pore wall of gap junctions are important to understanding processes like tissue homeostasis, cardiac pacemaker activity, and cardiac arrhythmias. If the permeation pathway is defined and the solute’s structure is known, then accurate predictions of permeation from one cell to another and subsequent effectiveness within a recipient cell are possible. A thorough understanding of connexin permeability will ultimately yield a better understanding of the role connexins play in processes such as multicellular coordinated tissue activity via inter-cellular second messenger signaling and regulation of gene expression.