A robust diffusion tensor model for clinical applications of MRI to cartilage

Abstract

Purpose

Diffusion tensor imaging (DTI) of articular cartilage is a promising technique for the early diagnosis of osteoarthritis (OA). However, in vivo diffusion tensor (DT) measurements suffer from low signal-to-noise ratio (SNR) that can result in bias when estimating the 6 parameters of the full DT, reducing sensitivity. This study seeks to validate a simplified 4-parameter DT model (zeppelin) for more robust and sensitive in vivo DTI biomarkers of cartilage.

Methods

We use simulations in a substrate to mimic changes during OA, and analytic simulations of the DT based in the range of fractional anisotropies (FA) measured with high quality DT data from ex vivo human cartilage. We also use in vivo data from the knees of a healthy subject and two OA patients with Kellgren-Lawrence (KL) grades 1 and 2.

Results

For simulated in vivo cartilage SNR (~25) and anisotropy levels, the estimated mean values of MD from the DT and zeppelin models were identical to the ground truth values. However, Zeppelin’s FA is more accurate in measuring water restriction. More specifically, the FA estimations of the DT model were additionally biased by between +2% and +48% with respect to zeppelin values. Additionally, both mean diffusivity (MD) and FA of the zeppelin had lower parameter variance compared to the full DT (F-test, p<0.05). We observe the same trends from in vivo values of patient data.

Conclusion

The zeppelin is more robust than the full DT for cartilage diffusion anisotropy and SNR at levels typically encountered in clinical applications of articular cartilage.

Introduction

The articular cartilage provides a low-friction bone-to-bone gliding, and transmits force efficiently to the subchondral bone. Most of its composition is water (~70%), in addition to a fibrous matrix of collagen (~20%) and proteoglycan (PG) (7%); only 3% of the volume is cellular (chondrocytes). The PG provides low water permeability and high swelling pressure to the matrix. The collagen fibrils balance the osmotic pressure generated by the PG and the shear forces which act on cartilage. The early stages of OA affect the cartilage, and so the assessment of its structure and composition is important for the early diagnosis of OA [1, 2, 3, 4]. But at present we lack reliable and quantitative biomarkers that measure the integrity of the cartilage matrix for early stage OA diagnosis and treatment [5].

Magnetic resonance imaging (MRI) has shown potential in providing information on the cartilage composition non-invasively. However, to date, there is no one unified MRI approach that can assess both cartilage PG and collagen architecture. Most MRI biomarkers target PG; such examples are sodium imaging [6, 7], delayed Gadolinium enhanced MRI of the cartilage (dGEMRIC) [8], T1ρ [9, 10], and glycosaminoglycan chemical exchange dependent saturation transfer (gagCEST) [11]. As for collagen, partial sensitivity is obtained from T2 relaxation time [12, 13] and magnetization transfer [14, 15, 16].

Diffusion Tensor Imaging (DTI) has emerged as a technique that can assess both cartilage structure and composition [17]. One of its two commonly-used indices, the fractional anisotropy (FA), is sensitive to the anisotropy of motion of water molecules along and across the collagen fibres [17, 18, 19, 20, 21, 22, 23, 24, 44], while changes in PG content affect another index, the mean diffusivity (MD) [23, 25, 26, 27].

A few technical challenges remain in the DTI of articular cartilage that arise as a result of various factors. The cartilage, where diffusion is mostly extracellular, is characterised by short T2 relaxation time. Because of the short T2, a measurement of the diffusion in vivo demands low b-values (of the range 0.3 - 0.6 ms/μm²), in order to balance SNR and resolution requirements. To minimise acquisition time, the DTI technique usually acquires six measurements in six non-parallel directions, to enable the evaluation of six parameters — geometrically, the Diffusion Tensor (DT) can be represented by a 3D ellipsoid, with three principal axes (eigenvectors) and three radii (eigenvalues). Low SNR, the number of measurements, and choice of the orientation of the diffusion probing gradients introduce instability in the estimated parameters. To improve the SNR of the images without sacrificing resolution or diffusion weighting one can either acquire more directions or perform repeated acquisitions. In both cases this will result in unacceptably long acquisition times for in vivo applications.

Here, we approach the above clinical cartilage DTI problem from a model point of view. We propose a simplification of the DT model: a cylindrically symmetric DT, i.e. a tensor characterised by just two radii and one direction. Our hypothesis is that, for in vivo applications, we cannot capture the small radial anisotropy of articular cartilage, and that this simplified model provides a more robust characterisation of the diffusion MRI signal from cartilage in a clinical setting. We compare the full and simplified tensor qualitatively and quantitatively using in silico and in vivo human data.

Methods

Numerical Simulation

The in silico data was obtained by using the Camino Toolkit (http://cmic.cs.ucl.ac.uk/camino/). For the Monte Carlo simulations, we placed 100,000 water molecules in a substrate that mimics the radial zone of the articular cartilage. Collagen fibrils were positioned randomly in the substrate. The collagen fibrils were modelled as circular cylinders whose radii follow a gamma distribution. The parameters of this distribution were derived from an earlier experimental measurement [28] of fibril diameter distributions, which yielded shape parameter κ=75 nm and scale parameter θ=1, corresponding to a mean radius of κθ=75 nm and variance of κθ²=75 nm. The random walkers have a diffusivity of 2.5 μm²/ms and are positioned randomly outside the cylinders. The number of cylinders in each substrate varies from 100 to 600, corresponding to a linear increase in 6 steps of fibril volume fraction, from 0.04 to 0.20. This is intended to model the changes in the cartilage as a result of OA progression. To avoid configuration bias for each volume fraction we considered 10 different substrate realisations. We also used the same 5 orientations of the b-matrix for each simulation combination.

The diffusion simulations were performed using the in vivo protocol detailed in the subsection below. Rician noise was added to the signal, sampling 100 times from the distribution with a mean signal-to-noise ratio (SNR) at one of {8, 10, 12, 15, 20, 25, 30, 40, 50, 1000}, a range covering typical noise levels which are normally observed in acquisitions in vivo (mean SNR~25). The SNR values relate to signal at b=0 — at b=0.3 ms/μm² and diffusivity D=2.5 μm²/ms the SNR would be attenuated by a factor of e^−bD ~0.47. The SNR at 1,000 was considered the standard of reference.

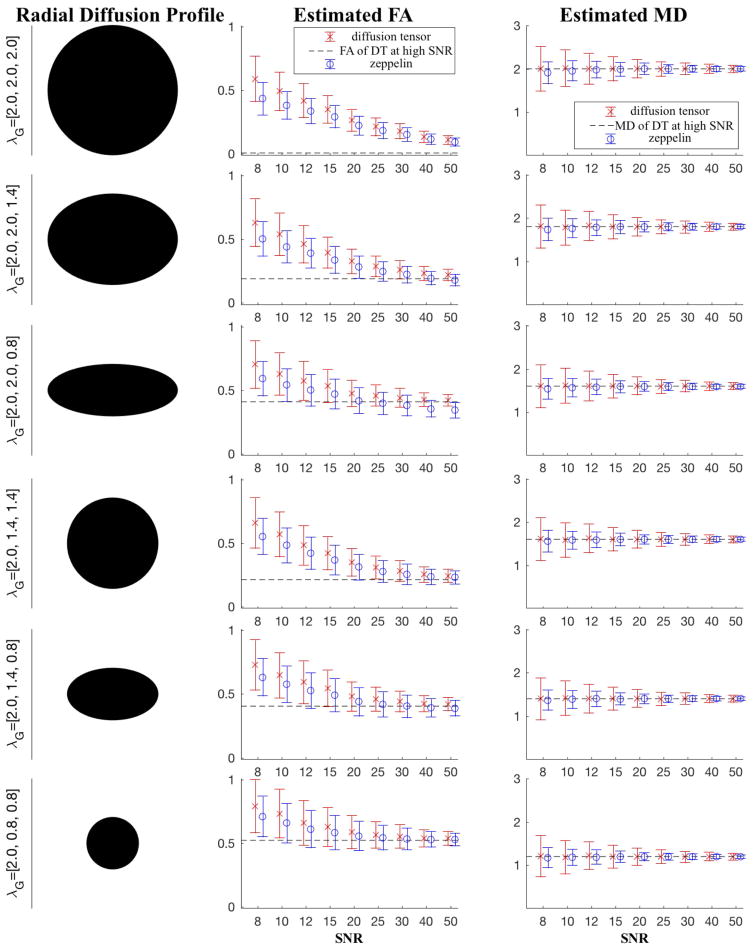
Finally, we simulated a cartilage dataset using the full DT analytical expression. The eigenvalues used here cover extreme cases of anisotropy as observed in high quality (SNR~400) ex vivo cartilage data of Raya et al. [29, 23]. This study’s diffusivities in the cartilage superficial layer returned a mean axial diffusivity 2.0 μm²/ms, while the radial diffusivities were a permutation (with repetition) of two values from {2.0, 1.4, 0.8} μm²/ms. (The ex vivo cartilage data was acquired at 18°, while the substrate values are based on in vivo data that is acquired at body temperature, 36°.) This dataset provides the advantage of having ground-truth known a priori, which is not available in substrate simulations.

In vivo Data

MRI was performed on three subjects: one healthy male subject, 38 years old; one male OA patient, 45 years old, with tibio-femoral Kellgren-Lawrence (KL) grade 1 in the left knee; and one female patient, 45 years old, with tibio-femoral KL2 right knee OA. The patients were selected from an ongoing clinical study at NYU Langone Medical Center. X-rays not older than 2 weeks were used to assess the KL grade. The study was approved by the Institutional Review Board and performed in compliance with HIPAA. All subjects provided informed written consent.

Diffusion MRI was performed on a 3T whole-body MRI (Magneton Prisma, Siemens Healthineers AG, Erlangen, Germany) using a 15-channel transmit-receive knee coil provided by the vendor. We used an optimized knee DTI protocol, with the radial spin-echo diffusion tensor imaging (RAISED) sequence [30] that includes a 2D phase navigator for motion correction, with repetition time/echo time TR/TE=1500/49 ms. The diffusion scheme has one b=0 and 6 diffusion-weighted measurements, sampled along 6 non-parallel directions and optimised with the downhill simplex algorithm [31]. A b-value of 0.3 ms/μm² was used with a diffusion time (Δ) of 19 ms, gradient duration (δ) of 14.45 ms and maximum gradient strength (|Gmax|) of 37.625 mT/m. The images were acquired in the sagittal plane perpendicular to the line tangent to the posterior aspects of the femoral condyles. The articular cartilage was segmented using PaCaSe software package [32].

Model Fitting

To all the simulated and in vivo datasets described above we fit two models which are based on the DT. The first model is the full DT, characterised by 6 parameters which are linearly fitted using a standard Matlab routine (MathWorks Inc, Natick, MA). This linear DT fitting produces three eigenvalues, λ₁, λ₂, λ₃ and their corresponding eigenvectors. Using the eigenvalues, we calculate the two most commonly used indices:

$$MD=\frac{{\mathrm{\lambda }}_1+{\mathrm{\lambda }}_2+{\mathrm{\lambda }}_3}{3}\text{and}FA=\sqrt{\frac{3}{2}\left[\frac{{({\mathrm{\lambda }}_1-\text{MD})}^2+{({\mathrm{\lambda }}_2-\text{MD})}^2+{({\mathrm{\lambda }}_3-\text{MD})}^2}{{{\mathrm{\lambda }}_1}^2+{{\mathrm{\lambda }}_2}^2+{{\mathrm{\lambda }}_3}^2}\right]}$$

The second model is a 4-parameter cylindrically-symmetric tensor, the zeppelin, in which the two radial diffusivities are set to be equal, i.e. λ₂=λ₃ [33, 34, 35]. The non-linear model fitting of the zeppelin was performed using Camino (http://www.camino.org.uk). In the fitting, the initial estimates are derived from the linear DT fitting, via the pseudo-linear inverse. Then, the optimisation uses the Levenberg–Marquardt algorithm, perturbing this starting point, to extract the set of zeppelin parameters, i.e. the eigenvalues (λ₁ and λ₂) and two angles (that define unit eigenvector n₁), given diffusion-encoding directions g, as in the signal equation:

$$S=exp(-b{\mathit{g}}^T[({\mathrm{\lambda }}_1-{\mathrm{\lambda }}_2){\mathit{n}}_{\mathbf{1}}{\mathit{n}}_1^T+{\mathrm{\lambda }}_2\mathit{I}]\mathit{g})$$

The zeppelin indices for MD and FA are calculated as for the full DT, i.e. assuming two equal eigenvalues.

Statistics

We tested the differences between the calculated MD values and ground truth using the two-sided t-test, after testing for normal distribution of the data using the Kolmogorov-Smirnov test. Differences in the standard deviation between the DT and zeppelin models were assessed using the F-test test. We used a p-value of 0.05 as threshold for statistical significance. Pearson’s correlation coefficient was used to assess the dependence of FA on the number of cylindrical fibrils.

Results

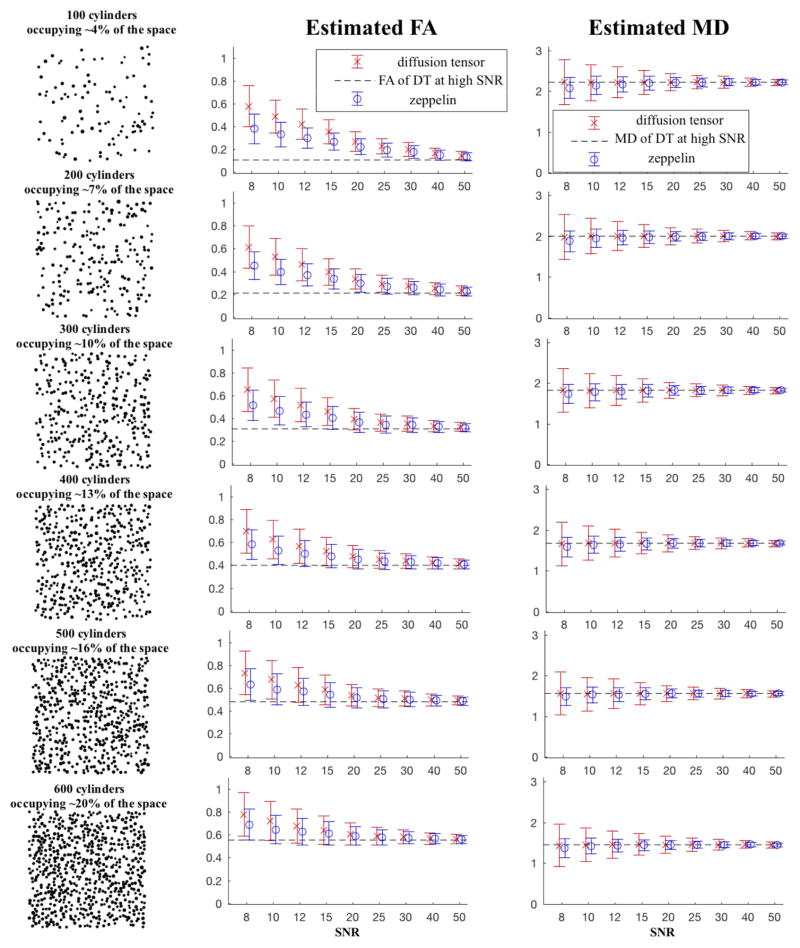
Figure 1 shows the variation, through Monte Carlo simulations, of diffusion MRI parameters of random walkers which diffuse in the synthetic substrate of cylinders under a typical in vivo protocol. The first column illustrates the substrate cross-section, as the number of cylinders in the substrate increases. The second column plots the model-derived FA for the corresponding substrate, and the third column plots the MD.

Figure 1.

Simulations using a substrate with different density of collagen fibrils, showing the variation of FA and MD across typical in vivo SNR. In the first column, each mesh substrate consists of cylinders randomly-spread in the cross-sectional plane, occupying area/volume fractions that vary from 4% to 20% of the whole plane/space. The distribution of (right circular) cylinders has a cross-section with mean radius R=75 nm. The second column is for FA and the third column is for MD; the circles represent the mean over 5,000 simulations (1000 instances of noise, 10 random realisations of the substrate, and 5 orientations of the b-matrix), with the bars showing standard deviation. Colour red denotes the DT values, and the blue denotes the zeppelin ones. The SNR references b0 signal, which at a b=300 ×10³ ms/μm² and diffusivity=2.5 μm ²/ms is attenuated by a factor of about 0.47. A typical SNR for in vivo experiments is about 25.

All estimates of the zeppelin FA have lower mean (t-test) and variance (F-test) than the full DT model with statistical significance below 0.05. For a substrate sparsely dense with fibres, as shown in the first row, occupying only about 4% of the space and with ground-truth FA at 0.11 (estimated as the FA of the DT under SNR=1,000) at a usual SNR=25 the zeppelin FA estimate is 0.19±0.06 while DT’s is 0.22±0.07 (which is about 17% higher than zeppelin’s mean). At a lower SNR=10 the zeppelin FA=0.33±0.11 while FA of DT is 0.49±0.15 (DT’s mean being about 48% higher than zeppelin’s). In a substrate more densely populated with cylindrical fibrils, as in the last row, with 20% of the space taken by fibrils and the ground-truth FA=0.55, at SNR=25 zeppelin’s FA is 0.58±0.07 compared with DT’s mean 0.59±0.08 at 1.4% higher; at SNR=10, zeppelin’s FA is 0.65±0.13 compared with DT’s 0.72±0.17, an increase on the mean of 11.5%. Across all simulation scenarios the estimated indices at SNR=1,000 coincide. The estimated FA from both Zeppelin and DT do increase as the number of cylindrical fibrils in the substrate increases. There was a linear relationship between the FA and the substrate volume (percentage fraction of collagen fibers relative to the whole volume); for this range the estimated FA increases at a gradient of 0.03 and offset 0.015 (p=4×10⁻⁵, R²=0.99).

The differences in mean MD values for both models were not-statistically significant across the range of in vivo SNR. The zeppelin, however, showed statistically significant lower parameter variance; e.g. in the last subplot of volume 20%, at SNR=10 the MD of zeppelin is 1.42±0.19 while DT’s is 1.45±0.41 μm²/ms, and at SNR=25 the MD of zeppelin is 1.45±0.09 while DT’s is 1.46±0.16 μm²/ms. MD values were also attenuated by the change in the substrate number of cylinders with an inversely linear gradient of −4.8 and offset of about 2.34 μm²/ms (p=3.8×10⁻⁴, R² =0.97).

Figure 2 is like Fig. 1, though here we generate the anisotropy instances through the DT model itself using eigenvalues encountered in a high SNR experiment of ex vivo cartilage data. Trends similar to that in Fig. 1 emerge: the zeppelin FA is consistently lower than DT’s, and it has lower variance. Within the normal clinical SNR values (~25) zeppelin FA is closer to ground-truth values; in particular, for the rather extreme anisotropy of third row, where one of the radial diffusivities is as large as the axial one, this zeppelin bias is only worse at SNR>40. The table summarises the key results from Figures 1 and 2, for the “clinical” case, i.e SNR=25.

Figure 2.

Simulations using an analytical expression for DT. The diffusivities are typical of those encountered in a high SNR ex vivo dataset. Error bars have the same meaning as in Fig. 1.

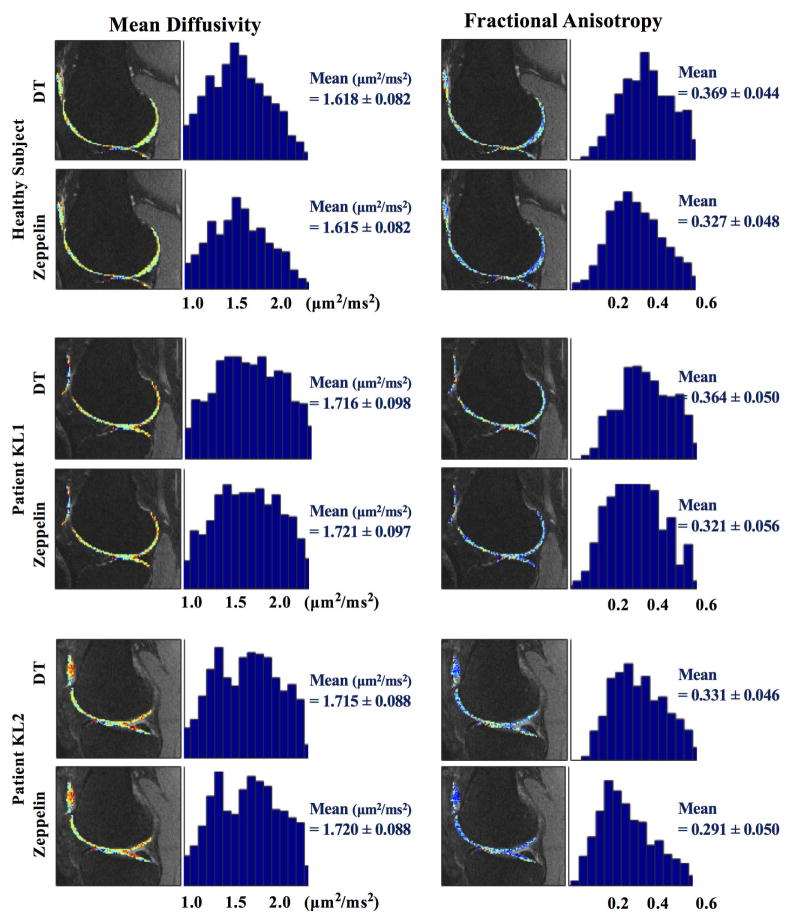
Figure 3 shows the plot of parameters for the scanned healthy subject and patients with OA severity KL 1 and KL 2. Qualitatively, the MD maps of the two OA patients appear to have higher values than the map of the healthy subject; similarly, FA maps of the OA patients show lower values than those of the healthy subject. Intra-subject variability is noticeable in the FA values, with zeppelin FA being lower than DT’s across all three datasets, while MD remains unchanged. The change in mean FA between KL0 and KL2 is −12.1% for the Zeppelin and −10.8% for DT.

Figure 3.

MD (left) and FA (right) of in vivo healthy subject and two OA patients (KL1 and KL2). Beside each image we show the histograms of parameter distribution of cartilage surface.

Discussion

DTI can provide useful biomarkers in the early diagnosis of OA [36, 37]. However, in clinical in vivo acquisitions, the benefits of this imaging are limited by low SNR and requirements of high resolution. In this study we compared the indices derived from the standard 6-parameter DT with the indices derived from a simplified DT model. Geometrically, the difference between the models arises in the estimation of the radial component of the diffusivity: radial cross-section of the DT can be ellipsoidal, whereas the cross-section of the zeppelin is necessarily circular. We showed through simulations the zeppelin can provide more robust estimations of anisotropy in the range of FA and SNR of in vivo cartilage. We illustrated this with in vivo human data. Strikingly, as Figs. 1 and 2 show, even under obvious anisotropy, in SNR values typical of clinical applications the zeppelin is an improvement over the DT. Because of overfitting, low SNR levels cause a bias in DT parameters. Thus, trying to capture differences in the radial anisotropy for the range of in vivo SNRs accentuates the bias on the eigenvalues, and thus on FA. Even if differences in the radial diffusivities exist, these cannot be accurately captured.

The fitting of the models, the full DT and zeppelin, is different. While the full DT is fitted utilising the standard (pseudo)linear inversion, the zeppelin is fitted using a non-linear optimisation routine with initial starting estimates derived from the DT. Since in our study the DT is the initial guess for the zeppelin model fit, 6 DW images are still required; though in general a zeppelin model could be estimated with 4 DW images, e.g. employing a nonlinear fitting routine that starts with arbitrary estimates for the four parameters, two Euler angles and two diffusivities. In our simulations, we observed that the zeppelin fitting is quite robust with respect to initial conditions. Only in a few cases of extreme anisotropy did the fitting become less stable, especially as radial diffusivities diverged from each-other.

The simplified tensor, the zeppelin, has seen early applications in the eye [42] and recently in the spinal cord [43], as well as in the brain [33,34,35]. In the brain, however, there are regions where the 3D geometry of the fibers is potentially important, e.g. in regions of complex fiber configurations the radial diffusivity profile can be anisotropic. But even in this such case, a rich protocol is required, whose rich signal can enable the model to distinguish between the two radial diffusivities. Additionally, the two tissues differ fundamentally: unlike the brain, the cartilage tissue has a mostly extracellular structure.

Specific to cartilage, previous work has touched on this problem of the two tensor models, the full DT and the zeppelin. Ferizi et al. [39] illustrated this disparity through ex vivo data. Later, Bajd et al. [40] use various sources of data to test the DT: through synthetic model simulations, a water phantom, and cartilage. Using DT’s analytical expression, they first synthesise data for an isotropic medium, akin to water, to test the bias in DT parameters for many popular diffusion-sensitising direction schemes; they also employ a cylindrically-symmetric tensor (i.e. a zeppelin) to generate data for testing the full DT at two SNR values (5 and 30), three FA values (0.0, 0.1 and 0.3), and various (6 to 100) diffusion directions. Lastly, the authors use ex vivo cartilage-on-bone bovine samples. For low SNR the authors demonstrated the bias in the estimates of FA as a function of SNR and choice of diffusion-sensitising gradients. In the end, the authors suggest ‘applying a larger number of diffusion sensitizing directions’, which is not feasible for clinical scans.

The important question is when to use the zeppelin, and when the DT model. While we cannot provide a general answer to this question, as this depends on many factors that have not been analyzed here (e.g. the gradient scheme), we can identify a range for the particular application that we have considered. According to our validation, we see that in the range of moderate SNR, between 10 and 50, and moderate FA, less than 0.4, the zeppelin model provides more accurate and precise estimation of the diffusion indices. It is worth mentioning that our in vivo experiments used an optimised gradient scheme. In other cases, where the gradient scheme is suboptimal our data showed that the zeppelin is even more robust to noise than the DT.

Beyond these two single-compartment tensor-based models, our attempt to use more advanced models, like those in Ferizi et al. [38], did not provide any added benefit. In particular, Watson-sticks, which could potentially describe the restricted water by the weave-like structure of the fibrils, provides too noisy a fit. The two-compartment ball-stick, which is computationally very efficient, provided similar maps to the zeppelin and DT; however, we see no obvious justification for a two compartment modelling, since the cartilage is essentially a one-compartment extracellular structure.

The in vivo observations from Fig. 3 are consistent with the results in the simulations. Zeppelin FA values are lower than DT’s, while MD values stay the same. By reducing the bias, we expect to increase the sensitivity to changes in the microstructure. However, caution is needed because, even though we correlate the change in substrate cylinder density with estimated FA, the correlation of DTI metrics with the cartilage damage (say KL grade) ignores the fact that the progression from one grade to another does not necessarily increase linearly.

This work has an obvious limitation. The simulations are simplifications of the cartilage: the fibrils are assumed to be straight; the extra-fibril space is considered isotropic, so that the simulation does not capture the full complexity of the extracellular matrix.

In summary, for the range of SNR of in vivo data the zeppelin provides a more robust fitting and accurate characterisation of the cartilage. Our specific hypothesis, that for clinical applications to the articular cartilage the zeppelin is better than DT, arises from the limitations of in vivo protocols. Due to the high resolution required, in vivo protocols are limited to the minimal 6+1 number of image acquisitions. In this case, the zeppelin fitting problem would become overdetermined, enabling a more accurate estimation of the DT parameters in the low-SNR regime; as our study showed. this would manifest in the lower [MD and FA] parameter variance. However, while the zeppelin clearly outperforms in this range of SNR, we do not claim a universal superiority of the zeppelin over DT in describing the complexity of the cartilage. A richer protocol, with more directions and higher SNR, will eventually show the DT outperforming the simpler zeppelin.

Table 1.

A summary of the most important results from Figures 1, 2 and 3.

Monte Carlo Simulations (SNR=25 of Fig. 1)
Fibril Fraction	4%	7%	10%	13%	16%	20%
DT (MD mean±std)	2.23±0.17	2.01±0.17	1.83±0.16	1.68±0.16	1.57±0.16	1.46±0.16
ZP (MD mean±std)	2.22±0.11	2.00±0.10	1.82±0.10	1.67±0.10	1.56±0.10	1.45±0.09
MD ground truth	2.22	2.00	1.82	1.68	1.56	1.45
DT (FA mean)	0.23±0.07	0.30±0.07	0.36±0.08	0.45±0.08	0.51±0.08	0.59±0.08
ZP (FA mean)	0.19±0.06	0.27±0.07	0.34±0.07	0.44±0.07	0.50±0.07	0.58±0.07
FA ground truth	0.11	0.21	0.31	0.40	0.48	0.55

DT-synthesised (SNR=25 of Fig. 2)
Diffusion Profile [λ1, λ2, λ3]	[2.0 2.0 2.0]	[2.0 2.0 1.4]	[2.0 2.0 0.8]	[2.0 1.4 1.4]	[2.0 1.4 0.8]	[2.0 0.8 0.8]
DT (MD mean±std)	2.00±0.17	1.80±16	1.60±0.16	1.60±0.16	1.40±0.16	1.20±0.16
ZP (MD mean±std)	2.00±0.10	1.80±0.09	1.59±0.09	1.60±0.09	1.40±0.08	1.20±0.08
MD ground truth	2.00	1.80	1.60	1.60	1.40	1.20
DT (FA mean±std)	0.21±0.07	0.29±0.08	0.46±0.08	0.31±0.09	0.46±0.09	0.57±0.11
ZP (FA mean±std)	0.18±0.06	0.25±0.08	0.40±0.09	0.28±0.09	0.42±0.10	0.54±0.10
FA ground truth	0.00	0.19	0.41	0.21	0.40	0.52

In Vivo (from Fig. 3)
Subjects	Healthy	Patient KL1	Patient KL2
DT (MD mean±std)	1.62±0.08	1.72±0.10	1.72±0.09
ZP (MD mean±std)	1.62±0.08	1.72±0.10	1.72±0.09
DT (FA mean±std)	0.37±0.04	0.36±0.05	0.33±0.05
ZP (FA mean±std)	0.33±0.05	0.32±0.06	0.29±0.05

^*All diffusivity (MD and λ’s ) units are in μm²/ms.