Not All β-Sheets Are the Same: Amyloid Infrared Spectra, Transition Dipole Strengths, and Couplings Investigated by 2D IR Spectroscopy

Abstract

We report the transition dipole strengths and frequencies of the amyloid β-sheet amide I mode for the aggregated proteins amyloid-β_1–40, calcitonin, α-synuclein, and glucagon. According to standard vibrational coupling models for proteins, the frequencies of canonical β-sheets are set by their size and structural and environmental disorder, which determines the delocalization length of the vibrational excitons. The larger the delocalization the lower the frequency of the main infrared-allowed transition, A_⊥. The models also predict an accompanying increase in transition dipole strength. For the proteins measured here, we find no correlation between transition dipole strengths and amyloid β-sheet transition frequency. To understand this observation, we have extracted from the protein data bank crystal structures of amyloid peptides from which we calculate the amide I vibrational couplings, and we use these in a model β-sheet Hamiltonian to simulate amyloid vibrational spectra. We find that the variations in amyloid β-sheet structures (e.g., dihedral angles, interstrand distances, and orientations) create significant differences in the average values for interstrand and nearest neighbor couplings, and that those variations encompass the variation in measured A_⊥ frequencies. We also find that off-diagonal disorder about the average values explains the range of transition dipole strengths observed experimentally. Thus, we conclude that the lack of correlation between transition dipole-strength and frequency is caused by variations in amyloid β-sheet structure. Taken together, these results indicate that the amide I frequency is very sensitive to amyloid β-sheet structure, the β-sheets of these 4 proteins are not identical, and the assumption that frequency of amyloids scales with β-sheet size cannot be adopted without an accompanying measurement of transition dipole strengths.

Graphical Abstract

INTRODUCTION

More than 20 human diseases are associated with the formation of β-sheet-rich amyloid fibers.^1,2 Their structures and aggregation mechanisms are of immense interest to better understand the origins of these diseases.^1,2 Both Fourier transform infrared (FTIR) and two-dimensional infrared (2D IR) spectroscopy have proven to be powerful tools for studying amyloid proteins in a structurally specific manner, including their kinetics.^3–8 Structural sensitivity stems from changes in vibrational couplings between amide I modes that correlate with secondary structure. Isotope labeling can also be employed to obtain site-specific resolution of secondary and tertiary structure, either for individual residues or larger domains of a protein.^9–14 2D IR spectroscopy is particularly useful, because of the nonlinear scaling of the signal, additional structural information from cross peaks, 2D lineshapes, and enhanced resolution.^15,16

For coupled amide I transitions, absorptions at specific frequencies can often be directly correlated with secondary structure. In aqueous solution, disordered random coil features typically absorb around 1645 cm⁻¹, native β-sheet features around 1630–1640 cm⁻¹, and amyloid β-sheet features in the 1610–1630 cm⁻¹ range.^15,17–19 Both native and amyloid β-sheets may also exhibit a higher frequency amide I transition in the 1670–1680 cm⁻¹ range, depending on if the sheet is parallel (absent) or antiparallel (likely present).^15,18–21 However, assignments like these can often be tentative, as these frequency ranges are based mostly on empirical observations and can vary by as much as 20 cm⁻¹, caused by differences in vibrational couplings and electrostatic environment for the specific protein under consideration.¹⁷ Furthermore, the frequencies are not always unique, such as for α-helicies and random coil structures, which can absorb at similar frequencies.^15,18,19,22 Transition dipole strengths can help with peak assignments, because they scale linearly with vibrational delocalization.^23–26 Delocalization is created by strong coupling between residues in extended secondary structures. It has been experimentally determined that the amide I vibrational modes extend over as many as 3.5 residues in α-helices²⁵ and 12.5 residues in β-sheets,²⁶ while random coils are largely localized onto a single residue. Thus, measuring both frequencies and transition dipole strengths provide a stronger basis for assignments than spectra alone. In principle, all one needs to extract transition dipole strengths from a spectrum is the concentration and path length, but in practice it is much more difficult (i.e., protein concentrations are difficult to measure accurately), and transition dipole strengths are hardly ever reported for complex molecules. Our group recently reported a simple, robust method for measuring transition dipole strengths using a 2D IR spectrometer.^25,26 The transition dipole strength dictates the absorption coefficient, ε, in Beer’s law (A = ε × c × l, c = concentration, l = path length) through the relationship $\epsilon \propto |\overrightarrow{\mu }{|}^2$. Thus, the signal of a linear absorption spectrum is proportional to $c\times |\overrightarrow{\mu }{|}^2$. Our method of measuring transition dipole strengths relies on the fact that the 2D IR signal is proportional to $c\times |\overrightarrow{\mu }{|}^4$; by taking the ratio of the 2D IR and linear signals we obtain a measurement of $|\overrightarrow{\mu }{|}^2$ that is independent of concentration. The spectrum of a calibrant molecule with known transition dipole strength is used to eliminate dependence of the measurement on experimental parameters, such as laser fluence and spatial overlap of laser pulses.²⁷ The transition dipole of the protein is calculated as the ratio of signal strengths shown in eq 1, where ΔOD_sample and ΔOD_calibrant are the intensities of the 2D IR spectra of the sample and calibrant, OD_sample and OD_calibrant are the OD of the sample and calibrant, and $|{\overrightarrow{\mu }}_{\text{calibrant}}{|}^2$ is the transition dipole strength of the calibrant. By using a calibrant molecule with a similar anharmonicity and line width to the protein vibrational transitions we are studying, the effects of the overlapping bleach and excited state absorption cancel (to a reasonable approximation) when taking the ratio of signals described in eq 1.

$$|\stackrel{\rightharpoonup }{\mu }{|}^2=\frac{\left(\frac{\mathrm{\Delta }{\text{OD}}_{\text{sample}}}{{\text{OD}}_{\text{sample}}}\right)}{\left(\frac{\mathrm{\Delta }{\text{OD}}_{\text{calibrant}}}{{\text{OD}}_{\text{calibrant}}}\right)}\times |{\stackrel{\rightharpoonup }{\mu }}_{\text{calibrant}}{|}^2$$ (1)

The amide I vibrational mode has a relatively large transition dipole strength due to its significant C=O stretching character. An amide I stretch consists primarily of C=O stretching (ca. 85%), but also has contributions from C–N (ca. 10%) stretching and in-plane bending of the N–H.^15,28 In proteins, several amide I groups couple to produce delocalized vibrational modes, leading to shifts in transition frequencies and redistribution of transition dipole strength. Vibrational coupling differs between secondary structure motifs, leading to characteristic frequencies observed for each type of secondary structure as discussed above. For each frequency, the procedure above gives a corresponding transition dipole strength. In samples with unknown concentration, kinetically evolving samples, complex structured samples like proteins, or heterogeneous samples, standard methods using absorption spectroscopy cannot accurately measure transition dipole strengths, whereas the method described above can be easily applied during data collection for any 2D IR experiment.

Figure 1a shows a cartoon that illustrates the relationship between vibrational couplings, transition dipole strengths, and the intensities of FTIR and 2D IR spectra. Two amide groups are shown in close enough proximity that they are coupled; their potential energy landscapes depend on one another. The normal modes of this system will be delocalized across both molecules and have transition dipole strengths that depend on the relative orientations of the local transition dipole vectors, ${\overrightarrow{\mu }}_1$ and ${\overrightarrow{\mu }}_2$.^28–31 In the geometry shown, the symmetric normal mode transition dipole, ${\overrightarrow{\mu }}_{+}$, will be larger than that of the antisymmetric mode, ${\overrightarrow{\mu }}_{-}$. The corresponding FTIR spectrum is given by the square magnitude of the normal mode transition dipoles, $|{\overrightarrow{\mu }}_{+}{|}^2$ and $|{\overrightarrow{\mu }}_{-}{|}^2$, respectively. The 2D IR signals are given by the fourth power, $|{\overrightarrow{\mu }}_{+}{|}^4$, and $|{\overrightarrow{\mu }}_{-}{|}^4$, respectively, and thus the ratio of intensities is much greater in the 2D IR than the FTIR spectrum. The redistribution of oscillator strengths caused by coupling does not alter the integrated area of the linear spectrum, but the integrated area of the 2D IR spectrum varies significantly.^32,33 Thus, FTIR spectroscopy is largely insensitive to changes in transition dipole strengths, while an increase in 2D IR signal intensity is strong evidence for coupling causing vibrational delocalization.

Figure 1.

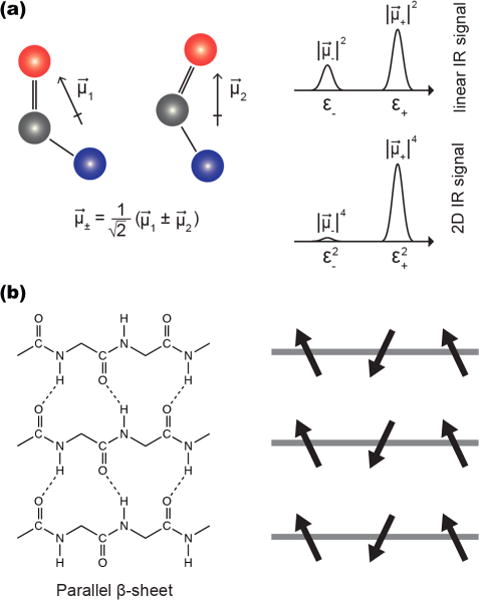
(a) Two coupled amide I oscillators and their transition dipole moments, ${\overrightarrow{\mu }}_1$ and ${\overrightarrow{\mu }}_2$. Their relative orientation affects the vector sum of their coupled vibrational modes, which dictates the magnitude of the coupled transition dipole moments. The linear IR spectrum scales as $|\overrightarrow{\mu }{|}^2$ while the 2D IR signal scales as $|\overrightarrow{\mu }{|}^4$. (b) The structure of a parallel β-sheet and a schematic of the local transition dipole moment orientations.

Delocalization and the accompanying change in transition dipole strength and 2D IR intensity can be dramatic for β-sheets. Figure 1b shows the backbone structure and hydrogen bonding pattern in parallel β-sheets, along with a schematic diagram showing the relative orientation of the local transition dipole moments. Similar to the example with two isolated amide groups, the amide I vibrational modes are in close enough proximity that they are vibrationally coupled. The strongest vibrational transition dipole moment involves in-phase oscillation of residues in-register between strands, generating a transition dipole perpendicular to the β-strands (termed the A_⊥ mode). For a canonical parallel β-sheet, the vibrational couplings between in-register residues of adjacent strands is on the order of −10 cm⁻¹, while that between neighboring residues of the same strand is on the order of about 2 cm⁻¹. These strong couplings cause the A_⊥ normal mode to delocalize over many residues for amyloid β-sheets, causing the local modes from each of the individual residues to sum into a normal mode with a significant increase in transition strength and a nonlinear enhancement in the 2D IR signal, as stated above. Accompanying the increase in transition dipole strength is a shift in the infrared allowed frequency from about 1650 cm⁻¹ to about 1620 cm⁻¹, creating the signature A_⊥ mode for amyloid fibers. Thus, these coupling models predict that the transition dipole strength and frequency of the A_⊥ mode are anticorrelated. Similar results are predicted for antiparallel β-sheets. Moreover, since these effects are caused by delocalization, they vary with the size of the β-sheet since size is the ultimate limiting factor for delocalization. Diagonal and off-diagonal disorder also influence delocalization. The link between β-sheet size, delocalization, disorder, and frequency has been extensively investigated theoretically.^{20,21,23,34,35} Experimentally, the link between these quantities has been much more difficult to study. The new ability to experimentally measure transition dipole strengths in proteins enables a more robust test of these models by providing what is essentially a measure of the delocalization length (related to the often-calculated inverse participation ratio).

In this article we measure the transition dipole strengths of several amyloidogenic proteins and discover that the anticorrelation between the A_⊥ transition dipole strengths and frequency predicted for canonical β-sheets does not exist in amyloid fibers. The proteins we selected for this study are the human variants of Aβ_1–40, calcitonin, α-synuclein, and glucagon. Amyloid fibers of Aβ_1–40 are associated with Alzheimer’s disease,³⁶ calcitonin fibers with medullary thyroid cancer,³⁷ and α-synuclein fibers with Parkinson’s disease.³⁸ Glucagon is used to treat hypoglycemia and shares a similar sequence to glucagon-like peptide 1 (a drug used in diabetes and obesity treatment), making its fiber formation interesting from a drug-formulation perspective.³⁹ Aβ_1–40^9,40,41 and α-synuclein^42,43 form parallel β-sheets in amyloid fibers. NMR studies suggest calcitonin forms antiparallel β-sheets in amyloid fibers,⁴⁴ though experiments on a D15N mutant⁴⁵ or on the pentapeptide comprising its amyloidogenic region suggest parallel β-sheets may form.^46–48 No A_‖ mode is observed in the linear⁴⁹ or 2D IR spectra of calcitonin, consistent with a parallel β-sheet structure, though this transition is not always clearly visualized in antiparallel β-sheets as mentioned above. Glucagon is known to form antiparallel β-sheets though we do not observe the A_‖ absorption in our 2D IR spectra.^50,51

For a given protein, we find very small variations (± 1.5 cm⁻¹ or less) in the measured A_⊥ frequency but a range of observed transition dipole strengths. No correlation exists between frequency and transition dipole strength across protein samples. Instead, by calculating vibrational couplings from amyloid crystal structure fragments in the protein data bank, we learn that different amyloid frequencies are related to differences in amyloid structure and that off-diagonal disorder alters the transition dipole strengths but not the average frequency. Thus, we conclude that amyloid infrared frequencies probe backbone structure, not size.

METHODS

Preparation of Protein Samples

Aβ_1–40 was purchased from Anaspec, α-synuclein from rPeptide, calcitonin from Bachem, and glucagon from Sigma-Aldrich. In the case of α-synuclein and calcitonin, the dried proteins as received contained trifluoroacetic acid. The trifluoroacetic acid was removed using a standard protocol in which the protein was dissolved in 5 mM HCl, flash frozen using liquid N₂, and lyophilized overnight. The lyophilization procedure was repeated three times.

Proteins were dissolved in deuterated hexafluoroisopropanol (HFIP-d) to deuterate exchangeable sites and to promote disaggregation of the protein samples. Concentration measurements for each protein were determined in aqueous solution and were made via 280 nm extinction coefficients using a NanoDrop 2000 (Thermo Sci.) The A₂₈₀ coefficients used were 1490 M⁻¹cm⁻¹ for Aβ_1–40⁵², 1400 M⁻¹cm⁻¹ for calcitonin,⁵³ 5960 M⁻¹cm⁻¹ for α-synuclein,⁵⁴ and 8480 M⁻¹cm⁻¹ for glucagon.⁵⁵ Lyophilization of the samples from HFIP-d were used to prepare aliquots at the desired concentration.

Proteins aggregated spontaneously upon dissolution in either a pD 7.5 20 mM tris buffer in D₂O at concentrations of ca. 1–3 mM for Aβ_1–40, calcitonin, and glucagon, and ca. 0.3–1 mM for α-synuclein. Each protein studied forms amyloid aggregates at different rates, and sample heterogeneity further leads to heterogeneity in the observed rate of aggregation. Aβ_1–40 aggregated within 1 h, and calcitonin aggregated within ca. 8 h as monitored by the rise of the amyloid transition in the 2D IR spectrum. Samples of glucagon and α-synuclein took a few days to aggregate; sonication of these samples for ca. 2–4 h in aqueous solution appeared to speed aggregation rates, as monitored by 2D IR spectra of aliquots taken from the aggregating solutions. Transition dipole strengths measured several days after the samples were already aggregated did not appear to change significantly, nor did the observed amyloid A_⊥ transition frequency.

2D IR Spectroscopy

The 2D IR spectrometer used has been described previously.^56–59 Briefly, a 3.2 W regenerative amplifier (Spectra Physics, Solstice) generates 100 fs pulses centered at 800 nm, which pump an optical parametic amplifier (Light Conversion, TOPAS) that outputs signal and idler pulses centered at 1417 and 1845 nm. The signal and idler undergo difference frequency generation to produce mid-IR pulses centered at ca. 1600 cm⁻¹ and are ca. 100 fs in duration. The mid-IR pulses are split into pump (95%) and probe (5%) beams using a CaF₂ wedge. The pump beam passes through a horizontal, fully reflective germanium acousto-optic modulator pulse shaper, described in detail previously.⁵⁹ The pulse shaper uses acoustic waves to generate a collinear pair of compressed pump pulses with variable delays that are scanned to generate the pump axis of the 2D IR spectrum. A four-frame phase cycling scheme is used to subtract background and suppress pump scatter.⁵⁸ Pump and probe beams are spatially overlapped and focused at the sample using parabolic mirrors, and the temporal delay (t₂) between the pump pair and probe beam is achieved using a motorized delay stage (Newport). The probe is spatially dispersed onto a 64-element mercury–cadmium-telluride (MCT) array (Infrared Associates), providing ca. 3 cm⁻¹ spectral resolution along the probe axis. Aqueous samples were placed between a pair of 2 mm thick CaF₂ windows separated by a 56 μm Teflon spacer for spectroscopic experiments.

Transition Dipole Strength Measurements

The transition dipole strengths of proteins samples were measured using a combination of 1D and 2D IR spectroscopy as described previously.^25,26 The 2D IR spectrometer allows simultaneous collection of the linear and 2D spectra for each sample using the 64-pixel MCT detector. For each measurement, data is collected for the protein solution, the buffer used to dissolve the protein, and a calibrant molecule dissolved in the same buffer. L-serine was used as the calibrant molecule with a previously reported transition dipole strength of 0.20 D², and the buffer used was 20 mM tris at pD 7.5. To minimize path length differences, small aliquots (ca. 1 μL) of all 3 solutions (protein, buffer, and calibrant) were simultaneously sealed in the same sample cell, spatially separated so that the spots did not mix.

Modeling Vibrational Spectra

Vibrational spectra were calculated using the amide I vibrational exciton Hamiltonian.¹⁵ We neglect local environment variations and set the local mode frequencies of each amide I transition to 1655 cm⁻¹ with identical transition dipole strengths. The couplings between each amide group were calculated using the transition dipole coupling (TDC) model.^29–31 Due to the well-known break down of the point-dipole approximation when the two chromophores are in close proximity, we substitute the nearest neighbor couplings with values obtained from the dihedral angle-based map of Jansen et al.⁶⁰ TDC generates interstrand couplings that are large in magnitude and negative in sign that produce spectra comparable to other coupling models for β-sheet proteins and amyloids.⁶¹ To further simplify our model, couplings below 0.4 cm⁻¹ were omitted from the Hamiltonian. The excitonically coupled modes are shown as sticks and were convoluted with a 5 cm⁻¹ full-width at half-maximum Lorentzian line shape to simulate peak broadening. Calculations were performed using a Matlab based vibrational spectroscopy simulation package, COSMOSS (coupled oscillator model spectrum simulator),⁶² or similar home-written Matlab scripts.

RESULTS AND DISCUSSION

Experimental Transition Dipole Strengths in Aggregated Amyloidogenic Proteins

We collected 2D IR and linear IR spectra for each protein as well as the calibrant molecule (L-serine) and the buffer, allowing us to calculate transition dipole strengths for each amyloid protein sample following the procedure outlined in the Introduction Section. Further details of this procedure have been reported previously.^25,26 All 2D IR spectra are collected at zero waiting time (t₂ = 0). Figure 2 shows 2D IR spectra of each protein along with diagonal slices though the fundamental transition and the corresponding linear IR spectra for the same samples. The 2D IR signal scales as $c\times |\overrightarrow{\mu }{|}^4$, while the signal in the linear IR spectra scales as $c\times |\overrightarrow{\mu }{|}^2$. This leads to a significant enhancement of vibrational transitions with higher transition dipole strengths (e.g., the A_⊥ amyloid β-sheet transition) in the 2D spectra, relative to the linear spectra. The transition dipole strength of the A_⊥ β-sheet transition was calculated from this data for several samples of each protein. In these experiments, we are primarily interested in the relationship between the observed A_⊥ transition frequency and its measured transition dipole strength, although one can use our method to generate a frequency-dependent “spectrum” of the transition dipole strengths.

Figure 2.

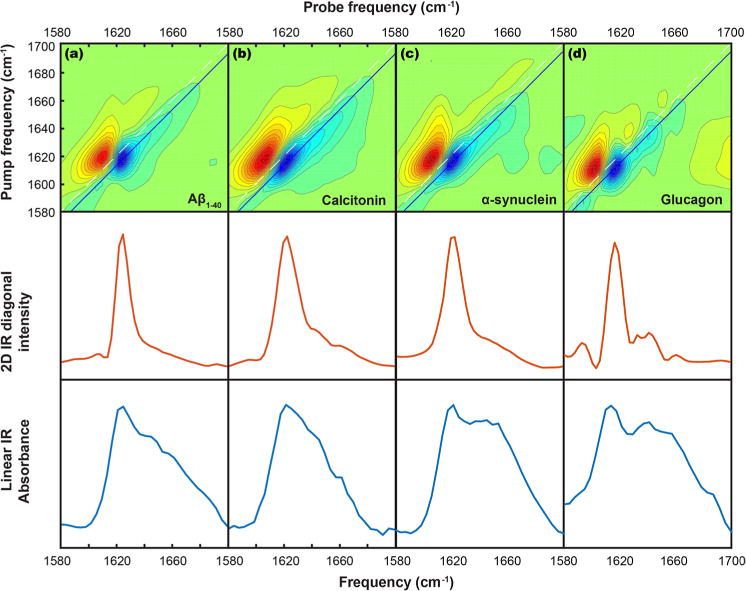
2D IR spectra (top row), diagonal traces through the 2D IR spectra (middle row), and linear absorbance spectra (bottom row) for (a) Aβ_1–40, (b) calcitonin, (c) α-synuclein, and (d) glucagon.

The A_⊥ transition is observed at 1625 cm⁻¹ for Aβ_1–40, at 1621 cm⁻¹ for calcitonin, at 1620 cm⁻¹ for α-synuclein, and at 1614 cm⁻¹ for glucagon. These frequencies are rounded to the nearest pixel in the detector and so have errors of ±1.5 cm⁻¹; fitting would likely produce more accurate frequencies but this method is sufficient for the present purposes. Figure 3 shows a plot of the measured transition dipole strength versus the observed β-sheet frequency. Each point on the plot is for a separately measured sample. We observe a range of transition dipole strengths for each protein, but, interestingly, we observe the same A_⊥ transition frequency for each sample of a given protein (±1.5 cm⁻¹). This result contrasts with the predicted expectation regarding the relationship between these two values, as outlined above. Specifically, for a canonical β-sheet, we would have expected that glucagon would have the largest transition dipole strength, Aβ the smallest, and the others in between.

Figure 3.

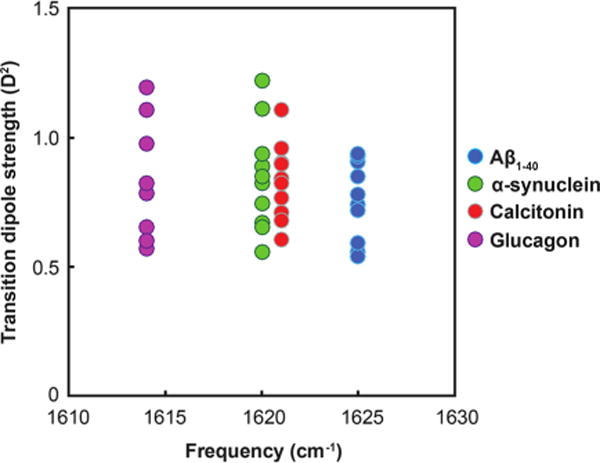
Plot of measured transition dipole strengths vs. β-sheet frequency maxima for ten samples of Aβ_1–40, calcitonin, α-synuclein, and glucagon.

Relating Transition Dipole Strengths to Delocalization of Vibrational Modes

As we discussed in the Introduction Section, the transition dipole strength for an excitonic mode depends on the number of residues over which excitons are delocalized. The transition dipole strength of an uncoupled amide I mode can be estimated as that for N-methylacetimide, which is 0.12 D². Thus, the observation of transition dipole strengths greater than 0.12 D² is indicative of vibrational coupling and delocalization of the amide I modes. The transition dipole strength is determined by the vector sum of local mode transition dipoles weighted by their eigenvector coefficients, c_i, as shown in eq 2). This is closely related to the inverse participation ratio (IPR), which is a measure of the number of local modes contributing to the normal mode. The IPR is calculated as defined in eq 7, where U_α,j is the j^th element of the eigenvector associated with the α^th vibrational mode.

$$\stackrel{\rightharpoonup }{\mu }={\displaystyle \sum c_i{\stackrel{\rightharpoonup }{\mu }}_i}$$ (2)

We see from eq 2 that for a delocalized amide I transition, α, with equal local mode transition dipole strengths, the transition dipole magnitude is

$$|{\stackrel{\rightharpoonup }{\mu }}_{\alpha }|=|{\displaystyle \sum c_i{\stackrel{\rightharpoonup }{\mu }}_{\text{loc}}|=}{c}_1|{\stackrel{\rightharpoonup }{\mu }}_{\text{loc}}|\text{cos}({\theta }_1)+c_2|{\stackrel{\rightharpoonup }{\mu }}_{\text{loc}}|\text{cos}({\theta }_2)+c_3|{\stackrel{\rightharpoonup }{\mu }}_{\text{loc}}|\text{cos}({\theta }_3)+\dots$$ (3)

where θ_i is the angle between local mode i and the excitonic mode transition dipole orientation. Deviations of the local mode transition dipole orientations from the excitonic mode transition dipole orientation lead to larger values for |θ_i|, thus decreasing individual terms in the sum, and decreasing $|{\overrightarrow{\mu }}_{\alpha }|$.

Taking the ratio of the experimentally measured transition dipole strength to the known local mode transition dipole strength gives

$$\frac{|{\stackrel{\rightharpoonup }{\mu }}_{\alpha }|}{|{\stackrel{\rightharpoonup }{\mu }}_{\text{loc}}|}=c_1\text{cos}({\theta }_1)+c_2\text{cos}({\theta }_2)+c_3\text{cos}({\theta }_3)+\dots$$ (4)

The normalization condition for the eigenvector coefficients is that their squares must sum to 1.

In the approximation that the vibrational mode is equally delocalized over N residues (c = √N/N) and that each residue lies at the same relative orientation to the normal mode transition dipole direction:

$$\frac{|{\stackrel{\rightharpoonup }{\mu }}_{\alpha }|}{|{\stackrel{\rightharpoonup }{\mu }}_{\text{loc}}|}=\sqrt{N}\mathit{cos}(\theta )$$ (5)

Thus, in units proportional to the linear absorption coefficienct, $|{\overrightarrow{\mu }}_{\alpha }{|}^2$, we obtain a ratio proportional to N.

$$\frac{|{\stackrel{\rightharpoonup }{\mu }}_{\alpha }{|}^2}{|{\stackrel{\rightharpoonup }{\mu }}_{\text{loc}}{|}^2}=N{\text{cos}}^2(\theta )$$ (6)

From the ratio in eq 6, we see that our experimentally measured value for $|{\overrightarrow{\mu }}_{\alpha }{|}^2$, divided by the local mode extinction coefficient, provides a lower bound for N, since deviations of θ from zero cause cos²(θ) to decrease, decreasing the measured transition dipole strength. In the case where θ = 0, this ratio would be equal to N. We will return to this equation shortly to see how knowledge of a protein’s secondary structure can be used to obtain a more realistic estimate for N.

The IPR, on the other hand, does not depend on the relative orientations of the local modes.

$${\text{IPR}}_{\alpha }={({\displaystyle \sum }{U}_{\alpha ,j}{}^4)}^{-1}=\frac{1}{{\displaystyle \sum c_i{}^4}}$$ (7)

Making the same approximation as above regarding equal delocalization over N residues:

$${\text{IPR}}_{\alpha }=\frac{1}{N\ast {\left(\frac{\sqrt{N}}{N}\right)}^4}=\frac{1}{\left(\frac{N^3}{N^4}\right)}=N$$ (8)

Thus, within the approximations made above, by measuring the ratio of the excitonic extinction coefficient to the local mode extinction coefficient we obtain a lower bound for the IPR, or the number of residues over which the excitonic mode is delocalized.

The IPR can be calculated from the eigenvector coefficients, but the eigenvector cannot be uniquely reconstructed from the IPR. It is worth pointing out that the IPR does not take into account the vector nature of the local mode transition dipoles and their relative spatial orientation, which will thus affect their sum in eq 2 (and thus the experimentally measured transition dipole strength) but not the IPR in eq 7. This leads to a lower experimentally measured transition dipole strength than would be interpreted from accurate knowledge of the IPR. For this reason, the experimentally measured transition dipole strength has been considered to be an approximate lower bound for the number of residues over which the vibrational mode is delocalized by simply taking the ratio of the experimentally measured transition dipole strength to the known local mode transition dipole strength. For example, using this interpretation, our experimental measurement of $|\overrightarrow{\mu }{|}^2$ for a single sample of α-synuclein of 1.1 D² suggests delocalization of the vibrational exciton over at least 9 amide I groups. The experimentally measured value is also a lower bound because when calculating the transition dipole strength we assume that there is only one vibrational transition, whereas there are usually several unresolved transitions caused by end effects and disorder.^63,64 We can also make use of knowledge of the β-sheet structure to adjust our estimate of the IPR. The local mode transition dipoles in a β-sheet are oriented at approximately 25° relative to the A_⊥ mode excitonic transition dipole.²⁸ Thus, we could scale the ratio of measured ratio of transition dipole strength to local mode transition dipole strength by cos⁻²(25°) = 1.22 (per eq 6) to obtain a more structurally based estimate for N, which for the example above would increase our estimate of delocalization from 9 to 11 amide I groups.

Finally, we also note that the approximation of equal delocalization over N residues will not always hold, and our derivation of this simple rule relies on that approximation. The vibrational mode may, in fact, be delocalized over a much larger number of residues with unequal weighting coefficients. This situation will occur, for example, when residues have different local model frequencies, causing diagonal disorder. An example are the edges of β-sheets that will be hydrogen bonded to solvent instead of peptide amides, and thus have a different frequency. Nonetheless, approximating them all as identical should be a reasonable assumption; a recent study on liquid N-methylacetamide, for example, suggested delocalization of the amide I transition over 42 molecules, despite the disorder inherent to a liquid.⁶⁵ Because of these factors, the delocalization lengths estimated here should be considered lower bounds, and the inverse participation ratio is likely to be much larger.

Modeling Vibrational Spectra of Extended β-Sheet Structures

As mentioned above, the observations in Figure 3 regarding changes in transition dipole strength without an accompanying change in frequency were unexpected for a canonical β-sheet. To investigate the origin of this observation, we turned to computational simulations of vibrational spectra. Transition dipole coupling (TDC)^29–31 was used to calculate the coupling constants for ideal β-sheet structures, generating the amide I Hamiltonian, and nearest neighbor couplings were computed separately based on dihedral angles using the map developed by Jansen et al.⁶⁰ Figure 4a shows a structural model for an ideal β-sheet focusing on the atoms involved in the amide I transition. We denote a β-sheet composed of n amide I groups and M repeating strands as an M_n β-sheet. Thus, the Hamiltonian for a 5₁₀ β-sheet, for example, describes 50 amide I groups (5 strands each containing 10 amide I groups), and the one-exciton vibrational Hamiltonian used to calculate the amide I frequencies and corresponding transition dipole strengths for this system is a 50-by-50 matrix. In these simulations we do not introduce diagonal disorder, which might be caused by variations in electrostatic environment and interactions with the solvent, for example,^66–69 but the results are qualitatively similar when 10–25 cm⁻¹ of diagonal disorder included.

Figure 4.

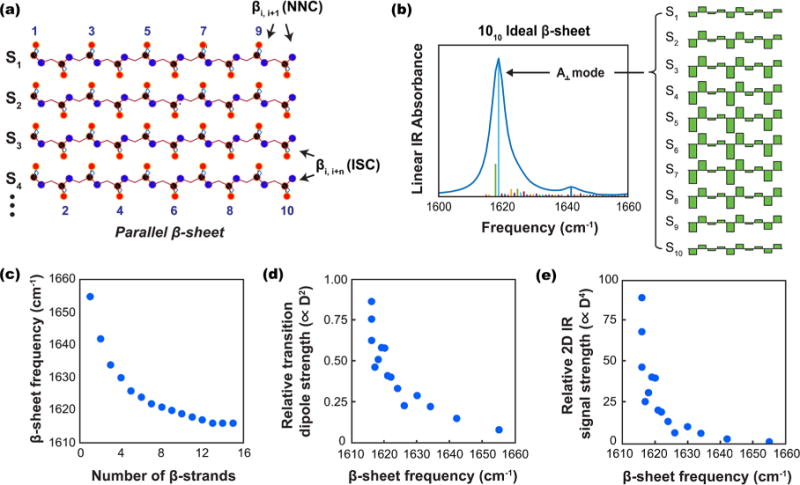
(a) Schematic structure of an ideal parallel β-sheet consisting of 10 amide I groups per strand, with strands indexed as S_n (red = oxygen, black = carbon, blue = nitrogen). (b) A linear IR spectrum and stick plot of the excitonic vibrational mode transition dipole magnitudes (proportional to $|\overrightarrow{\mu }{|}^2$) for a 10₁₀ parallel β-sheet vs frequency, along with a plot of the calculated eigenvector coefficients for the A_⊥ mode. (c) The calculated β-sheet frequency maximum vs number of β-sheet strands for a M₁₀ β-sheet (M = 1–15). (d) The relative transition dipole strength magnitude (proportional to $|\overrightarrow{\mu }{|}^2$) vs β-sheet frequency for the A_⊥ mode of a M₁₀ β-sheet (M = 1–15). (e) The relative 2D IR signal intensity (proportional to $|\overrightarrow{\mu }{|}^4$) for the A_⊥ mode of a M₁₀ β-sheet (M = 1–15).

We calculated vibrational spectra for various values of M_n, looking at changes in vibrational frequency and transition dipole strength as a function of the size of the β-sheet. In general, the most pronounced changes in frequency result from changes in the number of strands (M) rather than the number of residues in each strand. To select a relevant number of residues per strand, we considered structural models for amyloid fibers. Models of Aβ_1–40 indicate ∼6–12 residues being involved in each strand of the β-sheet (depending on the polymorph). Structural models for α-synuclein,⁴³ calcitonin,⁴⁴ and glucagon⁷⁰ also fall within this range. In Figure 4 we opted to use 10 residue β-sheets with varying numbers of strands, though we performed the same calculations with different values of n and the results are qualitatively and quantitatively similar. Lee and Cho have also previously reported that the number of residues included per strand did not have a significant effect on frequency.²³ The number of strands has a larger influence on the frequency than the number of residues per strands, because the couplings between residues on different strands is about 5-times larger than along a strand. Figure 4b shows an example of the linear IR spectrum calculated for a 10₁₀ parallel β-sheet along with an illustration of the eigenvector coefficients contributing to the A_⊥ vibrational mode. The eigenvector coefficients for the bright A_⊥ mode are in-phase for in-register residues from strand to strand, but out-of-phase for neighboring residues along each individual strand; this gives rise to a large oscillator strength oriented perpendicular to the individual strand orientations.

Figure 4c shows the effect of varying strand number for a M₁₀ β-sheet on the frequency of the A_⊥ mode (M varies from 1 to 15). Increases in M correlate with a red-shift in vibrational frequency. Note that the change in frequency with addition of successive strands decreases at higher values of M. Lee and Cho have previously described asymptotic behavior with regard to the splitting between A_⊥ and A_‖ modes in antiparallel β-sheets.²³ Figure 4d shows the calculated transition dipole strengths (proportional to $|\overrightarrow{\mu }{|}^2$) for the same values of M, and Figure 4e shows the calculated relative 2D IR signal strengths (proportional to $|\overrightarrow{\mu }{|}^4$) for the same values of M as a function of the A_⊥ frequency. Similar trends were observed when we repeated these calculations using an ideal model for antiparallel β-sheets, as well as when the number of residues per strand was varied (Figure S1). Experimentally, differences in hydration may cause shifts of a few wavenumbers in the local mode frequencies in different regions of the sheets, shifting the overall frequency slightly,⁷¹ but the overall trends we observe would remain.

It has been previously established that lower frequencies correlate to the number of strands in a β-sheet,^21,23 a conclusion that is consistent with spectra of soluble proteins containing β-sheets with between ca. 1–11 strands per sheet.¹⁷ Amyloid β-sheets are different, because they are highly extended β-sheet networks with hundreds if not thousands of strands in each fiber. Thus, while the edges of β-sheets in soluble proteins may confine delocalization and thereby the frequency, vibrational delocalization in amyloids can be constrained by the width of β-sheets but not the number of strands. The simulations in Figure 4c suggest that the frequency becomes less sensitive to the number of strands above ca. 15 strands, as the frequency approaches an asymptote. As mentioned above, the transition frequency is still sensitive to the number of strands in native proteins up to at least 11 strands, indicating delocalization over at least this many strands based on experimental observations.¹⁷ There are also structural differences between the β-sheets of amyloids and soluble proteins, with soluble proteins having curvature that deviates from the structure of a canonical β-sheet. To explore these factors for amyloid β-sheets, we predict the vibrational couplings between individual amide I oscillators that would be most responsible for shifting the excitonic transition frequencies away from the local mode frequency. In β-sheets, in-register interstrand couplings (henceforth denoted ISCs)¹⁵ and nearest neighbor couplings (NNCs)⁶¹ are two of the most important coupling parameters. ISCs for in-register residues in successive strands tend to be large and negative, causing a redshift in frequency for the A_⊥ mode. NNCs are smaller in magnitude, and positive values for NNCs give rise to a red-shift in frequency for the A_⊥ mode. Other couplings also influence the vibrational spectrum of the excitonic amide I transition, though we focus on these two here in the interest of developing a conceptually straightforward model for understanding our experimental observations.

The detailed atomic structure of most amyloid fibers are not known, and those that are known come from solid state NMR constraints with uncertainties too large to rely on for quantitative analysis of vibrational couplings. Multiple polymorphs also typically form in a single sample.^72,73 A detailed assignment of structure is not possible based solely on the observed amide I frequency due to the large range of potential structural changes that can give rise to the same frequency. For these reasons, we elected to use crystal structures of amyloid-forming protein fragments to estimate the values of ISCs and NNCs present in amyloid fibers, since these structures provide the highest resolution atomic structures available, and thus should provide the most realistic atomic-level structural models for amyloids, although they may represent only a subset of allowed strand and dihedral geometries. ISCs were computed using the transition dipole coupling model, while NNCs were computed based on the dihedral angles from the crystal structures using the map developed by Jansen et al.⁶⁰

Figure 5 shows histograms describing the distributions computed for NNC and ISC values for four representative structures that span the range of NNC and ISC values observed in the crystal structure models, along with the mean values computed for each structure. Histograms for additional structures are shown in the SI. Many of the crystal structures reported for amyloid fragments only contain a single strand; these were not considered in our analysis since they do not allow ISC values to be computed. Overall we observe a variation in the average NNC coupling of ∼3.4 cm⁻¹ and a variation of ∼3.2 cm⁻¹ in the average ISC coupling. We expect these to serve as lower bounds for the amount of variation observed in actual amyloids for several reasons. First, the crystal structures are of amyloid fragments; actual amyloids are formed from larger proteins and would therefore be expected to have more structural variation. Second, the crystal structures only contain two strands, which are used to compute the ISC values; increasing the number of strands in the model would also be expected to lead to more structural variation and thus more variation in the ISC values. Third, there are only a limited number of structures available, and knowledge of additional crystal structures could only serve to expand the total range of average NNC and ISC values observed.

Figure 5.

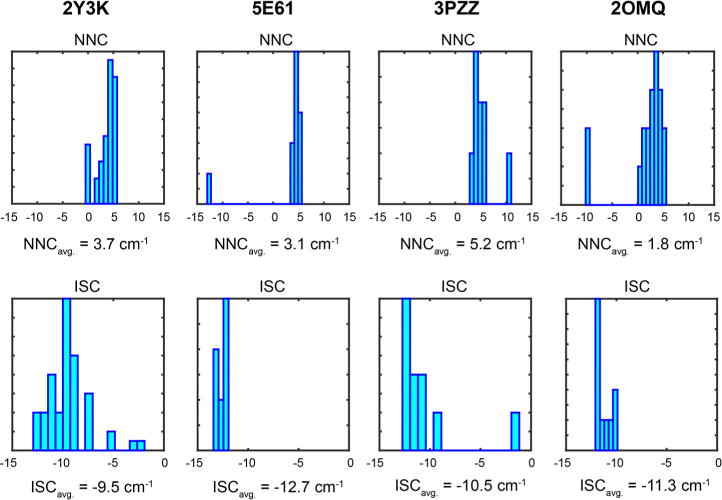
Histograms and mean values for nearest neighbor coupling constants and interstrand coupling constants computed for crystal structures of amyloid fragments in the PDB. Structure 2Y3K corresponds to Aβ_35–42, 5E61 to amylin_23–29, 3PZZ to Aβ_29–34, and 2OMQ corresponds to insulin chain B_12–17.

We used the range of mean NNC and ISC values determined from the crystal structures in a model amide I Hamiltonian to investigate the role of variation in NNCs and ISCs in establishing the frequency and transition dipole strength of the A_⊥ mode in extended β-sheets like those found in amyloid fibers. As mentioned above, more positive NNCs will lead to a red shift in frequency, as will more negative ISCs. For a fixed value of the NNC or ISC across all residues in the Hamiltonian, denoted β_NNC and β_ISC, the change in the A_⊥ frequency will scale approximately as −2*β_NNC + 2*β_ISC. For changes in the value of β_NNC or β_ISC, the shift in frequency Δν will scale as −2*Δβ_NNC + 2*Δβ_ISC. Thus, changes of 3 cm⁻¹ in the value of β_NNC and changes of 3 cm⁻¹ in the value of β_ISC can give rise to a range of 12 cm⁻¹ of observed values for the A_⊥ transition frequency.

We began by computing the one-exciton amide I Hamiltonian and corresponding local mode transition dipole vectors for an ideal parallel β-sheet using TDC. We substituted into the Hamiltonian a range of fixed values for NNCs and ISCs corresponding to values within the range of average NNCs and ISCs computed in crystal structures (2 to 5 cm⁻¹ for NNCs, and −12.5 to −9.5 for ISCs). Variation in the NNCs or ISCs produces a change in the frequency of the A_⊥ transition without an accompanying change in transition dipole strength. Diagonal disorder would serve to broaden the spectra and range of frequencies observed by diminishing the effects of couplings. Here we do not include diagonal disorder to better illustrate the effects of the structurally related NNCs and ISCs parallel β-sheet in which the ISCs and NNCs have been replaced with different fixed values for β_NNC and β_ISC. As is evident, the transition frequency shifts with changes in the ISC and NNC values, with little effect on the transition dipole strength. Thus, a frequency shift for the A_⊥ mode that is independent of transition dipole strength can be explained by changes in the magnitude of the ISCs and NNCs.

To generate the spectra in Figure 6a, we set all of the ISCs and NNCs to the same value. As we observed in our analysis of crystal structures in Figure 5 (and Figure S2), the ISCs and NNCs take on a distribution of values in a single structure. These variations in couplings correspond physically to variations in interstrand spacings, offsets between residues in neighboring strands, variations in dihedral angles along the strands, and the relative orientations of the amide I oscillators. Accordingly, we generated Hamiltonians with variation in the ISC and NNC values spanning a range similar to what is observed in the histograms computed from crystal structures. Figure 6b shows a scatter plot of the A_⊥ transition dipole strengths and center frequencies for the same average ISC and NNC values above in Figure 6a. Variation in the off-diagonal couplings, creating off-diagonal disorder in the Hamiltonian, gives rise to a range of transition dipole strengths all centered at the same frequency, similar to what we observed experimentally (Figure 3). The units on the y-axis of Figure 6b span a roughly 2-fold range of transition dipole strengths, similar to what is observed experimentally; these are scaled to the maximum calculated value as the simulations tend to delocalize over more residues than what is observed experimentally.

Figure 6.

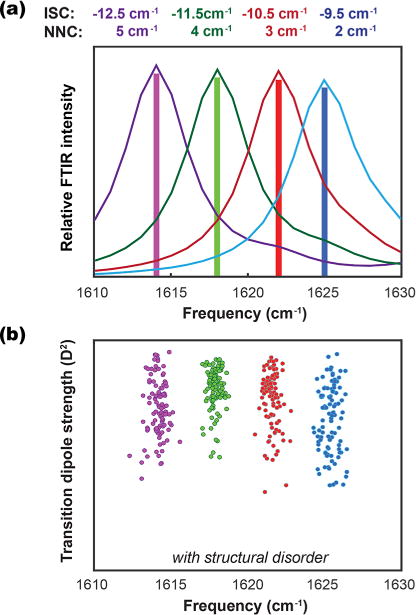
(a) Linear IR spectra for an ideal 10₁₀ β-sheet computed by manually varying the ISC and NNC values in the Hamiltonian to the fixed values indicated. (b) A scatter plot of transition dipole strengths and frequency maxima for the A_⊥ mode computed when variation about the average values from the above panel is introduced, representing structural disorder in the amyloid β-sheet.

As we saw from our analysis of the crystal structures, the variation in average values and from site-to-site in our model Hamiltonian is physically reasonable even in small crystal structure amyloid fragments. Vibrational couplings are sensitive to even subtle changes in structure. For example, transition dipole coupling predicts a 1/r³ dependence on the magnitude of the coupling constant for changes in the distance between the amide I modes. Thus, a change in distance of only 0.25 Å between amide I modes, independent of changes in orientation gives rise to a 3.5 cm⁻¹ change in ISC values. For the crystal structures examined, a range of 0.45 Å was found for the average nearest in-register neighbor (i.e. on adjacent strands) distances. The relative orientations of the amide I modes also lead to changes in coupling for both the ISCs and NNCs. For the NNCs, the map of Jansen et al. predicts a range of NNC values spanning approximately −12 to 12 cm⁻¹ for dihedral angles consistent with β-sheet structure, with the majority of NNCs centered at small positive or negative values for highly ordered β-sheets. As a result, we conclude that the natural variation of amyloid β-sheet structures, from the crystallographic structures measured to date, can account for both the observed (average) frequency for any given amyloid protein as well as off-diagonal disorder that leads to a loss of correlation between transition dipoles strengths and frequency.

SUMMARY AND CONCLUSIONS

We measured the transition dipole strengths of the A_⊥ amide I transition for aggregated samples of several amyloidogenic proteins. For a given protein, we observe a range of transition dipole strengths centered at the same amide I transition frequency maximum. Among the different proteins studied, we observe roughly the same range of transition dipole strengths, despite each protein having a different A_⊥ transition frequency. These observations cannot both be explained by modeling of canonical β-sheets. By modeling the spectra using couplings computed from crystallographic structures of amyloid peptide fragments, we conclude that the measured frequency of the A_⊥ transition in an amyloid fiber is set by the average magnitude of vibrational couplings. Variation in the ISCs and NNCs about their average values causes variation in the transition dipole strength without appreciable changes in frequency. For soluble proteins with a native fold containing β-sheets, the number of β-strands tends to correlate with a lower frequency absorption for the A_⊥ transition.¹⁷ Our results indicate that this trend does not hold for amyloid β-sheets. The vibrational modes of amyloid fibers extend over at least a dozen strands, indicating that delocalization occurs to such an extent that the β-sheet absorption reaches its asymptotic limit with regard to the influence of strand number. Hence, the vibrational frequency of an amyloid fiber is not significantly influenced by the number of β-strands available for delocalization, but is strongly determined by the couplings within the β-sheet. Vibrational couplings vary strongly with dihedral angles along the β-strands, interstrand spacings (perhaps mediated by side-chains), offsets between successive strands, and the relative orientations of the amide I groups. Thus, the amyloid frequency is very sensitive to amyloid β-sheet structure.

Knowledge of the transition dipole strength will also be useful for determining the concentrations of proteins in biological samples. Since the transition dipole strengths of proteins are often unknown, it is typically not possible to quantify even the relative quantities of random coil, native β-sheet, and amyloid β-sheet present in a sample. This will be particularly important in more complex samples, such as tissue. For example, a recent study used transition dipole strengths to estimate amyloid formation in the tissues of pigs, providing evidence that cataract formation may be an amyloid disease.⁷⁴ Transition dipole strengths can also be useful for determining secondary structure in congested regions of the spectrum where multiple secondary structures can absorb at the same frequency (e.g., random coil vs. α helix). With knowledge of both the transition dipole strength and frequency, secondary structures can be assigned with much higher confidence.²⁵ This method can also be applied to kinetically evolving samples, such as proteins that are in the process of folding, aggregating, or undergoing denaturation, and to monitor changes in transition dipole strength as a function of time. Indeed, oligomeric intermediates are thought to have different structures from amyloid fibers and so by kinetically measuring transition dipole strengths it might be possible to better observe oligomer formation.