Nonparametric dynamic modeling

Abstract

Challenging as it typically is, the estimation of parameter values seems to be an unavoidable step in the design and implementation of any dynamic model. Here, we demonstrate that it is possible to set up, diagnose, and simulate dynamic models without the need to estimate parameter values, if the situation is favorable. Specifically, it is possible to establish nonparametric models for nonlinear compartment models, including metabolic pathway models, if sufficiently many high-quality time series data are available that describe the biological phenomenon under investigation in an appropriate and representative manner. The proposed nonparametric strategy is a variant of the method of Dynamic Flux Estimation (DFE), which permits the estimation of numerical flux profiles from metabolic time series data. However, instead of attempting to formulate these numerical profiles as explicit functions and to optimize their parameter values, as it is done in DFE, the metabolite and flux profiles are used here directly as a scaffold for a library from which values are interpolated and retrieved for the simulation of the differential equations describing the model. Beyond simulations, the proposed methods render it possible to determine steady states from non-steady state data, perform sensitivity analyses, and estimate the Jacobian of the system at a steady state.

1. Introduction

Ever since the digital revolution drove analog computing to the brink of extinction, the design of computational models for complex systems has become an effort in choosing optimal mathematical representations and their parameter values. For most physical and engineering systems, the choice of model functions is directly guided by our rather solid understanding of basic physical concepts, such as mechanical or electrical forces, dilution and dispersion phenomena, optical processes, and the features of electric circuits. Biological systems are, of course, objects of the physical world and must therefore obey the laws of physics, but most processes that govern even moderately sized biological systems are so convoluted that they cannot be dissected into elementary physical representations [1]. As an example, the transmission of a neuronal signal at a dopamine synapse requires electrical activation, the prior biochemical production of dopamine and its packaging into membrane vesicles, the move of these vesicles through the crowded cytoplasm toward the synapse, the merging of vesicle and cell membranes, the opening of this membrane toward the synapse, the release of dopamine out of the vesicle and through the synaptic cleft to a receptor on the postsynaptic neuron, possible interactions with other neurotransmitters, and binding to the receptor. This binding in turn triggers a slew of additional mechanisms inside the signal receiving cell, including the complex process of signal interpretation which in the case of dopamine is often accomplished through multiple phosphorylation of the specific protein DARPP32, and the possible long-term adaptation to repeated stimuli [2–5]. Thus, a very coarse model could easily capture the fact that a signal moved from one neuron to another, but a detailed mechanistic model becomes quickly bogged down in the minutiae of the numerous intertwined biophysical processes that are involved in signal transduction.

Because elementary physical descriptions are often infeasible, the biological systems modeler is forced to resort to “higher-order” process representations, ad hoc models, suitable approximations, or combinations thereof. A good example is the Michaelis–Menten function of enzyme kinetics [6]. Its underlying concept is a process that postulates the reversible formation of a biochemical complex between an enzyme and its substrate and the subsequent release of the product of the reaction and of the enzyme, which is used over and over again. Under idealistic conditions in vitro, this concept is believed to be quite realistic. However, within living cells, the prerequisites for the involved mass-action functions are clearly not satisfied, and the so-called quasi-steady-state assumption, which is needed to formulate the process with a simple, explicit function, only holds under certain conditions. Thus, an idealized concept, formulated with the help of somewhat doubtful approximations, becomes a higher-order process representation for enzyme catalyzed reactions. Indeed, the Michaelis–Menten function performs well in vitro and, in an approximate sense, presumably in vivo, although this is not really known. For simulations of large pathway systems, this function is often used as well, but its mathematical features become rather cumbersome, even for standard model assessments such as sensitivity analyses [7].

Notwithstanding these mathematical issues, it is common for the biological modeling community to base simulation studies in a variety of fields on a rather small set of functions, which are used time and again and prominently include mass-action, Michaelis–Menten and Hill functions, which often include regulatory terms [8]. The users of these functions rely on the argument that these functions suit their purposes—quasi as black boxes—and are sufficiently accurate if one considers the typical noise encountered in biological data. Furthermore, these particular functions at least have some foundation and rationale in biology, whereas the use of a function like a shifted arctangent has very little justification, except that its graph is s-shaped and therefore might resemble some saturation processes in biology.

True alternatives to these ad hoc approaches are generic approximations. Linearization, the simplest of these, has been enjoying enormous successes in engineering applications for many decades. For the representation of biological phenomena, by contrast, linear models tend to run into conflicts with the genuine nonlinearities that characterize living systems. For instance, common features like saturation, stable oscillations, threshold phenomena, synergisms, or chaos cannot directly be modeled with linear equations. A logical solution might seem to be the expansion of linear models to second-order Taylor approximations, but these become so awkward for larger systems [9] that very few modelers have resorted to this option. Instead, many biological modeling groups have been using power-law approximations, which are nonlinear, but have linear characteristics in logarithmic space. Biochemical Systems Theory (BST; [10–13]) and Metabolic Control Analysis (MCA; [14–17]), which directly or indirectly utilize power-law representations [18,19], respectively, have had success with analyses of a wide variety of complex biological systems (for a review, see [20]). Notwithstanding their successes, power-law representations are local approximations and therefore genuinely limited in their accuracy of capturing phenomena over large ranges of variation in the involved variables. As a case in point, univariate power-law functions in BST do not saturate for large substrate concentrations, and lin-log models, which are associated with MCA, become negative for small substrate concentrations and tend toward −∞ for substrate concentrations approaching 0 [21–23]. As an alternative to these canonical power-law models, one could use sigmoidal basis functions, but for realistic models this option requires correspondingly larger numbers of parameters that need to be estimated [24,25].

Even if reasonable guideposts could be found to justify the choice of appropriate model representations, the second step of model identification is still to be performed, namely the estimation of parameter values. For moderately sized or large models, this estimation is always challenging [26–28], due to noise in the data, non-convergence of the search algorithm and other problems, or because the wrong model was chosen after all. To make matters worse, even an excellent fit is not necessarily optimal, and the parameterized model may perform poorly in extrapolations, because the original fit was obscuring the compensation of errors among some terms within the model (e.g., see [29,30]). Furthermore, an excellent fit may be the result of overfitting with a model containing too many parameters.

These challenges and compromises lead to the obvious question of whether it might be possible to glean appropriate functions directly from experimental biological data, without presupposing potentially unjustified mathematical formats. The method of Dynamic Flux Estimation (DFE), which permits a relatively unbiased estimation of fluxes within a system and which will be reviewed later, took a first step toward answering this question affirmatively, at least for metabolic systems under ideal conditions [31]. Still, DFE requires some choices of model frameworks when the task is setting up a model from scratch.

In this paper, we describe a novel variant of DFE that makes such choices unnecessary, at least under favorable conditions. Given such conditions, the overall result of the proposed strategy is that it is possible to develop dynamic models in a nonparametric manner. Intriguingly, the resulting nonparametric models, which make no assumptions regarding parameter values or even mathematical formats, beyond the topology of the system, permit most of the typical diagnoses and analyses that are possible with a fully parametric model, which may be considered the gold standard in the field. As a consequence, simulations and other analyses can be performed without the complicated and often biased step of choosing models and parameterizing them, if suitable data are available. The data needed for this purpose consist of sets of time series that representatively capture the dynamics of a system under relevant inputs.

Both DFE and the nonparametric variant proposed here are particularly well suited for nonlinear, dynamic, regulated compartment models, because these possess the property of mass conservation, which imposes strong, unbiased constraints that greatly aid the formulation of appropriate models. As an illustration, and for ease of discussion, we will focus here on metabolic pathway systems, but it appears that other nonlinear compartment systems, such as SIR models of epidemiology and pharmacokinetic models, can be treated in the same manner.

2. Methods

2.1. Dynamic flux estimation (DFE)

The stoichiometric equation

$$\dot{\mathbf{X}}=\mathbf{S}·\mathbf{V}$$ (1)

provides a generic description of the dynamics of a metabolic pathway system. This well-known equation collectively formulates dynamic changes in each metabolite of the system, $\frac{\mathit{\text{dX}}}{\mathit{\text{dt}}}=\dot{X}$, as a product between the stoichiometric matrix S and a vector of reactions or fluxes, V. This product formulation is remarkable, as it naturally separates the linear aspects of the system from its nonlinear features. Specifically, consider the situation where the slopes of all metabolites on the left-hand sides are known for some given time point. If so, Eq. (1) is a system of linear algebraic equations, where each variable V_j represents the state of a flux at this time point, rather than a metabolite. The nonlinear features enter the system secondarily, by virtue of the fact that each component of the flux vector is a possibly complicated function of metabolites and regulators, and therefore of time. Dynamic Flux Estimation (DFE) makes maximal use of this separation of the model into linear and nonlinear components.

In typical analyses, such as Flux Balance Analysis, the stoichiometric Eq. (1) is studied at a steady state of the system [32–34], where the vector on the left-hand side contains zeros. DFE reaches beyond the steady state, by addressing the system at many time points of a system’s trajectory, where the vector of derivatives is different from zero. In its first phase, DFE uses time series measurements of metabolite concentrations, X₁, …, X_n, along with estimates of the slopes of these time courses. Thus, DFE evaluates equations of the type

$$\frac{{\mathit{\text{dX}}}_i}{\mathit{\text{dt}}}\text{ at }{t}_k=\text{Slope of }{X}_i\text{ at }{t}_k=\sum _{j=1}^m{s}_{i,j}{V}_j(t_k)$$ (2)

where the slopes are numerical values, estimated from the data. Since data are typically noisy or incomplete, it is advisable to apply one of various available preprocessing, smoothing and data substitution techniques (e.g., [35–38]). We do not discuss these further in this paper, because data smoothing techniques and the methods proposed here constitute clearly distinct steps within the model design procedure. Thus, we will assume in the following that the data had been successfully smoothed.

The slope substitution is performed for m time points, with the result that each differential equation in (1) is replaced with a set of m linear algebraic equations at these time points. Collectively, these equations may be formulated as a matrix equation, where the variables are the fluxes V_j, rather than the metabolites [39–42]. If this matrix has full rank, the solution is unique, and if the equations are overdetermined, the best-fitting solution is computed via linear regression. In the most common case, the system is underdetermined. We will briefly skip this case here, but return to it later. The result of solving the linear equations is a set of numerical flux values at each time point. Collecting these sets for all time points it is straightforward to create a plot of each flux as a function of time. It is furthermore possible to plot each flux against the system variables upon which it depends. In the case of a single substrate and no regulation, the plot is a simple line graph. By the same token, if the flux depends on two or more variables, the result is a line on the manifold that is given by the unknown flux function in three or more dimensions. This first phase of DFE typically requires knowledge of the connectivity of the system. However, it is to some degree possible to infer formerly unknown reaction steps and regulatory signals [43,44] (Fig. 1).

Fig. 1. Dynamic Flux Estimation (DFE).

The method consists of two phases. Phase 1 (top) is model free in a sense that only the stoichiometry is assumed to be known, whereas functional forms of the process representations are not. The procedure in this phase is based on raw experimental time series data in the form of metabolite concentrations. It is beneficial to smooth these data with some numerical algorithm, such as a spline. Next, the rate of change in each metabolite is obtained from the smoothed time courses. These numerical slopes correspond to the values on the left-hand side of Eq. (2), so that numerical evaluation of the slopes at m time points converts each differential equation of the model into a set of m linear algebraic equations, in which the flux states are the driving variables. The system is solved, potentially with the aid of additional constraints, and the result is a time dependent, numerical profile of all fluxes. In Phase 2 (bottom), the dynamic flux profiles are fitted with appropriate functions or rate laws, and the result is a fully parameterized dynamic model.

In Phase 2 of DFE, the numerical flux representations are converted into mathematical functions. For this purpose, assumptions must be made regarding the functional format of each flux. In some cases, the shape of the flux profile or independent biological considerations may suggest a mathematical format, but this is not guaranteed (Fig. 2). Once a format has been chosen, the parameters of each flux representation are to be estimated from the available data, as it is typical for any other modeling effort. This estimation is much simpler than for the entire system, because it is performed for a single explicit function at a time, rather than simultaneously for all fluxes in the system of ODEs. The result of the two phases combined is a fully parameterized model of the pathway system.

Fig. 2. Typical results of Phase 1 of DFE.

The flux in panel A may be representable with a Michaelis–Menten function. By contrast, it might be difficult to choose appropriate formats for the fluxes in panels B and C.

It is not directly possible to solve the linear system when the stoichiometric matrix is underdetermined. Unfortunately, this is actually the most common case for metabolic systems, which typically contain more reactions than metabolite pools. In the case of an underdetermined system, the stoichiometric equation admits infinitely many solutions, and these can differ tremendously, even if the system is small, with some having monotonic shapes, while others may overshoot or exhibit oscillations [45]. To study these sets of solutions, it is advisable to reduce the system mathematically to a system whose dimension equals the degrees of freedom [45]; for instance, in a system with six metabolites and eight reactions, the dimension will typically be two.

A solution to the challenge of under-determination is the Moore–Penrose pseudoinverse [46–48]. While effective, the pseudoinverse usually contains negative values, which are not consistent with biological fluxes. Several other approaches have been proposed. First, characterizability analysis, based on the pseudoinverse, shows directly where additional information is needed about the system, or which metabolite pools could be merged, to make the equations uniquely solvable [49]. Second, it is sometimes possible to measure influxes or effluxes experimentally or to infer them from the data [43,44]. Third, it might be feasible to obtain additional biological information regarding some of the internal fluxes. For instance, one might be able to deduce internal fluxes from biochemical features of the involved metabolites [50]. Fourth, one may use the dynamic concentration profile associated with one metabolite to estimate flux functions for its influx and efflux [51]. This procedure requires assumptions regarding the functional forms of these fluxes, but if the variable does not change much in magnitude, an approximate representation is likely to be sufficient. Fifth, sufficiently many datasets may allow the inference of a few flux profiles directly from the data [52]. Finally, it might be possible to utilize biological constraints, such as energy minimization, to reduce the degrees of freedom within the system [45].

If independent information regarding a flux can be found, the system of equations becomes simpler. For instance, suppose that flux V₃ is known in sufficient detail. Then, Eq. (2) becomes

$$\frac{{\mathit{\text{dX}}}_i}{\mathit{\text{dt}}}-s_{i,3}·V_3=\sum _{j=1,j\ne 3}^m{s}_{i,j}{V}_j,$$ (3)

where the left-hand side is numerically known and the number of free degrees is typically reduced by 1.

2.2. Concepts of nonparametric dynamic modeling

Overview

The core idea of nonparametric modeling is to forgo Phase 2 of DFE and instead to replace the functional representations of the processes in the system with a library of numerical results directly obtained from Phase 1 of DFE. Of course, nothing comes for free: The proposed substitution requires good, comprehensive data. While such datasets may currently be scarce, the decreasing cost of generating rich datasets renders the proposed method increasingly more appealing.

Thus, let us suppose that rich data are available, where “richness” refers to more or less complete datasets and enough time series to represent the phenomenon under investigation appropriately. For instance, one could imagine sets of time series experiments with many combinations of different input and inhibitor concentrations. Collectively these datasets form the scaffold for the proposed modeling strategy. One should note that even a rich dataset rarely produces complete coverage of the imaginable metabolic profile space. One reason is that most metabolic systems have a single non-trivial steady state and that trajectories even from a variety of initial values tend to approach this steady state, so that many regions of the mathematically imaginable solution space are only scarcely covered or not at all. While this situation may seem to be undesirable, it actually reflects those portions of the metabolic profile space that are most relevant and reliably represented, while ignoring situations that may be biologically less relevant. Fig. 3 shows a generic example where the trajectories approach a common steady state.

Fig. 3. Illustrative example for scaffolding the library with different datasets.

The green surface is the graph of the unknown flux function V(x, y). Each white line represents the result of a time series experiment. All time series approach the same steady state (yellow) so that many regions of the surface, such as the top right, are not supported by measurements and may be biologically irrelevant. Thus, the set of time series results may be sufficient to interpolate between the data (white lines) but does not allow reliable extrapolations far beyond the data. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

For metabolic pathway systems and many other compartment models, the topology of the underlying network of components is typically known, or assumed to be known. It is also often, although not always, known which metabolites affect each flux as substrates or modulators. Nonparametric modeling takes advantage of this situation. It directly uses Eq. (2), where the stoichiometric coefficients are assumed to be given and where the flux states are the dependent variables on the right-hand sides. In contrast to parametric modeling, the explicit functions on the right-hand sides of the differential equations are here replaced with numerical flux descriptions. Thus, no mathematical formalism is used to represent the fluxes and hence no parameterization is needed. Instead, the numerical flux-substrate profiles are generated directly from the smoothed experimental data processed in Phase 1 of DFE and recorded in a library that is subsequently used for looking up values required by the ODE solver. As a result, the library, combined with an interpolation algorithm, constitutes the primary simulation tool for analyses with the nonparametric model (Fig. 4). Expressed differently, the processes of making functional assumptions and of parameterizing these functions are replaced by the use of a scaffolding library and geometric interpolations, once dynamic flux profiles have been obtained. The details of setting up the library and of the interpolation algorithm are discussed in the next sections.

Fig. 4. Nonparametric modeling framework.

Functional assumptions and the parameterization of fluxes are circumvented in nonparametric modeling. Instead, the flux values needed at each step of a system simulation are provided by look-up tables that are generated from the measured dynamic metabolite profiles and the inferred flux profiles. They are stored in a library for call-up.

Library construction

Phase 1 of DFE results in dynamic flux profiles that can be displayed against time or against the systems variables that affect the flux. Combining the smoothed metabolic time series and flux profiles, flux-substrate relationships are generated and recorded as arrays in which the columns contain values of substrates and regulatory agents that affect each flux, as well as the corresponding flux value itself. The rows represent snapshots of the state of the system at various time points and possibly from different experiments (Fig. 5). To ensure sufficient scaffolding of the flux-substrate subspace, each array should ideally include the dynamic profile of a flux for several experimental settings, for instance, with different initial conditions.

Fig. 5. Generic format of the flux library.

The data are arranged in arrays where the columns represent a specific flux along with all substrate(s) and regulator(s) that affect this flux directly. The rows represent snapshots of the state of the system for different time points and experiments. The specific numerical values shown here refer to the later example of a fermentation pathway but are not of import here.

Of course, the quality of further analyses and simulations depends on the quality of the library, which in turn depends on the quality of the available data. It is difficult to quantify how many data have to be available, as this quantity depends on the complexity of the flux functions. For example, oscillatory data will often require more data points than smooth monotonic data for a good representation of the true time trend. Thus, one can only pose a vague criterion that must be satisfied: the data must be representative of the trends they quantify.

In theory, every metabolite could be involved in every flux of the system, thereby causing an unmanageable combinatorial explosion for larger systems. In practice, this situation does not arise, and most metabolites are only affected by a few other metabolites.

Interpolation algorithm

To be useful, the nonparametric model must permit simulations of the evolution of the modeled system over time. The model is formally specified as a set of ODEs whose right-hand sides are defined by fluxes whose values are stored in the libraries described before. By its nature, each ODE solver needs to have flux values available for essentially arbitrary substrate and modulator amounts within reasonable ranges, which are, for instance, bounded by the experimental datasets. In the case of nonparametric modeling, the library consists of a discrete set of values, which covers only a finite subset of all values that are possibly needed. To overcome this issue, a method is needed that allows the ODE solver quickly to estimate each required flux value from the data in the library. Obviously, the quality of this type of gap-filling is directly correlated with the density and quality of the data in the library.

A convenient tool for this task is the function scatteredInterpolant in MATLAB (version R2014a, The MathWorks, Natick, MA), which is applied to the smoothed data obtained from DFE. This function generates 2D or 3D interpolations from the dataset in the library in an unbiased manner. Specifically, the interpolant passes through the original data and uses adjustable methods such as linear or nearest-neighbor interpolation, which enable the algorithm to estimate flux values for arbitrary substrate and modulator values during the ODE simulation.

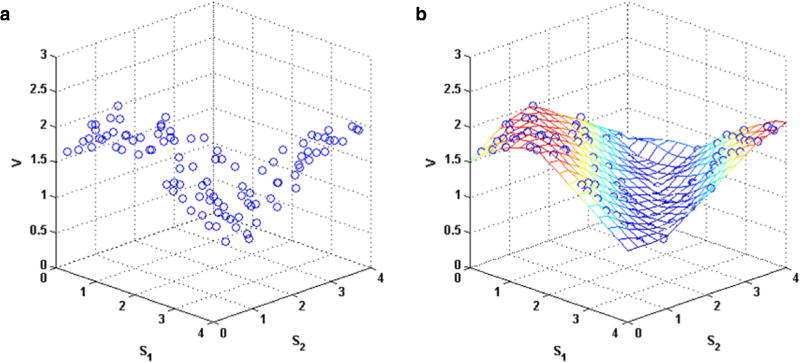
For our demonstration of the concepts of nonparametric modeling with fluxes of two or three arguments, we used the linear interpolation method. For fluxes with a single substrate and no regulators, the function interp1 was preferred, as it is more efficient for one-dimensional interpolations. Fig. 6 presents some output from this interpolation algorithm. Panel (a) exhibits data points for a flux V that depends on two substrates S₁ and S₂. Panel (b) visualizes the interpolated surface over a grid of inputs.

Fig. 6. Interpolation of a flux-versus-substrate surface for two substrates.

The algorithm uses an interpolant function that efficiently connects the data points. Panel (a) shows the raw data points, while panel (b) shows the interpolated surface.

Preliminary studies indicate that the interpolation, under favorable conditions, can generate sufficiently accurate libraries even for data that had not been smoothed. Indeed, skipping the smoothing step may lead to means of assessing the effects of intrinsic noise in the data. For instance, single data points or subsets could be removed from the library in Monte-Carlo simulations, thereby ultimately yielding distributions of slightly different trajectories and steady states. This option will be addressed elsewhere. It also remains to be more formally investigated under what conditions the chosen interpolation algorithm is optimal for the tasks discussed here or whether different, specifically customized interpolation methods might perform better.

Expanded data coverage by moderate extrapolation

Parametric models may typically be extrapolated without bounds. However, one must ask to what degree such extrapolations beyond the domain of experimental data are really justified. In our situation of nonparametric modeling, the interpolating function in MATLAB is able to extrapolate datasets to some degree. However, the accuracy of extrapolation is only guaranteed for relatively small ranges in the vicinity of the scaffolding data subspace. While the lack of far-reaching extrapolations may be seen as a disadvantage over parametric models, it also provides a healthy warning against extrapolations that are not supported by data and might even be biologically infeasible. We used the nearest-neighbor variant of the interpolation technique in MATLAB for extrapolations. An example will be shown later.

Library-based simulations

The flow of a typical simulation with a nonparametric model is illustrated in Fig. 7. Starting from an arbitrary initial state, within or sufficiently near the recorded flux-substrate subspace, the library, together with the interpolation algorithm, provides for each set of metabolites the appropriate flux values V_i. The flux values are then used to compute changes in the substrates, $\frac{d\mathbf{X}}{\mathit{\text{dt}}}$, using Eq. (1). These changes are utilized to compute the state of the system at the next time point; the base concept of this procedure is shown in Eq. (4).

$${\mathbf{X}}_{\tau +\mathrm{\Delta }t}\approx {\mathbf{X}}_{\tau }+\frac{d{\mathbf{X}}_{\tau }}{\mathit{\text{dt}}}·\mathrm{\Delta }t,$$ (4)

where $\frac{d{\mathbf{X}}_{\tau }}{\mathit{\text{dt}}}$ represents the collection of appropriate flux values at time τ. While Eq. (4) demonstrates the solution procedure with Euler’s forward method, modern ODE solvers employ more sophisticated methods, some of which are expansions of Euler’s method. Specifically, the standard ODE solver in MATLAB (version R2014a, The MathWorks, Natick, MA) uses the Runge–Kutta method with variable step size. In contrast to supplying the ODE solver with the parametric functions on the right-hand sides of the ODEs, as it is commonly done, we specify the appropriate interpolants from the library. This substitution does not affect the computation speed much.

Fig. 7. Flowchart for a typical nonparametric simulation.

Once initial conditions are specified, the algorithm extracts from the library the flux values that correspond to the metabolite profile at the initial time point. From these values, the algorithm computes the slopes of all variables and moves the simulation to the next time step, according to Eq. (4), until the desired final time point T_F is reached.

2.3. Typical model analyses

Analyses with the nonparametric model are primarily based on simulations. The simplest of these are changes in initial values of one or more of the dependent variables. Similarly easy to assess are changes in independent variables, which are often used to model constant quantities like an enzyme activity or a fixed input. As an example, suppose that some experimental technique raises the activity of an enzyme, which results in a concomitant 20% increase in the corresponding flux by. An analogous parametric situation would be a 20% raise in the V_max of a Michaelis–Menten or Hill rate law. In the nonparametric case, such an alteration is simply implemented by increasing all pertinent flux values in the library by 20%. The analogous strategy holds for an external inhibitor, as long as it decreases one or more fluxes in a multiplicative manner. A change in K_m corresponds to a different scale for the substrate concentration. For example, if K_m is to be doubled, an appropriate solution is to double the substrate concentrations in the library without changing the corresponding flux values. To see the rationale for this strategy, consider the standard Michaelis–Menten rate law, $V=\frac{V_{\mathit{\text{max}}}S}{K_m+S}$. If K_m is doubled, the same functional values of V are achieved if each value of S is doubled.

To some degree, it is even possible to perform analyses that at first seem to require functional forms. For instance, once a steady state has been identified, one may use the plots of each flux against each contributing variable and determine the slope(s) of the flux at the steady-state metabolite concentration. Entering all slopes into an appropriately laid-out array yields an approximate Jacobian matrix, which may then be used for numerical analyses characterizing the model behavior close to the steady state and, in particular, the stability of the steady state. We will discuss this option, as well as sensitivity analysis, within the context of the case study in the Results section.

Of course, the nonparametric model cannot entirely replace its parametric analog. For instance, it seems difficult to perform formal investigations of bifurcations and other features of complex dynamics, at least in a direct manner.

3. Results

3.1. Case study: nonparametric modeling of the fermentation pathway in yeast

To illustrate the nonparametric modeling capabilities without being encumbered by the idiosyncrasies of experimental datasets, we created artificial “data” from a model in the literature. This model describes in a simplified manner the anaerobic fermentation pathway in the baker’s yeast Saccharomyces cerevisiae. The pathway is comparatively well understood, and a considerable body of in vivo measurements of metabolites and fluxes at various steady-states is available [53]. This model was originally proposed by Galazzo and Bailey [54] and subsequently converted into a power-law model by Curto et al. [55–57] ; it has been used on numerous occasions to demonstrate new modeling and optimization techniques [58–63].

For the illustration here, we use Curto’s version of the model to generate datasets, which under typical conditions would have been obtained experimentally in the laboratory. We analyze the data without noise. Thus, we pretend that metabolic time courses had been measured and used in DFE to reveal plots of all fluxes versus time or versus the system variables that affect them. The system contains only a rather small number of metabolites and fluxes, which renders it a good candidate for illustration purposes.

The model captures the dynamics of the fermentation pathway from glucose uptake to ethanol yield (Fig. 8). The pathway has essentially a linear structure, although two minor pathways branch off. It is regulated through negative feedback from glucose-6-phosphate (G6P) on glucose uptake and feedforward activation of the enzyme pyruvate kinase by fructose-1,6-bisphosphate (FBP).

Fig. 8. Anaerobic fermentation pathway in Saccharomyces cerevisiae.

The model of the pathway contains five dependent variables and eight fluxes.

The independent variables and fluxes in the model (see Fig. 8) are as follows:

X1 : Glucose(Glc)	V1 : Vin	V5 : VGAPD
X2 : Glucose – 6 – phosphate(G6P)	V2 : VHK	V6 : VGOL
X3 : Fructose – 1, 6 – bisphosphate(FBP)	V3 : VPFK	V7 : VPK
X4 : Phosphoenolpyruvate(PEP)	V4 : VPOL	V8 : VATPase
X5 : ATP

Fig. 9 shows the model scheme in a simplified fashion; although regulation is not explicitly shown, it is taken into account by the model. One notes that flux V₅ splits a 6-carbon molecule into two 3-carbon molecules, which causes a doubled rate of influx into the pools of X₄ and X₅, and mandates corresponding elements of 2 in the stoichiometric matrix (Eq. 5).

$$\mathbf{S}=\left[\begin{array}{cccccccc}\hfill 1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill -1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill -1\hfill & \hfill 2\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill -1\hfill \end{array}\right]$$ (5)

Fig. 9.

Model scheme of the fermentation model.

The stoichiometric equation of the system, Ẋ = SV, is equivalent to the set of differential equations in Eq. (6).

$${\dot{X}}_1=V_1(X_2)-V_2(X_1,X_5)$$

$${\dot{X}}_2=V_2(X_1,X_5)-V_3(X_2,X_5)-V_4(X_2)$$

$${\dot{X}}_3=V_3(X_2,X_5)-V_5(X_3,X_5)-V_6(X_3,X_4,X_5)$$

$${\dot{X}}_4=2V_5(X_3,X_5)-V_7(X_3,X_4,X_5)$$

$${\dot{X}}_5=V_7(X_3,X_4,X_5)+2V_5(X_3,X_5)-V_2(X_1,X_5)-V_3(X_2,X_5)-V_4(X_2)-V_8(X_5)$$ (6)

The model has a stable steady state with concentration values, in [mM], Glc = 0.03456, G6P = 1.011, FBP = 9.188, PEP = 0.009532, and ATP = 1.128 [56].

3.1.1. Library for the fermentation model

In an actual systems analysis, experimental time series data would be used to populate the library. Instead, we use the Curto model and solve it multiple times, every time starting from different initial states of all metabolites. These states are located in a hypercube in ℝ⁵ that corresponds to the five substrates represented in the pathway model. Of course, experimental data would be noisy. For clarity, we consider noise-free or well-smoothed data.

The collective result consists of time series data of the substrate concentrations and corresponding fluxes, which in reality would have been obtained from DFE. In addition to time plots, the data allow us to establish flux-versus-substrate trajectories, whose values are recorded in arrays, as it was illustrated in Fig. 5. Fig. 10 shows examples of trajectories for the fermentation model. In all figures, the metabolite concentrations are in millimolar (mM), and all fluxes are in millimolar per unit of time (mM/min).

Fig. 10. Flux-substrate profiles corresponding to different initial conditions.

The dynamics of the system forms trajectories that are recorded and used in the form of look-up tables that substitute for explicit mathematical representations of the fluxes. The panels represent the different fluxes. For each panel, metabolite trajectories from different experiments are shown in different colors. Panel (a) shows V_in, V_POL and V_ATPase, which are single-substrate fluxes. Panels (b), (c) and (d) exhibit V_HK, V_PFK and V_GAPD respectively. These three fluxes have two substrates each. Lastly, panel (e) shows substrate trajectories for V_PK. This flux has three substrates so that the flux-substrate trajectory is four-dimensional. For this reason, only the substrate trajectory is shown. According to Curto et al. [55], the flux V_GOL is proportional to V_PK with a proportionality constant of about 0.03 and therefore not shown.

3.1.2. Dynamic simulations

Once the library is set up from the artificial data, the nonparametric model is ready to use. Fig. 11 confirms with simulation results that the nonparametric model returns essentially the same results for three distinct initial conditions as a parametric simulation with Curto’s model. For comparison, the nonparametric results (lines) are superimposed on the “data” (parametric results).

Fig. 11. Nonparametric and parametric simulations of the fermentation pathway.

Three different initial conditions were used; the results are shown in different colors. All simulations converge to the same steady state: Glc: 0.03456, G6P: 1.011, FBP: 9.188, PEP: 0.009532, ATP: 1.128. The initial conditions are: green: [0.0657 1.213 12.86 0.0086 1.410]; blue: [0.0518 0.6066 5.513 0.0148 0.6203]; red: [0.0207 1.820 17.46 0.0052 2.199]. The nonparametric simulation results (solid line) match the artificial data (circles) very closely. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

3.1.3. Jacobian at the steady-state

The library permits the estimation of the Jacobian of the system. Namely, once a steady-state metabolite profile has been determined, one estimates the slopes of the fluxes at this profile with respect to the various variables. The slopes of each flux, $\frac{d\mathit{V}}{{\mathit{\text{dX}}}_i}$, are computed numerically, using the flux values at the steady-state, V(X_i), and the flux values at points in the vicinity of the steady-state, V(X_i + ΔX_i). Using Eq. (1), the flux slopes together yield $\frac{d\dot{\mathbf{X}}}{{\mathit{\text{dX}}}_i}$. The quantities $\frac{d\dot{\mathbf{X}}}{{\mathit{\text{dX}}}_i}$ of all system variables constitute the elements of the Jacobian matrix. The most prominent use of the Jacobian is the determination of eigenvalues for local stability analysis. This analysis is directly comparable with the corresponding analysis of a linearized parametric model.

For the fermentation pathway, the eigenvalues of the nonparametric model at the steady-state are [−1734.0, −333.5, −14.04 ±7.581i, −1.635]. For comparison, the corresponding analysis for the parametric model yields quite similar eigenvalues: [−1689.0, −341.1, −13.66 ±7.853i, −1.843].

3.1.4. Sensitivity analysis

An important component of modeling is sensitivity and gain analysis. In the former case, a parameter is slightly altered and corresponding changes in critical system features are recorded. In the latter case, an independent variable is altered. Most prominent is the effect of changes in parameters or independent variables on the steady-state values of the system. While the nonparametric model obviously has no parameters, it is still possible to study sensitivities if one of the fluxes is either raised or decreased by a small percentage, which mimics a situation where the activity of an enzyme is altered. The results of such an analysis are shown in Fig. 12. As one would expect, the system reaches a new steady-state, which depends on the specific flux alteration. Comparisons with Curto’s model demonstrate that the nonparametric model matches the corresponding analytical results from the parametric model very well.

Fig. 12. Sensitivity analysis.

Each of the fluxes was separately perturbed by ±10% for the entire duration of each simulation. With each change in a flux, the simulation starts from the original steady state of the system and moves toward the new steady state. For all the flux perturbations other than V_POL and V_GOL (not shown here because they are insensitive), the system converges to new steady-states. The nonparametric model results (solid lines) closely match the parametric results (circles). One should note different scales for the five variables.

Fig. 13 exhibits simulation results representing the case where the K_m of an enzyme is altered. To mimic an increase in a K_m, more substrate is needed to compensate for the same flux magnitude. As was explained earlier, for example, doubling the K_m of a reaction corresponds to replacing the substrate concentration S with S/2 in the library. As can be seen, the steady-states take new values. Specifically, the substrate of the enzyme with altered K_m shows an increased steady-state value in each row. Again, the nonparametric and parametric model results agree quite closely.

Fig. 13. Trajectories and steady-states of the system for enzymes with altered K_m.

The system dynamics was replaced such that fluxes depict enzymes with increased K_m values. Each row represents simulation results for a flux catalyzed by an enzyme with an altered K_m, where the corresponding substrates respectively from top are: [Glc, G6P, FBP, PEP, ATP]. Each flux was modified to mimic a two-fold increase in K_m. Only V_ATPase was simulated for a 30% increase, because larger perturbations lead to instabilities in the parametric and nonparametric models. V_POL and V_GOL did not show any noticeable changes in steady-states and hence are not shown in here. Solid lines show the nonparametric results, while circles represent parametric results from Curto’s model.

3.2. Data collection from a bolus experiment

Model set-up

To test the nonparametric approach under more realistic circumstances, we used the Curto model to simulate an in vivo nuclear magnetic resonance experiment, which typically uses a bolus input rather than a constant substrate influx (for a pertinent example, see [64]).

In the original Curto model, the input flux of the system, V₁, is constant and set to simulate a saturated flux that corresponds to an exterior glucose concentration in excess. To model the transient dynamics of a bolus experiment, we converted external glucose into a dependent variable X₀, thereby expanding the system by one ODE:

$${\dot{X}}_0=-0.01V_1$$ (7)

The coefficient 0.01 reflects the compensation between the concentration within the large exterior volume of the medium and the much smaller interior volume of the cells. This coefficient quantifies how much a change in the external glucose concentration (e.g., from 4 mM to 3.99 mM) affects the internal glucose concentration (from 0 to 1 mM). For the uptake function, we use a Michaelis–Menten function with allosteric, noncompetitive inhibition, where the inhibitor, G6P, reduces the overall activity of the enzyme. This choice was based on the original article which considered the inhibition as not competitive, because G6P binds to the glucose transporter inside the cell while glucose binds on the outside [53]. Thus, we have

$$V_1=\frac{V_{\text{max}}{X}_0}{K_m+X_0}{(1+\frac{X_2}{K_I})}^{-1},$$ (8)

with K_m =4 mM [65]. V_max and K_I were retrieved from Curto’s model as about 16 and 394, respectively. With the exception of these two adaptations, the modified model is the same as in Eq. (6) and the pathway diagram is the same as in Fig. 9, where the input arrow now originates at X₀.

Commensurate with the K_m value for V₁, we used the modified Curto model to perform experiments with three different bolus amounts, where the initial values corresponded to a concentration of half the K_m, twice the K_m, and close to saturation, respectively. The results are shown in Fig. 14. Panel (a) corresponds to a bolus of exterior glucose resulting in an external initial concentration of 2 mM. In panel (b) the initial concentration is 8 mM, and in panel (c) it is 60 mM. In each panel, the left plot shows the dynamic metabolite profiles, while the right plot shows the dynamic flux profiles, which in a real experiment would have been inferred per DFE. In all cases, the input V_in initially causes the interior glucose concentration to rise, and this rise migrates throughout the pathway. The plots on the right side show how V_in and other fluxes start to decline once the exterior glucose becomes depleted. Correspondingly, each metabolite accumulates until the efflux from its pool becomes larger than the influx to the pool, due to the decline in exterior glucose. Eventually all metabolites become consumed and approach zero concentration.

Fig. 14. Simulation results for bolus experiments with different external glucose concentrations.

The time courses capture the transient behavior of the system very clearly. The left column exhibits concentration profiles, while the right column shows flux profiles. Amount of glucose bolus: Panel a: 2 mM; panel b: 8 mM; panel c: 60 mM.

The three experiments allow us to plot flux-versus-substrate trajectories (Fig. 15). Panels (a), (b), (c) and (e) correspond to V_in, V_HK, V_PFK and V_GAPD respectively. Panel (d) shows the trajectories for V_POL and V_ATPase, both of which are single-substrate fluxes with two-dimensional trajectories. Naturally, the trajectories converge since each flux value is a function of a substrate and the substrates approach steady state. In a bolus experiment however, the system only converges to a trivial steady-state. Panel (f) only shows the substrate trajectories since the flux-versus-substrate trajectories for V_PK are entities in a four-dimensional space.

Fig. 15. Flux-versus-substrate trajectories retrieved from the bolus experiment results.

The three experiments lead to different trajectories, which are shown in different colors.

Library construction

We took the simulation results of the three bolus experiments as artificial metabolite and flux data and used them to construct the library. The MATLAB function scatteredInterpolant (Fig. 6) provided a fast and effective interpolation for the data. Two examples of resulting surfaces are shown for V_in and V_HK in Fig. 16 (a) and (b), respectively. Panels (c) and (d) show the flux-versus-substrate surfaces with moderate extrapolations beyond the boundaries of the dataset.

Fig. 16. Interpolation and extrapolation of flux-versus-substrate surfaces.

Panels (a) and (b) exhibit how the interpolations provide approximations for desired values not included in the library. The algorithm can also provide approximate values slightly outside the dataset boundaries. The quality of this extrapolation often declines with the distance from the boundary (panels (c) and (d)).

Steady-state simulation

We simulated the system for a constant concentration of exterior glucose within the ranges recorded in the library. This experiment is fundamentally different from the bolus experiments that were used to stock the library. The results are shown in Fig. 17 for one of the fixed glucose inputs. Three different sets of initial conditions for the dependent variables were simulated, and the system converged to the same steady-state for all three. This steady state is essentially identical to that of Curto’s model if the same glucose input is simulated.

Fig. 17. Steady-state simulation results based on data from bolus experiments.

Although the data in the library were obtained from bolus experiments, the nonparametric simulation results for constant glucose inputs are very similar to their parametric analogues. Three different initial conditions were chosen, and the system was simulated for a constant exterior glucose concentration of 40 mM.

Computation of a steady-state

The computation of steady states is of great import, as most biological systems operate within the vicinity of a normal homeostatic state. For the case of parametric models, some structures, including linear systems, S-systems [66] and Lotka–Volterra systems (e.g., [67]), permit the algebraic calculation of steady-state solutions, while most other nonlinear systems require search algorithms.

Interestingly, the nonparametric model permits not only simulations toward a stable steady state, but even the option of direct computational assessments of steady states. In fact, the flux-versus-substrate library appears to be as effective as an explicit functional form. Here, we applied the MATLAB function fsolve to the task at hand. Similar to the traditional case involving explicit ODEs, fsolve starts from a given initial condition and at each iteration estimates the system derivatives using system equations and the library. These are used to determine the direction and size of the next step toward optimizing the objective function. It turned out that fsolve is quite sensitive to initial guesses. We therefore randomly sampled 10,000 initial conditions from the space of metabolite concentrations in the library, ran fsolve, and recorded the solutions that achieved zero derivatives within a reasonable tolerance. Fig. 18 compares the computed steady-states (blue circles) with the true steady-state from the parametric model (yellow circles). The left panel exhibits the metabolites, while the right panel shows the corresponding steady-state flux values.

Fig. 18. Steady-state metabolite and flux values.

The yellow circles show the true solutions for the constant input V_in = 8, according to Curto’s model, while the blue dots exhibit the ensemble of computed nonparametric solutions, which resulted from different initial values in fsolve.

4. Discussion

The term “nonparametric” is currently used almost exclusively within the context of statistics, where nonparametric tests are sometimes preferred to their parametric analogues because they require fewer assumptions and are often simpler to execute, although they are not always as discerning as parametric tests [68]. It is impossible to date the first use of nonparametric statistical methods, as standard features like histograms and sample means do not require a priori choices of parameters and have been used for a very long time. The terminology itself was apparently introduced by Wolfowitz in 1942 to characterize those methods that did not require specialized assumptions regarding the functional forms of the distributions characterizing the populations from which samples were analyzed [69,70]. As an alternative to “nonparametric,” some authors proposed the term “distribution-free,” while Ury suggested “assumption-freer” or ISD (incompletely specified distribution) statistics, openly admitting, however, that neither term was “especially felicitous” [71].

Notwithstanding the terminology, the statistics community at the time was of course not unanimously welcoming and initially considered nonparametric methods as “short cuts for well-established parametric methods” and later as “rough and ready (quick and dirty), inefficient methods, … that were wasteful of information” [70,72]. In today’s view, the advantages and drawbacks appear to have found a healthy equilibrium, and nonparametric methods are considered true alternatives to more traditional parametric methods, because they make less stringent demands on the data and sometimes reveal quick, although possibly coarser answers with a lesser amount of calculation. It is even possible that nonparametric methods utilize more information in large datasets, especially if the data do not stem from processes that have well-parameterized representations. Then again, by their very nature, nonparametric methods do not involve parameters that permit succinct descriptions, and they sometimes throw away information to a point where, for instance, differences between two populations can no longer be quantified [73]. It is also openly acknowledged that the interpretation of nonparametric statistical methods is sometimes difficult [74]. Overall, nonparametric methods are recognized as sometimes useful and maybe necessary, and on occasion superior, but certainly not perfect.

Similar to nonparametric models in statistics, the nonparametric dynamic models proposed here do not sweepingly solve all problems in nonlinear compartment modeling. In fact, one could say that they have similar advantages and drawbacks. They use fewer assumptions regarding mathematical formats, which immediately implies that these models cannot be described or compared succinctly with a set of parameter values. Similarly, they may be more difficult to interpret. They do not throw away information, however. For instance, if an appropriate format of a flux with correct kinetic parameter values is known from some outside source, this information can easily be used to reduce the degrees of freedom or to replace a unique analytical solution with a regression solution, which one might expect to be more robust. At any rate, the method and its solutions depend on the quantity and quality of available data, thus yielding a situation that is not genuinely different from parametric models.

Similar to parametric models that are obtained with DFE, the models here require solvability of the linear system of fluxes in the ODE model. This solvability issue can be assessed using the topology of the pathway through characterizability analysis, even in the absence of specific data [49]. Non-characterizable pathways incur estimation issues no matter what methods are applied, because such pathways admit entire spaces of solutions, some of which differ drastically from others [45]. In this situation, the DFE approach offers the advantage of identifying whether any, and if so which, fluxes can be determined uniquely, or what additional information would remedy the situation. For instance, Iwata and colleagues [51] demonstrated that it is possible to estimate a few fluxes with traditional methods and thereby to make a DFE solution unique. Similarly, it was shown that reasonable biological constraints may be able to ameliorate or even solve the under-determinedness of a pathway system [45]. The same arguments apply to our nonparametric approach, although the infusion of additional information may result in a hybrid model where some fluxes are parameterized and others are not.

Not long ago, the experimental characterization of metabolic time courses was considered a very difficult task, and metabolic time series data—and corresponding models—were extremely rare [75]. This situation has changed dramatically during the past decade, and various methods of molecular biology have rendered it feasible to generate time series data with reasonable effort (e.g., [76–79]). This type of data generation is crucial here, because the construction of nonparametric models depends on a data scaffold, from which a library of nonparametric flux representations can be established.

In contrast to metabolite concentrations, fluxes of a pathway system are presently difficult to measure, except possibly for influxes and effluxes that communicate with the exterior milieu. However, in analogy to the progress in time series measurements of concentrations, one might hope that flux measurements will follow in due time; e.g., see [80]. Indeed, if it becomes more widely known that a limited set of flux measurements may lead to a complete pathway characterization that does not make mathematical assumptions beyond the stoichiometry of the system, the community of molecular biologists may devote concerted effort toward such measurements in the future.

In addition to the difficulties of obtaining the right data, one could argue that experimental data often cover only a relatively small subspace of what an explicit mathematical function would be able to represent. This argument is certainly true, but one must ask to what degree extrapolations with these functions far outside the data domain are justifiable and biologically relevant.

Once experimental concentration and flux measurements become more readily available, the nonparametric method proposed here may actually become preferable over the tried and true approaches of parametric pathway modeling, at least for initial, unbiased assessments and various types of simulation studies. For deeper analyses, such as formal bifurcation studies, it appears that parametric representations will be difficult to replace. In this case, DFE may be executed to the end, where parametric functions are selected based on the inferred flux profiles.