Stochastic Community Assembly: Does It Matter in Microbial Ecology?

SUMMARY

Understanding the mechanisms controlling community diversity, functions, succession, and biogeography is a central, but poorly understood, topic in ecology, particularly in microbial ecology. Although stochastic processes are believed to play nonnegligible roles in shaping community structure, their importance relative to deterministic processes is hotly debated. The importance of ecological stochasticity in shaping microbial community structure is far less appreciated. Some of the main reasons for such heavy debates are the difficulty in defining stochasticity and the diverse methods used for delineating stochasticity. Here, we provide a critical review and synthesis of data from the most recent studies on stochastic community assembly in microbial ecology. We then describe both stochastic and deterministic components embedded in various ecological processes, including selection, dispersal, diversification, and drift. We also describe different approaches for inferring stochasticity from observational diversity patterns and highlight experimental approaches for delineating ecological stochasticity in microbial communities. In addition, we highlight research challenges, gaps, and future directions for microbial community assembly research.

INTRODUCTION

Biodiversity, a measure of the variety of life found on Earth (1, 2), is a central topic in ecology and for society, because the dramatic loss in biodiversity could alter the functions and services provided by ecosystems (3, 4). Since the last century, various facets of biodiversity have been intensively examined across space, time, and ecological gradients from different perspectives (e.g., taxonomic, phylogenetic, and functional diversity). Various fundamental biodiversity patterns have been observed in ecology, e.g., latitudinal diversity patterns (5–9), species abundance distributions (SADs) (10–12), species-area relationships (SARs) (13–16), distance-decay relationships (17–20), and species-time relationships (19, 21–25). However, the mechanisms and factors controlling such diversity patterns remain unclear and highly controversial. Traditional niche-based theory hypothesizes that deterministic factors such as species traits, interspecies interactions (e.g., competition, predation, mutualisms, and trade-offs), and environmental conditions (e.g., pH, temperature, salt, and moisture) govern community structure, which are often referred to as deterministic processes (26, 27). In contrast, neutral theory assumes that community structures are independent of species traits and governed by stochastic processes of birth, death, colonization, extinction, and speciation (28, 29). Although, recently, it has been generally accepted that both deterministic and stochastic processes occur simultaneously in the assembly of local communities (30–33), a central debate is on their relative importance in controlling community structure, succession, and biogeography (34–37).

Microorganisms are the most diverse group of life on Earth, inhabiting almost every imaginable environment (38). Although it is well known that microbial biodiversity is extremely high (12, 39–43), why and how such high diversity is generated and maintained are long-standing puzzles to microbiologists. Various deterministic factors, such as changes in environmental conditions (44–48), habitat conditions in hosts (49, 50), carbon and nutrient resource heterogeneity (40, 51), species traits and/or interspecies interactions (52–54), and plant diversity (55–60), are important in governing microbial community structure. However, they are alone not sufficient to explain the extremely high diversity of microbial communities observed in nature. Numerous studies (e.g., 13, 14, 61–63) revealed that substantial amounts of variation in microbial community structure could not be explained by environmental and/or distance effects despite extensive measurements of all routinely measured environmental variables. It is believed that in many cases, considerable amounts of the microbial community variation observed could result from stochastic processes of community assembly through historical contingency (e.g., priority effects), ecological drift, and/or dispersal limitation (29, 31, 32, 35, 36, 62, 64–66). However, the importance of stochastic processes in controlling microbial biodiversity has been recognized only in some recent studies (33, 35, 36, 67, 68). Partly due to the small organism size, vast diversity of microbial communities, and uncultivated status for the majority of microorganisms, the mechanisms underlying microbial community structure, succession, and biogeography are much less understood in general, compared to the ecology of macroorganisms (35).

Along with the rapid advance and application of large-scale high-throughput metagenomics technologies in the last decade (69), mechanisms underlying microbial community assembly have received great attention, especially within the last several years, with more emphasis on stochasticity (Fig. 1). While some great insights have been obtained, divergent controversial results have been reported (e.g., see references 32, 36, 64, 70, and 71). Several recent reviews/analyses have provided an excellent overview of the ecological processes controlling microbial community structure and biogeographic patterns in general (72, 73). However, a critical review on the importance of ecological stochasticity in governing microbial community structure and biogeographic patterns is lacking. Thus, to complement previous analyses, here, we focus primarily on the review and synthesis of most recent findings from studies of ecological stochasticity in microbial ecology. We first provide a historical overview of both the theoretical and empirical studies examining stochasticity, as well as determinism, in ecology. We describe the stochastic and/or deterministic components embedded in ecological processes, including selection, dispersal, diversification, and drift, with emphasis on microorganisms. Next, we describe different approaches for inferring stochasticity from observational diversity patterns in general by not being limited to microbial studies. In addition, we highlight experimental approaches for examining the importance of stochasticity in microbial ecology. Finally, we point out several research directions in microbial community assembly research.

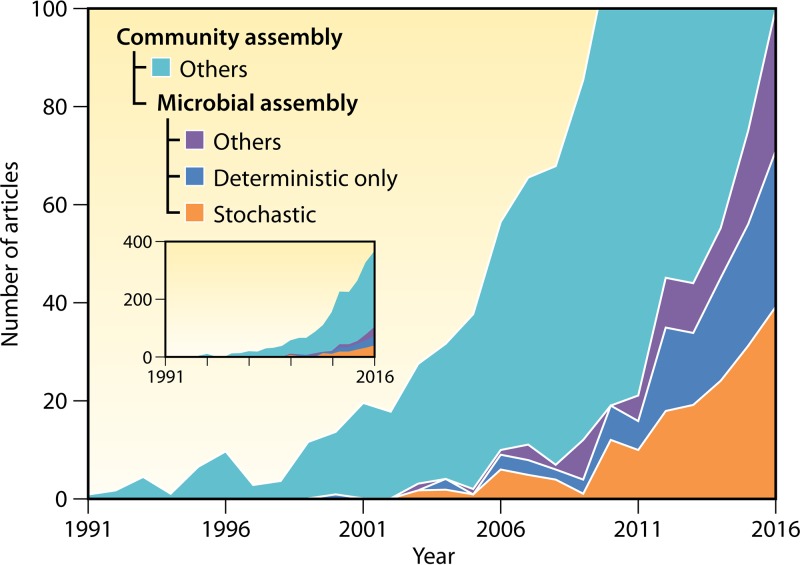
FIG 1.

Trends in studying community assembly mechanisms. The data shown are based on the annual number of articles on community assembly (any organisms, including microorganisms [inset]), articles on microbial community assembly, articles about only deterministic microbial assembly, and articles involving stochastic microbial assembly. We searched articles from 1990 to 2016 in the Web of Science Core Collection database on 10 January 2017. To find articles on “community assembly,” we searched by topic = “community assembly” and Indexes = SCI-EXPANDED and ESCI. To find articles on “microbial assembly,” we searched by topic = (microbi* or bacteri* or fungi or fungus or fungal or archaea* or protist or metazoa* or mycorrhiza) in addition to “community assembly.” For articles on “stochastic,” we searched by topic = (neutral or stochast* or dispersal or migration or immigration or (priority effect) or (historical contingency) or drift or diversification or speciation) in articles on “microbial assembly.” For articles on “deterministic only,” we searched by topic = (niche or deterministic or selection or filtering or competiti* or facilitati* or mutualism or predation or interaction) in articles on “microbial assembly,” except for those related to “stochastic.”

STOCHASTICITY VERSUS DETERMINISM: HISTORICAL OVERVIEW

Historically, much of traditional ecology has been built on niche concepts and theory. The basic assumption of niche theory is that species differ in their niches, which are sets of biotic and abiotic conditions under which species can persist (74, 75). Species niches are determined by their traits that enable them to obtain resources, evade enemies, and survive under various adverse environmental conditions (30). Species often show trade-offs (i.e., the benefits of performing one ecological function well comes at a cost of performing another function) (76), which allow them to coexist within communities for long periods of time (26, 77). Niche-based theory asserts that deterministic processes largely control the patterns of community structure. In general, a deterministic process is any ecological process that involves nonrandom, niche-based mechanisms (Table 1), including environmental filtering and various biological interactions (e.g., competition, facilitation, mutualisms, and predation) (30, 31, 35, 62). Over the last 100 years, niche concepts have been instrumental in the development of deterministic ecological theories and widely used in the fields of community ecology, biogeography, and evolutionary ecology (30, 75, 78–85).

TABLE 1.

Key terminology related to community assembly used in this review

Term	Definition	Reference(s)
Community assembly	Process by which species colonize and interact to establish and maintain local communities via sequential repeated immigration from the regional species pool	46, 99
Ecological stochasticity	Random changes in community structure with respect to species identities and/or functional traits due to stochastic processes of birth, death, immigration and emigration, spatiotemporal variation, and/or historical contingency (e.g., colonization order)	90–92
Selection	Major niche-based process that shapes community structure due to fitness differences (e.g., survival, growth, and reproduction) among different organisms, including effects of abiotic conditions (environmental filtering) and biotic interactions (e.g., competition, facilitation, mutualism, predation, and host filtering, etc.)	59, 94
Homogeneous selection	Selection under homogeneous abiotic and biotic environmental conditions leading to more-similar structures among communities	95
Heterogeneous selection	Selection under heterogeneous abiotic and biotic environmental conditions leading to more-dissimilar structures among communities; also called variable selection	95
Dispersal	Movement and successful colonization (establishment) of an individual organism from one location to another via both active and passive mechanisms	62
Priority effects	The organisms that arrive first at a location have negative or positive impacts on organisms that arrive later	98, 99
Homogenizing dispersal	Very high rate of dispersal among communities, which homogenizes the communities such that their structures are very similar	95, 96
Dispersal limitation	Movement of individuals to and/or establishment of individuals (colonization) in a new location is restricted, leading to more-dissimilar structures among communities	95, 96
Diversification	Evolutionary process of generating new genetic variants, which is a balance between speciation and extinction	59, 94, 109
Drift	Random changes, with respect to species identity, in the relative abundances of different species within a community over time due to the inherent stochastic processes of birth, death, and reproduction	28, 59, 94

Although the niche is one of the most important fundamental concepts in ecology, niche-based theory faces several grand challenges in explaining patterns of community structure. First, a niche is inherently highly dimensional (86). Defining the dimensions of a niche is an insurmountable task (30, 87). Second, niche-based theories focus primarily on trade-offs (e.g., see references 76, 88, and 89) to explain species abundance and distribution. If niche differences are observed among different species, there must be trade-offs among species to allow them to coexist. However, very limited evidence is available to support the assumption that niche differences cause trade-offs among species and, hence, influence stable species coexistences (30, 90). In addition, some nonrandom patterns of species distributions in space and time are consistent with predictions from non-niche-based stochastic processes (29, 91, 92). Thus, some key components/predictions of niche theory remain untested and therefore questionable. Since the mid-20th century, the niche paradigm has been directly challenged by neutral theory (29, 93, 94).

Neutral theory assumes that all species (e.g., see reference 95) or individuals (e.g., see reference 29) are ecologically functionally equivalent, and species dynamics are controlled by stochastic processes but not by the differences in their competitive abilities (28, 29, 95, 96). In contrast to deterministic processes, here, stochastic processes are referred to as ecological processes that generate community diversity patterns indistinguishable from those generated by random chance alone. These processes typically include probabilistic dispersal (e.g., random chance for colonization), random speciation and extinction, and ecological drift (e.g., random changes in organism abundance) (29, 30, 35, 62, 67) (Table 1). Neutral theory challenges the two fundamental concepts of niche theory: all species/individuals are ecologically and functionally different, and environments play important roles in governing species abundance and distribution (11, 97). Despite this extreme assumption of the ecological equivalence of all individuals, neutral theory successfully predicted, even better than niche theory, some fundamental ecological patterns of numerous communities, such as species abundance distributions and species-area relationships (11, 29, 74, 92, 98), suggesting that stochastic processes could play more important roles than species functional differences in generating community patterns (99).

Although neutral theory is attractive because of its surprising simplicity and tractability (93), neutral theory has been hotly debated since its publication because it challenges some foundational concepts in traditional ecological research (11). First, the assumption that all species are functionally equivalent (92, 98) is highly controversial because nothing is neutral in the real world (93). Second, the parameters in some neutral models are extremely difficult to estimate (11). In addition, it is difficult to infer underlying processes from diversity patterns (e.g., species abundance patterns) because different processes (or assumptions) can yield very similar, or even the same, diversity patterns (11, 74, 93). Therefore, if an observed pattern fit the neutral model (or null model) expectation, in principle, we could not reject the importance of deterministic processes unless we ensure that a deterministic process(es) could not generate the same or a similar pattern. Despite various heavy criticisms, neutral theory is still widely accepted as a valuable null hypothesis or approximation for developing new ecological theories and examining community assembly mechanisms (11, 93).

After intensive debates on niche versus neutral processes, researchers have now realized that both niche and neutral processes are not mutually exclusive. Instead, both processes are complementary and work together simultaneously in structuring communities (33, 74, 92, 98, 100, 101). Based on this perspective, various theoretical models considering both deterministic and stochastic processes have been developed (74, 89, 92, 102). However, the emerging consensus of a continuum from determinism to stochasticity was recently questioned by Clark and colleagues (86, 103), who argued that stochasticity could occur only in mathematical models and not in nature and thus can only stand in for unknown processes (34, 86). Nevertheless, some components of community changes (e.g., stochastic birth and death) are irreducibly stochastic, and thus, the hypothesis of a continuum from determinism to stochasticity is testable (34).

DEFINING ECOLOGICAL STOCHASTICITY

While it is important to unify niche and neutral perspectives on governing community structure, it is challenging to do so, partially due to the different meanings of stochasticity used in the literature, including environmental, demographic, genetic, ecological, compositional, and neutral stochasticity (34, 35, 104–106). Based on the standard dictionary definition, a process is considered stochastic (or random) with respect to a certain reference status if the outcome is probabilistic. For instance, Vellend et al. (34) defined neutral stochasticity in community ecology as random changes in community structure with respect to species identity due to stochastic processes of birth, death, immigration, and emigration. It could also mean variation explained by spatial rather than by environmental variables or random variation due to colonization order (34). Because neutral is often treated as being equivalent to stochastic in the ecological literature (e.g., neutral process is often a synonym for stochastic process), putting two words together could also potentially lead to confusion. In this review, we prefer to use the term “ecological stochasticity” to refer to this type of stochasticity used in community ecology research.

The term “ecological stochasticity” was used about 4 decades ago but has not been well defined (104). Here, we give a more straightforward definition of stochasticity used in community ecology. Based on general system theory, a system can be defined by two fundamental attributes: structure and functions. Community structure includes species composition and abundance distributions. Thus, in general, ecological stochasticity (Table 1) in community ecology can be defined as random changes in the community structure with respect to species identities and/or functional traits due to stochastic processes of birth, death, immigration and emigration, spatiotemporal variation, and/or historical contingency (e.g., colonization order [described in detail below]). One advantage of this term is that it encompasses the context of various other terms used in ecology research, e.g., demographic, compositional, or neutral stochasticity. It is also consistent with other terms used in the literature, such as genetic, physiological, and evolutionary stochasticity, corresponding to different biological fields of genetics, physiology, and evolutionary biology. Given this definition, below we describe stochastic components embedded in various ecological processes to reconcile both niche and neutral perspectives.

STOCHASTIC COMPONENTS OF ECOLOGICAL PROCESSES

Four Fundamental Ecological Processes

One of the most fundamental questions in ecology is how diversity is generated and maintained. Traditionally, the mechanisms governing the genetic diversity within species are referred to as evolutionary processes, including mutation, selection, gene flow, and genetic drift (107). In contrast, the mechanisms shaping the diversity among species are generally considered to be ecological processes (72). In parallel with evolutionary processes, Vellend (108) grouped ecological processes into the same four fundamental processes: speciation, selection, dispersal, and ecological drift. Because changes in evolutionary processes could lead to changes in community structure even without the creation of new species, Nemergut et al. (67) proposed the use of diversification instead of speciation. Hanson et al. (72) proposed the same four processes underlying microbial biogeographic patterns.

There are several advantages of Vellend's conceptual framework. First, this framework unifies niche and neutral perspectives by considering both deterministic (e.g., selection) and stochastic (e.g., ecological drift) processes. Three of the four fundamental processes (dispersal, drift, diversification, or speciation) are central to the neutral theory (29). Second, it explicitly recognizes the importance of evolutionary processes (i.e., diversification) in contributing to community structure because both evolutionary and ecological processes are intertwined in controlling community diversity and biogeography (67, 72). In addition, this framework provides an effective operational model under which all communities across different habitats can be compared under the same conceptual framework (37). Thus, Vellend's conceptual framework has the potential to unify various empirical and theoretical efforts and transform microbial ecology from descriptive observational studies to mechanistic predictive research (67). Below, we provide a brief description of stochastic and/or deterministic components associated with each of these processes within the context of their relative importance in controlling microbial community structure.

Selection

Ecological selection is referred to as the ecological forces that alter community structure due to fitness differences (e.g., survival, growth, and reproduction) among different organisms and is a main force governing community assembly (67, 72, 108, 109) (Fig. 2A). Selection results from deterministic factors at both local and regional scales, including abiotic conditions (e.g., temperature, moisture, pH, and salinity) and various antagonistic or synergistic biotic interactions (e.g., competition, facilitation, mutualism, and predation). In host-associated microbial communities, host filtering (i.e., the within-host environment allows only certain microbial taxa to colonize or persist) is another important selection process besides the biotic interactions among different microorganisms (50, 110). Selection is unambiguously not stochastic (30, 34) (Fig. 2E).

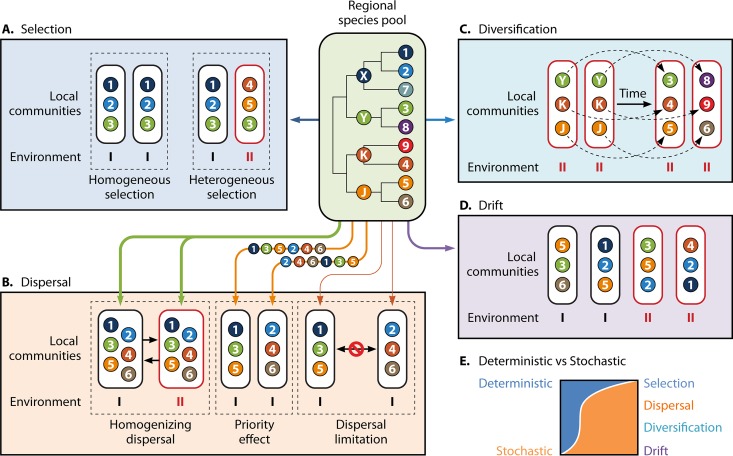
FIG 2.

Schematic representation of microbial community assembly processes. The middle panel represents the metacommunity species pool in a region. Each ball with a number is a contemporary species, while each ball with a letter is an ancestral species. The tree in the middle panel shows the phylogenetic relationships among different species. Species 1, 2, and 7 and their ancestor, species X, prefer environment I, while species 4 to 6, 9, K, and J prefer environment II, and species 3, 8, and Y live well in both environments I and II. (A to D) Extreme examples of the four different ecological processes. (A) Selection. The four local communities are strongly controlled by niche selection. While the local communities in environment I consist of only those species (species 1 to 3) that prefer environment I, the community in environment II is composed of only those species (species 3 to 5) that prefer environment II. The two local communities at the left have the same structure because of selection under the same type of environment (environment I), so-called homogeneous selection. The two communities at the right have different structures due to selection under different environments (environments I and II), so-called heterogeneous selection. (B) Dispersal. In the two communities at the left, there is very strong dispersal without any limitation between these two local communities. Even though the two communities are in different environments (environments I and II), they have exactly the same species (species 1 to 6) due to very strong dispersal, so-called homogenizing dispersal. In the middle two communities, species (species 1 to 6) moving along the arrow lines from the metacommunity have different orders of immigration to these two local communities. Due to priority effects, two different communities are formed even under identical environmental conditions. Species 1, 3, and 5 occupy the niches of one community because they arrive earlier than others, while species 2, 4, and 6 arrive earlier and dominate the other community. In the two local communities at the right, the arrow lines show immigration from the metacommunity, and there is very limited dispersal between these two local communities, so-called dispersal limitation. As a result, these two local communities have different structures even though they are in the same environment (environment I). (C) Diversification. This example of diversification assumes that there is no influence of either selection or dispersal. The two local communities (left) under the same environment, environment II, have the same ancestral species, species Y, K, and J, in the beginning. Due to diversification (speciation and extinction) in different communities, different new species could emerge from random mutations of the same ancestor (e.g., species 5 and 6 from species J). Consequently, the structures of these two communities could be different even under identical environmental conditions. (D) Drift. Species from the metacommunity occupy environmental niches only by chance due to random birth, death, and reproduction, etc., without any relevance to their niche preferences. For instance, taxon 5 prefers environment II, but because of drift, it is randomly present in communities in environments I and II. (E) Determinism versus stochasticity. The widths of the blue and orange parts represent the relative importances of determinism and stochasticity associated with each ecological process. Selection is solely deterministic, whereas drift is purely stochastic. In microbial ecology, dispersal and diversification are often considered stochastic processes but could be deterministic in some cases, although an example of deterministic dispersal or deterministic diversification is not shown.

By considering environmental heterogeneity, selection can be classified into two main categories. If “environmental conditions” (e.g., abiotic and biotic) are homogeneous, little variation in community structure or species/compositional turnover is expected. This is referred to as homogeneous selection (Fig. 2A) (37). In contrast, if environmental conditions change across space or time (i.e., heterogeneous), high variation in community structure could exist, which is referred as to variable selection (37, 108). For consistency, here, we refer to it as heterogeneous selection (Fig. 2A).

Dispersal

Dispersal is a fundamental process in ecology and evolution (111). In community ecology, dispersal is referred to as the movement and successful establishment of organisms across space (72, 108). Dispersal is considered limited if an organism's migration to new locations is restricted and/or its establishment is obstructed. If the probability of movement varies across space, in general, the movement of organisms by both active and passive pathways could be confined. Many factors could affect successful establishment, such as environmental filtering, biotic interactions, and priority effects (described in detail below) (72).

Unlike selection or drift, dispersal cannot be unambiguously treated as being deterministic or stochastic (34, 112) (Fig. 2E). It can depend on both deterministic and stochastic factors (72). For instance, if dispersal rates are dependent on the population size, dispersal is stochastic because more-abundant species have a greater probability of dispersal than do less-abundant species. However, dispersal rates could be quite different among different species, depending on species traits and active status (e.g., spores or dormancy). From this angle, dispersal is deterministic. In addition, environmental conditions in a new habitat will have dramatic effects on successful species establishment, which is deterministic. Therefore, theoretically, dispersal limitation alone could not be used as the sole evidence for stochastic processes (72) because dispersal can be either deterministic, stochastic, or both. However, in practice, many studies still treat dispersal as being neutral, because it is quite difficult for field studies to identify dispersal traits, link dispersal traits to community structure patterns, or assess dispersal processes and rates (112).

Due to the small size, high abundance, wide distribution, and short generation time of microorganisms, microbial dispersal processes are much less examined, and hence, they are poorly understood (66, 67). In microbial ecology, one of the main questions is whether microorganisms are dispersal limited, which is still controversial (113–115). Historically, microorganisms were considered to be everywhere and hence not dispersal limited (113, 114). After a decade of intensive studies, it is well recognized that microorganisms show strong biogeographic patterns, which is evidence for dispersal limitation (72, 116, 117). More importantly, although some microorganisms can propel themselves to a certain degree within a short distance, microbial dispersal is typically considered passive (67). Since passive dispersal is usually stochastic with respect to species identity (34), microbial dispersal can be largely viewed as stochastic (67). However, passive dispersal may not always be stochastic in some cases; e.g., the size or shape of a microorganism can affect its rate of dispersal through small soil pores.

Like diversification, dispersal is a key factor influencing the regional species pool and its associated community structure (108). A regional species pool is generally defined as what consists of all trophically similar individuals and species in a regional collection of local communities, also called a metacommunity, based on Hubbell's unified neutral theory (29). Within a large region, the degrees of dispersal could vary substantially among different taxa (101), ranging from being extremely limited to being very high. A high dispersal rate can homogenize the community structure and hence lead to little variation or turnover in the community structure (118, 119), which is referred to as homogenizing dispersal (37, 109). Low dispersal rates, coupled with drift or weak selection, could increase community variation or turnover, which is often referred to as dispersal limitation (37, 109).

Diversification

Diversification is an evolutionary process of generating new genetic variation (67, 108), and it is a balance between speciation and extinction (120). Diversification is central to understanding the origination, maintenance, and distribution of biodiversity and to predicting fundamental ecological patterns such as species abundance distributions, species-area relationships, and distance-decay relationships (67, 72, 120). Despite its importance in biodiversity research, diversification is very difficult to study, particularly in the ecology of macroorganisms, because it generally involves long-term evolutionary processes of thousands to millions of years for macroorganisms (120). Consequently, the roles of diversification are largely ignored in community ecology research (30, 67, 109, 118, 120). Many such studies generally aim to examine the ecological influences of “contemporary” species pools on community assembly over time scales within which diversification (speciation and extinction) largely does not affect regional diversity (30).

It is well recognized that diversification plays important roles in governing regional species pools over large spatial and temporal scales (Fig. 2), which could in turn be potentially important in determining community dynamics and patterns at smaller spatial and temporal scales (34, 108, 121–123) (Fig. 2C). Compared to plants and animals, diversification could be detected in the changes in microbial composition at a shorter time scale, particularly at a fine taxonomic/phylogenetic/genetic resolution (72), due to the short microbial generation time, fast growth, and rapid genetic mutations (124, 125). Since most genetic mutations are largely random at the molecular level (DNA level), without a substantial impact on the species trait(s) or identity, they may have little effect on microbial community composition. However, genetic mutations that alter a key functional trait(s) and/or species identity could have a considerable influence on microbial community dynamics over a relatively shorter temporal scale because microorganisms can evolve through mutations very rapidly (67, 124–128). Although mutation is widely accepted as being a stochastic process in evolutionary biology (34, 129), speciation could also be partly determined by the species traits and intertwine with the actions of selection in some cases. Therefore, diversification can be largely considered stochastic in ecology. In certain cases, it could encompass both deterministic and stochastic components (Fig. 2E).

Given the fact that some strong microbial biogeographic patterns cannot be fully explained by selection and dispersal (13, 14, 72, 116), the extremely high diversity and the capability for rapid mutations in microorganisms suggest that diversification could play an important role in shaping microbial community structure. However, to the best of our knowledge, no method is available to assess the relative importance of diversification in shaping microbial community structure. One reason for this is that the role of diversification was thought to be impossible to infer from contemporary diversity patterns (37). From an evolutionary perspective, various ecological processes interact with each other in space and time to structure biodiversity (30). Thus, contemporary diversity patterns at a single time point should reflect the combined actions of various ecological processes over time (72, 101). If so, contemporary diversity patterns should contain information to signify all deterministic and stochastic processes, including selection, dispersal, drift, as well as diversification. By the same token, similar to inferring the importance of selection, dispersal, and drift (29, 37, 109), the relative importance of diversification in shaping community structure should also be able to be inferred from the snapshot of contemporary diversity data, at least to some degree, but the difficulty is how to detect such signals.

Drift

Ecological drift is a central concept in community ecology. It is referred to as stochastic changes with respect to species identity in the relative abundances of different species within a community over time due to the inherent random processes of birth, death, and reproduction (34, 67, 108) (Fig. 2D). Various modeling and empirical studies showed that drift can alter community structure and biogeographic patterns even in the absence of selection (29), indicating the importance of ecological drift in shaping community structure (67, 72, 108). Drift is more important when selection is weak and the local community size is small (30). However, it is difficult to test pure ecological drift empirically because no species in nature are exactly demographically identical (108). Drift is unambiguously stochastic (34) (Fig. 2E).

Drift could play critical roles in shaping the structure of microbial communities (32, 35, 36). Although the size of a microbial community is typically large, substantial numbers of microbial taxa are rare. These rare taxa should be very vulnerable to ecological drift (67). In addition, functional redundancy, which means that different populations share a similar or the same function, appears to be quite high in a microbial community, especially compared to those in plant and animal communities (130–133). Functional redundancy increases neutrality and makes functionally redundant populations more susceptible to drift. However, it is challenging to directly examine ecological drift in microbial communities due to the uncertainty in assessing the extinction of microbial taxa and the existence of dormancy, which allows the species to avoid extinction and the effect of drift.

Historical Contingency and Contemporary Selection

Besides the four ecological processes described above, another widely used conceptual framework classifies assembly processes as historical contingency and contemporary selection. Broadly, historical contingency is referred to as the legacy effects on the current community structure left by historical processes, which typically include drift and/or past selection along with dispersal (72) and diversification. Thus, conceptually, historical contingency should encompass both stochastic and deterministic components, but in practice, historical contingency is considered to be more or less equivalent to stochastic processes in many studies (117, 134–136). It should be noted that the term historical contingency also more specifically refers to the effects of the order and timing of past biotic or abiotic events on community assembly (137). In contrast to historical contingency, contemporary selection (72, 138) is referred to as the selection imposed by present-day environments on the current community structure. Contemporary selection is deterministic regardless of the impacts of past environments on community structure.

Historical contingency can be caused solely by a priority effect (137), which is a phenomenon where early-arriving organisms have negative or positive impacts on late-arriving organisms (36, 72, 137, 139, 140) (Fig. 2B). Theoretically, niche preemption and niche modification are two important mechanisms underlying priority effects (137). The former is referred to as a situation where early-arriving species reduce the availability of resources (e.g., nutrients, space, and energy) to late-arriving species whose abundance will be limited (137), which always produces inhibitory priority effects. In contrast, the latter means that early-arriving species modify local niches affecting the colonization of late-arriving species, which can then lead to inhibitory or facilitative priority effects. Niche preemption generally affects species identity within functional guilds, whereas niche modification impacts species identity primarily across functional guilds (137). Thus, information on species distributions within and across functional guilds could provide insights into the mechanisms underlying priority effects. While niche modification should be deterministic, niche preemption can be either stochastic or deterministic, since resource consumption could be regardless of species identity.

Integrated View from Ecology and Evolution

Deterministic and stochastic processes represent two complementary parts along a continuum of ecological forces shaping community structure (30, 92). Deterministic processes are at one end of the continuum, whereas stochastic processes are at the other end (Fig. 2E). Within the context of the deterministic-versus-stochastic dichotomy, niche-based selection via interspecific interactions and abiotic environmental conditions is a deterministic process, and drift is a stochastic process (30). Generally speaking, dispersal and diversification are often considered components of stochastic processes, particularly in microbial ecology (30). However, both of them can be deterministic in some cases (Fig. 2E).

All four of these fundamental processes interact with each other directly or indirectly and work in combination to shape community structure (30, 66, 72, 101). For instance, selection and drift usually vary in opposite directions. If the local community size is small and selection is relatively weak, the effects of selection could be overridden by drift (108). A recent microbial population study showed that during evolution, demographic stochasticity was capable of reversing the direction of deterministic selection (141). However, the importance of drift in shaping community structure is also dependent on other forces. Strong diversification would enhance the influence of drift because diversification affects the size of the regional species pool. Drift will have larger role in governing the structure of local communities in regions with larger species pools in which there is a greater chance of producing stochastic variations among local communities (30). In addition, dispersal could have an impact on selection, and its roles can also be shaped by other processes. Homogenizing dispersal or dispersal limitation could potentially overwhelm the influences of selection on community structure (37, 66). Dispersal limitation alone does not create community variation without being coupled with drift and diversification (67, 109). Finally, the magnitude of the influences of diversification on community structure is dependent on the strength of dispersal. When dispersal rates are low, diversification is a major process contributing to the regional species pool (37, 109), and thus, diversification should be particularly important in shaping community structure (37). If dispersal rates are high, the influences of diversification on community structure variation or turnover would be minimal (37). From an evolutionary perspective, ecological communities can be viewed as being assembled primarily via dispersal or diversification within the context of natural selection (142). The final outcomes for community structure will be affected by the balance between dispersal and diversification rates, which have interactions with selection and drift (37, 142).

Although Vellend's conceptual framework on community assembly processes is attractive and well accepted in the field of microbial ecology in general (67, 72), determining how combinations of these four processes affect community assembly is difficult (67, 72). Translating this conceptual model into a quantitative operational framework is even more challenging (37). In the following sections, we describe different approaches for assessing the roles of various ecological processes in shaping community structure.

FROM PATTERNS TO PROCESSES: APPROACHES TO INFER STOCHASTICITY

With recent advances in large-scale high-throughput meta-omics (e.g., metagenomics, metatranscriptomics, metaproteomics, etc.) technologies (69), community-wide spatial and temporal information on microbial community structure, functions, and activities can be rapidly obtained, which enables microbial ecologists to address research questions that were previously difficult to approach, such as community assembly mechanisms. Recently, numerous studies have focused on understanding the mechanisms that control microbial community structure. Here, we focus on describing various approaches used for assessing the importance of ecological stochasticity in controlling community structure and highlighting some representative results, rather than providing a comprehensive review. Several major approaches have been used to infer ecological stochasticity, including multivariate analysis, neutral-theory-based process models, and null modeling analysis.

Inferring Ecological Stochasticity by Multivariate Analysis

In parallel with theoretical development, numerous statistical approaches have been developed and used to examine the relative importance of environmental control (i.e., selection) and dispersal limitation (143–147). Three major types of multivariate statistical methods are often used. The first one is direct comparisons of community structure differences between and within treatments (or different groups of communities in distinct environments), such as permutational multivariate analysis of variance (PERMANOVA or Adonis) (148), analysis of similarities (149), permutational analysis of multivariate dispersions (PERMDISP) (150), as well as more visualized ordination methods, e.g., principal-coordinates analysis (PCoA), nonmetric multidimensional scaling (NMDS), principal-component (PC) analysis (PCA), and detrended correspondence analysis (DCA) (e.g., see references 35, 70, 151, and 152). Significant dissimilarity between treatments or homogeneity within a treatment can be used to assess the effect of selection but has very low power for inferring the importance of stochasticity, since niche selection could also result in similarity between treatments and heterogeneity within a treatment. Thus, this type of multivariate analysis was usually applied along with null model analysis (described in detail below), e.g., comparing observed and null expectations by PERMANOVA or PERMDISP (e.g., see references 31, 35, 153), to infer assembly stochasticity.

The second type of analysis is correlation-type analyses between community structure and environment variables, such as the Mantel test (e.g., see reference 154), multiple regression on (dis)similarity matrices (MRM) (e.g., see references 155 and 156), redundancy analysis (RDA) (e.g., see references 61 and 157), and canonical correspondence analysis (CCA) (e.g., see references 36 and 157). A high proportion of community structure variation explained by environmental variables can provide evidence of the importance of selection, whereas a very low proportion of explainable variation may indicate the influence of stochastic processes. However, different processes (e.g., selection and dispersal) could produce similar spatial patterns (158), and hence, community variations due to environmental control and spatial influences need to be parsed out. Therefore, in most cases, correlation-type analyses have been extended to the third type of multivariate approach, variation-partitioning analysis (VPA) (e.g., see references 13, 14, 36, 45, 48, 72, 157, 158, and 159). To determine the relative importance of environmental control (i.e., selection) and dispersal limitation, typically, the correlation between community structure and environmental variables is estimated as an environment effect after controlling for the influence of geographic distance, whereas the correlation between community structure and spatial distance is quantified as a distance effect after controlling for the influence of environmental variables (72). In addition, the interaction between environmental variables and spatial distance can be quantified, and the remaining variation is termed unexplained variation (143). While the environment effect signifies the sole impact of selection, the distance effect is often considered to represent the influence of dispersal. However, it should be noted that the distance effect could also include other spatially structured effects caused by unmeasured variables or even drift. Unexplained variation could be due largely to unmeasured environmental variables, biotic interactions, drift, and/or methodological artifacts (13, 36, 37, 160, 161).

Basically, there are two types of VPA. One is a raw-data-based direct approach in which the raw environmental data and spatial x-y coordinates are directly used to correlate changes in community structure. Typical examples are VPA based on RDA for linear regression (e.g., see references 145 and 157) or partial CCA (pCCA) for unimodal regression (e.g., see references 14, 36, and 45). The other type of VPA is a distance-based indirect approach in which three distance matrices (community dissimilarity, geographic distance, and environmental similarity) are used to establish correlations among the environment, space, and community structure, e.g., VPA based on a partial Mantel test (rarely used now), MRM (e.g., see references 155 and 158), or distance-based RDA (e.g., see references 61 and 162). This type of approach was referred to as DIST (158, 163, 164). The raw-data-based direct approach addresses questions related to observed variations in community structure. In contrast, the distance-based indirect approach focuses on questions concerning the variation measured by various dissimilarity metrics (144, 163), e.g., differences in species occurrence measured by the Jaccard index, structure differences determined by the Bray-Curtis index, and phylogenetic dissimilarity determined by the UniFrac index, etc. Although one may choose an approach or a model with higher explained variation (e.g., R²) or more meaningful factors in practice, different complementary and reinforcing approaches should be used to explore relationships based on various dimensions of biodiversity.

By using multivariate statistical approaches, microbial ecologists tried to address the relative importance of contemporary selection and historical contingency in shaping community structure and biogeographic patterns over the last decades (72, 165–168). Contemporary selection is typically measured with the partial correlation between biotic structure and contemporary environmental variables by controlling for the influence of geographic distance (i.e., contemporary environment effect). Both contemporary selection and historical contingency were found to be important for governing microbial biogeographic patterns (72, 169), although in a recent meta-analysis, the selection imposed by the contemporary environment appeared to be more important than historical processes (72). Interestingly, it is generally expected that historical contingency might be more important at larger geographic scales and in less-connected habitats, primarily due to dispersal limitation, but such trends were not observed (72).

Multivariate analysis approaches are always compounded by the problem of unmeasured environmental factors, because it is almost impossible to measure all environmental variables in practice. As a result, for instance, the distance effect is most likely overestimated since it cannot exclude the impacts of unmeasured environmental variables (72). Recently, a new approach for isolating the effects of unmeasured environmental variables affecting microbial communities was proposed (109). First, spatial distance is decomposed into various spatial variables based on spatial eigenvector analyses. Next, the spatial variables are combined with other environmental variables and further decomposed into principal components (PCs). Next, the PCs are associated with β-diversity metrics related to selection (β nearest-taxon index [βNTI]) (described in detail below). If a PC is significantly associated with selection but has no obvious loading of any measured environmental variables other than spatial variables, it most likely represents unmeasured environmental factors. This is the first time that the impacts of unmeasured environmental variables on community structure could be possibly parsed out from stochastic processes. However, if not related to spatial variables, the impact of unmeasured environmental variables could still be tangled with the effects of drift and methodological artifacts in the unexplained part.

By using multivariate statistical approaches, the spatial distance effect on community structure is often interpreted as support for neutral theory (168, 170). Although VPA is widely used in ecology research to determine the relative importance of deterministic versus stochastic processes for community structure, several recent studies based on simulation models showed that VPA failed to correctly predict the environmental and spatial components of community variation (158, 171, 172), and hence, VPA could be difficult to use for inferring ecological processes (37). Nevertheless, great caution is needed when using VPA to partition community variation, and it should be used as an exploratory tool together with other approaches (e.g., neutral-theory-based models and null model analysis, as described below) to develop hypotheses and assess the relative importance of environmental variables and spatial distance (171).

Inferring Stochasticity by Neutral-Theory-Based Process Models

The second major approach for inferring processes from diversity patterns is testing for the presence of stochasticity using neutral-theory-based process models. There are over 10 different neutral models, each with slightly different predictions for different factors (11). The most influential one, Hubbell's neutral model (29), has only three parameters, the population size of the local community (J), the rate of immigration (i.e., dispersal) (m), and the “fundamental diversity number” (θ) (which depends on the population size of the metacommunity, J_M, and the speciation rate, v). Theoretically, it is possible to estimate all of these parameters directly from ecological data, but in practice, it is difficult to do so because estimating the population size of a metacommunity is problematic (11). Also, the rates of migration and speciation can almost never be measured directly (173). Thus, the parameters can be only indirectly estimated by fitting a neutral model(s) to the observed community structure data.

Neutral models have been applied to a wide range of ecological phenomena, but the majority of research related to neutral theory is focused on species abundance distribution (SAD), which characterizes the distribution of abundances of all species within a sample or ecological community (11). Along with distance-decay relationships and species-area relationships (SARs), SAD is one of the few universal patterns in ecology (174). An ecological community in nature consists of many species with different numbers of individuals of each species. One of the unique characteristics of an ecological community is that the distribution of numbers of individuals is very uneven. In general, there are a few species with many individuals but many species with a few individuals. SAD is a basic metric to describe how many individuals of each species are present in a community and is often used to test both niche and neutral models (29, 89, 175).

Despite their unrealistic assumptions, apparent simplicity, and very small numbers of parameters, neutral models remarkably fit very well with numerous ecological patterns, including SADs, SARs, abundance-occupancy relationships, species turnover, and distance-decay relationships, in a variety of communities from tropical trees to bacteria (32, 65, 176–186). Also, in some cases, neutral models fit the abundance of rare species better than those predicted from niche models (185, 187). Besides fitting numerous observed patterns, neutral models have been improved in terms of theory and methodology. One direction is substantial improvements in the fitting methods, including sampling theory, derived analytical forms, and likelihood functions (11, 94). The other direction is to make some original assumptions more realistic. For instance, some neutral models relaxed the zero-sum assumption (when an individual dies, it is immediately replaced by another individual, and thus, resources are fully saturated at all times), but the results showed that the form of SAD was not changed (11, 188). Other models improved the estimation of the speciation rate by incorporating protracted speciation into neutral models, where new species gradually evolve over a period of time instead of appearing instantaneously as point mutations (189). Another important advancement is spatially explicit neutral models. In the original spatially implicit models, dispersal occurs between only two distinct spatial scales, from the metacommunity to each local community. In spatially explicit neutral models, dispersal is simulated in multiscale structures, for instance, as migration between cells on a 2-dimensional grid (11, 190).

When applying neutral models to microbial studies, a particular acute problem is the sampling effect, the uncertainty/randomness due to a small sample size from a large population, although it is not unique to microbial studies. Even though applications of high-throughput sequencing technologies can greatly increase sampling efforts in microbiome studies, the sequencing depths typically used in current studies (e.g., 10⁴ to 10⁵ individuals per sample for the 16S rRNA gene) are still far smaller than the huge number of individuals in a microbial community (e.g., usually 10¹¹ to 10¹⁴ individuals per g soil sample). Thus, the vast rare species in a microbial community are mostly undetectable or detected just by chance. Accordingly, the traditional way to fit neutral models (e.g., SAD) is dramatically insensitive and problematic for microbial studies, since modest changes in neutral model parameter values are reflected only in the abundance of rare species (32, 191). Considering this problem, microbial ecologists developed some neutral models particularly suitable for microbial studies (32, 177, 178, 192). One solution is to calibrate and validate a mathematical model of microbial community assembly using a small sample size. A popular example is the neutral model developed by Sloan et al. (177, 192), which fits the observed abundance-frequency relationship with a beta distribution derived from neutral theory. Another solution is, instead of removing taxon identities and considering merely their abundance/frequency, to examine the dynamics of each abundant taxon with a modified neutral model by considering the niche effect (32). To incorporate the niche effect, the stochastic differential equation of the neutral birth-death process was extended by including environmental variables in a linear least-squares analysis. This method partly bypassed the above-described problems by focusing on abundant taxa, which are much less affected by a limited sampling effort, and by analyzing their dynamics separately instead of fitting patterns (e.g., SAD) of the whole community.

Although neutral models have been extensively examined against empirical data from plants and animals, efforts in microbial studies are very limited. Recently, neutral models have been applied to microbial communities in bioreactors (32, 36, 177, 178, 193), soils (64, 71, 157), lakes (194), and animal and human gut (195–197), but divergent and controversial results were obtained. For instance, based on neutral models, several related studies indicated that the microbial communities in wastewater treatment plants and bioreactors were primarily controlled by stochastic (neutral) processes, although deterministic processes were also important (32, 36, 177, 178, 193). Those observations contradict the previous common belief (198) and are different from some recent observations of anaerobic digesters, which showed that deterministic processes governed microbial long-term population dynamics (70). In another example, the importance of niche versus neutral processes also varied significantly among different microbial functional groups in soils. Both neutral and null model analyses showed that the phototrophic microbial communities in deserts are primarily controlled by stochastic processes (64). However, heterotrophic microbial communities were most likely shaped by deterministic processes (64). Therefore, it is compelling to further quantify the relative importance of niche and neutral processes across spatial/temporal scales, environmental gradients, and/or different functional groups.

Inferring Ecological Stochasticity by Null Model Analysis

The third major approach to understanding the potential importance of ecological stochasticity is the use of null models, which have been used widely in ecological studies (199). Different from the process-oriented mechanistic models (e.g., neutral model), null models generate statistically expected stochastic patterns via random permutations of ecological data by deliberately excluding certain mechanisms (e.g., species interactions) of interest (200, 201). Null model analyses involve several major steps (202). First, community similarity or dissimilarity is estimated based on empirical data with appropriate metrics, e.g., incidence based (e.g., Jaccard's and Sorenson's indexes) and abundance based (e.g., Bray-Curtis and Morisita-Horn indexes). Generally, dissimilarity metrics are used for detecting community assembly mechanisms. Next, community data are randomly shuffled by keeping some species properties constant. This process is generally repeated multiple times (e.g., 1,000 times) to obtain average null expectations. The standard deviation of the null expectation can then be estimated. With the expected random patterns from null assemblages, ecologists can ask whether the ecological patterns observed among local communities are different from the random patterns produced by null models. If the observed ecological patterns are not statistically different from null expectations, the community dynamics are largely considered stochastic with respect to the processes excluded (30). Otherwise, they are regarded as being deterministic.

Over the last 3 decades, numerous null models and algorithms (29–31, 195, 203, 204) have been developed to generate null expectations based on taxonomic (e.g., see references 31 and 205), phylogenetic (e.g., see references 62, 109, and 206), and/or functional (e.g., see references 155, 207, and 208) community structure data. Most of the reported null models keep the following properties constant in the regional species pool: the total number of taxa (richness), the number of individuals (abundance), and the sum of all taxon occurrence frequencies. For incidence (i.e., presence/absence) data, there are generally 9 null algorithms (also referred to as null models) (203), in which the richness in columns (representing sites, samples, or communities) can be equiprobable for each community (i.e., a taxon has equal probabilities of being present in all observed communities) (209–212) or proportional (199, 213–215) or fixed (31, 204, 205, 216, 217) to the observed richness. The rows (representing different taxa) can also be equiprobable for every taxon (i.e., all observed taxa have equal probabilities of being present in a community) (211, 212, 218) or proportional (205, 209, 210, 212, 216) or fixed (31, 204, 217, 219, 220) to the observed frequency. For abundance data, the abundances can be assigned in three different ways after randomizing the incidence pattern: (i) switching the above-described 9 incidence-based models (i.e., they consider only the presence and absence of each species [also called binary or unweighted]) to the corresponding individual-based models (i.e., they consider the abundance of each species [also called abundance weighted]) (212, 221, 222), (ii) shuffling the observed abundances within each community or each taxon (211), and (iii) a random draw where the probability of drawing individuals into a taxon is proportional to the relative abundance of the taxon in the regional species pool (109, 212, 216). Besides the above-described models of taxonomic assembly, 3 types of null models were reported to randomize phylogenetic relationships among taxa, including (i) shuffling the names of taxa (so-called phylogeny shuffle) (62, 68, 211, 218), (ii) abundance-constrained phylogeny shuffling (223), and (iii) randomizing the base pair composition of DNA sequences (195). When randomizing phylogeny, taxonomic β-diversity was usually fixed as observed. Since there are many different options, it is challenging to select the appropriate null models for a particular study. Depending on ecological questions, multiple null models should be explored for quantifying the mechanisms underlying community assembly.

As with any other approaches, inferring processes from patterns by null model analysis also faces some difficulties, with several major challenges. First, developing randomization algorithms to produce appropriate patterns against a specified null hypothesis is difficult. Imposing too few constraints on a null model will make it so random that it is very easy for the null expectation to be different from the observed pattern, which could increase the chances of a type I error. On the contrary, putting too many constraints will make the null results too close to the observed pattern, which could lead to greater chances of a type II error (201). Different methods to constrain the null model could lead to quite different results (201, 212). Thus, the experimental results from null model analyses are very sensitive to the models, approaches, algorithms, and diversity metrics used (201, 224).

Second, sample size, including the numbers of both taxa detected and communities analyzed, could also be a concern. Most of the data sets in plant and animal community ecology research are small or intermediate, often with fewer than 100 taxa and/or 100 communities (201). With the advance of high-throughput technologies, there are much larger data sets in microbial ecology research, e.g., thousands to up to hundreds of thousands of taxa. Null model analysis may be not well suited for such large data sets due to false-positive significant pairs and data autocorrelation (201).

Third, the choice of the appropriate regional species pool (i.e., γ-diversity) for null model analysis is very important but challenging. The species pool should not be too small or too large (205). As a rule of thumb, the regional species pool should include those species that can possibly colonize a given site within a reasonable period of time (205) (for microorganisms, weeks or months are usually reasonable, while years may also be fine for large-scale research). It is worth noting that the absolute magnitude of the deviation from the null model expectation will increase with the species pool size, but the relative deviations among different pairs of communities generally will not be affected (205). Thus, relative comparison (e.g., using a standardized effect size) should be used.

Fourth, the majority of null modeling approaches have been developed based on incidence data (203, 205). Abundance data potentially contain more information on species associations than do incidence data, and hence, they could be more suitable for inferring the underlying community assembly mechanisms (201). However, the inclusion of abundance data in null modeling randomization is much more complicated and challenging (109, 212), and further developments are needed (212).

In addition, null model analysis assumes that strong interactions always result in communities that are significantly different from null expectations. However, strong interactions, when combined with a variable immigration history, could produce an apparently random community structure (136, 225). Null model analysis based on time series data with an explicit or detectable immigration history could help to mitigate this potential problem (136). Despite various challenges in null model analyses, their applications to various ecological problems have continued to provide valuable insights into community ecology (201).

Null model analysis has also been incorporated into the development of new metrics to measure taxonomic β-diversity and phylogenetic α- and β-diversity for inferring community assembly mechanisms. Classical β-diversity metrics (without null model analysis) are useful for inferring the relative importance of stochastic versus deterministic processes (30, 31, 35, 153, 162, 170, 226–228). For instance, the significantly higher taxonomic β-diversity between biological replicate ponds with higher productivity indicated the increased influence of stochastic processes (31). However, comparison of classical β-diversity metrics among regions with different species pool sizes could lead to a poor estimation of the overall importance of stochastic factors with respect to environmental or spatial factors (162). Since classical β-diversity metrics are not independent of local diversity (α-diversity) and regional diversity (γ-diversity) (205), most of the metrics and statistical analyses used to estimate β-diversity (e.g., Jaccard and Sorensen dissimilarity indexes) are not always directly comparable, and it is difficult to generate meaningful results (205, 229, 230). This is because the classical metrics of all three diversity components (α, β, and γ) are interconnected, and any changes in two of the three components will affect the estimations of the third component (205, 231).

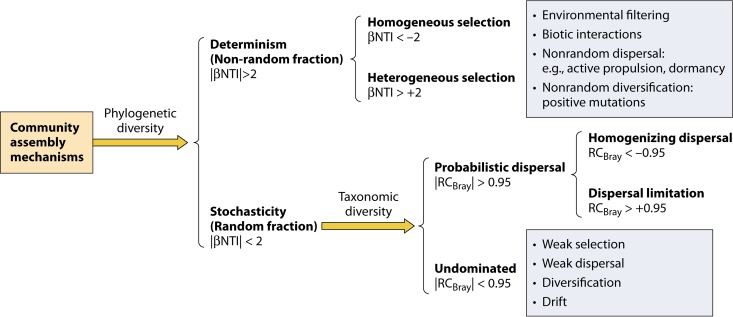
To remove the effects of α-diversity on the estimation of β-diversity, a probabilistic null-model-based β-diversity metric (β_RC) (205) was developed to control for the differences in species richness by modifying a Raup-Crick measure (232). β_RC can be estimated for each pair of communities based on taxonomic cooccurrence data. If the β_RC value is >0.95 (alpha = 0.05 by a two-tailed test), the given pair of communities shares significantly fewer species. If the β_RC value is less than −0.95, the given pair of communities shares significantly more species than expected by random chance (205). The mean β_RC can also be obtained across all pairwise combinations of communities. Based on the mean β_RC across communities, one can test whether the variation and/or turnover in the community structure is different from the null expectation, the degree to which the communities deviate from the null expectation, and how abiotic and biotic factors affect such a deviation (205). Assuming that the null model could reflect a real stochastic assembly and exclude determinism, the mean β_RC should be close to zero when stochastic processes dominate and/or dispersal is relatively high (neither limited nor too strong) among communities; if environmental conditions favor similar species (e.g., environment filtering) and/or dispersal is very strong (e.g., homogenizing dispersal), the mean β_RC will approach −1; and if environmental conditions select for dissimilar species (e.g., competitive exclusion) and/or dispersal is very limited, the mean β_RC will approach 1 (205). However, this metric uses only incidence data. Since abundance-based metrics are more informative and powerful than incidence-based metrics (229, 233), the Raup-Crick-based measure was extended to consider relative abundance data, and the resulting metric is referred to as RC_Bray (109).

Besides taxonomic metrics, the null model approach has also been widely incorporated into the development of phylogenetic α-diversity metrics, such as NRI (net relatedness index) and NTI (nearest-taxon index) (83, 206). The NRI is a standardized metric to measure phylogenetic clustering based on the observed mean phylogenetic distance (MPD_obs) and the randomly expected mean phylogenetic distance (MPD_exp) and its standard deviation, whereas the NTI is a standardized measure of phylogenetic clustering based on the observed mean nearest-phylogenetic-neighbor distance (MNTD_obs) and the null expectation of the mean nearest-phylogenetic-neighbor distance (MNTD_exp) and its standard deviation (83, 234). For a single community, if the NRI or NTI is >+2 or <−2 (i.e., 2 standard deviations from the null expectation), the coexisting taxa are phylogenetically more closely (i.e., phylogenetic clustering) or distantly (i.e., phylogenetic overdispersion) related than null expectations, respectively. A mean NRI or NTI across multiple communities that is significantly greater than zero indicates phylogenetic clustering, whereas a mean NRI or NTI that is significantly less than zero signifies phylogenetic overdispersion (62). Similar null model analyses have also been extended to measure phylogenetic β-diversity so that the βMNTD-based metrics (βNRI and βNTI) were developed (62, 235). Similarly, for a single pairwise comparison, a βNRI or βNTI value of >+2 or <−2 suggests that phylogenetic turnover is greater or less than the null expectation (62, 109). A mean βNRI or βNTI across all pairwise comparisons that is significantly greater or less than zero indicates that phylogenetic turnover is greater or less than the null expectation (62, 235). While a significant (β)NRI or (β)NTI value as described above is related to deterministic processes, a nonsignificant (β)NRI or (β)NTI value (between −2 and 2 for a single community or a single pairwise comparison) is usually considered to signify the influence of stochastic assembly. These null-model-based phylogenetic and taxonomic metrics have been used to assess the stochasticity of microbial assembly in a variety of environments, such as soil (228, 236), the ocean (237, 238), groundwater (33, 62), and animal feces (154). Recently, null-model-based β-diversity metrics (βNTI and RC_Bray) were employed to develop a new null-model-based framework for quantifying various community assembly processes (37, 68, 100, 101, 109) (see below).

Compared to neutral models, null model approaches are flexible due to various options of algorithms. In addition, since null model approaches can be based on taxonomic and phylogenetic diversity metrics and should extend to functional diversity metrics, it could be easier to develop a statistical framework based on null model approaches to disentangle the influences of different processes (see below). However, null model approaches are built on heuristic randomization algorithms that lack a clear biological mechanism (239). Neutral models are actually a special type of null model, but as mechanistic dynamical models, neutral models should be closer to “actual” stochastic population dynamics. Nevertheless, current neutral model approaches lack the ability to explore the information underlying phylogenetic and functional diversity whereas null model approaches are applicable, which significantly reduces the power of neutral models to infer the relative roles of different community assembly processes. Both null model and neutral model approaches have an inherent problem, that an observed pattern fitting a null/neutral model cannot reject the importance of deterministic processes, since a niche model could show a pattern similar to that of null/neutral models, as discussed above. To solve this problem, an important future direction is to effectively combine niche and neutral models. Although they have unsolvable drawbacks, as described above, multivariate analyses can help in the development of niche models and in linking community structures with environmental variables and ecosystem functioning parameters, which cannot be achieved by null or neutral models. Therefore, all three types of approaches should be simultaneously used in complementary and reinforcing fashions, and the results should be cautiously interpreted by considering their strengths and weaknesses. In the future, a unified framework of both niche and neutral theories will be built based on the further development and integration of different approaches.

EXPERIMENTAL APPROACHES FOR TESTING THE IMPORTANCE OF ECOLOGICAL STOCHASTICITY

Inferring the importance of ecological stochasticity from patterns determined by the various methods discussed above is difficult because observational survey data are always compounded by various other factors. Experimental tests of the role of ecological stochasticity in controlling the diversity of ecological communities in both the field and the laboratory are needed.

To directly test the relative importance of stochasticity in controlling community structure, Chase (153) established long-term experimental artificial ponds in the field (20 mesocosms, half under drought). The results showed that considerably higher β-diversity was observed in the pond community of producers and invertebrates without drought, which was most likely due to a combination of ecological drift and priority effects. In contrast, the communities in the ponds experiencing drought were much more similar due to niche selection imposed by drought. Also, higher β-diversity was observed in the ponds with greater productivity, suggesting that stochasticity increases with greater productivity (producers and small animals) (31). However, explanations for these experimental results could be complicated by the lack of control over assembly history in disturbed ponds and the initial environmental heterogeneity (153, 240).

To discern the existence of stochastic assembly and its relative roles in determining community assembly, an ideal experimental system should ensure that the initial conditions (e.g., initial density and initial environmental heterogeneity) and environmental conditions are identical among replicate communities (153, 240). Well-controlled laboratory systems such as microbe-based bioreactors could help meet such challenging requirements. Compared to plant- and animal-based systems, microbe-based laboratory systems have several unique advantages (36, 52, 241–243). First, microorganisms are very small and have short generation times, which allow us to manipulate and monitor the influences of stochastic and deterministic processes on community dynamics in tractable experimental units and at short time scales. Also, many replicate reactors can be established and maintained under identical environmental conditions with the same source communities so that any differences in initial conditions and the effects of compounding factors on experimental results can be minimized. The availability of sufficient replicate samples is critical for addressing questions related to stochasticity with the null model approach (35). In addition, laboratory systems are closed systems, and hence, various functional parameters of interest can be measured at the whole-system level to allow the linking of community structure to ecosystem functioning, which is critical but very difficult to achieve in nature. Several years ago, a microbial-electrolysis-cell-based reactor system was used to examine the roles of stochastic assembly in determining microbial community structure (36). After 2 months, the functional community structures determined by using a functional gene array, GeoChip (44, 69, 244, 245), were dramatically different among 14 replicate reactors that were operated under identical conditions with the same source community. Further null and neutral model analyses revealed that ecological drift (i.e., initial stochastic colonization) and subsequent biotic interactions via priority effects were critical in determining microbial community structure (36). This study provides explicit evidence of the dominant roles of stochastic assembly (i.e., stochastic colonization) in controlling microbial community structure.

The relative importance of contemporary selection and historical contingency in community structure and biogeography has been a central, but highly controversial, issue in microbial ecology research over the last decades (116, 138, 246). However, a great challenge in ecology is that it is difficult, if not impossible, to obtain detailed relevant historical information in most situations (137). Therefore, experimental manipulations with a known history are greatly preferred. Numerous experimental manipulation studies as well as theoretical analyses demonstrated the importance of historical contingency in affecting community structure. The strength of historical contingency (priority effects or stochasticity) is generally promoted by a small habitat patch (247, 248), a large species pool (137, 249–251), high productivity (31, 135, 156), low stress or disturbance (153, 240), and low predation (202, 252). Species functional traits involved in competitive and dispersal abilities (e.g., flagella, cell size, and metal resistance ability, etc.) are also important for historically contingent assembly (136, 137). Finally, through thorough synthesis of experimental and theoretical data it has been concluded that historically contingent community assembly occurs only when the regional species contain species that together can produce priority effects and when the early-arriving species can rapidly preempt or modify the niches before late-arriving species arrive (137).

Although various experimental studies revealed that historical contingency affects community structure, little is known about whether historical contingency affects community functioning (36, 253). Recently, several studies showed that historical contingency can influence ecosystem functional processes such as productivity, decomposition, and nutrient and energy fluxes (36, 253–256). For instance, by using 10 wood-degrading fungal species in laboratory microcosms, it was demonstrated that differences in early immigration histories resulted in dramatic variations in community structure and ecosystem functions (i.e., decomposition and respiration) (253), indicating that small differences in the species immigration history during community assembly could lead to large differences in community functioning. Similarly, stochastic colonization in microbial-electrolysis-cell-based reactors resulted in communities with not only different structures but also distinct functions (e.g., hydrogen production, methanogenesis, or CO₂ production via fermentation) (36).

The study of ecological succession remains at the core of ecology research because information on temporal community dynamics can help predict the responses of biodiversity and ecosystem services to environmental change (257, 258). While the mechanisms shaping the structure of ecological communities have been intensively studied (30–32, 36, 62, 64, 91, 157, 186, 193, 205, 221, 259), the drivers controlling ecological succession in response to environmental perturbations are poorly understood (260, 261). To understand the relative importance of stochastic and deterministic processes in mediating microbial community succession, the responses of groundwater microbial communities to nutrient inputs were examined (35). One of the main advantages of the use of groundwater ecosystems for examining the importance of stochasticity in controlling microbial community succession is that dispersal is not a major limiting factor influencing community assembly at the local scale examined (<10 m) due to high hydraulic conductivity. The experimental results indicated that the succession of groundwater microbial communities in response to nutrient amendment is primarily stochastic but that the drivers controlling biodiversity and succession are temporally dynamic rather than static (35). These results are also consistent with findings from several previous studies showing the importance of ecological stochasticity in driving macroorganism community succession (31, 153, 257).

QUANTIFYING COMMUNITY ASSEMBLY PROCESSES

A Quantitative Framework

Although ecological stochasticity has been widely studied by using various approaches, as described above, few approaches were available to further disentangle and quantify the relative importances of the four fundamental ecological processes until several recent attempts based on null model analyses were made. As an exploratory effort, a null-modeling-based statistical framework was developed by Stegen et al. (37, 109) to quantify the contributions of various ecological processes (e.g., selection and dispersal) to microbial community structure, succession, and biogeography (37, 68, 100, 101, 109, 152) (Fig. 3).

FIG 3.

Ecological processes shaping microbial community diversity in the context of the determinism-versus-stochasticity dichotomy. This scheme shows different steps in partitioning various ecological processes based on both phylogenetic and taxonomic diversity under the assumptions discussed in text. βNTI (β nearest-taxon index) is based on a null model test of the phylogenetic β-diversity index βMNTD (β mean nearest-taxon distance), and RC_Bray (modified Raup-Crick index) is based on a null model test of the Bray-Curtis taxonomic β-diversity index. The two boxes indicate the major components of deterministic selection and the undominated fraction, respectively. Besides less-influential selection, the weak selection in the undominated fraction may also result from counteracting influential selective factors and/or a contrasting selection of different taxa. The diagram was made primarily based on data reported previously by Stegen et al. (37, 109).

In this framework, the variation or turnover of both phylogenetic diversity and taxonomic diversity is first measured with null-model-based phylogenetic and taxonomic β-diversity metrics (βNTI, βNRI, and RC_Bray). The conservation of phylogenetic signals is then tested against different environmental variables, followed by the choice of appropriate phylogenetic metrics, βNTI or βNRI, for subsequent analysis. Next, selection is partitioned based on the phylogenetic diversity of a targeted gene across various communities. Since homogeneous selection leads to communities that are phylogenetically more similar, the percentage of homogeneous selection is estimated as the fraction of pairwise comparisons with a βNTI value of <−2. In contrast, heterogeneous selection, which results in communities that are less similar in phylogeny, is quantified as the fraction of pairwise comparisons with a βNTI value of >+2. Subsequently, the taxonomic β-diversity metric RC_Bray is used to further partition the pairwise comparisons with an absolute βNTI value of <2 (i.e., these pairwise comparisons are not assigned to selection). Similarly, because homogenizing dispersal produces communities that are more taxonomically similar, the relative influence of homogenizing dispersal is quantified as the fraction of the pairwise comparisons with an absolute βNTI value of <2 and an RC_Bray value of <−0.95. On the other hand, dispersal limitation leads to communities that are less similar in taxonomy, and hence, dispersal limitation is quantified as the fraction of the pairwise comparisons with an absolute βNTI value of <2 and an RC_Bray value of >0.95. Finally, the fraction of the pairwise comparisons with an absolute βNTI value of <2 and an absolute RC_Bray value of <0.95 was treated as an “undominated” fraction, which mostly consists of weak selection, weak dispersal, diversification, and/or drift (37).

At the moment, no methods are available to further partition different components. Besides the little influence of selection, “weak” selection could also be caused by influential selective forces counteracting each other and/or contrasting selection (i.e., some taxa are under homogeneous selection, but some others are under heterogeneous selection), which could lead to random phylogenetic patterns (101). In addition, it should be noted that the “selection” fraction detected by this approach could also include deterministic components of dispersal (e.g., active propulsion) and some degree of diversification, such as those derived from positive mutations (Fig. 3).

Simulation modeling analysis with predefined expectations indicated that this new framework could accurately predict the relative importance of various ecological processes in controlling spatial turnover among different communities (37). This new framework has been applied to a limited number of microbial communities, and some very interesting insights were obtained (37, 68, 100, 101, 109, 151, 152). For example, using this new framework, Stegen et al. (109) showed that the spatial turnover of the subsurface microbial communities in deeper finer-grained sediments were controlled majorly by selection (60% of the turnover). However, in shallower coarser-grain sediments, selection was weaker (∼30% of the turnover). Also, dispersal limitation contributed about 30% of the spatial turnover, while homogenizing dispersal explained about 20% of the spatial variation. In addition, undominated processes (37) control 25% of the spatial turnover. This new framework provides inferences of the relative importance of ecological processes in mediating community assembly, which could not be achieved by using previous approaches (109). This represents a significant advance in microbial ecology because this is the first time that microbial ecologists are able to obtain quantitative information on community assembly processes from a statistical perspective.

Although this new statistical approach provided valuable insights into the contributions of ecological processes to microbial community structure and succession (37, 68, 109, 152), there are several limitations of this approach. First, selection is estimated as the fraction of pairwise community comparisons with an absolute βNTI value of >2 at the whole-community level (37, 109). In this way, at an absolute βNTI value of >2, the turnover of the entire community is considered to be under strong selection. This may not be appropriate because it is well known that the action of natural selection typically occurs on the level of individual populations. Within a microbial community, while some populations are under natural selection, some could be under strong drift. This kind of difference cannot be identified by a metric at the whole-community level. In a recent study on a groundwater microbiome, this framework was applied to different classes separately instead of the whole community, and the results demonstrated taxon-specific assembly processes (101). Since this framework could also be applied to any functional gene/trait with a phylogenetic signal, further improvements can be achieved by focusing on functional genes to obtain higher resolution. Second, diversification is an important evolutionary and ecological process underlying microbial community assembly (67, 72, 108), but it is not accounted for in this framework (37). Third, in the extended framework, ecological drift was mixed with weak selection and dispersal (37, 68, 152). It would be highly desirable to determine the relative importance of ecological drift for controlling community dynamics by further parsing it out (37). In addition, a broad application of this framework to different microbial communities from diverse habitats is necessary to validate its generality and applicability.

Underlying Assumptions of the Statistical Framework

There are several important assumptions underlying the above-described framework, although they are not explicitly expressed in the original publications. The first assumption is that phylogenetic diversity reflects the diversity of functional traits. In community phylogenetics, one important belief is that community assembly is mediated through functional traits, and thus, the trait dispersion of a community is assumed to signify particular community assembly processes (262). Because of niche conservatism, that is, the tendency of species to retain ancestral ecological characteristics (263), phylogenetic diversity is often used as a proxy for functional trait diversity to infer the underlying community assembly processes if there is a strong correlation between phylogenetic distance and niche differences, i.e., phylogenetic signals (62). The existence of phylogenetic signals can be tested to some extent by multivariate analysis (62, 109), but this faces some difficulties. First, niche differences are the results of multiple parameters (e.g., pH, temperature, and salt), and not all of them will have a strong phylogenetic signal or similar phylogenetic signals (264). Many ecological niches are not or cannot be measured. It is not clear whether phylogenetic signals exist for these unmeasured niches. Also, due to rapid adaptive evolution, in general, a microbial phylogenetic signal exists only within a short phylogenetic distance, among closely related microorganisms (62, 68, 109, 265). The estimation of phylogenetic distance among closely related microorganisms could be highly susceptible to sequencing errors, quantitative accuracy, reproducibility, and the uncertainty of phylogenetic trees due to different tree construction approaches (69, 160, 266). In addition, horizontal gene transfer among microorganisms could be a significant problem by swiping out phylogenetic signals, especially for some functional traits (e.g., antibiotic resistance), which leads to a phenomenon where ecologically similar organisms are not phylogenetically closely related (267). Fortunately, a recent review showed that microbial traits appear to be phylogenetically conserved (268), and there were strong phylogenetic signals for many microbial traits (264). However, it should be noted that the results from such analyses could vary substantially with the taxonomic/phylogenetic resolutions of the molecular markers used. For instance, the widely used short sequences from the 16S rRNA gene (e.g., V3-V4 regions) are able to resolve differences only at the genus or family level (69). Such a coarse level resolution may not be sufficient to allow the detection of ecological forces at the species and strain levels.

The second underlying assumption is that phylogenetic information is better than taxonomic information for discerning some ecological processes, particularly selection. Historically, both phylogenetic diversity and taxonomic diversity have been used to infer community assembly mechanisms (e.g., deterministic versus stochastic) (31, 62, 83, 109, 153, 205). However, in this framework, both types of diversity are not considered equal in discerning community assembly mechanisms, particularly because of the phylogenetic signals detailed above. This framework first uses phylogenetic β-diversity to parse out the importance of selection, followed by the use of taxonomic β-diversity for dispersal and other processes. This implies that phylogenetic diversity is more informative than taxonomic diversity in reflecting selection. This assumption may be valid, as a recent perspective article argued that phylogenetic diversity better represents ecological differences of functional traits (269). This is because phylogenetic diversity, especially the abundance-weighted phylogenetic metric, encompasses information on both evolutionary history and the ecology of organisms (269).

The third underlying assumption is that there are differential effects of ecological processes on community structure. The proposed statistical framework partitions ecological processes in the following order: selection, dispersal, and undominated processes (including diversification, drift, weak selection, and weak dispersal). The underlying assumption for such a sequential analysis is that all ecological processes are important in shaping community structure, but selection has a more pronounced influence than dispersal and other processes. This assumption appears to hold, as numerous studies demonstrate that selection is critical for governing community structure at a small local scale, while dispersal and diversification are key contributors to the regional species pool (30, 142). If one is more interested in the research question of how deterministic and stochastic processes shape community structure at the local scale, diversification and dispersal should become less important than selection (108). Therefore, it should be reasonable to define the effects of selection on community structure first, followed by parsing out the effects of regional factors such as dispersal and diversification. Drift, as a pure stochastic process embedded in the null hypothesis of all null models, should be the remaining part.

Another underlying assumption is that the methods used at each step can effectively parse out the importance of various ecological processes: selection by phylogenetic β-diversity and dispersal by taxonomic β-diversity. Although simulation model analysis indicated that this approach can effectively delineate the effects of various processes on community assembly (37), it is still less certain whether this approach is effective for all communities. Intuitively, its effectiveness could vary with the complexity and dominant processes of the community assembly. For instance, this approach could be very effective if deterministic processes dominate, but it could be less reliable if stochastic processes are more important. The effectiveness of this approach could also vary with the spatial scales examined, sampling efforts, sampling errors, taxonomic/phylogenetic resolution of molecular markers, null model algorithms, and community similarity metrics (35, 203).

It is worthwhile to note that ecological selection, dispersal, diversification, and drift are generally not directly measurable in community ecology. Similar to the situation of ecological neutrality (270), the above-described framework provides statistical estimations of ecological processes, and they should be treated as statistical proxies for various ecological processes for several reasons. First, because of possible violations of the above-described assumptions underlying this framework, it could be difficult to obtain measurements close to the “true” values. Second, there are some statistical uncertainties associated with each step, especially with the variation of null model algorithms, community similarity metrics, regional pool size, and incidence or abundance data. The estimated values for various ecological processes could vary considerably with different choices. In addition, particularly for microbial studies, due to the complexity of natural ecosystems and the inherently high variation of molecular methods for sampling and associated analyses (160, 161, 266, 271), obtaining accurate estimations of experimental data could be very challenging. For the above-mentioned reasons, it might be wise to adopt a pragmatic definition for different terms, such as statistical selection, statistical dispersal, statistical diversification, and statistical drift. Similar to the situation for stochasticity and determinism (34, 272), the operational distinction among these processes can appear somewhat arbitrary. Although there might be differences, or even considerably large differences, between the statistically measured values and true values of ecological processes, this conceptual framework should be useful for comparative purposes. If all communities are analyzed in the same way, the results should be more comparative and meaningful on a relative basis.

CONCLUDING REMARKS AND FUTURE PERSPECTIVES

Unraveling the mechanisms underlying biodiversity has recently received a great deal of attention in microbial ecology research. In contrast to traditional wisdom, over the last decade, various theoretical, observational, and/or experimental studies clearly demonstrate the importance of stochastic processes in shaping microbial community structure, succession, and biogeography (e.g., see references 32, 33, 35, 36, 64, 177, 178, 193, and 273). However, most of those studies are based on taxonomic and/or phylogenetic diversity but not functional diversity. It is believed that species functional traits (i.e., functional diversity) could have critical impacts on mediating stochastic community assembly (137). Future microbial community assembly studies must consider functional diversity along with taxonomic and phylogenetic diversity (239, 274). New statistical approaches considering functional diversity within the context of microbial community assembly are also needed (63, 69). Such functional-trait-based approaches could be useful for inferring the relative importance of environmental filtering versus biotic interactions (e.g., competition) in shaping community structures (275–277). In addition, new methods to integrate all relevant data (e.g., taxonomic, phylogenetic, functional, environmental, and spatial) are needed to address interesting ecological hypotheses.

Vellend's conceptual framework for classifying ecological processes as selection, dispersal, drift, and diversification is well received in the field of microbial ecology (67, 72). Statistical approaches to quantify selection and dispersal have been developed in accordance with this framework (37, 68, 109). However, diversification is not incorporated into the theoretical framework (37, 68). Diversification could play key roles in shaping microbial community structure via mediating regional species pools over large spatial and temporal scales (34). Thus, novel approaches for quantifying the relative importance of diversification and integrating it into the existing framework are urgently needed. A recently developed approach using the randomization of nucleic acid sequences of a marker gene (195) could provide a useful way to quantify the relative importance of diversification.

Ecological drift is a central concept in community ecology. Because drift is strongly affected by selection, dispersal, and diversification, it is a great challenge to detect drift, especially in microbial communities. Given the large population sizes and high dispersal potential, it is often assumed that drift is not important in microbial communities, which may not be valid (72). To detect ecological drift in microbial communities, future studies should focus on investigating the dynamics of rare taxa and/or active populations under similar or identical environmental conditions with a well-replicated experimental design (35, 36, 72). Also, it is difficult to estimate the relative importance of ecological drift with recently developed frameworks (37, 68, 109), because it is mixed with other processes in the undominated fraction. Novel approaches to separate the effects of drift and diversification in the undominated fraction are needed. In addition, neutral and niche models, as well as different approaches (e.g., multivariate, neutral model, and null modeling approaches), should be integrated together in complementary and reinforcing fashions for systematically assessing the importance of ecological stochasticity (e.g., drift and stochastic colonization), because no approach is perfect (33, 100, 101, 239). Such integration will be even more powerful if combined with experimental approaches to determine the importance of ecological stochasticity. However, it is still challenging to integrate various approaches in data analyses and interpretation for quantifying ecological drift as well as other processes. Machine-learning-based new computational approaches could greatly help in ameliorating integration problems.

Although great insights have been obtained over the last decade, the majority of studies on disentangling the mechanisms controlling community assembly are based on observational surveys. Direct experimental manipulation of community diversity and assembly history is becoming increasingly important because observational survey data are always compounded by various other factors (34). However, experimental manipulation of assembly processes of microbial communities, especially in natural settings, is extremely difficult. New, well-replicated, and controlled experimental strategies and approaches, such as synthetic ecosystems that resemble natural ecosystems (278), should be very valuable for rigorously evaluating the relative importance of deterministic versus stochastic processes in community structure and succession (136, 279). Such synthetic ecosystems could allow researchers to precisely control microbial diversity (e.g., diversity level and species traits), the parameters of system inputs and outputs, assembly processes (e.g., colonization order and dispersal), and environmental factors (280). Also, directly altering microbial communities to test assembly theories in the field is even more challenging. Coupling theoretical analyses with ecosystem management efforts to obtain well-replicated time series data could be a viable way to test the concepts and theory of community assembly and succession in field settings (35, 136).

There is a very limited understanding of whether and how community assembly history affects ecosystem functioning (36, 253). Numerous studies demonstrated that biodiversity is important for ecosystem functioning (e.g., see references 281 and 282), but the underlying mechanisms shaping the relationships between microbial biodiversity and ecosystem functioning are less clear. Several recent studies indicated that stochastic processes are important for regulating both microbial community structure and functions (36, 253), but more systematic examinations across diverse ecosystems are necessary to understand whether stochastic community assembly processes affect ecosystem functioning and how environmental factors influence the relationships between microbial community assembly and ecosystem functioning. New, functional-trait-based frameworks to integrate various ecological processes (selection, dispersal, drift, and diversification) within the context of ecosystem functioning are needed, particularly from an evolutionary perspective (67). However, the identification and measurement of functional traits important for microbial community assembly and ecosystem functioning are a great challenge (67).

One of the main objectives in the field of microbial ecology is to be able to project a future scenario of microbial community structure and functions in a changing environment. However, stochastic community assembly poses a serious challenge to predictive microbial ecology research because stochastic processes make the structure and functions unpredictable (69). As a result, the majority of previous studies on microbial ecology were focused on deterministic processes and ignored the importance of stochastic processes (283). Despite this challenge, considerable progress was made in understanding the importance of stochastic community assembly in ecological communities. Although stochastic processes are unpredictable, the factors and conditions affecting stochastic community assembly are more or less predictable. For instance, as mentioned above, stochastic community assembly will more likely occur when there is a small habitat, a large species pool, high productivity, low disturbance, and/or low predation. By understanding the factors and conditions affecting stochastic community assembly, it is still feasible to predict the range of possibilities of stochastic community assembly (137). Thus, some important future research questions should focus on when ecological stochasticity should matter and when it should not (137). Microbial community ecology will become more predictable by determining when and under which conditions a microbial community will be more sensitive to stochastic processes. Such knowledge can also be used for assisting biodiversity preservation, ecosystem restoration, environmental management, agricultural management, and disease control (31, 35, 137). The appropriate manipulation of a community assembly history could serve as a useful tool in ecosystem management for achieving the desired ecosystem functions (137, 253).

Biographies

Jizhong Zhou is the George Lynn Cross Research Professor in the Department of Microbiology and Plant Biology and Director for the Institute for Environmental Genomics at the University of Oklahoma, Norman, OK. He is also a senior scientist at Lawrence Berkeley National Laboratory, Berkeley, CA, and a professor at Tsinghua University, Beijing, China. His expertise is in molecular biology, microbial genomics, microbial ecology, molecular evolution, theoretical ecology, and genomic technologies. He received a Presidential Early Career Award for Scientists and Engineers in 2001, and in 2014, he received an E. O. Lawrence Award, the highest scientific recognition by the U.S. Department of Energy. He won an R&D 100 Award in 2009 for one of 100 most innovative scientific and technological breakthroughs. He is an editor of the ISME Journal and mBio and a former editor of Applied and Environmental Microbiology. He is a Fellow of the American Academy of Microbiology and the American Association for the Advancement of Science.

Daliang Ning obtained his B.E. and Ph.D. in Environmental Science and Engineering with an emphasis on environmental microbiology from Tsinghua University in Beijing, China. After postdoctoral research at Tsinghua University, Dr. Ning joined Prof. Jizhong Zhou's laboratory as a postdoctoral research associate. He is currently a Research Scientist in the Consolidated Core Laboratory, Institute for Environmental Genomics, Department of Microbiology and Plant Biology, and the School of Civil Engineering and Environmental Sciences, University of Oklahoma, Norman, OK. His current research interests include microbial community assembly mechanisms in various ecosystems, global/continental-scale microbiome patterns and processes, and microbial ecology in environmental engineering.