Abstract
The observation of micrometer size spin relaxation makes graphene a promising material for applications in spintronics requiring long-distance spin communication. However, spin dependent scatterings at the contact/graphene interfaces affect the spin injection efficiencies and hence prevent the material from achieving its full potential. While this major issue could be eliminated by nondestructive direct optical spin injection schemes, graphene’s intrinsically low spin–orbit coupling strength and optical absorption place an obstacle in their realization. We overcome this challenge by creating sharp artificial interfaces between graphene and WSe2 monolayers. Application of circularly polarized light activates the spin-polarized charge carriers in the WSe2 layer due to its spin-coupled valley-selective absorption. These carriers diffuse into the superjacent graphene layer, transport over a 3.5 μm distance, and are finally detected electrically using Co/h-BN contacts in a nonlocal geometry. Polarization-dependent measurements confirm the spin origin of the nonlocal signal. We also demonstrate that such signal is absent if graphene is contacted to bilayer WSe2 where the inversion symmetry is restored.
Keywords: two-dimensional materials, spintronics, valleytronics, spin injection, graphene
Spintronics has been proposed for applications in logic devices as a complement or even an alternative to devices based on the charge degree of freedom.1,2 Searching for the ideal material that can transport spin-dependent currents beyond micrometer size distances (e.g., spin interconnects) has been one of the main focuses of spintronics research.2,3 In this respect, graphene is promising due to its low spin–orbit coupling,4 negligible hyperfine interaction,5 large Fermi velocity,6 and very high electronic mobility.7 Indeed, it exhibits the longest spin relaxation length at room temperature probed by magnetoresistance electrical measurements using ferromagnetic electrodes.8,9 However, even these record values are still orders of magnitude smaller than its intrinsic limit.6 The origin of this striking difference between theoretically predicted and experimentally observed spin relaxation lengths could still be spin-dependent scatterings at the graphene–ferromagnetic electrode interfaces despite the recent advances in creating high quality tunnel barriers.10−13 Nondestructive optical spin injection schemes could be an appealing alternative. However, the absence of sufficient spin–orbit coupling and weak optical absorption of graphene poses challenges for their implementation.14 The absence of optospintronics functionality in graphene is also a serious limitation for the prospect of potential graphene spintronics applications.
In contrast, transition metal dichalcogenides (TMDCs) exhibit strong light absorption even in their monolayers.15,16 Monolayer TMDCs also have spin-valley physics, which has captured the interest of the solid state physics community.17−19 Due to the broken spin degeneracy and the time-reversal symmetry, the spin and valley degrees of freedom are coupled in such a way that excitation by opposite handedness leads to preferential population of the K or K′ valley with a defined spin orientation. Among TMDCs, tungsten diselenide (WSe2) gets special attention due to the achievement of valley polarization value close to unity and large external quantum efficiency.20,21 More importantly, we choose WSe2 because it has the strongest spin–orbit induced splitting among TMDCs (∼450 meV22) and its use is expected to result in a more efficient spin injection than in the case of MoS2.23 As proposed by Gmitra and Fabian,14 the generation of spin polarized charge carriers by using its spin coupled valley selective absorption property24 could allow inducing spin dependent currents in the superjacent graphene layer through a tunneling process, without the need for a ferromagnetic spin injector.
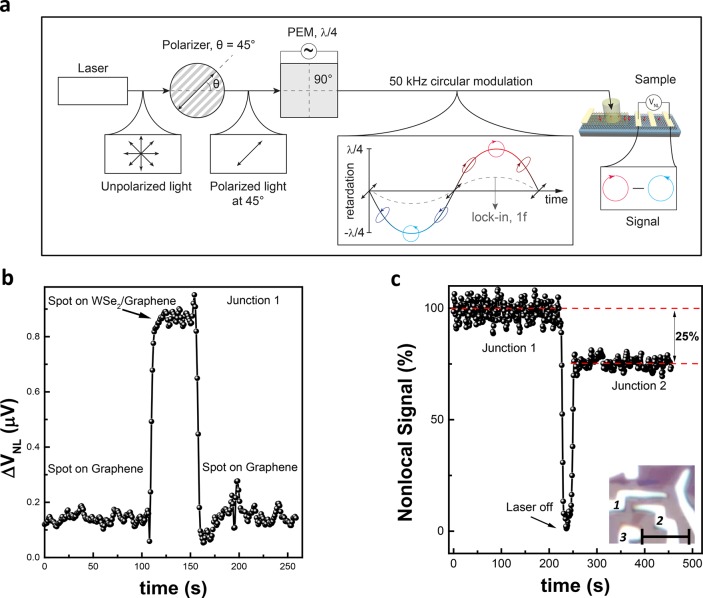
Toward this, we fabricated heterostructure devices consisting of monolayer WSe2, monolayer graphene, and h-BN on a conventional SiO2 (∼270 nm)/Si wafer (Figure 1a). In order to ensure clean interfaces in h-BN/WSe2/graphene heterostructure, we utilize the dry transfer method described in ref (6) and anneal samples under high vacuum conditions. Device fabrication is completed by forming the Ti/Co (10nm/35nm) electrodes. Figure 1b shows the optical images for one of our typical heterostructure devices at different fabrication steps. The final structure has an additional Co/h-BN/graphene region, which is crucial for the electrical detection of the generated spin signal. We note that such a stack could also host tunable magnetic proximity effects and hence allow the possibility of additional control of spin transport by gating.25 In order to detect the nonlocal voltage signal, the lock-in technique is combined with a photoelastic modulator (PEM), acting as a time-dependent variable waveplate. The linear polarizer in front of PEM is used to control the angle between incident light polarization and the optical axis of the modulator (See Methods and Supporting Information). In this study, we characterized five different devices. Here, we represent results obtained in two different optospintronic devices, labeled as device A and device B. Unless otherwise stated, the results shown are from device A. In order to achieve the highest signal-to-noise ratio for a clearer signal, we performed measurements at 4 K.
Figure 1.
Schematics and device fabrication. (a) Schematics of the device. Electrodes 1, 2, and 3 represent the Co electrodes, which have direct contacts to the graphene/h-BN portion of the device. Electrodes 1 and 2 are used as detector electrodes for junctions 1 and 2, respectively, and electrode 3 is used as the reference electrode during nonlocal measurements. The incident beam is focused on WSe2, close to the region at the graphene side. The red spheres with arrows represent the spin generation and diffusion during a nonlocal spin valve measurement. (b) Optical image of a typical device at various fabrication stages. WSe2 is transferred onto initially exfoliated graphene stripe. Then, the h-BN layer is transferred which is followed by the evaporation of the ferromagnetic Co electrodes.
Results and Discussion
Prior to any optical measurements, we first characterized a graphene-based spin valve device with trilayer h-BN used as a tunnel barrier. Figure 2a shows the device conductivity as a function of back-gate voltage (VBG). Our device characteristically shows the typical ambipolar field effect behavior. The charge neutrality point is observed at negative VBG values, which indicates the weak n-doped nature of graphene. Such doping is common for spin valve devices.12 From the four-terminal measurement configuration, we extract an electron mobility of ∼5500 cm2/(V·s) at ∼1 × 1012 cm–2 carrier concentration. At low bias range, we observe a nearly linear I–V relation (Figure 2b, inset). As the next step, we perform all-electrical spin injection, transport, and detection measurement in a nonlocal geometry (Figure 2a, inset).26 For this, we apply a fixed current of 5 μA between electrodes 1 and 2 and record the nonlocal voltage between electrodes 3 and 4 while sweeping the in-plane magnetic field B∥. This changes the relative polarization orientations of the injector (2) and detector (3) electrodes and induces a nonlocal spin signal of ∼0.2 Ω (Figure 2b). In order to determine the spin polarization (P) of electrodes (Co/3 layers of h-BN), which will be later employed for detecting the optically generated spin signal, we perform conventional Hanle precession measurements.26,27 Here, the nonlocal signal is recorded while the out-of-plane magnetic field B⊥ is swept in the range of ±150 mT (Figure 2c). Since the spin-dependent current precesses along the field, the signal decreases (increases) for the parallel (antiparallel) configuration as the strength of B⊥ is increased. The resulting signal can be fitted with the solution of the Bloch equation,11
where L ≈ 4 μm is the center-to-center separation between the injector and detector electrodes and ΩL is the Larmor frequency. This gives a spin relaxation time of τS ≈ 131 ± 1 ps, a spin diffusion constant of DS ≈ 0.123 m2/s, and hence, a spin relaxation length of λS ≈ 4 μm at VBG = 0 V. These spin transport properties are comparable to those of typical graphene spin valves11−13 but lower than for state-of-the-art graphene spin valves.9 In our device structure, the h-BN layer also acts as an encapsulation layer. This excludes polymer residues as the source of spin scattering in our devices.28 The limiting factor could be the contact-induced spin scattering. We believe that spin transport parameters in our device architecture could be enhanced by carefully engineering the number of h-BN layers to completely suppress the conductivity mismatch issue.10
Figure 2.
Electrical characterization of the graphene spin valve with a h-BN tunnel barrier. (a) Back-gate voltage dependence of graphene conductivity. Inset shows the I–V dependence of injector and detector electrodes. They are labeled 2 and 3, respectively in the schematics shown in the inset of panel b. (b) Nonlocal signal as a function of in-plane magnetic field. Black and red horizontal arrows represent the magnetic field sweeping directions. Vertical arrows represent the relative magnetization directions of the injector and detector electrodes. Inset: Schematics for nonlocal spin transport measurement. A charge current of 5 μA is applied from electrode 1 to 2, and the generated spin current is detected by probing the electrochemical potential differences between electrodes 3 and 4. (c) Hanle precession of the nonlocal signal as a function of the perpendicularly applied magnetic field. Measurements are performed at VBG = 0 V. (d) Back-gate voltage dependence of spin relaxation length, spin relaxation time, and spin injection efficiency.
Spin polarization value can be calculated from29
where w and σ are the width and conductivity of graphene, respectively. By inserting the λS extracted from spin precession measurements, we calculate P to be ∼0.6%. Next, we repeat spin Hanle precession measurements as a function of VBG. The spin parameters extracted above strongly depend on the VBG: both λS and τS values are observed to be highest near the Dirac point (Figure 2d). The extracted P values have opposite VBG dependence: P value is smallest near the Dirac point and enhances up to 2.85% at high VBG values. We consistently observe a very similar response at all measured junctions within this device, which indicates the large size uniformity of three-layer thick h-BN. Note that these spin polarization values are an order of magnitude smaller than for the best tunnel barriers ever created for graphene.30 However, they are comparable to the values obtained using oxide based tunnel barriers28 and reliable enough for detecting the optically injected spin currents.
Next, we characterize our WSe2-graphene-h-BN heterostructure device. Figure 3a shows the VBG dependence of graphene conductivity for device A which is similarly measured by using trilayer Co/h-BN electrodes. We observe ambipolar characteristic with a weak n-type doping. The corresponding I–V characteristic is also linear at low bias range. These results are consistent with the device performance shown in Figure 2a. This suggests that our electrode could serve as a spin detector. In order to determine how monolayer WSe2 affects electrical transport of the graphene channel when the former is transferred on top of the latter, we have fabricated another device, shown in Figure 3b inset. The design of this device allows us to perform four-terminal measurements independently on the pristine graphene as well as on the same graphene flake with monolayer WSe2 on top. Sheet resistance shown in Figure 3b reveals similar behavior of both regions in a reasonable proximity to the Dirac point. We extract an electron mobility of ∼5200 cm2/(V·s) and ∼5800 cm2/(V·s) at ∼1 × 1012 cm–2 carrier concentration for pristine graphene and WSe2/graphene heterostructure, respectively. This result indicates the absence of any obvious effect of large band gap material WSe2 on graphene transport properties while the Fermi level is kept in the band gap of the former material. Prior to optical spin injection, we also optically characterize the WSe2 flake in our device. In addition to the flake optical contrast, we confirm the monolayer nature of WSe2 by photoluminescence measurements using a 488 nm blue laser diode with low incident power of 40 μW. As shown in Figure 3c, we observe a strong peak X0 near 1.66 eV corresponding to the excitonic resonance in a monolayer flake. We can also distinguish the lower energy X′ peak that could be associated with the trion, localized exciton emission31 or shortwave plasmons (See Supporting Information).32
Figure 3.
Electrical characterization of the optospintronic devices. (a) Back-gate voltage dependence of graphene conductivity. Inset shows the I–V dependence of electrodes 1 and 2, which are indicated in the optical image in Figure 4c. (b) Back-gate voltage dependences of the four-terminal resistivity of the pristine graphene (black) and of the WSe2/graphene heterostructure (red). Inset shows the optical image of the device. Scale bar is 5 μm. (c) Photoluminescence measurements of monolayer WSe2.
Now we turn our attention to the optical spin injection aspect of our study. The schematic of the device setup is shown in Figure 4a. We polarize the initially unpolarized light beam using a linear polarizer oriented 45° to the optical axis of the photoelastic modulator (PEM). This orientation of the incident light provides the highest degree of modulated light circularity. PEM acts as a variable birefringent plate providing time-dependent retardation along one of the axes at a frequency of 50 kHz (1f). In the case of λ/4 modulation, applied retardation has maximal (minimal) value of λ/4 (−λ/4) with the PEM acting as a quarter wave plate at these moments, thus generating the right (left) circularly polarized light. Lock-in amplification of the nonlocal signal with the PEM (1f) fundamental frequency (50 kHz, gray dashed line) results in a signal that corresponds to the variation of the nonlocal signal caused by the right- and left-handed light. Therefore, the resulting light modulation is right-to-left (left-to-right) in the case of 45° (−45°) incidence angle. This measurement configuration minimizes background-related artificial signals. In order to ensure the full out-of-plane direction magnetization of Co electrodes, we first apply B⊥ = 2 T33 and then set the field to B = 0. By keeping B = 0 T, we exclude any contribution from the valley-Zeeman effect.34 We note that the remaining out-of-plane magnetization of Co is sufficient for contacts to be used as spin signal detectors. Next, we focus the laser beam under quarter-wave modulation on the device and detect the generated nonlocal signal electrically in a nonlocal geometry. As shown in Figure 4b, we do not observe any significant nonlocal signal while the light spot is parked on graphene. In contrast, once the spot is placed on the WSe2/graphene heterostructure, we observe a sudden increase in the nonlocal voltage reaching 1 μV, even though the laser beam is much further away from the detector electrodes compared to the initial case with the laser spot on graphene. The signal returns back to its initial value of ∼0.1 μV when the spot is placed back on top of the graphene region. This measurement suggests that the measured signal is not due to spurious effects, such as laser heating. The nonlocal origin of the signal is confirmed by the length-dependent measurement. As shown in Figure 4c, the magnitude of the signal decreases ∼25% from the initial value if the electrode 2 is utilized as the detector, which is ∼3.7 μm far away from the graphene/WSe2 interface. This is expected within the spin transport theory as the spin dephases more while it travels a longer distance and therefore the measured signal amplitude decreases.1 It is also worth mentioning that the measured signal has a weak dependence on the location of the laser spot (See Supporting Information). This could be related to the local interface homogeneity.
Figure 4.
Optical spin injection into graphene. (a) Measurement schematics for achieving quarter wave modulation and electrical detection of nonlocal signal. (b) Time dependence of nonlocal signal while laser spot is moved from graphene to WSe2 and then back to graphene. Photoelastic modulator is used for enhancing the signal quality. (c) Nonlocal signal measured at junction 1 and 2. Junction 1(2) refers to the nonlocal voltage measured between electrodes 1 (2) and 3. Inset shows the optical image of the device. Scale bar is 3 μm.
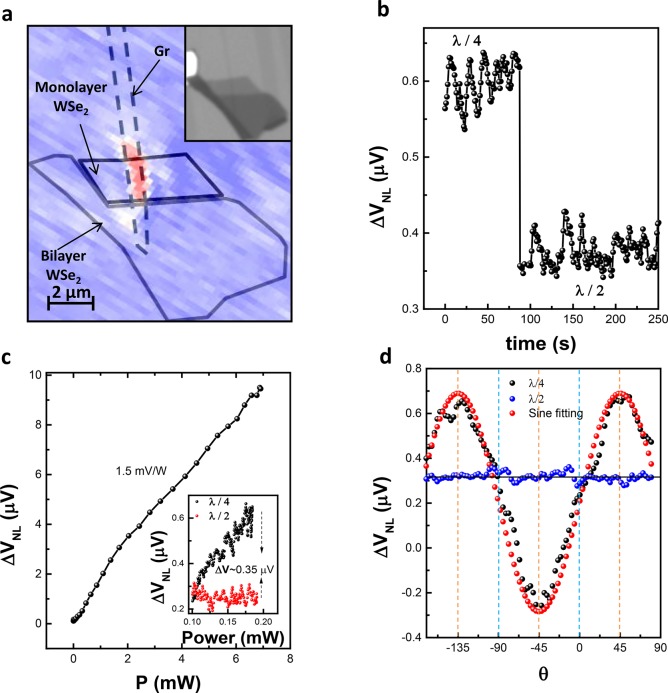
In order to confirm that the origin of the signal is the spin-coupled, valley-selective absorption, we compare the nonlocal signals generated at the monolayer WSe2/graphene and bilayer WSe2/graphene interfaces. Note that optical spin injection is not expected in the latter interface case as the inversion symmetry is restored in bilayer devices.18Figure 5a shows the spatial map of the nonlocal voltage signal measured in device B at VBG = 0 V. For direct comparison, the optical image of the device is shown in Figure 5a, inset. Similar to device A (Figure 4b), we detect the nonlocal voltage if only the laser spot is parked on the monolayer WSe2. As we move the spot on the bilayer WSe2 region, we observe a sudden suppression of the nonlocal voltage. This unequivocally proves the valley-selective origin of the signal.
Figure 5.
Polarization dependence of nonlocal signal. (a) Spatial map of the nonlocal voltage signal. The dotted line represents the monolayer graphene, black and blue solid lines represent the monolayer and bilayer WSe2 regions, respectively. The color scale bar is ∼1.2 μV as it moves from red to blue. (b) Nonlocal signal recorded with the incident light under quarter-wave and half-wave modulations. (c) Laser power dependence of nonlocal signal generated under quarter wave modulation. Inset: The dependence of nonlocal signal on the power of incident light. (d) Modulation of spin signal as a function of incident light polarization.
We also measure the nonlocal signal under quarter-wave (λ/4) and half-wave (λ/2) modulations of incident light so as to demonstrate the spin origin of this signal. Only the former modulation should result in the spin-dependent signal as the activation of a specific valley is only possible with the circularly polarized light, while the half-wave modulation does not meet this requirement (See Supporting Information). If the origin of the signal were not spin dependent, we would observe the same response under both modulations. Figure 5b shows the time dependence of the nonlocal voltage measured under λ/4, followed by λ/2 modulation. We observe a nonlocal signal of ∼0.62 μV for the case of λ/4 modulation and the signal drops significantly for the λ/2 modulation case. Unlike in the λ/4 modulation case, the signal is nearly independent of the incident laser power for the λ/2 modulation case as shown in Figure 5c, inset. We believe that this constant signal constitutes the background-related portion of our nonlocal signal. Its origin could be the finite resistance of graphene rather than any laser heating-related artifacts, as the signal does not change with increasing laser power. Importantly, the nonlocal signal under λ/4 modulation changes linearly with the laser power (Figure 5c). We measure ∼9.5 μV nonlocal signal under 6.2 mW laser power with slope close to ∼1.5 mV/W.
Importantly, we further prove the spin-valley coupling origin of the nonlocal signal by measuring its dependence on the ellipticity of the modulated light by modifying the incident angle (θ) (Figure 5d). A value of θ = +(−)45° indicates the modulation of polarization from right to left, R-L (left to right, L-R). As shown in Figure 5d, the nonlocal signal shows very strong dependence on θ, in a good agreement with the observation in Figure 5b. We observe a maximum signal of 0.6 μV under R-L modulation. The signal decreases and changes its sign as θ is changed. We observe a minimum signal of approximately −0.2 μV under L-R modulation. The signal for the linear/linear case is ∼0.3 μV and matches the value obtained for the λ/2 case, which was attributed to the background signal. As shown in Figure 5d, such incident angle dependence is completely absent for λ/2 modulation, which proves the optovalleytronic origin of the spin injection process.
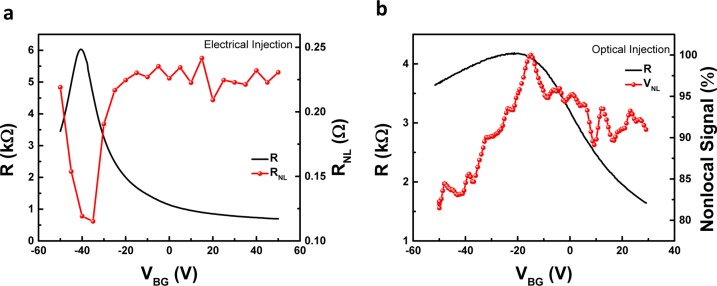
Finally, we compare the VBG dependence of the nonlocal signal generated by electrical and optical injection techniques. Figure 6a shows the VBG dependence of both charge resistance and the amplitude of the nonlocal resistance obtained by all-electrical measurements. We observe an inverse relation between the local resistance and the nonlocal resistance. The nonlocal signal is ∼0.12 Ω near the Dirac point, and as the VBG increases, the nonlocal signal increases 2-fold. Based on 1D diffusion spin transport theory,29 such inverse scaling indicates that our contacts are not tunneling, in a good agreement with the observation of linear I–V as shown in Figure 2a, inset. For the optical spin injection case, the scaling between device resistance and the nonlocal signal is completely different. The electrostatic doping decreases both the channel resistance and the nonlocal signal. We observe the maximum nonlocal signal at VBG = −20 V that matches the Dirac point of graphene (Figure 6b). Such direct scaling has previously been observed in graphene30 and black phosphorus35 spin valve devices and discussed to be the direct signature of tunneling spin injection.29 Here, note that the nonlocal signal at the hole conduction region decreases slightly faster than the electron conduction region, which could be due to enhanced barrier height between graphene and TMDC layers at lower VBG values.36−38
Figure 6.
Nonlocal signal as a function of back-gate voltage. Back-gate voltage dependence of local device resistance and nonlocal signal generated through (a) electrical and (b) optical injection.
Conclusion
In conclusion, we have demonstrated optical spin injection into graphene by benefiting from the spin-valley properties of monolayer WSe2. We activate the spin polarized charge carriers in the WSe2 layer by illuminating the crystal with circularly polarized light. The generated spin current diffuses into the graphene layer and transports over a distance of 3.5 μm before its electrical detection through a three layer thick h-BN tunnel barrier. A recent optical experiment in a graphene/TMDC based heterostructure suggests that induced charge carriers are electrons.39 We exclude any spurious effects by prudently studying the separation, power intensity and incident light polarization dependences on nonlocal signal. We also compare the nonlocal signals generated at the monolayer WSe2/graphene and bilayer WSe2/graphene interfaces in order to prove its spin-coupled, valley-selective absorption origin. Considering also the very recent Hanle precession measurements in similar structures,23 these results form the foundation of this emerging subfield of 2D heterostructures, which will be the key for the optospintronics functionality in graphene spintronics applications.
Methods
Device Fabrication
Our fabrication process starts with the mechanical exfoliation of monolayer graphene on a conventional SiO2 (∼270 nm)/Si wafer. Next, graphene is partially covered with monolayer WSe2 by utilizing the dry transfer method. Finally, a three-layer h-BN crystal is similarly transferred by targeting the uncovered region of graphene. Optical images for a heterostructure device at different fabrication steps are shown in Figure 1b. Before the metallization process, the heterostructure is annealed at 250 °C under high vacuum conditions (∼5 × 10–7 Torr) for 6 h. This process results in a cleaner interface between two-dimensional (2D) materials by removing the transfer-related residues. Electrode masks are prepared by utilizing a standard electron beam lithography technique. Device fabrication is finalized by forming the Co/Ti (35 nm/10 nm) electrodes. Deposition rate for both materials is ∼0.5 Å/s, and the Ti layer serves as a capping layer to prevent the oxidation of ferromagnetic Co electrodes.
Device Characterization Techniques
All-electrical spin transport measurements are performed with a standard AC lock-in technique at low frequencies and at fixed current bias in the four-terminal nonlocal spin valve geometry as a function of in-plane and out of plane magnetic field (B∥ and B⊥). For optoelectrical measurements, the monolayer WSe2 flake is resonantly excited at 720 nm (1.72 eV, black arrow in Figure 3b) using a supercontinuum laser with a maximal incident light intensity of 190 μW at 4 K. In order to detect the nonlocal voltage signal, the lock-in technique is combined with a photoelastic modulator (PEM), acting as a variable waveplate. The linear polarizer in front of PEM is used to control the angle between incident light polarization and the optical axis of the modulator. This way, in the case of quarter-wave modulation while using the fundamental frequency of PEM as the lock-in reference signal (50 kHz), the maximal amplitude of the signal should match the angle θ of +(−)45°, which corresponds to the right-to-left (RL) (left-to-right (LR)) modulation. During polarization dependent measurements, the ellipticity of the light is modified by changing the polarization angle θ. This decreases the signal amplitude, reaching the lock-in noise floor when incident light polarization is parallel to the PEM optical axis. For the experiment with linear light modulation, half-wave configuration of PEM was used with double frequency (100 kHz) as a reference signal.
Acknowledgments
We thank K. Marinov and J. Y. Tan for their help. We acknowledge the help of Z. Benes (CMI) with e-beam lithography. A.A., D.U., O.L.S., and A.K. acknowledge support by the H2020 European Research Council (ERC, Grant 682332), Swiss National Science Foundation (Grant 153298), and Marie Curie-Sklodowska-Curie Actions (COFUND grant 665667). A.K. acknowledges funding from the European Union’s Horizon H2020 Future and Emerging Technologies under grant agreement No 696656 (Graphene Flagship). B.Ö. acknowledges support by the National Research Foundation, Prime Minister’s Office, Singapore, under its Competitive Research Programme (CRP Award No. NRF-CRP9-2011-3), the Singapore National Research Foundation Fellowship award (RF2008-07), and SMF-NUS Research Horizons Award 2009-Phase II. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan, and JSPS KAKENHI Grant Numbers JP15K21722 and JP25106006.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b06800.
Further experimental results, half wave (λ/4) modulation by PEM, light modulation dependence on the polarization angle rotation, gate voltage dependence of extracted spin transport properties, photoluminescence spectra of WSe2, spot location dependence of nonlocal signal, and incident angle dependences of nonlocal signal for λ/2 and λ/4 modulations. (PDF)
Author Contributions
⊥ A.A. and D.U. equally contributed. A.A. and A.K. designed the experiments. A.A. fabricated the samples. A.A., D.U., J.L., and O.L.S. performed the measurements. K.W. and T.T. grew the h-BN crystals. B.Ö. supervised the all-electrical spin transport measurements. All authors discussed the results. A.A., D.U., and A.K. wrote the manuscript with input from all authors.
The authors declare no competing financial interest.
Supplementary Material
References
- Žutić I.; Das Sarma S.; Fabian J. Spintronics: Fundamentals and Applications. Rev. Mod. Phys. 2004, 76, 323–410. 10.1103/RevModPhys.76.323. [DOI] [Google Scholar]
- Wolf S. A.; Awschalom D. D.; Buhrman R. A.; Daughton J. M.; von Molnár S.; Roukes M. L.; Chtchelkanova A. Y.; Treger D. M. Spintronics: A Spin-Based Electronics Vision for the Future. Science 2001, 294, 1488–1495. 10.1126/science.1065389. [DOI] [PubMed] [Google Scholar]
- Dery H.; Wu H.; Ciftcioglu B.; Huang M.; Song Y.; Kawakami R. K.; Shi J.; Krivorotov I. N.; Telesca D. A.; Žutić I.; Sham L. J. Reconfigurable Nanoelectronics Using Graphene Based Spintronic Logic Gates. Proc. SPIE 2011, IV, 81000W. 10.1117/12.890318. [DOI] [Google Scholar]
- Gmitra M.; Konschuh S.; Ertler C.; Ambrosch-Draxl C.; Fabian J. Band-Structure Topologies of Graphene: Spin-Orbit Coupling Effects from First Principles. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 80, 235431. 10.1103/PhysRevB.80.235431. [DOI] [Google Scholar]
- Trauzettel B.; Bulaev D. V.; Loss D.; Burkard G. Spin Qubits in Graphene Quantum Dots. Nat. Phys. 2007, 3, 192–196. 10.1038/nphys544. [DOI] [Google Scholar]
- Han W.; Kawakami R. K.; Gmitra M.; Fabian J. Graphene Spintronics. Nat. Nanotechnol. 2014, 9, 794–807. 10.1038/nnano.2014.214. [DOI] [PubMed] [Google Scholar]
- Mayorov A. S.; Gorbachev R. V.; Morozov S. V.; Britnell L.; Jalil R.; Ponomarenko L. A.; Blake P.; Novoselov K. S.; Watanabe K.; Taniguchi T.; et al. Micrometer-Scale Ballistic Transport in Encapsulated Graphene at Room Temperature. Nano Lett. 2011, 11, 2396–2399. 10.1021/nl200758b. [DOI] [PubMed] [Google Scholar]
- Ingla-Aynés J.; Guimarães M. H. D.; Meijerink R. J.; Zomer P. J.; van Wees B. J. 24 – μ M Spin Relaxation Length in Boron Nitride Encapsulated Bilayer Graphene. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 201410. 10.1103/PhysRevB.92.201410. [DOI] [Google Scholar]
- Drögeler M.; Franzen C.; Volmer F.; Pohlmann T.; Banszerus L.; Wolter M.; Watanabe K.; Taniguchi T.; Stampfer C.; Beschoten B. Spin Lifetimes Exceeding 12 Ns in Graphene Nonlocal Spin Valve Devices. Nano Lett. 2016, 16, 3533–3539. 10.1021/acs.nanolett.6b00497. [DOI] [PubMed] [Google Scholar]
- Schmidt G.; Ferrand D.; Molenkamp L.; Filip A.; van Wees B. Fundamental Obstacle for Electrical Spin Injection from a Ferromagnetic Metal into a Diffusive Semiconductor. Phys. Rev. B: Condens. Matter Mater. Phys. 2000, 62, R4790–R4793. 10.1103/PhysRevB.62.R4790. [DOI] [Google Scholar]
- Tombros N.; Jozsa C.; Popinciuc M.; Jonkman H. T.; van Wees B. J. Electronic Spin Transport and Spin Precession in Single Graphene Layers at Room Temperature. Nature 2007, 448, 571–574. 10.1038/nature06037. [DOI] [PubMed] [Google Scholar]
- Avsar A.; Yang T.-Y.; Bae S.; Balakrishnan J.; Volmer F.; Jaiswal M.; Yi Z.; Ali S. R.; Güntherodt G.; Hong B. H.; et al. Toward Wafer Scale Fabrication of Graphene Based Spin Valve Devices. Nano Lett. 2011, 11, 2363–2368. 10.1021/nl200714q. [DOI] [PubMed] [Google Scholar]
- Kamalakar M. V.; Dankert A.; Bergsten J.; Ive T.; Dash S. P. Enhanced Tunnel Spin Injection into Graphene Using Chemical Vapor Deposited Hexagonal Boron Nitride. Sci. Rep. 2015, 4, 6146. 10.1038/srep06146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gmitra M.; Fabian J. Graphene on Transition-Metal Dichalcogenides: A Platform for Proximity Spin-Orbit Physics and Optospintronics. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 155403. 10.1103/PhysRevB.92.155403. [DOI] [Google Scholar]
- Li Y.; Chernikov A.; Zhang X.; Rigosi A.; Hill H. M.; van der Zande A. M.; Chenet D. A.; Shih E.-M.; Hone J.; Heinz T. F. Measurement of the Optical Dielectric Function of Monolayer Transition-Metal Dichalcogenides: MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 90, 205422. 10.1103/PhysRevB.90.205422. [DOI] [Google Scholar]
- Lopez-Sanchez O.; Lembke D.; Kayci M.; Radenovic A.; Kis A. Ultrasensitive Photodetectors Based on Monolayer MoS2. Nat. Nanotechnol. 2013, 8, 497. 10.1038/nnano.2013.100. [DOI] [PubMed] [Google Scholar]
- Zeng H.; Dai J.; Yao W.; Xiao D.; Cui X. Valley Polarization in MoS2 Monolayers by Optical Pumping. Nat. Nanotechnol. 2012, 7, 490–493. 10.1038/nnano.2012.95. [DOI] [PubMed] [Google Scholar]
- Mak K. F.; He K.; Shan J.; Heinz T. F. Control of Valley Polarization in Monolayer MoS2 by Optical Helicity. Nat. Nanotechnol. 2012, 7, 494–498. 10.1038/nnano.2012.96. [DOI] [PubMed] [Google Scholar]
- Sanchez O. L.; Ovchinnikov D.; Misra S.; Allain A.; Kis A. Valley Polarization by Spin Injection in a Light-Emitting van Der Waals Heterojunction. Nano Lett. 2016, 16, 5792–5797. 10.1021/acs.nanolett.6b02527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song X.; Xie S.; Kang K.; Park J.; Sih V. Long-Lived Hole Spin/Valley Polarization Probed by Kerr Rotation in Monolayer WSe2. Nano Lett. 2016, 16, 5010–5014. 10.1021/acs.nanolett.6b01727. [DOI] [PubMed] [Google Scholar]
- Withers F.; Del Pozo-Zamudio O.; Schwarz S.; Dufferwiel S.; Walker P. M.; Godde T.; Rooney A. P.; Gholinia A.; Woods C. R.; Blake P.; et al. WSe2 Light-Emitting Tunneling Transistors with Enhanced Brightness at Room Temperature. Nano Lett. 2015, 15, 8223–8228. 10.1021/acs.nanolett.5b03740. [DOI] [PubMed] [Google Scholar]
- Zhu Z. Y.; Cheng Y. C.; Schwingenschlögl U. Giant Spin-Orbit-Induced Spin Splitting in Two-Dimensional Transition-Metal Dichalcogenide Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 84, 153402. 10.1103/PhysRevB.84.153402. [DOI] [Google Scholar]
- Luo Y. K.; Xu J.; Zhu T.; Wu G.; McCormick E. J.; Zhan W.; Neupane M. R.; Kawakami R. K. Opto-Valleytronic Spin Injection in Monolayer MoS2 /Few-Layer Graphene Hybrid Spin Valves. Nano Lett. 2017, 17, 3877–3883. 10.1021/acs.nanolett.7b01393. [DOI] [PubMed] [Google Scholar]
- Muniz R. A.; Sipe J. E. All-Optical Injection of Charge, Spin, and Valley Currents in Monolayer Transition-Metal Dichalcogenides. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 085404. 10.1103/PhysRevB.91.085404. [DOI] [Google Scholar]
- Lazić P.; Belashchenko K. D.; Žutić I. Effective Gating and Tunable Magnetic Proximity Effects in Two-Dimensional Heterostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 93, 241401. 10.1103/PhysRevB.93.241401. [DOI] [Google Scholar]
- Johnson M.; Silsbee R. H. Interfacial Charge-Spin Coupling: Injection and Detection of Spin Magnetization in Metals. Phys. Rev. Lett. 1985, 55, 1790–1793. 10.1103/PhysRevLett.55.1790. [DOI] [PubMed] [Google Scholar]
- Jedema F. J.; Heersche H. B.; Filip A. T.; Baselmans J. J. A.; van Wees B. J. Electrical Detection of Spin Precession in a Metallic Mesoscopic Spin Valve. Nature 2002, 416, 713–716. 10.1038/416713a. [DOI] [PubMed] [Google Scholar]
- Avsar A.; Vera-Marun I. J.; Tan J. Y.; Koon G. K. W.; Watanabe K.; Taniguchi T.; Adam S.; Özyilmaz B. Electronic Spin Transport in Dual-Gated Bilayer Graphene. NPG Asia Mater. 2016, 8, e274. 10.1038/am.2016.65. [DOI] [Google Scholar]
- Takahashi S.; Maekawa S. Spin Injection and Detection in Magnetic Nanostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2003, 67, 052409. 10.1103/PhysRevB.67.052409. [DOI] [Google Scholar]
- Han W.; Pi K.; McCreary K. M.; Li Y.; Wong J. J. I.; Swartz A. G.; Kawakami R. K. Tunneling Spin Injection into Single Layer Graphene. Phys. Rev. Lett. 2010, 105, 167202. 10.1103/PhysRevLett.105.167202. [DOI] [PubMed] [Google Scholar]
- Yan T.; Qiao X.; Liu X.; Tan P.; Zhang X. Photoluminescence Properties and Exciton Dynamics in Monolayer WSe2. Appl. Phys. Lett. 2014, 105, 101901. 10.1063/1.4895471. [DOI] [Google Scholar]
- Van Tuan D.; Scharf B.; Žutić I.; Dery H.. Marrying Excitons and Plasmons in Monolayer Transition-Metal Dichalcogenides. 2017, https://arxiv.org/abs/1704.01981. [DOI] [PubMed]
- Tombros N.; Tanabe S.; Veligura A.; Jozsa C.; Popinciuc M.; Jonkman H. T.; van Wees B. J. Anisotropic Spin Relaxation in Graphene. Phys. Rev. Lett. 2008, 101, 046601. 10.1103/PhysRevLett.101.046601. [DOI] [PubMed] [Google Scholar]
- Srivastava A.; Sidler M.; Allain A. V.; Lembke D. S.; Kis A.; Imamoğlu A. Valley Zeeman Effect in Elementary Optical Excitations of Monolayer WSe2. Nat. Phys. 2015, 11, 141–147. 10.1038/nphys3203. [DOI] [Google Scholar]
- Avsar A.; Tan J. Y.; Kurpas M.; Gmitra M.; Watanabe K.; Taniguchi T.; Fabian J.; Özyilmaz B. Gate-Tunable Black Phosphorus Spin Valve with Nanosecond Spin Lifetimes. Nat. Phys. 2017, 13, 888. 10.1038/nphys4141. [DOI] [Google Scholar]
- Cui X.; Lee G.-H.; Kim Y. D.; Arefe G.; Huang P. Y.; Lee C.-H.; Chenet D. A.; Zhang X.; Wang L.; Ye F.; et al. Multi-Terminal Transport Measurements of MoS2 Using a van Der Waals Heterostructure Device Platform. Nat. Nanotechnol. 2015, 10, 534–540. 10.1038/nnano.2015.70. [DOI] [PubMed] [Google Scholar]
- Dankert A.; Dash S. P. Electrical Gate Control of Spin Current in van Der Waals Heterostructures at Room Temperature. Nat. Commun. 2017, 8, 16093. 10.1038/ncomms16093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan W.; Txoperena O.; Llopis R.; Dery H.; Hueso L. E.; Casanova F. A Two-Dimensional Spin Field-Effect Switch. Nat. Commun. 2016, 7, 13372. 10.1038/ncomms13372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roy K.; Padmanabhan M.; Goswami S.; Sai T. P.; Ramalingam G.; Raghavan S.; Ghosh A. Graphene-MoS2 Hybrid Structures for Multifunctional Photoresponsive Memory Devices. Nat. Nanotechnol. 2013, 8, 826–830. 10.1038/nnano.2013.206. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.