Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Oct 11;11(11):11024–11030. doi: 10.1021/acsnano.7b05033

Strong Carrier–Phonon Coupling in Lead Halide Perovskite Nanocrystals

Claudiu M Iaru †,*, Jaco J Geuchies ‡, Paul M Koenraad †, Daniël Vanmaekelbergh ‡, Andrei Yu Silov †,*
PMCID: PMC5707632  PMID: 29019652

Abstract

graphic file with name nn-2017-05033q_0005.jpg

We highlight the importance of carrier–phonon coupling in inorganic lead halide perovskite nanocrystals. The low-temperature photoluminescence (PL) spectrum of CsPbBr3 has been investigated under a nonresonant and a nonstandard, quasi-resonant excitation scheme, and phonon replicas of the main PL band have been identified as due to the Fröhlich interaction. The energy of longitudinal optical (LO) phonons has been determined from the separation of the zero phonon band and phonon replicas. We reason that the observed LO phonon coupling can only be related to an orthorhombically distorted crystal structure of the perovskite nanocrystals. Additionally, the strength of carrier–phonon coupling has been characterized using the ratio between the intensities of the first phonon replica and the zero-phonon band. PL emission from localized versus delocalized carriers has been identified as the source of the observed discrepancies between the LO phonon energy and phonon coupling strength under quasi-resonant and nonresonant excitation conditions, respectively.

Keywords: perovskite, nanocrystals, Fröhlich interaction, photoluminescence, phonon, carrier localization, crystal phase

Carrier–phonon scattering is a topic of great importance for understanding the transport properties of semiconductors, due to its impact on carrier mobilities. High mobilities are desirable in applications that rely on the efficient separation of electrons and holes, such as photovoltaics. Increased carrier mobilities in solar cell devices are linked to the efficient diffusion of carriers within the material.1−3 Similarly, light emitters benefit from increased carrier mobilities, which ensure efficient carrier injection and transport, and consequently high internal quantum efficiency for the devices.2 Additionally, the spectral width of light-emitting semiconductor devices is strongly linked to carrier–phonon interaction. As such, the importance of investigating the strength of carrier–phonon interaction in a given material becomes immediately clear.

In recent years, the scientific community has shown great interest in inorganic CsPbX3 (X = Cl, Br, I) perovskite nanocrystals, for use in optoelectronic devices, due to their highly efficient light emission and their highly tunable photoluminescence (PL) spectrum, which can be varied across the entire visible range.4 Interest in the photovoltaic applications of lead halide perovskites has led to extensive research on their transport properties, albeit mostly for organic–inorganic hybrid materials. While studies have proposed a number of mechanisms that could potentially limit carrier mobilities,5−7 longitudinal optical (LO) phonon scattering induces an intrinsic limit for room-temperature mobility in polar materials.8 LO phonon coupling via the Fröhlich interaction has been inferred from the temperature-dependent spectral broadening behavior of several commonly studied hybrid lead halide perovskite materials.9 In 2D Ruddlesen–Popper perovskite thin films, direct evidence of carrier–phonon coupling has recently been observed in the form of anti-Stokes lines, through low-temperature absorption and PL measurements.10 2D Ruddlesen–Popper perovskites represent a rather distinct class of perovskite materials, wherein the presence of long organic cations induces a crystal structure similar to quantum well superlattices. Consequently, exciton binding energies are significantly enhanced and effects such as carrier–phonon interaction become increasingly significant. As such, enhanced carrier–phonon interaction has been observed, involving different vibrational modes, which have been attributed to both the inorganic lead halide cage motion and rotations and bending of organic cations. Direct evidence of non-Fröhlich carrier coupling to low-energy transverse optical phonons has also been observed in the inorganic perovskite CsPbBr3.11,12

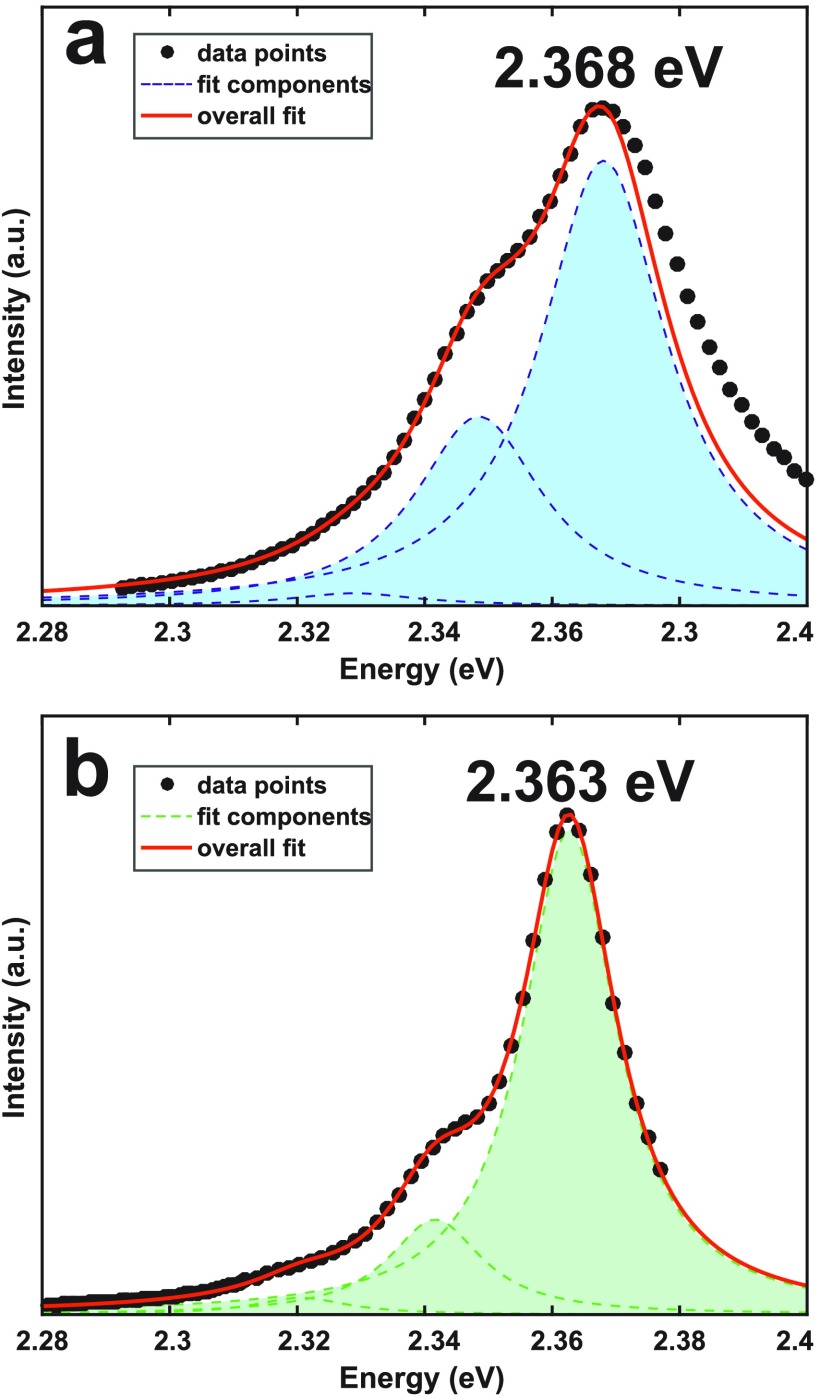
In this work we investigate the PL spectra of CsPbBr3 nanocrystals, under nonresonant and quasi-resonant excitation. Quasi-resonant conditions correspond to an excitation within the PL band of the nanocrystals, toward the higher-energy side of the nonresonant PL profile. Similar studies have been conducted for CdTe and CdSe colloidal nanocrystals, in the form of resonant photoluminescence excitation experiments, where LO phonon-assisted absorption led to size-selective excitation within the inhomogeneously broadened samples.13,14 In this study we observed three evenly spaced luminescence bands (see Figure 1), which we attribute to carrier–phonon coupling via the Fröhlich interaction. The luminescence spectrum is fitted as a sum of Voigt profiles. We provide a measure for the strength of the Fröhlich interaction, by calculating the ratio between the intensity of the first phonon band and that of the main emission band.

Figure 1.

Figure 1

Open in a new tab

PL spectrum of CsPbBr3 nanocrystals, obtained at 8 K, (a) under nonresonant (405 nm) and (b) under quasi-resonant (520 nm) excitation conditions. A narrowing of the PL band is observed at the lower excitation energy. The laser line situated at the high-energy end of the spectrum in (b) was blocked by the intermediate slit of the spectrometer, such that the data points shown here do not span the entire emission spectrum.

Results and Discussion

In polar semiconductors, an important scattering mechanism is the Fröhlich interaction, which represents the coupling to LO phonons via the Coulomb interaction between a carrier and the lattice. While the Fröhlich interaction is typically more important at higher temperatures, where kBT ≥ ℏωLO, such that the LO phonon occupation number is high15 (ℏωLO represents the LO phonon energy), at low temperature (i.e., reduced phonon occupation numbers), LO phonon coupling results in a specific PL line shape, consisting of multiple, evenly spaced luminescence bands of varying intensity. Low-temperature PL measurements allow us to quantify the Fröhlich interaction within a material, which at higher temperatures would be inaccessible, due to thermal contributions and acoustic line broadening. The separation between the observed PL bands corresponds to the LO phonon energy, such that the bands represent recombination events with zero, one, two, or more participating phonons. Phonon coupling via the Fröhlich interaction at low temperatures is due to the release of the polarization energy induced by the electrostatic interaction between the polar lattice and the charge carrier. Upon radiative recombination, the excess energy is released as polar lattice vibrations (i.e., LO phonons), and phonon side bands become visible in the PL spectrum of the material. Evidently, neutral excitons must possess a built-in dipole moment in order to interact significantly with the lattice, such that phonon emission can occur. By investigating the PL spectrum of a given material, we can visualize and measure the strength of carrier–phonon interactions. This also has implications for general transport behavior within the material, with consequences for both low- and room-temperature conditions.

Colloidal nanocrystals of CsPbBr3 were synthesized (as described in the Methods section), yielding average sizes ranging between 10 and 20 nm. For the measurements described here, nanocrystal sizes were around 10 nm (Supporting Information, Figure 1), whereas the reported exciton Bohr radius for CsPbBr3 is 7 nm.4 The processing of the acquired PL spectra consisted of applying a median filter (see Supporting Information), in order to reduce noise and remove artifacts such as cosmic rays, followed by a fitting procedure. The fit function consisted of a sum of three evenly spaced Voigt profiles, corresponding to the zero-phonon band and two phonon satellites, as shown in Figure 1. Phonon satellites were observed in the PL spectra taken under both 405 and 520 nm excitation. A reduction in the full width at half-maximum (fwhm) of the PL bands is observed under quasi-resonant excitation. This is indicative of strong carrier localization, which leads to inhomogeneous spectral broadening, due to local variations in localization energy, related to the electronic environment of each individual carrier. With increasing excitation energy, carriers can become delocalized, occupying so-called “extended” states, which cover a wide range of energies.16 Excitation closer to the band edge results in the occupation of only a subset of states (mostly localized), thus reducing the spectral width of the PL bands (hereafter referred to as “PL bandwidth”). The point in energy which separates the localized and delocalized states is called the mobility edge. As such, the quasi-resonant line narrowing is due to the positioning of the laser line within the nonresonant PL spectrum, which results in reduced extended state luminescence. Consequently, we also observe a red-shift of the main PL band under quasi-resonant conditions, as compared to nonresonant excitation. Similarly, Stoumpos etal. reported bound state emission from bulk single crystals of CsPbBr3.17 Additionally, experimental and theoretical reports have proposed different mechanisms for charge carrier binding in lead halide perovskite materials, including bound excitons16 or self-trapping of electrons18 or holes19 through the formation of small polarons. The dependence of PL energy on the chosen excitation scheme is highlighted via the difference in PL band maximum between the quasi-resonant and nonresonant spectra shown in Figure 1. The red-shift under quasi-resonant conditions is on the order of 5 meV, which is within the fwhm of the main PL band, suggesting that lower-energy states, below the mobility edge, are predominantly excited. This occurs via transfer from extended states to localized states. The positions of the satellites also exhibit a shift as the zero-phonon band is shifted in accordance with the excitation conditions. This enforces the idea of carrier–phonon coupling, as phonon replicas in the luminescence spectrum of a material are always shifted by an integer number of LO phonon energies with respect to the zero-phonon band. Moreover, a temperature-dependent study of the PL bandwidth is provided in the Supporting Information (Figure 2), as further proof of LO phonon coupling.

Figure 2.

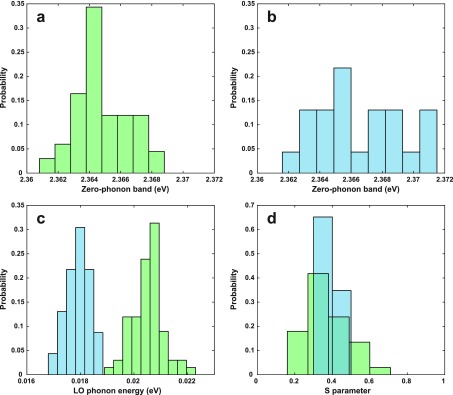
Figure 2

Open in a new tab

Histograms of the PL parameters under nonresonant (blue) and quasi-resonant (green) excitation: (a, b) position of the highest-energy PL band; (c) LO phonon energy; (d) coupling parameter S, obtained from the ratio of the intensities of the second and first phonon replicas. The data are normalized by probability, to account for the different number of measurements in the quasi-resonant and nonresonant case.

The histograms in Figure 2 show the distribution of zero-phonon band position, LO phonon energy, and S parameter across a large number of measurements. From transmission electron microscopy (TEM) analysis and the room-temperature PL spectrum (Supporting Information, Figure 1) we conclude that the average nanocrystal size is close to 10 nm. This is confirmed by the currently available literature on size-dependent PL energy.4,20 Each separate measurement was taken at a different position on the sample, such that variations in acquired values reflect the local nanocrystal dispersity. Additionally, nanocrystals in close proximity to each other have been shown to exhibit a modified band structure compared to isolated nanocrystals,20 and as such, fluctuations in the local nanocrystal density can also lead to fluctuations in the PL energy. Alternatively, shifts in emission energy may also arise from fluorescence blinking21 and from the crystal orientation of optically active dipoles with respect to the detection axis.22Figure 2a and b show the position of the highest-energy PL band, while Figure 2c corresponds to the LO phonon energies, and Figure 2d to the values of the S parameter. Within the data set shown here, consisting of 100 measurements, 75 spectra were obtained under quasi-resonant conditions, and 25 under nonresonant conditions, as quasi-resonant conditions produce a smaller line width and improved signal. To account for this difference in number of measurements, the data have been normalized according to the occurrence probability of each value.

Under quasi-resonant conditions, we determined a mean energy of the main PL band of 2.365 eV, with a standard deviation of 1.7 meV, whereas nonresonant excitation resulted in a mean energy of 2.366 meV, with a standard deviation of 2.6 meV. A detailed analysis of the Lorentzian and Gaussian components of the Voigt profiles, which reveals the different broadening mechanisms under the two excitation conditions, is given in the Supporting Information. The average LO phonon energy under quasi-resonant excitation is 20.5 ± 0.6 meV, which is in line with previous reports.17,23 Under nonresonant excitation, we found a lower average LO phonon energy of 17.9 ± 0.4 meV. Stoumpos etal. reported on the presence of a broad phonon mode in the low-energy Raman spectrum of CsPbBr3 single crystals.17 The mode is situated at 165 cm–1 (20.4 meV), with an fwhm on the order of 75 cm–1 (9.3 meV), which is considerably larger than the difference between the phonon energies corresponding to nonresonant and quasi-resonant excitation schemes in our measurements. We identify the 165 cm–1 mode as an LO phonon mode, in accordance with the value of the dielectric function and sample reflectivity at the corresponding frequency. Similarly, a broad band was reported in the Raman spectrum of the hybrid halide perovskite MAPbBr3 at 150 cm–1 (18.6 meV),24 along with a similar feature for MAPbI3. We infer that the modes in question all represent the same PbX6 octahedral mode, which is part of the lower-energy range of the lead halide perovskite Raman spectrum.25−27 The emission of different-energy phonons within the same broad mode can result from recombination of carriers in localized and extended states. This stems from the fact that the mean number of emitted phonons (i.e., the S parameter) is dependent on the ratio between the qth Fourier component of the charge density, ρq*, and the absolute value of q:28,29

graphic file with name nn-2017-05033q_m001.jpg 1

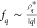where Inline graphic. Consequently, the phonon emission probability with wave vector q also depends on the localization potential, and as such, any variation in the latter changes the q value for the emitted phonon, resulting in a different energy. Additionally, the confinement of the carriers within the nanocrystals leads to an extended range of inaccessible ρq* values around the zone center, such that the high-q Fourier component values and their spread become determining factors for the fq values for a given transition. Evidently, the value of S also depends on the localizing potential, and this can be seen in relation to the spread in Figure 2d. We observe a similar mean value of the coupling parameter in both excitation conditions, with S = 0.37 ± 0.11 under quasi-resonant excitation and S = 0.38 ± 0.05 under nonresonant conditions. The significantly smaller spread of the nonresonant S values reflects the prevalence of extended-state emission under the respective excitation conditions, as opposed to bound-state emission in the quasi-resonant case.

In order to highlight the occurrence of carrier binding within the nanocrystals and establish the corresponding mechanism, we refer to the model introduced by Schmidt etal.,30 which describes the near-band-edge emission from direct-band-gap semiconductors in terms of a power law dependence between the PL intensity (I) and the excitation power (Pexc):

graphic file with name nn-2017-05033q_m003.jpg 2

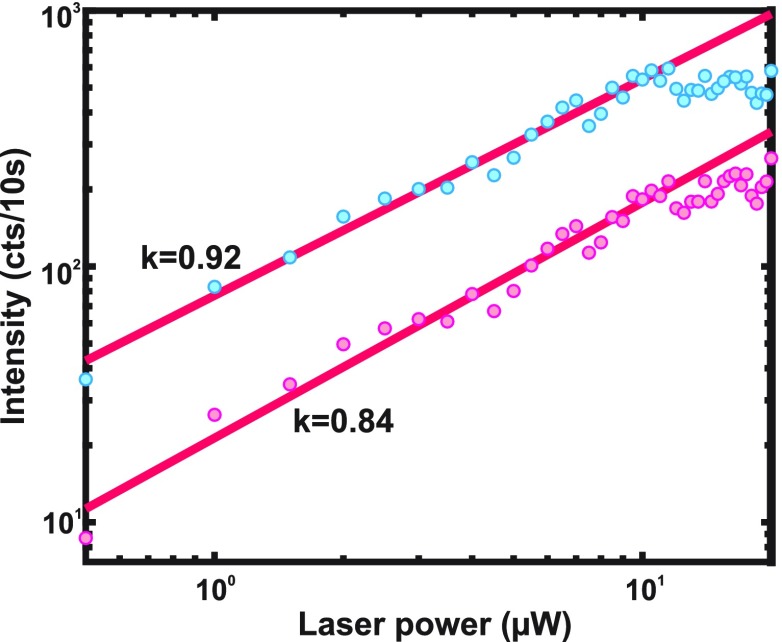
In accordance with this model, it is possible to determine the dominant recombination mechanism within our system. Thus, for above-band-gap excitation, a value of 1 < k < 2 corresponds to a predominantly free-exciton transition, while k < 1 values correspond to a situation where donor–acceptor pair or free-to-bound carrier recombination dominates. If neither free nor bound carrier recombination is dominant, the logarithmic power dependence of PL intensity becomes curved, being impossible to interpret in a straightforward manner. Under the quasi-resonant scheme we excite mostly the lower-energy side of the PL spectrum, which would correspond to excitation of mostly localized states. As such, a value of k < 1 is expected. Conversely, under nonresonant excitation, the resulting power dependence is influenced by the ratio of localized-versus-delocalized luminescent states, which contribute to PL, thus complicating the interpretation of results. Our quasi-resonant excitation-power-dependent study of the PL intensity of the perovskite nanocrystals, shown in Figure 3, revealed a saturation of the PL intensity at higher powers, whereas in the low power range, k is indeed lower than 1. This is indicative of free-to-bound carrier recombination, supporting our assumption that localized-state luminescence occurs. The case of free-to-bound carrier recombination would agree very well with the findings of both Neukirch etal.18 and Santomauro etal.,19 which report on the self-trapping of one type of charge carrier due to polaronic effects. Moreover, a recent report has revealed an electron Landé factor, g ≃ 2, corresponding to free electrons, while the value for holes was found to be much lower,12 corroborating the findings of Santomauro etal. It therefore seems plausible that the carrier localization mechanism involves the reported small polarons formed by holes.

Figure 3.

Figure 3

Open in a new tab

Dependence of the PL intensity of the zero-phonon line (blue markers) and the first phonon replica (pink markers) on the incident laser power.

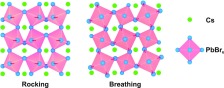
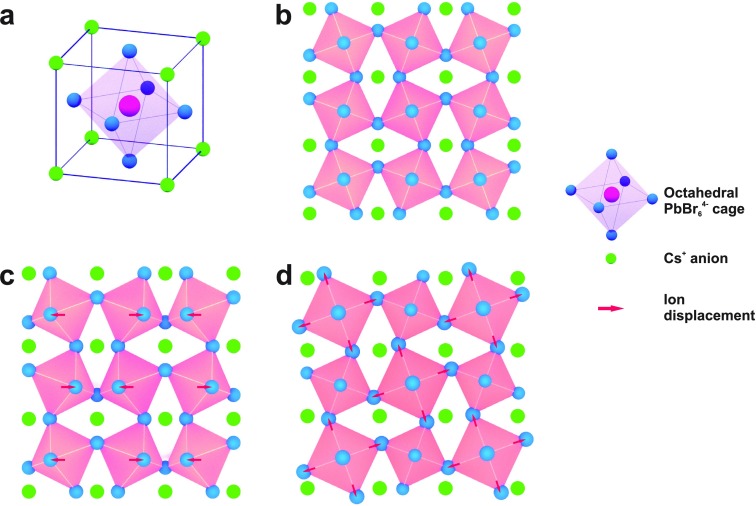
Investigations regarding the change in LO phonon energy under nonresonant excitation, as compared to the quasi-resonant case, have raised an interesting point of discussion, related to the crystal structure of perovskite nanocrystals at low temperature. It is as of yet unclear whether lead halide perovskite nanocrystals possess a stable cubic crystal phase, and different views on the subject have been expressed.4,31,32 Nuclear site analysis of the perovskite ABX3 structure has shown that zone-center LO phonon modes can only exist in rotationally distorted perovskite polymorphs.33 In the ideal cubic structure, no such modes are present within the first-order Raman spectrum, and as such, the mere occurrence of the Fröhlich interaction strongly suggests that the structure of CsPbBr3 nanocrystals is not cubic, but possesses a lower symmetry, as illustrated in Figure 4. Our results also agree with the Raman spectrum presented by Stoumpos etal.,17 containing the previously mentioned broad phonon mode. The crystal structure of the bulk single-crystal samples used in their work is orthorhombic, such that we can assume that the nanocrystals investigated here are of the same type. Furthermore, it has been recently shown that the orthorhombic distortion of the cubic perovskite lattice also plays an important role at room temperature, resulting in the high PL quantum yields which are typically observed.22

Figure 4.

Figure 4

Open in a new tab

(a) Ideal cubic unit cell of the CsPbBr3 perovskite crystal lattice; (b) orthorhombic crystal structure of CsPbBr3 nanocrystals, representing an octahedral distortion of the ideal lattice, which consists of a twist of the relatively rigid PbBr6 cage; (c) rocking and (d) breathing phonon mode, of the orthorhombic crystal phase, consisting of vibrations of the PbBr6 octahedra.

It is interesting to mention that even in single nanocrystals secondary PL bands have previously been observed. They have been attributed to charging effects34 or biexciton emission,35 whereas our interpretation of the results corresponding to nanocrystal ensembles can provide an alternative explanation. For example, in the single-nanocrystal spectra shown by Rainò etal.,34 an additional PL line is reported, appearing under higher-power excitation and red-shifted by 10–20 meV with respect to the main line. The splitting energy agrees very well with our findings, such that carrier–phonon coupling is a plausible alternative for explaining the additional luminescence band. Additionally, room-temperature broadening in hybrid perovskite thin films has been explained via the Fröhlich mechanism in the work of Wright etal.9 However, phonon side bands were not observed at cryogenic temperatures, as is the case in our experiments. The justification for the apparent difference in behavior stems in part from the different material structure (thin films, in the case of Wright etal.), as well as a significant difference in phonon energy, combined with a spectral broadening contribution. The latter two factors are especially important, as the shape of the PL spectrum is strongly dependent on the spectral width of the (phonon-assisted) transitions.36 Consequently, phonon replicas within the perovskite PL spectrum can only be resolved if the LO phonon energy is sufficiently large, such that the separation between the zero-phonon band and its satellites can compensate for the bandwidth. It is thus immediately clear that the study conducted here was made possible by the reduced PL bandwidth, characteristic of perovskite nanocrystals.

Conclusions

In conclusion, we have provided unambiguous evidence of carrier–phonon coupling in CsPbBr3 nanocrystals via the Fröhlich interaction. By fitting the nanocrystal PL spectrum, we were able to determine the energy of the involved LO phonons. We determine the ratio of one-phonon transitions to no-phonon transitions, which provides a measure for the strength of carrier–phonon interaction. It should be stressed that the occurrence of phonon coupling described here for CsPbBr3 has implications for inorganic as well as hybrid lead halide perovskites, due to the participation of low-energy, octahedral phonon modes, which do not depend on the nature of the cation.

The practical implications of this work are considerable, in relation to the main areas where lead halide perovskites have shown great potential, specifically solar cell applications and light-emitting devices. In relation to solar cell operation, a high rate of carrier–phonon coupling typically leads to increased carrier scattering during transport. Consequently, carrier mobilities are reduced, which could result in an increased loss of carriers through nonradiative recombination. We remark, however, that in metal halide perovskites carrier mobilities up to the same order as silicon have been reported,17,37 which correlates very well with their outstanding performance as solar cell materials. In regards to light-emitting applications, lead halide perovskite nanocrystals have become increasingly popular, due to high quantum efficiencies even at room temperature and their highly tunable emission wavelength. For light-emitting diodes, reduced mobilities due to strong coupling of carriers to optical phonons imply low device efficiencies, as a consequence of reduced carrier injection and transport efficiencies. Additionally, spectral broadening due to phonon coupling has implications regarding the color purity of light emitters. At low temperature, we have detected broad PL spectra of the CsPbBr3 nanocrystals, which can be attributed to two main broadening mechanisms. First, the bound nature of one of the carriers contributes to inhomogeneous broadening of each luminescence band due to variations in the local environment of each bound state. Second, the phonon-assisted emission, consisting of several overlapping bands, further increases the overall spectral width, in accordance with the number of phonon replicas and the LO phonon energy. Altogether, the results presented in this work provide a fundamental understanding of the properties of CsPbBr3 as a material with potential commercial applications.

Methods

CsPbBr3 Nanocrystal Synthesis and Materials Used

Cesium carbonate (Cs2CO3, Sigma-Aldrich, 99.9%), 1-octadecene (ODE, Sigma-Aldrich, 90%), oleic acid (OA, Sigma-Aldrich, 90%), lead bromide (PbBr2, Sigma-Aldrich, 99.999%), oleylamine (OLAM, Sigma-Aldrich, 70%), anhydrous toluene (Sigma-Aldrich, 99.8%), anhydrous hexane (Sigma-Aldrich, 95%) were used. OLAM and OA were degassed under reduced pressure at 120 °C for 1 h prior to use. All other chemicals were used as received.

The CsPbBr3 NCs were prepared according to the method described by Protesescu etal.4 First, a Cs-oleate precursor stock solution was prepared. Cs2CO3 (0.814 g), 2.5 mL of OA, and 40 mL of ODE were loaded into a 100 mL round-bottom flask. The mixture was dried under vacuum for approximately 1 h at 120 °C and then heated under N2 to 150 °C until all Cs2CO3 had reacted with OA. ODE (5 mL) and PbBr2 (0.069 g) were loaded into a separate 25 mL flask and dried under vacuum for 1 h at 120 °C. OLAM (0.5 mL) and OA (0.5 mL) were injected at 120 °C under a N2 atmosphere. After PbBr2 had dissolved, the temperature was raised to 180 °C and 0.4 mL of the Cs-oleate stock solution was quickly injected. We note that the Cs-oleate stock solution had to be preheated to 100 °C before injection. After five to ten seconds the reaction mixture was cooled by an ice–water bath in order to quench the reaction.

Purification of the Nanocrystals (NCs)

The CsPbBr3 NCs were purified following the method described by De Roo etal.38 (for a synthesis based on 69 mg of PbBr2). The crude synthesis solution was centrifuged for 3 min at 10000 rpm, and the colored supernatant was discarded. Then, 300 μL of hexane was added and the NCs were dispersed using a vortex mixer. Subsequently, the suspension was again centrifuged for 3 min at 10 000 rpm, after which the precipitate, containing larger NCs and agglomerates, was discarded. Another 300 μL of hexane was added to the supernatant, resulting in a colloidal dispersion of CsPbBr3 NCs.

Low-Temperature PL Measurements

Samples for low-temperature measurements were drop-cast on quartz substrates. The samples were cooled to cryogenic temperatures (8 K). Acquisition of the PL spectra was carried out using a diffraction-limited confocal microscope, coupled into a single-mode optical fiber. For signal analysis a spectrometer in triple-subtractive configuration, equipped with a silicon CCD detector, was used. The samples were nonresonantly excited using a 405 nm diode laser, while quasi-resonant excitation was achieved using a 520 nm diode laser.

Acknowledgments

This work is part of the research program entitled “Designing Dirac Carriers in Semiconductor Superlattices” (DDC13), which is supported by the Foundation for Fundamental Research on Matter (FOM), which is part of The Netherlands Organization for Scientific Research (NWO). A.Yu.S. also acknowledges the financial support from the Russian Science Foundation (Grant No. 14-42-00015). The authors thank Korneel Ridderbeek for technical assistance with PL measurements.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.7b05033.

  • Room-temperature PL/absorption spectrum, TEM analysis of the CsPbBr3 nanocrystals, description of the peak fitting method, discussion on the fwhm broadening behavior with temperature, and detailed analysis of the Lorentzian and Gaussian components of the Voigt profiles used in the fit of the PL spectra (PDF)

The authors declare no competing financial interest.

Supplementary Material

nn7b05033_si_001.pdf (830.9KB, pdf)

References

  1. Jiang C.; Yang M.; Zhou Y.; To B.; Nanayakkara S. U.; Luther J. M.; Zhou W.; Berry J. J.; Lagemaat J. v. d.; Padture P.; Zhu K.; Al-Jassim M. M. Carrier Separation and Transport in Perovskite Solar Cells Studied by Nanometre-Scale Profiling of Electrical Potential. Nat. Commun. 2015, 6, 8397. 10.1038/ncomms9397. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Singh J.Semiconductor Devices; McGraw-Hill Book Co., 1999; Chapters 5 and 11. [Google Scholar]
  3. Brenner T. M.; Egger D. A.; Kronik L.; Hodes G.; Cahen D. Hybrid Organic-Inorganic Perovskites: Low-Cost Semiconductors with Intriguing Charge-Transport Properties. Nat. Rev. Mater. 2016, 1, 15007. 10.1038/natrevmats.2015.7. [DOI] [Google Scholar]
  4. Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Krieg F.; Caputo R.; Hendon C. H.; Yang R. X.; Walsh A.; Kovalenko M. V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Wehrenfennig C.; Eperon G. E.; Johnston M. B.; Snaith H. J.; Herz L. M. High Charge Carrier Mobilities and Lifetimes in Organolead Trihalide Perovskites. Adv. Mater. 2014, 26, 1584–1589. 10.1002/adma.201305172. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Milot R. L.; Eperon G. E.; Snaith H. J.; Johnston M. B.; Herz L. M. Temperature-Dependent Charge-Carrier Dynamics in CH3NH3PbI3 Perovskite Thin Films. Adv. Funct. Mater. 2015, 25, 6218–6227. 10.1002/adfm.201502340. [DOI] [Google Scholar]
  7. Brenner T. M.; Egger D. A.; Rappe A. M.; Kronik L.; Hodes G.; Cahen D. Are Mobilities in Hybrid Organic-Inorganic Halide Perovskites Actually High?. J. Phys. Chem. Lett. 2015, 6, 4754–4757. 10.1021/acs.jpclett.5b02390. [DOI] [PubMed] [Google Scholar]
  8. Sendner M.; Nayak P. K.; Egger D. A.; Beck S.; Müller C.; Epding B.; Kowalsky W.; Kronik L.; Snaith H. J.; Pucci A.; Lovrinčić R. Optical Phonons in Methylammonium Lead Halide Perovskites and Implications for Charge Transport. Mater. Horiz. 2016, 3, 613–620. 10.1039/C6MH00275G. [DOI] [Google Scholar]
  9. Wright A. D.; Verdi C.; Milot R. L.; Eperon G. E.; Pérez-Osorio M. A.; Snaith H. J.; Giustino F.; Johnston M. B.; Herz L. M. Electron-Phonon Coupling in Hybrid Lead Halide Perovskites. Nat. Commun. 2016, 7, 11755. 10.1038/ncomms11755. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Straus D. B.; Hurtado Parra S.; Iotov N.; Gebhardt J.; Rappe A. M.; Subotnik J. E.; Kikkawa J. M.; Kagan C. R. Direct Observation of Electron-Phonon Coupling and Slow Vibrational Relaxation in Organic-Inorganic Hybrid Perovskites. J. Am. Chem. Soc. 2016, 138, 13798–13801. 10.1021/jacs.6b08175. [DOI] [PubMed] [Google Scholar]
  11. Isarov M.; Tan L. Z.; Bodnarchuk M. I.; Kovalenko M.; Rappe A. M.; Lifshitz E. Rashba Effect in a Single Colloidal CsPbBr3 Perovskite Nanocrystal Detected by Magneto-Optical Measurements. Nano Lett. 2017, 17, 5020–5026. 10.1021/acs.nanolett.7b02248. [DOI] [PubMed] [Google Scholar]
  12. Fu M.; Tamarat P.; Huang H.; Even J.; Rogach A. L.; Lounis B. Neutral and Charged Exciton Fine Structure in Single Lead Halide Perovskite Nanocrystals Revealed by Magneto-optical Spectroscopy. Nano Lett. 2017, 17, 2895–2901. 10.1021/acs.nanolett.7b00064. [DOI] [PubMed] [Google Scholar]
  13. Nguyen T. A.; Mackowski S.; Jackson H. E.; Smith L. M.; Wrobel J.; Fronc K.; Karczewski G.; Kossut J.; Dobrowolska M.; Furdyna J. K.; Heiss W. Resonant Spectroscopy of II-VII Self-Assembled Quantum Dots: Excited States and Exciton-Longitudinal Optical Phonon Coupling. Phys. Rev. B: Condens. Matter Mater. Phys. 2004, 70, 125306. 10.1103/PhysRevB.70.125306. [DOI] [Google Scholar]
  14. Rakovich Y.; Walsh L.; Bradley L.; Donegan J. F.; Talapin D.; Rogach A.; Eychmüller A. Size Selective Photoluminescence Excitation Spectroscopy in CdTe Quantum Dots. Proc. SPIE 2002, 4876, 432–437. 10.1117/12.463693. [DOI] [Google Scholar]
  15. Yu P. Y.; Cardona M.. Fundamentals of Semiconductors; Springer Verlag-Berlin: Heidelberg, 1999; Chapter 5. [Google Scholar]
  16. He H.; Yu Q.; Li H.; Si J.; Jin Y.; Wang N.; Wang J.; He J.; Wang X.; Zhang Y.; Ye Z. Exciton Localization in Solution-Processed Organolead Trihalide Perovskites. Nat. Commun. 2016, 7, 10896. 10.1038/ncomms10896. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Stoumpos C. C.; Malliakas C. D.; Peters J. A.; Liu Z.; Sebastian M.; Im J.; Chasapis T. C.; Wibowo A. C.; Chung D. Y.; Freeman A. J.; Wessels B.; Kanatzidis M. G. Crystal Growth of the Perovskite Semiconductor CsPbBr3: A New Material for High-Energy Radiation Detection. Cryst. Growth Des. 2013, 13, 2722–2727. 10.1021/cg400645t. [DOI] [Google Scholar]
  18. Neukirch A. J.; Nie W.; Blancon J. C.; Appavoo K.; Tsai H.; Sfeir M. Y.; Katan C.; Pedesseau L.; Even J.; Crochet J. J.; Gupta G.; Mohite A. D.; Tretiak S. Polaron Stabilization by Cooperative Lattice Distortion and Cation Rotations in Hybrid Perovskite Materials. Nano Lett. 2016, 16, 3809–3816. 10.1021/acs.nanolett.6b01218. [DOI] [PubMed] [Google Scholar]
  19. Santomauro F. G.; Grilj J.; Mewes L.; Nedelcu G.; Yakunin S.; Rossi T.; Capano G.; Haddad A. A.; Budarz J.; Kinschel D.; Ferreira D.; Rossi G.; Gutierrez Tovar M.; Grolimund D.; Samson V.; Nachtegaal M.; Smolentsev G.; Kovalenko M. V.; Chergui M. Localized Holes and Delocalized Electrons in Photoexcited Inorganic Perovskites: Watching Each Atomic Actor by Picosecond X-Ray Absorption Spectroscopy. Struct. Dyn. 2017, 4, 044002. 10.1063/1.4971999. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Lin J.; Gomez L.; Weerd C. d.; Fujiwara Y.; Gregorkiewicz T.; Suenaga K. Direct Observation of Band Structure Modifications in Nanocrystals of CsPbBr3 Perovskite. Nano Lett. 2016, 16, 7198–7202. 10.1021/acs.nanolett.6b03552. [DOI] [PubMed] [Google Scholar]
  21. Hu F.; Zhang H.; Sun C.; Yin C.; Lv B.; C Z.; Yu W. W.; Wang X.; Y Z.; Xiao M. Superior Optical Properties of Perovskite Nanocrystals as Single Photon Emitters. ACS Nano 2015, 9, 12410–12416. 10.1021/acsnano.5b05769. [DOI] [PubMed] [Google Scholar]
  22. Becker M. A.; Vaxenburg R.; Nedelcu G.; Servel P. C.; Shabaev A.; Mehl M. J.; Michopoulos J. G.; G L. S.; Bernstein M.; Lyons J. L.; Stöferle T.; Mahrt R. F.; Kovalenko M. V.; Norris D. J.; Rainò G.; Efros A. L.. Bright Triplet Excitons in Lead Halide Perovskites. ArXiv e-prints 2017, arXiv:1707.03071. [DOI] [PubMed]
  23. Sebastian M.; Peters J. A.; Stoumpos C. C.; Im J.; Kostina S. S.; Liu Z.; Kanatzidis M. G.; Freeman A. J.; Wessels B. W. Excitonic Emissions and Above-Band-Gap Luminescence in the Single-Crystal Perovskite Semiconductors CsPbBr3 and CsPbCl3. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 235210. 10.1103/PhysRevB.92.235210. [DOI] [Google Scholar]
  24. Ledinskỳ M.; Löper P.; Niesen B.; Holovskỳ J.; Moon S. J.; Ballif C. Raman Spectroscopy of Organic-Inorganic Perovskites. J. Phys. Chem. Lett. 2015, 6, 401–406. 10.1021/jz5026323. [DOI] [PubMed] [Google Scholar]
  25. Pérez-Osorio M. A.; Milot R. L.; Filip M. R.; Patel J. B.; Herz L. M.; Johnston M. B.; Giustino F. Vibrational Properties of the Organic-Inorganic Halide Perovskite CH3NH3PbI3 from Theory and Experiment: Factor Group Analysis, First-Principles Calculations, and Low-Temperature Infrared Spectra. J. Phys. Chem. C 2015, 119, 25703–25718. 10.1021/acs.jpcc.5b07432. [DOI] [Google Scholar]
  26. Brivio F.; Frost J. M.; Skelton J. M.; Jackson A. J.; Weber O. J.; Weller M. T.; Goñi A. R.; Leguy A. M. A.; Barnes P. R. F.; Walsh A. Lattice Dynamics and Vibrational Spectra of the Orthorhombic, Tetragonal, and Cubic Phases of Methylammonium Lead Iodide. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 92, 144308. 10.1103/PhysRevB.92.144308. [DOI] [Google Scholar]
  27. Yue S. Y.; Zhang X.; Qin G.; Yang J.; Hu M. Insight Into the Collective Vibrational Modes Driving Ultralow Thermal Conductivity of Perovskite Solar Cells. Phys. Rev. B: Condens. Matter Mater. Phys. 2016, 94, 115427. 10.1103/PhysRevB.94.115427. [DOI] [Google Scholar]
  28. Hopfield J. J. A Theory of Edge-Emission Phenomena in CdS, ZnS and ZnO. J. Phys. Chem. Solids 1959, 10, 110–119. 10.1016/0022-3697(59)90064-2. [DOI] [Google Scholar]
  29. Silov A. Y.; Marschner T.; Leys M. R.; Haverkort J. E. M.; Wolter J. H. Cation Sublattice Ordering in GaxIn1–xAs Quantum Wells: Evidence from Electron-Phonon Interaction. Phys. Status Solidi 1997, 164, 145–148. . [DOI] [Google Scholar]
  30. Schmidt T.; Lischka K.; Zulehner W. Excitation-Power Dependence of the Near-Band-Edge Photoluminescence of Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 1992, 45, 8989–8994. 10.1103/PhysRevB.45.8989. [DOI] [PubMed] [Google Scholar]
  31. Cottingham P.; Brutchey R. L. On the Crystal Structure of Colloidally-Prepared CsPbBr3 Quantum Dots. Chem. Commun. 2016, 52, 5246–5249. 10.1039/C6CC01088A. [DOI] [PubMed] [Google Scholar]
  32. Zhang D.; Eaton S. W.; Yu Y.; Dou L.; Yang P. Solution-Phase Synthesis of Cesium Lead Halide Perovskite Nanowires. J. Am. Chem. Soc. 2015, 137, 9230–9233. 10.1021/jacs.5b05404. [DOI] [PubMed] [Google Scholar]
  33. Islam M. A.; Rondinelli J. M.; Spanier J. E. Normal Mode Determination of Perovskite Crystal Structures with Octahedral Rotations: Theory and Applications. J. Phys.: Condens. Matter 2013, 25, 175902. 10.1088/0953-8984/25/17/175902. [DOI] [PubMed] [Google Scholar]
  34. Rainò G.; Nedelcu G.; Protesescu L.; Bodnarchuk M. I.; Kovalenko M. V.; Mahrt R. F.; Stöferle T. ‘Single Caesium Lead Halide Perovskite Nanocrystals at Room Temperature: Fast Single-Photon Emission, Reduced Blinking, and Exciton Fine Structure. ACS Nano 2016, 10, 2485–2490. 10.1021/acsnano.5b07328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Wang Y.; Li X.; Song J.; Xiao L.; Zeng H.; Sun H. All-Inorganic Colloidal Perovskite Quantum Dots: A New Class of Lasing Materials with Favorable Characteristics. Adv. Mater. 2015, 27, 7101–7108. 10.1002/adma.201503573. [DOI] [PubMed] [Google Scholar]
  36. de Jong M.; Seijo L.; Meijerink A.; Rabouw F. T. Resolving the Ambiguity in the Relation Between Stokes Shift and Huang-Rhys Parameter. Phys. Chem. Chem. Phys. 2015, 17, 16959. 10.1039/C5CP02093J. [DOI] [PubMed] [Google Scholar]
  37. Stoumpos C. C.; Malliakas C. D.; Kanatzidis M. G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. 10.1021/ic401215x. [DOI] [PubMed] [Google Scholar]
  38. de Roo J.; Ibàñez M.; Geiregat P.; Nedelcu G.; Walravens W.; Maes J.; Martins J. C.; van Driessche I.; Kovalenko M. V.; Hens Z. Highly Dynamic Ligand Binding and Light Absorption Coefficient of Cesium Lead Bromide Perovskite Nanocrystals. ACS Nano 2016, 10, 2071–2081. 10.1021/acsnano.5b06295. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

nn7b05033_si_001.pdf (830.9KB, pdf)

Articles from ACS Nano are provided here courtesy of American Chemical Society

RESOURCES