Statistical Significance for Hierarchical Clustering

Summary

Cluster analysis has proved to be an invaluable tool for the exploratory and unsupervised analysis of high dimensional datasets. Among methods for clustering, hierarchical approaches have enjoyed substantial popularity in genomics and other fields for their ability to simultaneously uncover multiple layers of clustering structure. A critical and challenging question in cluster analysis is whether the identified clusters represent important underlying structure or are artifacts of natural sampling variation. Few approaches have been proposed for addressing this problem in the context of hierarchical clustering, for which the problem is further complicated by the natural tree structure of the partition, and the multiplicity of tests required to parse the layers of nested clusters. In this paper, we propose a Monte Carlo based approach for testing statistical significance in hierarchical clustering which addresses these issues. The approach is implemented as a sequential testing procedure guaranteeing control of the family-wise error rate. Theoretical justification is provided for our approach, and its power to detect true clustering structure is illustrated through several simulation studies and applications to two cancer gene expression datasets.

1. Introduction

Clustering describes the unsupervised learning task of partitioning observations into homogenous subsets, or clusters, to uncover subpopulation structure in a dataset. As an unsupervised learning task, cluster analysis makes no use of label or outcome data. A large number of methods have been proposed for clustering, including hierarchical approaches, as well as non-nested approaches, such as K-means clustering. Since the work of Eisen et al. (1998), hierarchical clustering algorithms have enjoyed substantial popularity for the exploratory analysis of gene expression data. In several landmark papers that followed, these methods were successfully used to identify clinically relevant expression subtypes in lymphoma, breast, and other types of cancer (Perou et al., 2000; Bhattacharjee et al., 2001).

While non-nested clustering algorithms typically require pre-specifying the number of clusters of interest, K, hierarchical algorithms do not. Instead, hierarchical approaches produce a single nested hierarchy of clusters from which a partition can be obtained for any possible choice of K. As a result, hierarchical clustering provides an intuitive way to study relationships among clusters not possible using non-nested approaches. The popularity of hierarchical clustering in practice may also be largely attributed to dendrograms, a highly informative visualization of the clustering as a binary tree.

While dendrograms provide an intuitive representation for studying the results of hierarchical clustering, the researcher is still ultimately left to decide which partitions along the tree to interpret as biologically important subpopulation differences. Often, in genomic studies, the determination and assessment of subpopulations are left to heuristic or ad hoc methods (Verhaak et al., 2010; Wilkerson et al., 2010; Bastien et al., 2012). To provide a statistically sound alternative to these methods, we introduce statistical Significance of Hierarchical Clustering (SHC), a Monte Carlo based approach for assessing the statistical significance of clustering along a hierarchical partition. The approach makes use of the ordered and nested structure in the output of hierarchical clustering to reduce the problem to a sequence of hypothesis tests descending the tree. Each test is formulated such that the procedure may be applied even in the high-dimension low-sample size (HDLSS) setting, where the number of variables is much greater than the number of observations. This is of particular importance, as the number of measured variables in genomic studies continues to grow with advances in high-throughput sequencing technologies, such as RNA-seq (Marioni et al., 2008; Wang et al., 2009). A stopping rule along the sequence of tests is also provided to control the family-wise error rate (FWER) of the entire procedure.

Several approaches have been proposed to address the question of statistical significance in the non-nested setting. The Statistical Significance of Clustering (SigClust) hypothesis test was introduced by Liu et al. (2008) for assessing the significance of clustering in HDLSS settings using a Monte Carlo procedure. While well-suited for detecting the presence of more than a single cluster in a dataset, the approach was not developed with the intention of testing in hierarchical or multi-cluster settings. This approach is described in greater detail in Section 2.2. More recently, Maitra et al. (2012) proposed a bootstrap based approach (BootClust) capable of testing for any number of clusters in a dataset. However, in addition to not directly addressing the hierarchical problem, their approach has not been evaluated in the important HDLSS setting. As such, neither approach provides a solution for handling the structure and multiplicity of nested tests unique to hierarchical clustering.

For assessing statistical significance in the hierarchical setting, Suzuki and Shimodaira (2006) developed the R package pvclust. The hypothesis tests used in pvclust are based on bootstrapping procedures originally proposed for significance testing in the context of phylogenetic tree estimation (Efron et al., 1996; Shimodaira, 2004). Since the procedure is based on a nonparamateric bootstrapping of the covariates, while pvclust can be used in the HDLSS setting, it cannot be implemented when the dataset is of low-dimension. In contrast, SHC may be used in either setting. To our knowledge, no other approaches have been proposed for assessing the statistical significance of hierarchical clustering.

The remainder of this paper is organized as follows. In Section 2 we first review hierarchical clustering and describe the SigClust hypothesis test of Liu et al. (2008). Then, in Section 3, we introduce our proposed SHC approach. In Section 4, we present theoretical justifications for our method under the HDLSS asymptotic setting. We then evaluate the performance of our method under various simulation settings in Section 5. In Section 6, we apply our method to two cancer gene expression datasets. Finally, we conclude with a discussion in Section 7. The SHC procedure is implemented in R, and is available at http://github.com/pkimes/.

2. Clustering and Significance

We begin this section by first providing a brief review of hierarchical clustering. We then describe the K-means based SigClust approach of Liu et al. (2008) for assessing significance of clustering in HDLSS data.

2.1 Hierarchical Clustering Methods

Given a collection of N unlabeled observations, $\mathbb{X}=\{{\mathit{x}}_i,\dots ,{\mathit{x}}_N\}$ in p dimensions, algorithms for hierarchical clustering estimate all K = 1 ,…, N partitions of the data through a sequential optimization procedure. The sequence of steps can be implemented as either an agglomerative (bottom-up) or divisive (top-down) approach to produce the nested hierarchy of clusters. Agglomerative clustering begins with each observation belonging to one of N disjoint singleton clusters. Then, at each step, the two most similar clusters are joined until after (N − 1) steps, all observations belong to a single cluster of size N. Divisive clustering proceeds in a similar, but reversed manner. In this paper we focus on agglomerative approaches which are more often used in practice.

Commonly, in agglomerative clustering, the pairwise similarity of observations is measured using a dissimilarity function, such as squared Euclidean distance $(L_2^2)$, Manhattan distance (L₁), or (1 − |Pearson corr.|). Then, a linkage function is used to extend this notion of dissimilarity to pairs of clusters. Often, the linkage function is defined with respect to all pairwise dissimilarities of observations belong to the separate clusters. Examples of linkage functions include Ward’s, single, complete, and average linkage (Ward, 1963). The clusters identified using hierarchical algorithms depend heavily on the choice of both the dissimilarity and linkage functions.

The sequence of clustering solutions obtained by hierarchical clustering is naturally visualized as a binary tree, commonly referred to as a dendrogram. Figure 1A shows a simple example with five points in ℝ² clustered using squared Euclidean dissimilarity and average linkage. The corresponding dendrogram is shown in Figure 1B, with the observation indices placed along the horizontal axis, such that no two branches of the dendrogram cross. The sequential clustering procedure is shown by the joining of clusters at their respective linkage value, denoted by the vertical axis, such that the most similar clusters and observations are connected near the bottom of the tree. The spectrum of clustering solutions can be recovered from the dendrogram by cutting the tree at an appropriate height, and taking the resulting subtrees as the clustering solution. For example, the corresponding K = 2 solution is obtained by cutting the dendrogram at the gray horizontal line in Figure 1B.

Figure 1.

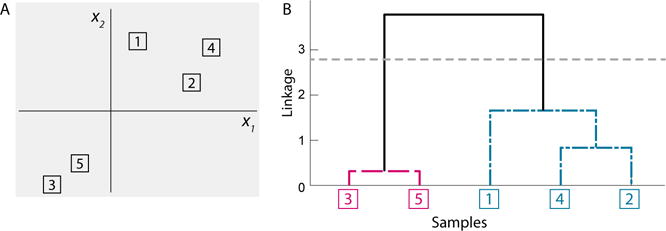
Hierarchical clustering applied to 5 observations. (A) Scatterplot of the observations. (B) The corresponding dendrogram. This figure appears in color in the electronic version of this article.

2.2 Statistical Significance

We next describe the SigClust hypothesis test of Liu et al. (2008) for assessing significance of clustering. To make inference in the HDLSS setting tractable, SigClust makes the simplifying assumption that a cluster may be characterized as a subset of the data which follows a single Gaussian distribution. While no universal definition for a “cluster” exists, the Gaussian definition is often used as a reasonable approximation (Mclachlan and Peel, 2000; Fraley and Raftery, 2002). While potentially restrictive, the Gaussian definition and SigClust approach have provided sensible results in real high-dimensional datasets (Verhaak et al., 2010; Bastien et al., 2012). Therefore, to determine whether a dataset is comprised of more than a single cluster, the approach tests the following hypotheses:

• H₀: the data follow a single Gaussian distribution

• H₁: the data follow a non-Gaussian distribution.

The corresponding p-value is calculated using the 2-means cluster index (CI), a statistic sensitive to the null and alternative hypotheses. Letting C_k denote the set of indices of observations in cluster k and using ${\overline{\mathit{x}}}_k$ to denote the corresponding cluster mean, the 2-means CI is defined as

$$\text{CI}=\frac{{\sum }_{k=1}^2{\sum }_{i\in C_k}{\Vert {\mathit{x}}_i-{\overline{\mathit{x}}}_k\Vert }_2^2}{{\sum }_{i=1}^N{\Vert {\mathit{x}}_i-\overline{\mathit{x}}\Vert }_2^2}=\frac{S{S}_1+S{S}_2}{\mathit{TSS}},$$ (1)

where TSS and SS_k are the total and within-cluster sum of squares. Smaller values of the 2-means CI correspond to tighter clusters, and provide stronger evidence of clustering of the data. The statistical significance of a given pair of clusters is calculated by comparing the observed 2-means CI against the distribution of 2-means CIs under the null hypothesis of a single Gaussian distribution. Since a closed form of the distribution of CIs under the null is unavailable, it is empirically approximated by the CIs computed for hundreds, or thousands, of datasets simulated from a null Gaussian distribution estimated using the original dataset. An empirical p-value is calculated by the proportion of simulated null CIs less than the observed CI. Approximations to the optimal 2-means CI for both the observed and simulated datasets can be obtained using the K-means algorithm for two clusters.

In the presence of strong clustering, the empirical p-value may simply return 0 if all simulated CIs fall above the observed value. This can be particularly uninformative when trying to compare the significance of multiple clustering events. To handle this problem, Liu et al. (2008) proposed computing a “Gaussian fit p-value” in addition to the empirical p-value. Based on the observation that the distribution of CIs appears roughly Gaussian, the Gaussian fit p-value is calculated as the lower tail probability of the best-fit Gaussian distribution to the simulated null CIs.

An important issue not discussed above is the estimation of the covariance matrix of the null distribution, a non-trivial task in the HDLSS setting. A key part of the SigClust approach is the simplification of this problem, by making use of the invariance of the 2-means CI to mean shifts and rotations of the data in the Euclidean space. It therefore suffices to simulate data from an estimate of any rotation and shift of the null distribution. Conveniently, by centering the distribution at the origin, and rotating along the eigendirections of the covariance matrix, the task can be reduced to estimating only the eigenvalues of the null covariance matrix. As a result, the number of parameters to estimate is reduced from p(p + 1)/2 to p. However, in the HDLSS setting, even the estimation of p parameters is challenging, as N ≪ p. To solve this problem, the additional assumption is made that the null covariance matrix follows a factor analysis model. That is, under the null hypothesis, the observations are assumed to be drawn from a single Gaussian distribution, N(μ, Σ), with Σ having eigendecomposition Σ = UΛU^T such that $\mathrm{\Lambda }={\mathrm{\Lambda }}_0+{\sigma }_b^2{\mathbf{I}}_p$, where Λ₀ is a low rank (< N) diagonal matrix of true signal, ${\sigma }_b^2$ is a relatively small amount of background noise, and I_p is the p-dimensional identity matrix. Letting w denote the number of non-zero entries of Λ₀, under the factor analysis model, only w + 1 parameters must be estimated to implement SigClust. Several approaches have been proposed for estimating ${\sigma }_b^2$ and Λ₀, including the hard-threshold, soft-threshold, and sample-based approaches (Liu et al., 2008; Huang et al., 2015). Descriptions of these approaches and a new estimator for ${\sigma }_b^2$ are presented in Web Appendix D.

3. Methodology

To assess significance of clustering in a hierarchical partition, we propose a sequential testing procedure in which Monte Carlo based hypothesis tests are preformed at select nodes along the corresponding dendrogram. In this section, we introduce our SHC algorithm in two parts. First, using a toy example, we describe the hypothesis test performed at individual nodes. Then, we describe our sequential testing procedure for controlling the FWER of the algorithm along the entire dendrogram.

3.1 SHC Hypothesis Test

Throughout, we use j ∈ {1,…, N − 1} to denote the node index, such that j = 1 and j = (N − 1) correspond to the top-most (root) and bottom-most merges along the dendrogram, respectively. In Figure 2, we illustrate one step of our sequential algorithm using a toy dataset of N = 150 observations drawn from ℝ² (Figure 2A). Agglomerative hierarchical clustering was applied using Ward’s linkage to obtain the dendrogram in Figure 2B. Consider the second node from the top, i.e. j = 2. The corresponding observations and subtree are highlighted in panels A and B of Figure 2. Here, we are interested in whether the sets of 43 and 53 observations joined at node 2, denoted by dots and ×’s, more naturally define one or two distinct clusters. Assuming that a cluster may be well approximated by a single Gaussian distribution, we propose to test the following hypotheses at node 2:

• H₀: The 96 observations follow a single Gaussian distribution

• H₁: The 96 observations do not follow a single Gaussian distribution.

Figure 2.

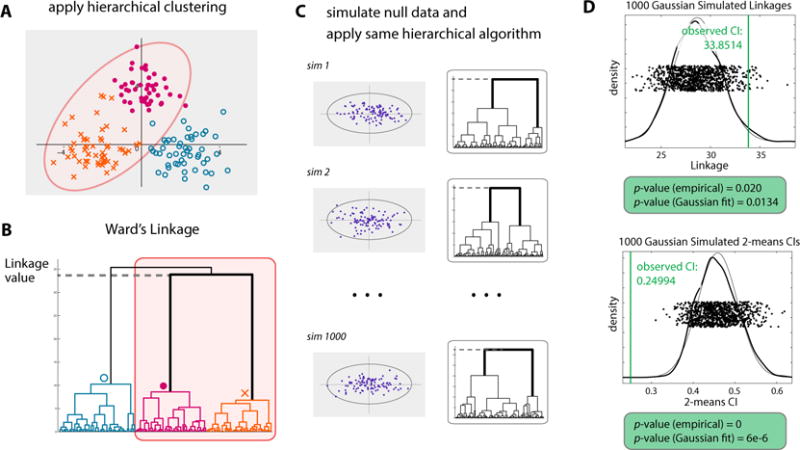
The SHC testing procedure illustrated using a toy example. Testing is applied to the 96 observations joined at the second node from the root. (A) Scatterplot of the observations in ℝ². (B) The corresponding dendrogram. (C) Hierarchical clustering applied to 1000 datasets simulated from a null Gaussian estimated from the 96 observations. (D) Distributions of null cluster indices used to calculate the empirical SHC p-values. This figure appears in color in the electronic version of this article.

The p-value at the node, denoted by p_j, is calculated by comparing the strength of clustering in the observed data against that for data clustered using the same hierarchical algorithm under the null hypothesis. We consider two cluster indices, linkage value and the 2-means CI, as natural measures for the strength of clustering in the hierarchical setting. To approximate the null distribution of cluster indices, 1000 datasets of 96 observations are first simulated from a null Gaussian distribution estimated using only the 96 observations included in the highlighted subtree. Then, each simulated dataset is clustered using the same hierarchical algorithm as was applied to the original dataset (Figure 2C). As with the observed data, the cluster indices are computed for each simulated dataset using the two cluster solution obtained from the hierarchical algorithm. Finally, p-values are obtained from the proportion of null cluster indices indicating stronger clustering than the observed indices (Figure 2D). For the linkage value and 2-means CI, this corresponds to larger and smaller values, respectively. As in SigClust, we also compute a Gaussian approximate p-value in addition to the empirical p-value. In this example, the resulting empirical p-values, 0.020 and 0, using linkage and the 2-means CI, both suggest significant clustering at the node.

In estimating the null Gaussian distribution, we first note that many popular linkage functions, including Ward’s, single, complete and average, are defined with respect to the pairwise dissimilarities of observations belonging to two clusters. As such, the use of these linkage functions with any dissimilarity satisfying mean shift and rotation invariance, such as Euclidean or squared Euclidean distance, naturally leads to the invariance of the entire hierarchical procedure. Thus, for several choices of linkage and dissimilarity, the SHC p-value can be equivalently calculated using data simulated from a simplified distribution centered at the origin, with diagonal covariance structure. To handle the HDLSS setting, as in SigClust, we further assume that the covariance matrix of the null Gaussian distribution follows a factor analysis model, such that the problem may be addressed using the hard-threshold, soft-threshold and sample approaches proposed in Liu et al. (2008); Huang et al. (2015).

Throughout this paper we derive theoretical and simulation results using squared Euclidean dissimilarity with Ward’s linkage, an example of a mean shift and rotation invariant choice of dissimilarity and linkage function. However, our approach may be implemented using a larger class of linkages and appropriately chosen dissimilarity functions. We focus on Ward’s linkage clustering as the approach may be interpreted as characterizing clusters as single Gaussian distributions, as in the hypotheses we propose to test. Additionally, we have observed that Ward’s linkage clustering often provides strong clustering results in practice.

Note that at each node, the procedure requires fitting a null Gaussian distribution using only the observations contained in the corresponding subtree. We therefore set a minimum subtree size, N_min, for testing at any node. For the simulations in Section 5, we use N_min = 10.

In this section, we have described only a single test of the entire SHC procedure. For a dataset of N observations, at most (N − 1) tests may be performed along the dendrogram. While the total number of tests is typically much smaller due to the minimum subtree criterion, care is still needed to account for the issue of multiple testing. In the following section, we describe a sequential approach for controlling the FWER to address this issue.

3.2 Multiple Testing Correction

To control the FWER of the SHC procedure, one could simply test at all nodes simultaneously, and apply an equal Bonferroni correction to each test. However, this approach ignores the clear hierarchical nature of the tests. Furthermore, the resulting dendrogram may have significant calls at distant and isolated nodes, making the final output difficult to interpret. Instead, we propose to control the FWER using a sequential approach which provides greater power at the more central nodes near the root of the dendrogram, and also leads to more easily interpretable results.

To correct for multiple testing, we employ the FWER controlling procedure of Meinshausen (2008) originally proposed in the context of variable selection. For the SHC approach, the FWER along the entire dendrogram is defined to be the probability of at least once, falsely rejecting the null at a subtree of the dendrogram corresponding to a single Gaussian cluster. To control the FWER at level α ∈ (0, 1), we perform the hypothesis test described above at each node j, with the modified significance cutoff:

$${\alpha }_j^{\ast }=\alpha \cdot \frac{N_j-1}{N-1},$$

where N_j is used to denote the number of observations clustered at node j. Starting from the root node, i.e. j = 1, we descend the dendrogram rejecting at nodes for which the following two conditions are satisfied: $(\mathrm{C}1)p_j<{\alpha }_j^{\ast }$, and (C2) the parent node was also rejected, where the parent of a node is simply the one directly above it. For the root node, condition (C2) is ignored. As the procedure moves down the dendrogram, condition (C1) and the modified cutoff, ${\alpha }_j^{\ast }$, apply an increasingly stringent correction to each test, proportional to the size of the corresponding subtree. Intuitively, if the subtree at a node contains multiple clusters, the same is true of any node directly above it. Condition (C2) formalized this intuition by forcing the set of significant nodes to be well connected from the root. Furthermore, recall that the hypotheses tested at each node assess whether or not the two subtrees were generated from a single Gaussian distribution. While appropriate when testing at nodes which correspond to one or more Gaussian distributions, the interpretation of the test becomes more difficult when applied to only a portion of a single Gaussian distribution, e.g. only half of a Gaussian cluster. This can occur when testing at a node which falls below a truly null node. In this case, while the two subtrees of the node correspond to non-Gaussian distributions, they do not correspond to interesting clustering behavior. Thus, testing at such nodes may result in truly positive, but uninteresting, significant calls. By restricting the set of significant nodes to be well connected from the root, in addition to controlling the FWER, our procedure also limits the impact of such undesirable tests.

4. Theoretical Development

In this section, we study the theoretical behavior of our SHC procedure with linkage value as the measure of cluster strength applied to Ward’s linkage hierarchical clustering. We derive theoretical results for the approach under both the null and alternative hypotheses. In the null setting, the data are sampled from a single Gaussian distribution. Under this setting, we show that the empirical SHC p-value at the root node follows the U(0, 1) distribution. In the alternative setting, we consider the case when the data follow a mixture of two spherical Gaussian distributions. Since SHC is a procedure for assessing statistical significance given a hierarchical partition, the approach depends heavily on the algorithm used for clustering. We therefore first provide conditions for which Ward’s linkage clustering asymptotically separates samples from the two components at the root node. Given these conditions are satisfied, we then show that the corresponding empirical SHC p-value at the root node tends to 0 asymptotically as both the sample size and dimension grow to infinity. All proofs are included in Web Appendix A of the Supplementary Materials.

We first consider the null case where the data, $\mathbb{X}=\{{\mathit{X}}_1,\dots ,{\mathit{X}}_N\}$, are sampled from a single Gaussian distribution, N(0, Σ). The following proposition describes the behavior of the empirical p-value at the root node under this setting.

Proposition 1

Suppose $𝕏$ were drawn from a single Gaussian distribution, N(0, Σ), with known covariance matrix Σ. Then, the SHC empirical p-value at the root node follows the U(0, 1) distribution.

The proof of Proposition 1 is omitted, as it follows directly from an application of the probability integral transform. We also note that the result of Proposition 1 similarly holds for any subtree along a dendrogram corresponding to a single Gaussian distribution. Combining this with Theorem 1 of Meinshausen (2008), we have that the modified p-value cutoff procedure of Section 3.2 controls the FWER at the desired level α.

We next consider the alternative setting. Suppose the data, $𝕏$, were drawn from a mixture of two Gaussian subpopulations in ℝ^p, denoted by $N({\mathit{\mu }}_1,{\sigma }_1^2{\mathbf{I}}_p)$ and $N({\mathit{\mu }}_2,{\sigma }_2^2{\mathbf{I}}_p)$. Let ${𝕏}^{(1)}=\{{\mathit{X}}_1^{(1)},\dots ,{\mathit{X}}_n^{(1)}\}$ and ${𝕏}^{(2)}=\{{\mathit{X}}_1^{(2)},\dots ,{\mathit{X}}_m^{(2)}\}$ denote the N = n + m observations of $𝕏$ drawn from the two mixture components. In the following results, we consider the HDLSS asymptotic setting where p → ∞ and n = p^α + o(p), m = p^β + o(p) for α, β ∈ (0, 1) (Hall et al., 2005). As in Borysov et al. (2014), we assume that the mean of the difference $({\mathit{X}}_i^{(1)}-{\mathit{X}}_j^{(2)})$ is not dominated by a few large coordinates in the sense that for some ε > 0,

$${\displaystyle \sum _{k=1}^p{({\mu }_{1,k}-{\mu }_{2,k})}^4=o(p^{2-\epsilon }),p\to \infty .}$$ (2)

Given this assumption, the following theorem provides necessary conditions for Ward’s linkage clustering to correctly separate observations of the two mixture components.

Theorem 1

Suppose (2) is satisfied and the dendrogram is constructed using Ward’s linkage function. Let n, m respectively be the numbers of observations sampled from the two Gaussian mixture components, $N({\mathit{\mu }}_1,{\sigma }_1^2{\mathit{I}}_p)$ and $N({\mathit{\mu }}_2,{\sigma }_2^2{\mathit{I}}_p)$, with σ₁ ≤ σ₂. Additionally, suppose n = p^α + o(p), m = p^β + o(p) for α, β ∈ (0, 1), and let μ² denote $p^{-1}{\Vert {\mathit{\mu }}_1-{\mathit{\mu }}_2\Vert }_2^2$. Then, if lim sup $\frac{n^{-1}({\sigma }_2^2-{\sigma }_1^2)}{{\mu }^2}<1$, X⁽¹⁾ and X⁽²⁾ are separated at the root node with probability converging to 1 as p → ∞.

Theorem 1 builds on the asymptotic results for hierarchical clustering described in Borysov et al. (2014). The result provides a theoretical analysis of Ward’s linkage clustering, independent of our SHC approach. In the following result, using Theorem 1, we show that under further assumptions, the SHC empirical p-value is asymptotically powerful at the root node of the dendrogram. That is, the p-value converges to 0 as p, n, m grow to infinity.

Theorem 2

Suppose the assumptions for Theorem 1 are satisfied. Furthermore, suppose ${\sigma }_1^2$ and ${\sigma }_2^2$ are known. Then, using linkage as the measure of cluster strength, the empirical SHC p-value at the root node along the dendrogram equals 0 with probability converging to 1 as p → ∞.

By Theorem 2, the SHC procedure is asymptotically well powered to identify significant clustering structure in the presence of multiple Gaussian components. While in this section we only considered the theoretical behavior of SHC using linkage value as the measure of cluster strength, empirical results presented in the following section provide justification for alternatively using the 2-means CI.

5. Simulations

In this section we illustrate the performance of our proposed SHC approach using simulation studies. Two implementations of SHC are considered, denoted by SHC_L and SHC₂, differing by whether the linkage value or the 2-means CI is used to measure the strength of clustering.

The performance of SHC is compared against the existing pvclust and BootClust approaches. In each simulation, Ward’s linkage clustering was applied to a dataset drawn from a mixture distribution in ℝ^p. A range of simulation settings were considered, including the null setting with K = 1 and alternative settings with K = 2, 3,…,8. To evaluate the robustness of the SHC approach to the underlying Gaussian assumption, simulations were completed with each cluster generated from Gaussian as well as t-distributions with 3 and 6 degrees of freedom, denoted t₃ and t₆. Simulation settings with both balanced and imbalanced cluster sizes were also considered. For all values of K, low (p = 10), moderate (p = 100), and high (p = 1000) dimensional simulations were explored. All settings were replicated 100 times. A representative set of results are reported in this section. Complete simulation results may be found in Web Appendix B of the Supplementary Materials. In the interest of space, all simulation results for K = 2 (Web Tables S5–S9), and K = 4 (Web Tables S18–S20) are left to Web Appendix B.

In all simulations, SHC p-values were calculated using 100 simulated null cluster indices, and the corresponding Gaussian-fit p-values are reported. When p = 10, the covariance matrix for the Gaussian null was estimated using the sample covariance matrix. Otherwise, the soft-threshold approach described in Huang et al. (2015) was used. The BootClust implementation was provided by the authors of Maitra et al. (2012). BootClust requires specifying an upper limit on the possible number of clusters, which was set to 10 for all simulations. In our simulations, the BootClust approach showed degenerate behavior when p = 1000, and therefore, performance using BootClust is not reported for these settings. A more complete discussion of this is provided in Web Appendix B and Web Table S1, along with a brief review of the fundamental differences between pvclust and our proposed SHC method. Both the pvclust and BootClust approaches were implemented using 100 bootstrap samples. The pvclust method of Suzuki and Shimodaira (2006) computes two values: an approximately unbiased (AU) p-value based on a multi-step multi-scale bootstrap resampling procedure (Shimodaira, 2004), and a bootstrap probability (BP) p-value calculated from ordinary bootstrap resampling (Efron et al., 1996). In the interest of space, results for pvclust BP p-values are left to Web Appendix B as the approach showed consistently negligible power throughout the simulations considered in this section. A significance threshold of α = 0.05 was used with all three approaches.

5.1 Null Setting (K = 1)

We first consider the null setting to evaluate the ability of SHC to control for false positives. In these simulations, datasets of size N = 50, 100, 200 were sampled from a single Gaussian, t₆ or t₃ distribution in p = 10, 100, 1000 dimensions with diagonal covariance and one dimension scaled by $\sqrt{v}$ to mimic low-dimensional signal for v ⩾ 1. The v = 1 case reduces to the spherical covariance setting. A subset of the simulation results are presented in Table 1, with complete results provided in Web Tables S2, S3, and S4.

Table 1.

Representative results for Simulation 5.1 (K = 1). Number of false positives at α = 0.05, and median computing time over 100 replications. (N: sample size, p: dimension, v: spike size, F: generating distribution.)

parameters				|p-value < 0.05|				median time (sec.)
N	p	v	F	pvAU	SHCL	SHC2	BC	pv	SHCL	SHC2	BC
100	10	1	Gaus.	0	0	0	0	22.38	0.16	0.23	0.78
100	100	1	Gaus.	0	0	0	46	28.59	1.2	1.38	7.35
100	1000	1	Gaus.	0	0	0	−	96.79	12.03	13.65	−
100	10	1	t6	1	0	0	0	22.44	0.16	0.24	0.79
100	100	1	t6	1	0	0	57	34.01	1.21	1.4	8.06
100	1000	1	t6	1	0	0	−	115.5	11.09	13.02	−
100	10	1	t3	18	16	20	28	22.02	0.22	0.31	1.09
100	100	1	t3	14	40	45	72	36.6	1.21	1.45	18.9
100	1000	1	t3	22	45	48	−	101.62	12.43	14.58	−
100	10	100	Gaus.	10	0	4	0	25.29	0.22	0.31	1.04
100	100	100	Gaus.	3	0	2	44	34.15	1.06	1.24	8.3
100	1000	100	Gaus.	0	0	0	−	94.58	12.16	13.74	−
100	10	100	t6	12	0	0	0	22.48	0.16	0.23	0.76
100	100	100	t6	3	0	0	48	34.52	1.2	1.39	8.25
100	1000	100	t6	1	0	0	−	99.47	12.09	13.78	−
100	10	100	t3	22	0	0	0	22.96	0.17	0.26	0.72
100	100	100	t3	16	0	2	51	36.05	1.2	1.39	10.15
100	1000	100	t3	11	9	9	−	117.9	12.28	14.23	−

For each method, we report the number of replications with false positive calls and the corresponding median computing time of a single replication. As both AU and BP p-values are computed simultaneously, only a single computing time is reported for pvclust.

In Table 1, both SHC_L and SHC₂ show generally conservative behavior in settings using Gaussian simulated data. The conservative behavior of the classical SigClust procedure was previously described in Liu et al. (2008) and Huang et al. (2015) as being a result of the challenge of estimating the null eigenvalues and the corresponding covariance structure in the HDLSS setting (Baik and Silverstein, 2006). As both SHC_L and SHC₂ rely on the same null covariance estimation procedure, this may also explain the generally conservative behavior observed in our analysis. The BootClust approach shows anti-conservative behavior for p = 100, and becomes intractable when p = 1000 under the Gaussian setting. The pvclust AU p-values shows slight anti-conservative behavior in the Gaussian setting with low-dimension and high variability (p = 10 and v = 100). Similar performance is observed across all methods for data generated from the heavy-tailed t₆ distribution. However, using the heavier-tailed t₃ distribution, both SHC_L and SHC₂ exhibit anti-conservative behavior similar to BootClust and pvclust, illustrating the effect of the Gaussian null assumption made by both SHC methods. The behavior is particularly pronounced for large sample sizes, as the null estimation of the t₃-distribution is improved. BootClust again shows the strongest anti-conservative behavior. Both SHC approaches required an order of magnitude less time than pvclust across all settings, and required less than one minute in high-dimensional settings.

5.2 Three Cluster Setting (K = 3)

We next consider the alternative setting in which datasets were drawn equally from three spherical Gaussian, t₆ or t₃ distributions. The setting illustrates the simplest case for which significance must be attained at multiple nodes to discern the true clustering structure from a dendrogram using SHC. Two arrangements of the three components were studied. In the first, the components were placed along a line with distance δ between the means of neighboring components. In the second, the components were placed at the corners of an equilateral triangle with side length δ. Several values of δ were used to evaluate the relative power of each method across varying levels of signal. For each dataset, N = 150, 300 or 600 samples were drawn randomly from the three components with probabilities π₁, π₂, π₃. Select simulation results for the triangular arrangement with equal cluster proportions (π₁, π₂, π₃ = 1/3, 1/3, 1/3) are presented in Table 2. Similar results were observed when clusters were arranged in a line, as well as when unequal cluster proportions were used. Complete results are presented in Web Tables S10–S17.

Table 2.

Representative results for Simulation 5.2 (K = 3) with N = 150 samples and clusters placed at vertices of an equilateral triangle with side length δ. Number of replications identifying the correct number of significant clusters, mean number of significant clusters, median computing time and mean ARI over 100 replications. (K: cluster count, $\widehat{K}$: predicted cluster count, p: dimension, δ: cluster separation, F: generating distribution.)

parameters			$\left|\widehat{K}=3\right|(\text{mean}\widehat{K})$				median time (sec.)				mean ARI
p	δ	F	pvAU	SHCL	SHC2	BC	pv	SHCL	SHC2	BC	pvAU	SHCL	SHC2	BC
10	4	Gaus.	1 (29.17)	21 (1.89)	36 (2.14)	41 (2.19)	42.2	0.52	0.7	1.59	0.08	0.43	0.52	0.53
10	8	Gaus.	25 (10.17)	89 (2.87)	94 (2.94)	94 (2.94)	42.04	0.64	0.86	1.56	0.64	0.93	0.96	0.96
100	4	Gaus.	11 (6.02)	5 (1.58)	3 (1.61)	0 (5.23)	56.64	2.73	3.2	13.07	0	0.26	0.27	0.13
100	8	Gaus.	6 (6.04)	59 (2.59)	62 (2.62)	0 (9.91)	55.97	4.08	4.75	21.42	0.23	0.8	0.81	0.38
1000	8	Gaus.	12 (4.32)	24 (2.09)	45 (2.35)	−	180.93	34.32	42.07	−	0.01	0.53	0.61	−
1000	16	Gaus.	23 (4.4)	82 (2.81)	90 (2.89)	−	194.7	34.69	38.96	−	0.38	0.91	0.93	−
10	4	t3	0 (28.7)	3 (1.29)	7 (1.45)	8 (5.36)	42.62	0.31	0.42	1.65	0.02	0.09	0.14	0.3
10	8	t3	2 (22.69)	48 (2.37)	55 (2.75)	55 (4.61)	42.24	0.62	0.85	1.6	0.2	0.63	0.73	0.73
100	4	t3	3 (4.79)	16 (1.89)	17 (1.91)	0 (6.4)	57.74	3.38	3.83	17.65	0	0	0	0.05
100	8	t3	2 (6.98)	31 (2.11)	36 (2.36)	0 (9.46)	64.76	2.96	3.89	22.27	0.03	0.38	0.43	0.57
1000	8	t3	16 (2.34)	22 (2.09)	25 (2.11)	−	171.07	35.54	43.33	−	0	0.01	0.01	−
1000	16	t3	19 (3.76)	28 (2.44)	32 (2.51)	−	187.08	40.22	45.36	−	0.03	0.5	0.51	−

For each method, we report the number of replications out of 100 in which statistically significant evidence was detected for the correct number of clusters as well as the mean number of significant clusters and the median computing time across replications. Additionally, to assess how well detected clusters agree with the true cluster labels, we report the mean adjusted Rand Index (ARI) for each method. The ARI provides a measure of cluster agreement corrected for randomness, with larger values corresponding to higher agreement.

Across all settings under the triangular arrangement, the SHC_L and SHC₂ approaches show the highest sensitivity, while pvclust AU p-values consistently over-estimate the number of clusters. The problem appears to be exacerbated in the low-dimensional (p = 10) setting. In contrast, the BootClust approach shows similar sensitivity to both SHC_L and SHC₂ when p = 10, but greatly over-estimates the number of clusters when p = 100 (Web Table S14) and becomes intractable when p = 1000 (Web Table S15). As expected, performance decreases when clusters are generated from the heavy-tailed t₃ distribution.

5.3 Increasing Cluster Count Setting (K = 5, 6, 7, 8)

Finally, we consider the alternative setting in which datasets were drawn from a mixture of K = 5, 6, 7 or 8 Gaussian or t-distributions. All simulations were performed with N = K·50 samples. Cluster sizes were determined by sampling from a multinomial distribution with equal probabilities across clusters. In each replication, the K cluster centers were uniformly randomly placed within a (K − 1)-dimensional sphere centered at the origin with radius δ, such that larger values of δ roughly correspond to greater separating signal between clusters. Select simulation results are presented in Table 3, with complete results presented in Web Tables S21–S24. As in Simulation 5.2, for each dataset, we report the number of replications in which the correct number of clusters were predicted, the mean number of significant clusters, the median computing time, and the mean ARI across replications.

Table 3.

Representative results for Simulation 5.3 (K = 5, 6, 7, 8) with N = K·50 samples. Number of replications identifying the correct number of significant clusters, mean number of significant clusters, median computing time and mean ARI over 100 replications. (K: cluster count, $\widehat{K}$: predicted cluster count, p: dimension, δ: cluster separation, F: generating distribution.)

parameters				$\left|\widehat{K}=K\right|(\text{mean}\widehat{K})$				median time (sec.)				mean ARI
K	p	δ	F	pvAU	SHCL	SHC2	BC	pv	SHCL	SHC2	BC	pvAU	SHCL	SHC2	BC
5	10	8	Gaus.	0 (8.13)	44 (4.28)	66 (4.65)	66 (4.65)	118.38	2.07	2.88	5.58	0.5	0.83	0.9	0.9
6	10	8	Gaus.	2 (6.73)	55 (5.26)	78 (5.72)	80 (5.78)	145.95	2.68	3.42	6.75	0.47	0.86	0.93	0.94
7	10	8	Gaus.	0 (7.02)	56 (6.23)	84 (6.79)	90 (6.9)	238.92	4.96	6.08	12.22	0.45	0.87	0.95	0.96
8	10	8	Gaus.	0 (5.06)	55 (6.99)	85 (7.79)	91 (7.91)	257.84	4.78	6.14	12.32	0.39	0.87	0.96	0.97
5	1000	15	Gaus.	3 (7.67)	53 (4.39)	69 (4.67)	−	623.62	111.32	125.83	−	0.22	0.86	0.9	−
6	1000	15	Gaus.	5 (8.1)	63 (5.58)	76 (5.76)	−	1014.4	136.28	146.92	−	0.33	0.91	0.93	−
7	1000	15	Gaus.	7 (8.57)	64 (6.54)	80 (6.7)	−	1294.04	184.71	198.92	−	0.37	0.92	0.94	−
8	1000	15	Gaus.	4 (8.98)	77 (7.66)	92 (7.88)	−	1620.74	262.55	279.85	−	0.41	0.95	0.97	−
5	10	8	t3	0 (42.22)	4 (2.73)	20 (3.43)	22 (7)	108.62	1.68	2.18	4.45	0.2	0.43	0.53	0.72
6	10	8	t3	0 (47.88)	9 (3.74)	26 (4.49)	20 (7.54)	178.72	2.91	3.87	9.36	0.2	0.54	0.61	0.77
7	10	8	t3	0 (63.18)	7 (4.3)	23 (5.33)	20 (8.4)	242.14	4.54	5.43	13.09	0.2	0.54	0.64	0.79
8	10	8	t3	0 (74.68)	2 (4.26)	13 (5.54)	23 (8.96)	289.16	6.24	7.38	17.53	0.17	0.46	0.58	0.8
5	1000	15	t3	20 (5.73)	13 (3.62)	10 (3.68)	−	687.27	115.76	124.45	−	0.02	0.4	0.4	−
6	1000	15	t3	15 (8.44)	4 (3.88)	8 (3.97)	−	921.06	150.42	161.42	−	0.01	0.39	0.4	−
7	1000	15	t3	7 (9.01)	10 (4.64)	12 (4.72)	−	1306.18	256.93	263.95	−	0	0.41	0.42	−
8	1000	15	t3	3 (10.07)	6 (5.53)	8 (5.7)	−	1387.78	340.85	360.39	−	0.01	0.44	0.45	−

The results presented in Table 3 largely support the results observed in Simulation 5.2. Again, the pvclust AU p-values provide little power to detect the correct clusters in the simulated settings, as shown by the relatively low mean ARI values achieved by the method. The BootClust approach achieves performance comparable to SHC_L and SHC₂ in the heavy tailed (t₃) setting. However, the approach shows poor performance in the moderate-dimensional (p = 100) settings (Web Tables S21–S24), and cannot be applied when p = 1000. Both SHC_L and SHC₂ methods show consistent performance across both low (p = 10) and high (p = 1000) dimensional settings.

6. Real Data Analysis

To further demonstrate the power of SHC, we apply the approach to two cancer gene expression datasets. In this section, we consider a cohort of 337 breast cancer (BRCA) samples, previously categorized into five molecular subtypes (Parker et al., 2009). Additionally, in Web Appendix C and Web Figures S1 and S2, we consider a dataset of 300 tumor samples drawn from three distinct cancer types. The greater number of subpopulations, as well as the more subtle differences between them, make the BRCA dataset more challenging than the dataset described in Web Appendix C. Data were clustered using Ward’s linkage, and the SHC₂ approach was applied using 1000 simulations. FWER was controlled at α = 0.05.

6.1 BRCA Gene Expression Dataset

A microarray gene expression dataset of 337 BRCA samples was obtained from the University of North Carolina (UNC) Microarray Database (https://genome.unc.edu/pubsup/clow/) and compiled, filtered and normalized as described in Prat et al. (2010). Gene expression was analyzed for a subset of 1645 well-chosen intrinsic genes (Prat et al., 2010). We evaluate the ability of our approach to detect biologically relevant clustering based on five molecular subtypes: luminal A (LumA), luminal B (LumB), basal-like, normal breast-like, and HER2-enriched (Parker et al., 2009). The dataset is comprised of 97 LumA, 54 LumB, 91 basal-like, 47 normal breast-like, and 48 HER2-enriched samples. Per-subtype separation and marginal variances are shown in Web Figure S3. The observed values illustrate that real data, indeed, fall within the range of parameters used in the simulations of Section 5.

The expression dataset is shown as a heatmap in Figure 3A, with the corresponding dendrogram and subtype labels reproduced in Figure 3B. The corresponding SHC₂ p-values and modified significance thresholds are given only at nodes tested while controlling the FWER at α = 0.05. SHC₂ identifies at least three significantly differentiated clusters in the dataset, primarily corresponding to luminal (LumA and LumB), basal-like, and all remaining subtypes. Diagnostic plots investigating the SHC model assumptions are shown in Web Figure S4. While the data appear to be heavier tailed than Gaussian, this may be partially attributed to the factor analysis model, which is also shown to hold in the plots. The diagnostics suggest that while still useful, the SHC test may lack some power as in the moderately heavy-tailed simulations of Section 5. The corresponding ARI for the clusters is 0.42, while the highest achievable ARI using Ward’s linkage clustering was 0.52 at K = 5. At the root node, the LumA and LumB samples are separated from the remaining subtypes with a p-value of 8.07e − 4 at a threshold of ${\alpha }_1^{\ast }=0.05$. However, Ward’s linkage clustering and SHC₂ are unable to identify significant evidence of clustering between the two luminal subtypes. The difficultly of clustering LumA and LumB subtypes based on gene expression was previously described in Mackay et al. (2011). Next, the majority of basal-like samples are separated from the remaining set of observations, with a p-value of 0.0198 at a cutoff of ${\alpha }_2^{\ast }=0.027$. The remaining HER2-enriched, normal breast-like and basal-likes samples show moderate separation by Ward’s linkage clustering. However, the subsequent node is non-significant, highlighting the difficulty of assessing statistical significance for larger numbers of clusters while controlling for multiple testing. When analyzed using pvclust as described in Section 5, only a single statistically significant cluster of more than 10 samples was identified, corresponding to the HER2 samples. Finally, when the BootClust approach was applied with a maximum of 30 clusters, as in the moderate and high-dimensional simulations of Section 5, the maximum possible number of clusters was predicted.

Figure 3.

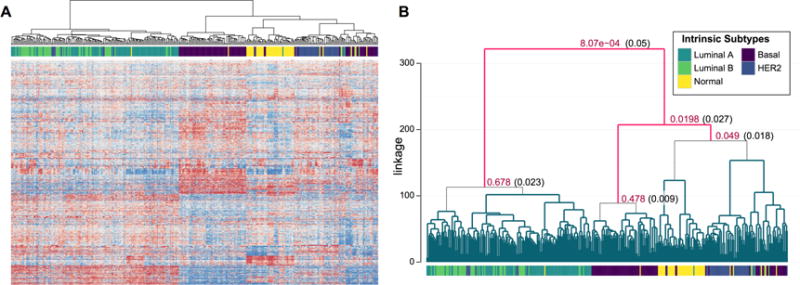
Analysis of gene expression for 337 BRCA samples. (A) Heatmap of gene expression for the 337 samples (columns) clustered by Ward’s linkage. (B) Dendrogram with corresponding SHC p-values and α* cutoffs given only at nodes tested according to the FWER controlling procedure at α = 0.05. This figure appears in color in the electronic version of this article.

7. Discussion

While hierarchical clustering has become widely popular in practice, few methods have been proposed for assessing the statistical significance of a hierarchical partition. SHC was developed to address this problem, using a sequential testing and FWER controlling procedure. Through an extensive simulation study, we have shown that SHC provides competitive results compared to existing methods. Furthermore, in applications to two gene expression datasets, we showed that the approach is capable of identifying biologically meaningful clustering.

In this paper, we focused on the theoretical and empirical properties of SHC using Ward’s linkage, and in general, we suggest using SHC₂ over SHC_L based on our simulation results. However, there exist several different approaches to hierarchical clustering, and Ward’s linkage may not always be the most appropriate choice. In these situations, as mentioned in Section 3, SHC may be implemented with other linkage and dissimilarity functions which satisfy mean shift and rotation invariance. Further investigation is necessary to fully characterize the behavior of the approach for different hierarchical clustering procedures.

Some popular choices of dissimilarity, such as those based on Pearson correlation of the covariates between pairs of samples, fail to satisfy the necessary mean shift and rotation invariance properties in the original covariate space. As a consequence, the covariance of the Gaussian null distribution must be fully estimated, and cannot be approximated using only the eigenvalues of the sample covariance matrix. When N ≫ p, the SHC method can still be applied by estimating the complete covariance matrix. However, in HDLSS settings, estimation of the complete covariance matrix can be difficult and computationally expensive. A possible direction of future work is the development of a computationally efficient procedure for non-invariant hierarchical clustering procedures.