Strategies for Comparing Metabolic Profiles: Implications for the Inference of Biochemical Mechanisms from Metabolomics Data

Abstract

Background

Large amounts of metabolomics data have been accumulated in recent years and await analysis. Previously we had developed a systems biological approach to infer biochemical mechanisms underlying metabolic alterations observed in cancers and other diseases. The method utilized the typical Euclidean distance for comparing metabolic profiles. Here we ask whether any of the numerous alternative metrics might serve this purpose better.

Methods and Findings

We used enzymatic alterations in purine metabolism that were measured in human renal cell carcinoma to test various metrics with the goal of identifying the best metrics for discerning metabolic profiles of healthy and diseased individuals. The results showed that several metrics have similarly good performance, but that some are unsuited for comparisons of metabolic profiles. Furthermore, the results suggest that relative changes in metabolite levels, which reduce bias toward large metabolite concentrations, are better suited for comparisons of metabolic profiles than absolute changes. Finally, we demonstrate that a sequential search for enzymatic alterations, ranked by importance, is not always valid.

Conclusions

We identified metrics that are appropriate for comparisons of metabolic profiles. In addition, we constructed strategic guidelines for the algorithmic identification of biochemical mechanisms from metabolomics data.

Introduction

Since entering the post-genomic era, high-throughput methods and biomedical instrumentation have been generating unprecedented amounts of data. The sheer size of these datasets is staggering and easily exceeds our capability of mining them for hidden information and novel insights. Among the high-throughput data, metabolomics profiles are of special interest because they form the bridge between enzymes, which govern biochemical mechanisms, with metabolites, which are directly tied to physiological function. This connection is important to study, because a healthy cell, tissue, or organ often exhibits different metabolic profiles when it enters a disease state or is subject to severe external perturbations. For example, cancer cells frequently alter their metabolism to facilitate rapid growth and proliferation [1, 2]. Since details underlying the pathogenic mechanisms of a disease are typically unclear, but their resulting altered metabolic profiles can be measured, an important question arises, namely: Do metabolomics data contain sufficient information for the inference of the underlying pathophysiological mechanisms?

In recent work, we proposed systems biological approaches to address this inference challenge and applied them successfully to analyses of colorectal cancer and Parkinson’s disease [3, 4]. Briefly, the methods we introduced strive to identify reaction steps that are altered by a disease or an external perturbation that becomes manifest at the metabolic level. The methods do so by repeatedly simulating very many combinations of changes in reactions and assessing their effects on the resulting metabolic profile. This ensemble approach involves intensive searches within the high-dimensional space of possible changes in enzymatic activities and is followed by various screens that filter out the most likely scenarios. It combines strategies from reverse engineering, optimization, machine learning, and statistics.

Thus the inference method requires means of quantitatively comparing simulated metabolic profiles against the observed metabolic profile extracted from the metabolomics data. Expressed differently, any comparison of this type mandates a distance metric. In our previous studies, we used the default of the Euclidian norm. However, numerous other metrics with quite different characteristics are available, thus begging the question whether the Euclidian norm is optimal for this type of comparisons. All metrics treat a metabolic profile as a high-dimensional vector, whose dimension equals the number of metabolites, and calculate the difference between two profiles (such as the profiles in a healthy and a cancer cell) using their own characteristic formulae. The most prevalent metrics fall into two broad groups: distance-based and similarity-based (Table I).

Table I.

Metrics for comparison of metabolic profiles and their characteristics

Metrics	Characteristics	Characteristics
Minkowski distance	$d(X,Y)={(\sum _{i=1}^N{|x_i-y_i|}^m)}^{\frac{1}{m}}$	A general metric, here implemented with m = 3.
Euclidean distance	$d(X,Y)={(\sum _{i=1}^N{|x_i-y_i|}^2)}^{\frac{1}{2}}$	Commonly used; increases influences of errors from large components on distance to some extent
Manhattan distance	$d(X,Y)=(\sum _{i=1}^N|x_i-y_i|)$	Each component has the same influence on distance
Jeffreys & Matusita distance	$d(X,Y)={(\sum _{i=1}^N{|\sqrt{x_i}-\sqrt{y_i}|}^2)}^{\frac{1}{2}}$	Based on Euclidean distance; increases influences of errors from small components on distance to some extent
Canberra distance	$d(X,Y)=(\sum _{i=1}^N|\frac{x_i-y_i}{x_i+y_i}|)$	A metric considering relative magnitudes of errors in components
Relative distance	$d(X,Y)={(\sum _{i=1}^N{(\frac{x_i-y_i}{y_i})}^2)}^{\frac{1}{2}}$	Similar to Euclidean distance but uses relative distance instead
Cosine of angle	$\mathit{\text{similarity}}(X,Y)=\frac{\sum _{i=1}^N{x}_i•y_i}{{(\sum _{i=1}^N{x_i}^2•\sum _{i=1}^N{y_i}^2)}^{\frac{1}{2}}}$	A similarity metric using the cosine of the angle between two vectors; not affected by absolute values of components
Dice’s coefficient	$\mathit{\text{similarity}}(X,Y)=\frac{2•\sum _{i=1}^N{x}_i•y_i}{\sum _{i=1}^N{x_i}^2+\sum _{i=1}^N{y_i}^2}$	A similarity metric comparable to the cosine similarity, using arithmetic averages instead of geometric averages
Jaccard similarity coefficient	$\mathit{\text{similarity}}(X,Y)=\frac{\sum _{i=1}^N{x}_i•y_i}{\sum _{i=1}^N{x_i}^2+\sum _{i=1}^N{y_i}^2-\sum _{i=1}^N{x}_i•y_i}$	A similarity metric similar to general Dice’s similarity

The metrics have been extensively used for various purposes in multiple areas. For example, distance metrics have been applied to mechanical engineering [5], imaging processing [6], robotics [7], text matching [8], and phylogenetic analysis [9]. For metabolomics data, these metrics were used for genotype discrimination [10], clustering [11], cancer subgroup identification [12], and etc. Some comparisons among various metrics, especially in the context of clustering, have already been mad [13, 14]. Differently, we are comparing the performance of various metrics for inference of biochemical mechanisms. For this purpose, the following questions could be asked:

• Question 1: Given that metrics suggest different degrees of similarity between two metabolic profiles, do some metrics exhibit better performance in discerning metabolic profiles. If so, is one metric always superior for the inference of biochemical mechanisms from metabolomics data?

• Question 2: Do some metrics deal better with uncertainties than others? When one searches for biochemical mechanisms that are affected by disease or perturbations, such as the activation or inhibition of an enzyme, one cannot necessarily expect to identify these mechanisms with mathematical precision when explore a high-dimensional parameter space. In other words, one should merely expect the correct identification of a relatively small neighborhood surrounding the true target point within the large space. Therefore, an effective search method should be able to recognize when it approaches the correct neighborhood, which requires that metrics can tolerate uncertainties and subsequently keep the search within this neighborhood.

• Question 3: Should absolute or relative changes in metabolite concentrations be used by a distance metric? Metabolites can be present in vastly different quantities even within the same system. For example, some metabolites have in vivo concentrations in the mM range, while others are at µM level. When a healthy system becomes perturbed or diseased, the changes in metabolites should be expected to differ correspondingly in magnitude, and these differences influence the distance between the healthy and perturbed metabolic profiles, especially if absolute changes are considered. As a consequence, absolute changes in a few metabolite concentrations may unduly dominate the distance between profiles and thereby bias the search for likely mechanisms in an unfavorable manner. By contrast, relative changes may provide certain advantages by reducing bias toward high metabolite concentrations.

• Question 4: Is it necessary to search for all alterations simultaneously or is it feasible to identify alterations in biochemical reaction steps in a ranked, sequential manner? It is generally not known how many metabolic processes are affected by a disease or perturbation, where these changes are positioned within a pathway, and what their magnitudes are. One could consider all possible sites simultaneously, but such a strategy could be computationally prohibitive. Alternatively, it might seem reasonable to search for the most significant contributor first and then to progress to other sites in a sequential manner according to their contributions to changes in the observed metabolic profile. This much cheaper alternative raises the questions of whether a sequential search is valid and to what degree the choice of a distance metric affects this validity.

In the following, we test and compare the metrics listed in the Table I against these questions and within the context of effectively identifying metabolic reaction steps that are affected by a disease or perturbation.

Materials and Methods

The main pathway system selected for this study is purine metabolism in human renal cell carcinoma, which is characterized by abnormal growth in the kidneys. This carcinoma is estimated to cause 62,000 new cases and 14,000 deaths in US in 2015 [15].

A mathematical model of purine metabolism

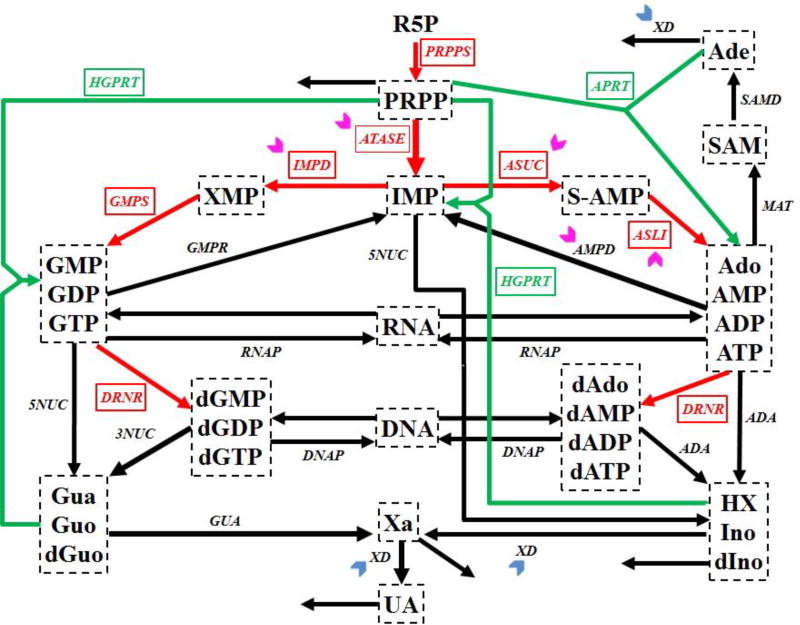
Purine metabolism supplies the body with purine nucleotides for DNA and RNA synthesis and synthesizes de novo compounds like ADP and ATP. Not surprising, it is of critical importance for cell growth and proliferation in cancers. The pathway constitutes a complex dynamical system (Fig. 1) that contains two routes for the synthesis of purines. The first is the de novo synthesis pathway for purine bases (red arrows in Figure 1), whose initial substrate is ribose-5-phosphate (R5P), while the second route is a salvage pathway (green arrows in Figure 1), through which purine bases can be recycled. Quite a detailed mathematical model of human purine metabolism was proposed by Curto et al. [16–18]. It consists of a system of ordinary differential equations with 16 variables and 37 fluxes. This mathematical model is used as the main test system in this study.

Figure 1. Simplified diagram of human purine metabolism.

Purine metabolism consists of a de novo synthesis pathway (red arrows) and a salvage pathway (green arrows) for purine bases. Reactions are represented with arrows. Metabolites are shown in dashed boxes and enzymes are indicated by italics. Table III lists enzyme names and their abbreviations. Chevron arrows point to altered enzymes in human renal cell carcinoma (magenta: activation; blue: inhibition). Regulatory signals are omitted for clarity. Metabolites and their abbreviations are: phosphoribosylpyrophosphate (PRPP), inosine monophosphate (IMP), adenylosuccinate (S-AMP), adenosine + adenosine monophosphate + adenosine diphosphate + adenosine triphosphate (Ado_AMP_ADP_ATP), s-adenosyl-L-methionine (SAM), adenine (Ade), xanthosine monophosphate (XMP), guanosine monophosphate + guanosine diphosphate + guanosine triphosphate (GMP_GDP_GTP), deoxyadenosine + deoxyadenosine monophosphate + deoxyadenosine diphosphate + deoxyadenosine triphosphate (dAdo_dAMP_dADP_dATP), deoxyguanosine monophosphate + deoxyguanosine diphosphate + deoxyguanosine triphosphate (dGMP_dGDP_dGTP), ribonucleic acid (RNA), deoxyribonucleic acid (DNA), hypoxanthine + inosine + deoxyinosine (HX_Ino_dIno), xanthine (Xa), guanine + guanosine + deoxyguanosine (Gua_Guo_dGuo), uric acid (UA), ribose-5-phosphate (R5P).

Chevron arrows

Metabolic information regarding human renal cell carcinoma

Weber performed an enzymatic assay for human renal cell carcinoma and discovered several changes in the activities of enzymes within purine metabolism [19]. The significantly affected enzymes are (indicated in Fig. 1): amidophosphoribosyltransferase (ATASE, 1.58), IMP dehydrogenase (IMPD, 2.53), adenylosuccinate synthetase (ASUC, 1.49), adenylosuccinate lyase (ASLI, 1.76), AMP deaminase (AMPD, 2.07), xanthine oxidase or xanthine dehydrogenase (XD, 0.25). In this list, the numbers in parentheses indicate the fold changes in activity between human renal cell carcinoma and normal kidney cells.

We used these experimental data with Curto’s model of purine metabolism to create “ideal” test data for the comparison of metrics. Namely, we introduced the measured changes in enzymatic activities into the model and computed the resulting metabolic profile for human renal cell carcinoma (Table II). This “dataset” constitutes an ideal metabolomics profile, because it is complete and mathematically precise. It allows us to know exactly what changes in enzyme activities led to this profile, which we consider as “observed.” Furthermore, we have complete information about the pathway in healthy individuals. Since the “data” are mathematically precise, all differences between results can be associated with the different metrics employed.

Table II.

Metabolic profile of normal and human renal cell carcinoma

Metabolite	Normal Cell (µM)	Cancer Cell (µM)	Absolute Change (µM)	Relative Change (%)
PRPP	5.017	4.698	−0.320	−6.376
IMP	98.264	82.785	−15.479	−15.752
S_AMP	0.198	0.156	−0.043	−21.484
Ado/AMP/ADP/ATP	2475.379	2177.100	−298.309	−12.051
SAM	3.992	3.887	−0.105	−2.618
Ade	0.985	0.878	−0.107	−10.851
XMP	24.793	925.311	900.518	3632.172
GMP/GDP/GTP	410.234	633.248	223.014	54.363
dAdo/dAMP/dADP/dATP	6.017	6.305	0.288	4.777
dGMP/dGDP/dGTP	3.026	3.293	0.267	8.816
RNA	28680.584	30152.000	1471.000	5.129
DNA	5180.797	5432.700	251.925	4.863
HX/Ino/dIno	9.519	9.579	0.061	0.639
Xa	5.06	34.879	29.819	589.310
Gua/Guo/dGuo	5.507	33.198	27.691	502.818

Each diseased or healthy metabolic profile is represented by a high-dimensional vector. In the case of purine metabolism, the dimension is 16, which corresponds to the number of metabolites or metabolite pools in the system. In the following, the “ideal” metabolic disease profile generated by the model is called “the target vector”, and vectors resulting from the simulation of other scenarios are called “simulated vectors”.

Normalization of metrics between vectors and statistical considerations

The general strategy for comparing metrics is to compute distances (similarities) between simulated vectors and the target vector. In this analysis, a shorter distance implies a closer similarity between two vectors. For fair comparisons, all metrics are normalized. Specifically, for the six distance-based metrics, the distance between the healthy metabolic profile and the cancer profile, as obtained from the model, is normalized to 100. For the three similarity-based metrics, which are based on angles between vectors, we first compute the inverse cosine of the computed similarities in order to obtain the angle between a simulated vector and the target vector. The angle of π/2 is then normalized to 100. Thus, the similarity is converted into a normalized distance.

Simulations

The All results are based on computer simulations. In each simulation, a certain perturbation of the activities of one or some purine enzymes is implemented in the model and the ODEs are integrated to yield the corresponding steady-state metabolic profile. Using the various metrics, the distance between this putative profile (a simulation vector) and the true disease target vector is computed.

The simulation study is performed in three phases. First, we implement all subsets of perturbations that are actually discovered in renal cell carcinoma, according to Weber [19]. Since six reactions are perturbed in this cancer, we implement changes in between one and six perturbations, where the six-perturbation case is used to compute the target vector. For these simulations, we use the measured magnitudes of perturbations. Secondly, we consider uncertainties in the quantification of the exact perturbations by considering a neighborhood surrounding the exact point in the high-dimensional parameter space. Different metrics are then compared with respect to their capability of reducing the distance when the search approaches the exact point within the neighborhood. Finally, we explore the feasibility of a sequentially nested identification strategy when different metrics are applied.

Statistics

Since uncertainties must be explored in these inferences, we devise a strategy that leads to ensemble results, which are collected as distributions. Statistical comparisons among the means of these distributions are performed with Student’s t-test and a significance level of 0.01.

Results

The metrics under the comparison are to be used for the inference of altered metabolic reaction steps from metabolomics data. The inference method itself was published elsewhere and is not discussed here [3, 4]. The following results focus exclusively on the qualities of the different metrics in Table 1.

Subsets of experimentally measured enzymatic alterations

If only one out of the six experimentally measured enzymatic alterations is implemented with the correct magnitude, there are six choices. These six perturbations are grouped and considered as the scenario of exact perturbations of one enzyme. Similarly, we construct scenarios of two (15 different combinations of exact perturbations), three (20 different combinations), four (15 different combinations), and five enzymes (6 different combinations).

Distances for relative changes

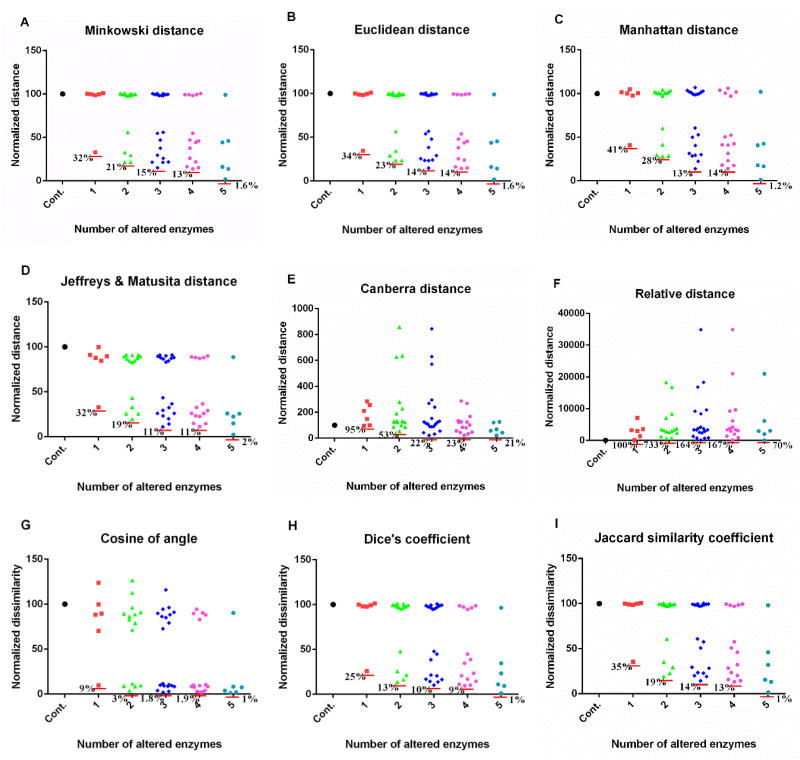
For each scenario, we compute distances between the simulated metabolic profiles and the target vector, using various metrics. Figure 2 shows the distances or dissimilarities between the same set of simulated metabolic profiles from the above scenarios and the target vector, using different metrics and relative changes of metabolites. Here and throughout the analysis, we use the parameter m = 3 in the Minkowski distance. The left-most symbol in each graph is the control, which corresponds to the distance between the healthy and diseased profiles and by definition has a normalized distance or dissimilarity of 100. The next set of symbols (red) corresponds to the scenario of a single perturbation, the following set (green) corresponds to the scenario of two perturbations, and so forth.

Figure 2. Performance of metrics on comparison of metabolic profiles resulted from experimentally measured enzymatic changes.

Out of six experimentally measured enzymatic changes, all possible combinations are implemented. When an exact enzymatic change is implemented, the result in each subpanel is shown in the column next to the control, which corresponds to no perturbation at all. Subsequent columns show the results of two (15 different combinations of exact perturbations), three (20 different combinations), four (15 different combinations), and five combinatory alterations of enzymatic activities (6 different combinations). The y-axis represents the distance or dissimilarity which is normalized. Results are based on relative changes. Each red horizontal line shows the smallest distance or dissimilarity in each column. A: Minkowski distance (m = 3); B: Euclidean distance; C: Manhattan distance; D: Jeffreys & Matusita distance; E: Canberra distance; F: relative distance; G: cosine of angle; H: Dice’s coefficient; I: Jaccard similarity coefficient. The corresponding plot for absolute changes is shown in Fig. S1. Note differences in magnitudes along the y-axis.

The dominant result of this analysis is that the metrics in subpanels A–D and G–H yield rather similar results, even though A–D refer to distances, while G–H are similarity metrics. For each case, the results are bimodal: Some perturbation combinations have distances close to 100, whereas others lead to much lower values. The former results are from perturbations of enzymes that are not very influential, so that the perturbation does not change the healthy profile much, whereas the latter results correspond to combinations of changes in influential enzymes. As a specific example, the red square with a normalized distance of 32 for a single perturbation identifies the most influential enzyme. In other words, one correct perturbation can account for about 70% similarity to the target vector that represents the renal cell carcinoma. A secondary result is that the Canberra metric and the relative metric yield extremely large distances, which are not seen in other metrics. These distances are much larger than the calibration distance, which has a value of 100 and represents the distance between the health and disease vectors. Finally, comparisons of different numbers of enzymatic alterations imply that the six perturbed enzymes may be divided into two groups of primary and secondary influence. Here, the terms primary and secondary indicate different magnitude of contributions of exact perturbations to the target vector.

Distances for absolute changes

When one uses absolute changes in metabolite concentrations instead of relative changes, similar results are obtained (Fig. S1). In this case, the single most significant perturbation accounts for about 80% of the difference between the control and target vector, whereas it accounts for about 70% when relative changes are used (Fig. 2). In both cases, two or three perturbations can be considered to have primary contributions to the cancer, while the remaining perturbations are of secondary importance.

Uncertainty in the quantification of exact perturbations

The identification of altered reaction steps requires an algorithmic search within a high-dimensional parameter space, where the probability of hitting the exact optimal point is zero. However, an efficient search algorithm is expected to identify the neighborhood surrounding the optimal point. This capability of recognizing a relatively small neighborhood containing the correct perturbations depends critically on the metric used to compare metabolic profiles. If this neighborhood is reached, can a good metric keep the search algorithm within this neighborhood (also refer to the Question 2 in the Introduction section)? To address this question, it is necessary to study the error space generated by a metric in response to uncertain perturbations surrounding the exact point that determines the performance of a search algorithm.

Among the enzyme alterations measured by Weber for renal cell carcinoma [19], two enzymes are most influential in terms of contributions to the metabolic alterations: IMPD is up-regulated 2.53 fold and ATASE is upregulated 1.58 fold. To model uncertainties, we consider solutions within 10% deviations of these values, without or with changes up to 10% in other enzymes. To obtain statistically significant results, we ran one million Monte Carlo simulations and report the corresponding distances between the simulated metabolic profiles and the target profile.

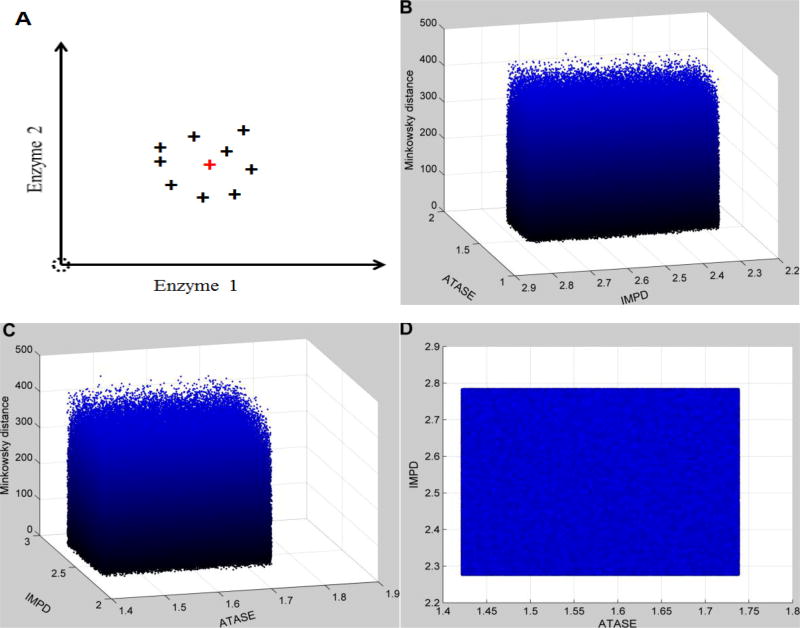
Effect of uncertainties for absolute changes

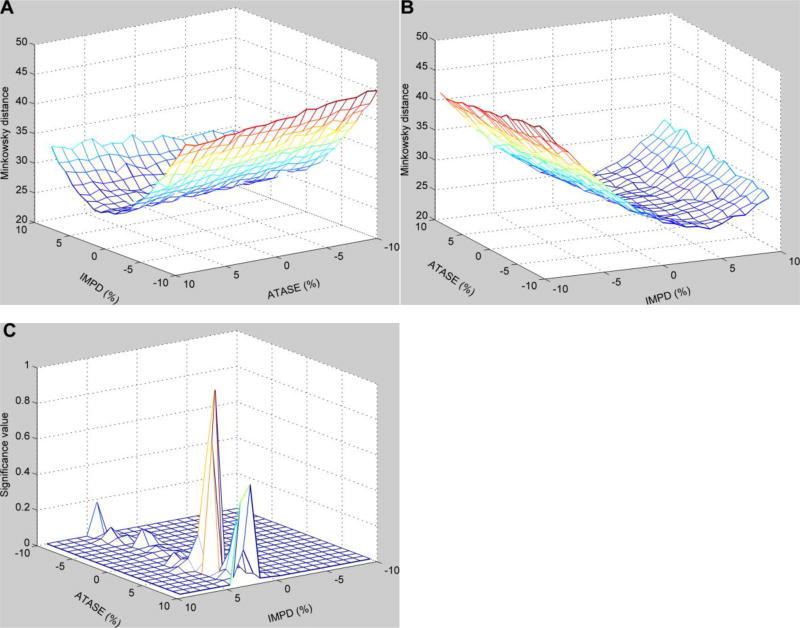
The results (Figure 3) show that the distances are similarly distributed with respect to changes in activities of the two most influential enzymes (IMPD & ATASE). In other words, when the algorithm searches a small neighborhood surrounding the exact perturbation (IMPD: 2.53; ATASE: 1.58), the uncertainty associated with these two enzymes and all other enzymes hamper the recognition of the target point, which corresponds to the correct perturbation in the cancer. Thus, this subspace containing the target point cannot be recognized as distinct even if it is reached. The effect of uncertainty in enzymes other than IMPD and ATASE is significant, because the distance landscape does provide a constraint (e.g., has local minima with statistical significance) to the search algorithm when these uncertainties are removed (Fig. S2).

Figure 3. Distance topology for the Neighborhood surrounding the targeted enzymatic changes using absolute changes.

For human renal cell carcinoma, the observed enzymatic changes include the activation of IMPD (2.53 in fold change) and ATASE (1.58 in fold change). This targeted set of enzymatic changes is disturbed by uncertainty (10% relative noise sampled from a normal distribution). In addition, all other enzymes are also affected by 10% relative noise over normal activities. The x- and y-axes represent relative enzymatic activities of IMPD and ATASE in regard to their normal values, respectively. The z-axis shows the Minkowski distances between the simulated metabolic profiles and the targeted disease profile, using absolute changes. Subplot A schematically illustrates the uncertainty surrounding the targeted enzymatic changes (red cross). The same distance topology is viewed from different angles. B: horizontal rotation (−105) and vertical elevation (20); C: horizontal rotation (−15) and vertical elevation (20); D: horizontal rotation (0) and vertical elevation (20). Distances are similarly distributed within the neighborhood surrounding the targeted enzymatic changes.

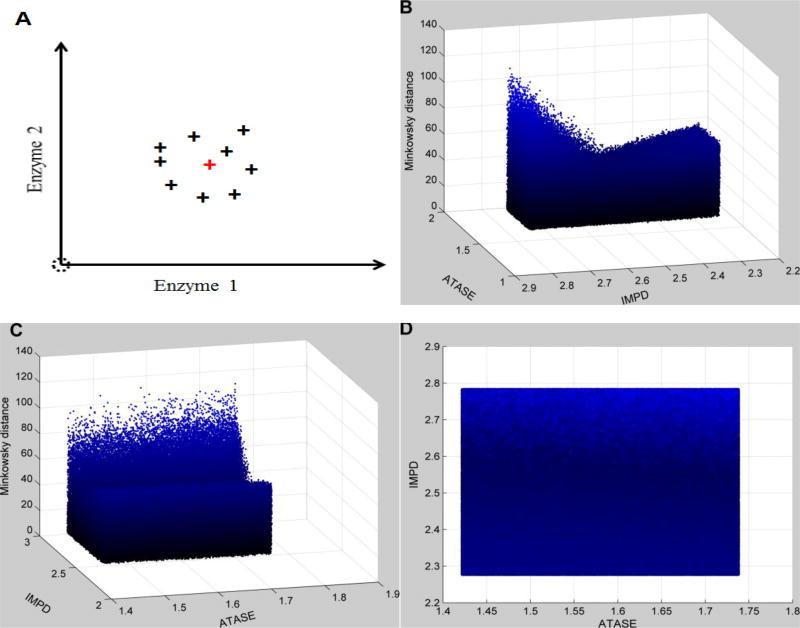
Effect of uncertainties for relative changes

When relative changes are used for the comparison of metabolic profiles, the results are quite different (the Minkowski distance is shown as an example). Here, the distance landscape corresponding to the small neighborhood surrounding the exact perturbation (IMPD: 2.53; ATASE: 1.58) shows that this neighborhood can be recognized by the search algorithm (e.g., has local minima with statistical significance) and that it is therefore possible to converge toward the correct solution (Fig. 4). This landscape looks like a trough, for which the enzyme IMPD is the most significant factor. When the search algorithm reaches this small neighborhood, it is guided toward the exact perturbation. One should note that the minimum in this case does not exactly correspond to the target point, due to uncertainties in all other enzymes. The same conclusions are obtained for most other metrics (data not shown). An exception is the similarity-based metric using the cosine of the angle between vectors, which does not tolerate uncertainties as well as the other metrics (data not shown).

Figure 4. Distance topology for the Neighborhood surrounding the targeted enzymatic changes using relative changes.

As described in Figure 3, the enzymatic changes consist of the activation of IMPD (2.53 in fold change) and ATASE (1.58 in fold change). Uncertainty is implemented as in Figure 3. The x- and y-axes represent relative enzymatic activities of IMPD and ATASE in regard to their normal values, respectively. The z-axis shows the Minkowski distances between simulated metabolic profiles and the targeted disease profile, using relative changes instead of absolute changes. Subplot A schematically illustrates the uncertainty surrounding the targeted enzymatic changes (red cross). The same distance topology is viewed from different angles. B: horizontal rotation (−105) and vertical elevation (20); C: horizontal rotation (−15) and vertical elevation (20); D: horizontal rotation (0) and vertical elevation (20). In contrast to Figure 3, distances are unevenly distributed within the neighborhood surrounding the targeted enzymatic changes. The surface looks like a trough, which identifies IMPD as the most significant factor.

Three-dimensional distance landscapes

The distance landscape is not a surface but a three-dimensional object for simultaneous changes in two enzymes (IMPD and ATASE). Every combination of IMPD and ATASE activities within a 10% range of the exact perturbation can possibly return a very small distance due to the influence of uncertainties in other enzymes. In other words, when the activities of IMPD and ATASE is fixed, changes in other enzymes produce a whole range of distances from very small to moderate. To analyze this situation, a statistical analysis is needed.

For the distance landscape shown in Figure 4, we composed a grid of enzymatic activities of IMPD and ATASE and calculated the mean value of distances for each grid box (Fig. 5A and 5B). The results show that there is a minimal mean value, which is close to the target point representing the exact perturbations to IMPD and ATASE. The significance of the differences in mean values between the distribution associated with the minimal mean value and all other distributions is shown in Figure 5C. The result shows that when the enzymatic activities of IMPD and ATASE deviate away from the small area containing the minimal mean Minkowski distance, the mean distances are statistically significantly different. Statistically speaking, this result suggests that uncertainties in other enzymes than IMPD and ATASE do not prevent the search algorithm from finding the target perturbations on these two enzymes. The same conclusion is obtained when other metrics are used (data not shown).

Figure 5. Mean values of distances for each grid area within the neighborhood surrounding the targeted enzymatic changes and significance of the differences in mean values.

Targeted enzymatic changes (IMPD and ATASE) with up to 10% relative variations are gridded, and the mean value is calculated for each grid box. All other enzymes have similar variations around their normal activities. The x- and y-axes represent relative enzymatic activities of IMPD and ATASE in regard to their normal values, while the z-axis exhibits the Minkowski distances using relative changes. The same distances are viewed from different angles. A: horizontal rotation (−125) and vertical elevation (20); B: horizontal rotation (−25) and vertical elevation (20). C: Significance of the differences in mean values between the distribution in the grid box with the minimal mean value and all other distributions.

Feasibility of a sequential identification strategy

Since it seems that enzyme perturbations can be divided into groups according to their metabolic influence, it is reasonable to devise a search algorithm with an iterative multi-phase strategy. According to such a strategy, the primary group of alterations would be targeted first, followed by a secondary. The problem is that it is not known which enzymes belong to which group. As a consequence, all enzymes need to be targeted simultaneously, which can quickly become computationally expensive if the metabolic system under investigation is complex.

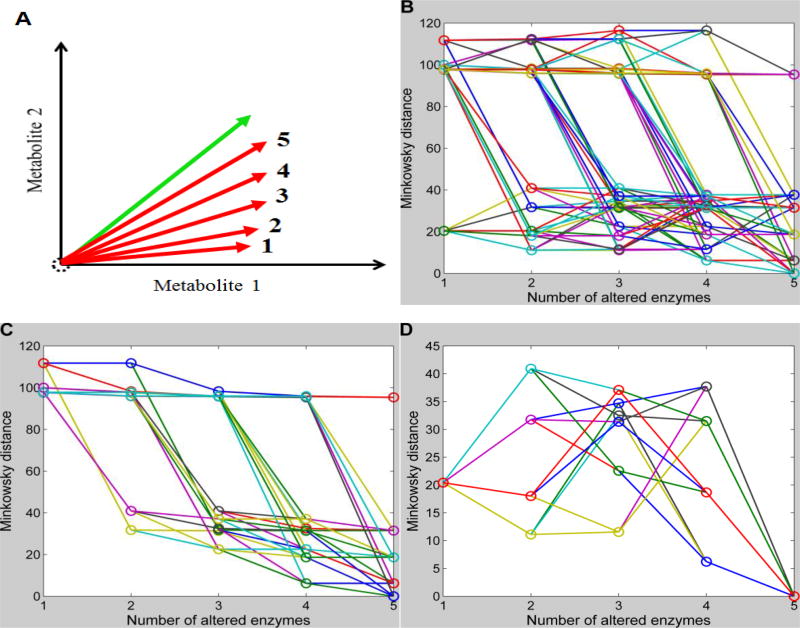
Alternatively, one could devise an algorithm that targets one enzyme at a time, retains the most influential enzyme, and then proceeds to a scan of the next important enzyme. Using the example of the Minkowski metric in Figure S1, we can easily simulate the results of this strategy. Namely, we connect the dots representing distances for a set of possible sequential perturbations involving one additional enzyme consecutively from 1 to 5 simultaneous perturbations. Each such a perturbation sequence starts with a randomly selected perturbation of a single enzyme and adds a new randomly selected but different perturbation at each step. This strategy leads to a total of 720 combinations of sequential enzymatic perturbations in the case of 6 enzymes. Figure 6B shows changes in the Minkowski distances along these paths of increasing numbers of enzymatic perturbations when absolute changes are used.

Figure 6. Feasibility of the sequential identification strategy.

Minkowski distances for all possible sequential enzymatic changes with one additional change per step are connected through lines. The x-axis shows the number of enzymatic changes in each sequential scenario, while the y-axis represents the Minkowski distances using absolute changes. With each increase in the number of enzymatic changes, the simulated vector might be expected to become closer to the target vector. A: Schematic illustration of positions of simulated vectors and the target vector for a demonstration system with only two metabolites. B: Changes in Minkowski distances with increasing numbers of sequential enzymatic changes (720 different combinations in the case of 6 enzymes). C: Out of all 720 possible sequential enzymatic changes, only those with decreasing Minkowski distances for subsequent steps are shown. D: Out of all 720 possible sequential enzymatic changes, only those are shown that start with the minimal Minkowski distance at 1^st step and end with a minimum at the 5^th step.

The most significant enzymatic perturbation returns a normalized Minkowski distance as small as 20; in other words, this alteration in enzyme activity explains 80% of the change in metabolic profile in human renal cell carcinoma. With the increase in the number of enzymatic perturbations, the simulated vector is expected to approach the target vector; a schematic illustration is shown in Figure 6A for a simple illustration system with only two metabolites. Ideally, the most significant enzymatic perturbation corresponds to a minimal distance in the scenario of one enzyme, and adding to it a second significant enzymatic perturbation has a smaller minimal distance in the scenario of two enzymes, and so forth. If a metric has this property, it allows the implementation of sequential identification strategy. Figure 6C shows sequential enzymatic perturbations with decreasing Minkowski distances. As shown, they have to start with some insignificant enzymatic perturbations to acquire a chain of decreasing distances with increasing number of perturbations, which disables the identification of the most significant perturbation at the beginning using this strategy. If the first perturbation is forced to be the most influential one, each of the subsequent sequential perturbations leads to an increasing Minkowski distance at some point (Fig. 6D). The same results were acquired for other metrics (data not shown). These results indicated the infeasibility of sequential identification strategy, and the optimal set of perturbations can only be detected through simultaneous perturbations.

As a practical alternative to searching the space of all possible enzyme perturbations, which could be costly or time prohibitive, one might start with all combinations of two or three enzyme alterations. Similar to a principal component analysis, such combinations are likely to explain a substantial portion of metabolic alterations found in a disease. Furthermore, because the distance between the healthy and diseased profiles is known a priori, the analysis of two or three simultaneous alterations immediately reveals what percentage of the disease alterations is explained. If this percentage is high, one might stop and not worry about additional enzyme alterations that are comparatively uninfluential. Then again, if only a relative small percentage is explained, one would continue with all combinations of four or five enzymes.

Comparisons of various metrics

The study of human renal cell carcinoma shows that three metrics (Canberra distance, relative distance, and cosine of angle) are inferior to the other studied metrics for the inference of biochemical mechanisms from metabolomics data. The remaining four distance-based metrics (Minkowski distance, Euclidean distance, Manhattan distance, Jeffreys & Matusita distance) are similarly well suited for this purpose. The general Minkowski distance (here with m=3) behaves almost the same as its two special cases: the Euclidean distance where m=2 and Manhattan distance where m=1. Occasionally, the Jeffreys & Matusita distance performs slightly better than the Minkowski distance (data not shown). Therefore, this metric could also be considered in addition to the typical Euclidean distance. Dice’s coefficient and Jaccard similarity coefficient are also valuable metrics even though they consider similarity in terms of the angle between metabolic profile vectors.

Implementation

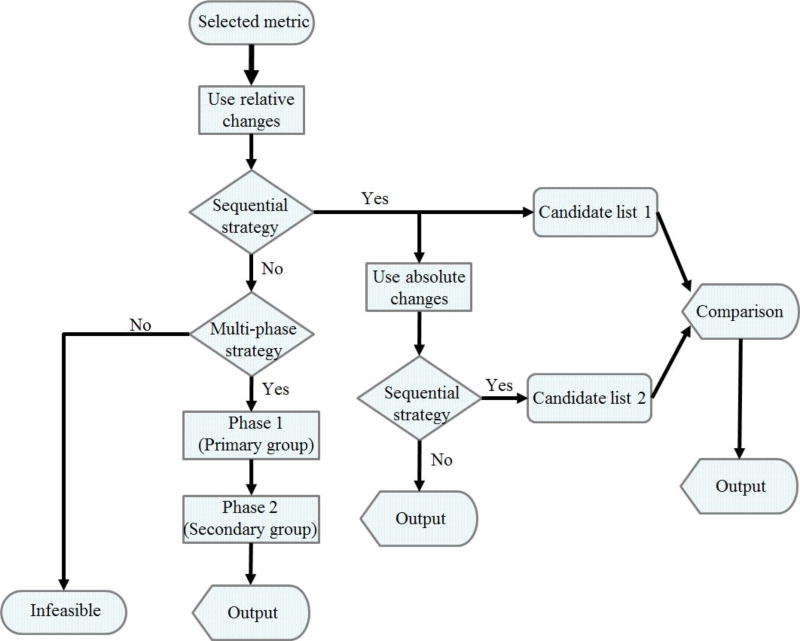
Some guidelines regarding the development of automated algorithms for the inference of biochemical mechanisms from metabolomics data are presented in the flow chart of Figure 7. While these are not iron-clad, they have proven beneficial in our experience. First, a metric is chosen among those shown as superior above. Also, it seems generally beneficial to perform the inference using relative changes of metabolites rather than absolute changes. A sequential strategy should be tried first, as it is much cheaper computationally than an immediate full search. If deemed appropriate, some steps in the sequence could be skipped. For instance, one could immediately start with two or three simultaneous alterations. The main criterion for stopping or continuing the search is the percentage of the health-disease distance that is explained at each step. The result is a candidate list of biochemical mechanisms of a disease or perturbation. For due diligence, this list could be compared with the corresponding list resulting from the use of absolute change. If the sequential strategy is not feasible, then the multi-phase strategy has to be considered. This multi-phase strategy allows the prediction of primary biochemical mechanisms at the phase one and secondary mechanisms at the phase two. There could be a possibility that both strategies are infeasible. However, our previous studies suggest that at least the primary mechanisms can be predicted using relative changes and the multi-phase strategy.

Figure 7. Strategic guidelines for the algorithmic inference of biochemical mechanisms from metabolomics data.

The flow chart shows recommendations for designing an algorithm for the inference of biochemical mechanisms underlying a disease from metabolomics data. Preferred metrics are Minkowski distance, Euclidean distance, Manhattan distance, Jeffreys & Matusita distance, Dice’s coefficient, and Jaccard similarity coefficient. These metrics have similar performance. The outputs from the sequential strategy and multi-phase strategy can be compared and provide further targets for experimental investigations.

Conclusions and Discussion

Experimental and clinical findings suggested that cancers reprogram their metabolism for particular needs, including cell growth, proliferation, and the escape from the immune system [20, 21]. However, it is unclear what biochemical mechanisms underlie metabolic reprogramming in cancers. We have developed an algorithm for the inference of biochemical mechanisms from metabolomics data and demonstrated its capability in the context of different diseases. The algorithm searches the high-dimensional space of enzymatic alterations and compares metabolic profiles, a process that requires the selection of an appropriate metric for the calculation of distances between metabolite profiles. The various available metrics have their own characteristics, which make them superior or inferior for the proposed inferences. Based on the results and analyses in this study, we now can answer these questions listed in the Introduction section.

We showed here that several metrics, including the Euclidean distance, perform well, while others do not. Six metrics (Minkowski distance, Euclidean distance, Manhattan distance, Jeffreys & Matusita distance, Dice’s coefficient, Jaccard similarity coefficient) perform similarly well, whereas three metrics (Canberra distance, relative distance, and cosine of angle) seem inappropriate for the inference of biochemical mechanisms from metabolomics data. The well performing metrics can be divided into distance-based metrics (the former four) and similarity-based metrics (the latter two). The metrics in the two groups consider different aspects of comparisons between metabolic profiles: the metrics in the first group measure a distance between two profiles, while these in the second group measure an angle between two high-dimensional vectors representing two metabolic profiles. It is possible to construct situations where two metabolic profiles have different distances but the same angle or different angles but the same distance. Thus, it might be beneficial to combine metrics from both groups.

While searching the high-dimensional space of possible enzymatic alterations, the proposed algorithm assumes that biochemical actions of a disease constitutes a point, which is surrounded by a neighborhood of acceptable solutions associated with small distances to the disease metabolic profile. Thus, if the search algorithm reaches this neighborhood, the distance landscape should allow the algorithm to recognize this neighborhood which contains the target point and lead the algorithm move toward the correct point. Interestingly, this is the case when relative changes in metabolites are used, whereas the use of absolute values makes the algorithm occasionally fail, presumably because in vivo concentrations may vary by orders of magnitudes and thus the high components dominate the error so that the algorithm is pushed out of the correct neighborhood.

For human renal cell carcinoma, most enzymatic alterations associated with purine metabolism increase enzymatic activity, which results in an elevation of most metabolites. In this case, the inexpensive sequential identification strategy is found as unlikely applicable. The feasibility of this strategy is also tested with an artificial metabolomics dataset, which is characterized by a mostly decreased metabolic profile in purine metabolism due to enzyme inhibition. In this case, the sequential identification strategy was found to be feasible, and the algorithm improved the solution with each enzyme addition, ultimately converging to the correct solution.

Metabolomics data contain rich but hidden information, such as the biochemical mechanisms underlying metabolic reprogramming in cancers. This theoretic study evaluated various metrics for the comparisons between metabolic profiles and provided a foundation for the selection of appropriate metric used in the inference of biochemical mechanisms by our algorithm. In addition, relative changes in metabolites are specifically suggested to be used in this context because it avoids the bias caused by metabolites with much higher concentrations than other metabolites, a usual characteristic of metabolism and metabolomics data. This is very beneficial since current metabolic platforms typically have difficulty in quantifying absolute metabolite levels but can provide relative changes reliably comparing different conditions or time points.

Table III.

Enzymes in purine metabolism

Enzyme or reaction	Abbreviation	EC Number
Hypoxanthine-guanine phosphoribosyltransferase	HGPRT	2.4.2.8
GMP synthetase	GMPS	6.3.5.2
Adenylosuccinate lyase	ASLI	4.3.2.2
GMP reductase	GMPR	1.7.1.7
AMP deaminase	AMPD	3.5.4.6
5’(3’) Nucleotidase	3NUC	3.1.3.31
Diribonucleotide reductase	DRNR	1.17.4.1
Adenosine deaminase	ADA	3.5.4.4
DNA polymerase	DNAP	2.7.7.7
DNases	DNAN	#
Guanine hydrolase	GUA	3.5.4.3
‘hypoxanthine excretion’	hx	$
‘xanthine excretion'	x	$
`uric acid excretion'	ua	$
Phosphoribosylpyrophosphate synthetase	PRPPS	2.7.6.1
Amidophosphoribosyltransferase	ATASE	2.4.2.14
Adenine phosphoribosyltransferase	APRT	2.4.2.7
`pyrimidine synthesis'	PYRS	#
IMP dehydrogenase	IMPD	1.1.1.205
Adenylosuccinate synthetase	ASUC	6.3.4.4
Methionine adenosyltransferase	MAT	2.5.1.6
Protein O-methyltransferase	MT	2.1.1.77, 2.1.1.80, and 2.1.1.100
S-adenosylmethionine decarboxylase	SAMD	4.1.1.50
5’-Nucleotidase	5NUC	3.1.3.5
RNA polymerase	RNAP	2.7.7.6
RNases	RNAN	#
Xanthine oxidase or xanthine dehydrogenase	XD	1.17.1.4 and 1.17.3.2

^#: Multiple enzymes.

^$: Non-enzymatic reaction.