Referenceless Acquisition of Phase-Sensitive Inversion-Recovery with Decisive Reconstruction (RAPID) Imaging

Abstract

Purpose

To describe a referenceless reconstruction approach to generate phase-sensitive inversion recovery images without relying on the extra acquisition of reference images.

Methods

The basic idea of the Referenceless Acquisition of Phase-sensitive Inversion-recovery with Decisive reconstruction, or RAPID, algorithm is to retrieve the magnetization polarity by estimating the background phase variation of a complex valued image. The theory and algorithm of RAPID is described in detail. To evaluate the performance of RAPID, seven patients were recruited then scanned in different anatomical regions (cardiac, brain, and vascular). Standard Phase Sensitive Inversion Recovery (PSIR) reconstructions using reference image information were compared with RAPID reconstructions using the same source data.

Results

RAPID reconstructed images were found to provide very good agreement with PSIR reconstructed images on all cases, although no reference image info was used in the RAPID algorithm. For neuroimaging applications, it was found that RAPID reconstruction is more robust compared with the PSIR algorithm as RAPID can avoid potential errors introduced by the reference acquisition.

Conclusion

The RAPID technique for phase-sensitive reconstruction is promising and can improve the imaging efficiency by a factor of 2 compared with PSIR. RAPID was also shown to provide more robust reconstruction by avoiding errors caused by the reference acquisition.

INTRODUCTION

MRI is known for its high soft tissue contrast which is useful in a broad range of clinical applications. Among the basic MRI sequences, there are a wide variety of magnetization preparation schemes which allow for very specific contrast tailoring. The inversion recovery prepulse, integrated as a magnetization prepared scheme, is an example of this: it improves T₁ contrast in a variety of clinical applications, like cardiac, brain, or body imaging.

This is especially useful in cardiac applications where contrast changes, after Gadolinium administration, can help differentiate infarcted myocardial tissue from the normal or hibernating tissues due to the slower rate of contrast washout (1,2). However, if the inversion delay time (TI) is not properly selected (3), the contrast between infarcted and normal regions of the myocardium can become so poor that reliable detection becomes challenging. One reason for this dependence on TI is that in regular MR images only the magnitude of the actual magnetization can be displayed, causing reduction of tissue contrast. Phase Sensitive Inversion Recovery (PSIR) imaging is, therefore, commonly used to detect myocardial infarction and to support quantification (4). The PSIR technique can restore the actual magnetization polarity, thus maintaining a strong contrast between normal and scarred myocardial tissues even if the inversion time (TI) is shifted away from the ideal value. This approach represents a great simplification of the imaging logistics and has been widely adopted in clinical evaluation of myocardial infarctions.

Beyond simplifying the protocol design and the parameter optimization process, the PSIR technique also provides improved tissue contrast in the images because the dynamic range of the MR images is doubled from only the positive realm to include both the positive and negative parts of longitudinal magnetization. Benefiting from this extra contrast, the PSIR technique has also found applications beyond cardiac imaging, such as brain (5–7) and vascular imaging (8,9) applications.

PSIR achieves the magnetization polarity restoration by interleaving a full size reference scan into the regular image acquisition scans (4). By acquiring this extra reference, phase variation caused by system imperfections can be identified and filtered out from the original acquisition and the magnetization polarity can be restored. A limitation of this practice is that, because of the extra reference acquisition, the total scan time of PSIR is essentially doubled compared with the regular IR-TFE sequence. This extra scan time has made the PSIR acquisitions less time-efficient and less applicable to time-sensitive clinical applications. Another limitation is that a successful PSIR reconstruction assumes that the reference scan was acquired after all the magnetization has recovered above zero. As a result, should the reference scan be acquired before that (due to protocol constraints, for example) artifacts can appear in the PSIR reconstructed images.

Various acquisition and reconstruction techniques have been proposed to improve the imaging efficiency of PSIR techniques. In one approach, a low-resolution reference scan was used to help reduce the overall acquisition time of PSIR (10). This study demonstrated that by using a reference scan with only ¼ of the size of the original scan; phase-sensitive reconstructed images can be obtained with very similar image quality. In another effort to reduce the imaging time for a series of PSIR acquisitions with different TI times, the same reference scan (essentially the image acquired with the longest TI) was shared by all other acquisitions so that a significant amount of time is saved by avoiding repetitive acquisitions of the reference images (11). These approaches, however, still require the acquisition of a reference image to successfully reconstruct the phase-sensitive images. To overcome this limitation, referenceless approaches have been proposed (12,13). These approaches either require a relatively large region of magnetizations from both polarities or rely on only one pair of pixels to determine the polarity, making them less robust in detecting magnetizations with opposite polarity. Furthermore, neither of the approaches has been compared with PSIR techniques for validation (12,13).

In this study, a novel Reference-less Acquisition of Phase-sensitive Inversion-recovery with Decisive reconstruction (RAPID) technique is described which can reconstruct phase-sensitive images without using the reference acquisition. As a reference-less approach it promises higher scanning efficiency and in particular more robust (less reference dependent) phase sensitive reconstruction. The basic concept is outlined and an experimental validation is performed. Phantom and in vivo experiments were then performed to compare RAPID with regular PSIR in different applications.

METHODS

Theory

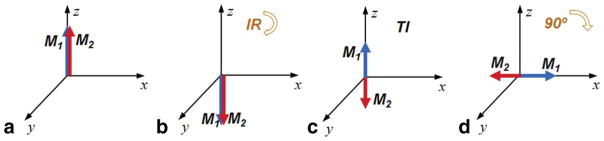
In phase-sensitive MR images, presumably as a result of the inversion recovery process, the magnetizations with different polarity exemplify themselves with flipped phases. This means the phase difference between magnetizations with different polarity will be exactly π (180°). As illustrated in Figure 1, magnetization of two different T₁ species can show a phase difference of π because of their opposite polarities. Here, a 90° flip angle is assumed for the simplification of illustration; in reality, any flip angle can be used for data acquisition and the same phase difference will be observed on the final image.

FIG. 1.

Signal evolution (amplitude and phase) of two different magnetizations after an inversion recovery pulse. The two magnetizations pointing to the z direction at equilibrium (a), will both be inverted after an inversion pulse (b). Due to the different T₁ relaxation rates, after a certain delay (TI), opposite polarities will result (c). If an image acquisition is performed at this time, using, for example, a 90° excitation, both of the magnetizations will be flipped to the x–y plane. But due to the opposite Mz polarities before excitation, they will present a π phase difference in the transverse plane (d).

Although the theory behind the phase difference is simple and straightforward, it cannot be directly used to restore the polarity information on a regular MR image. The main reason is that a spatially dependent background phase variation is always present in MRI. This background phase variation can be caused by a combination of B₀ field inhomogeneity, eddy current effect, gradient delay, receive phase variation, flow and other factors. In the previous PSIR implementations, the extra reference acquisition captures the background phase and the true phase polarity can be restored once the background phase is subtracted from the acquired phase. The key to a time-efficient referenceless phase-sensitive reconstruction, therefore, is to extract the background phase without using the extra acquisition, as proposed here.

The mathematical situation can be described as analogous to some water-fat Dixon imaging approaches (14,15). Both situations involve two magnetization species (original & inverted or water & fat) that present different phases on an MR image. Therefore, the overall signal in an inversion recovery experiments can be described as:

$$C(r)=(M_p(r)+e^{i\mathrm{\pi }}{M}_n(r))e^{i\mathrm{\psi }(r)}=(M_p-M_n)e^{i\mathrm{\psi }(r)},$$ [1]

where C is the measured complex MR signal; r is the spatial coordinates of the voxel of interest; M_p is the magnitude of the positive magnetization; M_n is the magnitude of the negative magnetization and ψ is the background phase shift at a particular spatial location. As M_p and M_n are aligned, any phase deviation from the magnetization is considered to be caused by the background phase ψ. If we assume each voxel is dominated by either the positive or negative magnetization, the image intensity can be described as:

$$C(r)=\{\begin{array}{c}{M}_p·e^{i\mathrm{\psi }(r)}(M_p\gg M_n)\\ -M_n·e^{i\mathrm{\psi }(r)}(M_n\gg M_p)\end{array}.$$ [2]

Knowing that the magnitude and phase can be described as:

$$M(r)=\{\begin{array}{l}{M}_p(M_p\gg M_n)\hfill \\ M_n(M_n\gg M_p)\hfill \end{array},P(r)=\{\begin{array}{l}\mathrm{\psi }(r)(M_p\gg M_n)\hfill \\ \mathrm{\psi }(r)+\mathrm{\pi }(M_n\gg M_p)\hfill \end{array}$$

and that the goal of the RAPID reconstruction is to retrieve the polarity info of the magnitude signal, we have:

$$S_{PS}(r)=\{\begin{array}{c}M(r)(M_p\gg M_n)\\ -M(r)(M_n\gg M_p)\end{array}=C(r)·e^{-i\mathrm{\psi }(r)},$$ [3]

where S_PS is the phase-sensitive corrected signal, commonly observed on the PSIR images, and its phase component corresponds to the “True Phase” (TP) of the underlining MR image: it is either 0 or π in this case. S_PS is also the true signal we are trying to retrieve using RAPID.

RAPID Algorithm

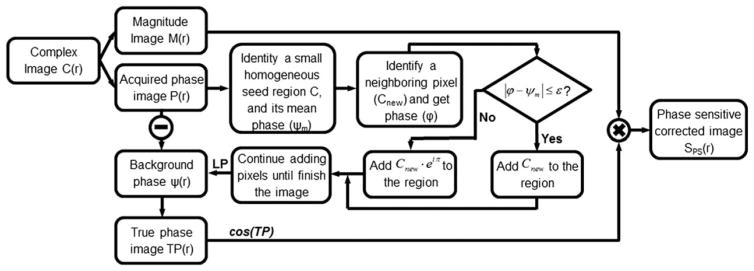
As can be observed in Eq. [3], the key to obtain S_PS is to first obtain the ψ(r) distribution in the MR images. Although ψ is the same as the phase image P(r) when the signal is dominated by positive magnetizations, it has a π difference with P(r) when the signal is dominated by inverted magnetizations. To retrieve ψ(r) without acquiring a standalone reference acquisition, an approach previously introduced for single-point Dixon was adopted and modified (16). The RAPID approach does not require a large portion of inverted magnetizations for them to be detected, nor does it base its decisions on only a very limited number of pixels. Essentially, RAPID differentiates background phase and true phase change (from inversion) by comparing the phase of a new pixel with the average phase of a neighboring region, if it is larger than a certain threshold, it is considered to be a true phase change caused by inversion; otherwise, it is considered to be contributed by the background phase. The fully automatic RAPID algorithm is described in the flow chart (Fig. 2). In summary, the RAPID algorithm first identifies a homogenous region in the image based on the low-pass (kernel: 5 × 5 boxcar) phase gradient map G(r) of the complex image. G(r) for a particular pixel is calculated by averaging the phase difference between this pixel and neighboring pixels in both x and y directions: G(r) is also squared to remove the contributions from inverted magnetizations. It then calculates the mean phase of the local region (ψ_m) and uses it as a base for expansion. Subsequently, all neighboring voxel’s phase gradients of the region are inspected, to identify the pixel with the minimum phase gradient, and to obtain this voxel’s phase (Φ). At this stage, there are two possibilities – if the new voxel has a similar phase to the mean (|ϕ − ψ_m| ≤ ε, where ε is a predetermined threshold with a value of π/2 used in this study), its signal (C_new) will be added to the region directly; otherwise, the flipped signal of the pixel (C_new · e^iπ) will be added to the region.

FIG. 2.

Flow chart of the fully automated RAPID algorithm. The key method is to retrieve the true phase image (TP) based on the acquired phase image (P). Once this is done, the true phase image can be combined with the magnitude image (M) to reconstruct the phase sensitive corrected image (SPS). For details, please see text. LP: Low Pass filter

After the new pixel is added to the region, the algorithm continues by re-inspecting all neighboring pixels and adds new ones as described above until the whole image is completed. A low-pass filter is applied on the background phase map (ψ) to remove noise. For simplicity, a boxcar low-pass kernel with the size of 1/20th of FOV is used in this study. Then, the background phase map (ψ) is subtracted from the original image to generate the true phase map (TP(r)).

Instead of using the TP map directly for determining the polarities of the magnetizations, a proper smoothing operation needs to be done to improve the visual appeal of the image. Two considerations come into play during the selection of this operation: (i) the method should help to filter out noise on the RAPID reconstructed images caused by local phase variation; and (ii) it should help to convert proper phase values into polarity info (1 or −1). In our case, a cosine operation was selected because it is efficient to implement and meets both criteria: for phases in the neighborhood of 0 (or π), the cosine values change slowly and are always close to 1 (or −1). Other operations that meet the criteria may also be used. By multiplying the magnitude image M(r) and the cosine of TP(r), the phase-sensitive corrected image S_PS(r) can be obtained.

A set of carotid artery images demonstrating the algorithm are shown in Figure 3. In this figure, using the algorithm detailed in Figure 2, the background phase image ψ(r) can be extracted from P(r). After subtraction, the true phase image TP(r) can be combined with the magnitude image M(r) to generate the phase sensitive corrected image S_PS(r).

FIG. 3.

Illustration of the RAPID algorithm. The phase image (a) contains both the inherent phase TP(r) and also the background phase ψ(r). As detailed in the flow chart in Fig. 2, the background phase ψ(r) (b) can be extracted from P(r). After subtraction, the true phase image can be obtained as shown in panel (d). The phase sensitive corrected (e) image S_PS(r) can be obtained after combining magnitude image (c) and true phase image (d).

Experimental Evaluations

To verify the RAPID technique, phantom and in vivo experiments were performed on two different whole-body scanners (Philips Achieva, Best, the Netherlands) operating at two different field strengths (1.5T and 3T). The scanners used different receiver coils but used the same scanning software (R3.2.1).

Phantom Experiment

A water phantom doped with copper sulfate (CuSO₄) was scanned using a body coil at 3T. The phantom has measured T₁/T₂ values of 425/340 ms. A slab-selective inversion prepared PSIR scan was conducted: the slab selective inversion pulse was applied at the center of the phantom with a slab thickness of approximately 5 cm. The scanning protocol was: 3D PSIR IR-Turbo Field Echo (TFE) sequence, TFE factor 48, TR/TE 4.2/1.9 ms, flip angle (FA) 12°, TI 30 ms, FOV 240 × 240 × 32 mm³, resolution 2 × 2 × 4 mm³, and the total scan time was 11 s.

In Vivo Experiments

Seven patients (four cardiac, two vascular, and one brain) were scanned using clinical MR scanners after approval from our local institutional review board. The cardiac patients were recruited because of suspected myocardial scar; the vascular patients were recruited because of suspected atherosclerotic disease in the carotid artery; and the brain patient was recruited because of suspected intracranial artery disease.

Cardiac scans were acquired using a five-channel cardiac coil at 1.5T. Two cardiac patients were scanned with only the PSIR techniques and the same source images were used to facilitate the quantitative comparison between RAPID and PSIR; another two cardiac patients were scanned with both PSIR and a standalone RAPID acquisition to demonstrate the feasibility of RAPID and its time efficiency. Both PSIR and standalone RAPID images were scanned ~10 minutes after the contrast injection. The imaging parameters for PSIR were: 2D IR-TFE sequence, IR separation 2RR interval, TFE factor 16, TR/TE 7.5/4.6 ms, FA 15°, TI 230–270 ms, FOV 360 × 360 mm², resolution 1.5 × 1.5 mm², slice thickness 10 mm, total scan time was 11 s/slice. The imaging parameters for RAPID were the same as PSIR except: IR separation 1RR interval, TI 30 ms less than PSIR and total scan time was 6 s/slice.

The vascular scans were acquired using an 8-channel carotid coil (17) at 3T. The imaging parameters were: 3D PSIR IR-TFE, IR interval 1970 ms, TFE factor 98, TR/TE 10/4.8 ms, FA 11°, TI 500 ms, FOV 160 × 160 × 32 mm³, resolution 1.0 × 1.0 × 1.0 mm³, fat saturation, the total scan time was 1 min 40 s.

The brain scans were acquired using an eight-channel brain coil at 3T. The scans were repeated twice using different TRs (80 ms and 15 ms) to explore the impact of the reference scan timing on PSIR and RAPID reconstructions. With these settings, the TI for the image acquisition for both scans was 500 ms, while the TI for reference acquisition would be ~7400 ms (80 ms TR, IR interval 13.8 s) and ~2200 ms (15 ms TR, IR interval 3.2 s), respectively. Due to the very long T₁ of CSF, it is expected that the CSF magnetization has relaxed to above zero at 7400 ms TI, while still negative at 2200 ms TI. The remaining imaging parameters were the same, specifically: 2D PSIR IR-TFE, TFE factor 80, TE 4.6 ms, FA 12°, TI 500 ms, FOV 240 × 240 mm², resolution 1.5 × 1.5 mm², slice thickness 4 mm, fat saturation, the total scan time was 1 min 50 s for 80 ms TR and 42 s for 20 ms TR.

Data Analysis

For both phantom and in vivo experiments, the magnitude images and the phase-sensitive reconstructed images were automatically displayed and saved on the scanner once the scan was completed. The complex images were also stored at the time of acquisition.

RAPID reconstruction was conducted off-line using only the complex images acquired without the reference acquisition, as detailed in the previous RAPID algorithm section. For 2D acquisitions, all images were processed on a slice-by-slice basis. For 3D acquisitions, all complex images were first reconstructed to 2D images along the acquisition direction as specified at the time of acquisition. The 2D images are then processed using the RAPID algorithm. Difference images between RAPID and PSIR reconstructed images were generated by comparing the signal polarity at a pixel level. A quantitative measurement was also used to compare RAPID against the PSIR algorithm: an S index is defined to measure the similarity between the two algorithms. As the primary goal of the phase-sensitive reconstruction is to retrieve the correct polarity of magnetizations, the S index is defined as,

$$S=\frac{n_{\mathit{Correct}\_\mathit{Polarity}}}{N_{\mathit{Total}\_\mathit{Number}\_\mathit{Pixel}}}$$

The S index is essentially a ratio between the correctly identified pixels and the total pixels, where the total number to be corrected pixels was defined from the fully relaxed reference image. Only those pixels which have an SNR higher than 2 were considered to avoid problems with void regions that contain only image noise. In this way also the ability of RAPID to deal with low SNR regions in the T1-weighted images can be judged. The index is expected to be a real number in the range of [0, 1], with a higher number indicating a higher agreement between the two.

For the two cardiac cases with standard RAPID and PSIR acquisitions, the RAPID algorithm was only applied on the RAPID acquisitions but not the PSIR images. The SNR and SNR effective of the myocardium region was measured on both images, using the equation defined below,

$$\mathit{SNR}=\frac{S}{\mathrm{\sigma }},{\mathit{SNR}}_{\mathit{eff}}=\frac{\mathit{SNR}}{\sqrt{T}}$$

Where, S is the average signal of the myocardium, σ denotes the noise measured as the standard deviation of lung in a small homogenous region and T is the average scan time per slice, in seconds. As the images were acquired on two separate acquisitions, no similarity comparison was applied on these images.

RESULTS

Phantom Experiment

In the phantom experiment, the inverted magnetizations are not expected to be recovered above zero at the time of acquisition given the very short TI time (30 ms). Low contrast was found between the inverted versus noninverted regions on the magnitude image (Fig. 4a) as only the absolute value of the magnetization is displayed. On both RAPID (Fig. 4b) and PSIR (Fig. 4c) images, the inverted regions were correctly identified and properly inverted. Along the boundary of the bottle, ringing artifacts can also be observed on all three images as the signal abruptly transitioned from high to low signal regions. The signal polarity of the artifacts was different between RAPID and PSIR, which is caused by the low-SNR region separation between them. This fact will be further discussed in the discussion.

FIG. 4.

The magnitude (a), RAPID (b), and PSIR (c) reconstructed images of a water phantom are shown. The inversion band applied is clearly visible in the middle of the bottle. Good agreement was found between RAPID and PSIR images with both correctly identifying and correcting for inverted regions as shown in (b) and (c).

In Vivo Experiment

The RAPID algorithm was successfully applied to all subject data with good agreement found when compared with the original PSIR reconstructed images.

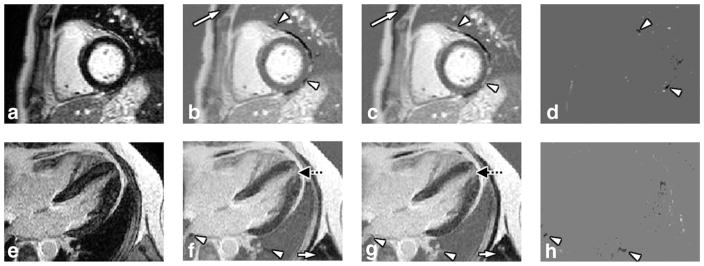
Figure 5 illustrates the RAPID reconstruction application on two cardiac viability scans: RAPID provides reconstructed images very similar to the PSIR images (S index for both are: 0.9525 and 0.9533). Species with long T₁s, and, therefore, with still negative magnetization at the time of acquisition, such as muscle (white arrows) and pericardial fluid were properly identified and inverted on the RAPID images. It is noticeable that the second patient presented with a suspected apical infarction which was properly identified on both the RAPID and PSIR images (dotted black arrows on Figure 5f,g). Differences (arrowheads) were mainly found in the tissues that were either surrounded by low SNR regions in the lung and/or impacted by the increased local field inhomogeneity next to the lung.

FIG. 5.

Magnitude, RAPID and PSIR reconstructed cardiac images. In the top row (a–d) patient 1 is shown, in the bottom row (e–h) data from patient 2 is presented. The different columns represent magnitude (a,e), RAPID (b,f), PSIR (c,g) reconstructed and difference (d,h) images, respectively. Good agreements were found for both cases. Tissues with long T₁ like muscle (white arrows) and pericardial fluid were properly identified and inverted by the RAPID algorithm. A suspected apical infarction is also identified by both reconstruction algorithms (dotted black arrows on (f,g)) on patient 2. To facilitate the comparison, locations of the differences were labeled using arrow-heads (b–d,f–h), which were mainly found in tissues isolated by air occupied regions in the lung or impacted by the increased local field inhomogeneity next to the lung.

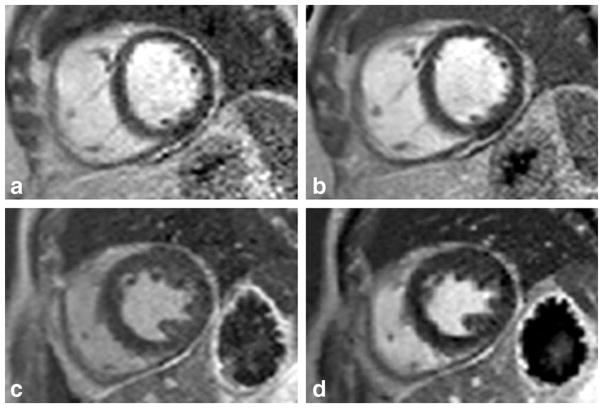
Figure 6 illustrates the performance of the RAPID algorithm on standalone acquisitions. Overall, RAPID was successfully applied on standalone time-efficient acquisitions: very similar image contrast was achieved on both RAPID and PSIR reconstructed images, and no artifacts were identified. The average measured SNR for both techniques are: 8.14 (PSIR) versus 6.88 (RAPID); the SNR_eff (unit s^−1/2) for both images are: 2.45 (PSIR) versus 2.81 (RAPID). Due to the reduced T₁ relaxation time used in 1RR RAPID acquisition, the overall signal SNR was slightly lower on the RAPID images. After normalizing against time, however, RAPID was found to provide ~15% higher SNR_eff.

FIG. 6.

Standalone RAPID and PSIR images for cardiac applications. The top (a,b) and bottom (c,d) row images are from two different patients. The two columns represent RAPID (a,c) and PSIR (b,d) images acquired at the same locations. Overall good agreements were found on both cases, although the standalone RAPID scan takes roughly only half of the scan time used by PSIR (6 s/slice versus 11 s/slice). Slightly lowered SNR were noticed on RAPID images due to the reduced T₁ recovery in a shorter IR separation (1RR versus 2RR).

The RAPID algorithm was also successfully applied (S index=0.901) for vascular imaging applications, as shown in Figure 7. In this application, a TI of 500 ms was used, thus only vascular structures are expected to be inverted due to the long T₁ relaxation time of blood. The data emphasize that the RAPID algorithm provided images very similar to the PSIR reconstructed images. Even the small vascular structures were faithfully reconstructed without error. Major differences were found on very low SNR regions such as the center of the image and at air-tissue interfaces (arrowheads).

FIG. 7.

Magnitude, RAPID and PSIR reconstructed images for vascular applications. The magnitude (a), RAPID (b), PSIR (c) reconstructed, and difference (d) images are shown. All magnetization with long T₁ (mainly blood here) was correctly identified by RAPID reconstruction (white arrows), including small structures (dotted white arrows). Differences were mainly found on regions with very low SNR (arrowheads).

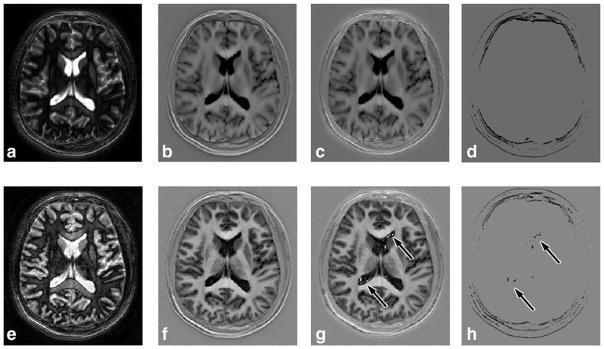
In the brain applications the RAPID algorithm also demonstrated good agreement when compared with the PSIR reconstruction. As shown in Figure 8, tissues with long T₁ values like CSF and grey matter were all correctly identified and properly phased by RAPID and PSIR algorithm (S index is 0.9361). For the images acquired with shorter TR (15 ms) and due to the much shorter TI for the reference acquisition (~2200 ms) the PSIR reconstruction was expected to present reconstruction errors. As shown in Figure 8e–h, the RAPID reconstructed images demonstrated a more robust reconstruction (Fig. 8f) without showing any artifacts, while the PSIR images (Fig. 8g) were impacted by the early reference acquisition as artifacts at the CSF region (arrows) can be clearly identified (S index is 0.9331). This is caused by the insufficient CSF relaxation at the time of reference acquisition. The magnetization was still negative and thus violated the PSIR reconstruction assumption. Because the RAPID reconstruction does not rely on the reference acquisitions, no artifacts were found (f). Other differences between RAPID and PSIR can mainly be found along the boundaries of the skull—suspected to be caused by the phase shifts from the unsuppressed fat along the skull.

FIG. 8.

Magnitude, RAPID and PSIR reconstructed images for neuroimaging applications. Images of the same subject are shown, with two different settings. Top row images (a–d) were acquired with 80 ms TR (reference image TI ~7400 ms), bottom row (e–h) were acquired with 15 ms TR (reference image TI ~2200 ms). Magnitude (a,e), RAPID (b,f), PSIR reconstructed (c,g) and difference (d,h) images are shown. Very good agreement was found between RAPID and PSIR images for long TR acquisitions (b,c). For short TR acquisitions, RAPID was able to reconstruct the phase-sensitive images while artifacts were found on PSIR images (arrows on g,h). Otherwise, certain differences were found along the periphery of the skull, mainly caused by unsuppressed fat (d,h).

DISCUSSION

In this manuscript, a Referenceless Acquisition of Phase-sensitive Inversion-recovery with Decisive reconstruction (RAPID) algorithm was proposed to reconstruct phase-sensitive images without using a reference acquisition. The technique has been implemented in several (cardiac, vascular, and brain) applications for phase-sensitive image generation. Compared with PSIR, RAPID was found to provide very similar information without using the reference image. Additionally, as demonstrated in the brain application, RAPID reconstruction allows for more flexible protocol design as it does not pose a restriction on how soon the reference scan can be acquired.

A key limitation of the current PSIR technique is the prolonged acquisition time due to the requirement of interleaving a full size reference matrix at the time of acquisition. This has been a key factor limiting the clinical adoption of 3D PSIR for whole heart applications. Techniques that can eliminate the reference image acquisition promise great clinical potential in reducing scanning time and/or trading for higher resolution imaging. Unlike other fast imaging techniques like SENSE (18), GRAPPA (19) and Compressed-sensing (20), RAPID reconstruction does not achieve accelerated imaging by under-sampling the data, but eliminates the need for a reference image. The reference image itself does not directly contribute to the improvement of image quality but merely provides an accurate estimation of the background phase map. As a result, RAPID can potentially cut imaging time by half without causing any image quality degradation. In this study, a standalone RAPID acquisition was demonstrated on two cardiac patients with an approximately two-fold scan time reduction. Although it was found that the standalone RAPID provided a reduced dynamic range on the final image due to the reduced T₁ recovery in a shorter time (1RR versus 2RR), RAPID still provides a higher SNR_eff than conventional PSIR due to the shortened scan time. Besides, this effect can be further mitigated by interleaving RAPID with a different, preferable low flip-angle, nonphase reference scan, answering a different diagnostic question. If RAPID is interleaved with a different clinically relevant acquisition, the tissue signal can be better T₁ recovered when the next RAPID acquisition starts and no extra scan time is spent on acquiring the reference matrix.

Another limitation of the PSIR technique is the acquisition timing assumption of the reference scan. When the reference scan is acquired, it is assumed that all magnetizations have recovered to above zero. For applications such as CSF suppression as in Figure 8, it means the reference scans cannot be acquired until after a very long delay (a few thousand milliseconds). If the reference scan is acquired too early and the magnetization has not yet fully recovered, errors can be observed from the PSIR reconstruction. This can result in unnecessarily long scan times for certain applications. The RAPID approach, however, is more suitable for this application as it does not rely on the reference scan for reconstruction. As seen in Figure 8, with the same TI time, a much longer protocol (1 min 50 s) has to be used by PSIR to generate artifact free images—while RAPID can reconstruct the brain images without causing artifacts. From this aspect, RAPID can not only save scan time by removing the reference scans, but also avoid prolonged waiting times for all the magnetizations to sufficiently recover.

The RAPID algorithm differentiates original and inverted magnetization by examining the phase change between magnetizations with different polarities. It, therefore, may encounter difficulties when a third phase exists (besides the original (0°) and inverted (180°) magnetizations). A common source of such a phase difference is from fat, which is known to have 3.5 ppm chemical shift from water molecules (21,22). In the in vivo scans done in this study, fat signal was either eliminated using fat saturation techniques (vascular and brain imaging) or an in-phase TE was used so that no water and fat phase difference was expected (cardiac imaging). When fat signal failed to synchronize due to issues like increased susceptibility, as shown in the brain imaging case, a reduced S index and certain image differences between RAPID and PSIR can be found. For this application, this is not considered to be a limitation as the difference was mainly observed outside of the common region of interest (brain parenchyma). We have included a theoretical calculation in the Appendix on RAPID’s robustness against phase bias caused by systemic imperfections.

The idea of reconstructing phase-sensitive images from regular MR images has been explored before. Borrello et al demonstrated that by examining the “phase-slope” among pixels, the abrupt 180° change on phase maps can be differentiated from the more gradual background phase change (12). Although it has been demonstrated in several anatomical regions, the algorithm generally requires a handful of neighboring pixels to generate a sufficiently accurate “phase-slope” estimation. Xiang proposed a technique that can determine the polarity of the magnetization by calculating background phase “layers” based on pixel-by-pixel phase change (13). This approach is similar to the RAPID but it relies on only one neighboring pixel to determine the polarity and thus might be more vulnerable to errors if the noise level is high. It has also been reported that, by solving a least-square problem for a set of phasing coefficients, phase sensitive reconstruction can be performed for low SNR TSE images (5,23). This approach requires a sufficiently low SNR region to accurately predict the polarity based on the description. It is also noteworthy that none of the abovementioned technique have been rigorously compared with a ground truth (i.e. PSIR images) as we have done in this study.

The complex image used by the RAPID algorithm is obtained from the scanner after the signals from different coil elements have been combined (18,24) using appropriate receive coil sensitivity information. If this is not available during the complex image combination, potential errors might result in the RAPID reconstruction. An alternative is a coil-by-coil RAPID reconstruction that could share information about the common true phase image.

An assumption made by the RAPID algorithm is that each pixel is dominated by either the positive or the negative magnetizations. This might not be entirely true for certain locations, i.e., positive and negative magnetizations may have comparable magnetization amounts. This fact, however, is not expected to be as significant as in the comparable situation for Dixon imaging—for PSIR, only the polarity of the residual signal is of interest; while for Dixon imaging, both water and fat magnetizations are expected to be reconstructed so a near complete signal cancellation may cause a higher level impact. In other words, for PSIR, should the amount of positive and negative magnetizations be comparable for a particular voxel, the expected signal from this pixel will be very close to zero—thus the polarity condition of the magnetizations would not be as critical.

A limitation of RAPID reconstruction is the sensitivity to the inherent image SNR, as RAPID relies solely on the phase of the original image to retrieve the background phase. Should the image SNR be very low, then generally a higher degree of phase variation exists and this variation tends to render the identification of true background phase more challenging. As the region-growing algorithm is used, tissue surrounded by low SNR regions can also be impacted as their phase values cannot be easily synchronized with the other body parts. In our experiments, this is a major source of disagreement between RAPID and PSIR. Although relatively high S index (0.9–0.95) were achieved in all RAPID versus PSIR comparisons, a majority of the differences were caused by the regions surrounded by low SNR, as can be seen at the inverted signal rim of the bottle phantom (Fig. 4) and in tissues surrounded by lung (the difference images in Fig. 5). This, however, is not considered a challenge for most clinical applications, as RAPID still performs relatively robustly on most diagnostically meaningful regions. Assume a normal distribution of the phase error and a conservative regional SNR of 3, in an approach similar to the one described in the Appendix, the probability of incorrectly detecting a magnetization polarity is less than 2.5 × 10⁻⁶. Besides, although the myocardium has previously been intentionally imaged at a delay time that lowers its signal, it was only done so because of the unavailability of proper techniques to restore the polarity of magnetizations in the region. With the adoption of techniques like PSIR and also potentially RAPID, this requirement will not be a necessity in the future. For the actual implementation of a standalone RAPID acquisition, it will be helpful to specifically design (not done in this study) new imaging protocols that will not force a low SNR in the myocardium or in other critical regions. In our experiment, nevertheless, most myocardial regions were still correctly identified as long as they are not surrounded by regions predominantly occupied by air (like tissues in the lung).

CONCLUSIONS

In this manuscript, a Referenceless Acquisition of Phase-sensitive Inversion-recovery with Decisive reconstruction (RAPID) algorithm was proposed and implemented. The RAPID algorithm can potentially improve the acquisition efficiency by eliminating the acquisition of a reference image, as compared with PSIR imaging. Phantom and in vivo experiments demonstrated that the phase sensitive image reconstructed by RAPID algorithm to be in very good agreement with the PSIR algorithm. RAPID was also shown to allow more robust reconstruction as it does not rely on reference image acquisition assumptions.

APPENDIX

The theoretical estimation of RAPID’s robustness against systemic imperfections

This appendix aims to present a theoretical estimation of the RAPID technique’s robustness in the presence of B₀ inhomogeneity and TE variations (if fat is unsuppressed). The phase variability among a homogenous region can be described as $\mathrm{\sigma }=\frac{1}{\mathit{SNR}}$, where σ is the standard deviation of the phase (25). If we assume the phase error distribution is normal, for an image region of SNR=5, we know the phase error in this region has a standard deviation of σ=0.2.

To estimate RAPID’s robustness, we first assume no B₀/TE variation present: the errors of the phase will come only from the measurement noise described by the standard deviation σ. In this study, a threshold of π/2 is used to determine the polarity of magnetizations, so the chance of making an erroneous detection by RAPID can be described by,

$$p=1-\left(\mathrm{\Phi }\left(\frac{\mathrm{\pi }/2}{\mathrm{\sigma }}\right)-\mathrm{\Phi }\left(-\frac{\mathrm{\pi }/2}{\mathrm{\sigma }}\right)\right)=2\left(1-\mathrm{\Phi }\left(\frac{5\mathrm{\pi }}{2}\right)\right)<1\times {10}^{-12}$$ [A1]

where p is the error rate, Φ(x) is the cumulative distribution function of the normal distribution and σ is the standard deviation of phase error.

Now, should a systemic phase error exists (either from B₀ or TE), it can be introduced as a phase bias θ. To simplify calculation and without loss of generality, θ is assumed to be > 0. Equation [A1] will become,

$$\begin{gathered} p=1-\left(\mathrm{\Phi }\left(\frac{\mathrm{\pi }/2-\mathrm{\theta }}{\mathrm{\sigma }}\right)-\mathrm{\Phi }\left(\frac{-\mathrm{\pi }/2-\mathrm{\theta }}{\mathrm{\sigma }}\right)\right) \\ \approx 1-\mathrm{\Phi }\left(\frac{\mathrm{\pi }/2-\mathrm{\theta }}{\mathrm{\sigma }}\right) \end{gathered}$$ [A2]

To achieve an error rate p of less than 0.01%, by solving the equation [A2], we know the value θ needs to be less than 0.827 (rad).

If the phase bias θ is caused by B₀, this means the phase change between neighboring pixels cannot be higher than 0.827. Using the cardiac protocol in this study (TE 4.6 ms, FOV 360 mm and resolution 1.5 mm), this B₀ inhomogeneity can be translated to a total of 6.87 × 10³ Hz (107 ppm at 1.5T) across the whole field of view. A B₀ inhomogeneity better than this condition can be easily achieved in most modern clinical scanners.

If the phase bias is introduced by a water-fat phase difference caused by shifted TE, it also should be less than 0.827. Knowing that the chemical shift between water and fat is 220 Hz at 1.5T, the maximum allowable TE shift for a pure fat voxel will be 0.598 ms assuming water being on the Larmor frequency. For an in-phase TE of 4.6 ms, this means any TE that ranges between 4.0 and 5.2 ms can be used.

It is noteworthy that this calculation is made by assuming the phase error mainly comes from one particular source. Should both B₀ and TE caused bias exist, the situation could worsen. It is, therefore, still suggested to use preferred TE time (in-phase) when a dedicated RAPID protocol is designed.