Abstract
Safe and effective planning for robotic surgery that involves cutting or ablation of tissue must consider all potential sources of error when determining how close the tool may come to vital anatomy. A pre-operative plan that does not adequately consider potential deviations from ideal system behavior may lead to patient injury. Conversely, a plan that is overly conservative may result in ineffective or incomplete performance of the task. Thus, enforcing simple, uniform-thickness safety margins around vital anatomy is insufficient in the presence of spatially varying, anisotropic error. Prior work has used registration error to determine a variable-thickness safety margin around vital structures that must be approached during mastoidectomy but ultimately preserved. In this paper, these methods are extended to incorporate image distortion and physical robot errors, including kinematic errors and deflections of the robot. These additional sources of error are discussed and stochastic models for a bone-attached robot for otologic surgery are developed. An algorithm for generating appropriate safety margins based on a desired probability of preserving the underlying anatomical structure is presented. Simulations are performed on a CT scan of a cadaver head and safety margins are calculated around several critical structures for planning of a robotic mastoidectomy.
Keywords: Robotic surgery, image-guidance, error modeling, mastoidectomy, bone milling
1. INTRODUCTION
Robot-assisted surgical systems can be beneficial for a variety of procedures due to their high accuracy and repeatability, ability to access and work in confined spaces, and capacity to integrate various imaging and sensing modalities into the execution of the surgical task. A subset of medical robots, called surgical CAD/CAM systems, help to execute a plan based on pre-operative imaging and modeling in a manner analogous to computer-integrated manufacturing.1 Examples include orthopedic bone milling systems2, 3 and needle placement systems.4 However, the field of otologic surgery has lagged behind other surgical fields in the incorporation of robots into the operating room, to date. This is likely due to the presence of complex and delicate anatomy in close proximity to the bone that must be removed (see Figure 1a,b). Thus, many otologic surgeries require high accuracy to avoid potentially serious complications. These stringent accuracy requirements make otologic surgery particularly well-suited for robotic assistance, provided that the robot can be made sufficiently accurate. Such a robotic system can use pre-operative imaging and registration to localize delicate bone-embedded structures before the procedure begins, and plan accordingly.
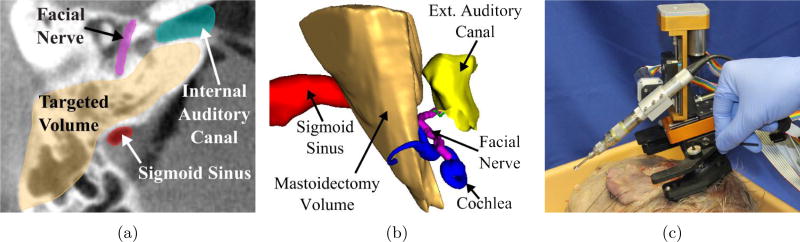
Figure 1.
(a) A computed tomography (CT) scan of a temporal bone showing several vital anatomical structures in the surgical field, (b) a 3D schematic of anatomy and the mastoidectomy volume, and (c) a bone-attached robot for mastoidectomy mounted on a cadaveric specimen before an experimental trial (the robot pictured is a revised version of the prototype described in [9]).
Several research groups have developed systems for image-guided otologic surgery. Federspil et al. used an industrial robot to mill a pocket for a cochlear implant bed.5 Labadie et al. developed customized, microstereotactic frames for minimally-invasive cochlear implantation (CI),6 performed the first robotic mastoidectomy in a cadaver using an industrial robot,7 and developed bone-attached robots for CI surgery8 and mastoidectomy.9 Bell et al. developed a robotic system for drilling a narrow path for minimally invasive CI surgery10 and have achieved high accuracy in vitro.11 Kobler et al. have developed a minimally invasive CI system, in which a passive parallel mechanism is manually adjusted to align the drill with the desired trajectory and mounted to the patient.12 Xia et al.13 and Olds et al.14 developed cooperatively-controlled robotic systems that enforce virtual fixtures around vital anatomy for skull base surgery. All of the above systems are intended to reduce the invasiveness and increase the safety of otologic surgery.
The purpose of the present work is to provide a statistical method to enhance the safety of image-guided surgical robots that must manipulate instruments in close proximity to delicate anatomical structures without damaging them. The method is applicable to any robot and procedure in which there is some anatomical structure to be preserved and system error that can be characterized. The algorithm described in this paper uses this information to produce a patient-specific, statistically-driven, variable-thickness safety margins around anatomical structures that preserve the underlying anatomy with probability levels specified by the surgeon.
Prior work toward developing statistically-informed planning methods of this type has incorporated target registration error (TRE) at the tip of an image-guided cutting tool for linear15 and three-dimensional trajectories.16, 17 However, these algorithms have not directly accounted for the physical hardware error in the surgical system or distortion in the images used to plan the procedure. Here, the framework of [16] (which considered only registration error) is extended to account for uncertainties arising from physical robot attachment, kinematic errors, and deflection during surgery as well as geometric uncertainty in the image. The algorithm is applied to a bone-attached robot for mastoidectomy (see [9] for system description) to generate safety margins around several vital structures. Mastoidectomy involves the removal of bone using a high-speed surgical drill to gain access to the middle and inner ear for a variety of surgical procedures. The requirement that bone must be removed close to vital anatomy makes mastoidectomy an excellent case study to demonstrate the use of this algorithm.
2. ALGORITHM OVERVIEW
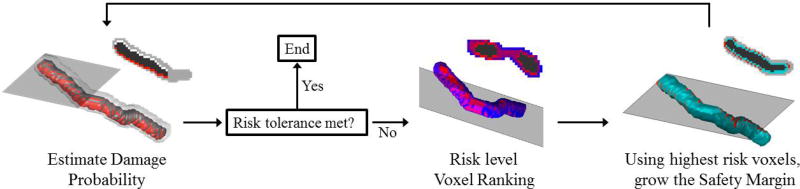
The inputs to the algorithm are the pre-operative images, segmentations of any vital structures that must be avoided during surgery (sensitive anatomical features such as the facial nerve), and a desired preservation rate for each vital structure (e.g. the surgeon can specify, “I want to be 99.9% sure that the facial nerve is not damaged”). The algorithm outputs safety margins unique to each vital structure. The safety margin thicknesses vary spatially, and combined with the underlying structure, define the set of points that must not be targeted by the robot to ensure that the vital anatomy is preserved at the rate specified pre-operatively. Thus, any portion of the original target volume that overlaps with the safety margins is removed from the planned volume to be drilled. Figure 2 shows a flow chart of the overall procedure planning process, showing how the safety algorithm fits into the work flow.
Figure 2.
Flow chart of surgical planning process including the proposed probabilistic safety algorithm. In this figure, processes are outlined in solid lines and data are outlined in dashed lines.
Starting with the original segmentation of the vital structure, the algorithm iteratively builds the safety margin until it is large enough to ensure the vital structure’s desired preservation rate. The image, vital structure, and safety margin are all considered as voxelized, i.e. a volumetric discretization, and the algorithm builds the safety margin by adding to it in units of voxels. For each iteration of the algorithm, the probability of preservation of the vital structure with the current safety margin is first estimated using a Monte Carlo simulation. This simulation considers the shell of all voxels surrounding the safety margin as targeted points. Note that the actual targeted volume of bone to be removed does not necessarily include these points; however, since the safety margin is independent of the target volume, all of the surrounding points are included as targets in the simulation. If the preservation rate predicted by the simulation is lower than the desired rate, the safety margin’s volume must be increased. The surrounding voxels are then ranked according to the probability that the vital structure would be damaged if the drill bit attempted to remove that voxel of bone. The highest risk voxels are then added to the safety margin. This process is then repeated by analyzing a new shell of voxels surrounding the updated safety margin (see Figure 3). Once the vital structure’s preservation rate is at or above the desired level, the algorithm stops and outputs the final safety margin. Since the errors used in estimating the probability of damage are spatially varying and anisotropic, the margins vary in thickness and are generally non-uniform.
Figure 3.
A schematic of the proposed safety algorithm. For each iteration, the probability of preserving the vital structure is calculated, given the current safety margin. If this probability is lower than the specified rate, then the highest risk voxels are added to the safety margin. The calculation is repeated until the calculated preservation rate is greater than the specified rate.
3. ERROR ANALYSIS AND MODELING
As discussed in Section 2, the preservation rate is calculated via Monte Carlo simulation at the beginning of each iteration of the algorithm. The various error sources are modeled as separate probability distributions. For each voxel in the shell surrounding the vital structure and safety margin, an error value from each probability distribution is sampled. These errors are combined to form an overall relative positioning error at the drill tip, for the point under consideration. If the positioning error at any point in the shell would cause the drill to hit the underlying vital structure, the structure is considered to be damaged for that calculation. The calculation is repeated N times with new values sampled from the error distributions for each calculation. The percentage of sample calculations in which the structure is not violated is the preservation rate for the current safety margin. When ranking the highest risk voxels to determine which ones to add to the safety margin, each voxel is subjected to a separate Monte Carlo simulation to determine the probability of damage to the vital structure if that particular voxel were to be targeted. The voxels with the highest damage probabilities are added to the safety margin. In this paper, imaging, registration, robot positioning and deflection errors are considered. These error sources are outlined in the following sections and model parameters are developed for the bone-attached robotic system for mastoidectomy described in [9] and shown in Figure 1c. All numeric error distribution values for this robot are listed in Table 1.
Table 1.
Parameter values used in simulation of safety algorithm described in this paper.
| Error Source | Parameter | Simulation Model Values | |
|---|---|---|---|
| Image distortion (affine transformation matrix) | A | σA(i=j) (diagonal terms) = 0.03%, σA(i≠j) (off-diag terms) = 0.03% | |
|
| |||
| Registration (fiducial localization error) | FLE | RMS FLE = 0.091 mm | |
|
| |||
| Joint initialization | eq,init | σq,init(Prism) < 0.01 mm, σq,init(Rot) = 3.4 × 10−4 rad | |
|
| |||
| Joint transmission backlash and clearance | eq,trans | σq,trans(Prism) = ±0.017 mm, σq,trans(Rot) ≈ 0 rad | |
|
| |||
| Joint sensing | eq,sens | eq,sens(Prism) ≈ 0 mm, eq,sens(Rot) < 1 × 10−4 rad | |
|
| |||
| Joint motion control and interpolation | ep,ctrl | |ep,ctrl| = rand([−0.05, 0.05]) mm | |
|
| |||
| Robot geometry calibration | G | σG(Length) = 0.08 mm, σG(Ang) = 5.24 × 10−4 rad, | |
| ûq,i | σu,ϕ = 1.1 × 10−3 rad | ||
|
| |||
| Prismatic joint compliance | ki (Prism) = [kqi, kα,i, kβ,i, kγ,i] |
|
|
|
| |||
| Rotational joint compliance | ki (Rot) = [kqi, kϕ,i] |
|
|
|
| |||
| Bone-attachment compliance | kanchor = [kaxial, krot] |
|
|
|
| |||
| Forces at drill tip | ftip | |ftip| (RMS) = 6 N | |
3.1 Image Distortion
Targeting based on pre- or intra-operative imaging is fundamentally limited by the geometric accuracy of the image. Inaccuracy leads to distortion, or non-rigid mapping, of points in the image relative to their true position in physical space. While any non-rigid distortion is, in principle, possible, it is assumed that components of second or higher degree are negligible. Therefore, the transformation between physical space and the image is assumed to be strictly affine, i.e. y = Tx + t, where x is a point in physical space and y is that point in the image after distortion. The translation vector, t, has no effect on the rigidness of the transformation, which is determined entirely by T. Thus, any measure of image distortion is a measure of the non-rigidness of T. To calculate the distortion of a particular scanner, it is necessary to first determine T and then calculate the non-rigid component of T.
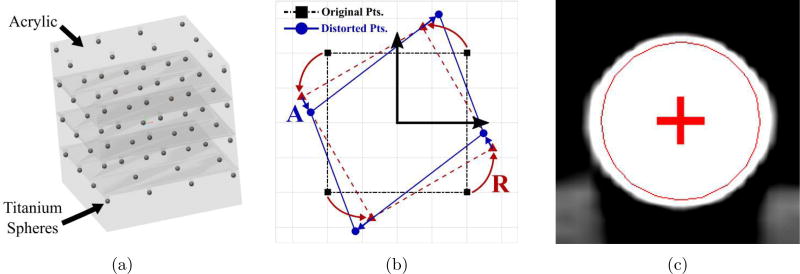
Computed tomography (CT) is the primary modality used in otologic surgery. Thus, a method was developed to quantify the geometric distortion in CT scanners (see Appendix A for details). Briey, a precise phantom with titanium spheres embedded at known locations (Figure 4a) was scanned multiple times. The locations of the titanium spheres in the image (Y) were determined for each scan and the points in physical space (X) are known from the phantom dimensions. Both sets of points were de-meaned to obtain X̃ and Ỹ, respectively, and the affine transformation, T, that maps X̃ to Ỹ was calculated in a least-squares sense. This transformation includes the image distortion as well as the rigid rotation between the image and physical space.18
Figure 4.
(a) A rendering of the custom phantom used to quantify the geometric accuracy of CT scanners. (b) A schematic of the decomposition of scanner affine transformation into rotation, R, and distortion, A. (c) A visualization of the localization of a titanium spherical fiducial marker in a CT scan.
To isolate the distortion, T is factored into rigid and non-rigid components using the polar decomposition, T = AR, where A is a positive-semidefinite Hermitian matrix and R is a rotation matrix (RtR = I). Figure 4b provides a schematic of this decomposition. The registration errors associated with calculating R are covered in the next section. A represents the stretching, or distortion, of the image and is given by
| (1) |
where the columns of U are the eigenvectors of TTt and Λ is a diagonal matrix of the singular values of T. A is calculated for each scan acquired of the geometric phantom. The mean of the A matrices for all scans is the characteristic transformation of the scanner, Ac.
The image distortion could be incorporated into the safety algorithm in two different ways. If no prior knowledge of the distortion of a particular scanner is known, a random characteristic transformation, Ac can be generated for each calculation of the Monte Carlo simulation based on known estimates of other similar scanners (see Appendix A for results from testing several commercially available scanners). The distorted point location, , can then be calculated using Ac as
| (2) |
where I is the identity matrix, and Imp̃i is the true location of the point relative to the centroid of the fiducial markers expressed in the image coordinate system.
Alternatively, if we have an estimate of the characteristic transformation for a particular scanner (Âc), the distorted image can be rectified by multiplying points in the image by . The error associated with image distortion is then reduced to the uncertainty in Âc. This uncertainty is the variance between the elements of A for each of the phantom scans. These distributions are sampled and added to I to construct Ai for each calculation in the simulation and the distorted point location is calculated by
| (3) |
3.2 Registration Error
Registration error can be estimated based on the method of registration and image quality. For the case of point-based registration, as is used in this application, it is possible to determine the distribution of target registration error (TRE) at a given point based on the locations of the fiducial markers and associated distributions of fiducial localization error (FLE).19 As was done in [16], a value from the TRE distribution for a particular point is sampled to determine the error associated with a “mis-registration” (i.e. a registration containing error due to imperfect fiducial localization). This error is added to the overall uncertainty of the system for a given calculation.
Knowledge of the FLE and the nominal fiducial marker locations with respect to the target positions is required to calculate the TRE. The FLE was computed using the same scans with the phantom described in Section 3.1 (see Figure 4). First, for each image, the demeaned points in image space were “rectified”, . Next, a rigid point-based registration of Yr to the demeaned phantom model X̃ was performed and the FRE for the registration was calculated. Finally, Eq. 8.25 from [18] was used to estimate the Root Mean Squared (RMS) FLE from the FRE.
Prior work by Kobler et al. characterized FLE for various sphere localization algorithms, marker materials, and image interpolation approaches.20 The values obtained in that work for titanium spheres using the cross correlation and least squares algorithms with image interpolation factors greater than 1 yielded FLE values similar to the value calculated for the Xoran xCAT. The data in [20] can be used as a reference to estimate FLE if the value for a particular setup is unknown.
3.3 Robot Kinematic Errors
Robot error analysis and modeling has been a significant area of research for many years (e.g. [21]) and has been studied within the context of medical robotics.22, 23 Thus, the various sources of kinematic error are well understood and can be applied to the robot analyzed here. This error arises from uncertainties in joint positioning and geometric parameters in the robot’s kinematic model.
More specifically, the joint positioning errors considered in this model are: (1) joint transmission backlash, (2) joint initialization inaccuracies, (3) joint sensing discretization, and (4) asynchronous control of joint positions. The joint transmission errors were calculated based on hardware specifications and transmission ratios. The linear joints have planetary gearboxes which result in slight backlash, although it is mitigated by a high reduction ratio of the lead screw. This error is modeled as a discrete distribution with two possible values (plus or minus the backlash value from the manufacturer’s specifications, multiplied by the gear ratio). The harmonic gearbox used in the rotational joint has negligible backlash, but the compliance of the flexible spline factors into the joint stiffness value. Inconsistent joint initialization (or homing) each time the robot is powered on results in a slightly different baseline from which all joint values are then calculated. This error was quantified by performing the initialization process, in which the joints are run to their end stops and zeroed, several times and analyzing the differences in zero positions. The sensor discretization error is a function of the encoder resolution and transmission gear ratios. The discretization error is modeled as a uniform distribution with bounds of plus or minus half of the joint discretization value. Given the high gear reduction ratios used, this error is low. Finally, since the controller cannot bring each joint to its desired position at exactly the same time, there is some error associated with this asynchronous joint movement. To quantify this, the maximum allowed positioning error defined in the control software (system shuts down if this is exceeded) is considered. This maximum error is then used to bound a random, uniform error distribution.
The geometric errors come from imperfect calibration of various robot dimensions and axes about which the robot joints move. To determine the geometric calibration errors, the full calibration procedure was performed ten times and the results for each model parameter were analyzed. This procedure involves moving the robot to a series of points, measuring these locations with a coordinate measurement machine (CMM), and fitting the data to the kinematic model of the robot. The variance in the resulting calibrated parameter values were used to select appropriate error distributions for each value in the kinematic model. Linear dimension errors (e.g. link lengths and position vectors between relevant coordinate frames) are simply added to the nominal value when calculating the error. Joint axis unit vectors and coordinate transformation errors are incorporated by multiplying the nominal value by a rotation matrix that represents a small rotation based on the range of calibration data.
3.4 Robot Deflection
Additional error is caused by deflection of the robot under loads during the surgical procedure, which result in a positioning error of the drill tip. All robots have some compliance in their joints and structural members. Bone-attached robots have additional compliance in the attachment interface between the bone and the anchoring screws. The analysis of the robot deflection is divided between these two modes and then combined to determine the total deflection under a given load.
3.4.1 Robot Compliance
A common method for computing the compliance of a robot is to assume quasi-static loading and infinitely stiff links relative to the joints.24 This enables a task space compliance matrix for the entire robot to be computed based on the individual joint stiffness values (acting about the joint motion axes) and the configuration of the robot.
| (4) |
where χ = Diag([k1, k2, …, kn]) represents the joint stiffness matrix, J is the robot Jacobian, and kj is the stiffness value along the motion of the jth joint (qj). kj is a linear stiffness coefficient for prismatic joints and torsional stiffness coefficient for rotational joints. The assumption of infinitely stiff structural members connecting the joints depends on the size and material selected for the links compared to the expected loads. This assumption is valid for the robot considered here as the robot is constructed from aluminum and stainless steel and the links were sized sufficiently large for the range of forces at the drill tip.
However, additional compliance can exist at the link-joint interfaces in off-axis directions, i.e. directions other than the joint motion axis. For example, a rotational joint can have some angular compliance perpendicular to the rotating shaft axis and/or linear compliance in one or more directions. Any additional compliance must be considered in an accurate model. Thus, experiments were performed on each joint of the robot to measure compliance in all directions. Forces and moments were applied in each orthogonal direction and the associated linear or angular deflection was measured. The data was then analyzed to determine which additional displacements must be included in the model and a stiffness coefficient was calculated for each direction of motion. The prismatic joints for this robot have angular compliance in all three directions but negligible linear compliance in the off-axis directions. The rotational joint has angular compliance perpendicular to the joint axis (specifically, about the vector that is orthogonal to the joint axis and the drill spindle axis). Figure 5 shows the directions of these relevant off-axis compliances for the prismatic and rotational joints of the robot. The stiffness coefficients along the joint motion directions (ki) were also measured in this manner. Note that both axis and off-axis stiffness values are assumed here to be constant throughout the range of motion of the joint.
Figure 5.
An Illustration of the off-axis deflection directions of robot joints considered in this paper. These are in addition to compliance model compliance about/along each joint axis, which were also modeled. (a) For linear joints, angular deflections resulting from moments in all three directions were considered. (b) For rotational joints, angular deflection resulting from a moment perpendicular to the joint axis was considered.
To account for the off-axis stiffness and generate a compliance matrix similar to Eq. (4), the kinematic model is augmented with additional “virtual joints” which represent motion about the additional directions of compliance that must be considered.25 When determining the position of the drill tip in the kinematic model, these additional joint values are set to zero; however, their contribution to the robot Jacobian enables them to contribute to the total robot compliance matrix. The full sets of joint displacements for the prismatic and rotational joints are given by
| (5) |
| (6) |
where αj, βj, and γj are the angular compliance displacements associated with the x-, y-, and z-axes of the prismatic joint coordinate frame (see Figure 5). ϕj is the angular compliance displacement about the axis perpendicular to the rotational joint axis and the drill spindle axis (ûj,ϕ). The columns of the linear velocity Jacobian for the full sets of prismatic and rotational joint displacements are
| (7) |
| (8) |
where ûj is the jth joint axis unit vector, rj is the position vector of the drill tip relative to the jth joint. Thus, the full set of displacements and the linear velocity Jacobian for the robot, including off-axis motions are
| (9) |
| (10) |
where q1, q2 and q3 are the displacement sets for the prismatic joints and q4 is the displacement set for the rotational joint. The compliance matrix for the entire robot, including the off-axis displacements is
| (11) |
where χFull is a 14×14 diagonal matrix that contains the joint axis and off-axis stiffness values.
3.4.2 Compliance of Attachment to Skull
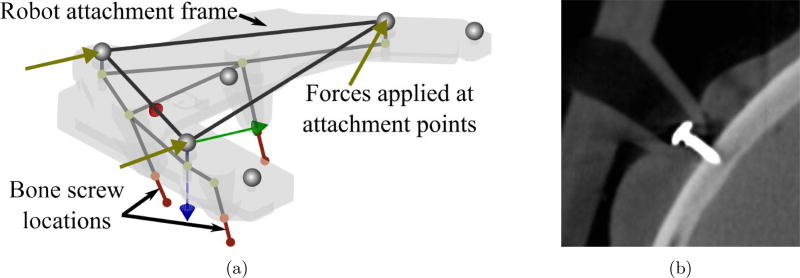
For a bone-attached robot, further deflection occurs at the interface of the bone anchor screws and the skull. To analyze and model this deflection, a finite element analysis (FEA) model of the robot attachment frame and bone anchor screws was developed. First, a structural model of the bone attachment frame was developed using the FEA software package ANSYS (ANSYS Inc., Canonsburg, PA, USA). However, since the deformation calculation must be performed many times and must be part of the overall error calculation, it was necessary to create a custom, simplified model in MATLAB (The Mathworks, Inc., Natick, MA, USA). The simplified FEA model treats the attachment frame as a structure with 18 nodes and 18 space frame elements (see [26] for MATLAB code and explanation of element types). Deflections at key points in the simplified model were compared to the full ANSYS model. The simplified model deflections averaged within 0.01 mm of the full model when tested under a range of simulated loads.
The bone anchoring screws (see Figure 6b) are also modeled as space frame elements with the matrix elements determined from experimental data. Data was used from experiments performed by Kobler et al. on cadaver temporal bones and phantom material in [27], which determined an axial stiffness coefficient of the anchor. Additional experiments were performed on fresh cadaver bones, which determined a torsional stiffness coefficient. Both of these stiffness coefficients were determined from experiments in ex vivo bones in controlled laboratory conditions and attachment in the operating room on a real patient would likely be more challenging, and perhaps result in less rigid fixation. To account for this imperfect attachment in practice, the stiffness values are randomly varied between 75% and 100% of the nominal values in the error model. For a given set of stiffness values, a three-dimensional space frame element is fit to this data and the compliance matrix associated with bone attachment, Cattach, is calculated.
Figure 6.
(a) A simplified Finite Element model of the robot positioning frame and the bone anchoring screws. The screw stiffnesses are based on experimental data. (b) A CT image of a bone anchoring screw inserted through positioning frame leg and into skull surface of cadaver.
4. COMBINING ERROR SOURCES
The various error sources are combined to estimate the total system error at a given point. Points are analyzed according to their proximity to the vital structures near the surgical site and discretized based on the voxel size of the image (can be down or up sampled as necessary). For each calculation, the point in the image, relative to the centroid of the fiducial markers, Imp̃i, is first transformed according to Eq. (3) to obtain . The elements of Ai are selected from the associated error distributions. is then converted to the robot base coordinate system, . Note that the error in this transformation is not considered here since the registration error between image and robot coordinate systems is considered separately below. The superscript indicating the frame of reference is dropped for brevity from this point forward and it is assumed that all positions are in the robot’s base coordinate frame (Frame {0}). Next, a nominal corresponding set of joint values, qi, is calculated using the inverse kinematics of the robot. A new set of joint values, , which includes additional joint positioning errors sampled from the error distributions described in Section 3.3, is then calculated as follows:
| (12) |
where the joint error values are sampled from the associated distributions. Geometric calibration errors (dimensions and joint axes) are also selected randomly from the probability distributions and combined with the calibrated geometry data to determine new values that include error. The set of joint axis unit vectors including error is defined as and the set of geometric parameters including error is defined as G*. Using this data, along with the joint values calculated above, the associated drill tip position, including kinematic error, is calculated as , where ep,ctrl is the error due to asynchronous joint control and interpolation.
The robot Jacobian and compliance matrix are also calculated using , G*, and . The overall system deflection is then computed based on the force at the drill tip (f) and weight of the robot. This force is estimated using prior research in evaluating the forces during mastoidectomy as guidance.28 Since the safety margin calculation is independent of the final robot trajectory, factors that influence the force magnitude and direction are not known at this stage of the planning process (e.g. cutting velocity, depth, drill angle at the specific voxel). Thus, forces associated with more aggressive cutting parameters (e.g. velocity of , depth of 1.6 mm) are used and applied in random directions at the drill tip. An additional factor of safety is applied to these values to account for lower spindle speeds compared to the value of 80,000 RPM used for all trials in [28]. The tip deflection due to milling forces and robot compliance is given by
| (13) |
The deflection of the positioning frame is caused by the same tip force as well as the weight of the robot, which depends on the orientation of the patient’s head in surgery.
| (14) |
where fweight = mrobotg and is equal to fweight except it is zero in the direction toward the skull since the tips of the legs cannot move downward into the skull. mrobot is the mass of the robot and g is the gravity vector. Since the robot is in series with the attachment frame, the deflections are added and
| (15) |
The drill tip position including error is then calculated from the kinematic error and tip deflection, , and the associated error relative to the true point location is . To determine the overall error for this target point, this value is combined with the registration error, ei,reg, which is calculated by sampling the TRE distribution at the given point. This overall error is given by:
| (16) |
The error is added to the corresponding point location. The calculation is repeated many times in the simulation, with the error distributions re-sampled for each calculation. Note that the registration and positioning errors are added at the end of the process rather than calculating a “mis-registration” (as described in Section 3.2) and using the mis-registered point location for subsequent calculations. This approach reduces the computation time by using the results of [19] to directly estimate the TRE distribution from the FLE.
It is also important to note that some of the error sources are coupled among target points, e.g. a rigid registration will apply the same transformation to all points and robot calibration error will affect the kinematic model that is used for all points. For this type of error, a single value is sampled from the error distribution and applied to each target point for that particular calculation. For error sources that are considered independent among target point locations, (e.g. joint backlash error and forces at the drill tip), a unique value is sampled from the error distributions for each point.
5. SIMULATION OF ROBOTIC MASTOIDECTOMY PLANNING
The algorithm was tested on a scan of a human cadaver skull that was used for prior experiments with the robot. Automatic segmentations of the facial nerve, chorda tympani, and external auditory canal were performed using the algorithms described in [29] and segmentations of the sigmoid sinus and internal auditory canal were performed manually. The segmentation boundaries were confirmed by a surgeon. These structures were provided as inputs to the algorithm along with their associated preservation probability values. The parameter values used for each error source, as outlined in Section 3, are provided in Table 1.
Results of the simulation are given in Table 2. The desired safety threshold for each structure is listed along with the volume of the associated safety margin. The targeted volume segmented by a surgeon was compared with the safety margins to determine how much (if any) overlap occurred. There was overlap into the target volume for the facial nerve safety margin and the sigmoid sinus safety margin. The facial nerve has the highest safety threshold (99.9%) and thus is most likely to impact the permissible workspace of the robot. The sigmoid sinus is not considered to be as critical of a structure so the desired preservation probability is lower. However, the large size of the sigmoid sinus increases the likelihood that there will be some overlap with its safety margin and the desired volume since there are so many nearby voxels that could potentially cause damage if targeted.
Table 2.
Simulation results
| Structure | Specified Preservation Rate |
Original Size (cm3) |
Safety Margin Size (cm3) |
Target Removed (cm3) |
|---|---|---|---|---|
| Facial Nerve | 99.9% | 0.117 | 1.118 | 0.063 |
| Chorda Tympani | 95.0% | 0.019 | 0.290 | 0.000 |
| External Auditory Canal | 95.0% | 0.693 | 1.337 | 0.000 |
| Sigmoid Sinus | 95.0% | 1.051 | 2.709 | 0.169 |
| Internal Auditory Canal | 99.0% | 0.235 | 0.824 | < 0.001 |
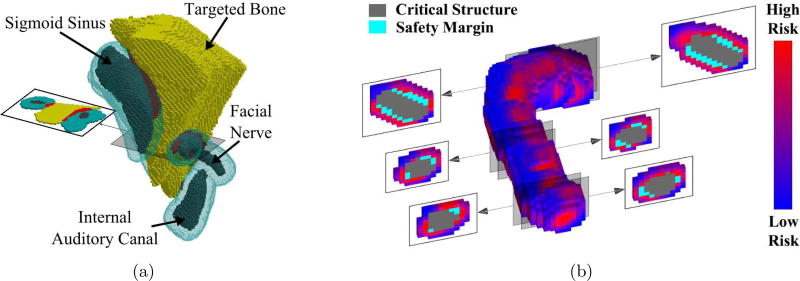
Figure 7 shows the resulting safety margins of several structures and cross-sectional views of the facial nerve. The red voxels in Figure 7a are the voxels that were removed from the planned volume to be removed with the drill. Figure 7b shows the dimensions of the facial nerve safety margin at a single iteration of the algorithm. The risk levels of the voxels surrounding the safety margin are indicated by shading. The anisotropic error sources result in the safety margin having an elliptical cross-section.
Figure 7.
(a) The final safety margins for several critical structures. Portions of the original target volume (in red) are removed where the safety margins overlap the volume originally identified for removal by the surgeon. (b) A schematic of the risk of drilling points surrounding the facial nerve and its current safety margin at one iteration of the algorithm. At each iteration, a percentage of the highest risk voxels are added to the safety margin to bring the probability of preserving the structure closer to the desired threshold.
6. CONCLUSIONS AND FUTURE WORK
This paper provides an algorithm for generating statistically-driven safety margins around vital structures based on estimates of imaging, registration, and robot errors. Prior work is expanded upon by incorporating a range error sources present in any image-guided, surgical robotic system and providing a method for combining various error distributions. The algorithm was applied to a bone-attached robotic system for mastoidectomy and generated variable-thickness safety margins around several vital anatomical structures. These safety margins were used to modify a segmented target volume so that it meets the desired preservation rates for each of the vital structures. The algorithm, however, can be applied to any surgical procedure in which a robot is moving through a planned path or region near vital anatomical structures that must be avoided. If stochastic estimates of the error sources are known, the formulation laid out in this paper can be followed to develop a safety algorithm for any such procedure. Additionally, this approach allows for analysis of system error in a way that is very specific for the intended use. By adjusting the different error distribution parameters and observing the effects on the size of the necessary safety margins for given preservation thresholds, the system components that cause meaningful error are apparent and system improvements can focus on these components.
Future work on this project should focus on additional improvements to the error modeling. Incorporating milling force estimates based on density and porosity of the bone near the vital structures would improve the accuracy of the force and deflection estimation. Additionally, a source of error that is not covered in this work is segmentation error. The errors at the boundaries of the critical structures should be analyzed and quantified since uncertainty in these locations impacts any margin that is built upon the structure. Using the framework described in this paper, these additional error sources, and any others, can be easily integrated into the algorithm once they are characterized as probability distributions.
Acknowledgments
This work was supported by award number R01 DC012593 from the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors thank Jack Noble and Benoit Dawant for use of their segmentation software.
APPENDIX A
GEOMETRIC DISTORTION OF CT SCANNERS
The geometric fidelity, or capability of a scanner to produce geometrically accurate images, was determined through a series of experiments using a custom manufactured, highly accurate phantom (see Figure 8). The phantom consists of 4 mm diameter titanium fiducial markers embedded in layers of Plexiglass. A total of 64 spheres are arranged in a 4 × 4 × 4 grid, with separation distances of 59.27 mm in the x- and y-directions and 50.8 mm in the z-direction. The array of spheres provides a three-dimensional grid of regularly spaced points that spans a volume large enough to encompass a human head. The material and shape of the spheres were chosen for ease of fiducial marker localization.
Holes for the spheres were created by a computer numeric controlled (CNC) milling machine (Ameritech Exact Junior, Broussard Enterprises, Inc, Santa Fe Springs, CA). The Plexiglas portion consists of four slabs glued together. Before gluing, the first slab was fixed to the CNC vise, sixteen holes were milled in the upper surface with a diameter appropriate for a press fit of the spheres, and the spheres were pressed into the holes and glued. Then, without disturbing the first slab, a second slab was glued to the first and allowed to set. Sixteen new holes were milled, and the process was continued until 64 spheres were placed. The accuracy of the CNC is 0.0002 inch (0.005 mm) absolute with a 0.0001 inch (0.0025 mm) repeatability. The placement error of the press fit of the spheres is estimated to be less than 0.001 inch (0.025 mm).
The phantom was imaged, and then a three-dimensional fiducial-localization algorithm was used to estimate the locations of the centers of the spheres in each image volume. As described in Section 3.1, it is assumed that the scanners distortion transformation is strictly affine, i.e. the second or higher degree components within the field of view of a calibrated instrument are negligible. As such, an affine registration is performed to calculate the matrix T, and the characteristic affine transformation for the scanner, Ac, is computed using the polar decomposition of T (see Section 3.1).
Figure 8.
Photo of custom phantom used to quantify the geometric accuracy of CT scanners; titanium spheres were embedded in layers of acrylic sheets using a CNC machine.
Additionally, a simple metric to provide an overall quantification of the geometric distortion of the scanner was calculated. A fundamental definition of a rigid transformation is that it preserves distances between points. This definition is used to define a measure of geometric distortion as the largest possible percentage change in distance, pd, between points. This change can be an expansion or contraction in any direction and is calculated using the singular value decomposition of T:
| (17) |
where Λi are the the singular values of T and |․| is the absolute value.
Five scanners were tested in this analysis. Image matrix sizes, voxel dimensions, peak voltages, and charge for each scanner are listed in Table 3. For each scanner three to four scans were acquired with the pose of the phantom changed for each scan. The Xoran xCAT, Siemens, and Medtronic O-Arm scans were acquired at Vanderbilt University Medical Center (Nashville, TN). The BodyTom scans were acquired by NeuroLogica (Danvers, MA, USA) and the Airo Mobile scans were acquired by Brainlab (Westchester, IL, USA). For each scan, the center of the phantom was roughly centered and the field of view covered as much of the phantom as possible.
Table 3.
Specifications of CT scanners tested
| Scanner | Image Matrix Size (X × Y × Z) |
Voxel Dimensions |
Peak Voltage |
Charge |
|---|---|---|---|---|
| Xoran xCAT ENT | 640 × 640 × 355 | x=y=z=0.4 mm | 120 kV | 120 mAs |
| Neurologica BodyTom (in Helical Mode) | 512 × 512 × 176 | x=y=1.16 mm, z=1.25 mm | 100 kV | 50 mAs |
| Siemens SOMATOM Definition AS | 512 × 512 × 333 | x=y=0.74 mm, z=0.75 mm | 120 kV | 300 mAs |
| Brainlab Airo Mobile | 512 × 512 × 249 | x=y=0.59 mm, z=1.0 mm | 120 kV | 270 mAs |
| Medtronic O-Arm | 640 × 640 × 640 | x=y=0.42 mm, z=0.83 mm | 110 kV | 230 mAs |
The results are summarized in Table 4. The FLE values and mean and standard deviation of the maximum distortion percentage are provided. These accuracies are far above any level needed for visual inspection of CT images for diagnosis or interventional planning. However, they may affect applications in which fixtures and/or fiducial markers are used for sub-millimetric targeting. If, for example, the distance between the centroid of the fiducial markers and the target is on the order of 100 mm, then each 1 percent of scaling error causes 1 mm of targeting error. The numbers in the table show that in this worst case, each of these scanners would produce a maximum geometrical targeting error of less than 0.234 mm.
Table 4.
Geometric fidelity of various commercially available CT scanners
| Scanner | FLE | Characteristic Transformation (Ac)a | Maximum Distortion (pd)c |
|
|---|---|---|---|---|
|
| ||||
| Diagonal Elements | Off-Diag. Elementsb | |||
| Xoran xCAT ENT | 0.091 | A11 = 1.0001 (0.0003) | A12 = 0.0002 (0.0001) | 0.125 (0.027) |
| A22 = 1.0012 (0.0002) | A13 = −0.0003 (0.0003) | |||
| A33 = 1.0004 (0.0001) | A23 = 0.0000 (0.0002) | |||
|
| ||||
| Neurologica BodyTom | 0.135 | A11 = 0.9993 (0.0001) | A12 = 0.0000 (0.0001) | 0.156 (0.040) |
| A22 = 0.9994 (0.0002) | A13 = −0.0003 (0.0002) | |||
| A33 = 0.9988 (0.0006) | A23 = −0.0003 (0.0001) | |||
|
| ||||
| Siemens SOMATOM Definition AS | 0.138 | A11 = 1.0004 (0.0001) | A12 = 0.0001 (< 0.0001) | 0.193 (0.104) |
| A22 = 1.0005 (0.0001) | A13 = −0.0015 (0.0011) | |||
| A33 = 0.9990 (0.0001) | A23 = −0.0002 (0.0001) | |||
|
| ||||
| Brainlab Airo Mobile | 0.124 | A11 = 0.9985 (0.0001) | A12 = −0.0000 (0.0002) | 0.198 (0.009) |
| A22 = 0.9985 (0.0002) | A13 = 0.0002 (0.0005) | |||
| A33 = 1.0001 (0.0001) | A23 = 0.0007 (0.0002) | |||
|
| ||||
| Medtronic O-Arm | 0.197 | A11 = 0.9981 (0.0003) | A12 = 0.0003 (0.0003) | 0.234 (0.023) |
| A22 = 0.9989 (0.0003) | A13 = 0.0000 (0.0002) | |||
| A33 = 0.9989 (0.0013) | A23 = 0.0001 (0.0004) | |||
Mean (Std. Dev.) of A matrix data from all scans for the given scanner.
Note that Aij = Aji.
pd calculated for each scan per Eq. (17).
References
- 1.Taylor RH, Stoianovici D. Medical robotics in computer-integrated surgery. Robotics and Automation, IEEE Transactions on. 2003;19(5):765–781. [Google Scholar]
- 2.Paul HA, Bargar WL, Mittlestadt B, Musits B, Taylor RH, Kazanzides P, Zuhars J, Williamson B, Hanson W. Development of a surgical robot for cementless total hip arthroplasty. Clinical Orthopaedics and related research. 1992;285:57–66. [PubMed] [Google Scholar]
- 3.Ho S, Hibberd R, Davies B. Robot assisted knee surgery. Engineering in Medicine and Biology Magazine, IEEE. 1995;14(3):292–300. [Google Scholar]
- 4.Kwoh YS, Hou J, Jonckheere E, Hayati S. A robot with improved absolute positioning accuracy for ct guided stereotactic brain surgery. Biomedical Engineering, IEEE Transactions on. 1988;35(2):153–160. doi: 10.1109/10.1354. [DOI] [PubMed] [Google Scholar]
- 5.Federspil PA, Geisthoff UW, Henrich D, Plinkert PK. Development of the first force-controlled robot for otoneurosurgery. The Laryngoscope. 2003 Mar.113:465–71. doi: 10.1097/00005537-200303000-00014. [DOI] [PubMed] [Google Scholar]
- 6.Labadie RF, Mitchell J, Balachandran R, Fitzpatrick JM. Customized, rapid-production microstereotactic table for surgical targeting: description of concept and in vitro validation. International journal of computer assisted radiology and surgery. 2009;4(3):273–280. doi: 10.1007/s11548-009-0292-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Danilchenko A, Balachandran R, Toennis JL, Baron S, Munkse B, Fitzpatrick JM, Withrow TJ, Webster RJ, III, Labadie RF. Robotic Mastoidectomy. Otology & Neurotology. 2010;(32):11–16. doi: 10.1097/MAO.0b013e3181fcee9e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kratchman LB, Blachon GS, Withrow TJ, Balachandran R, Labadie RF, Webster RJ. Design of a bone-attached parallel robot for percutaneous cochlear implantation. Biomedical Engineering, IEEE Transactions on. 2011 Oct.58:2904–10. doi: 10.1109/TBME.2011.2162512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Dillon NP, Balachandran R, Fitzpatrick JM, Siebold MA, Labadie RF, Wanna GB, With-row TJ, Webster RJ. A compact, bone-attached robot for mastoidectomy. Journal of Medical Devices. 2015;9(3) doi: 10.1115/1.4030083. 031003-1-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bell B, Stieger C, Gerber N, Arnold A, Nauer C, Hamacher V, Kompis M, Nolte L, Caversaccio M, Weber S. A self-developed and constructed robot for minimally invasive cochlear implantation. Acta oto-laryngologica. 2012;132(4):355–360. doi: 10.3109/00016489.2011.642813. [DOI] [PubMed] [Google Scholar]
- 11.Bell B, Gerber N, Williamson T, Gavaghan K, Wimmer W, Caversaccio M, Weber S. In vitro accuracy evaluation of image-guided robot system for direct cochlear access. Otology & Neurotology. 2013;34(7):1284–1290. doi: 10.1097/MAO.0b013e31829561b6. [DOI] [PubMed] [Google Scholar]
- 12.Kobler J-P, Nuelle K, Lexow GJ, Rau TS, Majdani O, Kahrs LA, Kotlarski J, Ortmaier T. Configuration optimization and experimental accuracy evaluation of a bone-attached, parallel robot for skull surgery. International journal of computer assisted radiology and surgery. 2015:1–16. doi: 10.1007/s11548-015-1300-4. [DOI] [PubMed] [Google Scholar]
- 13.Xia T, Baird C, Jallo G, Hayes K, Nakajima N, Hata N, Kazanzides P. An integrated system for planning, navigation and robotic assistance for skull base surgery. The International Journal of Medical Robotics and Computer Assisted Surgery. 2008;4(4):321–330. doi: 10.1002/rcs.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Olds KC, Chalasani P, Pacheco-Lopez P, Iordachita I, Akst LM, Taylor RH. Intelligent Robots and Systems (IROS 2014), 2014 IEEE/RSJ International Conference on. IEEE; 2014. Preliminary evaluation of a new microsurgical robotic system for head and neck surgery; pp. 1276–1281. [Google Scholar]
- 15.Noble JH, Majdani O, Labadie RF, Dawant B, Fitzpatrick JM. Automatic determination of optimal linear drilling trajectories for cochlear access accounting for drill-positioning error. The International Journal of Medical Robotics and Computer Assisted Surgery. 2010;6(3):281–290. doi: 10.1002/rcs.330. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Siebold MA, Dillon NP, Webster RJ, Fitzpatrick JM. SPIE Medical Imaging. International Society for Optics and Photonics; 2015. Incorporating target registration error into robotic bone milling; pp. 94150R–94150R. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Haidegger T, Győri S, Benyó B, Benyó Z. Engineering in Medicine and Biology Society (EMBC), 2010 Annual International Conference of the IEEE. IEEE; 2010. Stochastic approach to error estimation for image-guided robotic systems; pp. 984–987. [DOI] [PubMed] [Google Scholar]
- 18.Sonka M, Fitzpatrick JM, Masters BR. Handbook of medical imaging, volume 2: Medical image processing and analysis. Optics & Photonics News. 2002;13:50–51. [Google Scholar]
- 19.Danilchenko A, Fitzpatrick JM. General approach to first-order error prediction in rigid point registration. Medical Imaging, IEEE Transactions on. 2011;30(3):679–693. doi: 10.1109/TMI.2010.2091513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kobler J-P, Díaz JD, Fitzpatrick JM, Lexow GJ, Majdani O, Ortmaier T. SPIE Medical Imaging. International Society for Optics and Photonics; 2014. Localization accuracy of sphere fiducials in computed tomography images; pp. 90360Z–90360Z. [Google Scholar]
- 21.Veitschegger WK, Wu C-H. Robot accuracy analysis based on kinematics. Robotics and Automation, IEEE Journal of. 1986;2(3):171–179. [Google Scholar]
- 22.Mavroidis C, Dubowsky S, Drouet P, Hintersteiner J, Flanz J. Robotics and Automation, 1997. Proceedings., 1997 IEEE International Conference on. Vol. 2. IEEE; 1997. A systematic error analysis of robotic manipulators: application to a high performance medical robot; pp. 980–985. [Google Scholar]
- 23.Meggiolaro MA, Dubowsky S, Mavroidis C. Geometric and elastic error calibration of a high accuracy patient positioning system. Mechanism and Machine Theory. 2005;40(4):415–427. [Google Scholar]
- 24.Tsai L-W. Robot analysis: the mechanics of serial and parallel manipulators. John Wiley & Sons; 1999. [Google Scholar]
- 25.Abele E, Rothenbücher S, Weigold M. Cartesian compliance model for industrial robots using virtual joints. Production Engineering. 2008;2(3):339–343. [Google Scholar]
- 26.Ferreira AJ. MATLAB codes for finite element analysis: solids and structures. Vol. 157. Springer Science & Business Media; 2008. [Google Scholar]
- 27.Kobler J-P, Prielozny L, Lexow GJ, Rau TS, Majdani O, Ortmaier T. Mechanical characterization of bone anchors used with a bone-attached, parallel robot for skull surgery. Medical engineering & physics. 2015;37(5):460–468. doi: 10.1016/j.medengphy.2015.02.012. [DOI] [PubMed] [Google Scholar]
- 28.Dillon NP, Kratchman LB, Dietrich MS, Labadie RF, Webster RJ, III, Withrow TJ. An experimental evaluation of the force requirements for robotic mastoidectomy. Otology & Neurotology. 2013;34(7):e93. doi: 10.1097/MAO.0b013e318291c76b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Noble JH, Dawant BM, Warren FM, Labadie RF. Automatic identification and 3-d rendering of temporal bone anatomy. Otology & Neurotology. 2009;30(4):436. doi: 10.1097/MAO.0b013e31819e61ed. [DOI] [PMC free article] [PubMed] [Google Scholar]