Evolutionary algorithm optimization of biological learning parameters in a biomimetic neuroprosthesis

Abstract

Biomimetic simulation permits neuroscientists to better understand the complex neuronal dynamics of the brain. Embedding a biomimetic simulation in a closed-loop neuroprosthesis, which can read and write signals from the brain, will permit applications for amelioration of motor, psychiatric, and memory-related brain disorders. Biomimetic neuroprostheses require real-time adaptation to changes in the external environment, thus constituting an example of a dynamic data-driven application system. As model fidelity increases, so does the number of parameters and the complexity of finding appropriate parameter configurations. Instead of adapting synaptic weights via machine learning, we employed major biological learning methods: spike-timing dependent plasticity and reinforcement learning. We optimized the learning metaparameters using evolutionary algorithms, which were implemented in parallel and which used an island model approach to obtain sufficient speed. We employed these methods to train a cortical spiking model to utilize macaque brain activity, indicating a selected target, to drive a virtual musculoskeletal arm with realistic anatomical and biomechanical properties to reach to that target. The optimized system was able to reproduce macaque data from a comparable experimental motor task. These techniques can be used to efficiently tune the parameters of multiscale systems, linking realistic neuronal dynamics to behavior, and thus providing a useful tool for neuroscience and neuroprosthetics.

Introduction

Combining brain models and neuroprosthetics

The field of computational neuroscience has advanced significantly beyond artificial neural networks by using explicit experimental data to build biomimetic models of brain dynamics that can then be used to perform tasks [1–3]. The brain functions at many different but interdependent spatial and temporal scales, ranging from molecular interactions at the single neuron level, to small circuits of thousands of neurons, to information exchange between multiple areas involving millions of neurons. Biologically realistic models permit us to understand how changes at the molecular and cellular levels effect alterations in the dynamics of local networks of neurons and interconnected brain areas. At the highest levels, they allow us to connect neural activity to theories of behavior, memory, and cognition. The recent introduction of large neuroscience projects in the United States and the European Union—Brain Research through Advancing Innovative Neurotechnologies (BRAIN) [4] and the Human Brain Project (HBP) [1], respectively—will provide an opportunity to rapidly gather new and more accurate data to incorporate into the multiscale models.

On the other hand, neuroprostheses or brain-machine interfaces belong to an emerging field that aims at decoding electrical signals recorded from the brain. These techniques can, for example, be used to enable people with paralysis to control a robotic arm. Closed-loop neuroprosthetics move a step further, to encode neural signals such that the prosthetic arm transmits information back into the brain via neurostimulation, allowing users to feel what they are touching. This technology, which would have seemed like science fiction not many years ago, is already being tested in humans and has the potential to improve the lives of millions of people with paralysis [5]. Additional ongoing research is examining applications to other brain disorders, including precisely stimulating brain circuits to bring about memory restoration in patients with amnesia [6].

Embedding biomimetic brain models in neuroprosthetic systems has the potential to significantly improve their performance [7–9]. In our paradigm, biological brain circuits interact directly with biomimetic brain simulations, thereby employing biological mechanisms of co-adaptation and learning to achieve a functional task in a biological manner. Importantly, both networks employ neuronal electrical impulses or spikes to process information. This enables activity from the real brain to be seamlessly decoded by the model, and uses the simulated neural patterns to directly stimulate the brain. Potential applications of this approach are numerous, one of the most promising being the development of biomimetic brain-machine interfaces for people with paralysis. The biomimetic model can employ action selection signals from the patient’s brain to generate naturalistic motor signals that enable fine control of a prosthetic limb [7, 10, 11].

Similarly, the biomimetic model can be used to replace and/or rehabilitate a damaged brain region [12–15]. To achieve this, the biomimetic model can be connected to the remaining brain regions and tuned to reproduce healthy neural activity and stimulate the damaged region, restoring normal brain function.

Neuroprostheses based on biomimetic brain models are a clear example of a dynamic data-driven application system (DDDAS). They require simulation of a multiscale neural system in real time, while continuously learning and adapting the model parameters, based both on the neural activity from the real brain and on sensory feedback from the environment. We demonstrate here that combining the advantages of online biological learning methods [spike-timing dependent plasticity (STDP) and reinforcement learning] with those of an offline batch method (evolutionary algorithm optimization) can be an effective approach to building biomimetic neuroprostheses.

Biological learning and evolutionary optimization

The nervous system makes use of sensory information to rapidly produce behaviorally desirable movements, important for avoiding predators, finding shelter, and acquiring food. Primates use environmental sensory information to control arm movements to reach towards desirable targets.

Reinforcement learning via dopamine-modulated synaptic plasticity is one type of learning that is important in producing movements towards goals [16, 17]. Various studies of reinforcement learning-based motor learning have shown that the process begins with random exploratory movements that may be rewarded or punished via the dopamine neuromodulatory error signal [18]. A Hebbian or spike-timing dependent associated eligibility trace provides credit assignment [17, 19], determining which synaptic connections were responsible for the actions and should be strengthened or weakened. In primates, frontal areas, including primary motor cortex (M1), are innervated by dopaminergic projections from the ventral tegmental area (VTA). These projections have been shown to contribute to M1 plasticity [20], and to be necessary for motor skill learning but not for subsequent execution of the learned task [21].

These biological learning methods can be used in biomimetic neuroprosthetic systems to learn associations between real brain activity, a multiscale brain model, and environmental effectors, such as a prosthetic limb. The brain model synaptic connections could be adapted to map brain activity encoding the patient’s intentions to motor commands that drive the prosthetic limb. Reward signals recorded from the real brain could even provide the dopamine modulatory signals used to train the brain model via reinforcement learning [22, 23]. However, the reinforcement learning method itself also requires finding an optimal set of metaparameters that will maximize its efficiency. Examples of these metaparameters include the learning rate, the time window of eligibility traces, or the amplitude of the exploratory movements. Finding optimal solutions in such a complex multiscale system can be extremely time-consuming and inefficient if done manually.

One popular approach to optimizing complex multidimensional systems is the use of evolutionary algorithms, which use mechanisms inspired by biological evolution. Within the field of computational neuroscience, evolutionary algorithms have been predominantly applied to the tuning of single-cell models or small groups of neurons [24, 25]. Here, we use them for automated tuning of biological reinforcement learning metaparameters in large-scale spiking networks with behavioral outputs. A fitness function is used to measure the system’s performance associated with each set of metaparameters. This constitutes an example of using evolutionary optimization for indirect encoding, as opposed to direct encoding, since we are tuning metaparameters instead of directly tuning the network synaptic weights. Indirect encoding methods have the advantage of reducing the size of the search space, here from thousands of synaptic weights to a small set of metaparameters. In the present context, the use of indirect encoding was also motivated by our desire to use a biologically realistic learning rule.

Parallelization is usually required to make evolutionary algorithms a practicable solution to complex optimization problems. The advancement and proliferation of parallel computing architectures, such as high-performance computing (HPC) clusters and graphics processing units (GPUs), has provided a substrate for the implementation of parallelized evolutionary algorithms. Here, we parallelize an evolutionary algorithm to run in a large HPC cluster, significantly increasing the speed of the automated parameter tuning framework. We further reduce execution time by employing an island model implementation, a parallel computing technique that maximizes the efficiency of the HPC [26].

A similar version of this evolutionary optimization method was employed in our previous work [10], although a detailed description was not included. Here, we have improved the algorithm implementation by making use of an island model, and have applied it to a significantly more complex problem. Compared to [10], the current network contains 10 times more neurons, adds a spinal cord and modulatory input from real multielectrode recordings, and can learn to reach two targets instead of one.

In related work, a parallel evolutionary algorithm for spiking neural networks was implemented to execute on GPUs for two different scenarios: indirect encoding for a visual system model [27], and direct encoding for a sensorimotor system model [28]. Our methodology differs in that it is implemented on large HPCs instead of GPUs, employs island model techniques to increase efficiency, and uses indirect encoding for a brain model with reinforcement learning in the context of a neuroprosthetic system.

Motor system neuroprosthesis

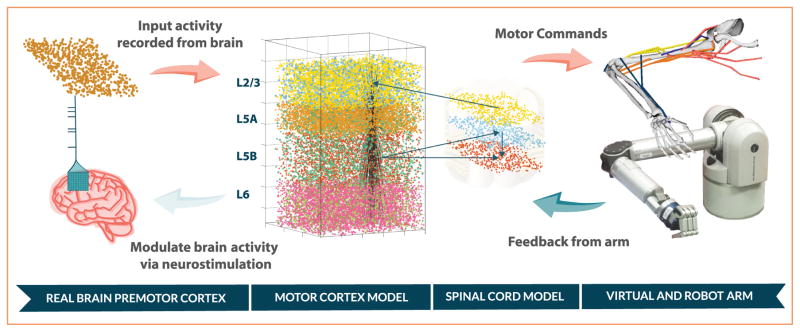
We evaluated the evolutionary optimization method using a biomimetic model of the motor system with over 8,000 spiking neurons and 500,000 synaptic connections (see Figure 1). The main component was a biologically realistic model of primary motor cortex (M1) microcircuits based on brain activity mapping [29–31]. This was connected to a spiking model of the spinal cord and a realistic virtual musculoskeletal arm. The arm model included anatomical and mechanical properties of bone, joint, muscle and tendon, as well as inertial dynamics of arm motion. Building on previous work [32, 33], we used reinforcement learning with STDP to adapt the motor system synaptic weights to drive the virtual arm to reach a target. Previously, we have shown that the virtual arm trajectories can be reproduced in real time by a robotic arm [10]. We therefore added the missing piece to obtain a neuroprosthetic system: we modulated the M1 network with activity recorded from macaque monkey premotor cortex [11]. These inputs acted as an action selection signal that dictated which target the virtual/robot arm had to reach. We have previously shown spiking activity from multielectrode recordings can be fed in real time to spiking network simulations [34]. In the future, the system could be extended to form a closed-loop neuroprostheses by neurostimulating the macaque monkey brain based on activity from the biomimetic network model.

Figure 1.

Overview of neuroprosthetic motor system model. Recordings from premotor cortex modulated the primary motor cortex (M1) to select the target to reach. M1 excited the descending spinal cord neurons that drove the arm muscles, and received arm proprioceptive feedback via the ascending spinal cord neurons. The virtual arm trajectory can be reproduced by a robotic arm in real time. To close the loop, neurostimulation could be fed back into the brain based on the motor cortex model activity. L2/3, L5A, L5B, and L6 refer to cortical layers.

Reinforcement learning was now responsible not only for learning appropriate motor and proprioceptive mappings between the M1, spinal cord and arm models, but also to associate premotor cortex spiking patterns to distinct reaching actions. This posed a significant challenge due to the complex multiscale dynamics, ranging from single neurons firing, to microcircuit oscillations, to musculoskeletal arm forces. The parallel evolutionary optimization method proposed managed to find reinforcement learning metaparameters that resulted in successful training of the system. The trained M1 network drove the arm to the target indicated by the recorded premotor cortex input. Arm trajectories and model neural activity were consistent with data from a similar experimental motor task [22].

The biological detail of our model is higher than that of previously published neural models that reproduce a similar reaching task: we implement a spiking neuron model with different synaptic receptors and many biological features, versus, for example, rate models [28]; we have cortical-based recurrent circuits with different cell types, versus more artificial task-oriented circuitries [7, 35, 36]; and we model anatomical and biophysical musculoskeletal arm properties, as opposed to simpler kinematic arm models [28, 35, 36]. Nonetheless, these models include regions that we do not explicitly implement, such as a population to encode reward information [35], posterior parietal cortex for sensory integration [28], or a cerebellum [36, 37].

The rationale for employing biologically detailed models is that it facilitates direct bidirectional interaction with the brain biological networks, including making use of synaptic plasticity at the single cell level to learn a specific behavior. We argue that for the model to respond in a biophysiologically realistic manner to ongoing dynamic inputs from the real brain, it needs to reproduce as closely as possible the structure and function of cortical cells and microcircuits.

This work demonstrates how to use parallel evolutionary algorithms to automate parameter tuning of reinforcement learning in multiscale brain models. This approach enabled translation of brain neural activity into realistic cortical spiking firing patterns that provided different motor commands to an external environment effector, thereby providing a useful tool to understand the sensorimotor cortex and develop neuroprosthetic systems.

In the remainder of this paper, we first describe the motor system model in more detail, as well as the biological learning methods and the evolutionary optimization approach. We then show the results of the optimization process, including the evolution of fitness over generations, as well as several performance measures of the optimized models. We end by discussing some implications of our work.

Methods

Motor system model

We implemented a model of the motor system with the following components: dorsal premotor cortex (PMd), primary motor cortex (M1), spinal cord, and musculoskeletal arm (Figure 1). PMd modulated M1 to select the target to reach, M1 excited the descending spinal cord neurons that drove the arm muscles, and received arm proprioceptive feedback (information about the arm position) via the ascending spinal cord neurons. Here, we describe each of the components in more detail.

The large-scale model of M1 consisted of 6,208 spiking Izhikevich model neurons [38] of four types: regular-firing and bursting pyramidal neurons, and fast-spiking and low-threshold-spiking interneurons. These were distributed across cortical layers 2/3, 5A, 5B, and 6, with cell properties, proportions, locations, connectivity, weights and delays drawn primarily from mammalian experimental data [30, 31], and described in detail in previous work [29]. The network included 486,491 connections, with synapses modeling properties of four different receptors: AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid), NMDA (N-Methyl-D- aspartic acid), GABAA (type A gamma-aminobutyric acid), and GABAB (type B gamma-aminobutyric acid). The model exhibits realistic physiological properties, including the distribution of firing rates and local field potential spectra.

PMd was modeled using a single population of 736 spike generators that reproduced activity recorded from the associated brain area of a macaque monkey during a reaching task. These were connected to M1 layer 5A cells via conductance-based synapses to provide the modulatory input used for target selection.

A simple model of spinal cord circuits was implemented using 1,536 regular spiking neurons, distributed into two descending populations and one ascending population. Corticospinal neurons in layer 5B were connected to excitatory and inhibitory descending spinal cord populations segregated into four muscle group subpopulations: flexor and extensor muscles of the shoulder and elbow. Regular-firing excitatory subpopulations modeled lower motoneurons by providing excitation to the corresponding muscles. Low-threshold spiking inhibitory subpopulations innervated the antagonist muscle motoneurons, modeling reciprocal inhibition and preventing antagonist muscles from contracting simultaneously. Proprioceptive feedback from the arm was encoded in an ascending spinal cord population, which then projected to M1 layer 2/3.

The virtual arm is a biomechanical model of human arm musculoskeletal system, constrained to two degrees of freedom in the horizontal plane. It includes 8 bones, 7 joints, and 14 muscle branches divided into four muscle groups: flexors and extensors of shoulder and elbow. Arm dynamics were calculated using an extended Hill-type muscle model [39], comprising two ordinary differential equations, which accounts for the force-length-velocity properties of muscle fibers and the elastic properties of tendons. The model takes as input an external muscle excitation signal, and calculates at each time step the overall muscle-tendon forces acting on bones. These forces then allow the arm model to obtain the position, velocity, and acceleration of each of the joints via a recursive Newton-Euler algorithm [40]. The model joint kinematics and dynamics were based on anatomical studies and match experimental measurements of an average-sized human adult male. A robotic arm can be made to follow the spiking network-driven virtual arm trajectories in real time. Although the robot arm was successfully tested with the current setup, the experiments in this study do not include the robot arm in the loop. More details on the virtual and robot arm implementations and their interface to the neuronal network can be found in our previous work [10].

Biological reinforcement learning

We modeled the brain’s dopamine-based reward circuits by providing a global reinforcement learning signal to modulate plasticity in the cortical neuronal network [41]. This signal was based on the state of the environment, which consisted of the virtual musculoskeletal arm and a fixed target in the 2D plane. The system can also be interpreted as an actor-critic reinforcement learning framework, where the neuronal network constitutes the actor, which maps sensory feedback to motor commands that alter the environment (control policy); and the reward system constitutes the critic (value function), which shapes the actor via plasticity to maximize its future rewards [35]. The aim was to learn a mapping between the M1 and spinal cord circuits that allowed driving the arm to a target, as well as a mapping between PMd and M1 that mediated target selection.

The reinforcement learning signal was calculated at short intervals (range 50 to 100 ms, optimized via the evolutionary algorithm) based on the distance between the virtual hand and the target. If the hand was getting closer to the target, then synapses involved in generating that movement were rewarded; if the hand was getting farther, those synapses were punished. To decide which synapses were responsible for the previous movement (credit-assignment problem), we employed spike timing-dependent plasticity and eligibility traces [19]. Eligibility traces are short-term memory mechanisms that record a temporal event, marking the synapse as eligible for undergoing learning changes. Synapses were tagged when a postsynaptic spike followed a presynaptic spike within the STDP time window. If a global modulatory signal was received within the eligibility time window, a trace was imprinted on tagged synapses, leading to an increase/long-term potentiation (for reward), or decrease/long-term depression (for punishment) of the weight [17]. Plasticity was present in the 158,114 excitatory synapses interconnecting M1 and spinal cord, PMd and M1, and M1 layers 2, 5A, and 5B.

We chose to reproduce the classical center-out reaching task, where subjects start with their hand at a center position, and need to reach to one of two targets placed 15 cm to the right or left [42–44]. During the training phase, exploratory movements of the arm were generated by randomly stimulating spinal cord subpopulations corresponding to different muscles. Exploratory behaviors facilitate learning linking a larger space of motor commands to its outcomes and associated rewards.

After training, input from PMd should modulate M1 activity and select which target the virtual arm will reach. To achieve this, activity from 96 PMd biological neurons of a macaque monkey was recorded during a center-out reaching task to left and right targets. PMd spike patterns were replicated using a model population of spike generators that provided input to the M1 L5A excitatory population. During training, the target to reach, rewarded via reinforcement learning, and the PMd input pattern were alternated every trial, in order to associate each PMd pattern to its corresponding target.

The testing or evaluation phase consisted of two 1-second trials with PMd input patterns corresponding to the left and right targets. This means the trained network needs to be able to generate two distinct spiking patterns, which move the virtual arm in opposite directions, depending on the input spiking pattern received from PMd. During testing, arm movements were enabled only after the network had reached a steady state (after 250 ms), to avoid the bursts of activity during the initial transitory period. The system’s performance was quantified by calculating the time-averaged pointwise distance between the arm’s endpoint trajectory and the target.

Parallel evolutionary optimization

The efficiency of the biological reinforcement learning method used to train the motor system is significantly affected by the choice of its metaparameters. Therefore, to maximize the system performance, we must optimize the learning metaparameters within the permitted biologically realistic range. Manually tuning these metaparameters can be a time-consuming and inefficient approach. Evolutionary algorithms provide an automated method to search for the set of parameters that maximize the system’s performance, quantified using a fitness function. Following the principles of biological evolution, a population of individuals, each representing a set of genes or parameters, evolves over generations until one of them reaches a desired fitness level. At every generation, individuals are evaluated and selected for reproduction, produce new offspring by crossing their genes and applying random mutations, and are replaced by the fitter offspring.

We employed evolutionary optimization to find reinforcement learning-related metaparameters that maximized the motor system performance. Importantly, we did not directly optimize the network synaptic weights (known as direct encoding), and instead we evolved the learning metaparameters of the model (indirect encoding). We optimized a total of 10 metaparameters within a range of values, such as the reinforcement learning interval or the amplitude of exploratory movements The range of values allowed for each metaparameter was based either on realistic biological constraints (e.g., the duration of the STDP or eligibility window), or on empirical observations derived from previous exploratory simulations (e.g., training duration or motor command threshold). See Table 1 for a list of metaparameters and their allowed range of values.

Table 1.

List of metaparameters optimized using the parallel evolutionary algorithm, including range and optimized value to obtain fitness of 0.619.

Description	Minimum (fitness using minimum)	Max (fitness using maximum)	Optimized value
STDP window duration (ms)	10 (0.557)	50 (0.581)	48.5
Eligibility trace window duration (ms)	50 (0.636)	150 (0.631)	117.8
Training phase duration (s)	30 (0.565)	180 (0.192)	85
RL learning rate	0.01 (0.619)	0.1 (0.444)	0.01
RL interval (ms)	50 (0.466)	100 (0.560)	76.8
Background rate (Hz)	50 (0.516)	150 (0.355)	134.5
Exploratory movements rate (Hz)	5 (0.619)	250 (0.426)	5
Motor command threshold (spikes)	500 (0.566)	2000 (0.531)	528.8
PMd to M1 probability of connection factor	1 (0.619)	8 (0.515)	1.0
Initial PMd to M1 weights	0.5 (0.508)	4 (0.433)	2.4

To evaluate each individual, that is, each set of metaparameters, we required a fitness function that quantified how well reinforcement learning worked using these metaparameters. Therefore, each evaluation consisted of training the network via reinforcement learning, and testing the reaching performance to the right and left targets using the different target selection PMd input patterns. The trained network had to generate spiking patterns that resulted in the virtual arm reaching towards the target indicated by the PMd input. The fitness function was calculated as follows:

$$\begin{gathered} d_{\text{avg}}=\left(\left(d_{\text{left}}+d_{\text{right}}\right)/2\right)-\mid d_{\text{left}}-d_{\text{right}}\mid \\ \mathit{fitness}=1-\left(\left(d_{\text{avg}}-d_{min}\right)/(d_{max}-d_{min})\right), \end{gathered}$$

where d_left and d_right represent the trajectory error, that is, the time-averaged distance between the arm’s endpoint and the left and right targets, respectively; d_avg represents the average trajectory error for both targets, and includes a term that penalizes differences between the two trajectory errors to reduce biases towards one of the targets; d_min represents the trajectory error for a best case scenario, reaching in straight line from the center to the target, starting after 250 ms and assuming a maximum speed of 1.0 ms⁻¹ and an acceleration of 5.0 ms⁻²; and d_max represents the trajectory error for a worst-case scenario, reaching to the opposite (wrong) target under the same conditions. Ergo, a fitness of 1 indicates a fast, straight line reach towards the correct targets, whereas a fitness of 0 indicates a fast straight line each towards the opposite targets. The evolutionary algorithm attempted to maximize the fitness of individuals, which resulted in minimizing the arm trajectory errors to both targets.

Each phase of the evolutionary algorithm has several parameters that affect, for example, how many individuals are selected for reproduction, the rate of mutation, or how individuals are replaced after each generation. We implemented a canonical evolution strategy technique [45] with a population of 60 individuals, default selection (i.e., all individuals are selected), “plus” replacement, and an internal adaptive mutation using strategy parameters. The “plus” replacement method means that only the fittest individuals will survive after each generation. In other words, out of 120 individuals (parents and offspring), only the 60 individuals with the highest fitness values will remain. Adaptive mutation means that a set of strategy parameters are used to determine the mutation rate of each gene or metaparameter i. The mutation rate is updated as follows:

$$p_i^{\prime }=p_i+N(0,{\sigma }_i),$$

where p_i represents the ith parameter, N(0; σ) represents the standard normal distribution of mean 0 and standard deviation σ, and σ_i is the standard deviation associated with the ith parameter. The strategy parameters are evolved along with the individuals using the following update equations:

$$\begin{gathered} {{\sigma }^{\prime }}_i={\sigma }_i+e^{\tau ·N(0,1)+{\tau }^{\prime }·N(0,1)} \\ {{\sigma }^{\prime }}_i=max\left({{\sigma }^{\prime }}_i,\epsilon \right), \end{gathered}$$

where the minimum allowed strategy parameter ε is 10⁻⁵; the learning parameters τ = 1/(2·n^1/2)^1/2 and τ′ = 1/(2·n)^1/2; and n is the number of parameters [45].

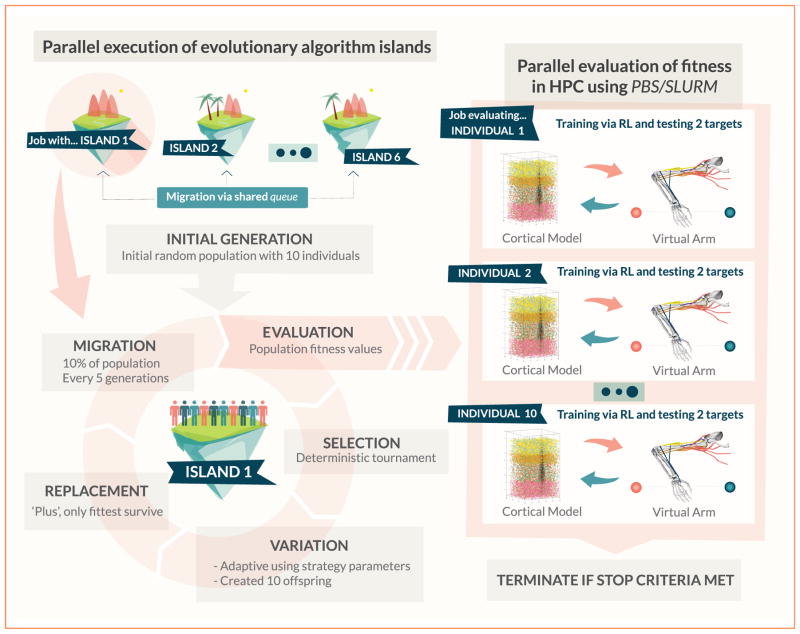
The parallel implementation of the evolutionary algorithm is illustrated in Figure 2. Obtaining an individual with a high fitness (optimized set of metaparameters) requires running the algorithm for many generations. However, each individual evaluation can take more than 1 hour if run serially (since the model must be trained and tested), making it an unfeasible option. Parallel computing techniques, such as GPUs, have been previously used to reduce execution time in similar problems [27]. Here, we employed an HPC cluster to execute the fitness evaluations in parallel, drastically reducing computation time. To implement the evolutionary algorithm we employed the open source Python library Inspyred (https://pypi.python.org/pypi/inspyred), and adapted it to exploit the parallel computation capabilities of the HPC. A custom Inspyred Evaluator function was defined to submit each function evaluation as a job to the HPC queue. Each fitness evaluation consisted of running a motor system simulation to train and test reaching to the two targets. The network model was parallelized [46] to run on 16 cores, and one additional core was used for the virtual musculoskeletal arm. The job scheduling system, Portable Batch System (PBS), together with the resource manager, Simple Linux^** Utility for Resource Management (SLURM), were then responsible for distributing the jobs across all computing nodes and returning the results to the master node. The Inspyred Evaluator function waited for all jobs to finish before submitting the fitness evaluations for the next generation.

Figure 2.

Parallel implementation of the island model evolutionary algorithm. A set of 6 islands is instantiated via multiprocessing parallel jobs, each with a population of 10 individuals that evolve independently. Information between islands is exchanged via migration of individuals implemented using a shared queue. Individuals are selected and mutated using internal adaptive strategy parameters to create new offspring. New individuals are evaluated to obtain their fitness values. Evaluation of fitness functions occurs in parallel in the HPC using PBS/SLURM, with each evaluation consisting of training the motor system model via reinforcement learning (RL), and testing its reaching performance to each of the targets. In every generation, the population is replaced by the fittest individuals out of all the parents and offspring.

Evolutionary algorithm parallelization typically results in a bottleneck effect, as moving onto the next generation requires waiting for the slowest individual to finish its fitness evaluation (synchronous master-slave mode). Given that one of the metaparameters evolved is the training time, the delay between the fastest and slowest fitness evaluation in populations of 60 individuals can be significant. A useful parallel computing technique to solve this problem is the use of island models. Under this paradigm, the population is divided into several subpopulations (islands), and each one evolves independently. This increases the overall diversity and allows efficient parallelization, given that each island can evolve asynchronously, waiting only for the slowest individual within its population. To add cooperation between islands, and thus regain the benefits a larger population size, migration between islands occurs periodically. Migration entails moving a set of randomly selected individuals to a temporary migration pool, and replacing them with different individuals from that pool [47].

Two parameters have a strong effect on the performance of island models: the migration interval (or number of generations between migrations) and the migration size (or the number of individuals migrated each time). Research has shown that island models with an appropriate balance between these parameters are not only more computationally efficient, but can improve the quality of solutions obtained [26]. This results from achieving higher diversity and exchanging enough information to combine the partial results from each island. A study suggests that best performance is achieved with moderate migration intervals (5 to 10 generations) and small migration sizes (5% to 10% of population size) [48]. Here, we chose to divide our single 60-individual population into 6 islands with 10 individuals each, with a migration interval of 5 generations and a migration size of 10%. The island model was implemented using Python’s multiprocessing library, where each island was run as separate job. Migration between islands was implemented via a custom Inspyred Migrator class, which employed a communication queue, shared by all jobs/islands, to exchange random individuals periodically.

The spiking network simulations were run in parallel using NEURON 7.4 [49] and Python 2.7, on the San Diego Supercomputer Center (SDSC) Comet HPC system with 2.5 GHz Intel Xeon^** E5-2680v3 processors. The code for the biomimetic neuroprosthetic system, including that used for the evolutionary optimization process, is open source and available via ModelDB (https://senselab.med.yale.edu/ModelDB/showModel.cshtml?model=194897).

Results

Fitness evolution

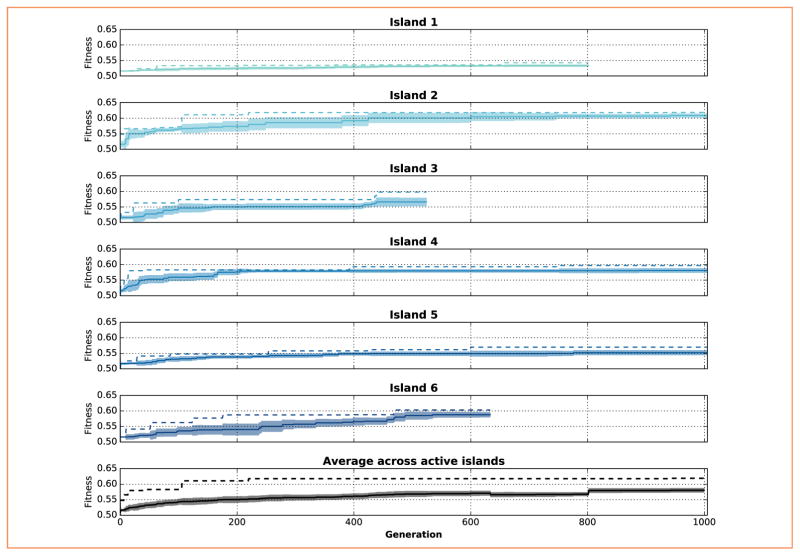
The evolutionary optimization algorithm increased the mean and best fitness values of the population over generations (Figure 3, black lines at bottom). Fitness values during the first generations exhibited a large variance (inappreciable/imperceptible in figure), which was rapidly reduced and kept approximately constant for the remaining generations. This is a consequence of the evolution strategy implemented, which only keeps the fittest individuals, and modifies them gradually in small search steps that result in small fitness changes. The best fitness value was 0.619, which was obtained by an individual of island 2 after 942 generations. To provide further intuition of the meaning of fitness values, consider that for reaching trajectories measured experimentally (see following section for details), the fitness value would be 0.6845. Also, if the arm remained at the center, the fitness value would be 0.508.

Figure 3.

Evolution of the average (solid lines, with shaded areas showing standard deviation) and best (dashed lines) fitness values over 1,000 generations, for each island (blue) and the entire population (black, at bottom). The width of shaded areas corresponds to the standard deviation of the fitness of individuals in each island. Each individual consists of a different set of metaparameters, which are evaluated using a fitness function that reflects the degree of accuracy of the resulting arm trajectory.

Both mean and best fitness values of the 6 island subpopulations (with 10 individuals each) also increased progressively over generations (Figure 3, blue lines). This monotonic increase was ensured by the “plus” replacement method, which only allows the fittest individuals to survive. Islands evolved asynchronously, therefore producing different numbers of generations within the same execution time. Although islands evolved independently, random migration occurred every 5 generations and increased the diversity of the islands by introducing an external individual. Therefore, although the highest fitness values were predominantly obtained by island 2; other islands could have had an effect via migration.

Parallelization of the evolutionary optimization process happened at three levels. First, each fitness evaluation consisting of a NEURON simulation to train and test the system was parallelized to use 16 cores. Second, the 10 fitness evaluations required by each island every new generation were also executed in parallel. Finally, the 6 islands were also executed as parallel processes. Every level of parallelization provided a speedup compared to the corresponding serial or sequential equivalent version (Table 2).

Table 2.

Speedup achieved by parallelization of the model and evolutionary optimization process for a population of 60 individuals (6 islands).

Description	Cores required (network + arm)	Time/generation (minutes)	Speedup
Purely sequential	1 + 1	2,945.2	1
Parallel simulation (sequential individuals + islands)	16 + 1	260.6	11.3
Parallel simulation + individuals (sequential islands)	160 + 10	44.9	11.3 × 5.8 = 65.6
Parallel simulation + individuals + islands	960 + 60	7.5	11.3 × 5.8 × 6.0 = 393.2
Parallel simulation + individuals (single population, no islands)	960 + 60	13.0	11.3 × 20.0 = 226.6

The speedup achieved by parallelizing each simulation on 16 cores was sublinear (11:3×), due to some fixed computational overhead to run and interface with the virtual arm, distribute cells across nodes and gather the spikes back. Parallelizing the execution of the 10 individuals per island also resulted in a sublinear speedup (5:8×), since advancing to the next generation required evaluating all individuals, which implies waiting for the slowest one. Finally, the speedup gained by parallelizing islands was linear (6:0×), since islands evolved independently—they can advance to the next generation once its 10 individuals have been evaluated, without depending on the stage of the remaining islands. In contrast, the single population approach (no islands) required the full population of 60 individuals to be evaluated each generation, leading to a strongly sublinear speedup—60 times more cores only achieved a speedup of 20:0×. The island model technique increased the speedup by a factor of 1.74. Overall, the island model technique together with parallelization of the model and the optimization process yielded a speedup of 393:2× over the single-core sequential approach (see Table 2).

Optimized model performance

The list of metaparameters optimized, the range of values explored for each, and the optimal set of values corresponding to the individual with the highest fitness, are shown in Table 1. To provide a better understanding of the effect of each metaparameter, Table 1 also includes the fitness of the system when the minimum or maximum value of each metaparameter was used (keeping the optimized values for the remaining metaparameters). Exploratory movements rate and training phase duration were the metaparameters with the highest sensitivity, whereas the system exhibited highest robustness to variations of eligibility trace window duration and STDP window duration. The optimized value of some metaparameters coincided with its lower bound value (RL learning rate, exploratory movements rate and PMd to M1 probability). This could indicate that fitness can be improved by increasing the range of values allowed for that metaparameter. However, it could also simply be a consequence of the stochastic nature of the evolutionary algorithm. Interestingly, fitness values improved slightly when using the minimum and maximum values of the eligibility trace window duration. This suggests that performing a standard parameter grid search after the evolutionary algorithm could be an effective method to further optimize the system’s performance.

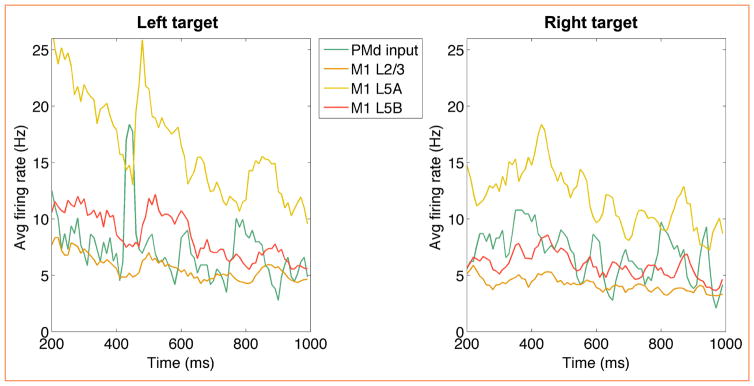
The optimized set of metaparameter values enabled the motor system model to learn the 2-target reaching task employing a biological reinforcement learning method. Premotor cortex (PMd) spiking activity, recorded from a macaque monkey during a reaching task, was used as a target selection input to the primary motor cortex (M1) model. After training, M1 populations produced different patterns of activity in response to the different PMd recorded spiking patterns for each target (Figure 4).

Figure 4.

Time-resolved average firing rates of the premotor and motor cortical populations during reaching to two targets. Premotor spiking activity was recorded from a macaque monkey, and is used as a target selection input to the primary motor cortex (M1) model. M1 population firing patterns are modulated by the PMd input and result in different reaching movement (see Table 3). The initial 200 ms of transient activity did not directly affect arm movements and are omitted.

We compared model results to macaque monkey experimental data, including arm trajectories and multielectrode array extracellular recordings of 110 neurons from M1 L5. The data corresponds to 10 trials of a center-out reaching task to right and left targets placed 4 cm away from the center. Arm trajectory errors were normalized by target distance to enable comparison between our motor system model and the experimental task. More details on the recording procedures and experimental task can be found in [22].

The average firing rate during reaching of layer 5 excitatory neurons for the 10 fittest models (14:0 Hz ± 4:5 Hz) was similar to that measured experimentally (19:3 Hz ± 1:4 Hz). The distribution of firing rates across cells also exhibited similar statistics for the top 10 models (median = 20:5 Hz ± 6:0 Hz and interquartile range = 26:2 ± 8:9 Hz) and experiment (median = 16:0 ± 1:4 Hz and interquartile range = 17:3 ± 1:9 Hz).

When the model learning metaparameters corresponded to individuals with the highest fitness values, the arm trajectory errors were closer to those measured experimentally (Table 3). Note that fitness takes into account the trajectory error to both targets. Table 3 also includes the model solutions that achieve the lowest trajectory error for a given target, but these show high trajectory errors to the alternative target. These results further illustrate the complexity of finding networks capable of generating good reaching trajectories to both targets.

Table 3.

Comparison of normalized arm trajectory error for experimental data vs. the best and worst model solutions (average and standard deviation).

Target	Experiment (10 trials)	Best 10 models (both targets)	Best 10 models (left target)	Best 10 models (right target)	Worst 10 models (both targets)	Worst 10 models (left target)	Worst 10 models (right target)
Right	0.63 ± 0.09	0.85 ± 0.02	1.14 ± 0.09	0.66 ± 0.01	1.08 ± 0.02	0.72 ± 0.04	1.26 ± 0.03
Left	0.73 ± 0.10	0.85 ± 0.02	0.69 ± 0.02	1.21 ± 0.08	1.08 ± 0.02	1.59 ± 0.03	0.80 ± 0.10

Conclusion

Our research lays the groundwork for a new generation of neuroprosthetic systems, where biological brain circuits interact directly with biomimetic cortical models, and employ co-adaptation and learning to accomplish a functional task. Such a multiscale approach, ranging from the cellular to the behavioral level, will furthermore provide deeper insights into brain dynamics and have applications for the diagnosis and restoration of brain disorders.

We have reproduced experimental data of a center-out reaching task using a biomimetic model of the sensorimotor system and a virtual musculoskeletal arm. To achieve this we have combined a biological reinforcement learning rule, used to adapt the synaptic weights of a cortical spiking network model during training, with an evolutionary algorithm to automatically tune the metaparameters of the system. By evolving a set of indirect parameters or metaparameters, instead of the direct network parameters (i.e., the synaptic weights), we were able to employ a biologically realistic sensorimotor learning approach, namely, dopamine neuromodulation of STDP. Previously, we had performed manual metaparameter tuning of similar models [32, 33]. However, the increased complexity of the virtual arm, which included many realistic biomechanical properties—and the more challenging dynamics of the detailed cortical model, spinal cord, and premotor cortex target selection inputs—required more sophisticated methods. We demonstrate the potential of parallel evolutionary algorithms in providing a solution to the problem of automated parameter optimization in biomimetic multiscale neural systems. The solutions found by our fitting algorithm yielded virtual arm trajectories and firing rates comparable to those measured experimentally.

The parallel implementation of the evolutionary algorithm over a large HPC cluster was achieved by combining the flexibility of a Python-based optimization package (Inspyred), with the HPC job scheduling software. Multiple fitness functions (up to 60) were evaluated concurrently, where each function consisted of running a NEURON simulation, which in turn executed, and interacted with, an instance of the musculoskeletal arm model, developed in C++. This demonstrates the modularity and adaptability of the parallel optimization framework, and suggests it could be useful for a diverse range of models, including those developed in different languages. Furthermore, our evolutionary algorithm implementation made use of an island model technique, whereby the population is subdivided into smaller groups that evolve independently and periodically exchange information via migration. This method significantly reduced the execution time and increased the HPC CPU usage, by eliminating the bottleneck caused by the slowest individuals in large populations.

Parallel evolutionary algorithms constitute an effective tool for automated parameter optimization in complex multiscale systems, such as those linking neural and behavioral models. These kinds of tools are likely to become indispensable in the development of hybrid co-adapting systems where in silico biomimetic brain models interact with real brains and prosthetic devices [13]. We previously showed that spikes from multielectrode recordings in macaque monkeys can be fed in real-time into a biomimetic model [34]. In this work, we extend this to show how spiking data recorded from macaque premotor cortex can be used to modulate a primary motor cortex (M1) model to select a desired target for reaching. This approach may enable the development of more advanced control of robotic limbs [10, 50], and have clinical applications by employing electrical or optogenetic stimulation neural control methods [12, 14, 51] to restore normal function in damaged brains [52, 53].

Biographies

Salvador Dura-Bernal Neurosim Lab, SUNY Downstate Medical Center, Brooklyn, NY 11203 USA (salvadordura@gmail.com). Dr. Dura-Bernal is a Research Assistant Professor in the Physiology and Pharmacology Department at SUNY Downstate Medical Center. He completed his B.Sc. and M.Sc. degrees in telecommunication engineering in Spain and received his Ph.D. degree in computational neuroscience (2011) from the University of Plymouth, United Kingdom. He then worked as a Postdoctoral Researcher for the University of Plymouth and Johns Hopkins University, developing biologically inspired, hierarchical models of auditory processing, and multimodal integration. In 2012, Dr. Dura-Bernal joined the Neurosim Lab at SUNY Downstate as a Postdoctoral Researcher for the Defense Advanced Research Projects Agency (DARPA) REPAIR project, aimed at replacing damaged brain motor regions with biomimetic neuroprosthetic systems. He currently works on a National Institutes of Health grant, developing a detailed multiscale model of primary motor cortex. Dr. Dura-Bernal also teaches computational neuroscience at the NYU Tandon School of Engineering as an Adjunct Professor. He is author or coauthor of 18 peer-reviewed journal papers or book chapters as well as 22 conference proceedings. He is a member of the Society for Neuroscience and the Organization for Computational Neurosciences.

Samuel A. Neymotin Brown University, Providence, RI 02912 USA (samuel_neymotin@brown.edu). Dr. Neymotin is Assistant Research Professor in Neuroscience at Brown University. He received a B.S. degree in computer science from Queens College in 2001, an M.S. degree in computer science from Columbia University in 2005, and a Ph.D. degree in biomedical engineering from SUNY Downstate/NYU-Poly in 2012. He subsequently joined Yale University as a Postdoctoral Associate in neurobiology. Afterwards, he joined SUNY Downstate Medical Center as Research Assistant Professor (2013). In 2017, he joined Brown where his research focuses on computational neuroscience and analysis of neural data. In 2012, he received the Robert F. Furchgott Award for Excellence in Research. He is an author on 32 peer-reviewed papers and 6 book chapters/review articles. Dr. Neymotin is a member of the Society for Neuroscience and the Organization for Computational Neurosciences.

Cliff C. Kerr Complex Systems Group, School of Physics, University of Sydney, Sydney, NSW 2006, Australia (cliff@thekerrlab.com). Dr. Kerr is an Australian Research Council (ARC) Discovery Early Career Research Award (DECRA) Fellow, focusing on investigating the interplay between small-scale and large-scale dynamics in biomimetic spiking network models of the brain. In addition to neuroscience, he works on human immunodeficiency virus epidemic modeling and big data analytics. He has authored 30 scientific papers and 4 book chapters. He is a member of the Organization for Computational Neuroscience.

Subhashini Sivagnanam Data Enabled Scientific Computing Division, San Diego Supercomputer Center, University of California, San Diego, La Jolla, CA 92093 USA (sivagnan@sdsc.edu). Ms. Sivagnanam is a computational and data science research specialist at the San Diego Supercomputer Center. She received a B.E. degree in electronics and communication from University of Madras, Chennai, India, in 2001, and an M.S. degree in computer engineering from North Carolina State University in 2004. She joined the San Diego Supercomputer Center in 2005 and has been working on web-based science platforms and high-performance computing applications and systems. She is author or coauthor of 16 papers and conference proceedings. She is a member of the Organization for Computational Neuroscience.

Amit Majumdar Data Enabled Scientific Computing Division and Department of Radiation Medicine and Applied Sciences, University of California, San Diego, La Jolla, CA 92093 USA (majumdar@sdsc.edu). Dr. Majumdar is the Director of the Data Enabled Scientific Computing Division at the San Diego Supercomputer Center and a faculty member at the Department of Radiation Medicine and Applied Sciences. He received his B.S. degree in electronics and telecommunication from Jadavpur University, Calcutta, India, in 1985, M.S. degree in nuclear engineering from Idaho State University in 1988, and Ph.D. degree in nuclear engineering and scientific computing from the University of Michigan in 1996. After working at the Ford Research Laboratory for one year, he subsequently joined the San Diego Supercomputer Center, working on high-performance computing and cyberinfrastructure software. Since 2009, he has been a faculty member in the Department of Radiation Medicine and Applied Sciences. He is author or coauthor of 50 papers and conference proceedings. He is a member of the Organization for Computational Neuroscience, the Institute of Electrical and Electronics Engineer, the Society for Industrial and Applied Science, and the American Physical Society.

Joseph T. Francis Cullan College of Engineering, University of Houston, Houston, TX 77004 USA (joey199us@gmail.com). Dr. Francis is an Associate Professor of the Cullen College of Engineering at The University of Houston. He graduated from the honors program in biology at SUNY Buffalo in 1994. Subsequently, he studied neural dynamics with an emphasis on non-linear dynamical systems theory applied to the nervous system, as well as ephaptic interactions, for which he obtained his Ph.D. degree in 2000 at The George Washington University in Washington, D.C. He had two postdoctoral fellowships; the first was in computational sensorimotor control and learning under the guidance of Reza Shadmehr at Johns Hopkins University. He then started researching brain-machine interfaces with John Chapin at SUNY Downstate, where he later obtained a faculty position. In 2015, he was appointed Associate Professor at The University of Houston, where he continues his work on brain-machine interfaces. He is author or coauthor of more than 60 publications. He is a member the Society for Neuroscience, the American Physiological Society, and the Institute of Electrical and Electronics Engineers.

William W. Lytton Neurosim Lab, SUNY Downstate Medical Center, Brooklyn, NY 11203 USA (billl@neurosim.downstate.edu). Dr. Lytton is a practicing Neurologist caring for the indigent at Kings County Hospital, and he is Professor of physiology and pharmacology at Downstate Medical Center. Dr. Lytton is an M.D., trained at Harvard, Columbia, Alabama, Johns Hopkins, UCSD, and Salk Institute. He is the author of From Computer to Brain, a basic introduction to computational neuroscience. His research is concerned with multiscale modeling, at scales from molecule to brain to assist in understanding of brain diseases including epilepsy, stroke, and schizophrenia, with a focus on using modeling for clinical translation from bench to bedside. He is author or coauthor of more than 80 publications. He is a member the Society for Neuroscience and the Organization for Computational Neurosciences.