Graph Theoretic Analysis of Resting State fMRI

Abstract

Graph theoretic analyses applied to examine the brain at rest have played a critical role in clarifying the foundations of the brain’s intrinsic and task-related activity. There are many opportunities for clinical scientists to describe and predict dysfunction using a network perspective. This primer describes the theoretical basis and practical application of graph theoretic analysis to resting state functional magnetic resonance imaging data. Major practices, concepts, and findings are concisely reviewed. The theoretical and practical frontiers are highlighted with observations about major avenues for opportunity in theoretical development and clinical translation.

Introduction

Given its complexity [1], the brain is perhaps the quintessential example of a network. Neural elements are interconnected by a large number of connections that can be studied across several orders of spatio-temporal magnitude. We are apt to seek a framework that can help us describe and understand brain organization, dynamics, and cognitive-behavioral phenomena. From the perspective of network science[2], the brain is a special case of a larger space of natural and possible networks [3]. The mathematical basis in which we can represent and study networks is graph theory, which provides fundamental mathematical knowledge and a generalizable basis in which to study networks.

In human brain networks, we can apply graph theoretic analysis to anatomical or functional networks at multiple scales to study the connectome [4]. An essential tool in our effort to understand functional brain networks is functional magnetic resonance imaging (BOLD fMRI), which allows us to indirectly study neural activity using the hemodynamic relationship between blood flow and neural firing in the brain [5]. BOLD fMRI is often used to examine contrasts between different cognitive conditions to examine changes in functional signal amplitudes and connectivity associated with behavior. In addition, and the focus of the current review, it can be used to understand the intrinsic [6] organization of functional brain networks to study the brain at rest [7] and its relationship with cognition and behavior.

To say that a living brain is ever at “rest” is incorrect; indeed, brains persistently bustle with complex neural and metabolic activity. “Resting state” fMRI (rsfMRI) is broadly used to refer to data acquired when subjects are instructed to look at a crosshair fixation or engage in no task in particular while in the scanner [7]. In contrast to studies that involve tightly controlled experimental paradigms, rsfMRI studies involve data that represent any number of cognitive-emotional mental activities that participants may engage in while at rest. Indeed, rsfMRI is used to investigate processes such as mind-wandering [8], introspection [9], and imaginative thought [10]. For these reasons, it has been suggested that less leading terminology such as “intrinsic connectivity” may be preferable in referring to “resting state” data [11]. Broadly, we can examine properties of network organization observable within rsfMRI to identify correlates of other cognitive variables and markers of dysfunction. While care should be applied when interpreting rsfMRI connectomes, we know that rsfMRI networks and network statistics are overall reliable enough to afford robust analysis of connectomic organization to examine major systems [12, 13]. Here, I review major approaches to and findings from graph theoretic analysis of rsfMRI data.

Data collection and preprocessing

Data collection for rsfMRI typically involves asking subjects to lie in the scanner with eyes open, closed, or fixated on a target in the center of participants’ visual field over several minutes of fMRI data acquisition [14] (see “Not all rsfMRI is equal”, below). “Preprocessing” techniques to ensure that data meet several assumptions prior to analysis. The most standard steps to preprocessing rsfMRI data include slice timing correction [15], motion correction ([16, 17]), realignment [18], coregistration of anatomical and functional images [19], spatial normalization [20], and smoothing [21]. Smoothing increases signal to noise, normalizing error distributions, and accomodates anatomical and functional variation between subjects. In addition, global signal regression (GSR), which refers to the statistical removal of the average signal across all voxels in the brain, is a contentious issue in rsfMRI analysis [22, 23]. On the one hand, GSR can increase the detection of localized neural signals and improve functional connectivity analysis specificity [24, 25]. On the other, GSR introduces negative correlations mean-centered around zero and may exclude important neural signatures [26, 22, 27, 28]. Finally, rsfMRI time series are often examined after applying a bandpass filter to BOLD data to reduce influences of nonphysiological and physiological nuisance signals (often between 0.01 Hz to 0.1 Hz or similar). Because no model can perfectly separate physiological nuisance variables from neurally-related signals, we must be cautious in our selection of GSR and bandpassing preprocessing techniques and appropriately discuss the limitations of each selection in empirical work. Readers are encouraged to consult primary sources for in depth empirical analysis and discussion of preprocessing issues.

Graph theoretic analysis of rsfMRI data

Once data are obtained and preprocessed, any number of techniques can be applied to examine the organization of rsfMRI data. The primary conceptual distinction between graph theoretic analysis of rsfMRI and other approaches is that the former directly links rsfMRI to much broader efforts with deep mathematical foundations in graph theory. This allows us to share concepts and language with investigators interested in other types of networks and encourages the potential for innovative crosstalk. In this section, I provide basic intuition for major ideas in graph theory analysis for rsfMRI data and findings from applied analysis.

Graphs in rsfMRI analysis

Graph theoretic analysis is a specific approach to analyzing brain networks in which the brain network is represented in the mathematical “graph”. A graph G is composed of N nodes (or vertices) and E edges (region-region relationships). The graph G can be encoded in an adjacency matrix, A, whose (i,j)^th element represents the weight of the edge between node i and node j. The edges of a graph can be binary (including only 0’s and 1’s) or weighted (including a range of other values). Graphs can be undirected, where the association between regions is bidirectional, or directed, where the association between regions may vary across directions. In rsfMRI analysis, the elements of the adjacency matrix A most often include full correlation coefficients representing the strength of functional communication between two regions. The elements can alternatively include covariance, partial correlation, coherence, and mutualized information shared between pairs of brain regions.

To construct A, one must define the nodes between which edges are calculated. This is typically achieved by selecting a parcellation of rsfMRI data voxels into coarse-grained units called parcels, which reduces the number of nodes in the system for simplicity, statistical economy, and computational efficiency. Several notable parcellations are available defined by functionally [29, 30, 12] or anatomically validated features. The proliferation of and continued interest in developing parcellations highlights the fact that there is no “perfect” parcellation established to date. Indeed, each parcellation relies on statistical optimization or anatomically-based boundary definitions paired with our intuitions about what matters in brain organization. It is essential to note that the absolute value of statistics in rsfMRI network analysis vary depending on the parcellation [31]. Thus, caution should be used in inter-parcellation comparisons and we should be well aware of the nature of the parcellation we select and rationale for selecting it.

Once the adjacency matrix is defined, we can apply a rich range of concepts and tools from graph theory to examine brain networks (See Fig. 1). In the following sections, I introduce commonly applied network statistics across scales of network organization. The reader is also referred to other excellent reviews concerning graph theoretic analysis in general [32] and specific to brain networks [33, 34].

Figure 1. Schematic flow for graph theoretic analysis of rsfMRI data.

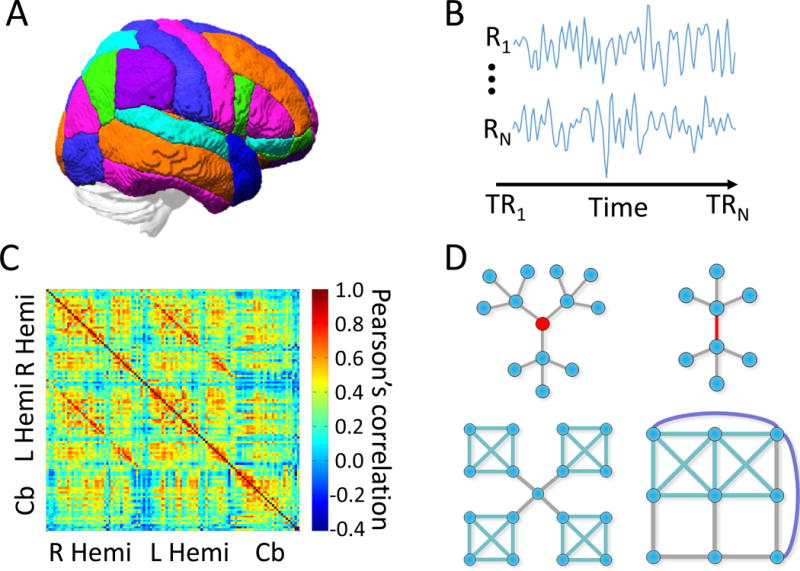
(A) Nodes are established with a parcellation representing distinct parts of the brain. (B) After preprocessing, time series of BOLD measurements from nodes (regions) R₁ to R_N are extracted along time for time points TR₁ to TR_N. Then (C) then adjacency matrix A can be constructed to represent measures of connectivity such as the Pearson’s correlation coefficient. Finally (D) we can compute measures representing the role of nodes and edges, community organization, and global characteristics of the A matrix.

Micro, meso, and macroscale network analysis

One of the advantages of applying a graph theoretic perspective is that it gives the ability to study intermediate and high levels of organization across the network as a whole. This is a fundamental distinction between rsfMRI and other approaches to functional brain network analysis: by allowing us to examine higher level statistics, we can identify properties of networks that are not evident in any particular node or edge and potentially what cognitive-behavioral processes they may support. The scales of network analysis can coarsely be separated into micro, meso, and macroscale, representing the configuration of the elements of the network, their modular configuration, and the overall topology of the network as a whole, respectively.

Microscale

The micro scale refers to the organization of nodes and edges in the network. In rsfMRI data, each node statistic emphasizes complementary information about brain region roles in the functional connectome. One major notion in networks is that hubs serve central roles in network organization and information processing. To represent this, hub coefficients [35, 36] constructed from measures of node centrality have been used to quantify nodes’ connectedness in the network (degree or strength in weighted networks; see 2), involvement in short paths across the network (betweenness centrality), connectedness with local neighbors (clustering coefficient or local efficiency), connectedness to important nodes in the network (eigenvector centrality), and interactions with multiple communities in the functional network (participation coefficient). Each of these statistics emphasizes a distinct aspect of nodes’ varying roles in organizing information procecssing across the brain. In rsfMRI data, we can examine variation in node centrality across the brain and distinct groups to identify characteristic roles for nodes.

Perhaps the simplest measure of node centrality is degree. In binary networks, degree is defined as the number of edges connected to a node. In weighted networks, the weighted degree (or strength) is the sum of edge weights connected to a node. Nodes of high degree or strength centrality are thought to be particularly influential on the network’s function. In rsfMRI networks, nodes with high degree are referred to as network hubs, and are thought to be critical for general information transmission and circuit-level computing [37, 38].

Other centrality statistics capture a node’s role in network organization beyond node-to-node connections. Commonly used examples include betweenness centrality, closeness centrality, and eigenvector centrality. Betweenness centrality quantifies the extent to which a node participates in shortest paths throughout the network. A shortest path is the path between node i and node j that traverses the fewest (or in weighted networks the fewest high-weight) edges. Nodes with high betweenness centrality are thought to be particularly influential across different efficient pathways of the network as a whole rather than just local direct connections. Closeness centrality quantifies the average shortest path between a given node and all other nodes in the graph. As a result, closeness centrality is used as a measure of a node’s ability to communicate quite broadly to every node in the network. Eigenvector centrality uses the eigenspectrum of the adjacency matrix to quantify the influence of a node based on its connectedness with other high-scoring nodes in a network (See Fig. 3). This statistic recursively captures the importance of a node: nodes that are connected to important nodes will rank higher in eigenvector centrality. Because each of these statistics putatively identify highly central nodes, nodes that score high on these statistics are sometimes referred to as hubs given their theoretical role in network function [39].

Figure 3. Example microscale statistics.

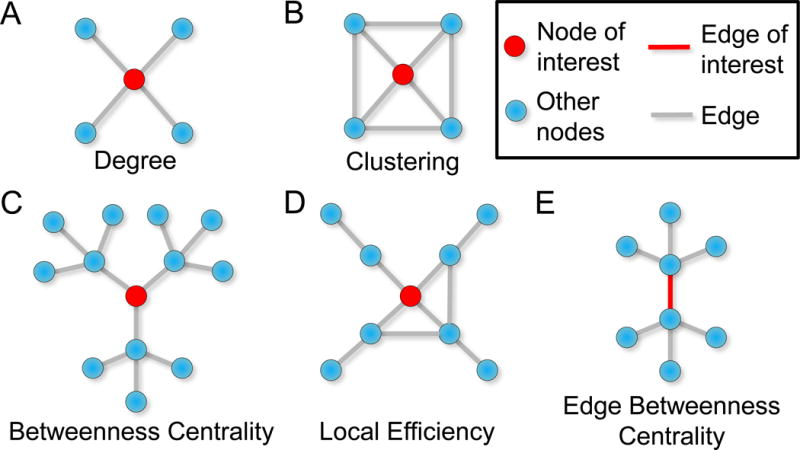
The red node in each image denotes the node of interest. (A) A node’s degree is the number of edges emanating from a node. (B) The node has a high clustering coefficient because the node’s neighbors are also connected to each other. (C) The red node has high betweenness centrality because it participates in many paths. In this case, the red node also has high eigenvector centrality because it is connected three other nodes with high importance in the network. (D) In this illustration, the local efficiency for the node of interest is low because few connections exist among the immediate neighbors of the node of interest. (E) The red edge has high betweenness centrality because of its position along a high number of paths across the network.

Some node statistics are designed to capture the role of nearby neighbors in the neighborhood (one step in topological distance) around the node. The clustering coefficient, which describes how close its nearest neighbors are to being a completely connected subgraph or clique). One specific example is the local clustering coefficient, which can be defined as the number of triangles in the network containing a node, divided by the number of connected triples containing that same node [40]. With this definition, the local clustering coefficient gives the density of local connections involving a given node and is often used to probe the node’s ability to participate in local information integration. A complementary notion is that of node “efficiency”, which assesses the connectedness of the edges among neighbors of a given node, thus offering a notion of the network’s local robustness to a node’s removal [41].

In addition to quantifying features of a node and its role in the network, one might also be interested in quantifying features of an edge. Perhaps the simplest statistic for an edge is its weight, which provides information about the strength of the relationship between two nodes. Moving beyond pairwise information, one can also compute something like the edge betweenness centrality, which measures the number of shortest paths between all possible pairs of nodes that pass through the edge of interest. Similar to the betweenness centrality of a node, the betweenness centrality of an edge is thought to represent its importance in efficient information transfer in networks. These are just a couple of examples of useful statistics for edges that can help one to understand the role of a node-node relationship in the broader network.

Mesoscale

Mesoscale organization refers to the arrangement of nodes into modules or communities. Mesoscale structure is that which is not easily characterized at either the local (node and edge) or global (entire network) scales. Networks may exhibit varying degrees and qualities of modular structure – also known as community organization – which refers to high within- and low between- module connectivity. A network exhibits a varying degree of modularity that can be quantified as the extent to which nodes exhibit non-trivial community organization relative to network null models [42].

A contrasting mesoscale organization in networks is core-periphery structure, which refers to the tendency for a network to have a core of densely interconnected nodes surrounded by a periphery of nodes that connect to the core but not to one another. Put differently, an extreme of thiswould be a single large module with more sparsely connected individual nodes attached to the module. More modular networks theoretically maintain a balance of information integration within and segregation between modules, while core-periphery structure can offer relatively more centralized processing [43].

In natural networks, mesoscale networks can exhibit community organization in which individual modules have mixtures of characteristic modular, core-periphery, or assortative organization. An assortative network is one in which like-degree nodes tend to connect to one another, and a disassortative network is one in which unlike-degree nodes tend to connect to one another. In some networks, assortativity can be a marker of robustness: the removal of one high-degree node can be overcome by the interconnectedness of the others [44, 45]. Promising techniques such as stochastic block models [46] allow us to identify the organization of network communities along these organizational subtypes and describe their potential diversity of network function.

Macroscale

Another key notion in graph theory is that networks can be represented holistically, potentially described with single scalar values representing a property of the network. This is a form of emergent feature of a system that is not represented in any particular part. To represent this, global statistics are important to characterize overarching network organizational principles. Perhaps the simplest statistic is a network’s density: the number of existing edges relative to the number of possible edges. Many natural networks exhibit low density because edges are costly [47]. Relatedly, one often studied characteristic of a network is the shape of its degree (or strength) distribution. Long-tailed degree distributions indicate that unexpectedly large hubs exist. As within individual modules, it is often interesting to ask whether these hubs preferentially connect to one another across the entire network, forming a basis for macroscale assortativity analysis [44].

In addition, we can examine whether a network is scale-free, which means that a network has a degree distribution that follows a power law [48]. Scale-free networks can emerge from theoretical mechanisms including preferential attachment [49] and node fitness [50], or rules that copy a fraction of links to existent nodes [51]. Regardless of the mechanism of generation, scale-free networks are notable because they represent relatively economical architectures for information transmission [47]. They are also robust against random damage but especially vulnerable to targeted attack to high-degree nodes [52]. Many natural networks demonstrate approximately scale-free degree distributions [53] that are characterized by power laws over some regimes of their degree distribution [54].

Another way to describe macroscale organization is to average the values of nodal statistics. For example, a network’s global clustering coefficient is equal to the average clustering coefficient of that network’s nodes. High global clustering in a network indicates that nodes tend to be highly connected across all possible cliques larger than two nodes. The characteristic path length refers to the average shortest path between all pairs of nodes in the network. A short characteristic path length is thought to represent the potential for high integration across the network [55]. Global efficiency is a notion that is complementary to the characteristic path length, and can be calculated as the inverse of the harmonic mean of the shortest paths in the network [41, 56]. A network with a smaller characteristic path length has a higher global efficiency, indicating a theoretical ability to communicate quickly across the network as a whole [57].

A composite statistic representing a network’s tendency to exhibit higher than expected clustering and shorter than expected path lengths is famously known as small-worldness [55]. Small-world network organization theoretically supports a balance of local segregated information processing in modules in conjunction with long distance integrating processing across modules. Many small-world networks are also scale-free [58]. One problem with calling a network “small-world” is that all networks fall on a continuum of this property and it is not often robustly defined in network analysis [59]. Because small-worldness is a continuous property that is defined by the clustering and path length in networks, it is important to interpret the contribution of both of these statistics to the small-worldness of the system. A statistically rigorous definition of small-worldness for weighted networks is small world propensity, which has been validated but not yet widely applied in brain network analysis [59].

If one is interested in studying not just the shortest path but also longer paths or walks through the network, then one might examine a generalization of network communicability [60]. Communicability describes all shortest paths as well as all walks – steps along the network including revisitations to nodes and edges – connecting two nodes. This accounts for the possibility that communication can occur in a network involving both the shortest path as well as longer and indirect paths across the network. This property may be interesting as a complement to other measures associated with network resilience. For example, nodes and networks with increased communicability may exhibit more robustness to the loss of specific edges because multiple pathways for communication exist across the nodes.

One feature of global network organization is the minimum spanning tree (MST), which is a subset of edges in a connected, weighted, undirected graph that connects all nodes together without any cycles and the minimum possible total edge weight [61]. Thus, the MST of a graph represents the least total cost architecture associating all nodes to one another with no redundancy. The size and configuration of a graph’s MST can be analyzed to identify efficient organization in network topology and its temporal and cross-sectional variation.

In practical network analysis, it is important to note that raw measures of global network organization are heavily influenced by the network’s density (or total node strength), and it is therefore important to normalize or statistically control for graph density (strength) prior to making statistical inferences across networks or in relation to extrinsic variables such as clinical status or cognition in the context of rsfMRI analysis. This allows us to examine the unique contributions of network topology above and beyond simple network density.

Major findings in rsfMRI graph theoretic analysis

Graph theoretic analysis has been applied broadly in rsfMRI in healthy and clinical populations to examine intrinsic network organization and how variations in intrinsic graph properties relate to cognition and clinical syndromes. From these studies, it is known that (1) not all rsfMRI is created equal (2) that human rsfMRI networks exhibit a complex organization that supports cognitive activity and (3) is altered in clinical populations.

Not all rsfMRI is equal

As alluded to previously, “resting state” fMRI is a misnomer given that the brain is a persistently active system with a rich cognitive repertoire. Neurophysiologically, the link between neural field potentials and BOLD is greater in eyes closed relative to open conditions in animal models, suggesting that visual and attention-related cognitive demands modulate hemodynamic coupling [26, 62]. In addition, important differences in connectivity can be observed across eyes closed, eyes open, and fixation cross rsfMRI collection designs. In eyes closed conditions, connectivity within the auditory network is higher than the other conditions. Connectivity within default-mode, attention, and auditory networks are more reliable when eyes are fixated on a cross. In an eyes open condition without a fixation cross, visual network connectivity is most reliable [14]. This highlights the fact that while rsfMRI data are thought to be relatively “task-free”, differences in how the rsfMRI paradigm is administered are associated with different network configurations, presumably as a function of differences in cognitive processing demands across the conditions. In addition, not all rsfMRI represents waking brain activity: as much as 30% of rsfMRI data may be acquired during transient or sustained periods of sleep in the scanner [14]. While eyes open and especially fixation cross designs reduce the incidence of sleep, it is an important potential confound to all rsfMRI analysis [14]. Thus, we should consider using fixation paradigms to help reduce the incidence of sleep in the scanner. We can also use technologies such as eye tracking, self report, and machine learning procedures to identify potential sleep in the scanner [14].

Human brain organization maintains a complex balance between randomness, small worldness, and modularity

In healthy humans, some major findings have resulted from rsfMRI network analysis. At a high level of organization, it is clear that healthy human brain networks exhibit economical sparse connectivity [47] and maintain a balance along extremes on dimensions of order, degree diversity, and heirarchy [47, 63]. Relatively high order is reflected by the high clustering and modularity of brain networks, but the presence of some randomness is reflected in short path lengths that connect modules [55, 64]. rsfMRI networks exhibit truncated power law distributions [31], demonstrating the presence of scale-free organization through some of the network’s regime with a pronounced “rich-club” of hubs that are highly connected to one another [65]. Hubs are variably defined in the literature, but are typically characterized by an unexpectedly high number of connections given all connections observed in the entire network, within specific modules, and/or between modules [36], and are thought to play key roles in regulating information processing across the network [36]. Interestingly, step-wise functional connectivity analyses in rsfMRI data corroborate the view that the brain is organized hierarchically, involving connections spreading from regions in primary and secondary sensorimotor regions to multimodal integration regions and finally converging on cognitive hubs in the cortex. This suggests that classically defined neuropsychological functions across these regions are represented in a low-cost hierarchy that privileges dense communication between cognitive control and default mode regions and the rest of the brain.

Resting state networks form a stable organization supporting cognitive function within and between individuals

rsfMRI studies demonstrate a rich mesoscale organization involving reliably detectable intrinsic networks that can be observed during rest [29] (See Fig. 7). These are often thought to represent systems with distinct cognitive roles, including fronto-parietal and cingulo-opercular control networks, dorsal and ventral attention networks, a salience network, a default mode network, primary somato-motor systems, and subcortical systems. The cognitive relevance of these networks is suggested by the fact that they co-activate as units during distinct cognitive tasks [68]. Notably, connections between the fronto-parietal control and other networks reconfigure most prominently across tasks, most notably in the left dorsolateral prefrontal cortex [68]. In addition, functional connections across the brain robustly predict cognitive activations among these systems during various tasks, suggesting that these systems form basic building blocks in high-level cognitive organization [69]. Interestingly, patterns of connectivity can be used to accurately identify individuals and intersubject variability in intelligence from rsfMRI data connectivity “fingerprints” [70], demonstrating a high information content in the brain’s intrinsic profile.

Figure 7. Intrinsic brain networks.

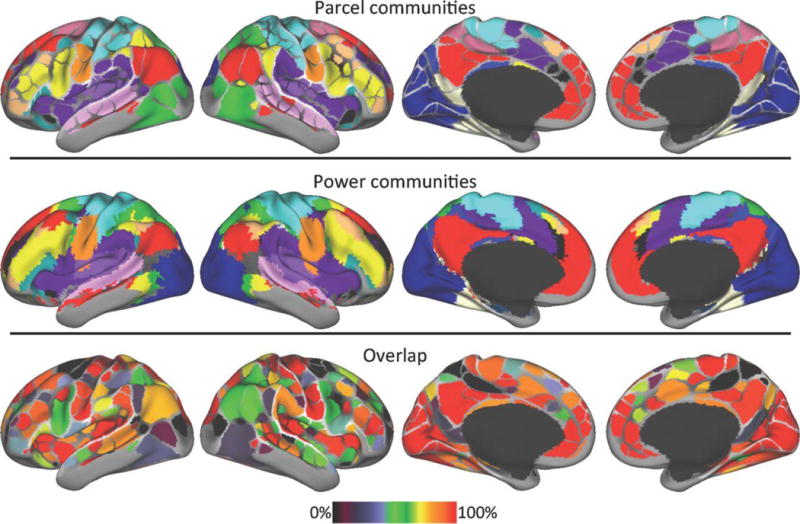
The network organization of intrinsic fMRI networks forms a mesoscale organization replicated in two studies. Top: Colors represent different communities identified with an “Infomap” community detection procedure using the boundary map-derived parcels as network nodes and an independent sample for cross-validation [12]. Middle: Colors represent different communities calculated using every voxel as a network node [29]. Bottom: spatial overlap of the two community assignments demonstrate that systems demonstrate variable but generally high overlap.

From Gordon EM, Laumann TO, Adeyemo B, Huckins JF, Kelley WM, Petersen SE. Generation and evaluation of a cortical area parcellation from resting-state correlations. Cerebral cortex. 2014;p. bhu239.

Resting state network graph characteristics are altered in numerous clinical populations

While major networks and organization can be identified in healthy rsfMRI analyses, we can also examine whether graph theoretic analysis contribute to our characterization and understanding of clinical syndromes. A major review is outside the focus of this primer, and the reader is encouraged to consult several excellent reviews concerning graph theoretic analysis in neurological and psychiatric syndromes [71, 63, 72, 73, 74]. So far, early studies span a wide range of syndromes with developmental, psychiatric, and neurological mechanisms of origin. Findings indicate that rsfMRI analysis can indeed identify altered network topology in clinical syndromes over the lifespan. Emerging findings from rsfMRI analysis suggest that psychiatric and neurological disorders across the lifespan are associated with altered intrinsic network organization. Across syndromes, disruptions in hub node activity are frequently identified, with common disruptions in cognitive control and default mode systems but notable differences in specific nodes across disorders [63, 73]. Network efficiency is often disrupted via alterations of path length and mesoscale community organization [73, 47]. Cognitively, general conscious activity may be supported by segregated information processing facilitated by specific functional hub organization [75, 76], and global cognitive function may depend on key long distance connections [77, 78, 79] and “connector” hubs that communicate between systems [80]. Emotionally, disrupted connectivity involving subcortical and frontal are associated with mood and anxiety syndromes and symptom profiles [81, 82]. While the number of studies for any specific disorder remains limited, it appears clear that rsfMRI can contribute a network-level perspective to characterize features associated with clinical diseases and disorders.

Open frontiers in rsfMRI analysis

With the increase in rsfMRI analysis and its early promise in identifying correlates of clinical syndromes and symptoms, it is useful to clarify important theoretical frontiers and opportunities. We can potentially make great strides by studying the neural basis of rsfMRI graph organization, its theoretical contributions to cognitive and clinical neuroscience, its clinical utility, and integration with other techniques.

What does rsfMRI graph organization represent?

It is prudent to reflect on the nature of rsfMRI data to evaluate its epistemological value. Because rsfMRI analysis is based on the BOLD signal, there are fundamental limits to its neural interpretation from the micro- to macroscale. rsfMRI data are thought to represent high and low frequency local field potentials [26]. Beyond hemodynamic responses, how can we understand the specific network configurations we observe in healthy brains? The fact that rsfMRI topology represents major cognitive systems may have a basis in environmental influences over development. There is evidence that rsfMRI network organization is a result of experience-dependent plasticity in humans following co-activation between brain regions [83]. This feature appears to persist in mature brain networks, where a relatively simple connectivity model of activity flow among brain regions predicts network-level activation [69]. Combined with observations about the neurovascular coupling that drives widespread rsfMRI activity, it is speculatively possible that intrinsic network organization is truly a robust marker of gross neurocognitive organization within and between individuals. This may be why cognitive variability can be associated with intrinsic network activity. However, we must still be wary about drawing inferences about any specific cognitive activity during any particular scanning session.

One prevailing limitation in many studies is that BOLD-based graph edges are demonstrably low-dimensional when computed along entire time series and thus very limited in their ability to represent brain interactions [84]. However, time-varying graph [85] and trial-wise analysis [86] are promising open areas that may add new dimensions of information to potentially link clinical nosology to brain network dynamics (See Fig. 8). As these efforts develop, it will remain critical to pair rsfMRI analysis with good experimental designs, genetic and environmental analyses, and replication and cross-validation studies.

Figure 8. Dynamic Network Analysis.

(A) The BOLD fMRI signal displays region-specific variability. (B) Windowing time series and estimating the functional connectivity (FC) between pairs of regions reveals dynamic FC matrices. Each edge describes the statistical relationship (strength of connectivity) between two brain regions. The organization of FC matrices changes over time. (C) Dynamic FC matrices can be used as input to community detection algorithms to generate estimates of the network’s modular structure at each time point. Modules, in this case, refer to collections of mutually-correlated brain regions that, as a group, are weakly correlated with the rest of the network. We can characterize the dynamics of community structure both in terms of individual brain regions and at the level of the whole network with the measure flexibility. Network flexibility indicates the extent to which brain regions change their community affiliation over time.

Adapted from Mattar MG, Betzel RF, Bassett DS. The flexible brain. Brain. 2016;139(8):2110–2112.

The unique theoretical value of graph theory rsfMRI analysis is at present unknown. Do the quantities afforded to us represent something cognitively meaningful in principle? Can they provide us theoretical or predictive information we otherwise would not see? It is clear that we can continue to study brain organization and dysfunction without using graph theory. It is also possible, as it commonly done, to rely heavily on reverse inference [87, 88] to interpret the graph statistics we observe and previously known ideas from cognitive neuroscience. To identify specific value of graph theory, we should search for consilience between graph theoretic analysis and other neuroscientific approaches [89].

Optimism for clinical identification, prediction, and translation

Nevertheless, cautiously optimistic view of rsfMRI for some clinical purposes is justified if we maintain several priorities. The features that distinguish useful clinical research include problem base, context placement, information gain, pragmatism, patient centeredness, value for money, feasibility, and transparency [90]. Many studies do not satisfy these features and fail to provide value because of their design. It has been suggested that a major reform could address the forces that drive this problem, and the reader is strongly encouraged to consult one particularly incisive perspective [90]. As it stands, careful hypothesis testing for specific clinical end-goals should increase in general [90].

Toward applied clinical utility, rsfMRI graph statistics analyzed can be combined with machine learning to build models that identify autism [91], Alzheimer’s disease [92, 93], schizophrenia [94] depression [95], relative to controls, in some cases with very high sensitivity and specificity. In general, the opportunities to apply machine learning to any type of neuroimaging data or derived measure are enormous and can provide novel observations [96]. The challenge in rsfMRI analysis is that in order to have clinical value, these approaches must be valid and replicable, portable to clinical environments, and either equally accurate to but cheaper than existing techniques, or demonstrably more accurate.

Integrated multimodal strategies offer potential value for treatment. For example, rsfMRI connectivity has been evaluated to guide or predict outcomes in neurosurgical approaches in brain injury [97], brain tumors [98], and epilepsy [99], and deep brain stimulation [100]. In addition, the effects of noninvasive brain stimulation have been linked to the connectivity profiles of intrinsic networks across many diseases. Specifically, suppressive transcranial magnetic stimulation (TMS) is effective if the site of stimulation is positively connected with the target, whereas facilitative TMS is effective in the opposite case [101]. Importantly, rsfMRI graph theoretic analyses have not been systematically linked to brain stimulation approaches to provide either neurocognitive criteria (e.g., target brain network states for stimulation) or surgical or brain stimulation targeting methods. This is substantial potential for development on this front. It is possible that computer simulation models that use simplifications of neural dynamics in anatomical networks to predict rsfMRI connectivity [102, 103, 104] and the effects of stimulation [105] may contribute to this effort.

Conclusion

Graph theoretic analyses in rsfMRI are becoming a significant tool for describing the human brain and characterizing clinical syndromes. It is becoming clear that clinical syndromes are marked by dysfunction in major brain networks and distinct hubs in intrinsic functional connectivity patterns. The specific contributions of rsfMRI to clinical nosology and translation will likely be understood with the benefits of hindsight. At present, our challenge is to embrace opportunities to robustly characterize network dysfunction and search for a meaningful framework to connect rsfMRI network analysis to clinical practice.

Figure 2. Notions of hubs in networks.

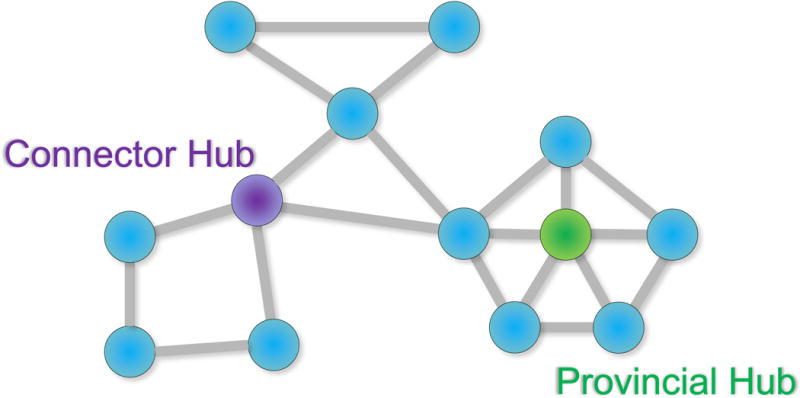
Provincial hubs are high-degree nodes that primarily connect to nodes in the same module. This provincial hub is also a hub of high degree overall because it has a high number of connections relative to other nodes in the network and contributes to many paths through the network. Connector hubs are high-degree nodes that show a diverse connectivity profile by connecting to several different modules within the network (see also [36]).

Figure 4. Example mesoscale statistics.

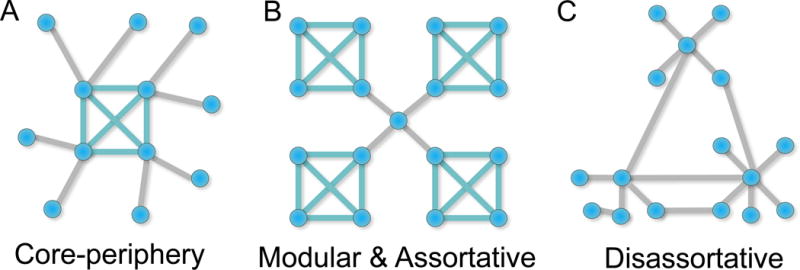
(A) A core-periphery organization involves a low number of primary modules (here marked by a single module of nodes sharing teal edges) and a number of sparsely connected peripheral nodes. (B) In contrast, a modular organization involves a few modules connected by a few intermediating nodes. In this example there is a single node that serves as a so-called “connector hub” between the modules. This network is also assortative because the highly connected nodes tend to connect to one another. (C) A disassorative network does not exhibit a high degree of connectivity among like nodes, and tends to be non-modular

Figure 5. Example macroscale statistics.

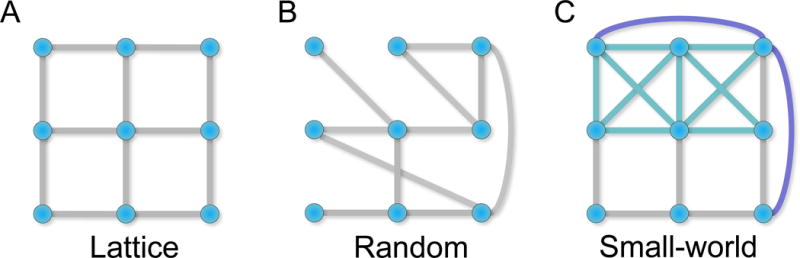
(A) A lattice network is a regular network that has an example of high clustering but a relatively long path length. (B) A random network tends to lack distinct modular organization but has short path lengths due to random connections across the network. (C) A small-world network has both clustering and short path lengths due to the presence of clusters and long distance connections.

Figure 6. Hubs and heirarchy in rsfMRI data.

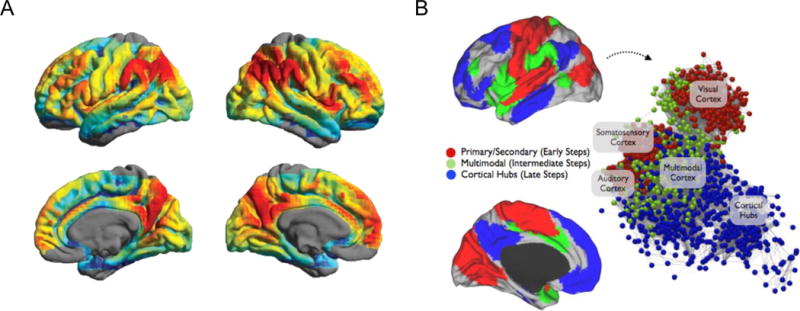
(A) rsfMRI studies report hubs with high density of functional connectivity in the precuneus/posterior cingulate cortex, lateral inferior parietal cortex, medial orbitofrontal cortex, and medial superior frontal cortex. (B) Step-wise functional connectivity analyses reveal a heirarchical progression of edges from primary motor and secondary sensorimotor regions to multimodal regions and finally hubs in the cortex. (A) Adapted from Zuo XN, Ehmke R, Mennes M, Imperati D, Castellanos FX, Sporns O, et al. Network centrality in the human functional connectome. Cerebral cortex. 2012;22(8):1862–1875. (B) Adapted from Sepulcre J. Stepwise Connectivity of the Modal Cortex Reveals the Multimodal Organization of the Human Brain. Journal of Neuroscience. 2012;32:10649–10661

KEY POINTS.

• -Graph theory is the mathematical basis of network science and is now widely applied to study rsfMRI networks
• -Several major themes have emerged in applied rsfMRI graph theoretic analysis
• -rsfMRI graph theoretic analysis has revealed several key principles of healthy and dysfunctional brain network organization
• -Open frontiers in rsfMRI graph theoretic analysis include evaluating the contributions of graph theory and potential for direct clinical applications

SYNOPSIS.

Graph theoretic analyses applied to examine the brain at rest have played a critical role in clarifying the foundations of the brain's intrinsic and task-related activity. There are many opportunities for clinical scientists to describe and predict dysfunction using a network perspective. This primer describes the theoretical basis and practical application of graph theoretic analysis to resting state functional magnetic resonance imaging data. Major practices, concepts, and findings are concisely reviewed. The theoretical and practical frontiers are highlighted with observations about major avenues for opportunity in theoretical development and clinical translation.