Altered tuning in primary motor cortex does not account for behavioral adaptation during force field learning

Abstract

Although primary motor cortex (M1) is intimately involved in the dynamics of limb movement, its inputs may be more closely related to higher order aspects of movement and multi-modal sensory feedback. Motor learning is thought to result from the adaption of internal models that compute transformations between these representations. While the psychophysics of motor learning has been studied in many experiments, the particular role of M1 in the process remains the subject of debate. Studies of learning-related changes in the spatial tuning of M1 neurons have yielded conflicting results. To resolve the discrepancies, we recorded from M1 during curl field adaptation in a reaching task. Our results suggest that aside from the addition of the load itself, the relation of M1 to movement dynamics remains unchanged as monkeys adapt behaviorally. Accordingly, we implemented a musculoskeletal model to generate synthetic neural activity having a fixed dynamical relation to movement and showed that these simulated neurons reproduced the observed behavior of the recorded M1 neurons. The stable representation of movement dynamics in M1 suggests that behavioral changes are mediated through progressively altered recruitment of M1 neurons, while the output effect of those neurons remain largely unchanged.

Introduction

Despite the complexity of the limb's dynamics, we make precise reaching movements with smooth hand kinematics, long thought to suggest that we plan reaches in a hand-centered reference frame (Morasso 1981; Flash and Hogan 1985). More recently, models based on optimal feedback control have been proposed that do not require explicit trajectory planning and transformation (Todorov 2004; Scott 2012). In either case, control signals must ultimately be expressed in the intrinsic, musculoskeletal coordinates of motor execution. Both approaches posit the use of internal models of the limb (Wolpert et al. 1995), whether to transform a desired kinematic trajectory into kinetic commands (Kalaska and Crammond 1992; Shadmehr and Mussa-Ivaldi 1994), or for optimal state estimation (Shimansky et al. 2004; Todorov 2004; Scott 2012). These internal models are learned during development, but it is also possible to modify them on a shorter time scale, for example, when using a heavy tool that requires altered forces to produce a given movement.

The psychophysics of this short-term motor adaptation process have been studied by using Coriolis forces to perturb reaches made in a rotating room (Lackner and Dizio 1994) and by perturbing reaches with forces imposed by a robotic manipulandum (Shadmehr and Mussa-Ivaldi 1994). Over time, subjects learn to alter their patterns of muscle activity to compensate for these external forces and restore normal kinematic trajectories. When normal movement dynamics are restored, the transient appearance of behavioral “aftereffects”, expressed as oppositely directed errors during re-adaptation to normal movement dynamics, is taken as evidence of internal model adaptation.

The pattern of generalization found in the experiments described above suggests that the learned internal model represents the dynamics of movement in terms of intrinsic coordinates of the limb (Shadmehr and Mussa-Ivaldi 1994). Given the considerable evidence that primary motor cortex (M1) encodes low-level details of motor execution (Evarts 1968; Fetz et al. 1986; Kalaska et al. 1989; Scott and Kalaska 1997; Morrow and Miller 2003; Sergio et al. 2005), it is reasonable to expect that this short-term adaptive process could be implemented by neurons in M1. Experimental evidence for the short-term adaptation of internal models within M1 comes from several studies of altered neural tuning as monkeys adapted to a curl-field (CF) perturbation (Gandolfo et al. 2000; Li et al. 2001; Richardson et al. 2012). These studies compared the spatial tuning properties of individual M1 neurons before, during, and after CF adaptation. They reported that a subset of M1 neurons (called “Dynamic” cells) changed their tuning in response to the altered dynamics. Intriguingly, they also found a number of cells whose change in tuning persisted even when the CF was removed, together with a second, complementary group of cells that had no initial change, but changed subsequently when the CF was removed. These “memory cells”, were thought to be evidence of the modification of internal models within M1 during CF adaptation. A follow-up study found no evidence of memory cells, with neural tuning changes simply mimicking the behavior of muscles (Cherian et al. 2013), although differences in task design between the studies made it difficult to compare the differing results directly.

The goal of the present study was to resolve the discrepancies between these studies and characterize the behavior of neurons in M1 prior to, in the presence of, and following a curl force field. Imposing the curl field led to apparent tuning changes in M1 that occurred as early as we were able to test, which were consistent with the altered dynamics of movement and directly proportional to the magnitude of the applied perturbation. Furthermore, simulated neurons with fixed dynamical relationships generated from a simple musculoskeletal model reproduced the critical features observed in the recorded units. These new results suggest that M1 neurons do not exhibit short-term learning-related changes reminiscent of internal model adaptation, but instead have a largely unchanging relation to the dynamics of movement that must have been formed over longer, perhaps developmental periods of time. Short-term behavioral adaptation thus appears to occur at a hierarchical level above the inputs to these cells, likely involving upstream areas that provide input to M1.

Methods

Behavioral Task

Two monkeys (male, macaca mulatta) were seated in a primate chair and grasped the handle of a 2-D planar manipulandum that controlled a computer cursor on a screen in a standard center-out (CO) task (Figure 1a). A trial began when the monkey moved to the center target. After a hold period of 500-1500 ms, a 2cm target was randomly displayed in one of eight regularly spaced outer positions at a radial distance of 8 cm, followed by a variable delay period of 500-1500 ms before an auditory go cue (Figure 1b). Monkey C was initially trained without the instructed delay (which had been used in the prior studies), and the first six curl field sessions with this monkey omitted it. As we were interested in the movement-related activity of M1 it is unlikely that the lack of a delay impacted our conclusions, though to ensure that there were not differences we later collected an additional seven sessions from Monkey C with the delay. The monkeys were required to reach to the target within one second and hold for 500 ms to receive a liquid reward.

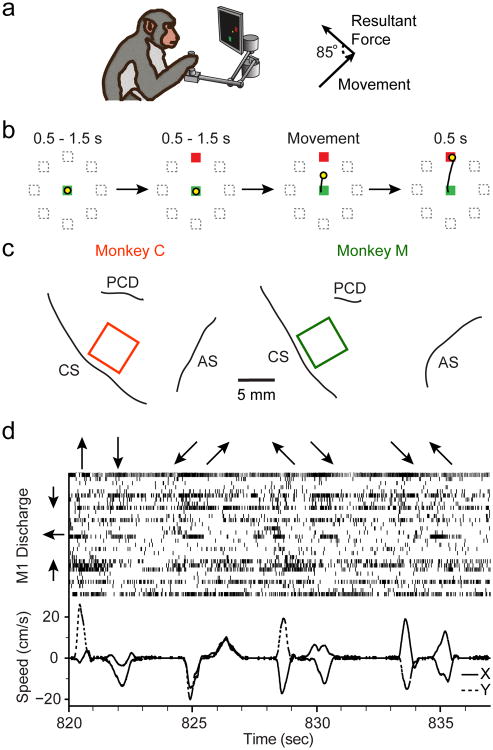
Fig 1. Behavioral tasks and neural recordings.

a) Macaque monkeys were seated in a chair and controlled a cursor on a computer screen using a 2-D planar manipulandum that covered a 20cm × 20cm workspace (top left). During the Adaptation epoch, the monkeys made reaches in a velocity-dependent force field applied to the endpoint of the hand, approximately orthogonal to its direction of motion (top right). b) The center-out task required that the monkey reach from the center of the workspace to one of eight outer targets (see Methods). c) We implanted electrode arrays, indicated by the squares, in the arm region of M1 of two monkeys. CS: Central Sulcus; AS: Arcuate Sulcus; PCD: Pre-central Dimple. d) Upper panel shows normalized neural spike rasters for 30 single units recorded simultaneously from Monkey M during a series of reaches. The arrows along the top illustrate the direction of each reach. The units have been sorted by their PDs, indicated approximately by the arrows to the left of the panel. The bottom panel illustrates X (solid) and Y (dashed) components of hand velocity.

Each experimental session had three task epochs: a short Baseline epoch in which the monkey made unperturbed movements, a longer Adaptation epoch when the monkey adapted to reaching movements made with the curl field, and a Washout epoch when the CF was removed and the monkey readapted to normal movement dynamics. During CF trials, motors in the manipulandum applied forces at the endpoint proportional to the velocity of the hand according to Equation 1.

$$\overrightarrow{F}=\left[\begin{array}{c}{F}_x\\ F_y\end{array}\right]=k\left[\begin{array}{cc}cos{\theta }_c& -sin{\theta }_c\\ sin{\theta }_c& cos{\theta }_c\end{array}\right]\left[\begin{array}{c}{\dot{p}}_x\\ {\dot{p}}_y\end{array}\right]$$ (1)

where F is the applied force, ṗ is hand velocity, and k is a constant (0.15 N•s/cm). The forces were exerted at a direction θ_c of 85° relative to the direction of hand movement to avoid instabilities that occurred when the force was applied at 90°. The CF was enabled for the duration of the Adaptation epoch including the return movement and intervals between trials.

Both monkeys required several experimental sessions to learn to tolerate the perturbation, initially completing only a small number of reaches in a given curl field session. Data analysis began with the first session in which a given monkey completed at least 25 reaches to each target during adaptation and had sufficient time in Washout for deadaptation. The data used for analysis began with the third and seventh interaction with the curl field for Monkey C and Monkey M, respectively. The experimental sessions reported here were typically not consecutive, but instead, had intervening sessions with adaptation to visual rotation. Consequently, we focus here on within-session learning, since the experiments were not designed to investigate long-term savings. The monkeys also performed a small set of control sessions of similar duration to the force field sessions, but with no applied force field. In these sessions, all other task parameters were identical to the curl field sessions. These control sessions allowed us to ascertain the baseline variability in our analyses in order to better understand the effect of the force field.

Implantation of Microelectrode Arrays

We implanted 100-electrode arrays with 1.5mm shaft length (Blackrock Microsystems, Salt Lake City) in the arm area of M1 of two monkeys. We placed the monkeys under isoflurane anesthesia and opened a craniotomy above the motor cortex. M1 was localized using visual landmarks and the arm area was identified using bipolar cortical surface stimulation to evoke twitches of proximal muscles. The arrays were then inserted pneumatically. Figure 1c shows array implant locations for the two monkeys and neighboring cortical surface landmarks, based on photographs taken intraoperatively.

Analysis of Behavioral Adaptation

We computed the “takeoff angle” error between one vector drawn from the position of the hand at the start of movement to the position of the hand at the time of peak speed, and a second vector pointing from the hand directly to the target. This metric was designed to focus on the ballistic phase of movement and ignored force-induced error corrections later in the reach.

Neural Data Acquisition

Neural data were amplified, band-pass filtered (250 to 5000 Hz) and digitized using a Cerebus system (Blackrock Microsystems, Salt Lake City, UT). We identified threshold crossings of 5.5 times the root-mean square (RMS) amplitude of the signal on each of the channels and recorded spike times and brief waveform snippets. Additionally, we recorded kinematic data from the robot handle and endpoint force data using a 6-axis strain gauge in the handle to measure the net forces acting on the hand. After each session, we used Offline Sorter (Plexon, Inc, Dallas, TX) to sort all the waveforms that crossed a detection threshold. Importantly, we sorted the waveforms for all three epochs together, to ensure that we did not inadvertently introduce sorting differences. Since we sought to study well-isolated neurons, they were included only if they had a waveform signal to noise ratio greater than three (calculated as the average waveform peak-to-peak value divided by two times the standard deviation of the waveform shapes). We ensured that each single unit was reliably held throughout the session by comparing the spikes from each epoch using a statistical test that incorporated the waveform shapes and inter-spike interval distribution (Tolias et al. 2007), an approach also used by a previous study in our lab (Rebesco et al. 2010). We excluded units with an average firing rate during movements <5 Hz to achieve adequate model fits.

Neural Tuning Analysis

For each unit, we fit directional tuning curves relating the firing rate (f) to the direction of movement kinematics (θ) (Georgopoulos et al. 1982) according to Equation 2.

$$f=f_m+\mathit{\text{DOT}}cos(\theta -PD)$$ (2)

where f_m is the mean firing rate across directions, DOT represents the depth of tuning, and PD represents the preferred direction. We grouped movements into 45-degree bins according to their mean directions, and fit the model to the average firing rates in the eight bins.

We obtained confidence bounds for the PD estimate using a bootstrapping procedure with 1000 iterations. We excluded from analysis, poorly-tuned units whose bootstrapped PD confidence bounds exceeded ±20 degrees and whose lower 95% confidence bound for R² was below 0.5. In practice, this yielded results similar to a requirement of mean R² ≥ 0.7, but ensured that every bootstrap fit used for the PD confidence interval was of acceptable quality.

The typical method for determining PDs uses target-based tuning, where the average neural activity throughout the movement is regressed to the target direction. We compared this target-centric tuning to similar tuning computed in a hand movement coordinate frame, relating average neural firing rate to the actual direction of hand motion. We selected a window of time beginning with the onset of movement (as determined by a velocity threshold crossing of 1.5 cm/s) until the time of peak speed. This window was chosen to focus on the ballistic, planned aspects of reach and to avoid the later error correction phases of movement, particularly in the Adaptation epoch. To compensate for typical neuronal transmission delays, we shifted neural activity forward by 100 ms to better align with the kinematics.

Neural Tuning Comparison

We tested for changes in PD estimates for each single unit during the Baseline, Adaptation, and Washout epochs. We determined the significance of PD changes by computing confidence bounds on the differences between the 1000 reference Baseline PD estimates obtained with the previously described bootstrapping procedure, and the 1000 bootstrapped PD estimates in each tested epoch. A change was considered significant if the 95% confidence bounds of the differences did not include zero.

We classified cells into five categories based on their tuning behavior in the three epochs (Li et al. 2001). “Kinematic” cells had no change in PD. “Dynamic” cells had a significant change from Baseline PD during Adaptation but returned to Baseline tuning in the Washout. As in prior studies, we also defined two types of “Memory” cells. Type I had a change in PD during Adaptation that persisted in the Washout, while Type II changed only between Adaptation and Washout. A final class, termed “Other”, had different tuning in all three epochs. To further characterize the behavior of these cells, we computed a “Memory cell” index, shown in Equation 3, to determine if Other cells more closely resembled Dynamic or Memory cells (Cherian et al., 2013).

$$\mathit{\text{Mem Ind}}=\frac{|P{D}_{WO}-P{D}_{BL}|}{\mathit{min}[|P{D}_{AD}-P{D}_{BL}|,|P{D}_{AD}-P{D}_{WO}|]}$$ (3)

Values greater than 1.0 indicated that the PD in Washout was closer to its value in Adaptation than in Baseline, and thus the cells were more like Memory cells, while values less than 1.0 were more like Dynamic cells.

Musculoskeletal model

We implemented a simple musculoskeletal arm model in order to generate simulated neurons with known relationships to behavior. The monkey's limb was modeled as a two-link planar manipulator fixed at the shoulder (Figure 7a). For each session of behavioral data, we used the real hand position and inverse kinematics to compute the joint angles (θ_e and θ_s) for the model system according to Equations 4 and 5.

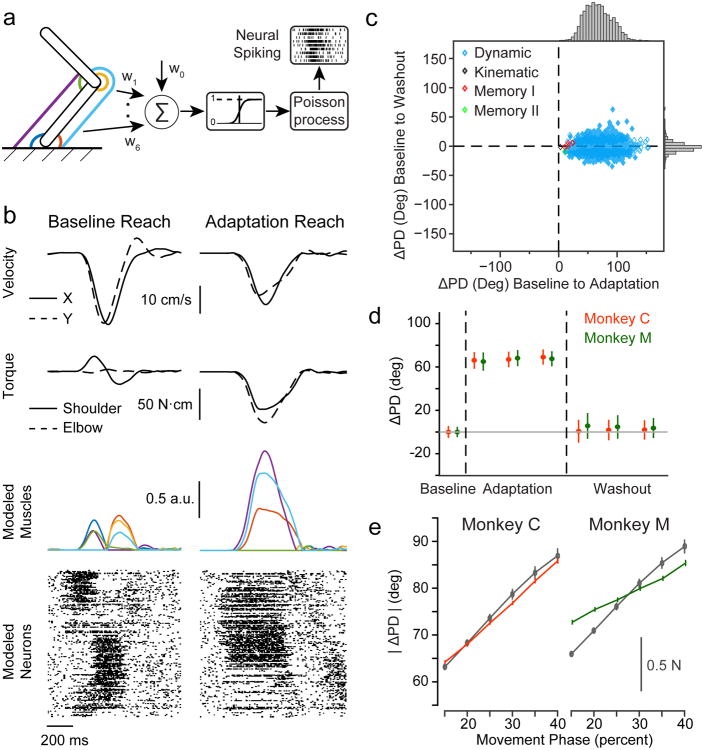
Fig. 7. Simulated dynamics neurons reproduce properties of recorded units.

a) Schematic of biomechanical model and neural generative model. The limb was modeled as a two-link manipulandum controlled by six muscles (colored lines). Neural activity was generated from weighted sums of these muscle activities (see Methods). b) Biomechanical model examples from one session with Monkey M. The left column is a representative reach to the -135° target in Baseline, while the right column is a reach to the same target with the curl field. Top row: endpoint velocities in the x (solid) and y (dashed) directions. Second row: joint torques for shoulder (solid) and elbow (dashed) computed using the model. Third row: muscle activations from the biomechanical model. Colors correspond to the muscles in Figure 7a. Bottom row: raster plots showing the spiking activity of a subset of the simulated neurons sorted by PD. c) Same as Figure 3b for simulated neurons. d) Same as Figure 4a for simulated neurons. e) Same as Figure 5a for simulated neurons.

$${\theta }_e(t)={cos}^{-1}\left[\frac{p_x{(t)}^2+p_y{(t)}^2-L_1^2-L_2^2}{2L_1{L}_2}\right]$$ (4)

$${\theta }_s(t)=\frac{[L_1+L_{2}cos\{{\theta }_e(t)\}]p_y(t)-L_{2}sin[{\theta }_e(t)]p_x(t)}{L_{2}sin[{\theta }_e(t)]p_y(t)}$$ (5)

where L is the length of each limb segment. We then computed joint torques at the elbow (τ_e) and shoulder (τ_s) using inverse dynamics (Equation 6) derived in (Murray et al. 1994). The equations are reproduced with our notation here:

$$\begin{array}{c}\left[\begin{array}{c}{\tau }_s(t)\\ {\tau }_e(t)\end{array}\right]=\left[\begin{array}{cc}A+2Bcos[{\theta }_e(t)]& Bcos[{\theta }_e(t)]+C\\ Bcos[{\theta }_e(t)]+C& C\end{array}\right]\left[\begin{array}{c}{\ddot{\theta }}_s(t)\\ {\ddot{\theta }}_e(t)\end{array}\right]+\left[\begin{array}{cc}-Bsin[{\theta }_e(t)]{\dot{\theta }}_e(t)& -Bsin[{\theta }_e(t)][{\dot{\theta }}_s(t)+{\dot{\theta }}_e(t)]\\ Bsin[{\theta }_e(t)]{\dot{\theta }}_s(t)& 0\end{array}\right]\left[\begin{array}{c}{\dot{\theta }}_e(t)\\ {\dot{\theta }}_e(t)\end{array}\right]\\ A=I_s+I_e+m_s{r}_s^2+m_e(L_s^2+r_e^2)\\ \begin{array}{c}B=m_e{L}_s{r}_e\\ C=I_e+m_e{r}_e^2\end{array}\end{array}$$ (6)

where for each limb segment, m is the mass, r is the distance to the center of mass (assumed to be half of L), and $I=\frac{1}{3}m{L}^2$. Note that we did not make precise measurements of the mass of each limb segment, but instead used approximate values based on morphometry studies (Cheng and Scott 2000) and the total body mass of each monkey (Monkey C: 12 kg, Monkey M: 10 kg). We measured approximate segment lengths for each monkey (Monkey C: L_s = 25 cm, L_e = 20 cm; Monkey M: L_s = 20 cm, L_e = 24 cm), though qualitatively our results were consistent even with relatively large changes in these parameters.

Based on the torque computed from actual trajectories, we calculated patterns of muscle activation to drive the modeled limb using shoulder, elbow, and biarticular muscles for both flexion and extension. The moment arms of each muscle were given by the matrix [2 -2 0 0 1.5 -2; 0 0 2 -2 2 -1.5] (Lillicrap and Scott 2013). Given the redundancy in these muscles, we performed static optimization at each time step to find the activations for the desired joint torques. We normalized the required muscle force by the physiological cross-sectional area (PCSA) of each muscle. We used PCSA values from (Cheng and Scott 2000), assuming that each of our modeled muscles represented the sum of the corresponding groups of synergistic muscles. We minimized the total squared activation across the six muscles, with the additional constraint that activations must not be negative. During curl field trials, we modeled the effect of the CF using the parameters and equations described previously. These forces caused an additional torque about each joint that altered the optimal muscle activations needed to drive the limb with the observed kinematics.

We simulated a population of M1 neurons with a firing rate generated using randomly weighted combinations of the activations α_i of the six muscles. For each neuron, we generated a weight ω_i pseudo-randomly for each muscle from a Gaussian distribution with a mean of zero and a standard deviation of one, modeling balanced excitatory and inhibitory effects on muscle activation (Kujirai et al. 1993; Mariño et al. 2005). We added the resulting sum to a random baseline spiking probability ω₀. These weighted sums were scaled to give physiologically realistic firing rates and treated as the mean rate of a Poisson process, λ, which generated a random spike count n for each time bin according to Equations 7 and 8.

$$\begin{array}{ccc}\lambda ={\omega }_0+{\sum }_i{\omega }_i{\alpha }_i;& -1\le {\omega }_i\le 1;& 0\le {\omega }_0\le 0.1\end{array}$$ (7)

$$n|\lambda ~\text{Poisson}(\lambda )$$ (8)

We included a threshold nonlinearity in the form of saturation at a λ value of 1 to avoid physiologically unrealistic firing rates. Neural activity was made to lead the intensity function by a latency drawn for each neuron from a uniform distribution between 70 and 130 ms to simulate the anticipated lag between neural activity and movement used for the recorded units. Importantly, we kept the weights between neurons and muscles constant throughout the session. Thus, the model provided time-varying patterns of neural activity sufficient to drive the limb in the presence of the curl field. We then performed the same kinematic analysis on these simulated neurons as we did on the recorded single units.

Results

Behavioral adaptation to the force field

We analyzed thirteen sessions of data with curl field learning from Monkey C and nine curl field sessions from Monkey M. Of the 22 sessions, 14 used a counter-clockwise (CCW) curl field and 8 used a clockwise (CW) curl field. We saw no clear difference in behavioral or neural data between the two directions, aside from the sign of the effects. The experimental sessions for both monkeys occurred over several months, and each learning session was treated independently. Additionally, we collected 11 control sessions that had a large number of trials with no imposed fields (five with Monkey C and six with Monkey M). We attempted to maximize the number of Adaptation trials that the monkey would perform in each session to provide more nearly complete adaptation. Consequently, the number of trials in each epoch varied from session to session depending on the monkey's motivation. The monkeys averaged 185±21 (mean±st.d.) movements in Baseline, 266±35 movements during Adaptation, and 196±100 movements for the Washout. Figure 1d shows representative kinematics and the discharge of 30 single units, sorted according to each cell's PD, recorded from Monkey M during the Baseline epoch. Note that the first movement (indicated by the upward arrow at the top of the panel, which was actually a movement away from the monkey) was accompanied by a burst from several units with upward PDs. These same units shut off during the subsequent return movement, and burst again (more weakly) for the later diagonal movements that had an upward component. Though somewhat noisy, similar observations can be made for the downward and leftward PD units.

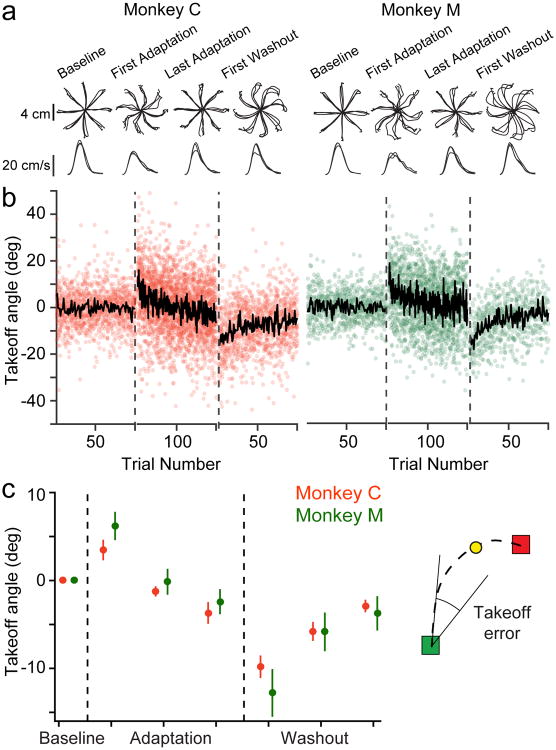
To quantify behavioral adaptation, we used the “takeoff angle” error metric (see Methods), which compares the direction of initial hand movement to the location of the target. The average speed traces for both monkeys had a characteristic biphasic profile during Adaptation that appeared to represent an initial open-loop movement, followed by a correction. This effect decreased during learning, yet was present to some degree even in the later, more-adapted trials (Figure 2a). We thus evaluated the takeoff angle error metric in the brief window between movement onset and the time of peak speed, prior to the apparent error correction. For the CW curl field sessions, we flipped the sign of the error to align it with the CCW-field errors and to simplify analysis and presentation of the results. The CF-induced errors decreased significantly for both monkeys with adaptation (Figure 2). At the beginning of Washout, both monkeys made significant errors due to the after-effects of adaptation.

Fig. 2. Behavioral adaptation to the force field.

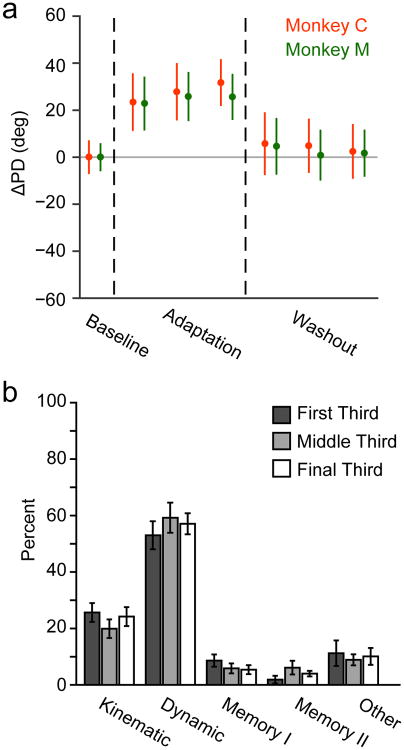
a) The top row shows reach position traces for three representative sessions with clockwise curl field perturbations for Monkey C (left) and Monkey M (right). For each monkey, we plotted the final reach to each target during Baseline (left), the first reach and final reach to each target during Adaptation (middle), and the first reach to each target during Washout (right) for each of the three sessions. Trajectories during Baseline and late Adaptation were generally straight, while the early Adaptation and Washout trajectories were markedly curved. The bottom row shows speed profiles, averaged over the trajectories plotted in the top row for each session. b) We used the average takeoff angle (see Methods) at movement onset to characterize behavioral adaptation. The left panel shows these angles for the first 100 Baseline reaches, 200 Adaptation reaches, and 100 Washout reaches for each session with Monkey C. The black line indicates the mean across sessions for each trial (13 with Monkey C and 9 with Monkey M). Takeoff angle increased when the force field was applied and gradually decreased during Adaptation. There were after-effects during Washout that returned gradually to Baseline values. Note that all three epochs contained additional trials beyond those shown here, that varied in number across sessions. c) Behavioral adaptation for Monkey C (red) and Monkey M (green). For the Adaptation and Washout epochs, we averaged the take-off angle in non-overlapping blocks of reaches, each containing one-third of the total number of successful trials. These blocks of trials are used again in the later neural analysis (see Figure 4). Plotted data represent mean ± SEM across all sessions.

Neural responses to altered dynamics

We identified a total of 523 single units across the 22 curl field sessions (Monkey C: 49 ± 7 units per session, Monkey M: 25 ± 10 units per session, mean ± st.d.). Since the recordings were made with chronically implanted arrays, these were certainly not all unique. However, groups of sessions were separated by as much as 18 months, increasing the diversity of the neural populations they represented. Many electrode channels yielded well-isolated single units (Across all channels: Monkey C: 28-49%; Monkey M: 12-35%; of these, rough one-quarter to one-half yielded more than one well discriminated, single unit).

We first examined the change in neural responses of M1 cells from Baseline to the Adaptation and Washout epochs. We computed the mean firing rate of each cell in the window of time from movement onset to peak speed, as described above. We determined the PD of each cell by fitting tuning curves with respect to the direction of hand motion in that window, rather than the target location. This approach did not require the assumption that the monkey reached straight to the target, as would otherwise be necessary. We divided the Adaptation and Washout epochs into three blocks, each one-third of the total movements. We looked initially at spatial tuning in the final block of each epoch when behavior was most likely to be stable.

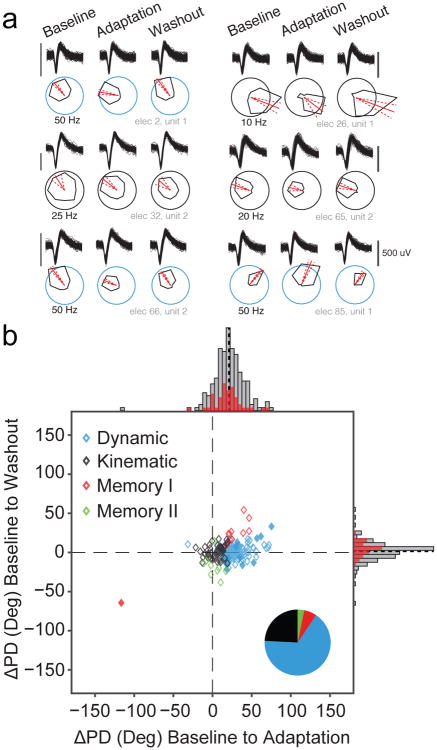
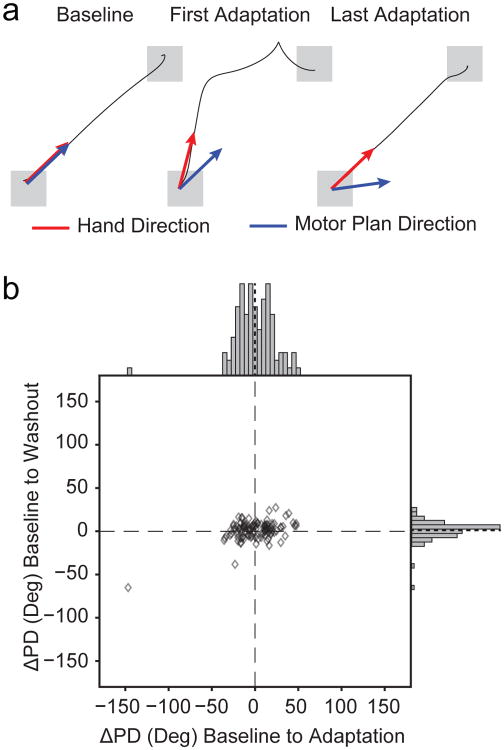
For the curl field sessions, 36% of cells (190/523) met our requirements for spatial tuning (see Methods). In the control sessions a higher percentage of cells (66%, 144/226) met the tuning criteria due to the more consistent trial-to-trial behavior compared to the perturbed trials. Figure 3a shows example waveforms and tuning curves throughout the three epochs for six representative cosine-tuned single units. The changes in PD (ΔPD) from Baseline to Adaptation and Baseline to Washout epochs for all cells are shown in Figure 3b. As we did with the behavioral adaptation data, we changed the signs of ΔPDs in the CW sessions to align them with the CCW metrics. Across the population, the mean PD shifted by 21° ± 19° (mean ± st.d.) between Baseline and Adaptation, but only 1.6° ± 12° between Baseline and Washout (Figure 3b, solid black lines). We divided these cells into five classes based on the significance of their changes across the three epochs. Combined across all sessions, 55% of cells (104/190) were classified as “Dynamic”, having a significant change of tuning between the Baseline and Adaptation epochs that returned to the Baseline PD during Washout. All of these cells are located near the horizontal axis with positive PD changes in Figure 3b. Fifty of the remaining cells (26%) were clustered near the origin, with statistically unchanged tuning and were classified as “Kinematic” cells.

Fig. 3. Neural PD changes.

a) Waveforms and tuning curves for six representative cosine-tuned units recorded from one session of Monkey C during the Baseline period and the final third of trials in the Adaptation and Washout periods. The black scale bar next to the waveforms indicates 500 uV. The red line indicates the PD, and the dashed red lines denote the 95% confidence bounds on the PD. The scaling circles are colored according to the cell classification. b) Change in preferred direction (ΔPD) from the Baseline to Adaptation epochs (abscissa) and from the Baseline to the Washout (ordinate). Histograms indicate marginal distributions, with gray being all tuned cells, and red being the best isolated cells (SNR > 6). Black dashed lines on the histograms represent the mean change from baseline for each distribution (21° in Adaptation and 1.6° in Washout). Most PDs changed significantly during Adaptation and reverted to their original tuning in Washout. Symbol colors and pie chart (inset) shows the proportion of each cell type for the population. The Dynamic and Memory I cells with solid fills represent Other cells that were reclassified using the Memory Cell index (see Methods).

We also found 13 (7%) cells that fit the definition of Memory I type cells, having PDs that rotated during the Adaptation epoch and kept the new tuning during Washout (Figure 3b, red diamonds). In addition, there were nine (5%) Memory II cells (stable tuning across the Baseline and Adaptation epochs but altered tuning in Washout). These cells (Figure 3b, green diamonds) were clustered near zero PD change during Adaptation. Lastly, we identified 14 (7%) cells with significantly different tuning in all three epochs, referred to in prior literature as “Other” cells. For these, we computed a “Memory cell index” (see Methods) describing whether the changes more closely resembled Dynamic cell behavior (values less than one) or Memory I cell behavior (values greater than one). Thirteen of the fourteen cells had an index below one and if included in the Dynamic cell group would bring the total Dynamic population to 62% of all cells (117/190). We could find no tendency for the Kinematic and Dynamic cells to be located differentially on the arrays.

Our decision to regress neural activity against the motion of the hand differs from earlier studies (Gandolfo et al. 2000; Li et al. 2001), which averaged neural activity over the duration of the reach and regressed against the target direction. To ensure our results did not depend on the differences between these coordinate frames, we repeated these analyses using the more typical target-direction regressor. We found qualitatively similar PD changes during Adaptation, although the ΔPD distribution was slightly smaller on average and more variable (17° ± 22°). The choice of coordinate system had little impact on our cell classifications, with 29% Kinematic, 46% Dynamic, 13% Memory I or II, and 12% Other.

As a control, we analyzed data from several sessions in which there was no curl-field perturbation, dividing the large number of trials into three equal portions. Under these conditions, we would expect no changes in PDs, and for all single units to be classified as Kinematic. In fact, we found only 81% of cells (117/144) to be Kinematic. There was a small number of Dynamic (6%, 19/144) and Memory I (4%, 5/144) cells, and a slightly larger group of Memory II cells (9%, 13/144). No cells were classified as Other.

The cell classification in Figure 3 used a block of trials from the final third of the Adaptation and Washout epochs when adaptation or de-adaptation would have been most nearly complete. We repeated the classification using PD changes in the first and second blocks of trials to assess the time course of neural PD changes. If changing PDs were related to adaptation, we would expect to find smaller changes earlier in the Adaptation epoch. However, that was not the case. Any cells that rotated did so fully in the first Adaptation block (Figure 4a). There was no progressive change in PD throughout the Adaptation or Washout epochs, even as behavioral performance continued to change (compare Figure 2c).

Fig. 4. PD changes did not correlate with behavioral adaptation.

a) ΔPD (mean ± SEM) of the population as the monkeys adapted for three different blocks of data during Adaptation and Washout. The PDs for Monkey C (red) and Monkey M (green) rotated when the force field was applied, with no progressive changes across these blocks despite the changing behavior (Figure 2c). b) Neural population classifications for each of the blocks of Adaptation and Washout trials from Figure 4a. Error bars represent standard error of the mean across experimental sessions. There were similar proportions of each cell class within the three blocks.

We then tested the stability of cell classifications using the first and second blocks of trials within Adaptation and Washout. If Memory cells result from motor learning, we would expect to find fewer early in Adaptation. At the population level, neuron classification rates were similar for all three blocks of trials (Figure 4b). However, at the single cell level, there were differences in the classifications of individual units. We compared each unit's classification during the middle and final blocks of the Adaptation and Washout epochs. Of the 190 cells that were tuned in the final block, 155 were tuned in all three blocks. The Dynamic population proved to be fairly robust; 76% (68/89) of Dynamic cells from block 3 were also classified as Dynamic in block 2, well above chance (approximately 20% given the five classes). A slightly lower proportion of Kinematic cells, (66%; 23/35), had consistent classification, while the classification of Memory (4/18) and Other cells (5/13) was close to chance. Together, these results show that short-term motor adaptation is not a product of progressive changes within M1, and that putative Memory cells are likely the result of statistical misclassification.

Magnitude of neural PD changes during the CO task depends on the instantaneous force

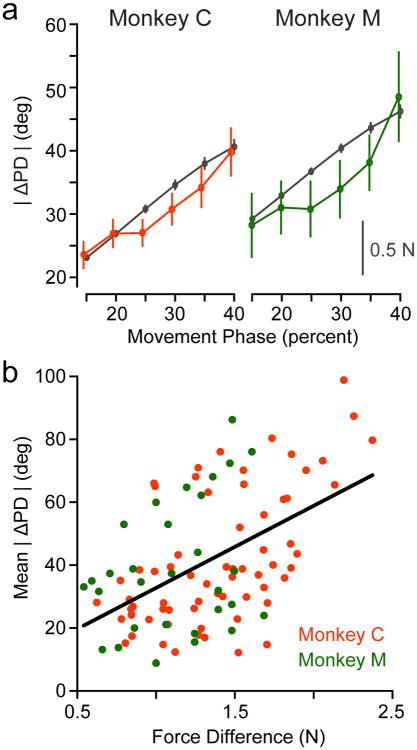
The previous results used PDs computed within a brief window between movement onset and peak speed. However, the speed and amount of force exerted by the curl field varied even within this window. If M1 activity is related to movement dynamics, we should observe larger ΔPD when the monkey experienced larger curl forces. We fit PDs within six overlapping windows (30% of the movement duration for each trial, typically ∼150 ms) from the beginning of movement. The last of these ended approximately at the time of peak speed. The magnitude of the CF force varied throughout this period, which we compared to the ΔPD for all cells that had significant cosine tuning in a given window (Figure 5a). There was a strong correspondence between the two measures. However, Figure 5a shows single units from the same time windows pooled across multiple sessions and thus removes the correlations with behavior on individual sessions. Each point in Figure 5b represents, for a single time window from Figure 5a, the mean ΔPD for the population of recorded cells on one session and the corresponding RMS curl force experienced on that session. A linear fit across all data points from both monkeys was highly significant (r=0.51, p∼0; black line of Figure 5b).

Fig. 5. Neural PD changes depend on force.

a) We fit PDs for all single units in overlapping, sliding time windows beginning at movement onset and computed ΔPD between Baseline and Adaptation in each window. Values represent mean ± SEM across the cells that were tuned in any given window. This plot compares the time-varying change in RMS force measured at the handle (black lines, scale bar) with the population ΔPD (red for Monkey C, green for Monkey M, left axis) in each window. b) Each data point shows the per-session average of the ΔPD change observed in each of the time windows shown in Figure 5a plotted against the difference in endpoint force in that window. The fitted line gives the relationship ΔPD = 6.6° + 26° × ΔForce

Neural tuning to the “motor plan” is stable during adaptation

The correlation between ΔPD and force suggests that endpoint kinematics may not be the appropriate reference frame with which to describe M1 activity. Therefore, we also expressed M1 activity in terms of the dynamics of the “motor plan”, using an approach developed by Mandelblat-Cerf, et al (Mandelblat-Cerf et al. 2011). Briefly, during the window between movement onset and peak speed, we used endpoint velocity to compute the underlying CF force, which we subtracted from the force recorded by the force transducer. The resulting force vector provided an estimate of the net force at the hand that would have been produced by the monkey in the absence of the curl field and serves as a proxy for the movement that the monkeys intended to make, referred to as the “motor plan” (Figure 6a). In early CF trials, this motor plan should be directed towards the target, then rotate gradually to counter the CF over the course of adaptation. We computed the average motor plan force vector during the time between movement onset and peak speed. We then fit cosine tuning functions to the firing rate of our M1 units regressed to the direction of this vector. We assessed the change in the resulting PDs between Baseline and Adaptation trials. If this dynamic coordinate frame more accurately captures M1 modulation, the average ΔPD should be significantly smaller than that shown in Figure 3b. Indeed, neural tuning in this “motor plan” reference frame was quite stable during Adaptation, with a population ΔPD = 0.8°±22° (mean ± st.d.; p=0.95, one-sample t-test), suggesting that M1 activity more consistently relates to the net forces produced by the limb (Figure 6b).

Fig. 6. M1 consistently encodes the desired motor plan.

a) We identified the direction of the intended force application (blue arrows), or the “motor plan”, by subtracting the effect of the curl field from the observed endpoint force vector (red arrows). In Baseline, these two coordinate frames were identical. Initially during Adaptation, the monkey intended to reach to the target, though the direction of the hand motion was altered by the curl field. In late Adaptation trials, the hand reached the target but the compensatory motor plan was rotated toward the direction of the perturbation. b) Despite the large behavioral effects, PD changes in the motor plan coordinate system, plotted as in Figure 3b, were centered near zero at the beginning of both adaptation and washout.

Musculoskeletal Model

We repeated the tuning analyses using our simulated, muscle-based neurons and found results qualitatively similar to those of the recorded single units. We generated 500 simulated neurons (Figure 7b) for each of the 22 curl-field sessions from both monkeys to give a total of 11,000 neurons. The randomly weighted muscle force inputs allowed cells to have equal activation from antagonist muscle groups. As a result, not all cells produced significant spiking activity. As with the recorded units, we considered only cells that had a firing rate greater than five Hz during the movement period, which removed 1827 cells from further analysis. Of the remaining neurons, 46% (4279/9173) also met our cosine tuning criteria.

The PD changes during Adaptation were broadly distributed, with a mean significantly larger than that of the recorded units (68° ± 22°; Figure 7c, top marginal distribution), while the distribution of model neuron PD changes during Washout was a bit narrower (-1° ± 7°; Figure 7c, right marginal distribution). The PDs rotated immediately due to the effect of the force perturbation, which altered the relationship between endpoint kinematics and joint torques (Figure 7d). The ΔPD was thereafter constant during Adaptation, with no temporal correlation to behavior. Although the majority of cells were classified as Dynamic (87%, 3726/4279), there were many Other type cells (13%, 543/4279) and far smaller numbers of Kinematic (2/4279) and Memory (8/4279) cells. Since the neural firing rates were generated using fixed dynamical relationships, any change in spatial tuning in the Washout that lead to Other or Memory cells must have been due to a misclassification resulting from chance and/or different kinematic behavior rather than a change in underlying neural processes. Assuming all Memory and Other cells were the result of altered behavioral statistics in Washout, then 13% (551/4279) of simulated neurons were classified erroneously, somewhat less than the proportion observed in the recorded units (19%, 36/190). The PD changes of modeled neurons also had a dependence on time (and force) throughout the reach (Figure 7e), as did the real units (Figure 5a).

Discussion

We investigated the spatial tuning of M1 neurons as monkeys made reaching movements against an externally imposed curl field that altered limb dynamics. We showed that the majority of single units were Dynamic, having PDs that changed when the field was imposed and returned to their Baseline tuning when it was removed. Importantly, the PDs of the units showed no progressive change even during ongoing behavioral adaptation, but instead, the size of ΔPD was well correlated with the magnitude of the CF force. This was true over the course of movements (Figure 5a) and across sessions (Figure 5b). When instead computed in terms of dynamic, “motor plan” coordinates, there was no change in PD. Lastly, we used a simple musculoskeletal model to generate a population of neurons with fixed relationships to joint torques. These modeled neurons had a broad distribution of ΔPDs that was qualitatively similar to that of the recorded units. It has been proposed that learning results by adapting the brain's internal inverse model of limb dynamics (Shadmehr and Mussa-Ivaldi 1994). Overall, our results suggest that short-term adaptation of such an internal model likely occurs before the inputs to these M1 neurons, which themselves maintain a consistent relationship to the dynamics of movement.

Tuning changes do not suggest internal model adaptation within M1

The progressive learning of new motor skills must be encoded within the brain, presumably by changes in discharge that mimic the time course of the behavioral adaptation. It is reasonable to expect that M1 participates in this process. M1 tuning curve changes, especially those of Memory cells, have been thought to be an expression of this process (Gandolfo et al. 2000; Li et al. 2001; Arce et al. 2010; Richardson et al. 2012). This theory suggests that changes in neural discharge are the result of altered functional properties either within M1 or in downstream neural circuits, embodying an adapted internal model. It is important to note that although these prior studies expressed neural activity within the classic kinematic coordinate frame, they did not assume that M1 acts as a kinematic controller. Indeed, they found that the activity of many M1 cells reflected movement dynamics, with a range of effects that was suggestive of a kinematic to dynamic transformation (Li et al. 2001). The critical difference between those studies and our own, however, is the suggestion that these properties are altered during the hour-long process of adaptation, for which we can find no compelling evidence.

In our experiment, there were progressive behavioral changes within sessions (Figure 2) and clear behavioral aftereffects during Washout. If changes within M1 mediate this short-term motor learning through internal model adaptation, we would predict that the magnitude of the change in neural tuning or the proportion of Memory cells should gradually change as the monkey adapts. However, although the CF affected the great majority of the recorded and simulated neurons, we found no progressive change in their PDs throughout the Adaptation epoch (Figures 2 and 4). Thus, we interpret the PD changes as a direct consequence of the altered dynamics, rather than the subsequent process of adaptation. Although the PD changes appeared at the earliest point at which we were able to examine them, a limitation of the tuning analysis is that we must average over a relatively large number of trials to achieve adequate statistical power. Much of the behavioral adaptation occurred early, within the first block in the session. However, it is important to note that there were still significant behavioral changes even between blocks two and three (Figure 2c). If the tuning changes were the consequence of learning, there should be evidence of further tuning changes across all three blocks.

Furthermore, we saw little evidence of Memory cells. Although there was no progressive change in their number during learning, the classification of individual Memory cells did change unpredictably. Finally, we even found a small number of Memory cells in the control sessions, in which there was no applied curl field. A similar study that recorded the activity of single units in the supplementary motor area also detected Memory cells in control sessions approximately as often as during the learning sessions (Padoa-Schioppa et al. 2004). These observations raise the concern that Memory cells may be the result of measurement noise rather than a robust change in neural tuning. There are several potential explanations for the differences between our results and those in the prior studies. First, we used a stronger force field (0.15 compared to 0.07 Ns/cm). Since neural PDs rotate in proportion to the magnitude of force (Figure 5), the larger effect size likely made our classifications more robust. Additionally, our experiments contained more movements during Adaptation (266 on average, versus ∼160-200 in prior studies), allowing us to exclude more of the earlier, less adapted trials. More movements likely also allowed for more complete adaptation and stable behavior. If Memory cells arise from noisy estimates, then larger fields, more trials, and more stable behavior should decrease the chance of misclassification.

Although we classified cells as Dynamic and Kinematic for consistency with prior literature, the units were not distributed bimodally in a manner that would suggest two distinct classes. Rather, in both the recorded and simulated neurons there was a continuum of ΔPD magnitudes. Those recorded units with small rotations may represent muscles that were only minimally affected by the CF. Alternatively, this continuous distribution may well represent an internal model that transforms motor commands from kinematic to dynamic coordinates (Fetz 1992; Kalaska and Crammond 1992; Shadmehr and Mussa-Ivaldi 1994). In that case, however, it appears that these neurons are not the source of the short-term behavioral adaptation in our experiments. Instead, the internal model represented by the outputs of this neural circuit remained stable, suggesting that compensation for the modified external dynamics occurred at a higher level and was simply transmitted to M1.

Neural tuning is related to movement dynamics

If the tuning changes in M1 in the presence of a curl field do not correspond to behavioral adaptation, how are they to be explained? We propose that PD changes are primarily due to the direct effect of force on M1 firing rates (Evarts 1968; Scott and Kalaska 1995, 1997; Sergio and Kalaska 2003; Sergio et al. 2005; Gupta and Ashe 2009). Our evidence for this includes the very rapid PD rotation with the onset of the CF, the strong correlation between ΔPD and force (Figure 5), and the stable PD representation that occurred for the dynamic motor plan. Although the discharge of these units changed during the course of learning to drive the adapted behavior, their spatial tuning throughout the Adaptation epoch was quite stable. Importantly, our conclusions do not need to assume that single M1 neurons necessarily encode specific variables (e.g., endpoint kinematics, endpoint force, joint angles, muscle activations) and indeed many studies of activity in M1 have suggested that individual neurons need not represent any particular movement covariate (Fetz 1992; Churchland and Shenoy 2007; Elsayed et al. 2016). We focused on a brief window, early in movement before online error correction, to simplify the interpretation of our results. Yet, there remains the possibility that some of the PD changes were the result of changes in short-latency proprioceptive feedback to M1 (Scott et al. 2015). Indeed, it has been proposed that proprioceptive feedback to M1 is necessary to learn curl field perturbations (Wolpert et al. 1995; Mathis et al. 2017), and that the adapted internal model is shared for both feedforward control and feedback control (Wagner and Smith 2008). Although afferent inputs likely influence the shape of at least some tuning curves, this influence is equivalent to that of premotor inputs with respect to our argument about the role of M1 in short-term adaptation. The rapid and sustained PD changes throughout adaptation, whether the result of altered premotor or afferent inputs to M1, suggest that the dynamical relation between M1 activity and movement was altered only by the addition of the load force, not subsequent adaptation. The very similar results in our musculoskeletal model, which lacked proprioceptive feedback, further support the conclusion that PD changes result primarily from the altered dynamics of the task.

It would be enlightening to pursue a more detailed model of the relation between M1 activity and muscle force, but that is well beyond the scope of this study. With their fixed generative relationship to dynamics, the simulated neurons exhibited tuning changes remarkably similar to those of the recorded M1 units. There were, however, some differences. Notably, our model had a large percentage of Dynamic cells, many Other cells, and virtually no Kinematic or Memory cells. These differences are likely due in large part to two factors. First, there were larger model PD changes during Adaptation, and generally smaller changes during Washout compared to the real neurons, yielding more robust statistical changes underlying the Dynamic classification. Second, there was much less variability in the discharge of the simulated neurons compared to the real units, leading to narrower confidence intervals on the PD estimates. The activity of real neurons likely includes a number of sources of signal-dependent noise, or variability that is not strictly stochastic but is also not well-captured by our cosine tuning model. Such sources could include the posture or load dependence of neurons (Scott and Kalaska 1995; Sergio et al. 2005), the control of muscles not included in the model or not strongly modulated in the task, and other activity that is not related explicitly to the motor outputs (Fetz 1992; Churchland and Shenoy 2007). This combination of factors caused virtually all modeled neurons to be statistically different in Adaptation from both other epochs. This greatly decreased the likelihood of observing Kinematic cells. It also meant that most cells that happened to differ between Baseline and Washout became Other (all epochs different) rather than Memory. A smaller PD change in Adaptation would have increased the probability that the Other cells would instead be classified as Memory, since no change would be observed in Adaptation.

The broader distribution of modeled PD changes may have been the result of simplifications in our biomechanical model and our generative neural model. First, we assumed that motion was limited to two joints in the horizontal plane, while the actual posture also involved movements of most of the limb's seven degrees of freedom, many of which would not have contributed directly to the planar tuning curves. Second, our neurons were based on a small number of modeled muscles, which are greatly simplified compared to the number of muscles that actually move the limb. This simple model did not include force-length and force-velocity characteristics, or posture-dependent pulling directions, and it minimized any co-contraction. Including these features would likely increase the number of single units with less than maximal responses to the curl field, thus providing a population that more closely resembles the recorded M1 cells.

It is important to note that the model was not intended to recreate the monkeys' behavior precisely; we used real behavioral kinematics simply to provide realistic movement speeds, trajectories, and effects of behavioral adaptation. We generated neural activity directly from the activity of the modeled muscles, maintaining a fixed dynamical relation between the two. Although the connectivity was random, there is much evidence that the real connectivity of corticomotoneuronal cells is more structured, with many cells favoring reciprocal activation of agonists and antagonists (Cheney et al. 1985). In practice, the majority of the modeled cells that were cosine-tuned had this structure. Although the firing of many M1 cells is closely related to forces at the hand and to patterns of muscle activity (Evarts 1968; Ashe 1998; Cabel et al. 2001; Sergio et al. 2005), a number of studies have shown that the discharge of M1 neurons correlates with many aspects of behavior beyond the activation of muscles (Fetz 1992; Churchland and Shenoy 2007). Our modeled neurons lack activity related to intrinsic network dynamics (Shenoy et al. 2013), movement planning and preparation (Alexander and Crutcher 1990), or afferent feedback (Asanuma et al. 1979; Cheney and Fetz 1984). As such, our modeled neurons cannot be expected to replicate the precise patterns of activity that would be observed in a real motor cortical population. Nevertheless, despite these simplifications, the generated neurons behaved in a qualitatively similar manner to the recorded units. The results from our experimental and modeled data are consistent with the conclusion that M1 activity encodes information related to the dynamics of the intended movement that remains unchanged during adaptation.

Comparison with prior studies

Including the original study in 2000 (Gandolfo et al. 2000), several studies have proposed that short-term tuning changes in M1 during curl field learning reflect modification of an internal, inverse model of limb dynamics that drives the behavioral adaptation (Li et al. 2001; Arce et al. 2010; Richardson et al. 2012). Another study reached a conclusion more like ours, that M1 activity was consistently correlated with the “motor plan” during adaptation (Mandelblat-Cerf et al. 2011). Their motor plan analysis, applied to our data, yielded similar results. However, that study did not include a Washout period, so they could not assess their neurons for any memory effects. Furthermore, they used a unique design, in which the CF was applied to a single reach direction (as did the 2010 Arce study). This difference makes comparison of both these studies with the earlier studies from Bizzi's group difficult.

Another important later study used chronically implanted electrode arrays, allowing some neurons to be tracked between sessions. That study replicated many of the earlier within-session findings, but also reported some neurons with persistent, cross-session PD shifts that were taken as evidence of long-term learning. However, they also acknowledged that the M1 tuning changes they described did not necessarily mean a change in the functional properties of M1 cells, but instead likely reflected altered recruitment by higher order brain areas, as we have concluded. Nonetheless, they interpreted the changes in PD and the presence of Memory cells as signatures of an adapted internal model, not simply the dynamics of the added load. Neither our results, nor those of the previous study from our group (Cherian et al. 2013), support this conclusion.

The discrepancies between Cherian et al. and the earlier studies have also been puzzling, though a number of differences in the design of the studies make direct comparison difficult. First, Cherian et al. compared movements between two oppositely directed curl fields. Interference between the two perturbations may have disrupted the learning process (Brashers-Krug et al. 1996), raising the possibility that the lack of Memory cells was simply a consequence of incomplete adaptation. Our experiment compared curl fields to null fields, as did the earlier studies. Second, Cherian et al. used a random-movement task with dynamics that were quite different from the standard center out movements used in prior literature. The lack of explicit planning and greater movement complexity may have led to different rates or signatures of learning (Smith et al. 2006; Sheahan et al. 2016). For the present study, we used the center-out task, which also allowed us to compare target-based and hand-movement reference frames. Finally, we added a biomechanical model, with known, fixed dynamics. Both our recording and modeling results remain at odds with the conclusions of the earlier studies (Gandolfo et al. 2000; Li et al. 2001; Arce et al. 2010; Richardson et al. 2012).

Behavioral adaptation is mediated by altered recruitment of M1 neurons

Motor adaptation is a complex process that is dependent on many factors, including the type of perturbation (Krakauer et al. 1999), the perturbation schedule (Orban de Xivry et al. 2011), and even whether the subject has explicit knowledge of the perturbation (Mazzoni and Krakauer 2006). It is likely that motor learning involves the concerted efforts of multiple cortical and sub-cortical areas (Kawato 1999). Our results suggest that short-term adaptation to a curl field is not mediated by persistent plastic changes in the functional characteristics of the units we recorded in M1. There remains the possibility that adaptation occurs upstream of our recording but still within M1. However, two studies investigating curl field learning by humans used repetitive transcranial magnetic stimulation to disrupt M1 and concluded that it is not a critical site for short term motor learning (Richardson et al. 2006; Overduin et al. 2009). The greater rate of adaptation for humans than monkeys and the possibility that humans may make more use of altered strategy than monkeys complicates the cross-species comparison. However, the inactivation results are consistent with the idea that the rapid adaptation to a novel dynamic environment results from changes in the recruitment of M1 neurons by higher cortical areas. Similar studies suggest that the supplementary motor area (SMA) helps to compensate for the altered dynamics, potentially by altering its inputs to M1. However, its responses to the CF varied quite broadly, during both learning and control conditions, suggesting a complex role for SMA (Padoa-Schioppa et al. 2002, 2004). Curl field adaptation is likely mediated as well by inputs from dorsal premotor cortex (Shadmehr and Holcomb 1997; Dum and Strick 2002, 2005), and undoubtedly involves cortical interactions with the cerebellum (Wolpert et al. 1998).