Modeling left ventricular blood flow using smoothed particle hydrodynamics

Abstract

This study aims to investigate the capability of smoothed particle hydrodynamics (SPH), a fully Lagrangian mesh-free method, to simulate the bulk blood flow dynamics in two realistic left ventricular (LV) models. Three dimensional geometries and motion of the LV, proximal left atrium and aortic root are extracted from cardiac magnetic resonance imaging and multi-slice computed tomography imaging data. SPH simulation results are analyzed and compared with those obtained using a traditional finite volume-based numerical method, and to in vivo phase contrast magnetic resonance imaging and echocardiography data, in terms of the large-scale blood flow phenomena usually clinically measured. A quantitative comparison of the velocity fields and global flow parameters between the in silico models and the in vivo data shows a reasonable agreement, given the inherent uncertainties and limitations in the modeling and imaging techniques. The results indicate the capability of SPH as a promising tool for predicting clinically relevant large-scale LV flow information.

INTRODUCTION

Cardiovascular diseases (CVDs) are the number one cause of death globally, with an estimated 31% of all deaths worldwide¹. In recent years, computational modeling of cardiac flow has made great progress and gained increased acceptance for investigating cardiac function in healthy and diseased conditions². Detailed study of left ventricular (LV) hemodynamics is not only expected to unfold new perspectives for the understanding of cardiovascular physiology, but also offer potential for patient-specific clinical diagnostic and prognostic information.

Investigation of cardiac flow using computational fluid dynamics (CFD) is an active research area that encompasses several numerical approaches, which can be broadly categorized into mesh-based methods and mesh-free methods. Most numerical LV studies to-date are based on mesh-based methods such as the arbitrary Lagrangian–Eulerian (ALE) approach³ or the immersed boundary (IB) method⁴. In general, complex geometries, boundaries with large deformations, and moving interfaces involved in the study of LV blood flow remain a major challenge for mesh-based methods⁵.

To overcome these limitations, a new generation of numerical methods called mesh- free methods have been developed and adapted in recent years. Mesh-free methods are based on a Lagrangian approach instead of the Eulerian approach, therefore the continuum medium, such as blood, is discretized as a set of particles distributed over the solution domain without the need of a spatial mesh⁶. In particular, the smoothed particle hydrodynamics (SPH) method, created originally to simulate compressible flows in astrophysics⁷, is a versatile fully Lagrangian approach that has been applied extensively to study a variety of physical phenomena^8–12.

While SPH or other mesh-free methods have been successfully used for blood flow simulations before, the majority of these studies have focused on vascular hemodynamics^13–15, which are far simpler than that of the heart. To date, a limited number of studies have used SPH to study cardiac blood flow^16–19. Shahriari et al.²⁰ presented the first work demonstrating the capability of SPH to simulate the intraventricular blood flow in a simplified LV model. In this study, the SPH code and methodology were validated against two benchmark cases, and then combined to simulate pulsatile flow in a rigid LV model. Although this study clearly demonstrated the ability of SPH to simulate the LV flow dynamics, the main limitations associated with this study were the assumption of a 2D geometry and a rigid LV wall.

Although SPH is a relatively new tool in the study of cardiac flow, this method is attractive for simulating the fluid-structure interaction (FSI) phenomenon involved in the LV blood flow. Due to its capability to handle complex geometric motion, SPH is particularly useful to model the complex LV-valve dynamics that involves nonlinear large deformations during the entire cardiac cycle with flow fragmentation during valve closure. However, there are some inherent limitations associated with SPH. For example, modeling of wall boundary conditions is non-trivial for SPH, requiring some special treatments such as placement of fixed ghost particles outside the computational domain^{21, 22}. Additionally, turbulence modeling has not been well developed in SPH and is currently an area of great interest^{23, 24}. These limitations are likely to affect the flow solution in the boundary layers and limit the study of the small-scale flow features seen in the intraventricular blood flow.

Recently, SPH has been implemented in Abaqus (SIMULIA, Providence, RI), a widely used commercial nonlinear FEA solver. In our recent study¹⁸ using ABAQUS/SPH coupled with nonlinear hyperelastic FE valve models, we compared SPH-FSI and FE-only simulations of a bioprosthetic valve deformation. It was found that SPH-FSI was able to generate more realistic leaflet spatial and temporal dynamics, as well as stress and strain fields. Our ultimate goal is to develop a comprehensive SPH-FE FSI model that incorporates the LV, the aortic valve and the mitral valve to simulate the valves structural response and the intraventricular blood flow phenomena. As a first towards this goal, we aim to investigate the capability of the SPH method to model the bulk flow dynamics in 3D LV models, which ultimately drive the deformation of the valves in the intraventricular flow.

Thus, in the present work, we focus on the quantitative comparison of the SPH results with those obtained using a traditional finite volume (FV)-based CFD method, and to in vivo hemodynamic data, in terms of clinically significant large-scale blood flow measurements. These results and comparisons are used to identify and discuss the key challenges and limitations, and practical implications when using SPH to study the 3D LV bulk flow.

MATERIAL AND METHODS

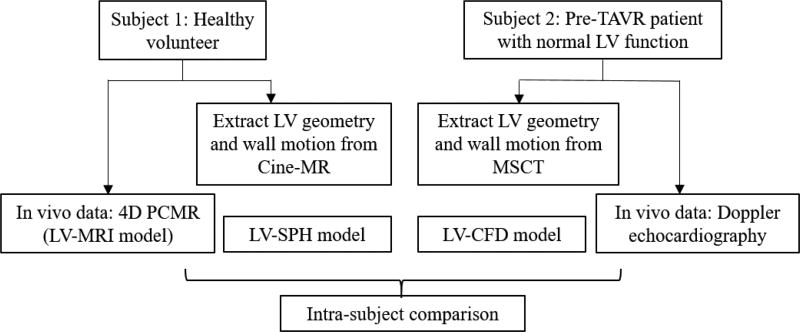
One healthy volunteer with no underlying disease and one pre-operative transcatheter aortic valve replacement (TAVR) patient with normal LV ejection fraction were selected for this study, herein denoted as Subject 1 and Subject 2, respectively. Institutional Review Board (IRB) approval was obtained for this study. Figure 1 shows the schematic of our study design. 3D LV geometries and wall motion were obtained from medical images. In silico LV-SPH and LV-CFD models were then developed for each subject, and simulation results were compared to clinical in vivo hemodynamic data in terms of bulk blood flow features.

Figure 1.

Schematic of study methodology

1. Patient anatomical data

1.1 Cine-MR

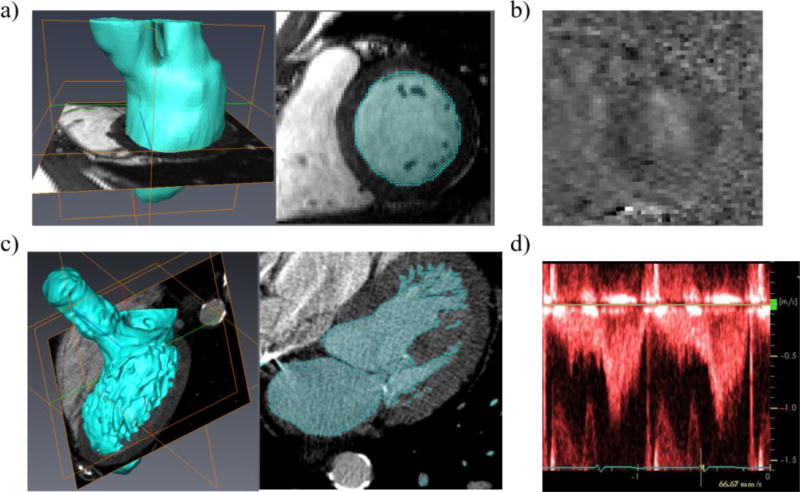
Cardiac magnetic resonance (CMR) imaging was performed in a 31-year-old healthy male volunteer (Subject 1) on a 3T scanner (Magnetom TRIO, Siemens Medical Systems, Erlangen, Germany) using a six-element body array coil. Retrospectively ECG-gated, short axis images covering the entire LV, proximal left atrium (LA) and aortic root were acquired using a balanced steady-state free precession (SSFP) cine sequence, as shown in Figure 2a. An acceleration factor of 2 was used using the GRAPPA technique. The SSFP cine images were acquired with an in-plane resolution of 1.3 × 1.3 mm, a slice thickness of 4.8 mm, and 19 phases. 23 short-axis slices were acquired to cover the entire volume of interest. Slices were acquired during and end-expiration breath-hold to minimize alignment errors caused by changes in breath-hold position.

Figure 2.

a) Cine images of the LV for Subject 1, b) PCMR velocity image of the LV for Subject 1, c) MSCT images of the LV for Subject 2, and d) Doppler echo velocity recordings at LVOT plane for Subject 2

1.2 Full phase MSCT

From our full phase cardiac multi-slice computed tomography (MSCT) database from patients at Hartford Hospital (Hartford, CT), a 72-year-old female pre-TAVR patient (Subject 2) with normal LV ejection fraction was selected for the study. The MSCT examination was performed on a GE LightSpeed 64-channel volume CT scanner. In general, a total of 2000 images with in-plane resolution of 0.82 × 0.82 mm and a slice thickness of 0.625 mm were collected for the whole cardiac cycle (Figure 2c). A collimation of 25–30 × 0.625 mm and a rotation time of 375 ms were used, resulting in 10 phases through the cardiac cycle.

2. In vivo hemodynamic data

Following acquisition of cine-MR images, LV flow was acquired for Subject 1 using a 4 dimensional phase-contrast MR sequence (4D PCMR) with the same orientation and anatomical position as the cine images. The 4D PCMR sequence provides time resolved 3D data, where each frame in time and space has 3D velocity components. The 4D PCMR sequence was an ECG-gated, gradient echo sequence with a slice thickness of 4 mm and in-plane resolution 1.8 × 1.8 mm. Other imaging parameters were as follows: repetition time (TR) 51.2 ms, echo time (TE) 3.475 ms, flip angle 15°, velocity encoding 150 cm/s. The volume of interest was resolved into 28 slices, and 17 phases were acquired through the cardiac cycle. 4D PCMR imaging provided four sets of images per time-point, i.e., magnitude image and flow-velocity encoded images at x-, y-, z-directions. Figure 2b shows a representative PCMR phase image with the velocity encoded along the vertical axis of the slice. PCMR data was processed using an in-house Matlab code (The Mathworks, Inc., Natick, MA) following the approach in Uribe et al.²⁵.

4D PCMR magnitude images had relatively low spatial resolution and therefore were only used for manual registration and localization of imaging planes between the cine-MR and the PCMR anatomical data. Getting clear flow data during the entire cardiac cycle was challenging due to various factors, such as artifact generation due to respiratory motion, high temporal-spatial averaging, and limited signal-to-noise ratio (SNR)²⁶. Hence, the results obtained from PCMR are only used in this study for a qualitative comparison.

For Subject 2, pre-operative transthoracic echocardiogram Doppler examination was obtained from Hartford Hospital (Hartford, CT). From this data, the pulsed-waved Doppler velocity recording at the LV outflow track (LVOT) plane seen in Figure 2d was digitized and compared to the numerical results.

3. Model reconstruction

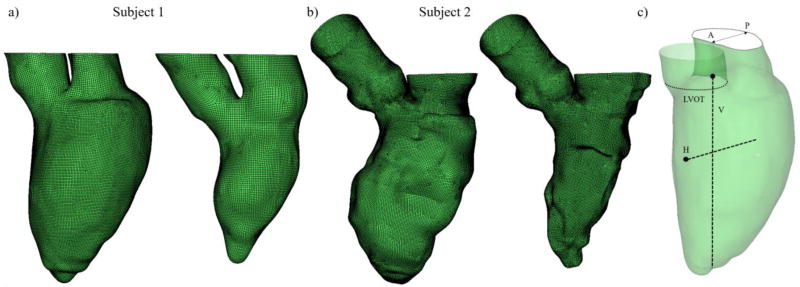
Cine-MR and MSCT images were imported into Avizo 9 software (VSG, Burlington, MA) to generate the 3D models in the form of smoothed LV surface meshes. The semiautomatic segmentation and processing methods of medical imaging data were developed and used in our previous studies^{27, 28}. The reconstructed geometries captured the LV internal structure and motion in detail, including the mitral annulus (MA) and proximal LA dynamics during the whole cardiac cycle. Figure 3a, b shows the successfully reconstructed subject-specific LV models at end-diastole and end-systole for Subjects 1 and 2, respectively. Although aortic (AV) and mitral (MV) valve motion was not simulated in this study, we approximated valve function numerically by changing the boundary conditions for the corresponding systolic and diastolic phases²⁹, and geometrically by image-based anatomically-driven dynamic annular structures. The reference planes and lines where the velocity measurements will be analyzed are indicated in Figure 3c.

Figure 3.

Subject-specific LV models at end-diastole and end-systole for a) Subject 1, b) Subject 2, and c) reference planes and lines. A and P represent anterior and posterior directions. H and V represent the horizontal and vertical lines, with the black circles indicating the origin of the lines

4. Numerical methods

4.1 SPH modeling

A detailed description of SPH fundamentals can be found in Monaghan et al.⁷ and Morris et al.⁹. Briefly, SPH is a fully Lagrangian particle solver where the particle connectivity evolves with time and needs to be determined by a particle search. This concept is interpreted numerically using a summation

$$A({\mathbf{r}}_{\mathrm{a}})=\sum _{\mathrm{b}}{m}_{\mathrm{b}}\frac{A_{\mathrm{b}}}{{\rho }_{\mathrm{b}}}W({\mathbf{r}}_{\mathrm{a}}-{\mathbf{r}}_{\mathrm{b}},h)$$ (1)

where A_b denotes any physical property at particle ‘b’ within the neighboring domain (limited by the influence length h of the kernel) of particle ‘a’ at position r_a. Particle ‘b’ has mass m_b, position r_b, and density ρ_b. In this study, a cubic spline kernel function W was adopted. Using this equation and its derivatives, the governing equations of fluid flow can be rewritten under the form of SPH formulation. The time derivative form of the conservation of mass gives

$$\frac{\mathrm{d}{\rho }_{\mathrm{a}}}{\mathrm{d}t}={\sum }_{\mathrm{b}}{m}_{\mathrm{b}}{\mathit{\nu }}_{\text{ab}}·{\nabla }_{\mathrm{a}}{W}_{\text{ab}}.$$ (2)

Here ∇_aW_ab is the gradient of the kernel function regarding the coordinates of given particle ‘a’ and ν_ab = ν_a − ν_b denotes the relative velocity vector between particles ‘a’ and ‘b’. Similarly, the conservation of momentum under the SPH scheme can be written as

$$\frac{\mathrm{d}{\mathit{\nu }}_{\mathrm{a}}}{\text{dt}}=-{\sum }_{\mathrm{b}}{m}_{\mathrm{b}}\left(\frac{P_{\mathrm{a}}+P_{\mathrm{b}}}{{\rho }_{\mathrm{a}}{\rho }_{\mathrm{b}}}\right){\nabla }_{\mathrm{a}}{W}_{\text{ab}}+{\sum }_{\mathrm{b}}{m}_{\mathrm{b}}\frac{({\mu }_{\mathrm{a}}+{\mu }_{\mathrm{b}}){\mathit{\nu }}_{\text{ab}}}{{\rho }_{\mathrm{a}}{\rho }_{\mathrm{b}}{\mathbf{r}}_{\text{ab}}^2}{\mathbf{r}}_{\text{ab}}·{\nabla }_{\mathrm{a}}{W}_{\text{ab}}$$ (3)

where P is pressure and μ is the dynamic viscosity of the fluid. More details on the implementation of the SPH formulation in Abaqus/Explicit (SIMULIA, Providence, RI) can be found in our previous publication¹⁸. In this study, blood was assumed as an incompressible Newtonian fluid of density ρ = 1056 kg/m³ and dynamic viscosity μ = 0.0035 Pa · s. SPH particles were initially uniformly distributed in the domain with a spatial resolution of 0.8 mm. This led to approximately 594,000 PC3D elements in the domain for the LV-SPH model of Subject 1, and 497,400 PC3D elements for Subject 2. The mesh sensitivity of SPH particles was checked previously¹⁸, thus a similar particle density was adopted here. Two cardiac cycles were conducted and the results from the second cycle were analyzed. It was found that the difference in the velocity results between the first and second cycle was within 5%.

4.2 CFD modeling

The Navier-Stokes equations for 3D unsteady flow with moving walls are solved using the FV-based CFD solver Star-CCM+ (CD-adapco, Melville, NY). For a control volume V with surface S moving with local surface velocity ν_b, the integral form of the continuity equation is

$$\frac{\partial }{\partial t}{\int }_V\rho \mathrm{d}V+{\int }_V\rho (\overrightarrow{\mathit{\nu }}-{\overrightarrow{\mathit{\nu }}}_b)·\overrightarrow{\mathit{n}}\mathrm{d}S=0$$ (4)

where n⃗ is the outward unit normal vector to the differential area dS, ρ is the density of the fluid, ν⃗ = (u, ν) is the velocity vector of the fluid in the fixed coordinate system, and ν⃗_b = (u_b, ν_b) is the velocity vector of the moving boundary S of control volume V. The momentum equation in integral form is given by

$$\frac{\partial }{\partial t}{\int }_V\rho \overrightarrow{\mathit{\nu }}\mathrm{d}V+{\int }_S\rho \overrightarrow{\mathit{\nu }}(\overrightarrow{\mathit{\nu }}-{\overrightarrow{\mathit{\nu }}}_b)·\overrightarrow{\mathit{n}}\mathrm{d}S=-{\int }_{S}P\overrightarrow{\mathit{n}}\text{ dS}+{\int }_S\overline{\mathit{\tau }}·\overrightarrow{\mathit{n}}\text{ dS}$$ (5)

where P is the pressure and τ̄ is the viscous stress tensor. In the above equation, the body forces are ignored. For an incompressible Newtonian fluid, τ̄ is expressed as

$${\tau }_{\mathit{\text{ij}}}=\mu (\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i})$$ (6)

For this type of problem where the mesh is moving, an additional equation called the space conservation law is solved for the moving coordinate velocity components

$$\frac{\partial }{\partial t}{\int }_V\mathrm{d}V-{\int }_S{\overrightarrow{\mathit{\nu }}}_{\mathrm{b}}·\overrightarrow{\mathit{n}}\mathrm{d}S=0$$ (7)

This relates the change in cell volume to the cell-face velocity. The simultaneous satisfaction of the space conservation law and all other equations of fluid motion facilitates the general moving mesh operations performed. The development and solution of the discretized forms of these equations is straightforward within the FV framework, provided that appropriate measures are taken to ensure obedience to the space conservation law³⁰. The Navier-Stokes equations for 3D flow with moving walls are solved by a second order segregated iterative method (SIMPLE algorithm). A detailed description of the numerical method can be found in^{30, 31}.

Approximately 200,000 elements for the LV-CFD model of Subject 1 and 270,000 elements for Subject 2 were found to be sufficient to provide mesh-independent results (see Appendix A). The final volume mesh consisted of five prism layers near the wall and hexahedral cells at the core region. Convergence criteria for all the flow parameters were set to 10⁻⁵. To reach a periodic solution, the CFD simulations were repeated for four cardiac cycles using a time-step size of 1 ms.

5. Boundary conditions

5.1 LV wall

The ventricular wall motion was pre-described according to the medical imaging data. For Subject 1, a total of 8 phases from the original cine-MR images were used to prescribe the LV wall motion for one cardiac cycle, while 10 MSCT phases were used for Subject 2. This approach keeps the correspondence of the surface nodes of the computational domain by creating a unique LV mesh for all time steps, thus the movement of each node can be tracked over time. Briefly, from the segmented mesh in end-systole, a high quality template mesh was created in Hypermesh (Altair Engineering, Inc., MI) using four-node shell elements (S4R). Then, a preprocessing inflation simulation in Abaqus/Explicit was implemented, in which the template mesh was inflated to match the mesh from the next cine-MR or MSCT phase. In this fashion, the LV models maintained the same number of nodes across all phases, thus ensuring one-to-one connectivity.

As numerical simulations typically involve time steps smaller than the time interval between two cine-MR or MSCT phases, displacements were interpolated in time. Previous studies with linear interpolation of the LV wall showed high discontinuities in the flow and pressure solution due to the resulting discontinuities in mesh acceleration³², thus, cubic spline was used to interpolate the displacement of each node in time. No-slip boundary condition was applied to the LV-CFD models. For the LV-SPH models, the interaction between SPH particles and the LV wall was based on node-to-surface contact. The node-to-surface contact interaction in SPH is directly related to the no penetration boundary condition. Thus, the combined effect of the smoothing kernel interpolation function near the wall and the node-to-surface contact interaction partially enforces the no-slip boundary condition.

5.2 Inlet and outlet

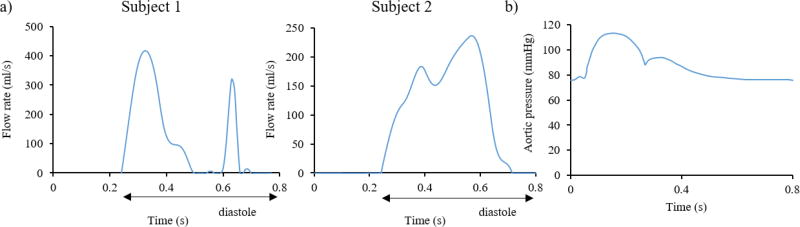
As blood is considered incompressible, reasoning based on mass conservation can be made to overcome the lack of detailed inflow and outflow information. The volume flow rates into and out of the model are thus driven by the expansion and contraction of the LV and proximal LA. For the inlet boundary condition, the CFD and SPH models employed the diastolic flow rate waveform derived from the LV volume change (including the proximal LA), with its value set to zero during systole^33–37 (Figure 4a). For the outlet boundary condition, a physiological aortic pressure waveform³⁸, as seen in Figure 4b, was applied. In order to avoid the boundary effects on the region of interest, the inlet and outlet boundaries of the models were moved away from the position of the mitral and aortic orifices by extending the proximal LA and LVOT with tubes^{39, 40} (not shown in Figure 3). Since the SPH formulation in Abaqus lacks periodic boundary conditions, the tubes were extended long enough to accommodate the inflow and outflow of particles for two full cardiac cycles. Rigid plates at the extensions were used to apply the boundary conditions in the LV-SPH models¹⁸. Similarly to the LV-CFD models, the diastolic flow rate waveform was applied on the inlet plate, while the aortic pressure curve was applied on the outlet plate of the LV-SPH models.

Figure 4.

a) Inlet flow rate for Subject 1 (left) and Subject 2 (right), and b) Outlet pressure

Note that differences in the diastolic flow rate between this study and normal physiological curves refer to 1) the fact that our flow curves included the volume change of not only the LV but also the volume change of the proximal LA, 2) imaging and segmentation uncertainties, as well as to the reduced number of imaging phases, since minor fluctuations in the volume curve lead to considerable changes in the flow rate waveform. Nonetheless, as explained in the following section, global flow parameters matched with in vivo clinical data and were within physiological range. The heart rate for both subjects was approximately 75 bpm, corresponding to a cardiac cycle of t=0.8 s.

RESULTS

Global flow parameters

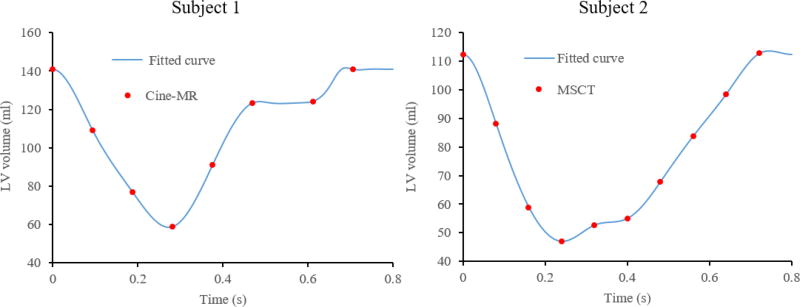
Figure 5 shows the LV blood volume over time for both subjects, where the points indicate the cine-MR or MSCT phases and the lines represent the cubic spline interpolation. For Subject 1, the end-diastolic (EDV) and end-systolic (ESV) volumes were 140 ml and 58 ml, respectively, which are within the physiological range typically measured in males⁴¹. The stroke volume (SV) and the ejection fraction (EF) were 82 ml and 58%, respectively. For Subject 2, the EDV and ESV were 112 ml and 47 ml, giving a SV of 65 ml and EF of 58%, values that closely match the patient-specific data obtained from Doppler Echo of 64 ml and 57%, respectively.

Figure 5.

Time variation of LV volume for Subject 1 (left) and Subject 2 (right).

Large-scale intraventricular flow patterns

Figures 6 and 7 show the velocity vectors in the anterior–posterior plane (see Figure 3c) for the LV-MRI (a), LV-SPH (b,d), and LV-CFD (c,e) models during peak systole (t=0.09 s) and early diastole (t=0.37 s), respectively. From the figures it can be seen that the intra-subject LV hemodynamics generated by the LV-SPH models had a similar overall topology as those measured in the LV-MRI and simulated in the LV-CFD models. At peak systole (Figure 6), a strong outward jet was developed at the LVOT, with an almost equal maximum velocity of 1.4 m/s. The LV-SPH models gave a good representation of the ejection phase, with the flow converging towards the outflow tract. As shown in Figure 6a, the LV-MRI maximum velocity for Subject 1 was highly localized in the central outflow region, as compared to the CFD and SPH results. Since the MV is not included in the numerical models, some minor backflow of blood into the LA can be observed, especially in the LV-CFD for Subject 1 (Figure 6c).

Figure 6.

Velocity vectors in the anterior-posterior plane for Subject 1 (a,b,c) and Subject 2 (d,e) during peak systole at t=0.09 s.

Figure 7.

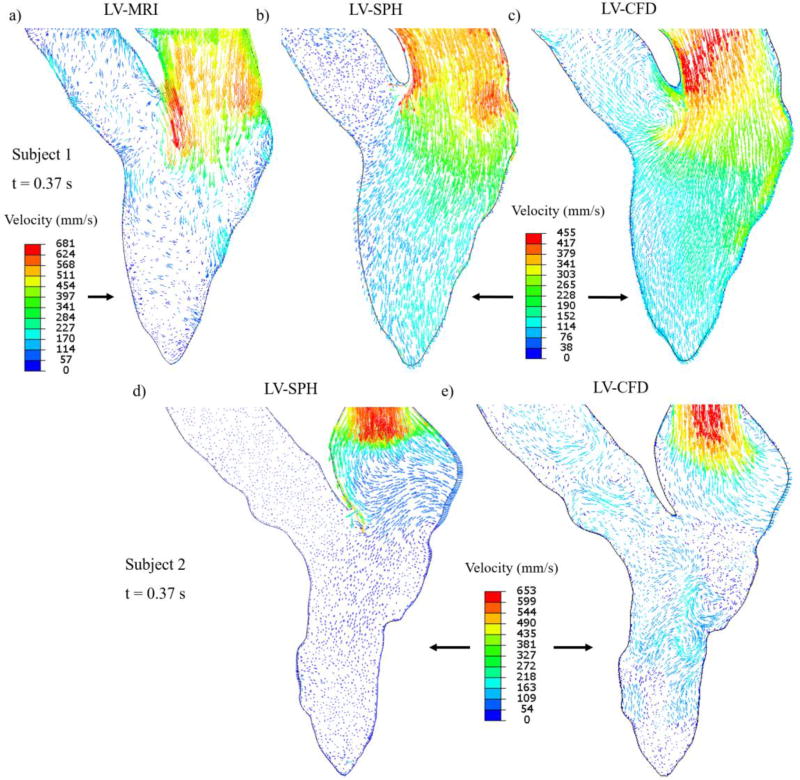
Velocity vectors in the anterior-posterior plane for Subject 1 (a,b,c) and Subject 2 (d,e) during early diastole at t=0.37 s. For clarity, for Subject 1, the scale of the velocity vectors is the same for the SPH and CFD models, while is different for the MRI model. For Subject 2, the velocity scale is the same for both SPH and CFD models.

Once diastole begins and the LV wall and MA start to expand, the blood enters from the LA to the LV, forming a jet through the mitral orifice. During early diastole (Figure 7), the intra- subject flow patterns of the LV-SPH models were similar to the CFD results and PCMR measurements. For Subject 1, the LV-MRI maximum velocity magnitude at the level of the MA was approximately 0.68 m/s (Figure 7a), compared to the 0.45 m/s of the numerical models (Figure 7b,c).

In diastole, due to the high velocity differences of the inflow blood and the retaining blood inside the LV, a vortex ring is developed in the LVOT region, as shown in a representative image for Subject 1 (Figure 8). The vortex seen in the SPH and CFD models is generated from the jet shear layer that is rolled up by viscous forces exerted from the resting fluid onto the jet core^{42,43, 44}. As shown in Figure 8a and further explained below, during this phase and late- diastole the velocities in the LV are low and the LV-MRI measurements do not show a clear distinction between the small-scale vortices and the background noise.

Figure 8.

Velocity vectors in the anterior-posterior plane for Subject 1 during E-wave deceleration at t=0.42 s. For clarity, the scale of the velocity vectors is the same for the SPH and CFD models, while is different for the MRI model

Quantitative comparison of velocity profiles

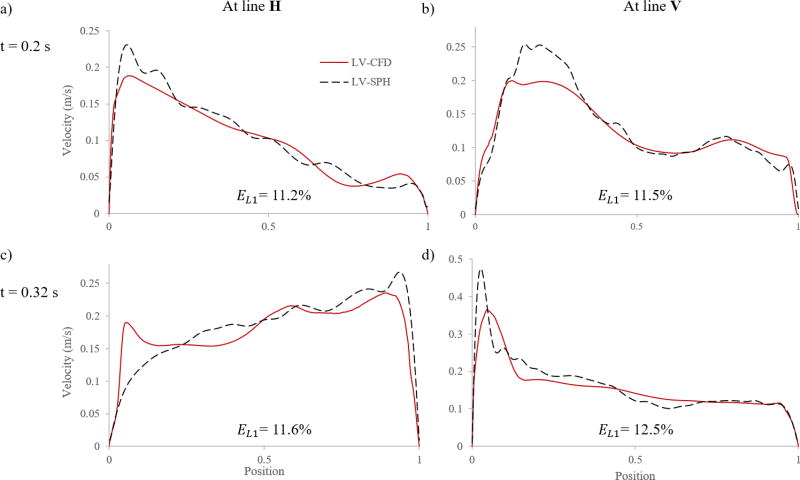
In order to quantitatively compare the SPH and CFD results, velocity profiles at different time instants at mid-horizontal (H) and mid-vertical (V) lines inside the LV (see Figure 2c) were measured and plotted in Figure 9 for Subject 1. Because of the Lagrangian nature of the SPH method, the velocity magnitude was calculated by averaging particle velocities enclosed from evenly space spheres of radius 1.5 mm along the lines. From Figure 9 it is clear that, in general, the SPH results were in good agreement with those extracted based on the CFD method. However, there was a discrepancy in the velocity magnitudes, and this difference was mostly concentrated in the regions near the LV wall. The discrepancy in the velocity profiles was quantified by the L₁- relative error norm (E_L1), defined as

$$E_{L1}=\frac{\Vert {\nu }_{\mathit{\text{SPH}}}-{\nu }_{\mathit{\text{CFD}}}\Vert }{\Vert {\nu }_{\mathit{\text{CFD}}}\Vert }$$ (5)

For E_L1, shown in Figure 9, it is found that the velocity difference between the two models was around 11%. The highest discrepancy was 12.5%, and this occurred for line V at t = 0.32 s.

Figure 9.

Velocity profiles and errors at different time instants at mid-horizontal (H) and mid-vertical (V) lines for Subject 1

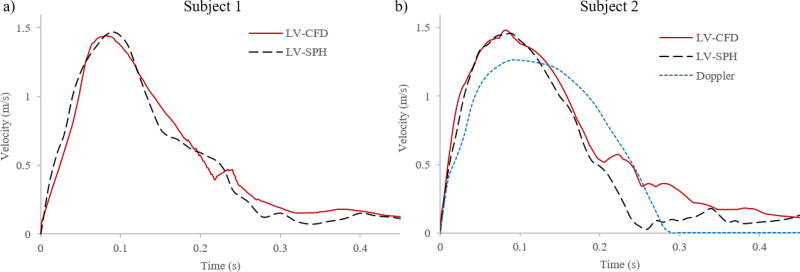
For a more clinically relevant quantitative evaluation, we compared the maximum flow velocity magnitude at the LVOT plane (see Figure 3c) during the systolic phase between the LV-SPH (dotted line) and the LV-CFD (solid line) models for both Subjects. Figure 10a shows that for both numerical models of Subject 1, the LVOT velocities reached a close agreement in regards to magnitude and velocity waveform with nearly identical value around t = 0.09 s. As discussed in the next section, inaccuracies, limited resolution, and multiple-beat ensemble averaging of the 4D PCMR data prevented a direct comparison of the LV-MRI velocity waveform with the SPH and CFD models at the LVOT plane for Subject 1.

Figure 10.

Maximum LVOT velocity from different data sets during systole for a) Subject 1, and b) Subject 2

Similarly, for Subject 2, the maximum flow velocity magnitude at the LVOT during systole was compared between the LV-SPH model, the LV-CFD model, and the patient-specific Doppler velocity recordings (Figure 10b). Figure 10b shows that for both computational models, the LVOT velocity reached a nearly identical maximum value at 0.09 s, with a close agreement in the velocity waveforms. For the Doppler waveform, however, a 12% lower peak velocity was observed compared to the numerical models.

Overall, the LV-SPH models quantitatively matched to a good degree with the LV-CFD models and to a reasonable degree with the patient-specific in vivo data. Despite the fact that the near wall flow features were not modeled accurately using Abaqus SPH formulation, we obtained similar bulk flow information as the traditional mesh-based CFD models.

DISCUSSION

This study investigated the capability of a SPH framework, implemented in commercial software ABAQUS, to simulate the bulk blood flow dynamics in realistic 3D LV models. Quantitative and qualitative comparisons of SPH simulation results with those of in vivo clinical flow measurements and a CFD approach have been presented. The comparison between the three data sets is encouraging, showing that the SPH method can capture the large-scale flow dynamics with a similar level of accuracy as a traditional mesh-based CFD method. The study by Shahriari and colleagues²⁰ was essential to validate the SPH approach when applied to the study of 2D cardiovascular flows. The main limitation of this study was, however, the assumption of a 2D rigid LV geometry. Cardiac flow with moving LV wall has also been investigated by Kulp et al¹⁷. Nevertheless, the model analyzed in this study lacked verification of simulation results.

The SPH results of this study indicate the capability of SPH as a promising tool for predicting clinically relevant large-scale LV flow information. First, there was generally a good match between the simulated and measured velocity fields at different time points of the cardiac cycle (Figures 6–8). During systole, the intra-subject flow patterns were qualitatively similar for the three data sets of Subject 1 (Figure 6a–c), and for the two data sets of Subject 2 (Figure 6d–e). However, as shown in Figure 5a, the highly localized velocity vectors at the LVOT for the LV-MRI measurements probably originate from the level of uncertainty in the acquisition and interpolation of the PCMR data, as well as from the stronger jet flow due to the AV dynamics, which was not incorporated in this study.

During early diastole, the intra-subject flow patterns were also similar; but the velocity magnitude of the LV-MRI measurement for Subject 1 (Figure 7a) was higher than that from the in silico models (Figure 7b,c). The absence of MV leaflets in the computational models affected the accuracy of the velocity calculations, as a bigger orifice area, and thus a smaller flow jet, was obtained for the in silico models. In PCMR measurements of the velocity through the MV during diastole, Kim et al.⁴³ and Fujimoto et al.⁴⁴ noted velocity magnitudes at the leaflet tips between 15%–20% greater than that at the MA. During mid- to late-diastole, the LV-MRI results did not show a clear presence of the vortices as the simulation results did (Figure 8). A possible reason of this phenomenon is that the velocity encoding factor used in the PCMR imaging was constant over the entire cardiac cycle, and was selected to exceed the expected peak systolic velocities in the LVOT to avoid velocity aliasing. As a consequence, small-scale vortical features and regions with low flow suffered from low signal in the PCMR data and thus lead to impaired depiction.

When the intra-subject systolic velocity waveforms at the LVOT were quantitatively compared between the different models (Figure 10), a good agreement in regards to magnitude and velocity waveform was obtained. Moreover, the level of discrepancy between the computational and Doppler velocity measurements for Subject 2 (Figure 10b) were in-line with the inherent uncertainties in the pulsed-waved Doppler flow recordings. Doppler velocity measurements are dependent on the ultrasound beam orientation, maximum velocity information should be obtained with the ultrasound beam aligned as parallel as possible to the flow, otherwise the maximum velocity will be underestimated⁴⁵.

It is also noted that along the centerlines in Figure 9, the shape of the velocity profiles was similar, but there was a discrepancy in the velocity magnitudes near the LV wall. This may be because the no-slip condition was not fully constrained in the Abaqus SPH formulation. This situation caused differences between the LV-SPH and LV-CFD velocity profiles for Subject 1 of approximately 11%. However, the SPH method was able to capture the bulk LV flow with reasonably accuracy, and the large-scale intraventricular hemodynamic features obtained were similar to what have been reported in previous mesh-based LV studies^{34, 46, 47}.

PCMR is currently considered the gold standard for non-invasive quantification of cardiac blood flow, as this technique has been validated extensively^{48, 49}. Nevertheless, there are some known limitations associated with PCMR flow measurements^{50, 51}. Blurring or ghosting artifacts are common due to breathing motion⁵². Particularly for 4D PCMR data acquisition, large amounts of data require measurement durations that often exceed normal human breath-holding capabilities. To achieve a high SNR, the patient needs to be scanned for multiple cardiac cycles, and the velocity fields from different cardiac cycles are combined to form a single 4D velocity field⁵³. To achieve a high spatial resolution, a long imaging time is also required, which will lead to more artifacts induced by respiratory movement. Therefore, there is a trade-off among SNR, time-resolution and spatial-resolution. Our comparison of the in vivo measured and in silico simulated velocity results should be interpreted with the consideration of these PCMR recording limitations.

In comparison with conventional CFD methods, implementation of boundary conditions, especially the no-slip condition, is not straightforward with SPH^{21, 22}. The default interaction between SPH particles and Lagrangian boundaries in Abaqus is based on node-to-surface contact. The SPH discretization relies on a kernel interpolation that requires full support to obtain an accurate approximation of the field quantities and derivatives. When particles are close to the boundary, part of the supporting domain of the smoothing kernel will not be filled with SPH particles. Therefore, the integration accuracy for those SPH particles close to the boundary may be affected⁵⁴. To improve the SPH solution near the wall, it is possible to specify in Abaqus the so-called ghost particle method⁵⁵. Ghost particles fill the boundary by mirroring real particles and their attributes are extrapolated such that the no-slip condition is satisfied. The two main drawbacks of this method are 1) the need of recreation of ghost particles at every time step, and 2) direct mirroring only works for simple geometries⁵⁶, thus, this boundary method could not be applied to our LV-SPH models.

Another intrinsic modeling limitation of this study was ignoring the native heart valve structures. Past studies have shown that by choosing appropriate inlet information together with global geometric and flow parameters that are within physiological range, computational models with simplified valve structures can reproduce the flow features associated with LV function with reasonably accuracy^{29, 35, 38, 57, 58}. It is well known that for a computational heart model to become a clinically relevant simulation tool it must be able to capture the FSI between the blood flow and the heart valves⁵⁹. Conventionally, many of the FSI approaches used to study LV function have been based on conventional CFD mesh-based methods, however, complex LV dynamics can lead to computational challenges. A fully-coupled modeling approach that combines the transparent meshless character of SPH together with a nonlinear FE formulation can be implemented in a natural and simple way to simulate the intraventricular hemodynamics and valves structural response. This is the subject of a study we are currently undertaking.

The final modeling simplification was the topology of the endocardium, by assuming a smooth-walled endocardium without papillary muscles and trabeculae. The influence of these structures on the LV flow field may be significant^{60, 61}, and should be explore in a future study. Given that the model simplifications were kept the same for the numerical models, it is expected that a comparison of these data sets provided useful insights into the capability of SPH to model the large-scale LV blood flow dynamics. The LV-SPH framework presented here is an initial step towards a versatile and simple mesh-free methodology to study the global 3D LV flow phenomena.

APPENDIX

Appendix A: Mesh independence study

Tests on mesh sensitivity were performed on the LV-CFD models by comparing results obtained with three different mesh densities: coarse (100,000 elements, 150,000 elements), medium (200,000 elements, 270,000 elements), and fine (500,000 elements, 640,000 elements), for Subject 1 and Subject 2, respectively. The L₁- relative error norm (E_L1) of the instantaneous velocity profile along the LVOT plane center line at peak systole for Subject 1 was 8.6 % between the coarse and fine meshes, and 4.8 % between the medium and fine meshes. For Subject 2, E_L1 was 5.2 % between the coarse and fine meshes, and 3.9 % between the medium and fine meshes. Similarly, E_L1 of the instantaneous velocity profile along the MA plane centerline at the E-wave for Subject 1 was 10.3 % between the coarse and fine meshes, and about 4.4 % between the medium and fine meshes. For Subject 2, was 9.8 % between the coarse and fine meshes, and 4.9 % between the medium and fine meshes. A reasonable convergence was therefore achieved on the medium grid resolution in terms of the intraventricular flow field. Therefore, the CFD results presented in this study employed the medium mesh density.

Figure A1.

Results of LV-CFD mesh sensitivity for Subject 1 (a,c), and Subject 2 (b,d) models