Modeling of Antilatency Treatment in HIV: What Is the Optimal Duration of Antiretroviral Therapy-Free HIV Remission?

ABSTRACT

A number of treatment strategies are currently being developed to promote antiretroviral therapy-free HIV cure or remission. While complete elimination of the HIV reservoir would prevent recurrence of infection, it is not clear how different remission lengths would affect viral rebound and transmission. In this work, we use a stochastic model to show that a treatment that achieves a 1-year average time to viral remission will still lead to nearly a quarter of subjects experiencing viral rebound within the first 3 months. Given quarterly viral testing intervals, this leads to an expected 39 (95% uncertainty interval [UI], 22 to 69) heterosexual transmissions and up to 262 (95% UI, 107 to 534) homosexual transmissions per 1,000 treated subjects over a 10-year period. Thus, a balance between high initial treatment levels, risk of recrudescence, and risk of transmission should be considered when assessing the “useful” or optimal length of antiretroviral therapy-free HIV remission to be targeted. We also investigate the trade-off between increasing the average duration of remission versus the risk of treatment failure (viral recrudescence) and the need for retreatment. To minimize drug exposure, we found that the optimal target of antilatency interventions is a 1,700-fold reduction in the size of the reservoir, which leads to an average time to recrudescence of 30 years. Interestingly, this is a significantly lower level of reduction than that required for complete elimination of the viral reservoir. Additionally, we show that when shorter periods are targeted, there is a real probability of viral transmission occurring between tests for viral rebound.

IMPORTANCE Current treatment of HIV involves patients taking antiretroviral therapy to ensure that the level of virus remains very low or undetectable. Continuous therapy is required, as the virus persists in a latent state within cells, and when therapy is stopped, the virus rebounds, usually within 2 weeks. A major question is how to reduce the amount of persistent virus and therefore allow a delay or remission until the virus returns after ceasing therapy. In this work, we consider the probability that HIV will still rebound even after this reduction and ask what the likelihood of viral transmission would be in this case.

INTRODUCTION

Combination antiretroviral therapy (ART) suppresses HIV replication below the level of detection in most subjects. However, if treatment is discontinued, the virus commonly rebounds within weeks. This rebound virus is most likely derived from long-lived latently infected cells, which persist for many years despite effective ART (1, 2). A large number of approaches are currently being developed to reduce the number of latently infected cells (3) or to reduce the frequency with which virus is released from latently infected cells (4). They include approaches aimed at reactivating and killing latently infected cells (5) and enhancing immune-mediated clearance of virus (6, 7), as well as gene therapy approaches aimed at making cells resistant to HIV or silencing the HIV genome within latently infected cells (8, 9). The goal of these approaches is either to completely eliminate latently infected cells or to completely silence virus in latently infected cells. However, the most effective current treatments are able to reduce the size of the latent reservoir only by approximately 2-fold (6) and have been able to achieve ∼10-week viral remission (10, 11). If the goal of complete eradication cannot be met, it is hoped that in future latency-reducing agents can at least safely and significantly delay viral rebound off ART to allow prolonged antiretroviral therapy-free remission in most patients.

Mathematical models suggest that following ART interruption, a viral reactivation event that leads to ongoing viral replication and viral rebound occurs within 4 weeks (12). In a minority of patients, this recrudescent virus may be controlled by immune effector mechanisms or other factors (13). Although there is no perfect biomarker that predicts the time to viral rebound, several studies have shown an association between time to viral rebound and the level of cell-associated RNA in patients on ART (12), total cellular HIV DNA in peripheral blood mononuclear cells (PBMC) (14), and expression of immune exhaustion markers prior to ART initiation (15). Interventions capable of reducing the size of the pool of latently infected cells (the latent reservoir), or the frequency of viral reactivation from latently infected cells, should delay the average time to viral rebound off ART.

Here, we use mathematical modeling to investigate the impacts of treatments designed to reduce the frequency of viral reactivation and to extend the time to viral rebound after ART interruption (ART-I). We use a stochastic modeling approach to investigate the effects of interventions that reduce the size of the latent reservoir and the impact they would have on the number of subjects experiencing viral rebound and the probability of viral transmission. We found that even if a 1-year average delay until viral remission is achieved, there will be an estimated 39 (95% uncertainty interval [UI], 22 to 69) HIV transmissions per 1,000 heterosexual treated patients and up to 262 (95% UI, 107 to 534) per 1,000 homosexual patients over a 10-year period. We also use a simplified analytical model to show that there is an optimal “target” average time to viral rebound of around 30 years.

RESULTS

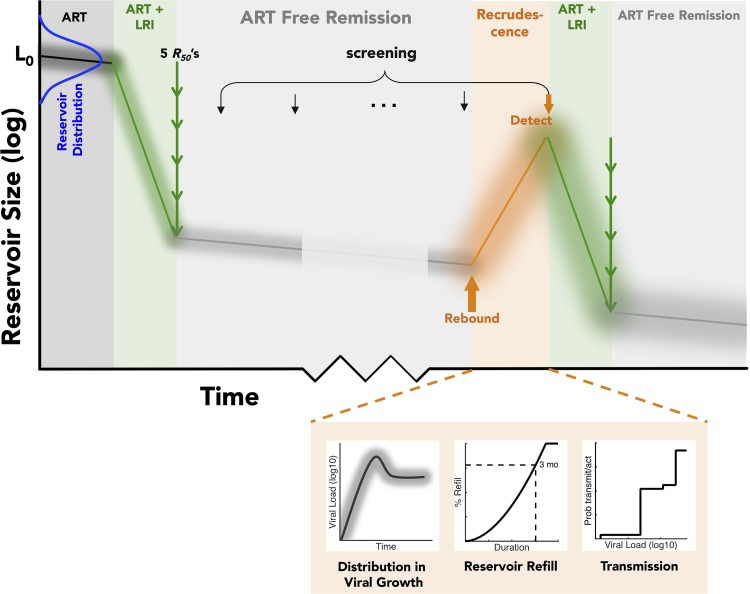
We first explored the relationship between the average time to viral rebound after treatment and the actual likelihood of both reactivation and transmission. It is likely that subjects have latent reservoirs of various sizes and different viral growth rates and will be screened intermittently for viral reactivation and that retreatment will take some time. To account for these possibilities, we implemented a stochastic model that mimics population heterogeneity in the size of the subjects' pools of latently infected cells and time to detection of viral rebound, as well as heterogeneity in viral transmission. Details of this model are given in Materials and Methods, but briefly, simulated subjects were given an intervention to reduce the size of their latent reservoir and then screened periodically for viral recrudescence. If virus was detected, they were placed on both ART and another course of the latency-reducing intervention for a fixed time. We allowed a population distribution in (i) the initial number of latently infected cells (14, 16), (ii) the reduction in reservoir size effected by a latency reversing agent (LRA), (iii) the growth rate of the virus upon rebound (6, 17), (iv) the rate of refilling of the pool of latently infected cells (estimated from reference 16), and (v) the probability of viral transmission upon rebound (18–20) We simulated a situation in which subjects were screened for viral rebound once every 3 months. A graphical depiction of the model, as well as a schematic of the numbers of latently infected cells over time, is shown in Fig. 1.

FIG 1.

Depiction of the stochastic model to determine the chance of viral reactivation from latency and subsequent viral growth and detection after introduction of a latency-reducing intervention.

Estimating the impact of an average 1-year delay to viral rebound.

We found that if an intervention is initially able to reduce the average frequency of viral rebound events to once per year, then 30% of patients would experience reactivation from latency within 3 months after completing the intervention, i.e., within the current screening interval. After 2 years, over 70% of patients would have experienced viral rebound. Thus, to achieve a meaningful ART-free remission for a significant proportion of subjects, the average duration of viral remission must be increased to considerably more than 1 year.

Long average duration of ART-free remission still leads to some early reactivation.

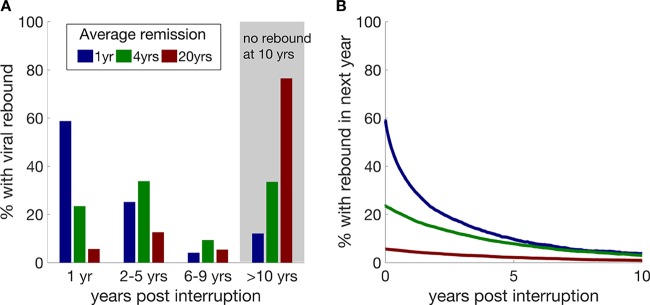
If the latent reservoir can be shrunk sufficiently to reduce the average duration of ART-free remission to 4 years, then nearly one-quarter of patients will still experience viral rebound within the first year, purely due to chance stochastic events. However, in parallel, a large proportion of the other patients (34% and 76% for 4- and 20-year average duration of remission, respectively) will still remain in remission 10 years after the intervention (Fig. 2A).

FIG 2.

Probability of viral rebound following treatment with latency-reducing interventions that achieve different durations of ART-free remission. (A) Proportions of patients experiencing viral rebound at various times after the latency-reducing intervention is completed if the initial average duration of ART-free remission effected by the intervention is 1 year, 4 years, or 20 years. (B) The probability of viral rebound within the next year decreases as the length of time already spent in ART-free remission increases.

Probability of reactivation decreases over time.

Latently infected resting central memory T cells have a natural half-life of approximately 4 years (1, 2, 21). Thus, the longer a subject remains in ART-free remission, the less likely it becomes that he/she will experience viral rebound (Fig. 2B). This could be used to advise subjects of their risk-of-rebound status and to decrease testing regime frequency in a way similar to that in which individuals' cancer risk is classified according to the time that they have been cancer free.

Does early treatment failure imply a large viral reservoir?

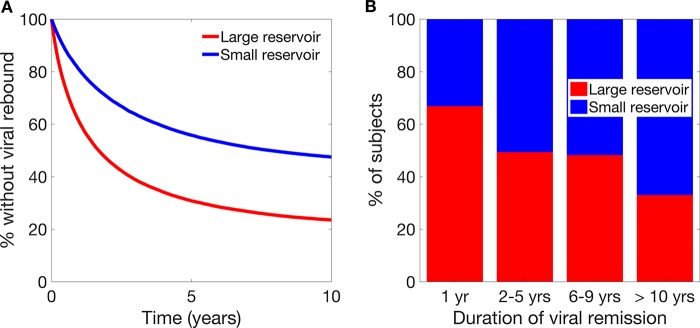
Recent studies suggest delayed recrudescence in subjects with fewer latently infected cells prior to ART interruption (12, 14, 22), so we used our stochastic simulation to explore whether a subject's initial number of latently infected cells could be used as a predictor of the time to viral rebound once all the other potential sources of variation were included. Indeed, as these studies suggest, if we divide our simulated subjects into two groups based on the simulated initial size of their population of latently infected cells, we can observe differences in the time until viral rebound from latency between those in the bottom 50% of subjects (small reservoir) and those in the top 50% of subjects (large reservoir) (33% versus 67% in the first year for those with small and large reservoirs, respectively) (Fig. 3A). However, closer inspection revealed that the pretreatment size of the latent reservoir is not directly related to the time until viral reactivation and on its own is unlikely to be a useful predictor of whether a subject will respond well to an intervention. Indeed, due to the stochastic nature of when a subject will recrudesce, a large proportion of subjects experiencing early viral rebound had a small population of latently infected cells (Fig. 3B), making it difficult to use the starting number of latently infected cells alone as a predictor of the time to viral rebound.

FIG 3.

Viral reservoir sizes and reactivation. (A) Survival curve of time to viral rebound for subjects with either a smaller than average or larger than average latent reservoir. (B) Duration of viral remission for subjects with a smaller than average or larger than average latent reservoir.

Probability of viral transmission.

Another fundamental question facing the use of latency-reducing interventions is what the likelihood is that a subject will attain high viral loads and be able to transmit virus prior to their viral rebound being detected. We found that with quarterly screening of plasma HIV RNA off ART, and assuming viral growth rates were as reported previously (6, 17), 92% of patients experiencing viral rebound would attain viral loads that were above 10,000 copies/ml (a viral load within the “normal” range for untreated individuals) prior to their viral rebound being detected, and of these, 65% would have had viral loads above this threshold for more than 1 month. Even if monitoring were increased to screen plasma viral loads every 14 days, 37% of patients experiencing viral rebound would have had virus at a level above 10,000 copies/ml for more than 1 day by the time of virus detection. These percentages are independent of the average time between viral reactivation events.

We next asked what was the chance that a subject would transmit virus prior to having their viral rebound detected. Incorporating both the viral-load-dependent probability of viral transmission per act of intercourse, the number acts of intercourse, and overall transmission rate estimates (18–20) into our model, we found that regardless of the time until viral rebound, for heterosexual transmission and given a 3-month screening regime, rebounding subjects across all income settings would have a 4.1% chance (95% UI, 2.28 to 7.28%) of transmitting HIV in the period prior to having their rebound first detected. This was reduced to a 1.76% chance (95% UI, 0.73 to 4.12%) in a high-income setting. The results for insertive homosexual transmission were similar to those for heterosexual transmission (3.61%; 95% UI,1.25 to 10.22%). However, the risk increased to up to 27.6% (95% UI, 11.3 to 56.23%) for receptive homosexual transmission. Our model suggests that this would result in 39 (95% UI, 22 to 69) transmissions per 1,000 treated heterosexual patients (17/1,000; 95% UI, 7 to 39 in a high-income setting) and up to 262 (95% UI, 107 to 534) transmissions per 1,000 treated homosexual patients over a 10-year period.

An intervention that achieved a 4-year average duration of ART-free remission would reduce the number of transmissions per 1,000 subjects by around 1.5-fold compared to an intervention that achieved only a 1-year delay in remission, and an intervention that allowed an average 20-year delay in remission would result in just over 3 times fewer transmissions per 1,000 treated subjects than a 1-year delay.

Impact of repeated dosing with LRA.

Intermittent screening and heterogeneity in the rate of refilling the latent reservoir means that individuals will have varying numbers of latently infected cells at the time when their viral rebound is detected. We found that with quarterly screening for viral recrudescence and a 1-year average delay in viral remission, a subject's latent reservoir would refill to a median value of 28% (95% confidence interval [CI], 0.25 to 74%) of its original size before viral reactivation was detected and treated (similar results were obtained for other average durations of viral remission). This means that subsequent interventions (should they be done after reactivation had occurred) might generally act upon a smaller number of latently infected cells. Thus, the effect that repeat interventions have on a smaller latent reservoir will ultimately determine their overall usefulness. We next considered a simplified model of reservoir reduction and reactivation to understand some of the implications of repeat dosing.

A simplified model including repeat dosing.

Given that most individuals have a normal life expectancy on ART and that toxicity is minimal, a key goal of any intervention to achieve ART-free remission is safety. In the absence of such safety, it may be preferable for a patient to remain on ART rather than achieve ART-free remission through a latency-reducing intervention, particularly if that intervention carries significant safety risks. A highly potent initial latency-reducing intervention to decrease the number of latently infected cells may increase the chance of prolonged remission but may also expose the patient to higher risks of adverse effects. Conversely, less potent interventions may lead to relapse and require resumption of ART, as well as repeated or new treatments to reduce the latent reservoir. This dilemma led us to ask whether there is an optimal reduction in the reservoir size that can minimize the total amount that the reservoir would need to be reduced once we account for repeat dosing.

We quantified the potency of a latency-reducing intervention by considering the extent to which it reduced the frequency of reactivation (and thus increased the duration of antiretroviral therapy-free remission). We quantified this as the number of “half-reductions” (R₅₀s) that an intervention achieved. A single half-reduction reduced the frequency of reactivation by 50% and thus approximately doubled the average time to rebound. Such a half-reduction might be achieved by either halving the total number of (competent) latent cells, halving the probability that an individual latent cell would reactivate, or a combination of the two. We noted that the magnitude and rapidity of the reduction in the size of the latent reservoir did not affect the results of our model. It could be via a daily tablet that removed a proportion of cells with each dose, or it could be a different intervention, such as a bone marrow transplant that removed the vast majority of the latent reservoir during treatment. In order to compare results across different treatment possibilities, we focused only on the total number of half-reductions effected.

Our simplified model assumes that a certain number of R₅₀s are administered initially and that whenever subjects rebound, they are once again given the same number of R₅₀s. Since we did not have any real information on precisely how retreatment would work, we made the simplified assumptions that the latent reservoir completely refills prior to retreatment and that retreatment causes the viral reservoir to be reduced to the same level as at the initial treatment. A full description of this model can be found in Materials and Methods.

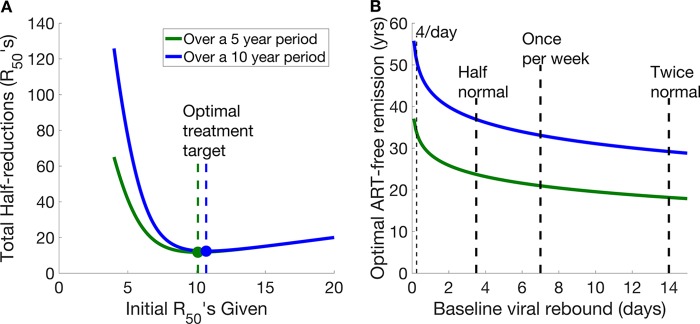
Figure 4A shows how the initial R₅₀s achieved when ART is first stopped are correlated with the total number of half-reductions that would be delivered over an extended period per individual (once all the retreatments are taken into account). To minimize the number of R₅₀s required over a 10-year period, it is optimal for an LRA to achieve ∼11 R₅₀s initially. This is equivalent to a reduction of over 1,700-fold in the size of the latent reservoir, equating to an average duration of remission of 33 years (assuming that the baseline frequency of reactivation is once per week) (Fig. 4A).

FIG 4.

(A) Total numbers of half-reductions that would be given over 5- and 10-year periods as the initial average duration of ART-free remission afforded by an intervention is varied. This assumes a baseline average time between reactivation events of 1 week. Minimum total numbers of half-reductions administered over 5- and 10-year periods are shown by the dots. (B) Optimal target duration of ART-free remission over 5 years (green) and 10 years (blue) given different initial baseline average times between viral rebounds. If the average time between viral reactivation events prior to a latency-reducing intervention is short, then the optimal duration of ART-free remission to be targeted is higher than if the baseline average time between viral reactivation events is longer.

If an intervention cannot achieve the optimal number of half-reductions during the initial course of treatment, the steepness of the left side of the curve in Fig. 4A makes it clear that even marginal improvements in the number of half-reductions achieved initially will dramatically reduce the total number of R₅₀s required over a prolonged period.

Effect of increasing initial dosage.

We next considered the difference between two interventions, one that effects 6 initial R₅₀s and another that effects 7 initial R₅₀s. An intervention effecting 6 initial R₅₀s (average time to viral rebound, just over 1 year) is far from optimal. Over 10 years, it results in multiple viral rebounds and retreatments in this simplified scenario, which together mean patients are required to receive 44 half-reductions over a 10-year period (i.e., they will need to be retreated approximately 6 times). In contrast, an intervention that effects 7 R₅₀s (only one additional R₅₀; average time to viral rebound, 2.5 years) would require only 26 half-reductions (i.e., an average of less than 3 retreatments with the same agent) over a 10-year period, a reduction in the total number of R₅₀s required of 42%. Indeed, the gain from an intervention that achieves more than 9 half-reductions (i.e., an ∼500-fold reduction in the reservoir, extending the average time to viral rebound beyond 10 years) is relatively low (only an 11% reduction to achieve the optimal number of R₅₀s over 10 years).

To illustrate this further, consider a population of 1,000 people given intervention A that achieves an average time between viral rebound events of 20 years through 10 half-reductions (a total initial treatment of 10 × 1,000 R₅₀s worth of initial treatment). Over a 10-year period, we would expect to observe 250 viral rebound events in these 1,000 subjects, who would each be retreated with the same intervention, meaning that retreatment of the cohort would require an additional 10 × 250 or 2,500 R₅₀s. In contrast, if we treated the 1,000 subjects with intervention B, which effects 13 half-reductions and achieves an average time between viral rebound events of 160 years (a total initial treatment of 13 × 1,000 R₅₀s worth of initial treatment), we would expect to see only 30 rebound events in these 1,000 subjects over a 10-year period, which would require 30 × 13 or 390 R₅₀s on retreatment. This is a saving of 2,110 R₅₀s on retreatment. However, it is achieved at the cost of an extra 3,000 R₅₀s in the initial treatment phase for intervention B over intervention A. If toxicity of the treatment is the key driver of acceptability, in total, intervention B is a less optimal intervention. If we were to consider only a shorter period (Fig. 1A) of 5 years, this balance between initial R₅₀s and retreatment R₅₀s is altered. Over 5 years, the optimal target duration of remission would be 21 years.

Is elimination worthwhile?

It is also useful to consider the difference between the number of half-reductions required for eradication versus the number required to achieve the estimated optimal time before viral rebound. For example, the number of latently infected cells has been estimated to be around 1 million (23). To reduce the number of latently infected cells from 1 million to <1 would require an intervention to achieve 20 half-reductions. However, as estimated above, beyond 11 half-reductions (average time to viral rebound, 33 years), the total number of R₅₀s required to be administered over a 10-year period actually increases due to an increase in the initial number of R₅₀s administered. Thus, intensifying treatment to achieve viral elimination may expose the patients to more latency-reducing treatment cycles than they would have required had this optimum level been targeted.

Impact of initial frequency of reactivation.

The analysis above assumes a baseline average frequency of viral reactivation of once per week (24); however, in reality, there is likely a distribution around this average (24, 25). Subjects in whom viral reactivation occurs more frequently than average have a higher optimal number of R₅₀s (Fig. 4B). If the baseline frequency of reactivation were extremely high (4 times per day, as has been proposed by others [26, 27]), the optimal initial target duration of ART-free remission would increase from 33 years to 51 years (Fig. 4B). The reason for this change is the altered “cost” of viral rebound and retreatment with the latency-reducing interventions in this scenario. With a higher baseline frequency of reactivation, an intervention requires additional R₅₀s to achieve the same duration of ART-free remission both on initial treatment and then later on subsequent reactivations. Thus, an intervention that achieves a longer duration of ART-free remission initially is preferable, as the higher penalty (in terms of number of retreatments) for HIV reactivation is not paid as often.

DISCUSSION

A major focus of current research is to provide HIV-infected subjects with prolonged periods of antiretroviral therapy-free remission. A recent study combining therapeutic vaccination and reversal of HIV latency with romidepsin showed a reduction in the level of total HIV DNA of approximately 2-fold (one R₅₀) (6). Other work has shown that treatment with broadly neutralizing antibodies was able to significantly delay the time of detection of recrudescent virus after treatment interruption, with some patients achieving ∼10 weeks of remission (10, 11). Multiple rounds or combinations of therapies may provide even longer remissions.

Recrudescence of virus raises significant risks of pathogenesis and transmission. Thus, a regime in which recrudescence occurred in a large proportion of patients would be problematic, even if retreatment were highly effective. Regular screening for virus would minimize these risks but must be balanced against the inconvenience, costs, and psychological effects of constant testing. Indeed, we found that with an average 1-year remission from reactivation, with testing at 3-month intervals, more than 60% of patients were likely to have virus at levels greater than 10,000 copies/ml for longer than 1 month, and there were likely to be an average of 39 transmission events per 1,000 treated subjects over a 10-year period. From this perspective, it is likely that either prolonged treatment with ART or complete eradication of latently infected cells may be preferable to simply extending remission from viral recrudescence.

It has been assumed in previous studies that the risk of viral reactivation decreases over time (28). The results of our modeling work support this assumption; however, we also show that the risk may not decrease as fast as has been previously assumed. We found that for interventions that initially reduce the average time between viral rebound events to between 1 year and 20 years, the risk of viral reactivation within the next year is decreased by between 15% and 27% each year due to the natural death of latently infected cells.

Another question to be asked of latency-reducing interventions is whether we need to completely eliminate the reservoir, or what the optimal duration of remission would be to reduce potential toxicity. Using a simple model, we showed that if latency-reducing interventions are to be used instead of ARTs, the optimal strategy of antilatency treatment of patients to minimize overall treatment dosing in the presence of high toxicity of drugs is not to eliminate the latently infected cells altogether but to increase the average duration of remission to around 30 years.

A more nuanced approach to minimizing the total latency-reducing treatment administered would be to identify an individual's risk of recrudescence, so that he or she can receive only the number of initial treatments required to achieve the desired reservoir size or remission duration. A number of approaches to measuring the viral reservoir have been proposed, although there is no consensus on the best measure. Some of these appear predictive of the time to recrudescence in cohort studies, although again, different studies observe different parameters as being predictive (for example, DNA or RNA) (12, 14, 15). If the latent reservoir and risk of recurrence could be accurately measured, this might allow reduced induction doses for some individuals (but require an increased number for others), although individual variation in reservoir size would have relatively little effect on the optimal target duration of remission. In the absence of an accurate measure of reservoir size and risk of recrudescence, one way of identifying high-risk individuals might be to target those patients who recrudesce early after interruption, as our work suggests that they have (on average) slightly higher numbers of latently infected cells. However, we show that, since failure to sustain ART-free remission is a random event, in most cases, early failure is not highly predictive of the underlying size of a subject's latent pool and hence the frequency of reactivation (Fig. 3B).

The modeling described here presents a novel approach to understanding the optimal length of ART-free remission to be targeted to both minimize drug dosage and maximize the chances of a patient remaining virus free. However, there are some limitations to our work. Our model relies on the assumption that the predicted time to viral rebound is related to the number of cells in the latent reservoir (as well as the frequency of reactivation of these cells). There is evidence from recent studies to support this relationship (12); however, it remains to be determined whether the relationship is as strong as we assume in our model. We also assume that all latently infected cells are independent of each other and that they are all essentially identical, thereby allowing us to use single rates of reactivation and decay for each patient. This is a realistic assumption based on the current understanding of latently infected cells (24); however, should evidence emerge that this is not the case, additional work will be necessary. Additionally, in our simple (deterministic) model, we have assumed that all patients have identical reservoir sizes and that reservoir refilling after viral rebound, ART, and the latency-reducing intervention occur instantaneously. Though this is an approximation that oversimplifies the actual distribution of reservoir sizes and timing, such assumptions allow us to use analytical tools to calculate an optimal dosing regime.

Using a combination of deterministic and stochastic modeling approaches, we have shown that aiming for a complete cure using latency-reducing intervention therapies may be setting the bar too high. Indeed, the optimal average duration of ART-free remission to be targeted is around 30 years. Achieving a remission period of significantly less than this will lead to some proportion of patients both requiring repeated rounds of therapy and also having unacceptably high probabilities of transmitting virus. Interestingly, due to the natural decay of latently infected cells, once a patient has remained virus free for over 5 years, their chances of relapse decrease significantly and continue to do so over time.

MATERIALS AND METHODS

Probability of reactivating from latency.

We have previously shown that viral rebound after treatment interruption occurs around once per week (T₀ = 5 to 8 days) (24, 25). We assume that the action of a latency-reducing intervention is to increase the average time between viral reactivation events by a factor of α, such that T is equal to αT₀, where T₀ and T are the average times between reactivation events before and after the intervention, respectively. This could be achieved either by reducing the size of the latent reservoir, by decreasing the frequency with which each cell in the latent reservoir reactivates virus, or a combination of the two approaches. For simplicity, we derive the model expressions for the case where the intervention acts to reduce the size of the latent reservoir. Thus, if L₀ is the initial size of the latent reservoir and L is the reduced size of the reservoir after treatment, then an α value of L₀/L is the fold reduction in the latent reservoir and the efficacy of the intervention.

The frequency of reactivation also decreases due to the natural loss of latently infected cells on ART. This decrease has been estimated to have a half-life of between 6 months (29) and 23 years (30), with the general consensus being around 4 years (1, 2, 21). We therefore also include a reduction in the size of the latent reservoir, with a half-life of 4 years [k_R = ln(2)/4].

The probability of viral rebound is governed by an exponential distribution with an instantaneous rate constant, k_a(t), that is determined by both the current size of the latent reservoir and the frequency with which a cell from the reservoir reactivates. If $k_a^I$ is the baseline rate of viral rebound (so that $k_a^I$ is equal to 1/T₀ initially), then after an intervention that decreases the average time between reactivation events by a factor of α, k_a(0) is equal to $\frac{k_a^I}{\alpha }$ and k_α(t) is equal to $\frac{k_a^I{e}^{-k_{R}t}}{\alpha }$. Thus, the probability of viral reactivation occurring at time t, given a preintervention reactivation rate of $k_a^I$ and an intervention of efficacy α, as well as a natural death rate of latently infected cells, k_R, is given by equation 1:

$$p(t,k_a^I,\alpha ,k_R)=\frac{k_a^I}{\alpha }{e}^{-\frac{k_a^I}{\alpha k_R}}{e}^{\hspace{0.17em}-\hspace{0.17em}{k}_{R}t}{e}^{\frac{k_a^I}{\alpha k_R}{e}^{\hspace{0.17em}-\hspace{0.17em}{k}_{R}t}}$$ (1)

Models. (i) Stochastic model.

We used a stochastic model to incorporate the effects of stochastic variations in the time to viral rebound with population heterogeneity in the initial number of latently infected cells, the potency of a latency-reducing intervention, and viral growth rates, as well as different monitoring regimes, and thus the extent to which the pool of latently infected cells is refilled following viral rebound.

The model was seeded with a cohort of subjects having a log-normal distribution in the average rate of viral reactivation from latency, and the latency-reducing intervention then acted to decrease this rate by a factor of α, where α also had a log-normal distribution in the population. We outline below how this is achieved for the case of a treatment that acts to reduce latent cell numbers, although it could also be considered in terms of reducing the per-cell frequency of reactivation or a mixture of both effects.

We assumed that prior to treatment the average time between viral rebound events in the population is given by T₀, and therefore, the average rate of viral reactivation is $k_a^I$, although this varies from one individual to another, as outlined below. The size of the latent reservoir for subject i is represented by L_i and is chosen from a log-normal distribution with a median value of L_median. The associated baseline rate of viral rebound for patient i is then given by $k_a^I$, equal to $k_{a_i}^I=\frac{L_i}{L_{median}}{k}_{\alpha }^I$/year. The latency-reducing intervention is chosen to have a median value of α; however, for each patient, the intervention has an effect of α_i, where α_i is chosen from a log-normal distribution with a median value of α. This intervention is then applied to all subjects, reducing the size of their latent reservoirs to L′_I, equal to L_i/α_i. This results in an increase in the average duration of ART-free remission by a factor of α, from T₀ to T′_avg, equal to αT₀ years. The initial rate of viral rebound for patient i is then given by $k_{a_i}^{\prime }$, equal to $\frac{k_{a_i}^I}{{\alpha }_i}$, and a subject experiences viral rebound at time t with a probability determined using equation 1.

Viral rebound is assumed to be detectable when the virus reaches 50 copies/ml. Viral growth and refilling of the pool of latently infected cells then occur subject to the parameters outlined below until viral rebound is detected at one of the screening time points.

(a) Model parameters. (i) Reservoir sizes.

The distribution in the number of latently infected cells between subjects is modeled using a log₁₀-normal distribution, with the standard deviation of the underlying normal distribution estimated from reference 14 as 0.3 log units.

(ii) Variations in the latency-reducing intervention across the population.

The distribution in the effect that a latency-reducing intervention has on the reservoir size is also modeled using a log₁₀-normal distribution, with the standard deviation of the underlying normal distribution set at 0.5 log units.

(iii) Viral growth.

Upon reactivation, virus grows from the limit of detection of 50 copies/ml at a rate selected from a log-normal distribution with a mean of 0.78/day and a standard deviation of 0.23/day (estimated from viral growth in patients following treatment interruption [6, 17]).

(iv) Refilling the pool of latently infected cells.

Once viral rebound occurs, so too does refilling of the pool of latently infected cells. The rate at which the latent reservoir is refilled is estimated from reference 16. Considering long-term HIV DNA levels in patients who initiated ART between 2 weeks and 3 months after infection, we estimate that complete refilling of the latent pool takes 104 days and that the proportion of refilling that occurs by time t, P_refill(t), follows a power law, such that

$$P_{\text{refill}}\left(t\right)=\{\begin{array}{ll}A{t}^m& t\le 104\\ 1& t>104\end{array}$$ (2)

with A equal to 0.0002 and m equal to 1.8332.

(b) Probability of transmission.

In order to estimate the probability of transmission, we used data on the probability of viral transmission at different viral loads per sexual act coupled with the estimated number of sexual acts per month, both estimated by Gray et al. (18). We then scaled this to reflect the average per-contact probability of HIV transmission, using either a meta-analysis of heterosexual transmission (19) or a cohort study of homosexual transmission rates (20). Details of the parameters used are given in Table 1. To obtain 95% uncertainty intervals, we bootstrapped 10,000 samples from a log-normal distribution, with the mean and standard deviation selected according to the parameters in Table 1.

TABLE 1.

Probabilities of HIV transmission used in the model

Parameter	Probability of transmission per act (%) (95% CI)	No. of acts/mo	Source
Viral load (no. of copies/ml)
<1,700	0.01	10.4	18
1,700–12,499	0.13	9.38
12,500–38,500	0.14	7.98
>38,500	0.23	7.91
Overall	0·11 (0.08–0.15)
Income setting
High Income	0.077 (0.037–0.161)		19
Overall	0.182 (0.110–0.299)
Mode of contact
Receptive anal intercourse with ejaculation	1.47 (0.51–2.93)		20
Insertive anal intercourse	0.16 (0.05–0.31)

(ii) Deterministic model.

We used a simplified deterministic model to assess the effect of repeated dosing with an LRA.

Since it is currently unclear by how much an intervention is able to reduce the size of the latent reservoir, we performed much of our analysis in terms of “half-reductions” (R₅₀s). We assumed that each half-reduction reduced the frequency of reactivation by half, with a concomitant increase in the average time between viral rebound events of 2-fold.

Our deterministic model assumes the following. (i) Subjects have a baseline reactivation rate of $k_{\alpha }^I$ and are given an intervention that effects D₀ half-reductions, reducing their reactivation rate to a $k_a$ equal to $\frac{k_a^I}{2^{D_0}}$. (ii) Upon viral rebound, a subject is immediately re-treated with both ART and an intervention that effects D_r half-reductions (in the work presented here, D_r is equal to D₀). (iii) The viral reservoir has a natural decay rate of k_R. In this work, k_R is equal to 4.76 × 10⁻⁴/day, equating to a reservoir half-life of 4 years. Additionally, since there is currently little evidence for how successful retreatment with a latency-reducing intervention would affect the size of the latent pool, we made the simple assumption that the result of retreatment is to reduce the number of latently infected cells to the same level that was achieved after the initial intervention and, thus, to reduce their reactivation rate to k_α once again. We can then derive an expression for the total average number of half-reduction units that would have been administered to a patient by time t, D_avg(t), that depends only on the initial number of half-reductions, the repeat number of half-reductions, and the natural death rate of latently infected cells.

(a) Derivation of the average number of half-reductions administered.

Given a reactivation rate of k_a after completing LRA therapy and a natural decay rate of the latent reservoir of k_R, the time-varying reactivation rate for a patient after receiving LRA therapy is as follows: $k_a\left(t\right)=k_a^I{e}^{-k_{R}t}$. The probability distribution function for observing the first reactivation event at time t is given by the following equation:

$$f_{1,k_R,k_a}\left(t\right)=k_a{e}^{-\frac{k_a}{k_R}(1\hspace{0.17em}-\hspace{0.17em}{e}^{\hspace{0.17em}-\hspace{0.17em}{k}_{R}t})\hspace{0.17em}-\hspace{0.17em}{k}_{R}t}$$ (3)

The probability distribution function for observing the nth reactivation event in a patient at time t is then given by the following equation:

$$f_{n,k_R,k_a}\left(t\right)={\int }_0^t{f}_{n\hspace{0.17em}-\hspace{0.17em}1,k_r,k_a}\left(x\right)f_{1,k_R,k_a}(t-x)dx$$ (4)

We can then integrate the equation above to obtain $F_{n,k_R,k_a}\left(t\right)$, the probability of having observed n reactivation events by time t, as follows:

$$F_{n,k_R,k_a}\left(t\right)={\int }_0^t{f}_{n,k_R,k_a}\left(x\right)dx$$ (5)

If we assume that a person is immediately put back onto LRA therapy when they reactivate from latency and that this acts instantly to reduce their latent reservoir to a level identical to the initial level, then the expected total number of reactivation events, E_TOT(t), observed in a patient until time t is given by the following equation:

$$E_{\text{TOT}}\left(t\right)=\sum _{i=1}^{\infty }{F}_{i,k_R,k_a}\left(t\right)\mathrm{.}$$ (6)

We can thus derive the average number of doses a patient would have been given by time t after completing their initial round of LRA therapy, D_avg(t), as follows:

$$D_{\text{avg}}\left(t\right)=D_0+D_r\sum _{i=1}^{\infty }{F}_{i,k_R,k_a}\left(t\right)$$ (7)

where D₀ is the initial number of doses given during LRA therapy and D_r is the number of doses given when a patient reactivates.

(b) Determining the optimal duration of latency.

To determine the optimal duration of latency that would minimize drug exposure, i.e., minimize D_avg(t), we assumed that each dose of a drug reduces the size of the latent reservoir by half and thus correspondingly halves the baseline rate of reactivation from latency. We assumed that multiple doses have a cumulative effect.

We also assumed that if a patient reactivates from latency he/she is given an identical repeat treatment with the LRA, resulting in the same drug exposure (i.e., the same number of doses), and the effect of this is to achieve the same reactivation rate from latency as after initial drug treatment (i.e., D_r = D₀).

The optimal number of doses to be given on treatment, D_opt, which would minimize the total number of doses given by time Y [i.e., that would minimize D_avg(Y)], depends on the time period, Y, over which we are considering our results and is given by the value of D₀ that minimizes the equation for D_avg(t) above.