Right Ventricular Strain, Torsion, and Dyssynchrony in Healthy Subjects using 3D Spiral Cine DENSE Magnetic Resonance Imaging

Abstract

Mechanics of the left ventricle (LV) are important indicators of cardiac function. The role of right ventricular (RV) mechanics is largely unknown due to the technical limitations of imaging its thin wall and complex geometry and motion. By combining 3D Displacement Encoding with Stimulated Echoes (DENSE) with a post-processing pipeline that includes a local coordinate system, it is possible to quantify RV strain, torsion, and synchrony. In this study, we sought to characterize RV mechanics in 50 healthy individuals and compare these values to their LV counterparts. For each cardiac frame, 3D displacements were fit to continuous and differentiable radial basis functions, allowing for the computation of the 3D Cartesian Lagrangian strain tensor at any myocardial point. The geometry of the RV was extracted via a surface fit to manually delineated endocardial contours. Throughout the RV, a local coordinate system was used to transform from a Cartesian strain tensor to a polar strain tensor. It was then possible to compute peak RV torsion as well as peak longitudinal and circumferential strain. A comparable analysis was performed for the LV. Dyssynchrony was computed from the standard deviation of regional activation times.

Global circumferential strain was comparable between the RV and LV (−18.0% for both) while longitudinal strain was greater in the RV (−18.1% vs. −15.7%). RV torsion was comparable to LV torsion (6.2 vs. 7.1 degrees, respectively). Regional activation times indicated that the RV contracted later but more synchronously than the LV.

3D spiral cine DENSE combined with a post–processing pipeline that includes a local coordinate system can resolve both the complex geometry and 3D motion of the RV.

I. Introduction

Measures of left ventricular (LV) cardiac mechanics are predictive of adverse cardiac events and poor clinical outcomes [1]. A multitude of studies have characterized LV function in both healthy individuals and patients with impaired cardiac function using various imaging techniques and modalities. The role of the right ventricle (RV), however, remains less clear. While more traditional measures of RV function, such as mass and volumes, are known to play an important role in a number of pathologies including arrhythmogenic right ventricular cardiomyopathy (ARVC), RV hypertrophy, pulmonary hypertension, and congenital heart disease [2], [3], very few studies have looked at advanced measures of function in the RV such as strain, torsion, and synchrony. These advanced measures of RV function could potentially provide better insight into the progression of these diseases and allow for the early detection of subclinical symptoms.

The lack of studies on RV function is due in part to the technical difficulties of measuring cardiac mechanics in the RV. Due to the lower pressures experienced by the RV, its myocardium is much thinner (3–5 mm) than the LV myocardium and can only be imaged with a high resolution technique [4]. Furthermore, while the geometry of the LV is readily modeled as a prolate spheroid, the shape of the RV does not adhere to any standard coordinate system and is highly variable even among healthy individuals. The contraction is also complex with mechanical activation beginning at the apex and propagating longitudinally towards the outflow tract [5]. This complex shape and contraction make it difficult to measure RV function using a standard two-dimensional imaging plane. Taken together, these factors make imaging, processing, and quantifying RV function difficult.

Despite these difficulties, several modalities have been used in an effort to measure advanced cardiac mechanics in the RV. While echocardiography is the most widely used modality for assessing LV function, the acoustic windows into the RV are narrow or even non–existent in many individuals. Magnetic Resonance Imaging (MRI) can overcome this limitation thanks to excellent tissue contrast as well as its ability to assess complex structures using multi–slice imaging. Traditional cine Steady State Free Precession (SSFP) MRI has been combined with feature tracking techniques to assess RV mechanics [6]–[8]; however, feature tracking techniques traditionally suffer from poor reproducibility, particularly when used to quantify regional strain, twist, and torsion. More advanced techniques such as 3D myocardial tagging have been used to measure bi–ventricular mechanics [9], but the thin wall of the RV makes tracking tag intersection points (on the order of 8 mm) difficult, ultimately leading to a poor estimate of transmural cardiac function.

Three–dimensional cine Displacement–encoded (DENSE) MRI, however, is a technique in which the displacement of tissue is encoded directly into the phase of the MRI signal [10], [11]. By applying this technique in both the LV and RV, it is possible to map the three–dimensional displacement of any pixel within the myocardium over the cardiac cycle with high temporal and spatial resolution. Using this displacement information, cardiac strains and torsion can be computed for any region of the RV and LV.

While DENSE has been used widely to measure and characterize LV function in both mice and humans [12], [13], very few studies have investigated its ability to assess RV function. In 2012, Auger et al. used three–dimensional cine DENSE to measure principal strains within the RV. Due to the limited spatial resolution of the technique at the time (2.8 mm in–plane resolution), they were only able to determine strain within the midwall of the myocardium. While this study represented a critical first step to understanding right ventricular function, transmural differences in strain have been shown to be important in the LV [14] and it would be beneficial to make such measurements in the RV as well. Moreover, this study was completed in a limited set of 5 volunteers and their post-processing framework did not include a local coordinate system adapted to the complex geometry of the RV. In this study, we sought to combine the advanced capabilities of 3D DENSE imaging with a robust post–processing framework to perform bi–ventricular assessment of cardiac mechanics including strain, torsion, and dyssynchrony. Our goal was to use this framework to characterize normal RV function in a cohort of healthy individuals and to compare measures of RV mechanics with their LV counterparts.

II. Materials & Methods

A. Image Acquisition

All scanning for this study was performed on a 3T Siemens (Erlangen, Germany) Tim Trio with a 6–element chest and 24–element spine coil. After acquiring the necessary localizing images, a single four-chamber image and a stack of 9–11 contiguous short–axis images were acquired spanning from the apex to the mitral valve plane at end–diastole. Spiral cine DENSE was acquired at each of the image locations with balanced 3D displacement encoding (Figure 1) [15]. DENSE parameters included: 12 spirals, 1 average, 360×360 mm² FOV, 180×180 image matrix, 8 mm slice thickness, ramped 20° flip angle, 17 ms repetition time, 1.8 ms echo time, 0.04 cyc/mm encoding frequency [16], two spirals per heartbeat (34 ms temporal resolution), and 3–point phase cycling for artifact suppression [11], [17]. Based on typical values of off-resonance and T2* decay, the estimated net spatial resolution from full width at half maximum analysis of the point spread function was 3.7 mm [18]. All acquisitions were performed using a respiratory navigator to eliminate respiratory artifacts and to ensure a consistent diaphragm position (acceptance window: ±3 mm/range: 7 mm).

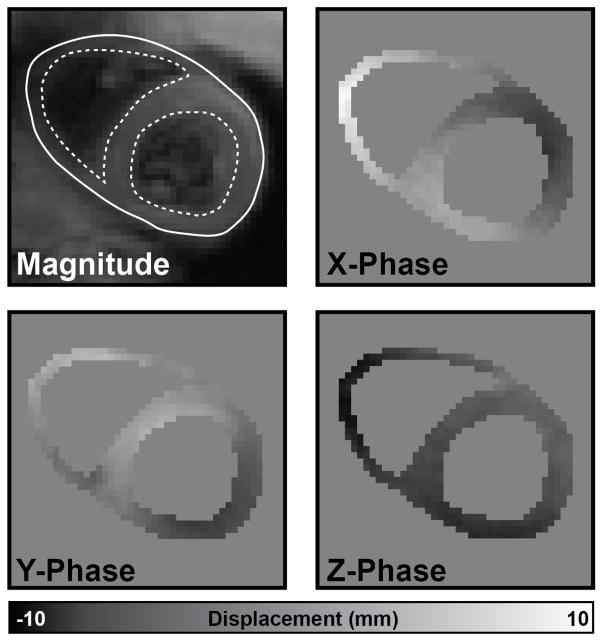
Fig. 1.

RV and LV endocardial boundaries (dotted lines) and a combined epicardial boundary (solid line) were delineated on the magnitude image for all slices and cardiac phases. These boundaries were used to create a mask of the myocardium and unwrap the X, Y, and Z displacement–encoded phase images. Using these images, a 3D displacement field could be constructed.

B. DENSE Post–Processing

Briefly, after manual segmentation of the myocardium, the displacement–encoded phase images were unwrapped. A 3D radial basis function interpolant was fit to these displacements and the spatial derivatives were computed analytically to construct the deformation gradient tensor and subsequently the Cartesian Lagrangian strain tensor. Using a local coordinate system based upon the endocardial surface mesh, the Cartesian strains were transformed into radial, circumferential, and longitudinal strains. Regional analysis was performed using standard segmentations of the LV and a comparable segmentation of the RV. All analysis was performed for both the RV and LV simultaneously.

1) Myocardial Segmentation

For each short–axis slice and cardiac phase, RV and LV endocardial boundaries (dotted lines in Figure 1) and a combined epicardial boundary (solid line in Figure 1) were manually delineated on the combined black–blood magnitude images. All trabeculations and papillary muscles were excluded from the segmentation to isolate mechanics calculations to the true myocardium. The open–source DENSEanalysis software [19] with a custom plugin for bi–ventricular segmentation was used to perform all segmentation and phase unwrapping. From these boundaries, a mask was created for each short–axis slice. The X, Y, and Z displacement–encoded phase images were unwrapped using manual seed points and a quality–guided path following phase unwrapping algorithm [20]. All cardiac phases were visually inspected to ensure no phase unwrapping errors were present (Figure 1).

2) Cartesian Strain Tensor Calculation

The coordinates of all pixels within the myocardium were converted to 3D coordinates using the position information stored within the image headers. By combining the 3D coordinates of each pixel with the unwrapped X, Y, and Z Eulerian displacement vectors, a 3D displacement field was generated for each cardiac frame.

Previous work has often utilized a finite-element based analysis where a mesh is fit to the geometry of the myocardium and then deformed using the measured displacements in order to derive cardiac strains [9], [11]. This methodology requires algorithms to construct the volumetric meshes and care must be taken to control the arrangement and size of the elements. Furthermore, the computation of strains and torsion from a displacement field are only dependent on the spatial gradients of the displacement field. We chose to compute the strains analytically from a continuous and differentiable interpolant of the displacement field.

Linear radial basis functions (RBFs, ϕ) were fit to the 3D Lagrangian displacement field [21]. The weights ω_i in Equation 1 were determined using the 3D coordinates and measured 3D displacements. Using the position x of a query point, it was possible to determine the 3D displacement D of this point using the calculated weights ω_i and the location of each of the M original data points, x_i.

$$\mathit{D}(\mathit{x})=\sum _{i=1}^M{\mathit{\omega }}_{\mathit{i}}\varphi (\Vert \mathit{x}-{\mathit{x}}_i\Vert )$$ (1)

To compute strains at any point, the deformation gradient tensor (F) was computed from gradients in the displacement interpolants at that point. D_x, D_y and D_z are the interpolants for the X, Y, and Z displacements, respectively. I is the identity matrix.

$$F=I+\left(\begin{array}{ccc}\frac{\partial D_x}{\partial x}& \frac{\partial D_x}{\partial y}& \frac{\partial D_x}{\partial z}\\ \frac{\partial D_y}{\partial x}& \frac{\partial D_y}{\partial y}& \frac{\partial D_y}{\partial z}\\ \frac{\partial D_z}{\partial x}& \frac{\partial D_z}{\partial y}& \frac{\partial D_z}{\partial z}\end{array}\right)$$ (2)

All of the derivatives in Equation 2 were computed analytically using the coefficients from the RBFs fit to the displacement field. The Green Cartesian strain tensor E_c was then computed using Equation 3, ultimately yielding the tensor shown in Equation 4.

$$E_c=\frac{1}{2}\left(F^{T}F-I\right)$$ (3)

$$E_c=\left(\begin{array}{ccc}{E}_{xx}& E_{xy}& E_{xz}\\ E_{yx}& E_{yy}& E_{yz}\\ E_{zx}& E_{zy}& E_{zz}\end{array}\right)$$ (4)

3) Local Coordinate System

The Cartesian strain tensor is not useful on its own for quantifying cardiac mechanics because the different components are dependent upon patient position and measurement position within the heart. To account for this dependency, Cartesian strains are typically transformed into a cylindrical coordinate system with radial, circumferential, and longitudinal components. In 2D LV analysis of a short–axis image, the radial direction is typically defined as pointing towards the centroid of the LV and the circumferential direction is defined as normal to this vector (within the same short–axis imaging plane). This works well for the middle region of the LV but breaks down near the apex, where the true radial direction is angled out of the image plane and points towards the base, and in the RV where the geometry is non–cylindrical. To transform the Cartesian strain tensor to a polar strain tensor, we defined an adaptive local coordinate system based upon a surface mesh fit to the endocardial boundaries of the myocardial segmentation. The endocardial mesh generation methodology introduced by Haggerty et al. [22] was used in this study.

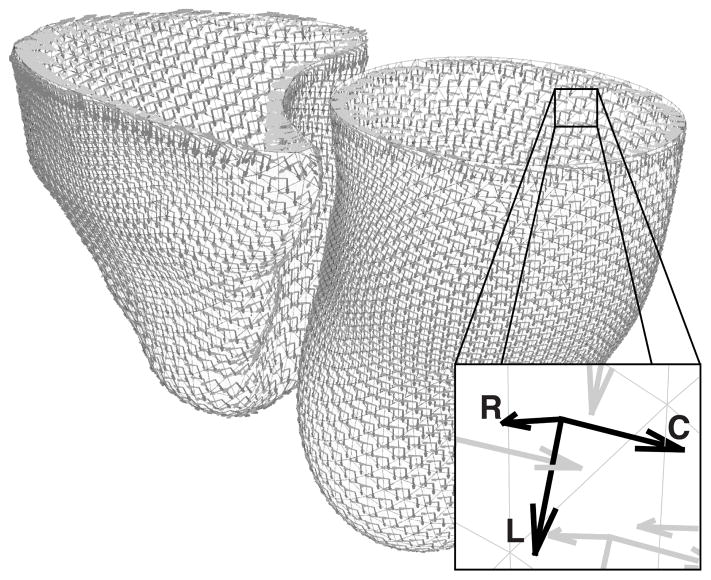
Radial r, longitudinal l, and circumferential c directions were defined for each vertex on the endocardial surface meshes of both the right and left ventricles. The radial direction was defined as the inward normal to the surface. The longitudinal direction was constrained to be tangent to the surface but pointing in the direction of the apex of the ventricle.

The apices of each ventricle were defined automatically from the point of maximum curvature of the LV and RV endocardial contours delineated on the four-chamber image. The four-chamber image was chosen for apex selection since it was planned such that it passed through the apices of the ventricles. These apical points on the 2D encodardial contours were then projected to the endocardial mesh of their respective ventricle to obtain the apical reference point for that ventricle.

The circumferential direction was then the cross product of the longitudinal and radial direction vectors (Figure 2).

Fig. 2.

For any point in either the left or right ventricle, a local coordinate system was defined with the radial direction (R) being the inward normal of the surface, the longitudinal direction (L) pointing towards the apex, and the circumferential direction (C) as the cross–product of the radial and longitudinal components.

The local coordinate system was used to construct a rotation matrix, R (Equation 5), that was then used to transform the Cartesian strain tensor, E_c, into the polar strain tensor E_p (Equation 6).

$$R=\left(\begin{array}{ccc}{r}_x& c_x& l_x\\ r_y& c_y& l_y\\ r_z& c_z& l_z\end{array}\right)$$ (5)

$$E_p=R^T{E}_{c}R$$ (6)

Using this polar strain tensor E_p, it is possible to derive the radial (E_rr), circumferential (E_cc) and longitudinal (E_ll) strains (Equation 7).

$$E_p=\left(\begin{array}{ccc}{E}_{rr}& E_{rc}& E_{rl}\\ E_{cr}& E_{cc}& E_{cl}\\ E_{lr}& E_{lc}& E_{ll}\end{array}\right)$$ (7)

Torsion was quantified using the circumferential–longitudinal shear angle α_cl (in degrees) computed from the polar strain tensor using Equation 8 [23].

$${\alpha }_{cl}=arcsin\frac{2E_{cl}}{\sqrt{(1+2E_{cc})(1+2E_{ll})}}$$ (8)

In addition to the polar strains, principal strains were derived from the eigenvalues and vectors of the polar strain tensor, E_p. Because principal strains are invariant to rotations of the coordinate system, either E_c or E_p could be used to derive them.

4) Regional Analysis

The American Heart Association (AHA) 17–segment model is widely used for characterizing regional function within the LV [24]. This representation of the ventricle requires parameterization in both the longitudinal and circumferential directions. In order to perform similar regional analysis in the RV, it is necessary to develop a method to do so that is flexible enough to handle the variable and irregular geometry of the RV.

For longitudinal parameterization, we used the normalized geodesic distance between the base and the apex for each ventricle independently. For every point in the endocardial surface mesh of each ventricle, we compute the geodesic distance of that point from both the apex of that ventricle as well as the base. We then used the ratio of these two distances to determine the normalized longitudinal distance. The heat method was used to compute geodesic distances across the surfaces meshes [25] using the freely available Geometry Processing Toolbox [26] (Figure 3).

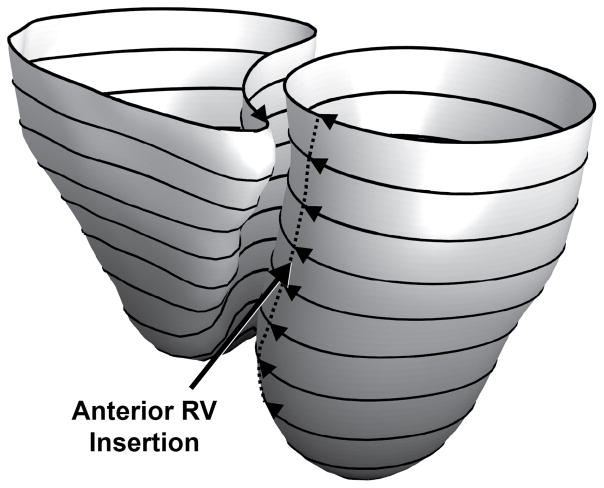
Fig. 3.

The normalized geodesic distance from the apex (0, black) to the base (1, white) was computed for each point on the encodardial surface for both the left and right ventricles to determine the longitudinal parameterization. Using the iso–value lines of the longitudinal parameterization (black rings), the circumferential position was parameterized using the normalized arc length of each iso–value line starting at the anterior insertion line of the right ventricle (dotted line) and continuing around the ventricles.

To perform circumferential parameterization, we determined the iso-value lines of the longitudinal parameterization (black lines in Fig. 3) [26]. This provided us with paths that traversed the ventricle circumferentially. We normalized the arc length of each of these paths with zero being defined as the anterior insertion of the RV (dotted line in Figure 3). The anterior and inferior insertion points were defined automatically for each short–axis image by finding the points on the LV endocardial contour that had the lowest sum of distances to the other two contours (the RV endocardial contour and the epicardial contour).

Radial parameterization is important if transmural differences in strain are to be studied. It has been shown that different disease states affect the different layers of the myocardium preferentially [14]. Here we present a method to perform this transmural parameterization; however, the results from this paper will only present transmural averages.

Radial parameterization was performed using a 3D version of a PDE–based thickness measurement [27]. Using the endocardial and epicardial surface meshes, the region within the RV endocardium was defined to have a potential of 0 and the epicardium and LV endocardium were defined to have a potential of 1. The PDE–based approach solved the heat equation for any point within the myocardium. Then, this procedure was repeated except that the LV endocardium was set to 0 and the epicardium and RV endocardium were set to 1. For any point in the myocardium, its transmural position (normalized between 0 and 1) was defined as the minimum of the two results.

Using the circumferential and longitudinal parameterization of the endocardial surfaces, any point within the myocardium was able to be mapped to the nearest point on the endocardial surface mesh to determine its circumferential and longitudinal position. Using this information, the LV and RV were divided into segments (17 and 13 segments, respectively) and all mechanics measures derived from DENSE were averaged within each of these segments. The LV segmentation used the standard AHA 17–segment model while the RV segmentation used four equal segments longitudinally and four equal segments circumferentially between the anterior and inferior insertion points for all but the apex where a single circumferential segment was used.

Peak strain and torsion values were determined by averaging the time series of all sampled points within a segment. The peak value of this average curve was then used as the representative peak value from that segment.

5) Dyssynchrony Analysis

To assess regional timing, the second principal strain curve was computed for each segment. Contraction timing was measured throughout the LV and RV by computing the mechanical activation delay of each segment relative to a patient–specific reference curve using cross–correlation analysis [28]. Using the R-R interval, the delays times were converted from milliseconds to percent of the cardiac cycle. After obtaining a delay time for each region, the dyssynchrony index (the standard deviation of segmental delay times) was computed for both the LV and RV. The septum was included with the LV, which is standard for the 17-segment LV model. The inter–ventricular delay time was computed as the difference between the median delay time of each ventricle with a positive value indicating that the LV contracts before the RV [7].

C. Reproducibility Analysis

In order to determine the inter–observer reproducibility of the 3D post–processing pipeline, 10 datasets were selected at random and analyzed by a second observer. No restrictions were placed on the independent observers regarding which slices to use for the analysis (i.e., selecting the most apical and basal slices to segment). All metrics including global and regional torsion, strain and dyssynchrony were compared between the two observers using Bland-Altman analysis. Additionally, a modified coefficient of variation (CoV) was computed using Equation 9 where x₁ and x₂ are the observations of a given metric by the two observers and N is the number of datasets for which reproducibility was assessed [29], [30].

$$\mathit{CoV}(x_1,x_2)=\frac{{\sum }_{i=1}^{N}St.\mathit{Dev}(x_1(i),x_2(i))}{{\sum }_{i=1}^{N}0.5(x_1(i)+x_2(i))}$$ (9)

To assess inter–test reproducibility, we acquired two 3D DENSE datasets in 6 healthy individuals. Each of the two acquisitions was performed by a different technician and the subject was completely removed from the scanner between acquisitions. Reproducibility of strain, torsion, and dyssynchrony was again assessed via Bland–Altman analysis and the modified CoV.

III. Results

To characterize healthy RV function, we scanned 50 healthy individuals (Age: 26 ± 8 years, 46% male) with no history of cardiovascular disease (Table I). All participants provided written and informed consent and the protocol used in this study was approved by the Institutional Review Board.

TABLE I.

Subject Characteristics

	Mean ± Std.	Range
Age (years)	26 ± 8	18 – 50
Height (cm)	173 ± 8	156 – 191
Weight (kg)	72 ± 13	43 – 106
Heart Rate (bpm)	67 ± 12	41 – 100
LVEF (%)	58 ± 4	47 – 69
RVEF (%)	53 ± 4	44 – 61
LVEDV (ml)	107 ± 28	49 – 175
RVEDV (ml)	91 ± 27	28 – 149
LVESV (ml)	45 ± 14	20 – 76
RVESV (ml)	43 ± 14	14 – 73

Bi–ventricular 3D imaging and post–processing were performed successfully on all 50 subjects. Average scan time for the 3D data was 28 ± 6 minutes with an average respiratory navigator efficiency of 63 ± 10% (nominal scan time of 18 ± 5 minutes). Average time for manual segmentation of the myocardium of the left and right ventricles was 15 minutes per slice. The computational processing time on a 3.40 GHz CPU with 16.0 GB of RAM was 28 ± 18 minutes.

A. Cardiac Strains

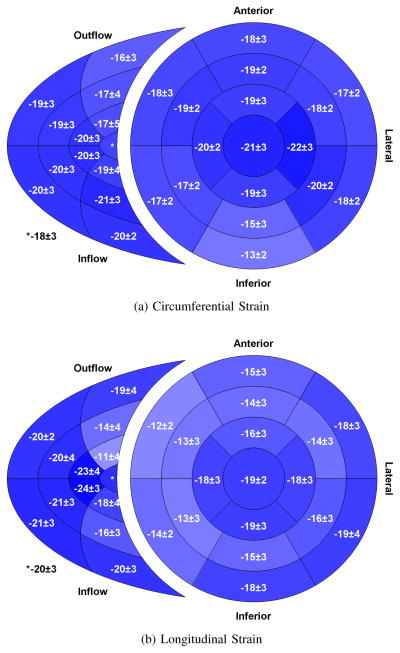
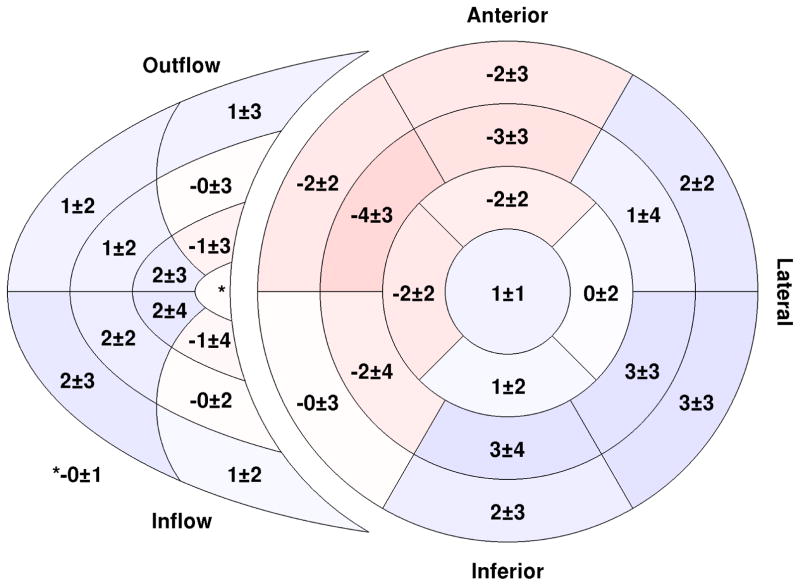
Peak global circumferential strain for the RV had a similar magnitude to the values observed in the LV (−18.0 vs. −18.0%); however, global RV longitudinal strain had a higher magnitude than in the LV (−18.1 vs. −15.7%) (Table II). Circumferential strain varied regionally within the RV with the lowest values (−16%) in the outflow region (Figure 4a). Longitudinal strain varied considerably throughout the RV free wall (11 – 24%) (Figure 4b).

TABLE II.

Global Cardiac Mechanics

	Left Ventricle	Right Ventricle
Circum. Strain (%)	−18.0 ± 1.8	−18.0 ± 2.0
Long. Strain (%)	−15.7 ± 1.3	−18.1 ± 1.6
Radial Strain (%)	31.5 ± 8.9	–
Torsion (°)	7.1 ± 1.1	6.2 ± 2.0
1,2 Delay Time (%)	0.0 ± 1.0	0.6 ± 1.0
2 Dyssynchrony (%)	3.4 ± 1.0	3.1 ± 1.1
Dyssynchrony (ms)	25.0 ± 6.9	23.3 ± 8.3
2 Inter–ventricular Dyssynchrony (%)	−0.0 ± 1.5
Inter–ventricular Dyssynchrony (ms)	−0.7 ± 10.6

¹Negative is early contraction; Positive is late contraction

²Expressed as a percent of the cardiac cycle

Fig. 4.

Bi–ventricular segment model showing regional peak circumferential (a) and longitudinal (b) strain in both the left and right ventricles. All values are expressed as a percent. Segments with greater strain magnitude are shown with a darker shade of blue. The inner–most region of the right ventricular segment model is the apical portion while the outer-most is the basal portion. (n = 50)

B. Mechanical Activation Times

Mechanical activation times were computed for each segment relative to a patient–specific reference strain curve and were reported as percent of cardiac cycle On average, the septum contracted first followed by the apex, the lateral wall of the RV, and finally the basal lateral regions of the LV (Figure 5). Globally, the RV contracted later than the LV (0.6 vs. 0.0%); however, once RV contraction began, it contracted more synchronously than the LV (dyssynchrony index: 3.1 vs. 3.3%) (Table II).

Fig. 5.

Regional delay times throughout both the right and left ventricles. A negative number (red) indicates an early–contracting segment while a positive number (blue) indicates a region with delayed mechanical contraction. All values are expressed as a percentage of the cardiac cycle. The inner–most region of the right ventricular segment model is the apical portion while the outer-most is the basal portion. (n = 50)

C. Cardiac Torsion

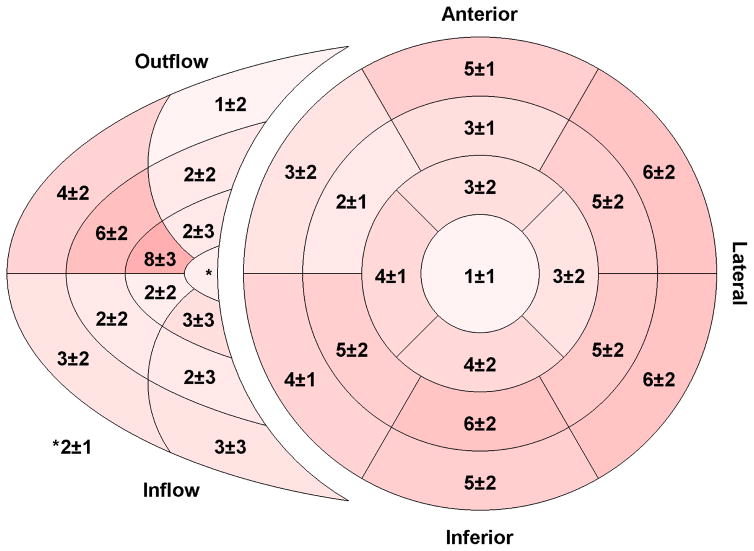
Significant torsion was observed in the RV with comparable global magnitude to that observed in the LV (Table II). The highest torsion values were seen in the lateral segments of the RV free wall and the basal lateral segments of the LV (Figure 6).

Fig. 6.

Regional torsion for the right and left ventricles. Torsion was computed from the circumferential–longitudinal shear angle and is expressed in degrees. Segments with greater torsion are shown with a darker shade of red. The inner–most region of the right ventricular segment model is the apical portion while the outer-most is the basal portion. (n = 50)

D. Reproducibility

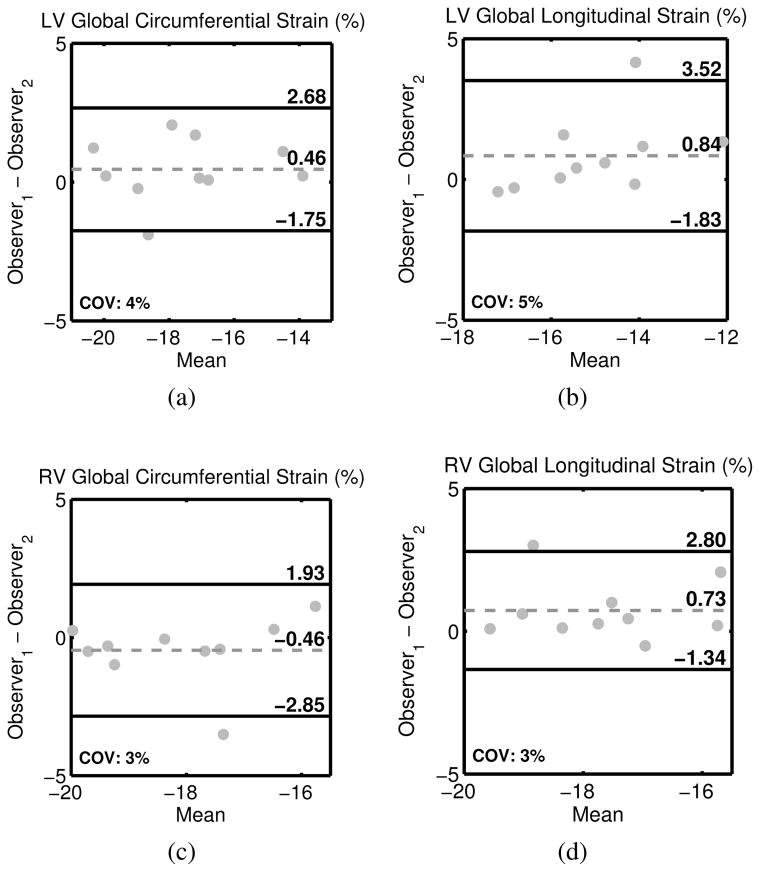
Inter–observer reproducibility assessed by two observers for 10 randomly–selected datasets including Bland–Altman biases and 95% limits of agreement and the modified coefficient of variation (CoV) is shown in Table III. Global circumferential and longitudinal strains demonstrated excellent reproducibility in both the right and left ventricles (CoV: 3–5%) (Figure 7). All global measures of LV and RV strain, torsion, and synchrony demonstrated excellent reproducibility with CoVs less than 15%. While slightly less reproducible, segmental strain, torsion, and dyssynchrony also demonstrated good inter– observer reproducibility with the exception of regional RV torsion (CoV = 44.4%). Inter–test reproducibility measured in 6 healthy individuals is shown in Table IV. Global measures of LV and RV strain, torsion, and dyssynchrony all demonstrated good inter–test reproducibility (all less than 20%) except for regional RV torsion (CoV = 28.0%).

TABLE III.

Inter–observer reproducibility

	Left Ventricle		Right Ventricle
Global	Bland–Altman Bias ± Limits	CoV	Bland–Altman Bias ± Limits	CoV
Circum. Strain (%)	0.5 ± 2.2	3.6	−0.5 ± 2.4	3.1
Long. Strain (%)	0.8 ± 2.7	4.8	0.7 ± 2.1	3.3
Radial Strain (%)	1.3 ± 8.4	7.1	–	–
Torsion (°)	0.1 ± 0.8	2.5	−0.4 ± 3.0	14.8
1 Dyssynchrony (%)	0.3 ± 1.6	5.6	−0.1 ± 2.2	9.8
Segmental
Circum. Strain (%)	0.3 ± 3.6	5.7	−1.1 ± 6.2	9.8
Long. Strain (%)	0.6 ± 4.6	7.7	0.3 ± 6.9	10.3
Radial Strain (%)	−1.0 ± 17.6	12.0	–	–
Torsion (°)	0.1 ± 4.4	16.8	−0.5 ± 8.9	44.4
1,2 Delay Times (%)	0.2 ± 4.0	–	0.2 ± 4.0	–

¹Expressed as a percent of the cardiac cycle

²Negative is early contraction; Positive is late contraction

Fig. 7.

Bland–Altman plots demonstrating inter–observer reproducibility for global circumferential (left) and longitudinal (right) strain in both the left (top) and right (bottom) ventricles.

TABLE IV.

Inter–test reproducibility

	Left Ventricle		Right Ventricle
Global	Bland–Altman Bias ± Limits	CoV	Bland–Altman Bias ± Limits	CoV
Circum. Strain (%)	0.7 ± 1.8	3.8	0.4 ± 1.5	2.8
Long. Strain (%)	0.0 ± l.3	2.4	−0.4 ± 3.1	4.8
Radial Strain (%)	0.6 ± 11.5	11.6	–	–
Torsion (°)	0.2 ± 1.2	5.6	0.6 ± 2.0	8.4
1 Dyssynchrony (%)	0.4 ± 3.6	11.8	0.3 ± 2.2	10.8
Segmental
Circum. Strain (%)	0.5 ± 4.0	6.6	0.8 ± 4.6	7.1
Long. Strain (%)	−0.1 ± 4.2	7.6	−0.3 ± 6.3	9.2
Radial Strain (%)	1.1 ± 21.3	18.0	–	–
Torsion (°)	0.2 ± 4.7	19.6	0.6 ± 8.2	28.0
1,2 Delay Times (%)	−0.8 ± 5.9	–	0.4 ± 5.6	–

¹Expressed as a percent of the cardiac cycle

²Negative is early contraction; Positive is late contraction

IV. Discussion

This study introduced a robust pipeline for processing 3D displacement–encoded images of both the left and right ventricles to yield measures of biventricular cardiac mechanics including global and regional strains, torsion, and dyssynchrony. By acquiring data in 50 healthy individuals, we were able to test the pipeline and characterize normal right ventricular function to serve as a baseline for future studies looking at impaired RV function. Our major findings included: 1) regional variations in circumferential and longitudinal strain were present within the RV, 2) global circumferential strain was comparable between the LV and RV while global longitudinal strain was larger in the RV, 3) the magnitude of RV torsion was similar to that observed in the LV, and 4) the RV contracts later but more synchronously than the LV.

A. DENSE Post-Processing

Several components of the post-processing pipeline were developed to adapt the typical processing of the LV to the more complex geometry of the RV. While the LV is often modeled as a cylinder or prolate spheroid, neither is well-suited for the RV. The local coordinate system introduced in this study is a generalization of the cylindrical model that defined radial, circumferential, and longitudinal directions for any point on the LV and RV endocardial surfaces. This model definition allowed for the evaluation of RV mechanics analogous to LV mechanics, overcoming a limitation that was noted in the first study to compute RV mechanics from 3D DENSE imaging [31]. This generalization, while developed for the RV, also improves the post-processing of the LV, as the true LV geometry will never be a perfect cylinder or prolate spheroid.

Another benefit of the local coordinate system is its independence to the orientation of the images. When considering a short-axis image, it is common to define the radial and circumferential directions to be in the plane of the image while the longitudinal direction is perpendicular to the image [20], [32]. While this is possibly true for a cylindrical geometry and perfectly-oriented short-axis image planes, it is unlikely to be the case for the actual geometry of the RV and LV. By extracting the local coordinate system from endocardial surfaces that were fit to the boundaries of the myocardial segmentation, the resulting radial, circumferential, and longitudinal directions were not restricted based on the prescribed image planes. Indeed, any combination of image planes could be inputted to the pipeline as long as they span the extent of the ventricular anatomy including four-, three-, and two-chamber long-axis views.

Another important component of the pipeline is the circumferential and longitudinal parameterization of the RV, which enabled regional analyses. The AHA 17-segment model is widely used for the LV (including the septum) and is based on a cylindrical model with equiangular sampling around the LV central axis [24]. This model is not well suited for the irregular shape of the RV (i.e. the RV is not cylindrical and has no obvious central axis). By using normalized arc lengths and geodesic distances around the surface of the RV endocardial mesh, every point on the mesh was represented by a circumferential and longitudinal parameterization. A 13-segment RV model was chosen to represent regional strains in this study. There is no standard model for RV segmentation, and several different models have been proposed in previous studies [2], [31], [33]. Importantly, the parameterization employed in our post-processing pipeline is generalizable and can be made compatible with any such RV segmentation scheme.

B. Strain Analyses and Timing of Contraction

Globally, peak circumferential strains were similar between the RV and the LV. In the RV, peak circumferential strain was lowest in the basal outflow region (−16%). The remainder of the ventricle demonstrated higher circumferential strain values. This trend is consistent with previous imaging studies using myocardial tagging [34] and strain imaging (SENC) [35]. Those two studies found the lowest principal strains and lowest circumferential strains in the basal region of the RV. An additional myocardial tagging study also found circumferential strain to be lowest in the outflow region (−16%) [36]. A previous 3D DENSE study found that the inflow region demonstrated the lowest circumferential strain (−10%), however the outflow region was the next lowest segment (−15%) [31].

Peak global longitudinal strain was larger in the RV compared to that in the LV and displayed more regional heterogeneity than circumferential strain. Longitudinal strain was highest in the lateral regions, particularly in the apical segments, which also demonstrated the highest longitudinal strain across both ventricles. The lowest longitudinal strains were seen in the apical and mid-ventricular segments of the outflow and inflow regions, however, the basal segments of those regions demonstrated higher strains. Both Hamdan et al. and Fayad et al. found the highest longitudinal strains in the apical (−19 and −29%, respectively) and basal (−19 and −25%, respectively) segments [35], [36], which is consistent with our findings of the highest strains in the apical-lateral segments (−24%) and relatively high strains in the basal segments in the outflow and inflow regions (−19 and −20%, respectively). Auger et al. found the highest longitudinal strain in the basal outflow region (−22%), consistent with our findings; however, their lowest reported strain was in the basal inflow region (−16%) where we observed higher strains (−19%) [31]. This discrepancy is likely due to differences in the strain computation and our use of a local coordinate system. Because Auger et al. did not define a local coordinate system for the RV, they resorted to separate 1-dimensional calculations in the direction that was perpendicular to the image planes.

Regarding both ventricles, the earliest contracting segments were in the septal and anterior regions of the LV while the latest segments were in the basal-lateral regions of the LV. Within the RV, the apical segments contracted earliest while the lateral wall contracted latest. We did not observe a gradient in contraction time from apex-to-base within the lateral regions. However, the basal segments of the outflow and inflow regions contracted later than their apical counterparts (difference in cross-correlation delay: 2% of cardiac cycle). Hamdan et al. found similar results to ours, with the apex contracting earliest and the base contracting latest (difference in time-to-peak: 55 ms) [35], which is consistent with the course of the right bundle branch that delivers electrical conduction down the septum to the apex and then out to the remainder of the ventricle [37]. In contrast, Auger et al. found the inflow region to contract earliest with the apex contracting latest (difference in time-to-peak: 96 ms). We also found the RV to contract more synchronously than the LV, which is likely due to the RV having a thinner wall and less myocardium, which takes less time to depolarize and contract.

C. Right Ventricular Torsion

To our knowledge, this is the first study to quantify RV torsion, likely because it has been suspected that torsion does not play a large role in the RV compared to the LV [38]. A previous study has qualitatively observed reduced RV torsion in patients with RV hypertrophy, however, there were no attempts to quantify it [39]. While previous studies in the LV have used basal and apical twist relative to a central axis to quantify torsion, this procedure is not appropriate for the RV where there is no well-defined central axis [40]. The incorporation of a local coordinate system to define local circumferential and longitudinal directions allowed for the calculation of the local circumferential-longitudinal shear angle, which has been widely used as a measure of torsion in the LV [40]. We found the magnitude of RV torsion to be comparable between the RV and LV, largely due to segments in the lateral wall of the RV that had the largest shear angles across both ventricles. Regional RV torsion may be an important, and now quantifiable, indicator of RV function.

D. Reproducibility

Global circumferential and longitudinal strains demonstrated excellent inter-observer reproducibility with CoVs less than or equal to 5%. These compare well with previous inter-observer results for global LV strains (circumferential: 3.6%, longitudinal: 3.9%) [41]. Global LV torsion demonstrated similarly excellent reproducibility, which agrees well with a previous study (CoV = 2.9%, [41]), while global RV torsion was less reproducible but still acceptable. As expected, regional mechanics were less reproducible than their global counterparts. This could be alleviated by dividing the ventricles into fewer segments and averaging the mechanics over a larger volume of tissue. Indeed, some segmentation models of the RV include only four segments (e.g. outflow, inflow, mid-ventricle, and apex) [31]. RV regional torsion was the least reproducible mechanic as measured by CoV (44%). This is likely due to the calculation of the circumferential-longitudinal shear angle, which is a combination of three components of the strain tensor, each with their own variability. In addition, there were many segments with nearly zero torsion such that a small variability leads to a high CoV. Regarding the timing of contraction, both the LV and RV dyssynchrony indices demonstrated good CoVs (6 and 10%, respectively), which is indicative of the good reproducibility of the regional delay times from which they were calculated.

E. Limitations

In this study, scan time for the 3D DENSE acquisition was 28 ± 6 minutes. This long scan time was partly due to the necessity of a respiratory navigator, which has imperfect efficiency, as well as the inherent duration of the scan. Unfortunately, this long scan duration is not clinically feasible, especially in patients with significant cardiac disease. There are several new developments in DENSE imaging including outer volume suppression [42], parallel imaging and compressed sensing [43] which can ultimately be adapted to 3D acquisitions to reduce the scan duration by an order of magnitude.

All 3D DENSE data was obtained as a multi–slice acquisition rather than a volumetric acquisition in an effort to minimize acquisition time and allow for easy re-acquisition of images with poor image quality. This type of acquisition results in non-isotropic voxels which can potentially result in partial voluming and issues in quantifying strains particularly in the right ventricle where the geometry of the free wall is irregular. Future studies can use the proposed pipeline to better understand the effect of voxel size on the quantification of cardiac mechanics.

To perform interpolation of 3D displacements and compute strains, linear radial basis functions were used. Fitting an RBF to data, even when optimized, is a computationally expensive operation. This computational cost is offset by the fact that linear RBFs extrapolate well and do not require post–processing such as spatial regularization which further influences the computed strains.

While this study sought to understand RV function in healthy individuals, no individuals with cardiac dysfunction were studied. Using this study as a reference, future studies can use the proposed framework in order to assess RV function in patients with heart disease.

V. Conclusion

The present study combined high–resolution displacement imaging from 3D spiral cine DENSE with a post–processing pipeline that included mesh–free strain analyses, a local coordinate system, and a flexible parameterization in order to quantify regional RV mechanics in 50 healthy individuals. Regional variations in circumferential and longitudinal strain were found throughout the RV while the RV lateral wall demonstrated torsion comparable that observed in the LV. The RV was also found to contract more synchronously than the LV. Future studies can now investigate deviations from these healthy contraction patterns to potentially gain new insights into the manifestation and/or prognosis for a variety of diseases affecting the right ventricle.