Retention and Effective Diffusion of Model Metabolites on Porous Graphitic Carbon

Abstract

The study of metabolites in biological samples is of high interest for a wide range of biological and pharmaceutical applications. Reversed phase liquid chromatography is a common technique used for the separation of metabolites, but it provides little retention for polar metabolites. An alternative to C18 bonded phases, porous graphitic carbon has the ability to provide significant retention for both non-polar and polar analytes. The goal of this work is to study the retention and effective diffusion properties of porous graphitic carbon, to see if it is suitable for the wide injection bands and long run times associated with long, packed capillary-scale separations. The retention of a set of standard metabolites was studied for both stationary phases over a wide range of mobile phase conditions. This data showed that porous graphitic carbon benefits from significantly increased retention (often > 100 fold) under initial gradient conditions for these metabolites, suggesting much improved ability to focus a wide injection band at the column inlet. The effective diffusion properties of these columns were studied using peak-parking experiments with the standard metabolites under a wide range of retention conditions. Under the high retention conditions, which can be associated with retention after injection loading for gradient separations, D_eff/D_m~ 0.1 for both the C18-bonded and porous graphitic carbon columns. As C18 bonded particles are widely, and successfully utilized for long gradient separations without issue of increasing peak width from longitudinal diffusion, this suggests that porous graphitic carbon should be amenable for long runtime gradient separations as well.

1. Introduction

The analysis of metabolites is becoming increasingly important for the progress of a variety of fields such as pharmaceuticals, disease detection and systems biology [1–4]. Liquid chromatography-mass spectrometry (LC-MS) is widely used in metabolomics with the LC method serving to separate components prior to detection [5–7]. Polar metabolites can be difficult to analyze with traditional reversed phase columns [8]. They will elute very early in a gradient, in some cases at the mobile phase breakthrough time, causing the loss of useful metabolomic information.

Capillary based ultrahigh pressure liquid chromatography (UHPLC) has a number of benefits when compared to standard bore columns. These include improved sensitivity for injections of the same mass, decreased mobile phase consumption, and improved column performance due to the ability to use smaller particles and longer columns [9–10]. However, there are a number of factors specific to capillary based gradient UHPLC that are important to consider when new stationary phases are implemented. Due to their inherently small volumes, capillary columns benefit from large volume sample injections that allow for sufficient loading of low abundance species for ease of detection. In practice it is common for the injection volume to be larger than the column volume. To accommodate such high sample volumes, solutes must have significant retention at the head of the column during the period of sample injection [11]. Without significant retention under initial gradient conditions, peaks will be broad due to the weakly retained species being swept along as the injection loads onto the column [12–13]. Sample focusing at the head of the column is vital to ensure that the injected analytes elute as narrow bands [14].

Due to its ability to retain polar compounds and use of solvents compatible with electrospray ionization (ESI)-MS, hydrophilic interaction liquid chromatography (HILIC) has been used to analyze polar metabolites [15–16]. HILIC, however, has limited ability to retain non-polar compounds that may be present in a sample. Porous graphitic carbon (PGC) as an LC sorbent offers alternative retention mechanisms that can provide significant retention for both non-polar and polar solutes [17]. In addition to the hydrophobic interactions expected for reversed phase systems, PGC exhibits increased retention for polar compounds due to the polar retention effect on graphite (PREG) mechanism [18]. Mechanistically, when a functional group with a permanent dipole comes in close proximity to the graphite surface, electron rearrangement occurs in the graphite, inducing an “image” dipole [17]. This “image” force causes a strong dipole-induced dipole attraction, and increased retention. In combination, these mechanisms allow for retention for both non-polar and polar solutes. Porous graphitic carbon is available commercially under the trade name of Hypercarb and has been demonstrated with polar samples such as neurotransmitters, explosives, carbohydrates, and glycans [19–22].

Assuming a stationary phase provides sufficient retention at the head of the column for effective sample focusing, there is an additional concern, namely the rate of effective longitudinal diffusion that an analyte experiences over the course of the gradient separation. The concern here is that the focused sample may spread axially during the long times spent retained, resulting in broadening of the previously focused band while the solute awaits the arrival of mobile phase of sufficient strength to effect elution [23]. When investigating longitudinal diffusion, it is easier to study isocratic conditions using traditional band broadening theory. The contribution of effective longitudinal diffusion (B-term) to the overall reduced plate height (h_B) can be written as [24]:

$$h_B=\frac{B}{v_0}=\frac{2(1+k^{\prime })}{v_0}·\frac{D_{\mathit{eff}}}{D_m}$$ (1)

where D_eff is the analyte effective diffusion coefficient, D_m is the analyte molecular diffusion coefficient in the mobile phase, ν₀ is the reduced mobile phase linear velocity, and k′ is the analyte retention factor. D_eff is a combination of the rate of diffusion in the mobile phase outside of the particles as well as the rate within the particle pores (this includes stationary phase diffusion). With the long run times associated with long capillary column gradients (at times upwards of 2 hrs), high rates of effective diffusion could lead to increased peak widths and a loss of resolution between peaks [25].

Effective longitudinal diffusion has been studied on traditional C18 stationary phases with a variety silica supports and measurement methods. Early studies utilized the residence-time weighted or parallel diffusion model, which assumes that the diffusional processes inside and outside of the particle are independent of one another, to separate the contributions of D_eff into mobile phase and stationary phase diffusion [26–30]. These studies showed that as retention increases, the rate of stationary phase diffusion decreases, limiting the impact of the surface diffusion on highly retained compounds. In 2008, Desmet et al. determined that this model of parallel diffusion was not physically accurate, and that effective medium theory (EMT) could be adapted to more accurately model effective diffusion under chromatographic conditions [31,32]. In the years that have followed, many studies using both simulations and experimental data have shown that while the rate of effective diffusion is seen to decrease with increasing retention, the contribution of intraparticle diffusion is much less dependent on retention [31–36]. In practice, this means that under conditions of high retention, such as initial gradient conditions, effective diffusion should have a limited effect on the overall peak due to the impact of low D_eff/D_m on Equation 1. Contrary to what was observed with the parallel-diffusion model, it has also been shown using peak-parking experiments with EMT models and molecular dynamics simulations, that the rate of surface diffusion increases as analytes become more retained due to the presence of an acetonitrile-rich “ditch” present in the interfacial region near the ends of the C18 chains. This region has a lower viscosity than the bulk mobile phase and results in faster surface diffusion [37–40]. Due to the differences in retention mechanism and surface chemistry (C18 bonded layer vs. flat graphite surface) it is thought that Hypercarb might exhibit different effective diffusion properties from a C18 bonded material.

In capillary UHPLC, gains in separation efficiency can be achieved by packing long capillary columns with sub-2 micron particles [10]. As the smallest commercially available PGC is 3 μm, it will be necessary to capitalize on column length and long run times for increased resolving power of complex metabolite samples [41]. Herein we study the pre-concentration and effective diffusion properties of model analytes on Hypercarb to assess the sorbent’s suitability for gradient separations with very long capillary columns at ultrahigh pressures. Comparison measurements are made to a traditional C18 bonded phase column.

2. Materials and Methods

2.1 Chemicals

Methanol (MeOH, HPLC grade), acetone (HPLC grade), potassium chloride (KCl) and L-ascorbic acid were purchased from Fisher Scientific (Fair Lawn, NJ). Deionized water was obtained using a Barnstead Nanopure ultrapure water system (Dubuque, IA). Formic acid (FA), mandelic acid (MA), hippuric acid (HA), 2-methylhippuric acid (2-MHA), 3-methylhippuric acid (3-MHA), 4-methylhippuric acid (4-MHA), potassium ferrocyanide and potassium ferricyanide were purchased from Sigma Aldrich (St. Louis, MO).

2.2 Measurement of Retention for Hypercarb and BEH-C18 Columns

Isocratic separations were carried out using an Acquity UPLC system equipped with a photodiode array detector from Waters Corporation (Milford, MA). The columns used for the study were: a Hypercarb column (100 mm × 4.6 mm, 3 μm) purchased from Thermo Fisher Scientific Inc. (Waltham, MA) and a Bridged Ethylene Hybrid C18 column (BEH, 50 mm × 2.1 mm, 1.7 μm) provided by Waters Corp. The manufacturers market these columns as having an average pore size of 250 Å and 130 Å and a surface area of 125 m²/g and 185 m²/g for the Hypercarb and BEH-C18 columns, respectively. The columns were kept at 30 °C during all retention measurements using the Acquity column heater.

In order to characterize the retention characteristics of BEH-C18 and Hypercarb for metabolites, a standard test mixture was separated under isocratic conditions. This mixture contained mandelic acid, hippuric acid, 2-methylhippuric acid, 3-methylhippuric acid, and 4-methylhippuric acid. Separations were performed using a range of water/MeOH + 0.1% FA mobile phase compositions in order to see how k′ changed with organic content.

Initially, the Hypercarb column exhibited significant drift in retention time day-to-day. In an attempt improve reproducibility in retention data, a column pre-treatment process was performed before measurements. The column was flushed for at least 90 column volumes with whichever mobile phase (water/MeOH + 0.1% FA) was intended for use, with 10 mM ascorbic acid added. Ascorbic acid was then washed off the column with standard mobile phase used for analysis for at least 30 column volumes. This process brings the redox state of the graphite surface to a reproducible state prior to any retention measurements. Pre-treatment was not necessary for the BEH-C18 column as retention times were repeatable.

2.3 Molecular Diffusion Coefficient Measurements

Molecular diffusion coefficients were measured in the mobile phase for a number of analyte/mobile phase combinations using a dual-UV detector setup that has been described previously [42]. A diagram of the experimental setup can be found in the Supplementary Material. Briefly, the polyimide was removed from two spots, roughly 2.5 m apart, on a piece of fused silica capillary, 360 μm outer diameter (o.d.) with a nominal inner diameter (i.d.) of 50 μm (Polymicro Technologies, Phoenix, AZ). This capillary was threaded through two Linear UVIS 200 UV-Vis spectrophotometers with the capillary windows each being centered in one of spectrophotometers. All measurements were made with a rise time of 0.1 s, while the sensitivity was adjusted for each analyte to maximize the signal-to-noise. The capillary inlet was inserted into a scintillation vial containing the desired solute (1–2 mg/mL) in mobile phase. The vial was placed in an in-house made pressure vessel. The outlet was also placed in a vial of mobile phase to prevent evaporation inside the capillary. Nitrogen pressure was applied to the vessel to force sample through the capillary. As the analyte traveled through the detection zones, sigmoidal signal curves were recorded. Data was then differentiated using Igor Pro (Wavemetrics, Inc, Lake Oswego, OR) to generate peaks. The peaks were then fit to Gaussians for the measurement of variance. All measurements were made at ambient lab temperature (22.5 ± 0.2 °C).

2.4 Peak-Parking Measurements

Peak-parking methods have been used previously for the measurement of diffusion coefficients in chromatographic systems [32,35,36,39,40,43,44]. Peak-parking experiments were carried out with the same columns as above and the Acquity UPLC. A four-port valve (Valco, Houston, TX) was placed between the injector and column to allow manual control of the flow stoppage. The columns were kept in the Acquity column heater at a temperature of 30 °C or 55 °C as denoted.

Runs were performed with no stop in order to get a baseline variance for the analyte under the specific mobile phase conditions. For a peak-parking run, the flow was diverted away from the column using the valve when the analyte band reached half way down the column length. The valve had a restrictor capillary to make sure the backpressure of the diverted flow was equal to that generated by the column. After the stop time, the valve was turned to direct flow back to the column, where the analyte band was eluted off for detection. Measurements using a range of stop times were recorded for each set of conditions. As described previously, ascorbic acid washing of the Hypercarb column was performed each day before use.

Peak-parking experiments were performed on both the Hypercarb and BEH-C18 columns using unretained species (ascorbic acid for BEH-C18 and acetone for Hypercarb) and the standard test metabolites under a variety of water/methanol + 0.1% formic acid mobile phase conditions at 30 °C. Measurements were also made for Hypercarb at 55 °C in order to see if significant variation occurred due to elevated temperature. The mobile phase and analyte used were both varied to obtain measurements over a range of retention factors (k′ ~ 0–40). Measurements were taken in at least triplicate for all conditions and stop times.

3. Results/Discussion

3.1. Retention of Model Metabolites on Hypercarb and BEH-C18 Columns

In order to understand and compare the ability of Hypercarb and BEH-C18 columns to pre-concentrate metabolite standards under initial gradient conditions, it was necessary to measure the retention characteristics of model compounds across a range of mobile phase compositions. The selected metabolites in the test mixture are a series of organic acids that result from exposure to styrene, xylene, and toluene. During our initial work with Hypercarb columns, a large amount of day-to-day variability in k′ was observed. It was thought that the redox state of the Hypercarb surface was the cause of the drift. Previous studies have shown that chemical or electrochemical treatments can alter the surface redox state and ultimately alter the retention of compounds on PGC [45–50]. Here, an ascorbic acid wash, which has previously been shown to reduce graphene oxide, was used before each day of experiments in order to reduce the surface to a repeatable initial state [51]. Figure 1 shows a comparison of the repeatability and retention of the metabolite mixture before and after treatment. Significant improvement in the repeatability is seen using this washing step, as well as a decrease in. k′ The decrease in retention of anions due to reduction of the surface is in line with what has been seen previously [52]. Retention measurements were made across a wide range of water/MeOH + 0.1% FA compositions, for both types of columns. As a comparison of the retention difference between Hypercarb and BEH-C18, Figure 2 shows a plot of k′ for 4-methylhippuric acid, which is the most retained compound on both columns under the conditions used, vs. the organic content in the mobile phase. Hypercarb, with its alternative mechanism for retaining polar compounds and ability to have π–π interactions with the aromatic ring of 4-MHA, shows significantly increased retention over the BEH-C18 column, even over the limited mobile phase composition range measured. Even in 92.5/7.5 (v/v) water/MeOH + 0.1% FA, which is close to the initial conditions of most reversed phase gradients, the BEH-C18 column provides a k′ of approximately 25 for 4-MHA while Hypercarb shows a similar level of retention in 65% methanol. Keep in mind that this is the most retained compound of the mixture on both columns, so all other species will have even lower k′. As mentioned previously, this lack of retention is a limiting factor for the gradient separations of polar metabolites with C18-bonded columns.

Figure 1.

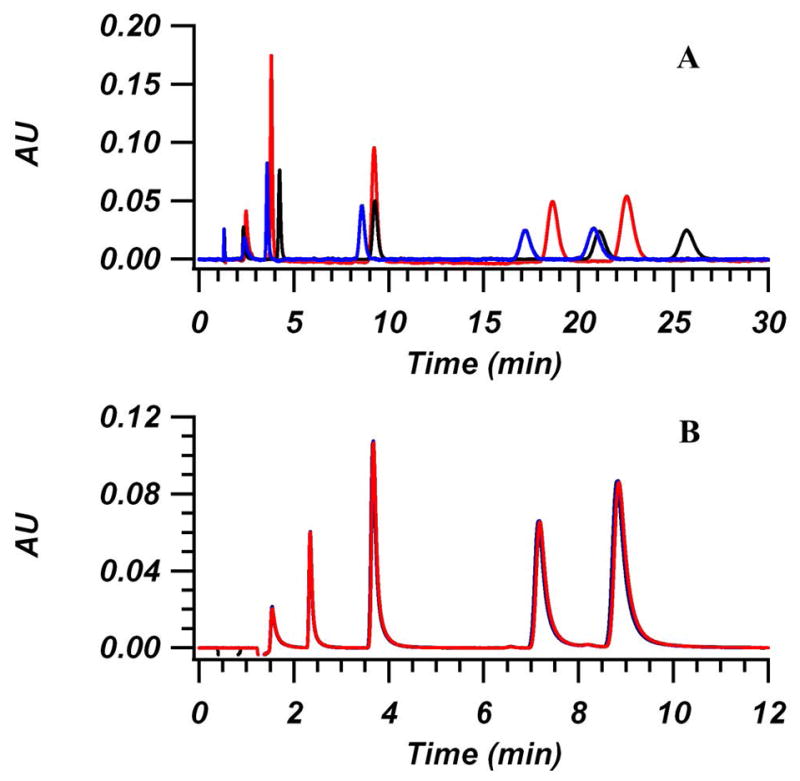
Chromatograms showing the change in day-to-day repeatability over three days for the standard test mixture before (A) and after (B) treatment using 10 mM ascorbic acid. Column was 4.6 mm × 100 mm packed with 3 μm Hypercarb. Mobile phase conditions were 5/95 (v/v) water/MeOH + 0.1% FA at a flow rate of 1 mL/min and 30 °C. For (A), measurements were taken over the course of 2 weeks at day 1 (red), day 4 (black) and day 14 (blue). For (B), ascorbic acid treatment was performed before use each day by flowing 10 mM ascorbic acid in mobile phase overnight. Before measurements, ascorbic acid was washed off column by flushing with mobile phase. Measurements were taken over a similar time span as in (A). Elution order: mandelic acid, 2-MHA, hippuric acid, 3-MHA, and 4-MHA. UV Detection: 240 nm.

Figure 2.

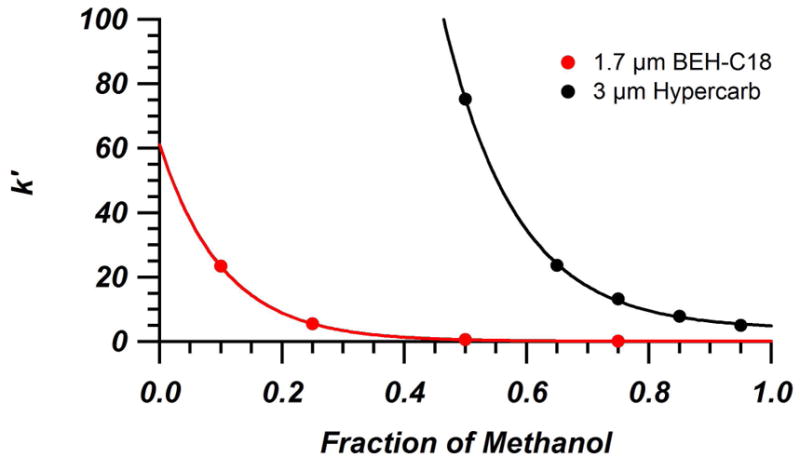
Retention factor of 4-methylhippuric acid on BEH-C18 (red) and Hypercarb (black) columns as a function of methanol volume fraction in the mobile phase. Columns were a 2.1 mm × 50 mm packed with 1.7 μm BEH-C18 and a 4.6 mm × 100 mm packed with 3 μm Hypercarb. Mobile phases consisted of mixtures of water/MeOH + 0.1% FA at 30 °C. Experimental data fit with exponential curves.

Due to the high level of retention for several of the test compounds on Hypercarb, it was not reasonable to measure k′ under still weaker mobile phase conditions. In order to project the retention of these test compounds to the conditions that would be expected under initial gradient conditions, it was necessary to fit the experimental data with an empirical model. It has been shown that the assumption of a linear relationship between the logarithm of k′ and organic content is an oversimplification, and that experimental data across a wide range of solvent compositions will show some curvature. Neue’s equation is used to empirically fit the observed curvature [53]:

$$ln{k}^{\prime }=ln{k^{\prime }}_{oo}+2ln(1+a\ast c)-\frac{B_{\mathit{sol}}\ast c}{1+a\ast c}$$ (2)

Here, k′₀₀ is the retention factor in 100% water, c is the fraction of organic in the mobile phase, B_sol is a solute dependent term largely determined by molecular weight, and a is a term that allows for curvature. Figure 3 shows the Hypercarb retention data for all of the standard metabolites, fit with Equation 2. A plot of the model metabolite retention data for BEH-C18 as well as values for a and B_sol for both columns can be found in the Supplementary Material. Table 1 compares the k′₀₀ factors for the five model analytes on Hypercarb versus BEH-C18. With the exception of mandelic acid, k′₀₀ values on Hypercarb are between 3,000 and 11,000, and offer more than 100-fold greater retention than BEH-C18 under the same 100% aqueous mobile phase conditions. For a given injection volume, the final band volume after loading the injection is related by the inverse of the retention factor in the sample solvent [14]. With this enhanced level of retention, these test compounds will pre-concentrate more significantly as they arrive at the head of the Hypercarb column than the BEH-C18 column. This suggests that a large injection onto a capillary column packed with Hypercarb will provide far more effective pre-concentration focusing than a BEH-C18 column for these metabolites.

Figure 3.

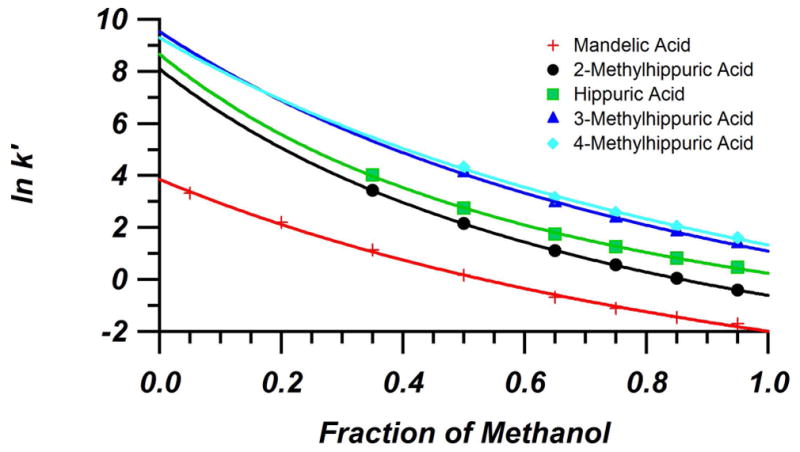
Plot of natural log of retention factors of the model metabolites as a function of methanol volume fraction in the mobile phase on the Hypercarb column (4.6 mm × 100 mm, 3 μm). Measurements made in water/MeOH + 0.1% FA mobile phases at 30 °C. Experimental data fit with Equation 2.

Table 1.

Projected retention of standard metabolites in 100% water (k′₀₀) on Hypercarb (4.6 mm × 100 mm, 3 μm) and BEH-C18 (2.1 mm × 50 mm, 1.7 μm) columns as well as the ratio of $\frac{{k^{\prime }}_{00}(\mathit{PGC})}{{k^{\prime }}_{00}(C18)}$. Retention was measured over a range of mobile phase compositions consisting of mixtures of water/MeOH + 0.1% FA at 30 °C. Experimental data was then fit with Equation 2, which was used to find k′₀₀.

Analyte	k′00 (PGC)	k′00 (C18)	$\frac{{k^{\prime }}_{00}(\mathit{PGC})}{{k^{\prime }}_{00}(C18)}$
MA	47	9.6	4.9
2-MHA	3300	23	140
HA	5800	15	390
3-MHA	13000	61	210
4-MHA	11000	61	180

3.2. Experimental Molecular Diffusion Coefficient Data

In order to determine the impact of the effective diffusion properties of these materials relative to bulk mobile phase diffusion, it was necessary to determine D_m for a number of analyte/mobile phase combinations. Due to the low pressures associated with the peak-parking experiments (< 500 bar), viscosity changes due to pressure do not need to be accounted for in D_m measurements [42]. The raw UV signal was differentiated to generate peaks (example in Supplemental Material). These differentiated peaks were then fit with Gaussians, whose variance can be used to find the temporal variance accumulated between the detectors ( ${\sigma }_{t\_\mathit{net}}^2$):

$${\sigma }_{t\_\mathit{net}}^2={\sigma }_{t2}^2-{\sigma }_{t1}^2$$ (3)

where ${\sigma }_{t1}^2$ and ${\sigma }_{t2}^2$ are the temporal variances of the peaks measured at the first and second detectors, respectively. D_m is then calculated from Equation 4 [42].

$$D_m=\frac{d_c^2\mathrm{\Delta }t}{96{\sigma }_{t\_\mathit{net}}^2}$$ (4)

In Equation 4 d_c is the capillary i.d. and Δt is the time between the detected peaks.

Accurate knowledge of d_c over the length between detectors is vital for determination of D_m because it depends on the square of d_c. For this reason, a calibration of d_c was needed. In order to calibrate d_c between the detectors, D_m of potassium ferrocyanide and ferricyanide were measured. D_m of these species in 1 M KCl has been studied using a number of methods at 25 °C [54]. By comparing the experimental D_m to the literature values, the diameter of the capillary between the detectors can be determined [54]. Due to the experiments being done at room temperature (22.5 ± 0.2 °C) it was necessary to account for the temperature difference between the literature and experimental measurements. This was done using the Stokes-Einstein equation [42]:

$$D_m=\frac{k_{B}T}{6\pi \eta r_H}$$ (5)

where k_B is Boltzmann’s constant, T is the absolute temperature, η is the mobile phase viscosity, and r_H is the hydrodynamic radius of the analyte. After calibration, d_c was found to be 46.4 μm. This value was then used, in conjunction with dual-UV measurements, to calculate D_m for a number of standard metabolite and mobile phase combinations. All measurements were taken at ambient lab temperature (22.5 ± 0.2 °C). Values were adjusted using Equation 5 for temperatures under which peak-parking measurements were conducted (30 °C and 55 °C). The viscosities of water/methanol mobile phases at various temperatures have been previously reported [55]. Tables 2, 3, and 4 show the measured D_m for all analyte and mobile phase combinations used for the BEH-C18 at 30 °C, Hypercarb at 30 °C, and Hypercarb at 55 °C peak-parking studies. At least triplicate measurements were made for each analyte/mobile phase pair. These values have some error inherent to them from the estimations made for temperature and viscosity, but this is likely less than the 10–15% error often associated with the Wilke-Chang method for calculating D_m [56–57].

Table 2.

Measured values for k′, D_m, D_eff, and $\frac{D_{\mathit{eff}}}{D_m}$ along with the conditions used for the BEH-C18 column (2.1 mm × 50 mm, 1.7 μm) at 30 °C.

Analyte	Mobile phase	k′	Dm (cm2/s)	Deff (cm2/s)	$\frac{D_{\mathit{eff}}}{D_m}$
Ascorbic acid	50/50 water/MeOH	0	4.43 ± 0.08 × 10−6	2.01 × 10−6	0.45
MA	60/40 water/MeOH	0.75	5.07 ± 0.09 × 10−6	2.95 × 10−6	0.58
4-MHA	75/25 water/MeOH	5.50	5.07 ± 0.09 × 10−6	1.43 × 10−6	0.28
4-MHA	85/15 water/MeOH	13.7	5.96 ± 0.11 × 10−6	1.12 × 10−6	0.19
4-MHA	92.5/7.5 water/MeOH	34.8	6.49 ± 0.12 × 10−6	8.42 × 10−7	0.13

Table 3.

Measured values for k′, D_m, D_eff, and $\frac{D_{\mathit{eff}}}{D_m}$ along with the conditions used for the Hypercarb column (4.6 mm × 100 mm, 3 μm) at 30 °C.

Analyte	Mobile phase	k′	Dm (cm2/s)	Deff (cm2/s)	$\frac{D_{\mathit{eff}}}{D_m}$
Acetone	5/95 Water/MeOH	0	2.61 ± 0.05 × 10−5	1.25 × 10−5	0.48
2-MHA	5/95 Water/MeOH	0.87	9.62 ± 0.17 × 10−6	2.9 × 10−6	0.30
Hippuric acid	5/95 Water/MeOH	1.95	9.51 ± 0.17 × 10−6	2.0 × 10−6	0.21
3-MHA	5/95 Water/MeOH	4.72	9.45 ± 0.17 × 10−6	1.5 × 10−6	0.16
4-MHA	5/95 Water/MeOH	6.40	9.25 ± 0.16 × 10−6	1.4 × 10−6	0.15
4-MHA	25/75 Water/MeOH	16.3	5.82 ± 0.10 × 10−6	7.2 × 10−7	0.12
4-MHA	40/60 Water/MeOH	41.2	4.81 ± 0.09 × 10−6	4.7 × 10−7	0.10

Table 4.

Measured values for k′, D_m, D_eff, and $\frac{D_{\mathit{eff}}}{D_m}$ along with the conditions used for the Hypercarb column (4.6 mm × 100 mm, 3 μm) at 55 °C.

Analyte	Mobile phase	k′	Dm (cm2/s)	Deff (cm2/s)	$\frac{D_{\mathit{eff}}}{D_m}$
2-MHA	5/95 Water/MeOH	0.81	1.54 ± 0.03 × 10−5	4.7 × 10−6	0.31
Hippuric acid	5/95 Water/MeOH	1.66	1.52 ± 0.03 × 10−5	3.25 × 10−6	0.21
3-MHA	5/95 Water/MeOH	3.75	1.51 ± 0.03 × 10−5	2.7 × 10−6	0.18
4-MHA	5/95 Water/MeOH	4.81	1.48 ± 0.03 × 10−5	2.3 × 10−6	0.16
4-MHA	25/75 Water/MeOH	11.1	9.92 ± 0.18 × 10−6	1.20 × 10−6	0.12
4-MHA	40/60 Water/MeOH	28	8.42± 0.15 × 10−6	1.02 × 10−6	0.12

3.3. Peak-Parking Experiments

Peak-parking measurements were performed under a variety of retention conditions for both BEH-C18 and Hypercarb columns in order to measure the effective diffusion of various solutes. Figure 1(B), shows that the Hypercarb columns produced a significant amount of tailing for the metabolite peaks. This tailing was observed throughout the peak-parking experiments and made it difficult to accurately measure peak variance with the commonly used methods of statistical moments or by fitting Gaussians. The most accurate way to fit these peaks was with the Foley-Dorsey model of the Exponentially-Modified Gaussian (EMG) function [58–59]:

$$f(t)=A_{\mathit{peak}}\frac{{\sigma }_{\mathit{fit}}}{{\tau }_{\mathit{fit}}}\sqrt{\frac{\pi }{2}}exp\left(\frac{{\sigma }_{\mathit{fit}}^2}{2{\tau }_{\mathit{fit}}^2}-\frac{t-t_r}{{\tau }_{\mathit{fit}}}\right)\left(1-\mathit{erf}\left[\frac{2}{\sqrt{2}}\left(\frac{{\sigma }_{\mathit{fit}}}{{\tau }_{\mathit{fit}}}-\frac{t-t_r}{{\sigma }_{\mathit{fit}}}\right)\right]\right)$$ (6)

where f(t) is the measured signal, A_peak is the peak amplitude, t_r is the peak retention time, σ_fit is used to describe the Gaussian, “sigma-type” broadening contribution, and τ_fit is used to describe the exponential decay, “tau-type”, broadening. Traditionally when fitting peaks using the EMG, the temporal variance of the fit peak ( ${\sigma }_{t,\mathit{EMG}}^2$) is calculated using Equation 7.

$${\sigma }_{t,\mathit{EMG}}^2={\sigma }_{\mathit{fit}}^2+{\tau }_{\mathit{fit}}^2$$ (7)

When using this equation on the measured analyte peaks for the Hypercarb column, ${\sigma }_{t,\mathit{EMG}}^2$ was dominated by ${\tau }_{\mathit{fit}}^2$ due to the strong tailing observed, masking any sigma-type broadening. Tau-type broadening can originate from several sources such as poorly swept volumes in the injector, connecting tubing and also slow kinetics of adsorption/desorption [60–62]. In the peak-parking experiments, there is no convective flow. This lack of flow means that the only broadening processes that can affect peak width during flow stoppage are axial diffusion in the mobile phase and intraparticle volumes. Since molecular diffusion has no directionality (it is equally probable toward the inlet or outlet of the column) it will only contribute toward increasing the sigma component of the total variance [62]. As the purpose of peak-parking experiments is to solely measure the effect of these diffusional processes on an injected band over a range of stop times, it was thought that simply using ${\sigma }_{\mathit{fit}}^2$ alone would be a more accurate descriptor of the diffusional broadening [62]. For consistency, this method of peak fitting was also used for measurements made with the BEH-C18 column, even though the tailing was far less on this column. It is necessary for the variance to be taken from the temporal domain that it was measured in, to the spatial domain ( ${\sigma }_{ax,L}^2$) using the analyte band velocity (u).

$${\sigma }_{ax,L}^2={\sigma }_{\mathit{fit}}^2{u}^2$$ (8)

By plotting the spatial variance versus the stop time for an analyte/mobile phase combination, it was possible to calculate D_eff that an analyte experiences while stopped using [24,63]:

$${\sigma }_{ax,L}^2=2D_{\mathit{eff}}{t}_{\mathit{stop}}$$ (9)

where t_stop is the stop time. Figures 4 illustrates the linearity between ${\sigma }_{ax,L}^2$ and t_stop for the analytes on Hypercarb at 30 °C. Plots for BEH-C18 at 30 °C and Hypercarb at 55 °C, as well as data for trend line fits of these plots, can be seen in the Supplementary Material. Even though the Hypercarb peaks were highly tailed, the EMG function fit the peaks very accurately and allowed determination of ${\sigma }_{\mathit{fit}}^2$ of the peaks. If the EMG function was not accurately or consistently fitting these tailed peaks, it would be expected that the R² values would likely be very poor. The fit of all these trend lines had R² ≥ 0.98 for BEH-C18 and Hypercarb at 30 °C and R² ≥ 0.96 for Hypercarb at 55 °C, suggesting that use of the EMG function was satisfactory in determining D_eff The values for D_eff measured using the slopes of the these trend lines can be found in Tables 2, 3, and 4 for BEH-C18 at 30 °C, Hypercarb at 30 °C, and Hypercarb at 55 °C peak-parking studies along with the corresponding solvent conditions and k′. The decreasing slope with increasing retention factor, which can be seen in Figure 4, arises from two factors. The first being that the increased water fraction in the mobile phase that caused the increased k′, also caused a decrease in D_m due to increased viscosity. The second factor causing the decrease in slope is the decrease in D_eff that has been seen previously [32,35].

Figure 4.

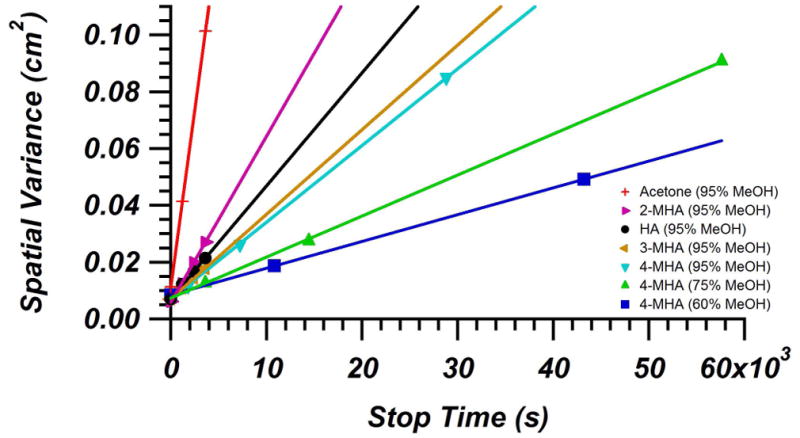
Change in spatial variance of acetone (unretained marker) and several model metabolites as a function of peak-parking time for Hypercarb column (4.6 mm × 100 mm, 3 μm) at 30 °C. Based on Equation 9, the slope of these trend lines are equal to 2 D_eff. In order to cover a range of retention factors, different analytes and mobile phase conditions were used.

In order to eliminate any bias introduced by changing mobile phase conditions, it is useful ratio the values of D_eff for the analyte/mobile phase combinations to the corresponding D_m. Figure 5 shows the values for D_eff/D_m plotted against their corresponding retention factor for BEH-C18 and Hypercarb. The values for D_eff/D_m can also be found in Tables 2, 3, and 4 for BEH-C18 at 30 °C, Hypercarb at 30 °C, and Hypercarb at 55 °C. In depth analysis of the calculation of error bars can be found in the Supplementary Material. It was seen that both BEH-C18 and Hypercarb at 30 °C decrease as they move from low to high k′. This trend has been reported previously for C18 bonded columns [35,36]. For very lightly retained species (k′ ~ 0.8), D_eff/D_m for BEH-C18 is roughly double that of Hypercarb, suggesting that diffusion occurs more rapidly on the BEH-C18 column. In order to determine whether this difference was truly due to differences in surface diffusion or in internal pore diffusion and column obstruction, peak-parking experiments were performed on unretained species (k′ = 0) on both the BEH-C18 and Hypercarb columns at 30 °C. It can be seen in Figure 5 (as well as Tables 2 and 3) that D_eff/D_m for unretained species are in close agreement, falling just below 0.5, meaning that the combined intra and inter-particle obstruction factors for both columns are very similar. With similar obstruction factors, the differences in D_eff/D_m that are seen for lightly retained species must be due to differences in surface diffusion rates. This difference in diffusion should not have a significant impact on gradient separations as the majority of time that an analyte spends on the column is under generally highly retained conditions. It should be noted that the D_eff/D_m data for BEH-C18 goes through a maximum at low k′. This trend has been seen previously when simulating particle packed chromatographic beds with a high rate of intraparticle diffusion [33,64]. At high k′ the two data sets converge and settle around similar values of D_eff/D_m ~ 0.1–0.13. It was seen that even at the elevated temperature of 55 °C, D_eff/D_m for Hypercarb is essentially identical to what was observed at 30 °C across the full range of k′. The similarity of the data is significant since elevated temperatures are often used in capillary separations to promote rapid diffusion as well as reduce backpressure and analysis time [25]. Previous studies using C18 bonded particles showed a similar overlay of surface diffusion data at different temperatures [29]. Since surface diffusion is derived from the effective diffusion, it is expected that the same trend be seen with effective diffusion. This trend suggests a correlation between effective diffusion and molecular diffusion [29]. D_eff/D_m appears to be constant for a given k′, regardless of temperature. For a given mobile phase composition and analyte, the data points at 55 °C are moved to slightly lower k′ than the corresponding points at 30 °C. Even with the slight decreases in k′ from the higher temperature, the ratio of D_eff/D_m has changed to fit the curvature of the overall data set, rather than staying equal to that of the data at 30 °C.

Figure 5.

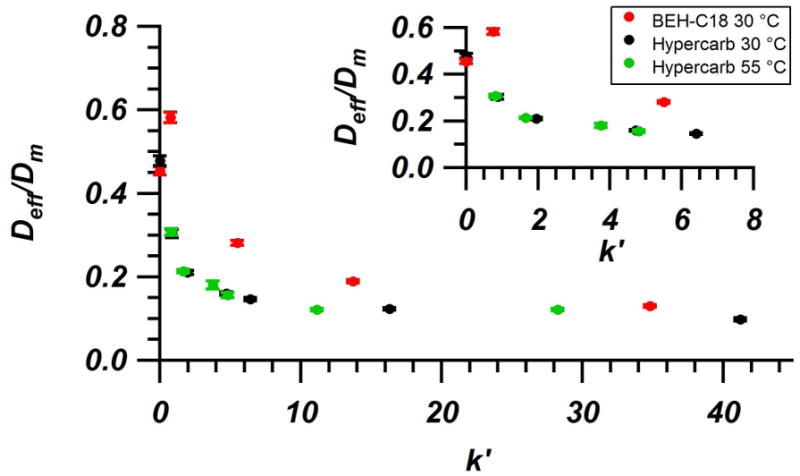
Comparison of D_eff/D_m at 30 °C for BEH-C18 (red), Hypercarb at 30 °C (black), and Hypercarb at 55 °C (green) as a function of analyte retention factor. The choice of analyte and mobile phase composition were varied in order to cover a wide range of retention factors for each column. Inset zooms on the region of moderate to low retention where curvature occurs. Error bars are shown for each data point. In-depth discussion of error calculation can be found in the Supplementary Material.

Previous studies have been able to further decompose D_eff to determine the contribution from intraparticle diffusion using Torquato’s model of effective diffusion [34,36]. Due to the lack of knowledge on the external column porosity for Hypercarb and likely difficulty adapting traditional pore blocking methods used for reversed phase columns to a system with significantly more complex retention, it was not possible to analyze the data presented here using Torquato’s model to determine specific values of intraparticle diffusion. However, based on simulations by Desmet and Deridder, the quick drop in D_eff/D_m seen for both BEH-C18 and Hypercarb suggests that the intraparticle diffusion is relatively low in comparison to diffusion in the interparticle volume [34]. As k′ increases, the analyte spends more time in the particle and its effective diffusion is more highly influenced by the intraparticle diffusion coefficient. Therefore, the lower the intraparticle diffusion coefficient, the more rapidly D_eff/D_m will decrease with increasing k′. Nonetheless, it is important to see the bigger picture as it applies to gradient separations. BEH-C18 and Hypercarb columns reach a similar value of D_eff/D_m ~ 0.1–0.13 at the highest k′ tested. It is known from experience that BEH-C18 particles provide low enough effective diffusion to allow for minimal contribution to peak broadening under conditions of high k′ prior to elution by the mobile phase gradient. The data for Hypercarb suggests that it too will provide minimal contributions to broadening of focused bands prior to elution, as D_eff/D_m are at even lower values on Hypercarb over the whole range of k′ at both 30 °C and 55 °C. This factor is critical since long capillary columns packed with Hypercarb will require long run times at the flow rates and gradient rates needed for coupling to MS systems.

Conclusions

In this work, the retention and effective diffusion characteristics of Hypercarb columns were studied for a standard mixture of model metabolites. This was done in order to determine whether long capillary columns packed with Hypercarb would be applicable to the separation of these types of samples. Whereas polar metabolites tend to have low retention on C18 bonded stationary phases, Hypercarb showed to have significantly increased retention for these compounds, likely due to electrostatic induction interactions between the graphite surface and the analyte functional groups. By having this high level of retention, Hypercarb should be able to focus large volume injections of these types of analytes on the head of the column when they are injected under initial gradient conditions. Data for Hypercarb shows that D_eff/D_m decreases across the range of k′ measured, settling around D_eff/D_m ~ 0.1 even at the elevated temperatures often used to speed up analysis time of capillary separations. BEH-C18 data shows increasing D_eff/D_m with k′ from 0 to 0.8 before ultimately falling to D_eff/D_m ~ 0.1 as k′ continues to increase. Since BEH-C18 is widely and successfully utilized for long, capillary-scale gradient separations without a significant increase in peak width from effective diffusion, this suggests that the impact of longitudinal diffusion on gradient separations using Hypercarb columns should be minimal as well. The data shown here suggests that Hypercarb should be amenable to long capillary column separations of polar metabolites based on the improved retention of these compounds and the low level of effective diffusion seen at high retention.

Highlights.

• Hypercarb shows increased retention of metabolites compared to a C18 bonded phase

• Retention on Hypercarb allows for focusing of large injections in gradient elution

• Potential impact of effective diffusion on gradient runs studied using peak parking

• Diffusion characteristics make Hypercarb suitable for long gradient runs