Molecular simulations of cellular processes

Abstract

It is, nowadays, possible to simulate biological processes in conditions that mimic the different cellular compartments. Several groups have performed these calculations using molecular models that vary in performance and accuracy. In many cases, the atomistic degrees of freedom have been eliminated, sacrificing both structural complexity and chemical specificity to be able to explore slow processes. In this review, we will discuss the insights gained from computer simulations on macromolecule diffusion, nuclear body formation, and processes involving the genetic material inside cell-mimicking spaces. We will also discuss the challenges to generate new models suitable for the simulations of biological processes on a cell scale and for cell-cycle-long times, including non-equilibrium events such as the co-translational folding, misfolding, and aggregation of proteins. A prominent role will be played by the wise choice of the structural simplifications and, simultaneously, of a relatively complex energetic description. These challenging tasks will rely on the integration of experimental and computational methods, achieved through the application of efficient algorithms.

Graphical abstract

Introduction

The simulation of biological events has become a fundamental tool in contemporary molecular and cellular biophysics (Tomita 2001; Avila et al. 2011; Trovato and O’Brien 2016). Computer simulations are often integrated with experiments performed in vivo to provide a microscopic interpretation of cellular phenomena (Hihara et al. 2012; Coquel et al. 2013; Di Rienzo et al. 2014; Earnest et al. 2017). Although powerful to predict macromolecule behavior, this technique, defined as the “computational microscope” by Schulten (Lee et al. 2009), has some limitations (Takada 2012; Piana et al. 2014; Ivani et al. 2016; Song et al. 2017; Wang et al. 2017a). The most challenging is the difficulty to simulate large systems represented at full atomistic resolution for timescales longer than a few μs. Simulations of slower processes occurring in a cell, such as protein (mis)folding, macromolecular (dis)assembly, chromosome (de)condensation, and co-translational events, are, therefore, unfeasible with today’s resources (Bhattacharya et al. 2013; Phillip and Schreiber 2013; Redler et al. 2014; Perilla et al. 2015; Nilsson et al. 2015; Korolev et al. 2016; Zheng and Wen 2017), unless coarser-than-atomistic representations are employed (Takada 2012; Trovato and Tozzini 2012).

One frequent simplification found in biological models is the elimination of the cellular components because of the computational cost associated with their representation. This often limits the scope of the studies, as it is now well recognized that the cellular environment perturbs the dynamics and thermodynamics of proteins and nucleic acids, as well as the solvent, with consequences on cell physiology (Luby-Phelps 1999; Foffi et al. 2013; Mourão et al. 2014; Huang et al. 2016; Rivas and Minton 2016; Wang et al. 2017b) . A factor that has been demonstrated early to modify the activity and mobility of biomolecules in vivo is the concentration of bystander macromolecules, also known as crowders, that can be as high as 40% of the cell volume (Muramatsu and Minton 1988). Accordingly, crowders have often been modeled as inert hard spheres to capture the effect of volume occlusion. This approximation has led to the prediction that inert crowders promote folding and chemical reactions (Muramatsu and Minton 1988; Zhou et al. 2008), as well as to observing the reversible transition from a swollen to a compact chromosome (Shendruk et al. 2015) and the assembly of nuclear bodies in computer simulations (Cho and Kim 2012b; Kim and Szleifer 2014).

The limitations of the assumption of inert crowders are now becoming evident, especially in the cell milieu, where promiscuous and attractive interactions are frequent (Robinson et al. 2012; Sarkar et al. 2013; Gnutt et al. 2015; Smith et al. 2016; Pérez Santero et al. 2016; Minton 2017; Rotta et al. 2017). The stabilizing effect arising from the crowder excluded volume has been observed to be counteracted in several cases where weakly interacting biological crowders were employed (Zhou et al. 2008; Peixoto et al. 2015; Gnutt et al. 2015; Smith et al. 2016; Rothe et al. 2016; Starzyk et al. 2016). However, the largest effect of favorable interactions is experienced during diffusion (Saxton 1996; Putzel et al. 2014; Peixoto et al. 2015; Bucciarelli et al. 2016; Smith et al. 2016). Indeed, by allowing the macromolecules of a model bacterial cytoplasm to associate transiently, computer simulations have predicted a consistent motion slowdown that inert crowders were unable to explain (Trovato and Tozzini 2014).

An additional consequence of the high concentration of macromolecules in vivo is that mobility can be anomalous, i.e., the diffusion coefficients can be time-dependent, contrary to the constant values expected in isolation (Banks and Fradin 2005; Dix and Verkman 2008; Smith et al. 2017). A positive rate of diffusion, termed super-diffusion, often suggests a mechanism of active transport (Reverey et al. 2015). A negative rate, so called sub-diffusion, can originate from weak macromolecular associations and increase, for example, the search efficiency of enzymes for their DNA binding sites (Golding and Cox 2006; Guigas and Weiss 2008; Sereshki et al. 2012; Lampo et al. 2017). The different regimes can alternate on different timescales, reflecting the underlying heterogeneity of and interactions among cellular structures (Di Rienzo et al. 2014; van den Berg et al. 2017).

Nonspecific interactions contribute not only to the stochastic diffusion of macromolecules (Saluja and Kalonia 2008; de Nooijer et al. 2009; Johansson et al. 2014; Staneva and Frenkel 2015; Luchinat and Banci 2017), but also to the formation of localized structures such as organelles and supramolecular assemblies (Lécuyer et al. 2007; Rudner and Losick 2010; Coquel et al. 2013; Wei et al. 2016; Luo et al. 2016). Hence, they determine the macroscopic properties of the cytoplasm both in physiological conditions and under stress (Parry et al. 2014; Joyner et al. 2016; Munder et al. 2016). These and the previous examples are clear evidence of the importance of chemical interactions between macromolecules, despite their weak strength, and suggest that they are as relevant as the specific interactions responsible for biomolecule folding and complex formation. The predominantly biological classification based on interaction specificity is inherently blurred and differs from the definitions of hydrophobic, hydrogen bond, electrostatic, and Van der Waals forces accepted in the physical sciences (Israelachvili 1992; Curtis and Lue 2006). Nevertheless, it is useful to adopt both the physical and the biological interpretations in light of the models that we will present in this work.

This review will discuss the insights gained from computer simulations on the behavior of macromolecules within cell-mimicking spaces. Special attention will be devoted to the inter-molecular interactions employed in the different models. Since a complex landscape of modeling techniques exists, we will first describe the main strategies used to represent biological systems and their limitations. The paper will be concluded by highlighting the challenges in simulating biological processes on a cell scale and for cell-cycle-long times, which will likely benefit from the integration of experimental and theoretical methods.

System representation, force field parameterization, and dynamical algorithms

To alleviate the problem of simulating cellular processes at full atomistic resolution, the system can be structurally simplified by grouping selected atoms together into a single interacting center or bead. The number of beads and their positions within the molecule are chosen according to considerations about the spatiotemporal scales to be explored and the physicochemical features deemed important to the cellular processes (Tozzini 2005; Rudzinski and Noid 2014; Dunn et al. 2016).

A wide variety of simplified models for biomolecules exists, as discussed in several excellent reviews (Tozzini 2005; Clementi 2008; Takada 2012; Zheng and Wen 2017). Here, we classify them into either particle-based coarse-grained and mesoscale models, or continuous models, in which the concept of granularity is lost. Coarse-grained models employ from a few beads per residue to one bead per few residues. This corresponds to a structural resolution ranging from few to roughly 10 Å (Trovato and O’Brien 2016). These models reproduce the shape of biomolecules and the slower, biologically more relevant modes of vibration (Tozzini 2010). Mesoscale models represent each biomolecule with one or a few beads and, therefore, have structural resolutions larger than ~ 10 Å (for simplicity, we include also models with a much larger resolution). Because of the aggressive simplifications, mesoscale models are typically suitable to explore genome organization or macromolecular diffusion over timescales longer than the ones of internal fluctuations. Continuous models are based on equations for the probability of observing a target quantity and they can access the longest timescales, being computationally very convenient (Manning et al. 1996; Argudo et al. 2016).

As a consequence of the structural simplifications, the free energy of the system becomes smoother and, therefore, its dynamics accelerates (Kmiecik et al. 2016). While the acceleration is an advantage that allows a faster exploration of the system conformations, the smoother energy landscape implies that some states are lost. Because of this intrinsic dynamical acceleration, any calculated time-dependent quantity (e.g., reaction rate) has to be rescaled appropriately before it can be compared with experiments.

Another consequence of the structural simplifications is the loss of chemical detail. This results in bead–bead interactions that are less physically and chemically specific. Nonetheless, the interactions among the lost degrees of freedom must be accounted for in effective energies between the beads, the sum of which constitutes the simplified force field:

$$U=U_{\mathit{\text{conf}}}+U_{\mathit{nb}}+U_{\mathit{ext}}=U_b+U_{\theta }+U_{\varphi }+U_{\mathit{nb}}+U_{\mathit{ext}}.$$ 1

In Eq. 1, the conformational term U _conf includes the forces responsible for a biomolecule bond connectivity and local chain orientation (Trovato and Tozzini 2012). This term is absent in mesoscale models where each biomolecule is represented with a spherical bead. The non-bonded term U _nb describes the longer-ranged forces responsible for biopolymer folding and complex formation, as well as nonspecific interactions. By influencing the biomolecular associations, U _nb also affects diffusion in dense macromolecular environments. Finally, U _ext accounts for any external or confining force.

A force that is not explicitly included into Eq. 1, but that naturally emerges in heterogeneous mixtures of macromolecules, is the depletion force. In its original formulation, this force was attributed to small particles (e.g., osmolytes and small biomolecules in a cell) that, in order to increase their entropy, diffuse away from and push together the bigger particles (Asakura and Oosawa 1954). The main assumption underlying this formulation is that the interaction among particles is purely repulsive. Following studies highlighted that soft inter-molecular interactions might generate depletion forces with an enthalpic origin (Louis et al. 2002; Egorov 2004; Marenduzzo et al. 2006; Sukenik et al. 2013; Sapir and Harries 2015).

The simplified force field in Eq. 1 is fully specified once each functional form and the associated parameters are defined. The task of force field parameterization is complex and constantly improving (Ayton et al. 2007; Trovato and Tozzini 2012; Ivani et al. 2016; Song et al. 2017). Whereas most simplified models employ simple non-bonded functional forms, a complex functional form can often be more accurate because a larger number of parameters is able to better capture the several physical interactions condensed in Eq. 1. Therefore, the functional form of a non-bonded potential is the second important choice in a simplified model. The Lennard-Jones potential is a simple functional form, in which the single well describes an isotropic, short-ranged attraction. More complex functional forms, such as isotropic multiwell potentials, have been used to model desolvation between amino acids during protein folding, allosteric transitions, DNA supercoiling, and protein aggregation (Okazaki et al. 2006; Chu and Voth 2007; Trovato and Tozzini 2008; Trovato et al. 2013; Ruff et al. 2014). Non-isotropic potentials have been used to describe the interactions between crystallins mediated by patches of amino acids (Staneva and Frenkel 2015; Bucciarelli et al. 2016). We remark that the success of a force field depends on the choice of complex enough functional forms and the method used for its parameterization (Trovato and Tozzini 2008, 2012, 2014; Trovato et al. 2013; Leonarski et al. 2013).

Water molecules are eliminated in simplified models to speed up the computation. This operation eliminates the solute–solvent affinity, as well as the hydrodynamic interactions. Whereas the solute–solvent affinity is introduced as an effective energy between beads in Eq. 1 (e.g., the hydrophobic effect), the collisions between solvent and the solute are accounted for by introducing viscous and random forces into Newton’s equations of motion. The resulting equation used to propagate a system’s motion in implicit-solvent coarse-grained models is the Langevin equation:

$$m_I{\mathit{a}}_I=-{\zeta }_I{\mathit{v}}_I+{\mathit{W}}_I-{\nabla }_{I}U,$$ 2

and it satisfies the conditions ⟨W _I(t)⟩ = 0 and ⟨W _I(t + t ₀)W _I(t)⟩ = 2ζ _I k _B Tδ(t ₀), where t is the time, I is the bead index, and m _I, ζ _I, W _I, T _I, and U are, respectively, the mass, friction coefficient, random force, temperature, and internal energy given in Eq. 1. In the limit of vanishing inertia m a _I ~ 0 or ζ_I = 0, the Langevin equation describes, respectively, either the Brownian or Newtonian dynamics (Długosz and Trylska 2011). Hydrodynamic interactions are not included into the Langevin equation and they can be added using several available algorithms (Mereghetti et al. 2011; Mereghetti and Wade 2012; Wang and Brady 2016; Blanco et al. 2017). Albeit popular, Eq. 2 and most treatments of hydrodynamic interactions do not account for the perturbation of the solvent caused by crowding agents (Harada et al. 2012; Mukherjee et al. 2015; Wang et al. 2017b) or by protein-specific effects (Huang et al. 2016).

Simulations of processes in cell-mimicking environments

Below, we will discuss the progress made in the simulation of different cell compartments, omitting the processes involving the cytoskeleton and the membranes. The reader is referred to excellent works in these fields (Neri et al. 2013; Smith et al. 2014; Unterberger and Holzapfel 2014; Mak et al. 2015, 2016; Gao et al. 2015; Nguyen et al. 2016; Popov et al. 2016; Reddy and Sansom 2016; Chavent et al. 2016; Foffano et al. 2016; Niesen et al. 2017; Tachikawa and Mochizuki 2017).

Computational models of diffusion in the cytoplasm

The total concentration of proteins and nucleic acids has been estimated to range from 20 to 400 mg/mL, depending on the cell type (Zimmerman and Trach 1991; Luby-Phelps 1999), which corresponds to a fraction of the cell volume between 10% and 40%. Macromolecule concentration, mass distribution, shape, polydispersity, as well as confinement, and inter-molecular and hydrodynamic interactions (HI), are the features that have been included in the various models of the cytoplasm discussed here. In the remainder of the paper, we will refer to the long-time translational diffusion coefficient simply as the diffusion coefficient.

McGuffee and Elcock (2010) were the first to simulate the Escherichia coli cytoplasm at full atomistic resolution, without solvent and without HI. They included 50 types of the most abundant E. coli biomolecules in their model and treated them as rigid bodies. Despite the approximations, their computations lasted more than a year, demonstrating the intensive demand of these simulations. In a first atomistic model, where the macromolecules interacted through purely repulsive potentials, diffusion of the green fluorescent protein (GFP) was reduced by a factor of three compared to the value of 87 μm²/s in dilute solution (Elowitz et al. 1999). Because experiments reported a ten-fold reduction (Elowitz et al. 1999; Mullineaux 2016), the authors introduced nonspecific attractive interactions among molecules to further slow down GFP mobility. For several proteins, diffusion was found to be anomalous in both repulsive and attractive regimes. The lowest anomalous exponents α were calculated in the attractive cytoplasm and ranged between 0.75 and 0.85 over timescales shorter than 1 μs. At the end of the simulation, α increased toward unity, at variance with experiments predicting an exponent of 0.75 for RNAs over the timescale of seconds (Golding and Cox 2004, 2006). This discrepancy was probably due to the force field parameterization, which used a single Lennard-Jones potential for the nonspecific attraction, and to the absence of slow macromolecules, which are known to increase the timescales of sub-diffusion (Saxton 1994). HI are not expected to affect the timescale of sub-diffusion, as we will discuss later.

Driven by high-throughput experiments, Yu et al. (2016) built a very large system made of 103 million atoms to represent the flexible biomolecules in the cytoplasm of Mycoplasma genitalium (MG), ions, water, and other small molecules. Diffusion of the GFP was normal, similarly to the other molecules, and compared well with the experimentally measured value of 7.7 μm²/s (Elowitz et al. 1999; Mullineaux 2016). We remark that HI, which are automatically accounted for in this explicit-solvent model, contribute, in part, to the GFP deceleration (Ando and Skolnick 2010). Beyond this average trend, a large spread of diffusion coefficients (ca. 12–15 μm²/s) at fixed macromolecule size indicates that transport is influenced by the different local environments within the MG cytoplasm. A similar scatter was also observed in a mesoscale E. coli cytoplasm model, composed of nonspecifically interacting biopolymers (Trovato and Tozzini 2014), suggesting that diffusion in the MG cytoplasm is sensitive to the local distribution of enthalpies. An interesting result of the MG simulations is the fast decrease of the diffusion coefficients of small molecules as a function of their size. Experimentally unexpected, this result was attributed to nonspecific interactions with bystander macromolecules. The importance of the electrostatic contribution to small molecule diffusion in crowded environments has also been emphasized recently (Acharya et al. 2015; Kekenes-Huskey et al. 2016). The impressive size of the simulated MG cytoplasm allowed a statistically accurate calculation of macromolecule transport properties. However, the insight into normal and sub-diffusive regimes was restricted to the short simulation length of ~ 100 ns.

The first stochastic dynamics simulation of macromolecular diffusion in the cytoplasm could exploit only limited computational resources. This was the main reason why Bicout and Field (1996) modeled the E. coli cytoplasm at a simplified level of one bead per biomolecule. In their model, the authors included ribosomes, proteins and tRNAs as spherical particles interacting via electrostatic and dispersive forces. The parameterization of the force field was based on the DLVO approximation, widely used in the colloidal sciences (Curtis and Lue 2006). Diffusion of all the species was slowed down at increasing crowder volume fractions and charges on the ribosomes. No separation of the large ribosomes from the small proteins was observed, suggesting that the depletion force was counteracted by the attractive part of the potentials (Louis et al. 2002).

The instrumental mesoscale approach used by Bicout et al. has undergone several improvements over the years. Ridgway et al. (2008) represented the E. coli cytoplasm with 12 types of inert spherical crowders, whose sizes and abundances reflected the ones measured in the bacterium. They used a continuous reaction–diffusion equation, solved for discrete particle jumps, to efficiently simulate particle motion and also binding. Diffusion of a particle with mass similar to the GFP was observed to decrease by a factor of two, which is consistent with other models that employed inert crowders.

An additional level of realism was introduced by Ando and Skolnick (2010), who explored the consequences of HI and favorable interactions on the diffusion of 15 types of macromolecules mimicking the E. coli cytoplasm. Because the macromolecule shape was found to play a marginal role over a wide range of crowder concentrations, the authors employed a computationally faster mesoscale model. HI were introduced using a combination of Brownian and Stokesian dynamics, accurately accounting for both short- and long-ranged hydrodynamics effects. In the first version of the cytoplasm (repulsive cytoplasm), where the crowders interacted through HI but not attractively, the GFP diffusion was reduced almost ten-fold, which is in excellent agreement with experiments (Elowitz et al. 1999). A smaller effect produced by HI, on the order of two-fold reduction of mobility, was observed in other studies of concentrated protein solutions (Mereghetti and Wade 2012; Balbo et al. 2013; Hasnain et al. 2014) and in experiments (Roosen-Runge et al. 2011). In the second version of the cytoplasm (attractive cytoplasm), the frequent crowder–crowder associations triggered a more pronounced dependence of diffusion on the crowder size and the formation of long-lived clusters around the ribosomes. The approximations used to parameterize the attractive and electrostatic interactions, based on the DLVO theory, might have been responsible for the observed aggregation tendency (Bicout and Field 1996; Boström et al. 2001; Curtis and Lue 2006; Prausnitz 2015). The two versions of the E. coli cytoplasm also differ by the repulsive barrier of the crowder–crowder potentials. Therefore, considering that the details of the interaction potentials affect diffusion (Tokuyama et al. 2011; Rovigatti et al. 2015), a quantitative understanding of whether attraction or HI dominates diffusion in vivo is not straightforward based on this work. It is clear, instead, that both HI and nonspecific interactions contribute to reduce mobility in vivo. Interestingly, the timescale of sub-diffusion calculated using the repulsive cytoplasm was on the order of 1 μs, remarkably similar to the results of full atomistic simulations without HI (McGuffee and Elcock 2010). Therefore, excluded volume interactions are mainly responsible for the anomality, while HI do not affect the timescale of sub-diffusion, as also emphasized recently (Blanco et al. 2017).

The same group analyzed the effects of confinement and HI on macromolecular diffusion using a spherical system, in which both the membrane-mimicking shell and the interior volume were composed of monodisperse particles (Chow and Skolnick 2015). Mobility of the freely diffusing particles was slower near the membrane than in the bulk volume, partly because of an effective attraction with the membrane, caused by the depletion force, and partly because of correlated motions caused by HI. This resulted in longer residence times near the membrane, which could have a regulatory role on signaling proteins.

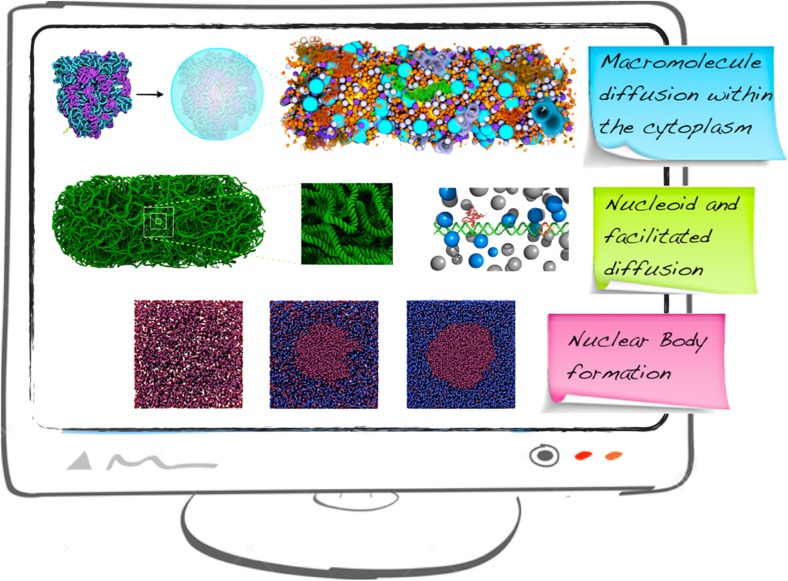
To overcome some limitations of previous cytoplasm models, namely the absence of the genetic material and the moderate cell-specificity of the inter-molecular interactions (Bicout and Field 1996; Boström et al. 2001; Curtis and Lue 2006; Ando et al. 2016), Trovato and Tozzini (2014) devised an original strategy to parameterize the nonspecific associations characteristic of E. coli. For the first time, the authors represented also the nucleoid, in addition to 12 species of macromolecules, therefore spanning three orders of magnitude in macromolecule size (Fig. 1a). In the first step of the force field parameterization, the interactions between any two spherical biomolecules were fitted on the energies calculated employing a coarse-grained model with E. coli characteristic amino acid distributions (see Trovato et al. 2013 and Trovato and Tozzini 2014 for details). These interactions were refined in the subsequent phase, until the calculated diffusion coefficients of all macromolecules approached a cell-scale reference curve (Fig. 2c) (Kalwarczyk et al. 2012; Sozański et al. 2013; Feng et al. 2016). The final nonspecific interactions, which accounted for the many body effects ignored in the first phase, were moderate enough to reduce aggregation and correlated strongly with binding energies between E. coli macromolecules. We remark that only nonspecific effects are included into this force field, as macromolecules with the same size have the same average amino acid distribution, therefore implying the absence of specific interactions.

Fig. 1.

Simulated macromolecular models and cellular processes. a Structural simplification of a coarse-grained ribosome (shades of blue and purple represent nucleotide and amino acid beads, respectively) into a spherical particle of corresponding size, for the purpose of defining a mesoscale cytoplasm model of Escherichia coli. The nascent chain is yellow. The nucleoid is represented as three spherical particles (orange) in the middle of the cytoplasm (Trovato and Tozzini 2014). b Coarse-grained conformation of the nucleoid, consistent with experimental data (Hacker et al. 2017). Note that the nucleoid here has finer resolution (one bead per nucleotide) than the nucleoid model in a or d. c Model of facilitated diffusion, where the DNA is shown in green and orange (binding site), the DNA binding protein (DBP) in red and the crowders in blue and gray. d Model of nucleoid compaction: states of the nucleoid (red particles, top and bottom) in the presence of ribosomes and polyribosomes (green particles, top) and 30S and 50S ribosomal subunits (blue and yellow particles, bottom) (Bakshi et al. 2015). e Nuclear body particle (red) assembly under the influences of a weak inter-molecular attraction and crowding agents (blue) at increasing volume fraction ϕ (Cho and Kim 2012b)

Fig. 2.

Depiction of the three challenges to advance the modeling and simulation of cellular processes. a In challenge 1, a template space is filled with molecular components of the HIV-1 virus (CellPack image). b In challenge 2, structural simplifications are devised (for a ribosome in this example) to make the relevant timescales accessible to simulations. Subsequently, the functional form of the interactions between any two simplified particles is chosen (single-well potential in this case, black and cyan lines) and the parameters (indicated) on which it depends are calculated. For models including bimolecular reactions, the criteria for each reaction need to be evaluated as well. c In challenge 3, the interactions calculated in challenge 2 are refined by using here, for the specific case of diffusion within the cytoplasm, a reference curve describing diffusive data measured in vivo, over 3 to 4 orders of magnitude in the biomolecule (hydrodynamic) radius. This refinement phase validates the model against experimental cell-scale quantities and produces a more realistic force field compared to the one obtained from challenge 2

A number of insights were gained from Langevin simulations of this interacting cytoplasm model. Polydispersity was responsible for retarding the motion of the largest macromolecules, through the depletion force (Egorov 2004; Marenduzzo et al. 2006). We emphasize that the magnitude of the deceleration caused by polydispersity is likely a fingerprint of the E. coli cytoplasm because depletion forces depend on particle concentrations and sizes, which are cell-specific. The favorable inter-crowder interactions improved the calculated diffusion coefficients relative to the approximation of inert crowders. Moreover, the transient associations between crowders allowed to predict a spread of the diffusion coefficients comparable to experimental values (Golding and Cox 2004, 2006; Lampo et al. 2017). This spread, like the average diffusion coefficients, was underestimated in the approximation of inert crowders, consistent with previous findings (Saxton 1997).

The interactions tuned on E. coli macromolecular affinities and diffusion are responsible for a biphasic behavior of this model cytoplasm (Trovato and Tozzini 2014), viscous between 30 and 100 Å and glassy-like up to the largest size of 800 Å (the nucleoid). This view, consistent with experiments (Weber et al. 2010; Parry et al. 2014), is confirmed by the calculated anomalous exponents α. While small biomolecules diffuse almost normally, crowders with sizes between 100 and 800 Å show anomalous diffusion with α ranging between 0.75 and 0.85 over 350 μs of simulation. Compared to full atomistic simulations without HI (McGuffee and Elcock 2010) and mesoscale simulations with HI (Ando and Skolnick 2010; Blanco et al. 2017), the much longer timescale over which sub-diffusion occurs is a consequence of the stronger attractive interactions (Saxton 1996), suggesting that sub-diffusion in E. coli is caused by nonspecific interactions. The nucleoid also diffuses anomalously, in agreement with the general idea that immobile obstacles are one of the causes of sub-diffusion (Saxton 1994). However, the nucleoid anomalous exponent is larger than the experimental value of 0.45 (Weber et al. 2010; Javer et al. 2013), since neither the DNA flexibility nor DNA binding proteins were accounted for in its representation (Weber et al. 2010; Javer et al. 2014). Worth noting, the simulated sub-ms timescales, on which anomalous diffusion persists, are consistent with the longer experimental timescales because the dynamics of simplified models is accelerated.

Based on the surveyed models, at biologically relevant volume fractions, the timescale on which sub-diffusion persists and the slope of the diffusion coefficient versus the molecular weight are the signatures of the inter-molecular interactions. A relatively short timescale (< 1–10 μs) and a soft slope indicate mostly inert and mobile cytoplasmic crowders; a longer timescale (> 10 μs) and a steep slope can indicate mobile and chemically interacting crowders, as well as inert and immobile obstacles, or a combination of them.

Whereas the effects of macromolecular crowding on protein internal dynamics, and translational and rotational diffusion have been studied employing a multiscale model by Trovato et al. (2013), investigations on the influence of protein flexibility on diffusion are lacking, albeit they could be potentially relevant (Illien et al. 2017). In part, this is a consequence of the limitations of most discussed models and, in part, it is due to the less frequent use of multiscale models. Another limitation is that particle-based simulations have not been designed to probe non-uniform configurations arising, for example, from the cellular co-localization of macromolecules. Toward this aim, Smith et al. (2017) combined theory and Brownian simulations to demonstrate that, in a non-uniform distribution of inert crowders, a particle may experience a transient super-diffusion upon transitioning from a dense to a less dense region of the cytoplasm. Their simulations showed that the biologically relevant scenario of non-uniform macromolecular distribution might induce super-diffusion, therefore directing macromolecule motion even in the absence of active transport.

The localization of macromolecules was observed to influence macromolecule diffusion also by Putzel et al. (2014). The authors found that the diffusion coefficient of a mobile particle is a non-monotonous function of the binding energy ε between the mobile particle and the immobile obstacles. Specifically, diffusion was fastest at ε values of ~ 2k _B T. Such an effect might be relevant for macromolecules that diffuse nearby membranes or the cytoskeleton, and that experience only a moderate attraction. Interestingly, this finding is reminiscent of the process with which a DNA binding protein searches for its site on the chromosome (see the next section titled Computational models of the genetic material).

Stefferson et al. (2017) addressed the diffusive behavior of a mobile molecule that is able to bind immobile obstacles, and either move on their surfaces (slippery regime) or remain fixed (sticky regime). The authors observed that, as the volume fraction ϕ of the sticky obstacles increased, diffusion became more anomalous and lasted longer. On the other hand, the presence of slippery obstacles shortened considerably the timescale of sub-diffusion because the mobile molecule could rearrange around the obstacles. Interestingly, the dependence of the diffusion coefficient on ϕ is qualitatively different in the two cases. Diffusion is monotonously decreasing with ϕ for sticky obstacles and non-monotonous for slippery obstacles. In the latter case, the diffusion coefficient tends to the value in dilute solution at large ϕ values. This apparently surprising behavior is a consequence of the slippery regime, which, at high ϕ values, allows the mobile molecule to first slide on one of the many obstacles and then to hop on the neighboring one. These effects might be relevant to biological systems such as membrane-less organelles and lipid rafts that expose large surfaces to the incoming macromolecules.

Computational models of the genetic material

Regulation of the genetic material is among the most complex processes occurring in a cell. Nonspecific interactions, especially of electrostatic nature, largely contribute to the behavior of this charged biopolymer and its regulatory proteins. Here, we will discuss the results of computer simulations regarding the genetic material in cell-mimicking spaces. Chromosome modeling and folding in isolation are discussed elsewhere (Rosa and Zimmer 2014; Ozer et al. 2015; Korolev et al. 2016).

In bacteria, the chromosome, also called the nucleoid (Fig. 1b), is free in the cytoplasm and, therefore, it is influenced by the high concentration of surrounding macromolecules. Mondal et al. (2011) simulated the E. coli nucleoid, represented as a coarse-grained hyper-branched polymer, embedded within inert spherical ribosomes sizing 100 Å. In these conditions, the authors observed that the DNA assumes a compact conformation at the center of the cell, while ribosomes and polyribosomes segregate to the cell periphery, to maximize the translational entropy (Fig. 1d). Although in line with some experimental observations (Pelletier et al. 2012), this finding disagrees with evidence supporting the co-transcriptional translation, the mechanism by which ribosomes penetrate into the nucleoid and translate the mRNA transcripts while bound to the nucleoid.

The testing for a possibly more expanded state of the genetic material, compatible with the co-transcriptional translation, was explored by Bakshi et al. (2015), who refined the model in Mondal et al. (2011) by allowing for the reversible disassembly of 70S ribosomes into the 30S and 50S subunits. Indeed, the authors observed that the ribosomal subunits were able to penetrate into the nucleoid and expand it (Fig. 1d). These works demonstrate that the nucleoid switches between a compact state, favored when 70S ribosomes crowd the cell, and an expanded state, favored when the ribosomes are disassembled into the 30S and 50S subunits. These simulations do not account for the transertion mechanism, i.e., the partial tethering of the nucleoid to the membrane, which contributes to nucleoid expansion (Roggiani and Goulian 2015).

Macromolecular crowders are unlikely to be the only determinants of chromosome compaction, as Shendruk et al. (2015) concluded from observing a continuous rather than first-order transition as in experiments (Pelletier et al. 2012). One such factor, i.e., DNA binding proteins (DBPs), has been studied by Brackley et al. (2013b). In their work, the chromosomal DNA was represented at a mesoscale resolution of 7 bps, whereas DBPs were approximated as spherical particles able to bind nonspecifically the DNA. Despite the absence of DBP–DBP attraction, the DNA underwent a strong compaction owing to local distortions caused by DBP binding.

Chromosome fluctuations are crucial to the accessibility of macromolecular complexes also in eukaryotic cells. Hihara et al. (2012) simulated the diffusion of complexes sizing from 13 to 20 nm within a dense state of chromatin, represented as a collection of spherical particles mimicking the nucleosomes. Only when the nucleosomes were allowed to move ca. 10 nm from their initial position could the complexes diffuse freely; otherwise, they remained trapped locally. As for the nucleoid, the magnitude of genome fluctuations relative to the macromolecule sizes determines whether the macromolecules are able to move inside the meshwork of the genetic material.

Using a mesoscale model, Maeshima et al. (2015) studied how the accessibility into chromatin and mobility of transcription factors contribute to transcriptional regulation. The authors observed that small transcription factors penetrate into chromatin domains and bind the DNA. Recruitment of large protein complexes, needed for transcription, occurs subsequently, when the target gene moves toward the chromatin surface. Because of their size, such large complexes prevent the genes from moving back to the inner regions of chromatin, therefore keeping the genetic material in a transcriptionally competent state.

Other computational investigations have been devoted to understand the process of facilitated diffusion, through which many proteins search for their target genes using a combination of 1D diffusion (sliding) along the DNA and 3D diffusion (Halford 2009; Hammar et al. 2012). This mechanism is known as facilitated diffusion because the time to find the target is smaller compared to a search based exclusively on 3D diffusion (Klenin et al. 2006).

The tradeoff between 1D and 3D diffusional searches has been studied by Krepel and Levy (2016) using a coarse-grained DBP model, a rigid, 100-bp coarse-grained DNA, and spherical crowders with tunable interactions (Fig. 1c). The tunable interactions served to mimic the variation of ionic strength, charge (q), and nonspecific binding (ε). In the absence of crowders, the authors found a clear anti-correlation between the number of 1D sliding and 3D diffusion events over a range of ionic strengths. At large ionic strength, 3D diffusion dominated, suggesting an electrostatic mechanism of this DBP–DNA binding. A similar anti-correlation was observed when crowders were introduced and their positive charges increased. In this case, however, 1D diffusion contributed much more than 3D diffusion and, for this reason, τ _D decreased compared to dilute solution conditions. For crowders interacting nonspecifically, the mechanisms of 1D and 3D diffusion anti-correlated and were roughly independent from ε. In this case, τ _D increased proportionally to ε, becoming larger than the search time in dilute conditions. The results of this work suggest that, when the binding mechanism between DNA and DBP has a strong electrostatic component, inert or electrostatically interacting crowders accelerate the search. When the crowders bind DNA through non-electrostatic forces, the search slows down already at small ε values because the crowders act as roadblocks: they hinder 1D diffusion and simultaneously promote 3D diffusion.

A different scenario was observed by Marcovitz and Levy (2013) in simulations of DPBs interacting nonspecifically with both the DNA and the obstacles bound to it. The authors found that the confinement of DBPs between obstacles decreases at higher obstacle concentrations because of a concomitant increase in hopping events. Albeit counterintuitive, the results of this work imply that the genomic search can exploit the different mechanisms of 1D sliding, hopping, and 3D diffusion, depending on the conditions and conformations of the genetic material. It also suggests that the distribution of obstacles on the DNA might be a strategy to finely tune the time of the genomic search.

Brackley et al. (2013a) explored how the crowder volume fraction ϕ and the affinity ε of a DBP (patchy colloid) for the DNA influence the average τ _D. The authors found that τ _D depends linearly on ϕ as τ _D(ϕ) = c(ε)ϕ, where c(ε) is the slope. Interestingly, in the absence of other proteins bound to the DNA, τ _D is a non-monotonous function of ε, which can be explained in terms of two effects: DBP binding to and 1D sliding along the DNA. At intermediate values of the binding energy (ε* ~ 2k _B T), the search time reaches the minimum value ${\tau }_D^{\ast }$ and the two effects balance each other, resulting in a flat profile of τ _D(ϕ). For ε values around ε*, the lines with variable slopes c(ε) intersect, locating a range of binding energies between 2k _B T and 4k _B T and a range of volume fractions between 0.2 and 0.25, at which ${\tau }_D\backsim {\tau }_D^{\ast }$. The authors speculated that these ranges might reflect why different transcription factors can search for their DNA sites quickly and efficiently in a cell. A qualitatively similar conclusion was reached by Ma et al. (2016). However, in this case, τ _D displays a steeper increase with ϕ, due to a constant time of 3D search as a function of ϕ. Regardless of the relative weights of 1D and 3D diffusion in the different models of facilitated diffusion, the structural correlations arising from the crowder concentration are responsible for the non-monotonous behavior of τ _D versus ε and they are sensitive to the polydispersity of the solution (Das and Kolomeisky 2010).

The role of cell confinement on the search of the DNA site was explored by Mondal and Bhattacherjee (2015) using a coarse-grained model of a 200-bp DNA, a coarse-grained DBP, and a sphero-cylindrical potential mimicking a prokaryotic cell. The authors found that both DNA flexibility and confinement increase the probability of binding between the DBP and the DNA. This enhancement implies a faster search for the binding site through an increase in the number of hoppings between DNA segments. A eukaryotic-type confinement facilitates diffusion even more markedly compared to a prokaryotic cell, owing to more frequent hopping events (Foffano et al. 2012).

Cellular confinement and chromosome flexibility affect also nucleoid replication and segregation, as Fan et al. (2007) demonstrated by simulating a mesoscale model of the E. coli chromosome over an entire cell cycle. The employed chromosome model is a linear polymer of beads sizing 210 kbp, constrained by an external force to occupy a cylindrical volume and driven to segregate by a free energy gradient. The authors found that the external force that mimics the cellular confinement is fundamental to maintain the chromosome in a compact state, which, in turn, guarantees a correct segregation of the daughter chromosomes. These simulations indicate that a balance between flexibility and confinement is necessary to allow chromosomal segregation and correct loci positioning. Macromolecular crowders, absent in this model, have also been found to contribute to segregation of the genetic material (Shin et al. 2014).

The consequences of DNA curvature and helical twist on DBP search were explored using coarse-grained plasmids of various sizes and torsional stresses by Bhattacherjee et al. (Guardiani et al. 2014; Bhattacherjee and Levy 2014; Bhattacherjee et al. 2016). The authors found that the DBP search occurs via the combination of 1D hopping and 1D sliding events, rather than with a helical motion, as observed when the DNA molecule is straight. Specifically, the geometry of under-twisted plasmids favors the sliding mode, while over-twisting favors the hopping mode. Although not performed under cell-like conditions, these simulations suggest the importance of accounting for the structural details of the DNA into future mesoscale models. Hydrodynamic interactions are another factor that can influence DBP helical motion on a straight DNA, adding to their relevance for in vivo processes (Ando and Skolnick 2010; Długosz 2015).

Benedetti et al. (2014) investigated the structural consequences of plasmid self-crowding, using molecules with different degrees of supercoiling, which might help to understand how loops and supercoiled arms in a chromosome are influenced by the surrounding genetic material. Plasmids transitioned to more elongated and supercoiled shapes as their concentration was increased. Negatively supercoiled plasmids showed a larger increase of the probability of interaction between enhancer and promoter sites compared to relaxed plasmids, because of the additional supercoiling induced by self-crowding.

The effect of macromolecular crowding on eukaryotic gene expression was addressed by Matsuda et al. (2014) using a multiscale model. The microscopic processes of polymerase recruitment to the promoter site, mediated by the interactions with transcription factors, as well as facilitated diffusion, were explicitly simulated as a function of crowder volume fraction ϕ. The resulting gene expression, i.e., the macroscopic production of mRNA at different crowding conditions, was calculated by solving a reaction-rate equation, whose rates were obtained from simulations. The authors observed that the mRNA levels follow a non-monotonous curve as a function of ϕ because diffusion and transcription are affected by macromolecular crowding in opposite directions. Up to moderate ϕ values, the mRNA concentration increases as a function of ϕ because the binding and transcription rates grow to a much larger extent compared to the decrease in the rate of diffusional encounter (see also the Appendix). A further increase in ϕ hinders diffusion heavily, with the consequence that the rate of diffusional encounter becomes comparable to or smaller than the transcription rate. In this non-equilibrium regime, mRNA production decreases. Together with the sensitivity of the mRNA production to the transcription rate, reactant concentrations, and protein affinity for the DNA, these results imply that gene expression can follow multiple biophysical pathways. In extreme cases, such as cancer, it is plausible that deviations of one or more of these factors from their physiological values could lead to an abnormal gene expression.

Nuclear organization: assembly and disassembly of nuclear bodies

Nuclear bodies (NBs) are membrane-less organelles found in the nucleus, composed mostly of unstructured proteins and RNAs. They play important roles in regulating transcription and RNA processing. NB formation is driven by nonspecific inter-molecular interactions, which are modulated by post-translational modifications and ions, as well as by macromolecular crowding (Richter et al. 2008; Zhu and Brangwynne 2015; Banani et al. 2017; Staněk and Fox 2017).

Recently, Cho and Kim (2012a, b) proposed a phenomenological model suitable to study the general features of NB formation. The authors represented the protein and RNA molecules as spherical objects, possessing a weak nonspecific attraction ε to drive their association into NBs. In the absence of crowders, this model predicted that NBs form already at weak ε values (k _B T/ε ≤ 1.085) and that particles exchange at the boundary between the NB and the nucleoplasm, in agreement with a liquid–liquid phase transition mechanism (Zhu and Brangwynne 2015).

By adding inert crowders, Cho and Kim (2012b) observed that NBs could grow even using ε values that were unable to nucleate the NB in isolation, provided the crowder concentration was sufficiently high (Fig. 1e). Additionally, NB diffusion was found to be retarded, with a characteristic asymmetry: particles moved more slowly toward the outside than toward the inside of the NB (Cho and Kim 2012b). This asymmetry is probably due to surface effects and implies that NB particles are retained for a longer time close to the surface of the NB when crowders are present. Despite a reduced diffusional encounter rate, the binding rates within the NB were found to be larger by ~ 20%. Because NBs are often found associated with chromatin, this increase might be relevant to the regulatory role that NBs have on transcription.

With the aim of understanding some aspects of NB formation in proximity of the chromosome, Oh et al. (2015) simulated NB particles interacting with a long, condensed polymer chain. Macromolecular crowders were not included, but their effect was implicitly accounted for by varying the NB particle number. The authors observed an interesting phenomenology. NB formation occurs independently from the long, condensed polymer, when the density of NB particles is high enough. In the regime of intermediate NB–polymer attraction and low NB particle number, the polymer triggers NB formation. This result suggests a possible mechanism for the formation of activity-dependent NBs, such as the nucleoli. The sequential growth of NBs, followed by association with the polymer chain, is observed at a higher NB density and weak NB–polymer attraction. The last scenario is consistent with the formation of activity-independent NBs, such as Cajal bodies.

The formation of NBs might have deep consequences on macromolecule transport within and outside the nucleus. Not only do NBs hinder the mobility of the surrounding macromolecules by virtue of their size, they might also perturb the concentration of macromolecules, during their own assembly or disassembly, to such an extent as to modify locally the macromolecular crowding effect. These and future simulations have and will continue to elucidate the poorly understood relation between NBs, chromatin, and the surrounding nuclear compartment.

Toward realistic molecular simulations of cellular events

Cell viability relies on a delicate balance between dynamical processes and macromolecule localization, between specific and nonspecific inter-molecular interactions (Lécuyer et al. 2007; Rodnina and Wintermeyer 2016). In spite of this general picture, most computer simulations have investigated the stability of and binding between compact proteins in cell-mimicking environments composed of passively diffusing and inert macromolecules (Cheung et al. 2005; Minh et al. 2006; Ridgway et al. 2008; Wieczorek and Zielenkiewicz 2008; Wojciechowski and Cieplak 2008; Mittal and Best 2010; Wojciechowski et al. 2010; Wang and Cheung 2012; Denesyuk and Thirumalai 2013; Qi et al. 2014; Naddaf and Sayyed-Ahmad 2014; Starzyk et al. 2016; Yu et al. 2016).

Only fewer computational studies have addressed the effects that the cellular environment has on the stability of intrinsically disordered proteins (IDPs) (Minton 2005; Qin and Zhou 2013; Goldenberg and Argyle 2014; Miller et al. 2016; Rusinga and Weis 2017). The development of models of IDPs within the cytoplasm will be highly desirable to understand how the structural heterogeneity of and interaction between cellular components influence IDP stability, aggregation propensity, and, consequently, the progression of neurological disorders and cancer (Theillet et al. 2014; Terakawa et al. 2014; Bai et al. 2017). Such models are expected to contribute also to understanding the specific behaviors of the different NBs, provided that the necessary physicochemical details are included in their parameterization.

Simulating macromolecule stability and interactions in a eukaryotic-like cell requires a large effort for the presence of localized and pervasive structures (Neri et al. 2013; Smith et al. 2014; Unterberger and Holzapfel 2014; Mak et al. 2015, 2016; Gao et al. 2015; Nguyen et al. 2016; Popov et al. 2016; Reddy and Sansom 2016; Chavent et al. 2016; Foffano et al. 2016; Niesen et al. 2017; Tachikawa and Mochizuki 2017). Future investigations will be devoted to simulating dynamical processes involving the cytoskeleton and the membranes, such as the trafficking of macromolecules and vesicles to their sub-cellular localization (Miller et al. 2016). Chromosome organization and fluctuations in vivo will benefit from the combination of simplified structural models (Hacker et al. 2017), with appropriate coarse-grained force fields for the DNA (Trovato and Tozzini 2008) and mesoscale force fields for the cytoplasm (Trovato and Tozzini 2014).

A cellular model should also include non-equilibrium processes, for their importance in regulating protein stability (Samiotakis et al. 2009; Gershenson and Gierasch 2011; Wang et al. 2015; Bui and Hoang 2016; Gorensek-Benitez et al. 2017). Toward this goal, recent simulations of co-translational folding showed that translation rates may affect the structure and stability of misfolding-prone proteins (Trovato and O’Brien 2017), as well as of multidomain proteins (Tanaka et al. 2015). Elucidating the frequency, on a proteomic scale, and the mechanisms of protein misfolding–aggregation during synthesis is an emerging topic (Buhr et al. 2016; Jacobson and Clark 2016). A promising strategy would be to combine past models (Jefferys et al. 2010; Tanaka et al. 2015; Trovato and O’Brien 2017) with a cell-mimicking environment (Trovato and Tozzini 2014) and non-uniform translation rates (Siwiak and Zielenkiewicz 2013) to highlight the consequences of synonymous codon substitutions on protein homeostasis.

Conclusions and future challenges

The studies that we have reviewed in this article have broadened our knowledge about various cellular processes and have demonstrated the effort that computational biophysics is undertaking to shift toward simulations performed in cell-mimicking conditions. They have also advanced computational methods to parameterize automatically realistic models, such as the evolutionary algorithms (Trovato and Tozzini 2012; Leonarski et al. 2013; Seffens 2017) or to access equilibrium and dynamical properties of both the solute and the solvent (Ayton et al. 2007; McGuffee and Elcock 2010; Długosz et al. 2011; Mereghetti and Wade 2012; Dama et al. 2013; Elcock 2013; Qin and Zhou 2013, 2016; Trovato et al. 2013; Ciccotti and Ferrario 2013; Trovato and Tozzini 2014; Ozer et al. 2015; Wang and Brady 2016).

From a theoretical and computational perspective, the aspects that need to be addressed are several. The first one is the static modeling of a cell’s interior (Fig. 2a). Far from being trivial, this point requires algorithms to fill a 3D space with cellular components, which should satisfy a number of experimental constraints to capture each compartment spatial ordering (Lučić et al. 2013; Mahamid et al. 2016; Danev and Baumeister 2017). CellPack, Chrom3D, and LipidWrapper are examples of software that address this first challenge and that might be employed to model the eukaryotic cell architecture (Durrant and Amaro 2014; Johnson et al. 2015; Earnest et al. 2017; Paulsen et al. 2017).

The second challenge is to derive a set of “rules” to accurately describe the interactions and reactive collisions between any two cellular components, once an appropriate simplification of their structural details has been devised (Fig. 2b). In the language of molecular simulations, these rules are the functional forms and parameters of a force field and are applied by the algorithm that propagates the dynamics of the cell over time. The criteria for bimolecular reactions also belong to this challenge and they are decided a priori in simplified models (Andrews 2017). When particle-based simulations are impractical, mathematical modeling and stochastic simulation algorithms might be employed (Gillespie 1977; Erban and Chapman 2009; Fange et al. 2012). As highlighted in this review, the input quantities of the latter methods can be experimentally measured or calculated from detailed particle-based simulations. The second challenge will likely trigger the development of accurate force fields (Leonarski et al. 2013; Ivani et al. 2016; Song et al. 2017; Wang et al. 2017a) that are transferable to different cell conditions (Rebelo et al. 2013; Parry et al. 2014; Joyner et al. 2016; Munder et al. 2016; Sun and Fang 2016), as well as diffusion–reaction schemes (Schöneberg et al. 2014; Michalski and Loew 2016; Epstein and Xu 2016) and agent-based simulations (Azimi et al. 2011).

Ultimately, the goal is to simulate an entire cell (Tomita 2001; Feig and Sugita 2013). As an example of the complexity of this task, we have reported the success of different models in reproducing diffusion in E. coli, despite them using different assumptions and ingredients. Not only a careful assessment of the modeled factors is necessary, but it is also important to expand the scope of the current studies to the simultaneous description of macromolecular trafficking, localization, and reactions. The third challenge, here defined, shall try to overcome the limitations of the previous steps. Specifically, the force field and reaction scheme of a cell model, parameterized through the two-body approximation in challenge 2, shall be refined by using a large number of data measured under minimally perturbing conditions for the cell (Xia et al. 2013; Di Rienzo et al. 2014; Gnutt et al. 2015; Luchinat and Banci 2017; Liu et al. 2017) (Fig. 2c). Images of the cell ultrastructure, obtained through cryo-EM, the technique awarded the Noble Prize in Chemistry this year, diffusion maps (Dross et al. 2009; Capoulade et al. 2011), micro-rheological data (Rigato et al. 2017), FRET (Dimura et al. 2016), and in-cell NMR (Smith et al. 2016; Luchinat and Banci 2017) are a few examples of such data. Because each technique is more or less sensitive to specific or nonspecific interactions, the simultaneous use of different quantities is recommended for having an accurate and predictive model of the cell.

Appendix: Diffusion and reactivity in the cell

A common order parameter used to describe the extent of macromolecular crowding is the volume fraction ϕ = V _cr/V, where V _cr and V are the volumes occupied by the crowders and the total volume of the cell or of the simulation box. While ϕ accounts only for the hard-core repulsion between crowders, other quantities might be important as well, as discussed in the paper.

Bimolecular reactions occurring in a cell can be described by summing up two times, one spent by the two molecules to diffuse nearby and the time to react once the molecules are in contact. This relationship can be expressed in terms of rates via the equation 1/k = 1/k _R + 1/k _D, where k, k _R, and k _D are, respectively, the observed rate of the reaction in the cell, the rate of the reaction when the biomolecules are in contact, and the rate of diffusional encounter. As discussed in the introduction, k depends on the crowding conditions because the diffusion of and reaction between macromolecules depend on the crowding conditions as well.

Diffusion regimes that are measured in a cell range from normal to anomalous. During normal diffusion, the mean square displacement of the system satisfies MSD(t) = 2nDt, where t indicates the time, n is the space dimensionality (n = 3 for diffusion in a volumetric space, n = 2 for diffusion on a surface, like a membrane), and D is the long-time translational diffusion coefficient, hereafter referred to as the diffusion coefficient. Normal diffusion is also observed in isolation, in which case the diffusion coefficient is D ₀. A system that diffuses anomalously satisfies MSD(t) = 2nD _α t ^α, where α is the anomalous exponent. Values of α larger than 1 indicate super-diffusion, whereas values less than 1 indicate sub-diffusion (Dix and Verkman 2008). The diffusion coefficient D _α is usually recast in terms of an apparent diffusion coefficient, which satisfies D(t) = D _α t ^α − 1. It is important to emphasize that D(t) is time-dependent when diffusion is not normal, i.e., when α ≠ 1. A thorough discussion of the conditions that yield anomalous diffusion as well as mathematical models of diffusion in crowded media can be found elsewhere (Bouchaud and Georges 1990; Höfling and Franosch 2013; Cherstvy and Metzler 2015).

Compliance with ethical standards

Conflict of interest

Fabio Trovato declares that he has no conflict of interest. Giordano Fumagalli declares that he has no conflict of interest.

Ethical approval

This article does not contain any studies with human participants or animals performed by any of the authors.