Abstract
Estimates of the effectiveness of influenza vaccines are commonly obtained from a test-negative design (TND) study, where cases and controls are patients seeking care for an acute respiratory illness who test positive and negative, respectively, for influenza infection. Vaccine effectiveness (VE) estimates from TND studies are usually interpreted as vaccine effectiveness against medically-attended influenza (MAI). However, it is also important to estimate VE against any influenza illness (symptomatic influenza (SI)) as individuals with SI are still a public health burden even if they do not seek medical care. We present a numerical method to evaluate the bias of TND-based estimates of influenza VE with respect to MAI and SI. We consider two sources of bias: (a) confounding bias due to a (possibly unobserved) covariate that is associated with both vaccination and the probability of the outcome of interest and (b) bias resulting from the effect of vaccination on the probability of seeking care. Our results indicate that (a) VE estimates may suffer from substantial confounding bias when a confounder has a different effect on the probabilities of influenza and non-influenza ARI, and (b) when vaccination reduces the probability of seeking care against influenza ARI, then estimates of VE against MAI may be unbiased while estimates of VE against SI may be have a substantial positive bias.
Keywords: Influenza, vaccine effectiveness, test-negative design, bias
Introduction
The test negative design (TND) has become the most commonly used study design for estimating the effectiveness of vaccines against influenza and other infectious diseases [1–9]. The influenza TND is a prospective study design where patients with symptoms of acute respiratory illness (ARI) seeking medical care are tested for influenza infection. Those who test positive are classified as cases of medically-attended influenza (MAI), while ARI patients testing negative serve as controls. The influenza vaccine effectiveness (VE) is then estimated as one minus the odds ratio (OR) in the 2×2 table cross-classifying vaccination and case/control status. Several publications discuss the bias of VE estimates from TND studies [2, 10–15]; however, they do not provide numerical evaluations of the magnitude and direction of the bias under realistic conditions.
We present a simple numerical method to evaluate the bias of a TND-based estimate of influenza VE. This method is based on a probability model [16] where the probabilities of being vaccinated, contracting influenza or non-influenza ARI, and seeking care for ARI depend on a (possibly unobserved) covariate. In our earlier paper [16] we found that in some cases, the bias of the VE estimates depends on the outcome against which the vaccine is supposed to protect. VE estimates from TND studies are usually interpreted as estimates of the effectiveness of the influenza vaccine against medically-attended influenza (MAI), defined as influenza illness resulting in medical consultation. We believe that from a broader public health perspective it may be also important to estimate VE against symptomatic influenza (SI) i.e., against any influenza illness. Evaluating VE against SI is important as influenza patients who do not seek medical care are still capable of infecting others, missing work or school, and developing severe complications. In addition, lay persons may misinterpret the estimated VE against MAI as VE against SI. We will see that under certain circumstances, TND studies may provide unbiased estimates of VE against MAI while substantially overestimating VE against SI.
In this work, we focus on two sources of bias: (a) confounding bias, resulting from the presence of a (possibly unobserved) covariate that is related to both the probability of being vaccinated and the probability of experiencing the outcome of interest, and (b) bias resulting from the fact that the vaccination may modify the probability of seeking medical care against influenza ARI, because vaccinated influenza patients may have less severe symptoms compared to unvaccinated patients. We will examine the magnitude and direction of each of these sources of bias.
Methods
We assume that every member of the study population is assigned a dichotomous unobserved covariate representing her/his health awareness. In other words, each person is classified as having either a ‘higher’ or a ‘lower’ health awareness. Individuals who are more concerned about their health are more likely to be vaccinated and to seek medical care when they develop ARI symptoms. The probabilities of being vaccinated, contracting influenza and non-influenza ARI, and seeking medical care may depend on this covariate. Hence, our method allows us to examine the effects of non-random vaccination where the probability of being vaccinated depends on an unobserved covariate. Since a person’s health awareness cannot be easily determined, we assume that it may be difficult to adjust the VE estimate for this potential confounder.
As we want to focus on the two types of bias mentioned in the Introduction we make a few simplifying assumptions to eliminate other potential sources of bias:
Vaccination does not affect the probability of contracting non-influenza ARI. This is a basic assumption for the validity of the TND [15].
Every ARI patient seeking medical care is tested for influenza infection.
The test has perfect sensitivity and specificity, and vaccination status is determined without an error
Our model [16] allows a person to have an influenza and a non-influenza ARI at the same time, however, we only consider their influenza ARI in this case. The model does not incorporate time, thus a person who has repeated infections may be included more than once. Figure 1 shows a diagram of our probability model.
Figure 1. Directed acyclic graph of influenza vaccine studies with a covariate.
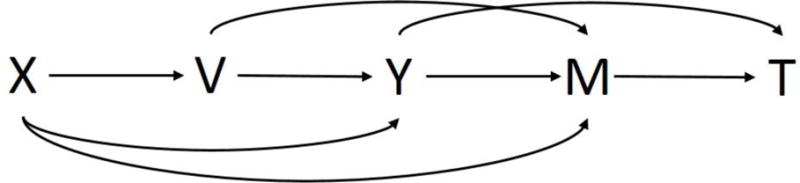
X=health awareness (unobserved), V=vaccination status, Y=ARI status, M=seeking medical care for ARI, T=influenza test result.
First, we present the baseline scenario and use it to illustrate the proposed method for calculating bias of VE estimates. In this baseline scenario, the two types of bias mentioned above are absent.
Without loss of generality we assume that 50% of the population have a higher health awareness
The probabilities of being vaccinated are 80% and 40% for persons with higher and lower health awareness, respectively. Hence, the overall vaccination coverage is 60%.
Based on results from 14 randomized clinical trials [11], the average probability of contracting a non-influenza ARI is 0.084 regardless of vaccination status and health awareness. The average probability of influenza ARI among unvaccinated persons is 0.027.
We assume that the effectiveness of the vaccine is 50%, hence the probability of influenza ARI among vaccinees is 0.0135.
Studies found that probabilities of seeking medical care for ARI vary between 0.2 and 0.6. Therefore, we set these probabilities to 0.2 and 0.4 in non-influenza ARI patients with lower and higher health awareness, respectively. We assume that influenza ARI patients are more likely to seek care than non-influenza ARI patients, therefore we set the corresponding probabilities in influenza ARI patients with lower and higher health awareness to 0.3 and 0.6, respectively.
Tables 1 and 2 present our assumptions and the values we assign to various probabilities in general and under the baseline scenario.
Table 1.
Model assumptions made throughout the entire article and additional assumptions made for the baseline scenario.
| Situation | Assumption |
|---|---|
| Entire Article | Every member of the study population is classified as having either high or low health awareness. |
| The probabilities of being vaccinated, contracting influenza and non-influenza ARI, and seeking medical care may be associated with health awareness. | |
| The probability of non-influenza ARI does not depend on vaccination status. | |
| Every ARI patient seeking medical care is tested for influenza infection. | |
| The test for influenza infection has perfect sensitivity and specificity. Vaccination status is determined without error. | |
| The probability of contracting a non-influenza ARI does not depend on vaccination status and health awareness. | |
| Additional for Baseline Scenario | The probability of influenza ARI does not depend on health awareness |
| The probability of seeking medical care does not depend on vaccination status. |
Table 2.
Parameters and their corresponding values used in general and in the baseline scenario. HA represents health awareness.
| Parameter | Value | |
|---|---|---|
| Entire Article | Baseline Scenario | |
| Percent of population with high HA | 50% | 50% |
| Probability of being vaccinated | 80% - high HA | 80% - high HA |
| 40% - low HA | 40% - low HA | |
| Vaccine effectiveness | 50% | 50% |
| Probability of contracting ARI | May vary | 0.084 – non-influenza ARI |
| 0.027 – influenza ARI (unvaccinated) | ||
| 0.0135 – influenza ARI (vaccinated) | ||
| Probabilities of seeking medical care | May vary | 0.3 – influenza ARI, low HA |
| 0.6 – influenza ARI, high HA | ||
| 0.2 – non-influenza ARI, low HA | ||
| 0.4 – non-influenza ARI, high HA | ||
The bias of an estimate is defined as the difference between the observed value of the estimate and the true parameter of interest. Therefore, we must determine the true values of VE against SI and MAI. Since the true VE is calculated under the assumption of random vaccination, we assume the probability of being vaccinated does not depend on a person’s health awareness. The common value of the probability of vaccination is 0.6, as 60% of the population received the vaccine. In other words, the risks of SI in non-vaccinees and vaccinees are 0.027 and 0.0135, respectively (as one would expect from probabilities of influenza ARI used in these calculations). The true VE against SI is, therefore, 1 – RR = 1 – 0.5 = 0.5, or 50%. The risks of MAI in non-vaccinees and vaccinees are 0.0243 and 0.01215, respectively. Therefore, the true VE against MAI is also 1 – 0.5 = 0.5, or 50%. We obtain the estimated VE from the proportions of cases of SI and MAI among vaccinated and unvaccinated person within the population. We present the expected number of influenza and non-influenza ARI patients by health awareness and vaccination status in a hypothetical population of size 100,000 under the baseline scenario in the Appendix.
Results
As stated in the Introduction, we focus in this work on two important sources of bias, confounding and bias resulting from effects of vaccination on the probabilities of seeking medical care.
(a) Confounding bias
Confounding is the result of exposed (vaccinees) and non-exposed (non-vaccinees) having different probabilities of the outcome for reasons other than the direct effect of the vaccine. In our case, the probability of vaccination is associated with health awareness, which may be also be associated with the probability of contracting influenza and non-influenza ARI. For example, a person with high health awareness may make healthier lifestyle choices (periodic visits to the doctor, regular exercise, frequent hand washing, etc.) compared to a person with low health awareness. We expect this behavior to reduce the risk of both influenza and non-influenza ARI regardless of vaccination. Conversely, a person with co-morbidities may have higher health awareness due to their pre-existing conditions, but may also have increased risk of contracting an ARI. The magnitude of the confounding bias is expected to depend on the following risk ratios:
RR1 = probability of non-influenza ARI in a person with higher health awareness divided by the same probability in a person with lower health awareness.
RR2 = probability of influenza ARI in a person with higher health awareness divided by the same probability in a person with lower health awareness.
For simplicity, we assume that these risk ratios are the same for vaccinees and non-vaccinees. Table 3 presents the estimated VE for different combinations of RR1 and RR2. The true VE against SI and MAI is 0.5 for all these combinations. From Table 3, we learn that the TND-based VE estimate is unbiased only if RR1=RR2, i.e., the confounder (health awareness) has the same effect on the probabilities of influenza and non-influenza ARI. This confounding bias may be quite severe when these risk ratios are very different. For example, when the confounder reduces the risk of non-influenza ARI by 50% (RR2=0.5) and increases the risk of influenza ARI by 50% (RR1=1.5) then the estimated VE is 0.222, while the true VE against either of the outcomes of interest is 0.5. For a given RR2, the VE estimate increases with increasing RR1. Similarly, for a given RR1, the VE estimate decreases with increasing RR2.
Table 3.
Estimated VE for different combinations of relative risk of influenza ARI (RR1) and non-influenza (RR2) in high versus low health awareness.
| RR1 | RR2 | |||||
|---|---|---|---|---|---|---|
| 0.5 | 0.7 | 1.0 | 1.5 | 2.0 | ||
| 0.5 | 0.500 | 0.407 | 0.333 | 0.222 | 0.143 | |
| 0.75 | 0.578 | 0.500 | 0.438 | 0.344 | 0.277 | |
| 1.0 | 0.625 | 0.556 | 0.500 | 0.417 | 0.357 | |
| 1.5 | 0.679 | 0.619 | 0.571 | 0.500 | 0.449 | |
| 2.0 | 0.708 | 0.654 | 0.611 | 0.546 | 0.500 | |
(b) Bias resulting from the effect of vaccination on the probability of seeking care against influenza ARI
A few recent studies [17–19] suggest that vaccination may reduce the severity of influenza symptoms. This may reduce the probability of seeking medical care in vaccinated cases of influenza ARI, compared to that of unvaccinated cases. We let RR3 denote the ratio of the probability of seeking medical care in a vaccinated case of influenza ARI divided by the corresponding probability in an unvaccinated case. Figure 2 displays the estimated VE and the true VE’s against SI and MAI as RR3 varies from 0.5 to 1.0 (we assume that vaccination does not modify the probability of seeking care for non-influenza ARI).
Figure 2.
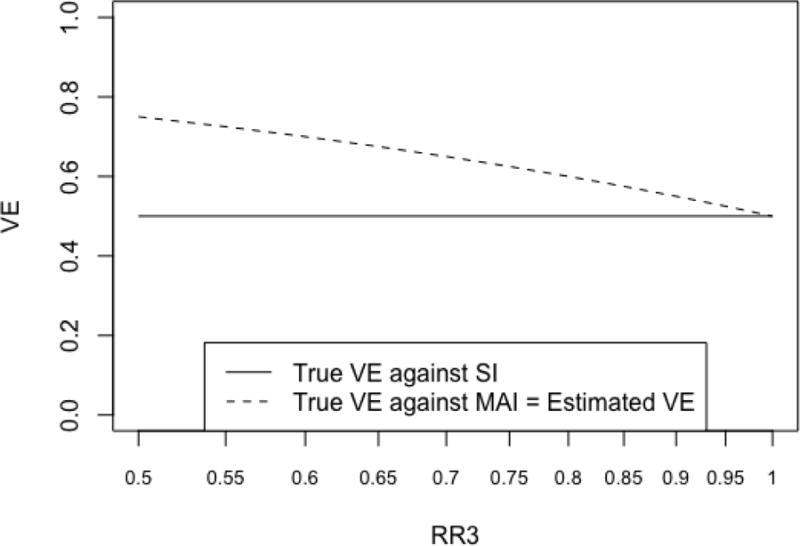
Estimated VE, true VE against SI, and true VE against MAI as the log of the ratio of the probability of seeking medical care in a vaccinated case of influenza ARI divided by the corresponding probability in an unvaccinated case (RR3) varies
Figure 2 demonstrates that when vaccination reduces the probability of seeking care against influenza ARI, i.e. RR3 < 1, then the true VE against MAI varies with RR3 and is higher than the true VE against SI (which does not depend on RR3). The bias of the VE estimate depends on the outcome of interest. While the estimate is still unbiased when assessing VE against MAI, it overestimates the true VE against SI when RR3 < 1. For example, when vaccinated influenza patients are 50% less likely to seek medical care compared to unvaccinated patients (RR3=0.5) then, the true VE against SI equals 0.5, while the estimated VE from the TND study is 0.75!
Discussion
We have presented a numerical method that allows for the evaluation of the bias of TND-based estimates of influenza VE against two outcomes of interest, SI and MAI. In the absence of sources of bias, we show that the estimates of VEs from TND studies are unbiased for both outcomes of interest. When a covariate (such as health awareness) is associated with both the probability of vaccination and the probability of contracting influenza and non-influenza ARI, (i.e., confounding bias is present), then TND-based estimates are unbiased only when the confounder has the same effect on the probabilities of influenza and non-influenza ARI (RR1=RR2, where RR1 and RR2 are the probabilities of non-influenza ARI and influenza ARI, respectively, in a person with higher health awareness divided by the same probability in a person with lower health awareness). When the confounder has a different effect on the risk of influenza ARI than on the risk of non-influenza ARI (RR1≠RR2), VE estimates may suffer from substantial bias, especially when RR1 and RR2 are very different. In practice, it is difficult to verify that these risk ratios are equal, particularly when the potential confounder is unrecognized or unobserved. The TND has become widely used because it is supposed to reduce confounding bias by trying to eliminate differences in care seeking behavior between vaccinees and non-vaccinees [1–3, 10, 14, 20]. However, we show that when a confounder is associated with the probabilities of influenza and non-influenza ARI, then the TND may still produce biased VE estimates. The decision to use the TND over other study designs to evaluate VE should be carefully considered if a confounder is suspected to have a different effect on the risks of influenza ARI and non-influenza ARI.
When vaccination affects the probability of seeking medical care against influenza ARI, perhaps due to a reduction in symptom severity in vaccinated influenza patients, the bias of TND-based VE estimates depends on the outcome of interest. When this source of bias is present, VE estimates are unbiased against MAI. However, VE against SI may be substantially overestimated when the probability of seeking medical care for influenza ARI is lower in vaccinated patients than unvaccinated patients. Our results emphasize the importance of specifying the outcome of interest when evaluating the bias of VE estimates and clearly stating the interpretation when reporting VE estimates.
It is important to consider the bias of VE estimates when the outcome of interest is SI as individuals with influenza who do not seek medical care still impact the disease burden. First, there are a variety of reasons a person with influenza may not seek medical care for flu beyond having mild symptoms. Second, there is no scientific evidence to suggest that a person with mild illness will only cause mild illness in individuals they infect. A person with mild influenza can still infect others, and a secondary infection may develop more severe disease (due to other risk factors) than the originally infected individual. For example, if a healthy twenty-something with mild influenza infected an elderly person with a compromised immune system, the elderly person may develop more severe symptoms. Ultimately, the mild illnesses are not caused by different viruses. They are caused by potential underlying immunity or general health of the host. The viruses are not different; it is the host that is different.
As stated in the Methods Section, we made simplifying assumptions to eliminate other sources of bias to focus on the two sources of bias discussed above. We considered each source of bias separately. It is entirely possible that both sources of bias may be present, but it is difficult to interpret the impact of multiple sources of bias on VE estimates. Finally, we only considered unadjusted VE estimates because (a) we assume that the confounder (health awareness) is unobserved, and (b) we aimed to focus on characterizing the impact of sources of bias rather than on how one can reduce bias using statistical techniques. We are currently working on a dynamic model that incorporates a near-real-time process of developing influenza and non-influenza ARI, seeking medical care, and being tested for influenza infections. The new model also includes confounders that may simultaneously affect the probabilities of being vaccinated, contracting influenza and non-influenza ARIs, and seeking medical care. The results from the new model, in terms of the bias of the TND-based VE estimate, are similar to those we report in this work.
TND studies are widely used to obtain influenza VE estimates, which have strong influence on both policy and public knowledge. This work highlights that 1) investigators should exercise caution when using the TND as resulting VE estimates may suffer from considerable bias due to confounding, and 2) if vaccination reduces the probability that vaccinated influenza patients seek medical care then TND-based VE estimates may be reliable when the outcome of interest is MAI, but they may substantially overestimate the true VE against SI. Thus, care should be taken to correctly interpret VE estimates from this study design and make policy makers and the public aware that these estimates may be too ‘optimistic’ when one is concerned about reducing the risk of any influenza illness, regardless of whether it results in seeking medical care.
Supplementary Material
Highlights.
VE estimates are unbiased only when the confounder has the same effect on the probabilities of influenza and non-influenza ARI.
VE against MAI is unbiased, but VE against SI is overestimated when vaccination affects seeking care for influenza ARI.
Investigators should exercise caution when using the TND as VE estimates may suffer from considerable bias.
Acknowledgments
This research was supported by the National Institute of Allergies and Infectious Diseases of the National Institutes of Health (NIH) under Award R01AI110474, and by IPA 1110376-05 with the Centers for Disease Controls and Prevention (CDC). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIH or the CDC. The authors wish to thank Dr. Ivo Foppa and to the reviewers for helpful comment.
Appendix
Table A1 presents the expected number of influenza and non-influenza ARI patients by health awareness and vaccination status in a hypothetical population of size 100,000 under the baseline scenario. The table also presents the corresponding expected number of influenza and non-influenza ARI patients who seek medical care and are therefore tested for influenza infection.
Table A1.
Calculation of the expected numbers of influenza and non-influenza ARI patients seeking medical care by health awareness and vaccination status in a hypothetical population of N=100,000 under the baseline scenario.
| Lower health awareness (N=50,000) |
Higher health awareness (N=50,000) |
||||
|---|---|---|---|---|---|
| Type of ARI | Vaccinated (N=20,000) | Unvaccinated (N=30,000) | Vaccinated (N=40,000) | Unvaccinated (N=10,000) | |
| Influenza | Probability of contracting | 0.0135 | 0.027 | 0.0135 | 0.027 |
| Number of cases | 270 | 810 | 540 | 270 | |
| Probability of seeking care | 0.3 | 0.3 | 0.6 | 0.6 | |
| Number seeking Care | 81 | 243 | 324 | 162 | |
| Non-influenza | Probability of contracting | 0.084 | 0.084 | 0.084 | 0.084 |
| Number of cases | 1,680 | 2,520 | 3,360 | 840 | |
| Probability of seeking care | 0.2 | 0.2 | 0.4 | 0.4 | |
| Number seeking care | 336 | 504 | 1,344 | 336 | |
As health awareness status is unobservable, we collapse the number of influenza and non-influenza patients seeking medical care over the two categories of health awareness. For example, the number of unvaccinated non-influenza patients is obtained by adding the numbers in the 2nd and 4th columns in the 8th row of Table 3, i.e., 504 + 336 = 840. Therefore, we expect to observe the 2×2 table shown in Table A2. The VE estimate from this hypothetical TND study is one minus the odds ratio in Table A2, i.e., 1 −0.5 = 0.5, or 50%.
Table A2.
Expected 2×2 table resulting from the calculations in Table A1.
| Vaccinated | Unvaccinated | |
|---|---|---|
| Test positive (cases) | 405 | 405 |
| Test negative (controls) | 1,680 | 840 |
The bias of an estimate is defined as the difference between the observed value of the estimate and the true parameter of interest. Therefore, we must determine the true values of VE against SI and MAI. Since the true VE is calculated under the assumption of random vaccination, we repeat the calculations in Table A1 where the probability of being vaccinated does not depend on a person’s health awareness. The common value of the probability of vaccination is 0.6, as 60% of the population received the vaccine. We then find that 1080 out of the 40,000 unvaccinated and 810 of the 60,000 vaccinees contract influenza illness (symptomatic influenza). In other words, the risks of SI in non-vaccinees and vaccinees are 0.027 and 0.0135, respectively (as one would expect from probabilities of influenza ARI used in these calculations). The true VE against SI is, therefore, 1 – RR = 1 – 0.5 = 0.5, or 50%. If we use the probabilities of seeking medical care in the above calculations we find that of the persons contracting SI, 486 non-vaccinees and 364.5 vaccinees are expected to seek medical care, i.e. to become cases of MAI. Therefore, the risks of MAI in non-vaccinees and vaccinees are 486/40000 = 0.01215 and 364.5/60000 = 0.006075 respectively, resulting in a true VE against MAI of 1 – 0.006075/0.01215 = 0.50 (50%). Thus, in our baseline scenario the estimated VE of 50% equals both the true VE against SI and against MAI. In other words, the estimate is unbiased for both outcomes of interest.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflicts of Interest
The authors report no conflicts of interest.
References
- 1.Skowronski DM, Masaro C, Kwindt TL, Mak A, Petric M, Li Y, et al. Estimating vaccine effectiveness against laboratory-confirmed influenza using a sentinel physician network: results from the 2005–2006 season of dual A and B vaccine mismatch in Canada. Vaccine. 2007;25:2842–51. doi: 10.1016/j.vaccine.2006.10.002. [DOI] [PubMed] [Google Scholar]
- 2.Sullivan SG, Shuo F, Cowling BJ. Potential of the test-negative design for measuring influenza vaccine effectiveness: a systematic review. Expert Rev Vaccines. 2014;13:1571–91. doi: 10.1586/14760584.2014.966695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Belongia EA, Simpson MD, King JP, Sundaram ME, Kelley NS, Osterholm MT, et al. Variable influenza vaccine effectiveness by subtype: a systematic review and meta-analysis of test-negative design studies. The Lancet Infectious Diseases. 2016;16:942–51. doi: 10.1016/S1473-3099(16)00129-8. [DOI] [PubMed] [Google Scholar]
- 4.Ohmit SE, Thompson MG, Petrie JG, Thaker SN, Jackson ML, Belongia EA, et al. Influenza vaccine effectiveness in the 2011–2012 season: protection against each circulating virus and the effect of prior vaccination on estimates. Clin Infect Dis. 2014;58:319–27. doi: 10.1093/cid/cit736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sullivan SG, Chilver MB, Higgins G, Cheng AC, Stocks NP. Influenza vaccine effectiveness in Australia: results from the Australian Sentinel Practices Research Network. Med J Aust. 2014;201:109–11. doi: 10.5694/mja14.00106. [DOI] [PubMed] [Google Scholar]
- 6.Jimenez-Jorge S, Pozo F, Larrauri A, cyc EVAST Interim influenza vaccine effectiveness: A good proxy for final estimates in Spain in the seasons 2010–2014. Vaccine. 2015;33:3276–80. doi: 10.1016/j.vaccine.2015.03.051. [DOI] [PubMed] [Google Scholar]
- 7.Castilla J, Martinez-Baz I, Navascues A, Fernandez-Alonso M, Reina G, Guevara M, et al. Vaccine effectiveness in preventing laboratory-confirmed influenza in Navarre, Spain: 2013/14 mid-season analysis. Euro Surveill. 2014;19 doi: 10.2807/1560-7917.es2014.19.6.20700. pii=20700. [DOI] [PubMed] [Google Scholar]
- 8.Fielding JE, Grant K, Tran T, Kelly H. Moderate influenza vaccine effectiveness in Victoria, Australia, 2011. Euro Surveill. 2012;17 pii=20115. [PubMed] [Google Scholar]
- 9.Kissling E, Valenciano M, Buchholz U, Larrauri A, Cohen JM, Nunes B, et al. Influenza vaccine effectiveness estimates in Europe in a season with three influenza types/subtypes circulating: the I-MOVE multicentre case-control study, influenza season 2012/13. Euro Surveill. 2014;19 doi: 10.2807/1560-7917.es2014.19.6.20701. pii=20701. [DOI] [PubMed] [Google Scholar]
- 10.Orenstein EW, De Serres G, Haber MJ, Shay DK, Bridges CB, Gargiullo P, et al. Methodologic issues regarding the use of three observational study designs to assess influenza vaccine effectiveness. Int J Epidemiol. 2007;36:623–31. doi: 10.1093/ije/dym021. [DOI] [PubMed] [Google Scholar]
- 11.Haber M, An Q, Foppa IM, Shay DK, Ferdinands JM, Orenstein WA. A probability model for evaluating the bias and precision of influenza vaccine effectiveness estimates from case-control studies. Epidemiol Infect. 2015;143:1417–26. doi: 10.1017/S0950268814002179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jackson ML, Nelson JC. The test-negative design for estimating influenza vaccine effectiveness. Vaccine. 2013;31:2165–8. doi: 10.1016/j.vaccine.2013.02.053. [DOI] [PubMed] [Google Scholar]
- 13.Foppa IM, Haber M, Ferdinands JM, Shay DK. The case test-negative design for studies of the effectiveness of influenza vaccine. Vaccine. 2013;31:3104–9. doi: 10.1016/j.vaccine.2013.04.026. [DOI] [PubMed] [Google Scholar]
- 14.Sullivan SG, Tchetgen Tchetgen EJ, Cowling BJ. Theoretical Basis of the Test-Negative Study Design for Assessment of Influenza Vaccine Effectiveness. Am J Epidemiol. 2016;184:345–53. doi: 10.1093/aje/kww064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.De Serres G, Skowronski D, Wu XW, Ambrose CS. The test-negative design: validity, accuracy and precision of vaccine efficacy estimates compared to the gold standard of randomised placebo-controlled clinical trials. Euro Surveill. 2013;18 doi: 10.2807/1560-7917.es2013.18.37.20585. pii=2058. [DOI] [PubMed] [Google Scholar]
- 16.Shi M, An Q, Ainslie KEC, Haber M, Orenstein WA. A comparison of the test-negative and the traditional case-control study designs for estimation of influenza vaccine effectiveness under nonrandom vaccination. BMC Infect Dis. doi: 10.1186/s12879-017-2838-2. to appear. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Castilla J, Godoy P, Dominguez A, Martinez-Baz I, Astray J, Martin V, et al. Influenza vaccine effectiveness in preventing outpatient, inpatient, and severe cases of laboratory-confirmed influenza. Clin Infect Dis. 2013;57:167–75. doi: 10.1093/cid/cit194. [DOI] [PubMed] [Google Scholar]
- 18.Deiss RG, Arnold JC, Chen WJ, Echols S, Fairchok MP, Schofield C, et al. Vaccine-associated reduction in symptom severity among patients with influenza A/H3N2 disease. Vaccine. 2015;33:7160–7. doi: 10.1016/j.vaccine.2015.11.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.VanWormer JJ, Sundaram ME, Meece J, Belongia E. A cross-sectional analysis of symptom severity in aduls with influenza and other acute respiratory illness in the outpatient setting. BMC Infect Dis. 2014;14 doi: 10.1186/1471-2334-14-231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lipsitch M, Jha A, Simonsen L. Observational studies and the difficult quest for causality: lessons from vaccine effectiveness and impact studies. International Journal of Epidemiology. 2016;45:2060–74. doi: 10.1093/ije/dyw124. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


