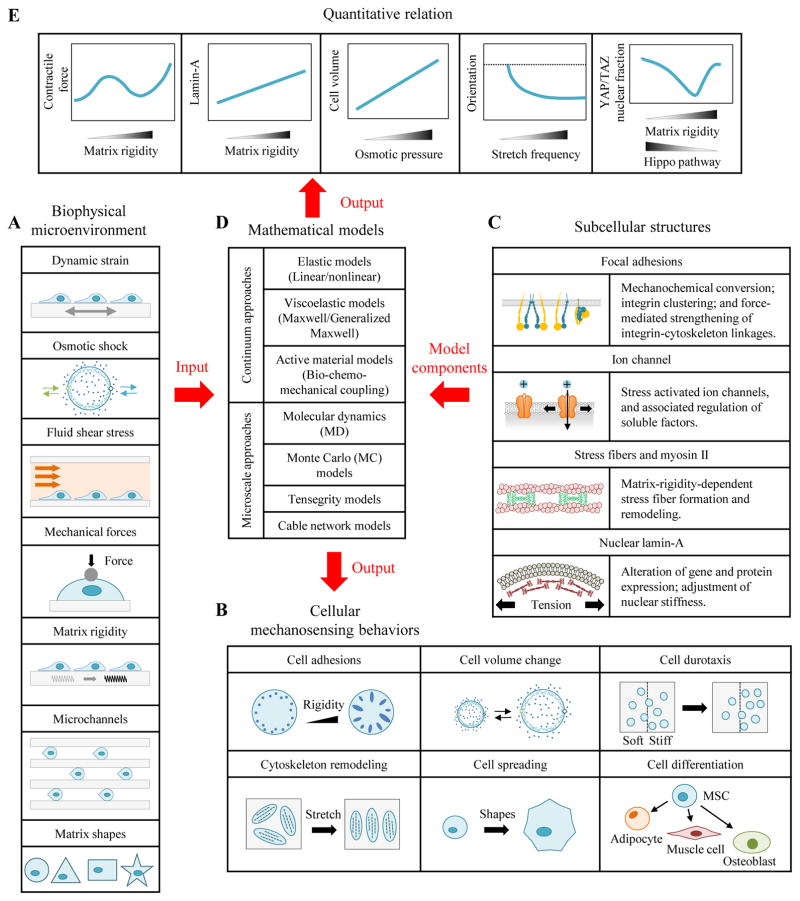
Abstract
Cells in vivo reside within complex microenvironments composed of both biochemical and biophysical cues. The dynamic feedback between cells and their microenvironments hinges upon biophysical cues that regulate critical cellular behaviors. Understanding this regulation from sensing to reaction to feedback is therefore critical, and a large effort is afoot to identify and mathematically model the fundamental mechanobiological mechanisms underlying this regulation. This review provides a critical perspective on recent progress in mathematical models for the responses of cells to the biophysical cues in their microenvironments, including dynamic strain, osmotic shock, fluid shear stress, mechanical force, matrix rigidity, porosity, and matrix shape. The review highlights key successes and failings of existing models, and discusses future opportunities and challenges in the field.
Keywords: Cellular mechanosensing, mathematical modeling, focal adhesions, stress fibers, signaling pathway, mechanobiology, biomechanics, cell models
1. Introduction
Cells in vivo reside within a complex microenvironment that is rich in biochemical and biophysical cues [1–7]. Cells react to these cues through behaviors such as spreading, migration and differentiation [8–14], and can thereby initiate major pathologies such as metastasis and fibrosis [15–25] (Fig. 1). The need to understand how cells transduce these the nature of their environment, especially mechanical elements such as matrix rigidity, mechanical stretch and fluid shear stress, has motivated the development of a broad range of new mathematical models. A great many of these models trace their genesis to efforts to explain the observation that the lineage of mesenchymal stem cells (MSCs) is strongly affected by the modulus of the substratum upon which they are cultured [26–29]. For example, matrices that mimic the compliance of brain or fat promote neurogenesis or adipogenesis of MSCs, matrices that mimic the compliance of muscle promote myogenesis, and matrices that mimic the compliance of bone promote osteogenesis [26]. However, the molecular mechanisms driving these phenomena remain elusive. The field has grown substantially to integrate a broad range of integrated intracellular protein structures and signaling systems. The goals of this review are to highlight some important breakthroughs and to critically assess the capability of existing models to capture the breadth of mechanobiological responses known to govern the behavior of animal cells.
Figure 1. Application of cellular mechanosensing models in mechanobiology.
Cells sense and respond biophysical cues such as dynamic strain, osmotic shock, shear flow, external forces, matrix rigidity, and steric constraints. For example, cells have bigger focal adhesions on stiffer substrata; cells can actively regulate their volume in response to osmotic shock; and cells reorient in response to mechanical strain. This review summarizes mathematical models based upon different cellular mechanosensing components that have been applied to interpret these phenomena.
The focus of the review is how cellular mechanosensitivity arises from the range of biophysical sensing modes inside the cells. Protein structures at the interface of the cell and extracellular matrix (ECM), including those that comprise focal adhesions, are known to sense ECM rigidity and tension. For example, chemomechanical signal conversion at the cell-ECM interface can arise through force-induced conformational or organizational changes in proteins or structures near the transmembrane domains. However, as is emphasized throughout this review, many possible pathways exist for this, and these pathways are likely redundant, with multiple pathways acting in parallel. Tension can unfold certain proteins to reveal cryptic binding domains and stabilize adhesions [17, 19, 30–34]. Both integrin clusters and cadherin clusters that link neighboring cells might serve as micro-platforms for biochemical reactions that help transduce force, with the dependence of cluster lifetime upon external mechanical cues a possible mechanism for mechanochemical signal conversion [30]. Stress-activated ion channels are also known to sense membrane tension [35, 36]. Cytoskeletal elements connect to the LINC (linker of nucleoskeleton and cytoskeleton) complex and possibly enable mechanical forces to affect gene expression and transcription directly via nuclear deformation [37, 38]. All of these result mechanical transduction to activate intracellular signaling [39–42] and to thereby enable cells to respond to microenvironmental biophysical cues [43, 44]. The identification of these mechanotransduction pathways has required predictive mathematical models that enable testing of hypotheses. As the functional relationships between the biophysical microenvironment and cellular behaviors have come to light, a range of such predictive models has emerged.
Advances in biomaterials, especially hydrogels that mimic ECM and micro/nano technologies, have enabled a wealth of cellular mechanosensing phenomena to be characterized experimentally [3, 17, 45–48]. Many of these phenomena seem tuned by cells to enable distinct, cell type-specific behaviors. For example, dorsal root ganglion neurites show maximal outgrowth when cultured on substrata with a rigidity analogous to that of brain parenchyma, approximately 1 kPa [49]. Several sets of technologies have proven particularly informative for quantifying how cellular behaviors and their underlying molecular interactions depend upon the cell microenvironment. The first is two-dimensional substrata with defined mechanical properties [50–52]. The second is micropost arrays with tunable flexural and material rigidity [53]. The third is three-dimensional tissue constructs with defined ECMs [54, 55]. The fourth is the external loads applied to cells by micropipette, magnetic or optical tweezers and atomic force microscopy (AFM) [56–58]. These systems have been used to quantify behaviors at the whole cell level, such as traction (“traction force”) distribution, spreading area, migration rate, and force regulation [59–64]. However, integrated models are required for gaining insight into the molecular mechanisms of mechanosensing, and molecular probes (e.g., fluorescence resonance energy transfer, FRET) are required to quantify protein conformation changes and probe receptor-ligand rupture events [65–67].
Despite the large number of experimental developments, many fundamental features of cellular mechanosensing are still not fully understood, including the complex relationship of matrix rigidity, integrin clustering and biochemical signal activation [68, 69]. Mathematical models have been central to reconciling seemingly divergent experimental observations into simpler and universal sets of principles describing how different component processes cooperate to produce mechanosensing [70–73]. A key model highlighted in this review is the “molecular clutch model”, which helped uncover talin-vinculin binding dynamics as pivotal to matrix rigidity sensing across cell types [10, 74, 75]. Emerging models seek to explain how cellular mechanosensing integrates dynamic interactions between biomolecules across wide temporal and spatial scales in the cell microenvironment [76–78]. Mathematical models based upon hypotheses of the mechanics and kinetics of biochemical and biophysical processes are needed to further unravel the biophysics of cellular mechanosensing.
A wealth of experiments and mathematical models exist for this purpose, and a range of excellent reviews can be found of both experiments (synthesis and measurement) [37, 45] and mathematical models [44, 79, 80]. A critical review of mechanistic and kinetic mathematical models for cellular mechanosensing is still lacking, however, and this review aims to fill that void. The review categorizes models into different biophysical cues based on the current biotechnology methods for perturbing and probing the cell microenvironment: dynamic strain, osmotic shock, fluid shear stress, external mechanical forces, matrix rigidity, and microchannel and matrix shapes. We critique these modeling efforts, highlight their strengths and limitations, then conclude with a perspective on important open challenges to understanding how cell mechanosensing affects cell physiology.
2. Cellular mechanosensing of dynamic strain
For many types of cells, dynamic deformation is a key component of both the physiological and pathophysiological cell microenvironment. For example, cardiac fibroblasts and cardiomyocytes experience periodic deformations of the heart wall, endothelial cells experience pulsatile shear flows and pressures, and cancer cells can bear compression deformation in a tumor [81]. Numerous studies seek to understand why and how cells could sense and respond to external dynamic strain, in hopes of finding potential ways to cure diseases of mechanotransduction.
2.1 Cellular reorientation and cytoskeletal remodelling
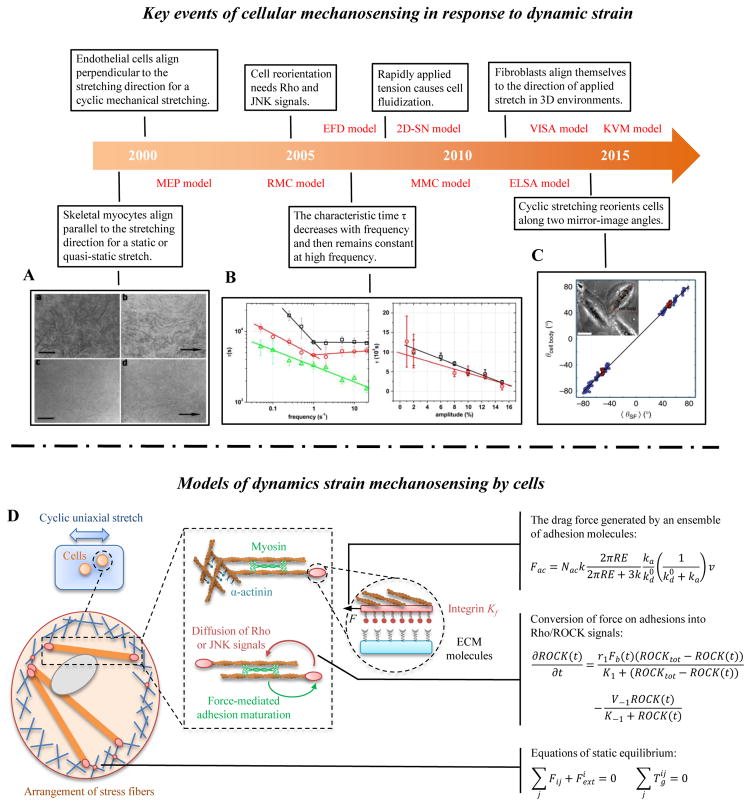
Cells actively sense the dynamic strain of their environments, resulting in cytoskeletal remodelling and cellular reorientation. This was shown many years ago in a series of innovative experiments that monitored cells stretched on flexible 2D substrata. Myocytes tend to align parallel to the direction of a static or quasi-static (low frequency) stretch [82] (Fig. 2A). However, many tissue cells (e.g., fibroblasts and endothelial cells) prefer to align perpendicular to the direction of applied cyclic strain at high frequency (>1 Hz) and larger stretching magnitude (>5%) [83] (Fig. 2B). Cyclic stretching can reorient cells along two mirror-image angles [84] (Fig. 2C). The story has only recently begun to unfold for cells in 3D environments. More interestingly, it has been shown that fibroblasts align themselves in the direction of applied stretch in 3D environments [85]. At higher strain rates, cell reorientation gives way to cell fluidization, a rapid disassembly of stress fibers (SFs) along the direction of deformation, in both 2D [86] and 3D [87].
Figure 2. Cellular mechanosensing in response to dynamic strain.
(A) Under conditions simulating mammalian long bone growth (e.g., a static or quasi-static stretch), cultured myocytes respond to mechanical forces by lengthening and orienting along the direction of stretch [82]. (B) Many tissue cells (e.g., fibroblasts and endothelial cells) prefer to align perpendicular to the direction of applied cyclic strain, especially at high frequency and larger stretching magnitude [83]. (C) Cells can reorient to a uniform angle in response to cyclic stretching of the underlying substrate [84]. (D) A mechanical model of SFs, showing adhesion complexes, myosin motors and actin filaments. Myosin motors generate force between antiparallel actin filament bundles, one of which is anchored to the matrix by adhesion complexes. Proteins in adhesion and actin filaments system are drawn as masses on springs in order to indicate how they function in the model.
Although the mechanisms for cellular mechanosensing in response to dynamic strain are not known fully, signaling molecules including Rho and JNK are known to have important effects. For example, inhibition of Rho will abolish cell reorientation in response to cyclic stretch [88]. Integrated mathematical models and experiments are essential to understanding cellular mechanosensing in response to dynamic strain (Fig. 2D).
2.2 Chromatin condensation and remodeling
A second class of response to mechanical strain is stretch-regulated nuclear reconfiguration, and potentially associated chromatin condensation and remodeling [89–93]. A potential pathway for nuclear mechanotransduction is force- or stretch-initiated ATP and Ca2+ release into the cytoplasm through hemichannels (possibly membrane-tension-mediated ion channels), with ATP-dependent purinergic signals (e.g., G protein coupled P2Y receptors) then reinforcing or reorienting SFs and thereby deforming the nucleus to alter chromatin condensation. Transforming growth factor beta (TGF-β) can enhance this, perhaps through increases of cell traction from interactions of TGF-β/Smad signaling and Rho signaling.
The kinetics of these changes reveal that intermediate steps are likely involved. In a 1 Hz dynamic stretch, ATP-release requires 10–20 sec, but changes to the chromatin structure require on the order 10 min. This suggests that mechanical cues may be firstly converted into chemical signals (e.g., ATP, Ca2+ and Rho) at cell-ECM surface rather than directly transmitted into nucleus in this process. However, mechanical forces transmitted directly through the actin cytoskeleton from the cell-ECM surface to the nuclear envelope are also important for cellular mechanosensing [92]. Integrated mathematical models and experiment are needed to identify these pathways as well.
2.3 Mathematical models
2.3.1 One-dimensional stress fiber model
A simple 1D stress fiber model is sufficient to explain several key features of cellular mechanosensing. Qian et al. proposed a viscoelastic-sarcomere-adhesion (VISA) model to describe the cell reorientation in response to cyclically stretching of a substratum [94]. The model includes four main parts: substrate stiffening, adhesion bond dynamics, stress fiber (SF) assembly/disassembly dynamics, and cell rotational diffusion. Matrix rigidity is assumed to increases with cyclic stretching via strain stiffening. Therefore, the effective stiffness of an adhesion bond (adhesion molecule-fibronectin-substrate bond) increases with increasing stretching amplitude, and in turn decreases the adhesion bond dissociation rate. Then, adhesion bond dynamics are connected to SF dynamics by coupled first order kinetic equations that model the density of SFs as proportional to the adhesion bond density:
| (1) |
| (2) |
where k+ (s−1) and k− (s−1) are on and off-rates of receptor-ligand bonds; c0 and ca are the total and connected bond density; and are the assembly and disassembly rates of SFs; and cf is the density of SFs. SFs are constituted by a parallel configuration of viscoelastic and contraction elements; note that some experiments support that a tandem configuration [95]. Finally, the stretching amplitude and frequency are sensed by SFs and transmitted to adhesion plaques, thereby influencing the adhesion bond dissociation rate. When cells cannot develop stable adhesions and SFs, they will undergo rotational diffusion to explore new orientations until stable adhesions and SF structures are formed. This integrated mechanochemical model could explain a broad range of experimental observations of cell reorientation on cyclic stretch substrata, such as the tendency of cells to align perpendicular to the stretching direction at a high cyclic stretch frequency (>1Hz) and stretching magnitude (5%~6%).
Chen et al. also proposed an elastic-sarcomere-adhesion (ELSA) model, in which SFs are modeled by linear elastic sarcomeres). Results of this model suggest that catch bonds in adhesions and two intrinsic time constants of the stress fiber play an important role in cell reorientation induced by cyclic stretch [96]. These two time constants are those for localized activation of sarcomere units at low stretching frequency, and homogenous activation of sarcomere units at high stretching frequency.
However, these simplified models cannot explain some other experimental observations, e.g., the cell fluidization (cytoskeletal disassembly) mechanism [86, 87], mechanochemical molecules such as activation of the Rho pathway [88], and inhomogeneous SFs contraction [97]. Recently, Wu et al. proposed a Kelvin-Voight-myosin (KVM) model, which couples assembly-disassembly of myosin motors with a single viscoelastic Kelvin-Voigt stress fiber [98]. Their model predicts that tension-regulated myosin detachment is the main reason for cell fluidization in response to transient loading.
2.3.2 Two-dimensional stress fiber model
The two-dimensional SF-network (2D-SN) model of Kaunas and colleagues is based on constrained mixture theory and has been used to explain SF reorganization in response to the cyclic uniaxial stretch [99–102]. The model concludes that SFs tend to dissociate in the direction of stretch and reach a stable configuration in the direction of lowest stretch at high frequencies. Cells undergo affine deformation in response to cyclic stretches. This result in a stretch λi of SFs oriented in a particular direction i and a stretch-dependent increase in the rate at which those SFs disassemble:
| (3) |
where k0 (s−1) is the intrinsical stress fiber dissociation rate without tension; k1 (s−1) represents the stretch-dependence of this rate; λ0 is the homeostatic pre-stretch level in the ith family of SFs. This model differs substantially from the KVM model as described in section 2.3.1, which predicts that only compression causes stress fiber disassembly, and also from the model of Deshpande and colleagues described below. The fact that all of these models are capable of predicting cellular behaviors despite vastly different assumptions is strong motivation for additional experimentation in this area.
The multiscale mechano-chemical (MMC) model proposed by Ji and colleagues suggests that a biphasic relationship between cell reorientation time and stretching frequency may be caused by the competition between instability of adhesions and reassembly of SFs [103]. The 1D elastic force-dipoles (EFD) model (note that this is a 1D cell model) of Safran and colleagues addresses this by considering that cells prefer to maintain homeostatic local stress and strain fields by adjusting a force dipoles which characterize the contraction force of cells [104–106].
SF networks have also been modeled as networks of discrete rod structures, which may be more consistent with their intrinsical states in vivo. For example, a two-dimensional SF-network (2D-SN) model based on coarse grained Monte Carlo models has been proposed by Puskar and colleagues [107]. Similarly, a cytoskeletal tensegrity system (CTS) model has been proposed, which consists of four struts (representing the longitudinal SFs and a lateral actin network) and eight cables (denoting the microfilaments) [108]. This model predicts that the lateral struts (actin network) play a vital role in regulating cellular orientation.
2.3.3 Rho-regulated mechanochemical stress fiber model
Stress fibers are regulated not only by mechanical forces but also by chemical signals, such as Rho and ROCK. This motivates mathematical models that integrate both mechanical and chemical factors. The Rho-regulated mechanochemical (RMC) model of Schwarz and colleagues models inhomogeneous stress fiber contraction [109]. In their model, mechanical forces can trigger Rho signals (e.g., Rho/ROCK/MLCP/myosin), leading to adhesion reinforcement and increasing contraction force in SFs; note that other studies suggest that forces caused by mechanical stretch would reduce the stability of adhesion clusters [110]. The mechanosensing process (e.g., the conversion of mechanical force into biochemical signals at focal adhesions) is treated as an enzymatic reaction in the framework of Michaelis-Menten kinetics:
| (4) |
where Fb(t) (pN) is the mechanical force applied on focal adhesion depending on SF deformation; ROCKtot (nM) and ROCK(t) (nM) are the concentrations of total and active ROCK; K1 (nM) is the Michaelis-Menten constant. The second term accounts for the degradation of active ROCK with maximum velocity V−1 (nM s−1) and Michaelis-Menten constant K−1 (nM). Mechanical forces acting on focal adhesions lead to a position-dependent feedback loop for adhesion maturation. The myosin motors and biochemical signals are described by a system of reaction-diffusion equations and myosin-filaments are modeled as a viscoelastic contractile actin bundle (a serious of viscoelastic-contraction elements). This model predicts that the contraction force of SFs displays spatial gradients corresponding to the deformation pattern of SFs, i.e., upon stimulation of contraction, only the sarcomeres in the cell edge shorten while those in the center elongate.
Another model of Kaunas and colleagues explains how the activity of JNK can be upregulated by reassembly of SFs. The model shows how uniaxial stretch induces the transient activation of JNK by formation of new adhesion bonds [111]. Their JNK-regulated mechanochemical (JMC) model models the JNK activation rate by the first-order kinetics,
| (5) |
where k1 (s−1) and k2 (s−1) are the rates for activation and deactivation of JNK; CPJNK (mol) and CJNK (mol) are the concentrations of the activation and deactivation forms of JNK, respectively; u (s−1) is the formation rate of integrin bonds independent of SF dynamics; is the formation rate of integrin bonds because of assembly of new SFs (this key value is calculated from the matrix stretch patterns by their 2D-SN model). Thus, matrix stretch and chemical factors are exquisitely incorporated into SF network dynamics, providing an explanation for how cells sense and adapt to their cyclic stretch matrix.
2.3.4 Minimum free energy stress fiber model
Another mathematical model is based on energy minimization is proposed to understand the cell reorientation in response to dynamic stretch [112, 113]. This model explains realignment of SFs in cells by the following factors: 1) SFs begin with a basal-strain-energy in their unstretched initial state; 2) substrate strain deforms individual SF from this initial state; 3) SFs disassemble when their strain energy reaches 0 or exceeds twice the baseline stain energy. Thus, the model suggests that SFs prefer to orient in the direction where their basal-strain-energy is minimally perturbed. This model is in rough analogy to the Kaunas 2D-SN model, in which rates of stress fiber disassembly scale with the square of the difference between the current and baseline stretch. However, caution is required in this model because, unlike the Kaunas 2D-SN model, the energy minimization model is strictly thermodynamic and not kinetic: all changes happen instantaneously, and the model cannot predict the time evolution of stress fiber patterns. Instead, the model predicts only the steady state distribution of SFs other than time-dependent cell reorientation process. Energy minimization arguments have been used in another model from the Geiger group, proposed to understand why and how cells reorient themselves along two mirror-image angles in response to certain cyclic loadings [84]. This model includes kinetic arguments to explain the temporal evolution of SFs as a function of cyclic loading frequency.
3. Cellular mechanosensing of osmotic shock
Cells can sense cycles of osmotic shock, e.g., cycles in which cells are subjected to a hypotonic shock followed by a hypertonic shock. These responses are mediated by activation of mechanosensitive ion channels at the cell membrane-cortex surface. The mechanosensitive ion channels are regulated by the mechanical force balance at the cell membrane-cortex surface, and their action determines homeostatic values of cell volume and membrane tension (Fig. 3E–F) [71].
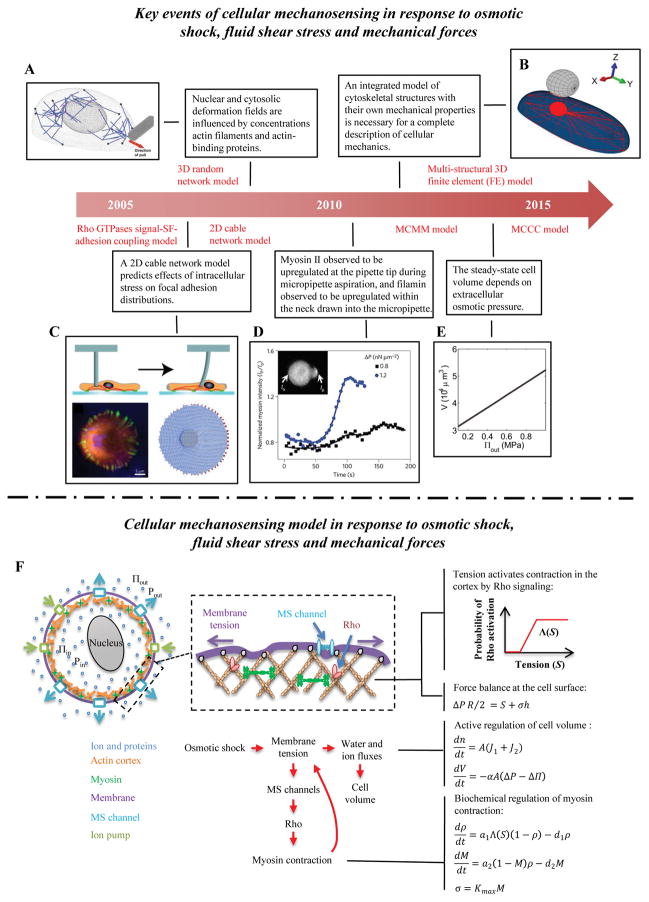
Figure 3. Cellular mechanosensing in response to osmotic shock, fluid shear stress and mechanical forces.
(A) The 3D random network model of the actin cytoskeleton to study the nuclear deformation under micropipette aspiration [124]. (B) The multi-structural 3D finite element (FE) model can be used to study how cytoskeletal mechanical properties affect cell responses under AFM indentation [121]. (C) A 2D cable network model predicts how stress is transmitted through the actin cytoskeletons of adherent cells and consequentially distributed at focal adhesions sites (FAs) [120]. (D) Myosin and α-actinin accumulation increase at the pipette tip and filamin increases in the neck region during micropipette aspiration [117]. (E) Steady state cellular volume increases with increasing extracellular osmotic pressure [71]. (F) Schematic of the model prediction of volumetric changes in response to osmotic shock. The model includes the Rho signaling pathway, which activates myosin assembly and active contraction in the cell cortex. At mechanical equilibrium, the membrane tension balances both osmotic pressure and active cortical contraction.
To understand the pathways underlying this volumetric regulation, a chemomechanical model was proposed by Tao & Sun, which modeled activation of the Rho signaling pathway by the opening of mechanosensitive ion channels [71]. There are two main assumptions in this model. The first is that the model considers a spherical (e.g., a suspended cell) or cylindrical cell (e.g., a cell between plat cantilevers) so as to simplify both cell geometry and cell adhesion; i.e., no adhesions or fixed adhesion area. The second is that the cortical actomyosin layer coupled to membrane is modeled as an active viscoelastic gel-like fluid. The ion channel chemomechanical model contains three main parts: force balance at the cell edge, membrane tension mediated myosin activation, and cell volume change that depends upon local traction. Force balance at the cell surface arises from balancing the osmotic pressure difference with tension in the membrane and mechanical stress in the cortex. For a spherical cell:
| (6) |
where ΔP (Pa) is the hydrostatic pressure difference (positive when the internal pressure exceeds the external pressure), R (nm) is the radius of a spherical cell, S (pN/nm) is the tension in the membrane, σ is the active contractile stress (Pa), and h (nm) is the cortical layer thickness. An increase in membrane tension and mechanical stress in the cortex leads to an increase in myosin contraction tension via the Rho pathway. The authors model the probability of Rho activation as depending nonlinearly on the membrane tension, S, according to a Michaelis-Menten type function Λ(S). Then, the fraction M of myosin that is engaged can be calculated from:
| (7) |
| (8) |
| (9) |
where ρ is the fraction of activated Rho; M is the fraction of engaged myosin; respectively; a1 (s−1) and d1 (s−1) are activation and deactivation rates of Rho, respectively; a2 (s−1) and d2 (s−1) are the myosin assembly and disassembly rates of myosin, respectively; and Kmax (nN/μm) is the maximum contractile stress. Finally, in addition to active regulation of myosin contraction, cells can also regulate their internal osmotic pressure via water and ion fluxes, leading to cell-volume change governed by the following:
| (10) |
| (11) |
where ΔΠ (Pa) is the osmotic pressure difference; n (mol) is the total osmolytes in the cell; V (m3) and A (m2) are cell volume and surface area, respectively; J1 (mol/m2s) is the ion flux out of the cell through passive membrane channels; J2 (mol/m2s) is the ion flux through active ion pumps. The mechanosensitive ion channel model successfully predicts cell mechanosensing of osmotic shock for a variety of environmental perturbations. Most importantly, the model implicates Rho signaling as a mediator of volumetric responses to osmotic shock for the first time, thereby revealing a key step in the pathway for a cell to maintain a homeostatic level of volume and membrane tension.
4. Cellular mechanosensing of shear stress
Endothelial cells are subjected to two kinds of mechanical cues from their vascular microenvironment: shear stress from blood flow and tensile stretch from the cardiac pressure cycle [114]. The shearing can influence signal activation, cytoskeletal realignment and gene expression. For example, cells align SFs along the direction of the fluid flow [114].
A Rho GTPase signal/SF-adhesion coupling model was proposed by the Mogilner group to study cellular mechanosensing in response to fluid shear stress [115]. In the model, a cell’s actin cytoskeleton network transfers shear stress to cell adhesions on the basal surface of the cell, leading to changes in adhesion dynamics. Subsequently, the concentration of Rho decreases transiently, resulting in SF disassembly. The decrease in mechanical traction at the basal surface results in there being more focal complexes other than focal adhesions, i.e., the maturation of FAs is inhibited. The increasing number of focal complexes enhances the concentration of Rac, which in turn promotes the polarized assembly of focal complexes at the downstream edge of the cell along the direction of fluid flow. When the concentration of Rho increases back its baseline value, the SFs would assemble in new polarized direction and then promote the maturation of focal complexes, thus leading to a reorientation of SFs in response to shearing.
In the Mogilner group’s model, SFs exhibit the full range of dynamic behavior, including nucleation, shortening, merging, splitting and disappearing. A limitation of the model is that fluid shear stress is not explicitly introduced as an input; instead the model applies a transient decrease of the Rho concentration to represent shear stress loading on the cell. Therefore, a model which considers the interplay of fluid and the actin cytoskeleton is still a pressing need.
5. Cellular mechanosensing of external forces
Cellular responses to mechanical forces have been studied for decades, beginning with the invention of the first AFM-like (atomic force microscope) apparatus in the Elson lab in the 1970s [116] and the development of micropipette aspiration techniques. New techniques continue to be developed, including magnetic and optical tweezers and nanoparticles. Cells sense and respond to external loads by dynamic changes to the actin cytoskeleton and focal adhesions [17]. In this section we summarize a few key examples of insight gained from integrated experimental and theoretical efforts.
5.1 Multiscale cytoskeleton-myosin-membrane (MCMM) model
Although much focus has been placed on cell-adhesion complexes as the main mechanosensors, mechanical cues can also be transmitted by the cortical actomyosin cytoskeleton, a mechanosensitive system containing myosin II, actin cross-linkers and actin filaments. During micropipette aspiration, in which a portion of a cell membrane is pulled into a micropipette tip by a controlled aspiration, myosin and α-actinin accumulate within the cell at the pipette tip, and filamin accumulates within the neck of the cell drawn into the micropipette [117] (Fig. 3D). Robinson and colleagues proposed a multiscale cytoskeleton-myosin-membrane (MCMM) model to decipher the cortical cytoskeleton mechanosensing mechanism [117, 118]. In analogy to integrin-fibronectin bonds, the dynamics of myosin-actin bonds are described by a catch-bond model, leading to mechanosensitive (stress-dependent) accumulation of myosin II as applied force decreases the effective off-rate of myosin motors from the actin filaments deceases [119]:
| (12) |
where the koff (s−1) and are the off-rate in the presence and absence of force; f (pN) is the mechanical force acting on myosin; x (nm) is the bond length; kB is Boltzmann’s constant; and T is absolute temperature (kBT ~4.1 pN·nm at physiological temperature).
Myosin II is one of several proteins that can serve as the force transducer and actin cross-linker. α-actinin and filamin can also transmit force from the cell membrane to the actin cortex. Robinson and colleagues suggested that myosin and α-actinin are sensitive to dilation stress [117]. Specifically, assembly rates of the bipolar thick filament and α-actinin dimer can change with the sliding of parallel actin filaments during dilation. Filamin is sensitive to shear stress, with off-rates for filamin from actin filaments changing with the angle between actin filaments during shear deformation. These factors have been demonstrated through a multi-scale simulation, including coarse-grained molecular dynamics, force-dependent reaction-diffusion dynamics and a viscoelastic model for the mechanical properties of actin cytoskeleton-membrane complexes [117].
5.2 Cable network model and tensegrity model
A two-dimensional cable network model has been proposed by Schwarz and colleagues to study the effect of stress propagation inside the cell on the spatial distribution of focal adhesions [120] (Fig. 3C). The intracellular stress perturbations modeled are motivated by experiments in which the actin cytoskeleton of fibroblasts was perturbed by a microfabricated pillar. The actin cytoskeleton is modeled as a 2D elastic cable network, constituted by one of three different topologies: regular triangles, reinforced squares and a random network. In the cable network model, the cable (actin cytoskeleton) is stretchable like a linear spring, but does not show any mechanical resistance in compression. The cable network is fixed by adhesion points that are immobile at its rim. The model predicts that the focal adhesions in the front of the pillar decrease in size while those at the back increase in size, consistent with experimental observations.
The multi-structural 3D finite element (FE) model based on tensegrity of Lacroix evaluates cell responses to AFM indentation [121–123] (Fig. 3B). The model highlights the roles of cytoskeletal mechanical properties, including those of the actin cortex, stress fibers and microtubules. It also captures interactions between the cytoskeleton network, cell adhesions and the cytoplasm.
Zeng et al. proposed a 3D random network model of the actin cytoskeleton to study nuclear deformation under micropipette aspiration [124] (Fig. 3A). This model assumes that nuclear deformation arises mainly from direct transmission of force from the cell membrane to the nucleus through the cytoskeletal network, the logic being that mechanical stress will quickly dissipate when transmitted into a viscous or viscoelastic cytoplasm. The 3D random network model concludes that nuclear deformation and displacements within the cytosol increase with increasing concentration of actin filaments and are maximized by an optimal concentration of actin-binding proteins.
6. Cellular mechanosensing of matrix rigidity
Matrix rigidity plays an important role in cell migration, shape and differentiation [45]. For example, fibroblasts display a behavior known as “durotaxis” that directs their migration toward stiffer substrata [125]. Neurons develop more neurites on softer substrata [49]. MSC differentiation is affected by matrix rigidity (Fig. 5A) [26]. In this section, we describe models for cellular mechanosensing phenomena underlying these behaviors.
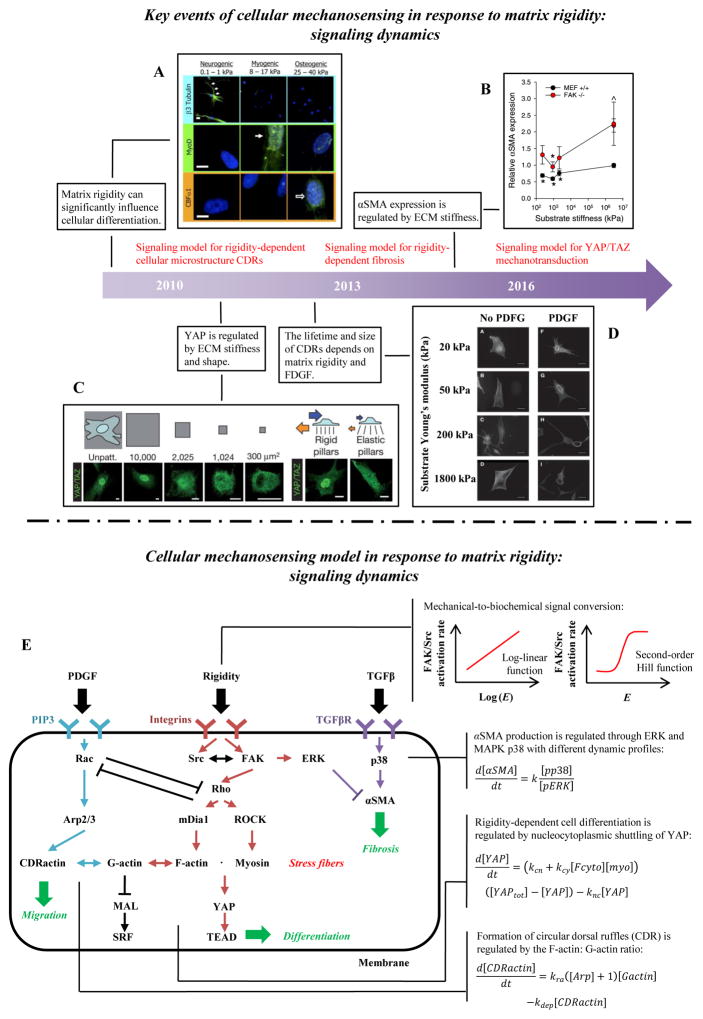
Figure 5. Cellular mechanosensing in response to matrix rigidity: signaling dynamics.
(A) The lineage of mesenchymal stem cells (MSCs) is strongly affected by the modulus of the substratum upon which they are cultured [26]. (B) The conversion of fibroblasts into myofibroblast is also regulated by external mechanical cues [73]. (C) YAP/TAZ nuclear translocation has been shown to be influenced by ECM stiffness and shape [145]. (D) FDGF can significantly increase the lifetime and size of CDRs on stiff substrata [14]. (E) Signaling pathway dynamic model for cell shape, migration and differentiation. The matrix rigidity is transduced into intracellular signals via adhesion molecules such as FAK and Src. Adhesion-mediated mechanosensing signals include Rho/ROCK/myosin II, Rho/mDia1/F-actin, SF/YAP/TEAD and SF/MAL/SRF. Other related signals related to soluble factors are TGFβ/p38/αSMA and PDGF/Rac/Arp2/3. A synergistic effect between the mechanical sensing and the chemical signals is predicted due in part to the interaction of Rac/Rho and ERK/p38.
6.1 Cell-adhesion dynamics at cell-ECM interface
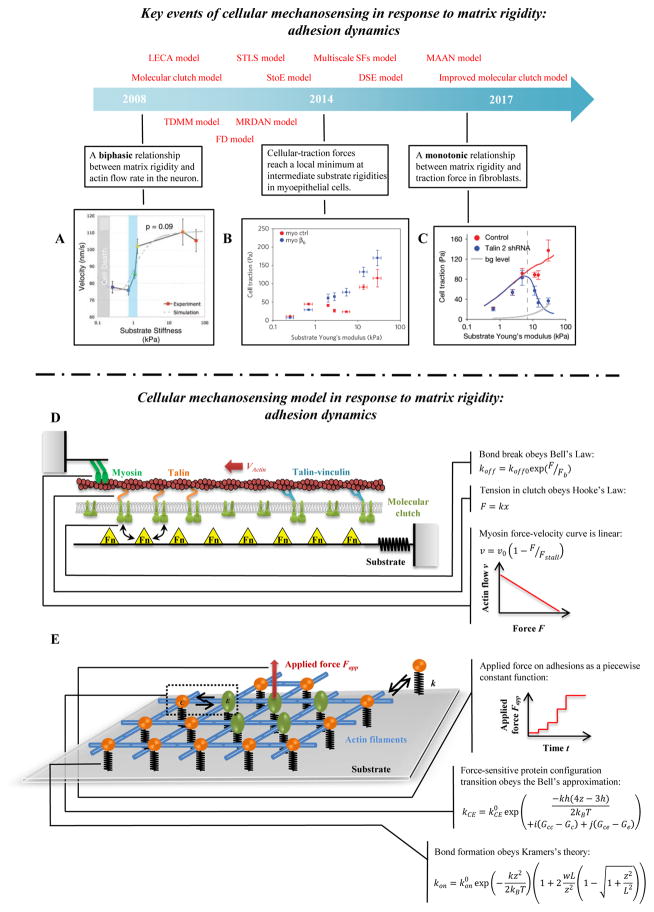
An effective cellular mechanosensitive system firstly needs mechanical sensing modes at the cell-ECM interface (e.g., cell-adhesions) that could transform microenvironmental mechanical properties (e.g., elasticity and viscoelasticity) to intracellular signals [33]. Cell adhesion sites are composed of a group of highly dynamic structures which can directly connect extracellular matrix to intracellular components (e.g., the actin cytoskeleton). The cell adhesions have two main roles in cellular mechanosensing: stress (strain) propagation and chemical signal activation. Cells sense the stress (strain) of the external matrix by forming a dynamic mechanical bond system (e.g., slip/catch bond, sliding-rebinding/allosteric catch bond) involving hundreds of known adhesion proteins, such as integrin, talin and vinculin [126]. It has been shown that talin is a “force buffer”, with cryptic vinculin binding sites in talin revealed as the molecule unfolds over a force range of 5–10 pN; this is believed to play an important role in rigidity sensing under physiological conditions in vivo [127]. Interestingly, cells can exhibit distinct behaviors for rigidity sensing because of slight differences in the talin unfolding threshold between talin isoforms (talin 1 and talin 2) [128]. Despite the complexity of focal adhesion components and dynamics, much of the mechanosensitivity of focal adhesions has been well described by the mathematical models based upon the ‘molecular clutch’ hypothesis of Mitchison and Kirschner [129], which postulates that engagement of a molecular clutch, now recognized to be the elements of focal adhesions [130], enables transmission of forces from the actin cytoskeleton to the ECM. This engagement reduces the retrograde flow rate of actin filaments, and downregulates both protrusion of the leading edge and activation of adhesion-mediated downstream signals.
Recently, integrin clusters have been proposed as a critical functional module for matrix rigidity sensing [30]. Sheetz et al. show that cell adhesions are loose aggregates of integrin clusters. These tight clusters of integrins each have a size of ~100 nm, and is each composed of ~20–50 molecules [131]. Interestingly, it has been concluded that clustered, but not individually distributed, plasma membrane proteins (e.g., Ras nano-clusters) can recruit and activate their downstream signals; this might be related to higher local concentration of reactants and associated higher probability of molecular collisions [132]. Thus, a single integrin cluster may act as a platform where chemical signals (e.g., phosphatase and kinase) are activated sequentially. Activation of FAK (e.g., phosphorylation of focal adhesion kinase on Y397) depends on integrin clustering and only happens inside the integrin clusters [133, 134]. Thus, a focal adhesion including many integrin clusters can be regarded as a highly dynamic mechanosensitive system capable of responding to alterations of matrix rigidity.
In spite of the large number of experimental findings, the steps and mechanisms of adhesion-dependent mechanosensing remain elusive. Computational models have been developed to simulate the protein clustering on a two-dimensional plane [135]. These models assume that protein clustering is mainly influenced by (1) confined diffusion resulting from special membrane structures, such as lipid raft or the cortical cytoskeleton [136, 137], and (2) enhanced activation rate of integrin by talin [138]. However, the effects of structure on integrin clustering are still unclear. It is also still unclear whether assembly-disassembly of integrin clusters is influenced by matrix rigidity, and if so, whether some quantitative features of matrix rigidity are related to integrin organization or intracellular signal activity through these integrin clusters.
6.2 Myosin-filament system in the cytoplasm
Mechanical cues sensed by cells at the cell-ECM interface have to be transduced several microns to the nucleus to regulate gene expression [37]. Two important cellular components respond to the mechanical cues at cell-ECM interface: the myosin-filament system (a structural path), and cytoplasmic, mechanically-regulated bio-signaling networks (a soluble path). The myosin-filament system can be classified two categories: actomyosin-based sarcomere-like contractile units at the cell edge and SFs which directly connect the cellular membrane to the cell nuclear membrane. The contractile units test matrix rigidity by pulling integrin clusters and reinforcing links between the actin cytoskeleton and integrin clusters via vinculin or α-actinin [30]. The SFs test matrix rigidity via an actin cap in cells which are cultured on stiff substrata. The actin cap, formed above the nucleus, compresses and tenses the nucleus, deforming the nucleus sufficiently to affect chromatin packing [139]. The arrangement of ventral SFs at the bottom of cells also depends on matrix rigidity. For example, SFs display a random arrangement on soft substrata, but align on stiff substrate [72].
In contrast to myosin-filament system, the mechanically-regulated bio-signaling network works primarily via soluble biomolecules associated with mechanical cues, such as FAK, Src and Rho whose activation rates are enhanced on stiff substrata [140]. The corresponding downstream signaling events such as the FAK-RhoA-ROCK cascade are produced sequentially, and likely crosstalk with other signaling pathways such as the TGFβ cascade and Hippo cascade to regulate nuclear events [43].
Several differences exist between these mechanotransduction pathways. The first is signaling directionality: biochemical signals in network dynamic models depend on signal diffusion while mechanical signals in myosin-filaments system depend on physical displacement. Another difference is the relationship between signaling strength and transmission distance: the strength of biochemical signals decreases with distance at a rate of 1/distance2, while mechanical signals transmitted via the cytoskeleton do not lose their intensity with distance. Instead, transduction of these latter signals depends on the mechanical properties cytoskeleton.
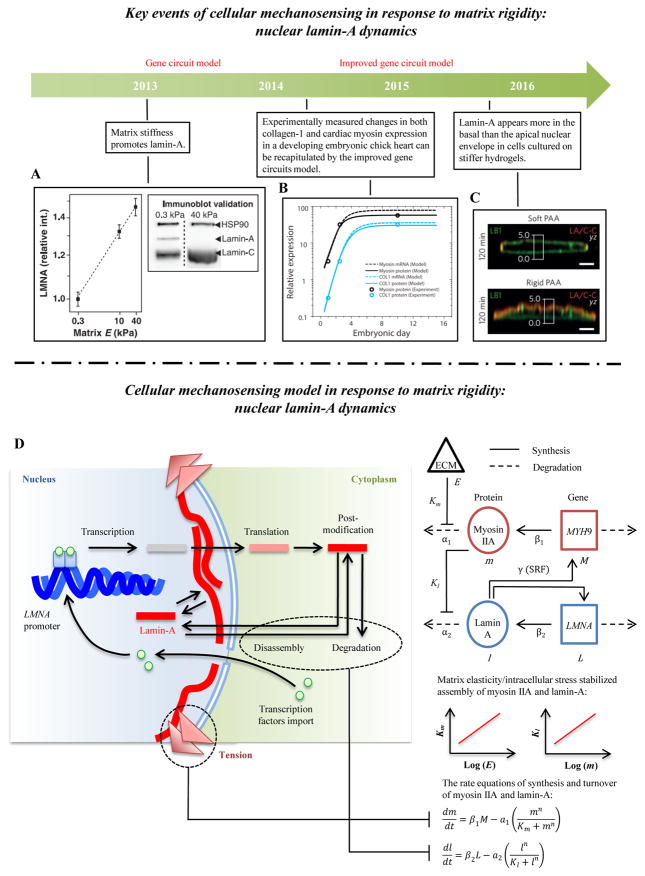
6.3 Matrix rigidity sensing by nuclear lamin-A
Nuclear structures, such as nuclear lamina, are mechanosensitive [11, 141] (Fig. 6A, C). The level of nuclear lamin-A follows a power-law scaling with matrix rigidity, and the rates of phosphorylation (turnover) of lamin-A are inversely related to matrix rigidity [142]. From the viewpoint of dynamics, matrix rigidity promotes myosin-mediated cellular contraction formation and therefore enhances tension in nuclear lamin-A, thus inhibiting lamin-A disassociation and stiffening the nucleus. The level and conformation of nuclear lamin-A also regulates the location of proteins involved in gene expression (e.g., nucleocytoplasmic shuttling of RARG and YAP) and thus lamin-A provides a potential mechano-chemical mechanism to explain the dependence of stem cell differentiation on substrata of varying rigidity. However, some questions still need to be addressed. For example, why and how does tension inhibit lamina degradation and what regulates the rate constants? The answers to these questions are important and require integrated experiments and models.
Figure 6. Cellular mechanosensing in response to matrix rigidity: nucleus lamin-A dynamics.
(A) Lamin-A concentration increases with increasing matrix stiffness [11]. (B) The levels of collagen-1 and cardiac myosin increase first and then reach a maximum value during the development of embryonic chick hearts [170]. (C) Lamin-A is found more in the basal than the apical nuclear envelope of fibroblasts adhering to stiff (but not soft) polyacrylamide hydrogels [206]. (D) Schematic of the gene circuit model predicting how matrix rigidity regulates levels of nuclear lamin-A. Stiffer matrices enhance cellular contraction and increase the tension in nuclear lamin layer, thereby decreasing the lamin-A degradation rate. Tension acting on the nucleus by stress fibers can also influence transcription factors associated with nucleoplasm shuttling, which can further regulate lamin-A expression.
6.4 Matrix-rigidity-dependent intracellular signaling pathways
Matrix rigidity can significantly influence cellular differentiation, but the details of this regulation remain elusive [26] and are likely complex and multi-scale. Several studies focused on the mechanosensitive role of nucleocytoplasmic shuttling of transcriptional regulators (e.g., YAP/TAZ, MAL/MRTF). For instance, increasing matrix rigidity or exerting a static stretch has been found to promote YAP/TAZ or MAL/MRTF nuclear translocation and its downstream transcription activity [143]. Actin cytoskeleton remodeling also plays an important role in this mechanosensing process. For example, the entry of MAL/MRTF into the nucleus to interact with SRF transcription factor is regulated by the ratio of G-actin and F-actin, because G-actin can bind to MAL/MRTF to prevent it from binding to SRF [144]. Although YAP/TAZ has behavior similar to MAL/MRTF (e.g., more YAP/TAZ in the nuclei of cells on stiffer substrata), their nucleocytoplasmic shuttling is regulated by distinct mechanisms that appear to be linked to cellular contraction caused by SFs [145] (Fig. 5C). Some recent studies investigate how crosstalk between chemical signaling pathways regulated by chemical factors such as growth factors like TGFβ and mechanotransduction pathways regulated by matrix rigidity affect cellular differentiation [146]. Although the details about individual pathway are well known, little is known about their interactions. Elucidating the mechanisms of conversion of mechanical signals to biochemical signals via adhesion molecules is a fundamental question of mechanobiology and offers many opportunities to understand underlying mechanisms through mathematical models.
6.5 Mathematical models
6.5.1 Uniaxial molecular clutch model
The uniaxial molecular clutch model based upon the molecular clutch hypothesis was first developed by Chan & Odde [147–149] (Fig. 4D). In this model, stretchable adhesion proteins and a deformable substrate are modeled as a spring system loaded by mechanical traction from the flow of actin filaments. Three mechanical equations describe the system mathematically, accounting for equilibrium of actin cytoskeleton contraction (actomyosin sliding), stretching of focal adhesion proteins, and deformation of the substrate. These relate to the effective dissociation rates of the mechanical bonds (i.e., the weakest links in an adhesion) between the actin cytoskeleton and ECM molecules, which are modeled by the Bell model:
| (13) |
where koff (s−1) is the effective dissociation rate of the weakest bond in the cell-ECM interaction (e.g., an integrin-fibronectin bond or an actin-talin bond, see reference [126] for more details), is the intrinsic dissociation rate, F (pN) is the tension on the mechanical bond, and Fb (pN) is the characteristic bond breakage force. The contractile force originating from elongation of adhesion proteins and the substrate is represented by Hooke’s Law:
| (14) |
where k (pN/nm) is the stiffness of adhesion proteins or substrate and δx (nm) is the elongation of adhesion proteins or substrate. A linear force-velocity relationship is used to relate the traction force F and the actin flow rate:
| (15) |
where v (nm/s) and v0 (nm/s) are the effective actin flow rate and its force-free value, respectively, and Fstall (pN) is the stall force of myosin motors.
Figure 4. Cellular mechanosensing in response to matrix rigidity: adhesion dynamics.
(A) Neurons have higher actin flow rate on stiffer substrata [147]. (B–C) The distinct actin flow/matrix rigidity relationships in breast myoepithelial cells and fibroblasts [10, 25]. (D) Schematic of the uniaxial molecular clutch model. Actin polymerization and depolymerization at the tips of filopodia are coupled to the substrate through molecular clutches, and these molecular clutches resist the retrograde actin flow driven by myosin motors and membrane fluctuations. With increasing tension, the following transformations of molecular clutches are possible: talin unfolding and refolding, clutch reinforcement by vinculin binding, signal activation from clutch reconfiguration, and weakest-link rupture. (E) Schematic of the 2D molecular-mechanical adhesion model. Each molecule may bind to the substrate through a flexible spring, and may transition from a circular to an elliptical state under mechanical loading.
The Chan-Odde model predicts a relationship between actin flow rate and matrix rigidity that is biphasic, consistent with experimental observations in filopodia in neuronal growth cones [147] (Fig. 4A). The model shows two regimes: a “frictional slippage” regime with low traction force on stiff substrate, and a “load-and -fail” regime with higher traction force on soft substrata. However, the model predictions are not consistent with observations of monotonic actin flow/matrix rigidity relationship in fibroblasts [10] (Fig. 4B–C). To address this, the Bangasser-Odde motor-clutch model proposes the concept of “optimum stiffness” [148]. This model predicts a monotonic relationship between retrograde flow and stiffness appears over experimentally accessible values mainly because of the shift of optimal stiffness, but that the relationship essentially remains biphasic over a wide range of stiffnesses. Recently, Roca-Cusachs and colleagues incorporated the molecular behaviors of talin and vinculin into molecular clutch model, which succeeded in predicting how integrin-mediated actin flow relates to matrix rigidity in fibroblasts [10]. In their improved molecular clutch model, talin (acting as a clutch) can directly bind with actin and integrin to mediate force transmission between the actin cytoskeleton and ECM. Importantly, tension in talin can expose cryptic vinculin binding sites and lead to vinculin binding, thus resulting in adhesion reinforcement. Besides talin and vinculin dynamics, distinct bond dynamics of different integrin types have an important effect on the substrate stiffness/actin flow relationship in breast myoepithelial cells [25]. For example, αvβ6 integrin (expressed in cancer cells) has higher affinity with fibronectin than α5β1 (expressed constitutively). Therefore, a molecular clutch model with force-dependent integrin recruitment predicts an additional third reinforcement regime, i.e., the traction force will increase with substrate stiffness even on stiff substrata.
These two sets of models were unified under a single set of governing principles by Xu and co-workers in an integrated molecular clutch model that accounted for (1) the kinetics of adaptor proteins (e.g., the talin exchange rate) and (2) the fact that the “weakest link” in the adhesion dynamics can shift under certain circumstances from the actin-integrin bond to the integrin-fibronectin bond [126]. These two factors are known to play an important role in adhesion dynamics and mechanosensing [150]. The integrated molecular clutch model predicts that both the shift of weakest link location and the development of integrin clustering affect the actin flow/matrix rigidity relationship, cell spreading, and migration, and provides a mechanism by which different types of cells can differ in their mechanosensing.
Later, Mooney and co-workers proposed a viscoelastic molecular clutch model which predicts that cell spreading area on soft, viscoelastically relaxing substrata is similar in magnitude to that of cells cultured on stiffer substrata [61], indicating that both substrate stress relaxation and substrate stiffness can influence cell behaviors such as cell spreading, cell traction, and YAP localization. Gardel et al. also find that the spatial distribution of retrograde flow and traction force is biphasic rather than monotonic at the cell leading edge on the substrata of certain stiffness [151]. An adhesion clutch model was proposed by Mogilner and co-workers to explain this [152]. Taken together, these models and observations suggest that there are still many mechanisms of cellular mechanosensing that need to be further explored through both experimental and modeling approaches.
6.5.2 Two-dimensional molecular mechanical (TDMM) model
The molecular clutch model predicts cellular rigidity-sensing due to (1) a cell adhesion layer that is more easily deformed and strengthened on a stiff substrate, and (2) concentric actin flow that is inhibited by such adhesion. However, some experimental observations cannot be explained by the molecular clutch model, including substrate rigidity-mediated anisotropic growth of focal adhesions [15] and lateral interconnection and clustering of adhesion proteins [76]. To solve these issues, a two-dimensional molecular mechanical (TDMM) model was proposed by Walcott & Sun for describing rigidity-sensitive adhesion nucleation, growth and decay [153] (Fig. 4E). In the TDMM model, integrin molecules are placed in a two-dimensional cell membrane plane. A single integrin molecule can connect to four neighboring integrin molecules by the actin cytoskeleton. Below this plane, each adhesion site is attached to a substratum that is represented by a linear spring of stiffness k (pN/nm), and above this plane, a force Fapp can be applied. A typical simulation begins with such a force applied to a single integrin to initiate adhesion growth. The model predicts that, although substrate rigidity influences whether an adhesion is initially formed, the adhesion lifetime is independent of substrate rigidity. To make the model mechanosensitive to matrix rigidity, two important factors are incorporated into the TDMM model: an adhesion molecule force-dependent state transition, and a strain-dependent binding to matrix.
The TDMM model idealizes an adhesion site as being comprised of adhesion molecules that shift between a resting “circle” state and a stretched “elliptical” state when loaded with sufficient force. The kinetics is approximated using a Bell model:
| (16) |
where kCE (s−1) is the circle-to-ellipse transition rate constant; h (nm) is the extension of the circle associated with the transition to an ellipse; k (pN/nm) is the effective stiffness of a linkage to the substratum; kBT (pN·nm) is the product of absolute temperature and Boltzmann’s constant; i is the number of circular state neighbors that a bond has; j is the number of elliptical state neighbors that a bond has; Gc (kBT) and Ge (kBT) are the normalized free energies of the ellipse and circle bonds of the transition state, respectively; Gcc (kBT) and Gce (kBT) are the free energy of circle-circle binding and circle-ellipse binding, respectively. Note that kCE0 (s−1) is the reaction rate in a reference state when z = 3h/4 and the molecule has no neighbors.
Another important factor, strain-dependent binding, is described using Kramers’s theory:
| (17) |
where kon and kon0 (s−1) are the effective and baseline binding rates of the circle state, w (nm) is the width of binding sites, and L (nm) is the offset of binding sites. This equation indicates that varying the ECM rigidity will change the probability of forming molecular-ECM bonds. More compliant ECM undergoes larger deformation and results in greater equilibrium distances between adhesion molecules and ECM, which downregulates bond formation; stiffer ECM undergoes smaller deformation and results in shorter equilibrium distances, which upregulates bond formation. Thus, matrix rigidity could upregulate the adhesion growth by strain-dependent bond binding and stress-dependent bond unbinding.
6.5.3 Linear elastic chain adhesion (LECA) model
Although the TDMM model can explain the relationship between the focal adhesion size or number and matrix rigidity, anisotropic growth and shrinkage of focal adhesions in the direction of cell contraction can be explained by neither the TDMM model nor the molecular clutch model [154, 155]. The one-dimensional linear elastic chain adhesion (LECA) model proposed by Nicolas and Safran identifies the physics underlying this behavior [156]. In their model, local contraction force originating from stress fibers will deform the adhesion layer leading to compression at the leading edge and expansion at the trailing edge. Adhesions are modeled as thin films whose stress-induced deformation is modeled by an infinite, thin plate using standard continuum elasticity theory. Gradients of strain in a single focal adhesion lead to different local biochemical signaling that will influence the local adhesion protein density. The spatially-varying adhesion protein density leads to structural changes that produce the directional, anisotropic growth of adhesions. Adhesion proteins (thin films), for simplicity, which are modeled as chains of particles connected by linear elastic springs, can sense the elastic properties of the ECM through an interaction represented by a sinusoidal potential:
| (18) |
where km (pN/nm) is the stiffness of the substrate; a (nm) is the equilibrium distance between the particles, and x (nm) is the current distance between the particles. The particle-spring system finally reaches mechanical equilibrium when pulled by the cellular contractile force. The LECA model not only accounts for the anisotropic growth and shrinkage of focal adhesions in the direction of force, but also concludes that adhesions grow only within a range of force. Interestingly, in LECA model, adhesions are pulled by a shear force which is ignored in the TDMM model. Therefore, the direction of traction force should play a key role in adhesion-mediated mechanosensing. Recently, some studies show that talin orients at ~15° relative to the plasma membrane [78]. This conclusion may constitute the theoretical basis for future mathematical models. Later, an improved two-layer adhesion model also proposed by the Safran group concludes that adhesions will finally reach a finite size which is proportional to the matrix rigidity [157, 158].
6.5.4 Stochastic-elasticity (StoE) model
A stochastic-elasticity (StoE) model proposed by Gao and colleagues describes the dynamics of adhesion clusters between substrate and cell (both modeled as elastic media) subjected to a perpendicular/inclined tensile load [159, 160]. In the StoE model, stochastic dynamic simulation of molecular bonds and continuum elastic predictions of traction distributions on the surface are integrated into a single modeling framework. A scaling law for the traction distribution within the adhesion domains calculated from classical contact mechanics solutions shows that stress at the adhesion edge increases with increasing adhesion size, bond density and bond stiffness, but deceases with increasing substrate rigidity and cell rigidity (e.g., cytoskeletal stiffening). According to this scaling law, bonds near the adhesion edge are subjected to larger forces, resulting in a larger dissociation rate as described by the Bell model [161]. The binding on-rate is attenuated in this region according to:
| (19) |
where kB T is the thermal energy; kon (s−1) is intrinsical on-rate when the receptor-ligand pairs are within a binding radius lbind (nm); Z is the partition function for a receptor confined in a harmonic potential between zero and the current degree of bond separation δ (nm); and kLR (pN/nm) is the linear spring stiffness of the bond. From the perspective of the model, rupture of adhesion clusters is mainly caused by stress concentrations near the adhesion edge, which increase with increasing adhesion size; increasing matrix rigidity can alleviate these stress concentrations and thereby stabilize adhesions. Using reasonable parameters, the StoE model predicts, correctly, that the size of stable adhesions lies in the range of a few hundred nanometers to a few micrometers.
6.5.5 Adhesion clustering model
As described in section 6.1, integrin clusters play an important role in cellular mechanosensing. Peng et al. developed a Monte Carlo simulation of matrix-rigidity-dependent adhesion clustering and nucleation [162]. The model simulates three chemical reactions: activation/deactivation of integrins, integrin-substrate binding, and cross-linking between integrins. Integrin is modeled as being activated by thermal undulations of the local cell membrane, and all chemical factors such as Mn2+, talin and ECM are ignored. The rationale of the authors is that these thermal undulations reduce the matrix-rigidity-dependent activation energy barrier of integrin, which helps cells sense the matrix rigidity in the same way that cell contraction tests substrate rigidity by pulling integrin-ECM links. The matrix-rigidity-dependent mechanical energy barrier Em can be denoted as:
| (20) |
where fb (pN) is the thermal fluctuation force to activate the integrin; le (nm) and lb (nm) are the length of bent/extended integrin, respectively; E (pN/nm2) and v are the Young’s modulus and Poisson’s ratio; and a (nm) is the radius of a single integrin molecule. The model suggests that increasing matrix rigidity and integrin density both can increase the integrin cluster size.
Several additional models have added insight to these phenomena. The mechanics of the glycocalyx that lies between the membrane and ECM can also induce integrin clustering, as confirmed by experimental observations interpreted through the spatial-temporal lattice spring (STLS) model [163, 164]. A diffusion-dependent stochastic-elastic (StoE) model of molecular bond clustering between two elastic media, proposed by He and colleagues, also suggests that matrix rigidity can promote the formation of stable bond clusters [165]. The matrix-adhesion-actomyosin-nucleus (MAAN) model of Shenoy and colleagues suggests that a stiffer substrate or nucleus could also promote adhesion clustering [166].
6.5.6 Multi-scale stress fiber model
A mechanical model incorporating adhesion complexes, myosin II, actin filaments and a substratum proposed by Sun and colleagues [72] predicts rigidity-sensing that is determined by three interacting mechanical elements: adhesion complexes, myosin and actin filaments. Adhesion complexes provide a matrix surface rigidity-dependent viscous drag that increases with increasing matrix rigidity, suggesting that adhesion complexes will move faster and bear less force on softer matrices than on stiff matrices. Then, the drag force can be written as:
| (21) |
where Nac is the number of sliding molecules; is the series protein stiffness of link between the matrix and actin cytoskeleton, R (nm2) is the adhesion area; E (pN/nm) is the matrix rigidity; k (pN/nm) is the protein stiffness of adhesion and matrix surface; ka (s−1) is the overall attachment rate; is the off-rate at zero strain; and v (nm/s) is the sliding rate. Myosin motors provide a steady-state force which obeys the Hill force-velocity relationship, suggesting that myosins generate smaller force when adhesion complexes slide faster. The Hill model can be written as:
| (22) |
where Fmyo (pN) is the myosin stall force; F0 (pN) is the drag force experienced by myosin; v0 (nm/s) and v (nm/s) are the sliding rates of actin filaments without and with drag force, respectively; and c is free parameter. Actin filaments in their model are modeled as rigid rods anchored or connected by the crosslinking protein α-actinin, which forms rigid nodes. As force is applied, the actin-filament network is assumed to stay in mechanical equilibrium. Single actin filament experiences three different types of forces/torques and the equations as follows:
| (23) |
| (24) |
where is the contractile force on actin filament i; Fij (pN) and are the friction and torque about the center of mass applied on filament i by relative sliding of filament j, respectively. The model concludes that a random actin filament network would bundle together and orient along force direction (contraction force of SFs) on stiff matrix, and the authors propose this restructuring as an effective cellular mechanosensing mechanism. Additionally, adhesion complexes and myosin motors can participate in mechanosensing: adhesion complexes slide faster and myosin generates a smaller force on softer substrata. The model of Sun et al. thus provides a simple, physically based model of cellular mechanosensing, which offers a different and novel view to traditional biochemical models.
In addition to formation of SFs, the alignment of SFs on substrata of varying stiffness is an important phenomenon whose underlying mechanisms are still unclear. SFs are known to polarize by aligning along the long axis of cells. Zemel et al. propose a force-dipole (FD) model to address this question, which suggests that such anisotropic alignment of SFs depends non-monotonically on matrix rigidity [167]. These findings provide useful insight into stress-fiber-based cellular mechanosensing of matrix rigidity.
6.5.7 Nucleus polarization and alignment model
A multiple-cell model proposed to study the mechanism of matrix rigidity-induced nuclear alignment and polarization [168, 169] predicts a critical role of perturbations to the magnitude and distribution of in-plane stresses due to cell-cell interactions. Structurally, the nuclear envelope integrates with the cytoskeleton through the lamin network, and the cytoskeleton links to the ECM or neighboring cells through adhesion molecules. Hence, the lamin network and possibly the nucleus are exposed to forces transmitted from extracellular microenvironment via the cytoskeleton.
Cells in patterned monolayers reorient and polarize along the direction of the maximum principal stress, accompanied by the reorientation of actin cytoskeleton. The actin cytoskeleton is believed to provide structural support and geometric shape to cells via tensile stress, but not to resist shear stress. Shear stress in the cell might thus induce cytoskeletal reorientation into the direction of principal stress, where the shear stress is equal to zero. The mechanical stresses within the cytoskeleton can then be propagated to the nucleus, resulting in nuclear reorientation and polarization into the direction of the maximum principal stress. From this vantage, in-plane stresses are the driving force of collective behaviors of cells and their subcellular structures, and provide a mechanism for how changes of matrix rigidity influence the nuclear behaviors.
6.5.8 Gene circuit model
Cells form more stress fibers on stiffer substrata, and hence apply greater tension on their nuclear lamina. This increased tension on the nuclear lamina could suppress the affinity of enzyme initiating phosphorylation and degradation of lamin-A filaments, leading to a higher levels of lamin-A and thus a stiffer nucleus. To investigate the effect of matrix rigidity on nuclear structural changes (e.g., lamin-A concentration), a gene circuit model was proposed by Discher and colleagues [170] (Fig. 6D). The gene circuit model contains a series of rate equations including synthesis (βi) and turnover (αi) rates of myosin II and filamin-A,
| (25) |
| (26) |
where m and M are concentrations of myosin II and its mRNA (MYHN9), respectively; l and L are levels of lamin-A and its mRNA (LMNA) respectively; β1 (s−1) and β2 (s−1) are first-order mRNA translational rates for myosin II and filamin-A, respectively; a1 (s−1) and a2 (s−1) are maximal protein degradation rates for myosin II and filamin-A, respectively; Km and Kl are Michaelis constant of myosin II and lamin-A; and n is a cooperativity coefficient. The novelty of this model is that cell and matrix mechanics are incorporated into the reaction rate constant. For example, protein turnover rates of myosin II and lamin-A are coupled to matrix rigidity and myosin-generated stress, respectively, by log-linear functions obtained by fitting experimental data. These phenomenological log-linear functions simulate the increase of cytosolic tension on stiff substrata and the inhibition of lamin-A degradation under high cytosolic tension. The overall rate of degradation is represented by Michaelis-Menten kinetics. Two relationships between myosin II (m) and myosin structural gene (M) and between lamin-A (l) and lamin structural gene (L) could be obtained by solving the rate equations (25–26). The model successfully predicts changes in collagen and cardiac myosin expression in a developing embryonic chick heart. The gene circuit model thus holds potential for predicting tissue-level and long-time biological mechanosensing (Fig. 6B). However, its foundation, including whether tension could inhibit lamin-A degradation and the appropriate rate constants, are still unclear.
6.5.9 Signaling model of cellular differentiation
A rich literature of mathematical models of mechanochemical conversion provides quantitative insight into interactions of actin cytoskeletal remodeling and nucleocytoplasmic shuttling of transcription factors. The integrated signaling pathway dynamic model of Zaman and colleagues includes substrate rigidity, YAP/MAL (Yes-associated protein/megakaryoblastic leukemia) dynamics, and actin cytoskeleton remodeling [171]. The model not only reproduces experimental observations of the regulation of location of YAP by tensioned cytosolic F-actin or SFs, but also provides a number of new predictions. These include a synergistic effect between chemo- and mechano-transduction by multilevel crosstalk between the YAP/TAZ (transcriptional coactivator with PDZ-binding motif) and Hippo signaling pathway networks. The inputs of the model are ECM rigidity and concentrations of LATS (large tumor suppressor), while the output is the nuclear translocation of the transcriptional molecule YAP/TAZ. The authors use a second-order Hill function to describe the relationship of FAK activity and ECM rigidity (Fig. 5E). The influence of SFs and RhoA on YAP/TAZ nuclear translocation is modeled as follows:
| (27) |
where [YAP], [YAPtot], [Fcyto] and [myo] are concentrations of YAP in nucleus, YAP in nucleus and cytoplasm, tensional F-actin, and activated myosin, respectively; kcn (s−1) is the rate of YAP translocation from the cytoplasm to the nucleus with no active cytoplasmic F-actin and myosin; kcy (s−1) is the change of YAP nuclear translocation rate due to SFs or tensional cytoplasmic F-actin; knc (s−1) is the rate of YAP translocation from the nucleus to the cytoplasm. Note that the tensional cytoplasmic F-actin filaments are characterized by the product of the cytoplasmic F-actin concentration and active myosin concentration, i.e., [Fcyto] × [myo]. Although early literature questioned whether SF structures exist in 3D culture exist [172], later literature identified these [85, 87]. Nevertheless, even in the early literature more F-actin was observed in cells in rigid ECMs, supporting the idea of tensional cytoplasmic F-actin filaments [173].
MAL in the cytoplasm has been shown to bind with G-actin, which inhibits its ability to enter the nucleus. MAL is associated with SRF (serum response factor) and forms the active SRF/MAL complex,
| (28) |
where [MAL], [MALtot] and [Gactin] are the concentrations of MAL in nucleus, total MAL in the cell, and total G-actin in the cytoplasm, respectively; kcnm (s−1) is the rate of MAL translocation from the cytoskeleton to the nucleus; kmg (s−1) represents the decrease in this effect due to cytoplasm MAL binding with G-actin and being thus retained in the cytoplasm (an inhibition effect described as a second-order Hill function); and kncm (s−1) is the rate of MAL translocation from the nucleus to the cytoplasm. Overall, their model provides a platform to study cell-ECM and cell-cell interactions, including the conversion of mechanical cues to biochemical signals and crosstalk among signaling pathway networks. These include mechanical-cue-dependent YAP/TAZ signals and chemical-cue-dependent LATS and Smad signals [143].
6.5.10 Signaling model of cellular remodeling
Cell microstructure influences cellular differentiation. A mathematical model of circular dorsal ruffles (CDRs) (i.e., actin-rich ringlike structures that form on the dorsal surface of growth factor stimulated cells) proposed by Chiam and colleagues suggests that the lifetime and size of CDRs depend on matrix rigidity via Rac-Rho antagonism [14] (Fig. 5D). This model has two inputs: matrix rigidity that enters the model via increasing concentration of activated FAK (a logarithmic function of matrix rigidity), and PDGF (platelet-derived growth factor) stimulation that activates Arp2/3 through activation of Rac to form CDRs. These chemo/mechanotransduction signaling networks can be written in the form of mass action and Michaelis-Menten kinetics to form a set of coupled ordinary differential equations, including the following equation for the concentration of CDR-actin:
| (29) |
where [CDRactin] and [Arp] are the concentrations of CDR-actin and Arp2/3 complexes; kra (s−1) is the rate of CDR-actin formation without Arp2/3; and kdep (s−1) is the rate of CDR-actin dissociation. The mathematical model also contains a set of coupled partial differential equations which represent the diffusion of various proteins between different simulation compartments.
6.5.11 Signaling model of fibrosis
Conversion of fibroblasts into myofibroblasts is also regulated by matrix rigidity (Fig. 5B). An ODE-based model was developed to analyze the mechanisms of mechanical-regulation of αSMA production [73]. The model has two inputs: growth factor signals (e.g., TGF-β and FGF) that activate the downstream signals (e.g., p38 and ERK), and matrix rigidity. Matrix rigidity is incorporated into the model via the levels of intracellular kinases (e.g., Src and FAK), which scale with the log of matrix rigidity. The output is αSMA production,
| (30) |
where [αSMA], [pp38] and [pERK] are the concentrations of αSMA, pp38 and pERK, respectively; k (s−1) is the rate of pp38 promotion of αSMA. This model suggests that αSMA production is enhanced by p38 and Src and inhibited by ERK.
Modeling these behaviors is challenging because of numerous interactions between different types of proteins and challenges obtaining quantitative data for intracellular chemical reaction kinetics. Computational models of mechanical-cue-related signaling networks have been used in many biological systems to clarify complex interactions, especially when intracellular protein activation states are difficult to quantify.
7. Cellular mechanosensing in response to various micropatterned geometries and microchannels
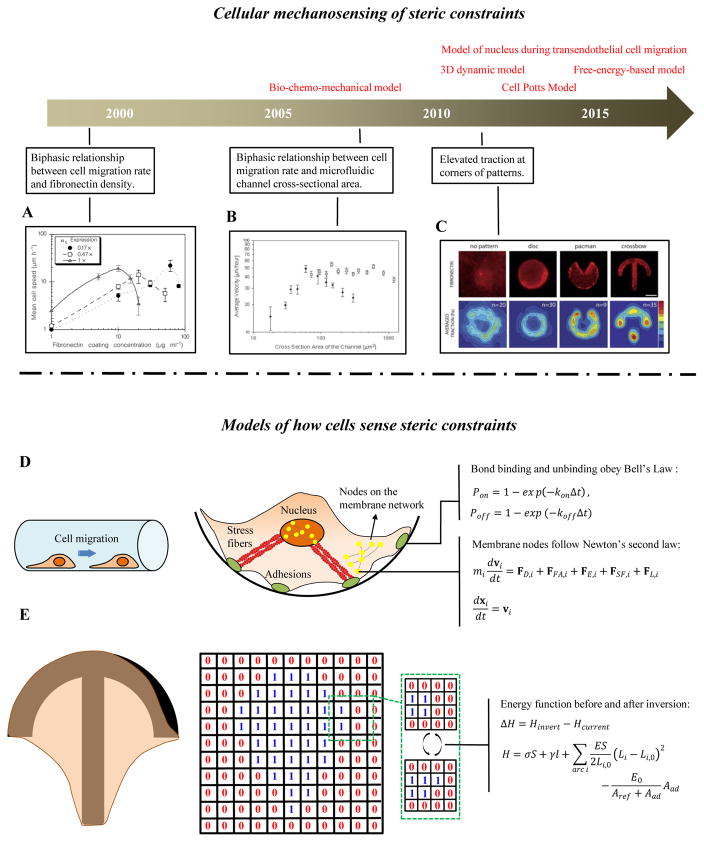
Cell migration on 2D substrata is influenced by ligand density and integrin-fibronectin binding affinity. For example, a biphasic relationship exists between cell migration rate and fibronectin density: cell migration rate is maximal at a particular fibronectin density [174] (Fig. 7A). Interestingly, in cell migration experiments conducted on 3D microfluidic platforms, a biphasic relationship also exists between cell migration rate and a microchannel’s cross-sectional area [175] (Fig. 7B). Cell spreading experiments conducted on micropatterned geometries including disk, “Pac-Man” and “crossbow” shapes show that strong tractions appear at the corners of the patterns [176] (Fig. 7C).
Figure 7. Cellular mechanosensing of steric constraints.
(A) A biphasic relationship exists between cell migration rate and fibronectin density: cell migration rate is maximal at a particular fibronectin density) [174]. (B) A biphasic relationship exists between cell migration rate the cross-sectional are of a microfluidic channel [175]. (C) Tractions are elevated at the corners of cell spread on micropatterned geometries [176]. (D) A 3D integrated dynamic model of cell migration on a curved substrate. The plasma and nuclear membranes are modeled as elastic meshes that interact with the ECM through integrin-fibronectin bonds, and with each other through actin stress fibers. (E) A cellular Potts model, in which cells which are modeled as a collection of spins, and overall energy during cell spreading is evaluated as cells probe possible expansion onto nodes of a regular lattice.
7.1 A three-dimension dynamic model of cell migration and spreading
The 3D integrated cell migration model of Asada and colleagues studies cellular mechanosensing behaviors such as migration of cells plated in different micropatterned geometries and microchannels [177, 178] (Fig. 7D). The cell plasma membrane and nuclear membrane are modeled as the two-layer elastic mesh structures, which can be connected by SFs. Integrin clusters are placed at nodes on the membrane mesh and associate or disassociate with ligands on the substrate according to:
| (31) |
where Pon and Poff are the binding and unbinding probabilities, respectively, of integrin-FN bonds within a time interval Δt; kon and koff (s−1) are the association and dissociation rate constants, respectively. The nodes on the plasma membrane and nucleus membrane displace according to Newton’s second law:
| (32) |
| (33) |
where vi (nm/s) is the velocity vector of the i-th node; FD,i, FFA,i, FE,i, FSF,i and FL,i (N) are frictional dissipative force, adhesion force, elastic energy force, SF force and lamellipodium force vectors, respectively; xi (μm) is the coordinate of the i-th node; and mi is the effective mass of a node, set at 1. When solved numerically, the above system of equations correctly predictions experimental observations of how cell migration rate varies with both fibronectin density and the cross-sectional area of a microchannel, suggesting that the model provides a powerful platform for simulating dynamic cell processes on 2D manifolds including cylindrical lumens in a 3D ECM.
7.2 The Cellular Potts Model (CPM)
The cellular Potts model predicts the dynamics of cell shape and traction on various micro-patterned substrata via simple tension-elasticity elements [179–181] (Fig. 7D). Cells, modeled as a collection of spins, can adopt arbitrary shapes. Each spin configuration has an energy function, which depends upon cell traction. Evolution of cell shape and cell traction is predicted via a quasi-static energy minimization principle. Simulations typically proceed on a lattice using Metropolis dynamics. In each time step, spin at a randomly chosen lattice sites at the edge of the cell is inverted, and the inversion is accepted with the probability eΔH/kBT, in which ΔH represents the energy difference between current state and inverted state,
| (34) |
| (35) |
where Hinvert and Hcurrent are the energy functions after and before inversion, respectively; σS represents the surface tension (S represents the cell spreading area); γl represents the line tension (l represents the cell perimeter); the third term represents the cell traction in concave actin fibers at the cell edge, in which Li is current length of a fiber, Li,0 is the reference length of fiber i, E is the elastic modulus of a fiber, and A is the cross-sectional area of a fiber; and the last term represents the energetic cost of adding adhesion sites, in which Aad is adhesive area, Aref is saturation of the adhesive area, and E0 is strength of the adhesive energy. Thus, the evolution of cell shape with time can be obtained from the above methods for cells on 2D substrata. The CPM is useful for predicting cell shapes on micro-patterned substrata with units that are well represented by a lattice.
7.3 Bio-chemo-mechanical model of Deshpande and co-workers
Deshpande et al. proposed a bio-chemo-mechanical model to explain the cell contraction on 2D micro-patterned substrata [182–184]. The work has since been expanded to model cells in a range of 3D microenvironments. Several phenomenological equations are incorporated into their continuum model to describe the following biochemical processes: 1) the formation of SFs triggered by a time-decaying activation signal C (such as the concentration of Ca2+),
| (36) |
where ti is the time since initial activation of Ca2+ signals and θ is the decay time constant; 2) signal-dependent assembly and tension-dependent disassembly of SFs following a first-order kinetic equation for the relative concentration of stress fibers η(φ) in any direction φ,
| (37) |
where k̄f and k̄b are SF assembly and disassembly rates, respectively, σ(φ) is the tension in SFs along the direction of φ, and σ0(φ) is a homeostatic target stress in that direction; and 3) contraction in SFs generated by actomyosin cross-bridge dynamics following a modified Hill equation. The bio-chemo-mechanical model can successfully predict that: 1) cell contraction increases with increasing matrix rigidity; 2) the boundary and cell shapes have an important influence on the anisotropic development of cell structure; and 3) the concentration of SFs is high in the vicinity of focal adhesions. This model for the first time provides an integrated mechanochemical description of the cell spreading and contraction on 2D various micro-patterned matrices.
7.4 The free-energy-based chemo-mechanical coupling model
Shenoy et al. proposed a free-energy-based chemo-mechanical coupling model to explain why cells prefer to migrate towards stiffer substrata (via durotaxis) and display a rigidity-dependent cell contraction [185]. In this model, the second law of thermodynamics is used to describe the decreasing total free energy of cell:
| (38) |
where dUmech and dUchem are the changes of mechanical energy and chemical energy, respectively; dUmotor is the mechanical work done by myosin motors. When the cell is subjected to the external tension, several tension-dependent signaling pathways are activated (e.g., the Rho- and Ca2+-cascades), which increase the binding rate of myosin motors. Finally, more engaged myosin motors lead to an increase in cell contraction (i.e., cytoskeleton tension), in turn, increasing the external tension. Uchem is related to the external tension and engaged myosin density, with an increasing external tension causing a decrease of chemical free energy. Thus, the chemical and mechanical processes are integrated into a unified framework. The strain and contraction distributions predicted by this model are consistent with experimental observations such as behavior of cells on 2D micropost arrays and in 3D matrices. Interestingly, the model also suggests that increasing substrate stiffness decreases the chemical contribution to the free energy and increases the mechanical contribution, resulting in a net free energy decrease with increasing substrate stiffness. This provides an explanation of cell durotaxis from the perspective of thermodynamics.
A mathematical model to describe cellular nuclear morphology and stresses during transendothelial cell migration in a microfluidic channel was also proposed by Shenoy et al. [186]. This model can predict the effect of large and small constriction during cell transmigration on the nuclear envelope and on chromatin deformation, which provides a very useful platform to understand the cell behaviors in 3D ECMs, and may shed light on how cell differentiation is influenced by the nuclear shape and chromatin disposition.
The Shenoy group’s models and the other models reviewed in this section predict a great many cell behaviors including migration and spreading, but prediction of more complex behaviors such as differentiation cannot be fully captured by any existing mechanical model. Therefore, a pressing need exists for more detailed models of how mechanical and chemical cues enable a cell to react to its complex mechanical environment.
8. Outlook and conclusions
Cells are complex living systems that integrate signals from the molecular (e.g., bond dynamics in adhesions) to the subcellular (e.g., arrangements of SFs) to the cellular (e.g., differentiation and migration) levels. Cellular mechanosensing is therefore a multiscale process across wide temporal and spatial scales, including interactions between numerous proteins during transduction via cell adhesions, actomyosin filaments, stress activated ion channels, and the nuclear envelope. Understanding cellular mechanosensing and signal transduction is full of challenges and opportunities for integrated modeling and experiment.
Existing cellular mechanosensing models span cell-ECM interactions to cytoplasmic mechanotransduction to nuclear responses, and can explain a broad range of experimental observations at each length scale. However, many key issues remain to be addressed:
What are the effects of a 3D environment on living cells? Much of what we have learned about cell mechanobiology derives from experiments performed on cells that are plated on 2D substrata. Many important questions that arise when translating these 2D data to cells in 3D remain unanswered. Especially important is the understanding of how differences in stress fiber disposition, focal adhesion structure, nuclear shape, and nuclear connectivity to the ECM differ between 2D and 3D, and how these differences affect cellular mechanotransduction.
Do cells follow universal principles? Can a generic mathematical model explain phenomena occur in different cell types? Different cell types, normal and diseased variants of the same cell time, and identical cell types in different microenvironments (e.g., 2D vs. 3D) can display significantly different cellular mechanosensing behaviors [141, 187–192]. In view of the complexity of both mechanical and biochemical signals controlling cellular mechanosensing, coupled modeling and experimentation are required to answer this question. Manipulation of one particular component of one mechanosensing process may change the behavior of that process alone, but it may also affect several other related processes, leading to different behaviors. Perhaps as a result of this complexity, many experimental studies have produced apparently contradictory conclusions [10, 147]. For example, the relationships between matrix rigidity and actin flow are distinct in different cell types, e.g., a biphasic relationship in neurons and a monotonic relationship in fibroblasts [126]. Normal fibroblasts align to specific angles in response to 3D compression while cancer-associated fibroblasts show a random distribution [113]. Fibroblasts align themselves along the stretch direction in 3D, while perpendicular to the stretch direction in 2D [85, 193, 194]. As of yet, no universal mathematical model explains these distinct observations.
How does cellular mechanosensing integrate across spatial and temporal scales? The events involved in cellular mechanosensing often occur at disparate timescales. Mechanosensitive ion channels can be activated on timescales of 0.1 s [195]; tension-dependent association and dissociation of adhesion proteins usually happens within seconds [133, 196–199]; the turnover of mature adhesions happens within minutes [200]; viscoelastic relaxation of the ECM can last minutes to hours [201–203]; gene regulation and protein translation in cellular differentiation can last for hours [204] or days [205]. Molecular and subcellular models like the molecular clutch model explain cell adhesion dynamics in mechanosensing over seconds to hours. Cell and tissue models (e.g., signaling network models) explain macroscopic cellular mechanosensing (e.g., cell differentiation) over several days to weeks. However, a framework that integrates these timescales has yet to be developed, and the development of such a framework represents an important need for understanding how cells make long-term and possibly irreversible decisions based upon mechanical inputs.
How are mechanical cues converted into nuclear signals? Mechanical force and matrix rigidity can directly influence nuclear shape and gene location, but how they affect long-term cell behaviors remains elusive [38, 206, 207]. Competing with the nuclear shape hypothesis is the hypothesis that conversion of mechanical cues into biochemical signals sequentially activates intracellular signaling pathways to determine cell behaviors via soluble signals to the nucleus. Identifying the pathways for this signaling is a critical direction. Cells are known to sense force and matrix rigidity via specific sensors, including several amongst the hundreds of known adhesion-associated proteins [208] such as Src, FAK and Rho that can activate downstream signal pathways. However, uncertainty exists at nearly every step of the pathway from the ECM to the nucleus. New features of the structure and function of integrin and cadherin clusters are being discovered constantly [30, 131], and the mechanisms for mechanical transmission of force to the nucleus are still not unclear [37, 38]. Integrated models and experiments are needed to understand how these participate in cellular mechanosensing.
Mechanobiology as a tool to control living cells holds much promise for next-generation therapies. Harnessing this potential requires crossing the frontiers described above. Progress in these areas will undoubtedly continue to hinge upon mathematical modeling that interprets experimental findings in terms of fundamental governing principles.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (11372243, 11522219, 11532009, 11402192), the Chinese Ministry of Education through a Changjiang Scholar award to GMG, the National Institutes of Health through grants U01EB016422 and R01HL109505, and the NSF Science and Technology Center for Engineering Mechanobiology, grant CMMI 1548571.
References
- 1.Dufort CC, Paszek MJ, Weaver VM. Balancing forces: architectural control of mechanotransduction. Nature Reviews Molecular Cell Biology. 2011;12:308. doi: 10.1038/nrm3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Janmey PA, Miller RT. Mechanisms of mechanical signaling in development and disease. Journal of Cell Science. 2011;124:9–18. doi: 10.1242/jcs.071001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Baker BM, Chen CS. Deconstructing the third dimension: how 3D culture microenvironments alter cellular cues. Journal of Cell Science. 2012;125:3015–24. doi: 10.1242/jcs.079509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Schwartz MA, Chen CS. Deconstructing Dimensionality. Science. 2013;339:402–4. doi: 10.1126/science.1233814. [DOI] [PubMed] [Google Scholar]
- 5.Han F, Zhu C, Guo Q, Yang H, Li B. Cellular modulation by the elasticity of biomaterials. Journal of Materials Chemistry B. 2015;4:9–26. doi: 10.1039/c5tb02077h. [DOI] [PubMed] [Google Scholar]
- 6.Engler AJ, Humbert PO, Wehrle-Haller B, Weaver VM. Multiscale Modeling of Form and Function. Science. 2009;324:208–12. doi: 10.1126/science.1170107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eyckmans J, Boudou T, Yu X, Chen CS. A Hitchhiker’s Guide to Mechanobiology. Developmental Cell. 2011;21:35. doi: 10.1016/j.devcel.2011.06.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vitriol EA, Zheng JQ. Growth cone travel in space and time: the cellular ensemble of cytoskeleton, adhesion, and membrane. Neuron. 2012;73:1068–81. doi: 10.1016/j.neuron.2012.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lowery LA, Van VD. The trip of the tip: understanding the growth cone machinery. Nature Reviews Molecular Cell Biology. 2009;10:332. doi: 10.1038/nrm2679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Elosegui-Artola A, Oria R, Chen Y, Kosmalska A, Pérez-González C, Castro N, et al. Mechanical regulation of a molecular clutch defines force transmission and transduction in response to matrix rigidity. Nature cell biology. 2016:18. doi: 10.1038/ncb3336. [DOI] [PubMed] [Google Scholar]
- 11.Swift J, Ivanovska IL, Buxboim A, Harada T, Dingal PCDP, Pinter J, et al. Nuclear Lamin-A Scales with Tissue Stiffness and Enhances Matrix-Directed Differentiation. Science. 2013;341:65. doi: 10.1126/science.1240104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hui TH, Zhou ZL, Qian J, Lin Y, Ngan AH, Gao H. Volumetric deformation of live cells induced by pressure-activated cross-membrane ion transport. Physical review letters. 2014;113:118101. doi: 10.1103/PhysRevLett.113.118101. [DOI] [PubMed] [Google Scholar]
- 13.Jungbauer S, Gao H, Spatz JP, Kemkemer R. Two characteristic regimes in frequency-dependent dynamic reorientation of fibroblasts on cyclically stretched substrates. 2008;95:3470–8. doi: 10.1529/biophysj.107.128611. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zeng Y, Lai T, Gee Koh C, LeDuc P, Chiam K-H. Investigating Circular Dorsal Ruffles through Varying Substrate Stiffness and Mathematical Modeling. Biophysical journal. 2011;101:2122–30. doi: 10.1016/j.bpj.2011.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Buxboim A, Ivanovska IL, Discher DE. Matrix elasticity, cytoskeletal forces and physics of the nucleus: how deeply do cells ‘feel’ outside and in? Journal of Cell Science. 2010;123:297–308. doi: 10.1242/jcs.041186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kang H, Bayless KJ, Kaunas R. Fluid shear stress modulates endothelial cell invasion into three-dimensional collagen matrices. Ajp Heart & Circulatory Physiology. 2008;295:H2087–97. doi: 10.1152/ajpheart.00281.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Vogel V, Sheetz M. Local force and geometry sensing regulate cell functions. Nature Reviews Molecular Cell Biology. 2006;7:265–75. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
- 18.Schwartz MA. Cell biology. The force is with us. Science. 2009;323:588–9. doi: 10.1126/science.1169414. [DOI] [PubMed] [Google Scholar]
- 19.Hoffman B, Grashoff C, Schwartz M. Dynamic molecular processes mediate cellular mechanotransduction. Nature. 2011;475:316–23. doi: 10.1038/nature10316. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Higuchi A, Ling QD, Chang Y, Hsu ST, Umezawa A. Physical cues of biomaterials guide stem cell differentiation fate. Chemical Reviews. 2013;113:3297–328. doi: 10.1021/cr300426x. [DOI] [PubMed] [Google Scholar]
- 21.Dalby MJ, Gadegaard N, Oreffo RO. Harnessing nanotopography and integrin-matrix interactions to influence stem cell fate. Nature materials. 2014;13:558–69. doi: 10.1038/nmat3980. [DOI] [PubMed] [Google Scholar]
- 22.Ivanovska IL, Shin JW, Swift J, Discher DE. Stem cell mechanobiology: diverse lessons from bone marrow. Trends in Cell Biology. 2015;4:523. doi: 10.1016/j.tcb.2015.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Huang X, Yang N, Fiore VF, Barker TH, Sun Y, Morris SW, et al. Matrix Stiffness–Induced Myofibroblast Differentiation Is Mediated by Intrinsic Mechanotransduction. American Journal of Respiratory Cell & Molecular Biology. 2012;47:340–8. doi: 10.1165/rcmb.2012-0050OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schroer AK, Merryman WD. Mechanobiology of myofibroblast adhesion in fibrotic cardiac disease. Journal of Cell Science. 2015;128:1865. doi: 10.1242/jcs.162891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Elosegui-Artola A, Bazellières E, Allen M, Andreu I, Oria R, Sunyer R, et al. Rigidity sensing and adaptation through regulation of integrin types. Nature materials. 2014;13:631–7. doi: 10.1038/nmat3960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126:677–89. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 27.Chaudhuri O, Luo G, Klumpers D, Darnell M, Bencherif SA, Weaver JC, et al. Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nature materials. 2015;15:326. doi: 10.1038/nmat4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Chaudhuri O, Koshy ST, Cunha CD. Extracellular matrix stiffness and composition jointly regulate the induction of malignant phenotypes in mammary epithelium. Nature materials. 2014;13:970–8. doi: 10.1038/nmat4009. [DOI] [PubMed] [Google Scholar]
- 29.Trappmann B, Gautrot J, Connelly J, Strange D, Li Y, Oyen M, et al. Extracellular-matrix tethering regulates stem-cell fate. Nature materials. 2012;11:642–9. doi: 10.1038/nmat3339. [DOI] [PubMed] [Google Scholar]
- 30.Changede R, Sheetz M. Integrin and cadherin clusters: A robust way to organize adhesions for cell mechanics. Bioessays. 2016 doi: 10.1002/bies.201600123. [DOI] [PubMed] [Google Scholar]
- 31.Thomas I, Wolfenson H, Sheetz M. Appreciating force and shape - the rise of mechanotransduction in cell biology. Nature Reviews Molecular Cell Biology. 2014;15:825–33. doi: 10.1038/nrm3903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Wehrlehaller B. Protein conformation as a regulator of cell-matrix adhesion. Physical Chemistry Chemical Physics Pccp. 2014;16:6342. doi: 10.1039/c3cp54884h. [DOI] [PubMed] [Google Scholar]
- 33.Schiller HB, Fässler R. Mechanosensitivity and compositional dynamics of cell–matrix adhesions. Embo Reports. 2013;14:509–19. doi: 10.1038/embor.2013.49. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bershadsky A, Kozlov M, Geiger B. Adhesion-mediated mechanosensitivity: a time to experiment, and a time to theorize. Current Opinion in Cell Biology. 2006;18:472–81. doi: 10.1016/j.ceb.2006.08.012. [DOI] [PubMed] [Google Scholar]
- 35.Lansman JB, Hallam TJ, Rink TJ. Single stretch-activated ion channels in vascular endothelial cells as mechanotransducers? Nature. 1987;325:811–3. doi: 10.1038/325811a0. [DOI] [PubMed] [Google Scholar]
- 36.Ping DJ, Pickard BG. Mechanosensory calcium-selective cation channels in epidermal cells. Plant Journal for Cell & Molecular Biology. 1993;3:83. doi: 10.1111/j.1365-313x.1993.tb00013.x. [DOI] [PubMed] [Google Scholar]
- 37.Wang N, Tytell JD, Ingber DE. Mechanotransduction at a distance: mechanically coupling the extracellular matrix with the nucleus. Nature Reviews Molecular Cell Biology. 2009;10:75–82. doi: 10.1038/nrm2594. [DOI] [PubMed] [Google Scholar]
- 38.Tajik A, Zhang Y, Wei F, Jian S, Jia Q, Zhou W, et al. Transcription upregulation via force-induced direct stretching of chromatin. Nature materials. 2016 doi: 10.1038/nmat4729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Provenzano PP, Keely PJ. Mechanical signaling through the cytoskeleton regulates cell proliferation by coordinated focal adhesion and Rho GTPase signaling. Journal of Cell Science. 2011;124:1195–205. doi: 10.1242/jcs.067009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Small EM. The Actin–MRTF–SRF Gene Regulatory Axis and Myofibroblast Differentiation. Journal of Cardiovascular Translational Research. 2012;5:794–804. doi: 10.1007/s12265-012-9397-0. [DOI] [PubMed] [Google Scholar]
- 41.Mendez MG, Janmey PA. Transcription factor regulation by mechanical stress. International Journal of Biochemistry & Cell Biology. 2012;44:728–32. doi: 10.1016/j.biocel.2012.02.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Dingal PC, Discher DE. Combining insoluble and soluble factors to steer stem cell fate. Nature materials. 2014;13:532. doi: 10.1038/nmat3997. [DOI] [PubMed] [Google Scholar]
- 43.Jin H, Zhang Y, Jing D, Yu S, Ge T, Huang S, et al. Mechanobiology of mesenchymal stem cells: A new perspective into the mechanically induced MSC fate. Acta biomaterialia. 2015;20:1–9. doi: 10.1016/j.actbio.2015.04.008. [DOI] [PubMed] [Google Scholar]
- 44.Chen B, Ji B, Gao H. Modeling Active Mechanosensing in Cell-Matrix Interactions. Annual Review of Biophysics. 2015;44:1–32. doi: 10.1146/annurev-biophys-051013-023102. [DOI] [PubMed] [Google Scholar]
- 45.Schoen I, Pruitt BL, Vogel V. The Yin-Yang of Rigidity Sensing: How Forces and Mechanical Properties Regulate the Cellular Response to Materials. Annual Review of Materials Research. 2013;43:589–618. [Google Scholar]
- 46.Pertz O. Filopodia: Nanodevices that sense nanotopographic ECM cues to orient neurite outgrowth. Communicative & Integrative Biology. 2011;4:436–9. doi: 10.4161/cib.4.4.15325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Polacheck WJ, Chen CS. Measuring cell-generated forces: a guide to the available tools. Nature methods. 2016;13:415. doi: 10.1038/nmeth.3834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Infanger DW, Lynch ME, Fischbach C. Engineered culture models for studies of tumor-microenvironment interactions. Annual Review of Biomedical Engineering. 2013;15:29–53. doi: 10.1146/annurev-bioeng-071811-150028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Daniel K, Rosoff WJ, Jiang J, Geller HM, Urbach JS. Strength in the periphery: growth cone biomechanics and substrate rigidity response in peripheral and central nervous system neurons. Biophysical journal. 2012;102:452–60. doi: 10.1016/j.bpj.2011.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Lo CM, Wang HB, Dembo M, Wang YL. Cell movement is guided by the rigidity of the substrate. Biophysical journal. 2000;79:144. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Discher DE, Janmey P, Wang YL. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310:1139–43. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 52.Wang HB, Dembo M, Hanks SK, Wang Y. Focal adhesion kinase is involved in mechanosensing during fibroblast migration. Proceedings of the National Academy of Sciences of the United States of America. 2001;98:11295–300. doi: 10.1073/pnas.201201198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Tan JL, Tien J, Pirone DM, Gray DS, Bhadriraju K, Chen CS. Cells Lying on a Bed of Microneedles: An Approach to Isolate Mechanical Force. Proceedings of the National Academy of Sciences of the United States of America. 2003;100:1484–9. doi: 10.1073/pnas.0235407100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Li Y, Huang G, Li M, Wang L, Elson EL, Lu TJ, et al. An approach to quantifying 3D responses of cells to extreme strain. Scientific reports. 2016;6:19550. doi: 10.1038/srep19550. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Elson EL, Genin GM. Tissue constructs: platforms for basic research and drug discovery. Interface Focus. 2016;6:20150095. doi: 10.1098/rsfs.2015.0095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Pajerowski JD, Dahl KN, Zhong FL, Sammak PJ, Discher DE. Physical plasticity of the nucleus in stem cell differentiation. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:15619. doi: 10.1073/pnas.0702576104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Na S, Collin O, Chowdhury F, Tay B, Ouyang M, Wang Y, et al. Rapid signal transduction in living cells is a unique feature of mechanotransduction. Proceedings of the National Academy of Sciences of the United States of America. 2008;105:6626–31. doi: 10.1073/pnas.0711704105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Guilluy C, Osborne LD, Landeghem LV, Sharek L, Superfine R, Garciamata R, et al. Isolated nuclei adapt to force and reveal a mechanotransduction pathway within the nucleus. Nature cell biology. 2014;16:376–81. doi: 10.1038/ncb2927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jannie KM, Ellerbroek SM, Zhou DW, Chen S, Crompton DJ, García AJ, et al. Vinculin-dependent actin bundling regulates cell migration and traction forces. Biochemical Journal. 2015;465:383–93. doi: 10.1042/BJ20140872. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wolfenson H, Meacci G, Liu S, Stachowiak MR, Iskratsch T, Ghassemi S, et al. Tropomyosin controls sarcomere-like contractions for rigidity sensing and suppressing growth on soft matrices. Nature cell biology. 2016;18:33. doi: 10.1038/ncb3277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chaudhuri O, Gu L, Darnell M, Klumpers D, Bencherif SA, Weaver JC, et al. Substrate stress relaxation regulates cell spreading. Nature communications. 2015:6. doi: 10.1038/ncomms7365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Schiller HB, Hermann MR, Polleux J, Vignaud T, Zanivan S, Friedel CC, et al. β1- and αv-class integrins cooperate to regulate myosin II during rigidity sensing of fibronectin-based microenvironments. Nature cell biology. 2013;15:625–36. doi: 10.1038/ncb2747. [DOI] [PubMed] [Google Scholar]
- 63.Elson EL, Genin GM. The role of mechanics in actin stress fiber kinetics. Experimental Cell Research. 2013;319:2490–500. doi: 10.1016/j.yexcr.2013.06.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Genin GM, Abney TM, Wakatsuki T, Elson EL. Cell-Cell Interactions and the Mechanics of Cells and Tissues Observed in Bioartificial Tissue Constructs. 2011 [Google Scholar]
- 65.Bader AN. Homo-FRET Imaging Enables Quantification of Protein Cluster Sizes with Subcellular Resolution. Biophysical journal. 2009;97:2613–22. doi: 10.1016/j.bpj.2009.07.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kim M, Carman C, Yang W, Salas A, Springer T. primacy of affinity over clustering in regulation of adhesiveness of the integrin αLβ2. Journal of Cell Biology. 2004 doi: 10.1083/jcb.200404160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Askari JA, Tynan CJ, Webb SE, Martinfernandez ML, Ballestrem C, Humphries MJ. Focal adhesions are sites of integrin extension. Journal of Cell Biology. 2010;188:891–903. doi: 10.1083/jcb.200907174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Iskratsch T, Yu CH, Mathur A, Liu S, Stévenin V, Dwyer J, et al. FHOD1 is needed for directed Forces and Adhesion Maturation during Cell Spreading and Migration. Developmental Cell. 2013;27:545. doi: 10.1016/j.devcel.2013.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Pasapera AM, Plotnikov SV, Fischer RS, Case LB, Egelhoff TT, Waterman CM. Rac1-Dependent Phosphorylation and Focal Adhesion Recruitment of Myosin IIA Regulates Migration and Mechanosensing. Current Biology. 2015;25:175–86. doi: 10.1016/j.cub.2014.11.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.He S, Su Y, Ji B, Gao H. Some basic questions on mechanosensing in cell–substrate interaction. Journal of the Mechanics & Physics of Solids. 2014;70:116–35. [Google Scholar]
- 71.Tao J, Sun SX. Active Biochemical Regulation of Cell Volume and a Simple Model of Cell Tension Response. Biophysical Journal. 2015;109:1541–50. doi: 10.1016/j.bpj.2015.08.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Walcott S, Peskin CS. A Mechanical Model of Actin Stress Fiber Formation and Substrate Elasticity Sensing in Adherent Cells. Proceedings of the National Academy of Sciences of the United States of America. 2010;107:7757–62. doi: 10.1073/pnas.0912739107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Schroer AK, Ryzhova LM, Merryman WD. Network Modeling Approach to Predict Myofibroblast Differentiation. Cellular and molecular bioengineering. 2014;7:446–59. doi: 10.1007/s12195-014-0344-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Swaminathan V, Waterman CM. The molecular clutch model for mechanotransduction evolves. Nature cell biology. 2016;18:459. doi: 10.1038/ncb3350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.García JR, García AJ. Cellular mechanotransduction: Sensing rigidity. Nature materials. 2014;13:539–40. doi: 10.1038/nmat3996. [DOI] [PubMed] [Google Scholar]
- 76.Patla I, Volberg T, Elad N, Hirschfeldwarneken V, Grashoff C, Fässler R, et al. Dissecting the molecular architecture of integrin adhesion sites by cryo-electron tomography. Nature cell biology. 2010;12:909–15. doi: 10.1038/ncb2095. [DOI] [PubMed] [Google Scholar]
- 77.Case LB, Baird MA, Shtengel G, Campbell SL, Hess HF, Davidson MW, et al. Molecular mechanism of vinculin activation and nanoscale spatial organization in focal adhesions. Nature cell biology. 2015;17:547–55. doi: 10.1038/ncb3180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Liu J, Wang Y, Goh WI, Goh H, Baird MA, Ruehland S, et al. Talin determines the nanoscale architecture of focal adhesions. Proceedings of the National Academy of Sciences. 2015;112:4864–73. doi: 10.1073/pnas.1512025112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Holmes WR, Edelsteinkeshet L. A comparison of computational models for eukaryotic cell shape and motility. Plos Computational Biology. 2012;8:e1002793-e. doi: 10.1371/journal.pcbi.1002793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Tao J, Li Y, Vig DK, Sun SX. Cell mechanics: a dialogue. Reports on Progress in Physics Physical Society. 2017;80:036601. doi: 10.1088/1361-6633/aa5282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Tse JM, Cheng G, Tyrrell JA, Wilcox-Adelman SA, Boucher Y, Jain RK, et al. Mechanical compression drives cancer cells toward invasive phenotype. Proceedings of the National Academy of Sciences of the United States of America. 2011;109:911–6. doi: 10.1073/pnas.1118910109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Collinsworth AM, Torgan CE, Nagda SN, Rajalingam RJ, Kraus WE, Truskey GA. Orientation and length of mammalian skeletal myocytes in response to a unidirectional stretch. Cell and Tissue Research. 2000;302:243. doi: 10.1007/s004410000224. [DOI] [PubMed] [Google Scholar]
- 83.Kurpinski K, Chu J, Hashi C, Li S. Anisotropic mechanosensing by mesenchymal stem cells. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:16095–100. doi: 10.1073/pnas.0604182103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Livne A, Bouchbinder E, Geiger B. Cell reorientation under cyclic stretching. Nature communications. 2014;106:42a-a. doi: 10.1038/ncomms4938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Lee SL, Nekouzadeh A, Butler B, Pryse KM, Mcconnaughey WB, Nathan AC, et al. Physically-induced cytoskeleton remodeling of cells in three-dimensional culture. PloS one. 2012;7:e45512. doi: 10.1371/journal.pone.0045512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Krishnan R, Canovic EP, Iordan AL, Rajendran K, Manomohan G, Pirentis AP, et al. Fluidization, resolidification, and reorientation of the endothelial cell in response to slow tidal stretches. Ajp Cell Physiology. 2012;303:C368–75. doi: 10.1152/ajpcell.00074.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Nekouzadeh A, Pryse KM, Elson EL, Genin GM. Stretch-activated force-shedding, force recovery, and cytoskeletal remodeling in contractile fibroblasts. Journal of biomechanics. 2008;41:2964–71. doi: 10.1016/j.jbiomech.2008.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Kaunas R, Nguyen P, Usami S, Chien S. Cooperative effects of Rho and mechanical stretch on stress fiber organization. Proceedings of the National Academy of Sciences of the United States of America. 2005;102:15895. doi: 10.1073/pnas.0506041102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Heo SJ, Han WM, Szczesny SE, Cosgrove BD, Elliott DM, Lee DA, et al. Mechanically Induced Chromatin Condensation Requires Cellular Contractility in Mesenchymal Stem Cells. Biophysical journal. 2016;111:864–74. doi: 10.1016/j.bpj.2016.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Heo SJ, Thorpe SD, Driscoll TP, Duncan RL, Lee DA, Mauck RL. Biophysical Regulation of Chromatin Architecture Instills a Mechanical Memory in Mesenchymal Stem Cells. Scientific reports. 2015;5:16895. doi: 10.1038/srep16895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Iyer KV, Pulford S, Mogilner A, Shivashankar GV. Mechanical Activation of Cells Induces Chromatin Remodeling Preceding MKL Nuclear Transport. Biophysical journal. 2012;103:1416–28. doi: 10.1016/j.bpj.2012.08.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Driscoll TP, Cosgrove BD, Heo SJ, Shurden ZE, Mauck RL. Cytoskeletal to Nuclear Strain Transfer Regulates YAP Signaling in Mesenchymal Stem Cells. Biophysical journal. 2015;108:2783–93. doi: 10.1016/j.bpj.2015.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Heo SJ, Driscoll TP, Thorpe SD, Nerurkar NL, Baker BM, Yang MT, et al. Differentiation alters stem cell nuclear architecture, mechanics, and mechano-sensitivity. Elife. 2016:5. doi: 10.7554/eLife.18207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Qian J, Liu H, Lin Y, Chen W, Gao H. A mechanochemical model of cell reorientation on substrates under cyclic stretch. PloS one. 2013;8:e65864. doi: 10.1371/journal.pone.0065864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Russell RJ, Xia SL, Dickinson RB, Lele TP. Sarcomere Mechanics in Capillary Endothelial Cells. Biophysical journal. 2009;97:1578. doi: 10.1016/j.bpj.2009.07.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Chen B, Kemkemer R, Deibler M, Spatz J, Gao H. Cyclic Stretch Induces Cell Reorientation on Substrates by Destabilizing Catch Bonds in Focal Adhesions. PloS one. 2012;7:e48346. doi: 10.1371/journal.pone.0048346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Peterson LJ, Rajfur Z, Maddox AS, Freel CD, Chen Y, Edlund M, et al. Simultaneous Stretching and Contraction of Stress Fibers In Vivo. Molecular biology of the cell. 2004;15:3497–508. doi: 10.1091/mbc.E03-09-0696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Wu T, Feng JJ. A biomechanical model for fluidization of cells under dynamic strain. Biophysical journal. 2015;108:43–52. doi: 10.1016/j.bpj.2014.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Hsu HJ, Lee CF, Kaunas R. A dynamic stochastic model of frequency-dependent stress fiber alignment induced by cyclic stretch. PloS one. 2009;4:e4853. doi: 10.1371/journal.pone.0004853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Kaunas R, Deguchi S. Multiple Roles for Myosin II in Tensional Homeostasis Under Mechanical Loading. Cellular and molecular bioengineering. 2011;4:182–91. [Google Scholar]
- 101.Kaunas R, Hsu HJ. A kinematic model of stretch-induced stress fiber turnover and reorientation. Journal of theoretical biology. 2009;257:320. doi: 10.1016/j.jtbi.2008.11.024. [DOI] [PubMed] [Google Scholar]
- 102.Na S, Sun Z, Meininger GA, Humphrey JD. On atomic force microscopy and the constitutive behavior of living cells. Biomechanics and Modeling in Mechanobiology. 2004;3:75. doi: 10.1007/s10237-004-0051-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Zhong Y, Kong D, Dai L, Ji B. Frequency-Dependent Focal Adhesion Instability and Cell Reorientation Under Cyclic Substrate Stretching. Cellular and molecular bioengineering. 2011;4:442–56. [Google Scholar]
- 104.De R, Zemel A, Safran SA. Dynamics of cell orientation. Nature Physics. 2007;3:655–9. [Google Scholar]
- 105.Safran SA, De R. Nonlinear dynamics of cell orientation. Physical Review E Statistical Nonlinear & Soft Matter Physics. 2009;80:060901. doi: 10.1103/PhysRevE.80.060901. [DOI] [PubMed] [Google Scholar]
- 106.De Rumi, Zemel, Assaf, Safran, Samuel A. Do Cells Sense Stress or Strain? Measurement of Cellular Orientation Can Provide a Clue. Biophysical journal. 2008;94:L29–L31. doi: 10.1529/biophysj.107.126060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Kang J, Steward RL, Kim YT, Schwartz RS, Leduc PR, Puskar KM. Response of an actin filament network model under cyclic stretching through a coarse grained Monte Carlo approach. Journal of theoretical biology. 2011;274:109. doi: 10.1016/j.jtbi.2011.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Xu GK, Li B, Feng XQ, Gao H. A Tensegrity Model of Cell Reorientation on Cyclically Stretched Substrates. Biophysical journal. 2016;111:1478. doi: 10.1016/j.bpj.2016.08.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Besser A, Schwarz US. Coupling biochemistry and mechanics in cell adhesion: a model for inhomogeneous stress fiber contraction. Quantitative Biology. 2007;43:707–20. [Google Scholar]
- 110.Kong D, Ji B, Dai L. Stability of Adhesion Clusters and Cell Reorientation under Lateral Cyclic Tension. Biophysical journal. 2008;95:4034–44. doi: 10.1529/biophysj.108.131342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.Kaunas R, Huang Z, Hahn J. A kinematic model coupling stress fiber dynamics with JNK activation in response to matrix stretching. Journal of theoretical biology. 2010;264:593–603. doi: 10.1016/j.jtbi.2010.02.020. [DOI] [PubMed] [Google Scholar]
- 112.Wang JH. Substrate deformation determines actin cytoskeleton reorganization: A mathematical modeling and experimental study. 2000;202:33–41. doi: 10.1006/jtbi.1999.1035. [DOI] [PubMed] [Google Scholar]
- 113.Yang L, Erdogan B, Ao M, Brewer BM, Webb DJ, Li D. Biomechanics of cell reorientation in a three-dimensional matrix under compression. Experimental Cell Research. 2017;350:253–66. doi: 10.1016/j.yexcr.2016.12.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Davies PF. Flow-mediated endothelial mechanotransduction. Physiological Reviews. 1995;75:519. doi: 10.1152/physrev.1995.75.3.519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Civelekoglu-Scholey G, Orr AW, Novak I, Meister JJ, Schwartz MA, Mogilner A. Model of coupled transient changes of Rac, Rho, adhesions and stress fibers alignment in endothelial cells responding to shear stress. Journal of theoretical biology. 2005;232:569–85. doi: 10.1016/j.jtbi.2004.09.004. [DOI] [PubMed] [Google Scholar]
- 116.Petersen NO, McConnaughey WB, Elson EL. Dependence of locally measured cellular deformability on position on the cell, temperature, and cytochalasin B. Proceedings of the National Academy of Sciences. 1982;79:5327–31. doi: 10.1073/pnas.79.17.5327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Luo T, Mohan K, Iglesias PA, Robinson DN. Molecular mechanisms of cellular mechanosensing. Nature materials. 2013;12:1064–71. doi: 10.1038/nmat3772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Luo T, Mohan K, Srivastava V, Ren Y, Iglesias P, Robinson D. Understanding the Cooperative Interaction between Myosin II and Actin Cross-Linkers Mediated by Actin Filaments during Mechanosensation. Biophysical journal. 2012;102:238–47. doi: 10.1016/j.bpj.2011.12.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Stam S, Alberts J, Gardel M, Munro E. Isoforms Confer Characteristic Force Generation and Mechanosensation by Myosin II Filaments. Biophysical journal. 2015;108:1997–2006. doi: 10.1016/j.bpj.2015.03.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Paul R, Heil P, Spatz JP, Schwarz US. Propagation of Mechanical Stress through the Actin Cytoskeleton toward Focal Adhesions: Model and Experiment. Biophysical journal. 2008;94:1470–82. doi: 10.1529/biophysj.107.108688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Barreto S, Clausen CH, Perrault CM, Fletcher DA, Lacroix D. A multi-structural single cell model of force-induced interactions of cytoskeletal components. Biomaterials. 2013;34:6119–26. doi: 10.1016/j.biomaterials.2013.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Ingber DE. Tensegrity I. Cell structure and hierarchical systems biology. Journal of Cell Science. 2003;116:1157–73. doi: 10.1242/jcs.00359. [DOI] [PubMed] [Google Scholar]
- 123.Ingber DE. Cellular tensegrity: defining new rules of biological design that govern the cytoskeleton. Journal of Cell Science. 1993;104:613–27. doi: 10.1242/jcs.104.3.613. [DOI] [PubMed] [Google Scholar]
- 124.Zeng Y, Yip AK, Teo SK, Chiam KH. A three-dimensional random network model of the cytoskeleton and its role in mechanotransduction and nucleus deformation. Biomechanics and Modeling in Mechanobiology. 2012;11:49. doi: 10.1007/s10237-011-0292-4. [DOI] [PubMed] [Google Scholar]
- 125.Plotnikov S, Pasapera A, Sabass B, Waterman C. Force Fluctuations within Focal Adhesions Mediate ECM-Rigidity Sensing to Guide Directed Cell Migration. Cell. 2012;151:1513. doi: 10.1016/j.cell.2012.11.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Cheng B, Lin M, Li Y, Huang G, Yang H, Genin GM, et al. An Integrated Stochastic Model of Matrix-Stiffness-Dependent Filopodial Dynamics. Biophysical journal. 2016;111:2051–61. doi: 10.1016/j.bpj.2016.09.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Yao M, Goult BT, Klapholz B, Hu X, Toseland CP, Guo Y, et al. The mechanical response of talin. Nature communications. 2016;7:1–11. doi: 10.1038/ncomms11966. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Austen K, Ringer P, Mehlich A, Chrostekgrashoff A, Kluger C, Klingner C, et al. Extracellular rigidity sensing by talin isoform-specific mechanical linkages. Nature cell biology. 2015 doi: 10.1038/ncb3268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Mitchison T, Kirschner M. Cytoskeletal dynamics and nerve growth. Neuron. 1988;1:761–72. doi: 10.1016/0896-6273(88)90124-9. [DOI] [PubMed] [Google Scholar]
- 130.Case LB, Waterman CM. Integration of actin dynamics and cell adhesion by a three-dimensional, mechanosensitive molecular clutch. Nature cell biology. 2015;17:955. doi: 10.1038/ncb3191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Changede R, Xu X, Margadant F, Sheetz MP. Nascent Integrin Adhesions Form on All Matrix Rigidities after Integrin Activation. Developmental Cell. 2015;35:614–21. doi: 10.1016/j.devcel.2015.11.001. [DOI] [PubMed] [Google Scholar]
- 132.Tian T, Harding A, Inder K, Plowman S, Parton RG, Hancock JF. Plasma membrane nanoswitches generate high-fidelity Ras signal transduction. Nature cell biology. 2007;9:905–14. doi: 10.1038/ncb1615. [DOI] [PubMed] [Google Scholar]
- 133.Hamadi A, Bouali M, Dontenwill M, Stoeckel H, Takeda K, Rondé P. Regulation of focal adhesion dynamics and disassembly by phosphorylation of FAK at tyrosine 397. Journal of Cell Science. 2005;118:4415–25. doi: 10.1242/jcs.02565. [DOI] [PubMed] [Google Scholar]
- 134.Seong J, Tajik A, Sun J, Guan J-L, Humphries MJ, Craig SE, et al. Distinct biophysical mechanisms of focal adhesion kinase mechanoactivation by different extracellular matrix proteins. Proceedings of the National Academy of Sciences of the United States of America. 2013;110:19372. doi: 10.1073/pnas.1307405110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Radhakrishnan K, Halász Á, Mccabe MM, Edwards JS, Wilson BS. Mathematical Simulation of Membrane Protein Clustering for Efficient Signal Transduction. Annals of Biomedical Engineering. 2012;40:2307–18. doi: 10.1007/s10439-012-0599-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Fallahisichani M, Linderman JJ. Lipid Raft-Mediated Regulation of G-Protein Coupled Receptor Signaling by Ligands which Influence Receptor Dimerization: A Computational Study. PloS one. 2009;4:e6604. doi: 10.1371/journal.pone.0006604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 137.Costa MN, Radhakrishnan K, Edwards JS. Monte Carlo simulations of plasma membrane corral-induced EGFR clustering. Journal of Biotechnology. 2011;151:261–70. doi: 10.1016/j.jbiotec.2010.12.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 138.Ali O, Guillou H, Destaing O, Albigèsrizo C, Block MR, Fourcade B. Cooperativity between Integrin Activation and Mechanical Stress Leads to Integrin Clustering. Biophysical journal. 2011;100:2595–604. doi: 10.1016/j.bpj.2011.03.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Versaevel M, Braquenier JB, Riaz M, Grevesse T, Lantoine J, Gabriele S. Super-resolution microscopy reveals LINC complex recruitment at nuclear indentation sites. Scientific reports. 2014;4:7362. doi: 10.1038/srep07362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Giannone G, Sheetz MP. Substrate rigidity and force define form through tyrosine phosphatase and kinase pathways. Trends in Cell Biology. 2006;16:213–23. doi: 10.1016/j.tcb.2006.02.005. [DOI] [PubMed] [Google Scholar]
- 141.Swift J, Discher DE. The nuclear lamina is mechano-responsive to ECM elasticity in mature tissue. Journal of Cell Science. 2014;127:3005–15. doi: 10.1242/jcs.149203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Cho S, Irianto J, Discher DE. Mechanosensing by the nucleus: From pathways to scaling relationships. Journal of Cell Biology. 2017 doi: 10.1083/jcb.201610042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Dupont S. Role of YAP/TAZ in cell-matrix adhesion-mediated signalling and mechanotransduction. Experimental Cell Research. 2016;343:42–53. doi: 10.1016/j.yexcr.2015.10.034. [DOI] [PubMed] [Google Scholar]
- 144.Miralles F, Posern G, Zaromytidou AI, Treisman R. Actin Dynamics Control SRF Activity by Regulation of Its Coactivator MAL. Cell. 2003;113:329–42. doi: 10.1016/s0092-8674(03)00278-2. [DOI] [PubMed] [Google Scholar]
- 145.Dupont S, Morsut L, Aragona M, Enzo E, Giulitti S, Cordenonsi M, et al. Role of YAP/TAZ in mechanotransduction. Nature. 2011;474:179–83. doi: 10.1038/nature10137. [DOI] [PubMed] [Google Scholar]
- 146.Speight P, Kofler M, Szászi K, Kapus A. Context-dependent switch in chemo/mechanotransduction via multilevel crosstalk among cytoskeleton-regulated MRTF and TAZ and TGFβ-regulated Smad3. Nature communications. 2016:7. doi: 10.1038/ncomms11642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 147.Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–91. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 148.Bangasser B, Rosenfeld S, Odde D. Determinants of Maximal Force Transmission in a Motor-Clutch Model of Cell Traction in a Compliant Microenvironment. Biophysical journal. 2013;105:581–92. doi: 10.1016/j.bpj.2013.06.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 149.Bangasser BL, Odde DJ. Master equation-based analysis of a motor-clutch model for cell traction force. Cellular and molecular bioengineering. 2013;6:449–59. doi: 10.1007/s12195-013-0296-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 150.Aratyn-Schaus Y, Gardel ML. Transient frictional slip between integrin and the ECM in focal adhesions under myosin II tension. Current Biology Cb. 2010;20:1145–53. doi: 10.1016/j.cub.2010.05.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Gardel ML, Sabass B, Ji L, Danuser G, Schwarz US, Waterman CM. Traction stress in focal adhesions correlates biphasically with actin retrograde flow speed. Journal of Cell Biology. 2009;183:999–1005. doi: 10.1083/jcb.200810060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 152.Craig EM, Stricker J, Gardel M, Mogilner A. Model for adhesion clutch explains biphasic relationship between actin flow and traction at the cell leading edge. Physical Biology. 2015;12:035002. doi: 10.1088/1478-3975/12/3/035002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 153.Walcott S, Kim DH, Wirtz D, Sun SX. Nucleation and Decay Initiation Are the Stiffness-Sensitive Phases of Focal Adhesion Maturation. Biophysical journal. 2011;101:2919–28. doi: 10.1016/j.bpj.2011.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 154.Zaidel-Bar R, Ballestrem C, Kam Z, Geiger B. Early molecular events in the assembly of matrix adhesions at the leading edge of migrating cells. Journal of Cell Science. 2003;116:4605. doi: 10.1242/jcs.00792. [DOI] [PubMed] [Google Scholar]
- 155.Besser A, Safran SA. Force-induced adsorption and anisotropic growth of focal adhesions. Biophysical journal. 2006;90:3469–84. doi: 10.1529/biophysj.105.074377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 156.Nicolas A, Geiger B, Safran SA. Cell mechanosensitivity controls the anisotropy of focal adhesions. Proceedings of the National Academy of Sciences of the United States of America. 2004;101:12520–5. doi: 10.1073/pnas.0403539101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 157.Nicolas A, Besser A, Safran SA. Dynamics of cellular focal adhesions on deformable substrates: consequences for cell force microscopy. Biophysical journal. 2008;95:527. doi: 10.1529/biophysj.107.127399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Nicolas A, Safran SA. Limitation of cell adhesion by the elasticity of the extracellular matrix. Biophysical journal. 2006;91:61–73. doi: 10.1529/biophysj.105.077115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 159.Qian J, Wang J, Lin Y, Gao H. Lifetime and strength of periodic bond clusters between elastic media under inclined loading. Biophysical journal. 2009;97:2438–45. doi: 10.1016/j.bpj.2009.08.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 160.Qian J, Wang J, Gao H. Lifetime and strength of adhesive molecular bond clusters between elastic media. Langmuir. 2008;24:1262–70. doi: 10.1021/la702401b. [DOI] [PubMed] [Google Scholar]
- 161.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200:618–27. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 162.Peng X, Huang J, Xiong C, Fang J. Cell adhesion nucleation regulated by substrate stiffness: a Monte Carlo study. Journal of biomechanics. 2012;45:116–22. doi: 10.1016/j.jbiomech.2011.09.013. [DOI] [PubMed] [Google Scholar]
- 163.Paszek MJ, Boettiger D, Weaver VM, Hammer DA. Integrin clustering is driven by mechanical resistance from the glycocalyx and the substrate. Plos Computational Biology. 2009;5:e1000604. doi: 10.1371/journal.pcbi.1000604. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Paszek MJ, Dufort CC, Rossier O, Bainer R, Mouw JK, Godula K, et al. The cancer glycocalyx mechanically primes integrin-mediated growth and survival. Nature. 2014;511:319–25. doi: 10.1038/nature13535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Jiang H, Qian J, Lin Y, Ni Y, He L. Aggregation dynamics of molecular bonds between compliant materials. Soft Matter. 2015;11:2812. doi: 10.1039/c4sm02903h. [DOI] [PubMed] [Google Scholar]
- 166.Cao X, Lin Y, Driscoll T, Franco-Barraza J, Cukierman E, Mauck R, et al. A Chemomechanical Model of Matrix and Nuclear Rigidity Regulation of Focal Adhesion Size. Biophysical journal. 2015;109:1807–17. doi: 10.1016/j.bpj.2015.08.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 167.Zemel A, Rehfeldt F, Brown AE, Discher DE, Safran SA. Optimal matrix rigidity for stress-fibre polarization in stem cells. Nature Physics. 2010;6:468–73. doi: 10.1038/nphys1613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.He S, Liu C, Li X, Ma S, Huo B, Ji B. Dissecting Collective Cell Behavior in Polarization and Alignment on Micropatterned Substrates. Biophysical journal. 2015;109:489–500. doi: 10.1016/j.bpj.2015.06.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Liu C, He S, Li X, Huo B, Ji B. Mechanics of Cell Mechanosensing on Patterned Substrate. Journal of Applied Mechanics. 2016:83. [Google Scholar]
- 170.Dingal PC, Discher DE. Systems Mechanobiology: Tension-Inhibited Protein Turnover Is Sufficient to Physically Control Gene Circuits. Biophysical journal. 2014;107:2734–43. doi: 10.1016/j.bpj.2014.10.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Sun M, Spill F, Zaman M. A Computational Model of YAP/TAZ Mechanosensing. Biophysical journal. 2016;110:2540–50. doi: 10.1016/j.bpj.2016.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Toh YC, Zhang C, Zhang J, Khong YM, Chang S, Samper VD, et al. A novel 3D mammalian cell perfusion-culture system in microfluidic channels. Lab on A Chip. 2007;7:302–9. doi: 10.1039/b614872g. [DOI] [PubMed] [Google Scholar]
- 173.Peyton SR, Kim PD, Ghajar CM, Seliktar D, Putnam AJ. The Effects of Matrix Stiffness and RhoA on the Phenotypic Plasticity of Smooth Muscle Cells in a 3-D Biosynthetic Hydrogel System. Biomaterials. 2008;29:2597. doi: 10.1016/j.biomaterials.2008.02.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 174.Palecek SP, Loftus JC, Ginsberg MH, Lauffenburger DA, Horwitz AF. Integrin-ligand binding properties govern cell migration speed through cell-substratum adhesiveness. Nature. 1997;385:537. doi: 10.1038/385537a0. [DOI] [PubMed] [Google Scholar]
- 175.Irimia D, Toner M. Spontaneous migration of cancer cells under conditions of mechanical confinement. Integrative Biology Quantitative Biosciences from Nano to Macro. 2009;1:506–12. doi: 10.1039/b908595e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 176.Tseng Q, Wang I, Ducheminpelletier E, Azioune A, Carpi N, Gao J, et al. A new micropatterning method of soft substrates reveals that different tumorigenic signals can promote or reduce cell contraction levels. Lab on A Chip. 2011;11:2231–40. doi: 10.1039/c0lc00641f. [DOI] [PubMed] [Google Scholar]
- 177.Kim MC, Neal DM, Kamm RD, Asada HH. Dynamic modeling of cell migration and spreading behaviors on fibronectin coated planar substrates and micropatterned geometries. Plos Computational Biology. 2013;9:e1002926. doi: 10.1371/journal.pcbi.1002926. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 178.Kim MC, Kim C, Wood L, Neal D, Kamm RD, Asada HH. Integrating focal adhesion dynamics, cytoskeleton remodeling, and actin motor activity for predicting cell migration on 3D curved surfaces of the extracellular matrix. Integrative Biology. 2012;4:1386–97. doi: 10.1039/c2ib20159c. [DOI] [PubMed] [Google Scholar]
- 179.Albert PJ, Schwarz US. Dynamics of cell shape and forces on micropatterned substrates predicted by a cellular Potts model. Biophysical Journal. 2014;106:2340–52. doi: 10.1016/j.bpj.2014.04.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 180.Barziv R, Tlusty T, Moses E, Safran SA, Bershadsky A. Pearling in cells: a clue to understanding cell shape. Proceedings of the National Academy of Sciences of the United States of America. 1999;96:10140–5. doi: 10.1073/pnas.96.18.10140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 181.Vianay B, Käfer J, Planus E, Block M, Graner F, Guillou H. Single cells spreading on a protein lattice adopt an energy minimizing shape. Physical Review Letters. 2010;105:128101. doi: 10.1103/PhysRevLett.105.128101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 182.Deshpande VS, Mcmeeking RM, Evans AG. A bio-chemo-mechanical model for cell contractility. Proceedings of the National Academy of Sciences of the United States of America. 2006;103:14015–20. doi: 10.1073/pnas.0605837103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 183.Deshpande VS, Mrksich M. A bio-mechanical model for coupling cell contractility with focal adhesion formation. Journal of the Mechanics & Physics of Solids. 2008;56:1484–510. [Google Scholar]
- 184.Deshpande VS, Mcmeeking RM, Evans AG. A Model for the Contractility of the Cytoskeleton including the Effects of Stress-Fibre Formation and Dissociation. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences. 2007;463:787–815. [Google Scholar]
- 185.Shenoy VB, Wang H, Wang X. A chemo-mechanical free-energy-based approach to model durotaxis and extracellular stiffness-dependent contraction and polarization of cells. Interface Focus A Theme Supplement of Journal of the Royal Society Interface. 2016;6:20150067. doi: 10.1098/rsfs.2015.0067. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Xuan C, Moeendarbary E, Isermann P, Davidson P, Xiao W, Chen M, et al. A Chemomechanical Model for Nuclear Morphology and Stresses during Cell Transendothelial Migration. Biophysical journal. 2016;111:1541–52. doi: 10.1016/j.bpj.2016.08.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 187.Doyle AD, Nicole C, Jin A, Kazue M, Yamada KM. Local 3D matrix microenvironment regulates cell migration through spatiotemporal dynamics of contractility-dependent adhesions. Nature communications. 2015:6. doi: 10.1038/ncomms9720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Li Y, Huang G, Gao B, Li M, Genin GM, Lu TJ, et al. Magnetically actuated cell-laden microscale hydrogels for probing strain-induced cell responses in three dimensions. Npg Asia Materials. 2016;8:e238. [Google Scholar]
- 189.Boudou T, Legant W, Mu A, Borochin MA, Thavandiran N, Radisic M, et al. A Microfabricated Platform to Measure and Manipulate the Mechanics of Engineered Cardiac Microtissues. Tissue Engineering Part A. 2011;18:910–9. doi: 10.1089/ten.tea.2011.0341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 190.Marquez JP, Genin GM. Whole cell mechanics of contractile fibroblasts: relations between effective cellular and extracellular matrix moduli. Philosophical Transactions. 2010;368:635. doi: 10.1098/rsta.2009.0240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 191.Marquez JP, Genin GM, Zahalak GI, Elson EL. The Relationship between Cell and Tissue Strain in Three-Dimensional Bio-Artificial Tissues. Biophysical journal. 2005;88:778–89. doi: 10.1529/biophysj.104.041947. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 192.Thomopoulos S, Das R, Birman V, Smith L, Ku K, Elson EL, et al. Fibrocartilage tissue engineering: the role of the stress environment on cell morphology and matrix expression. Tissue Engineering Part A. 2011;17:1039–53. doi: 10.1089/ten.tea.2009.0499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Riehl BD, Park JH, Kwon IK, Lim JY. Mechanical stretching for tissue engineering: two-dimensional and three-dimensional constructs. Tissue Engineering Part B Reviews. 2012;18:288. doi: 10.1089/ten.teb.2011.0465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Henshaw DR, Attia E, Bhargava M, Hannafin JA. Canine ACL fibroblast integrin expression and cell alignment in response to cyclic tensile strain in three-dimensional collagen gels. Journal of Orthopaedic Research. 2006;24:481. doi: 10.1002/jor.20050. [DOI] [PubMed] [Google Scholar]
- 195.Kobayashi T, Sokabe M. Sensing substrate rigidity by mechanosensitive ion channels with stress fibers and focal adhesions. Current Opinion in Cell Biology. 2010;22:669–76. doi: 10.1016/j.ceb.2010.08.023. [DOI] [PubMed] [Google Scholar]
- 196.Lele TP, Pendse J, Kumar S, Salanga M, Karavitis J, Ingber DE. Mechanical forces alter zyxin unbinding kinetics within focal adhesions of living cells. Journal of Cellular Physiology. 2006;207:187–94. doi: 10.1002/jcp.20550. [DOI] [PubMed] [Google Scholar]
- 197.Lele TP, Thodeti CK, Pendse J, Ingber DE. Investigating complexity of protein–protein interactions in focal adhesions. Biochemical & Biophysical Research Communications. 2008;369:929–34. doi: 10.1016/j.bbrc.2008.02.137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 198.Born S, Diez G, Goldmann WH, Merkel R, Hoffmann B. Becoming stable and strong: The interplay between vinculin exchange dynamics and adhesion strength during adhesion site maturation. Cell Motility & the Cytoskeleton. 2009;66:350–64. doi: 10.1002/cm.20375. [DOI] [PubMed] [Google Scholar]
- 199.Wolfenson H, Bershadsky A, Henis YI, Geiger B. Actomyosin-generated tension controls the molecular kinetics of focal adhesions. Journal of Cell Science. 2011;124:1425–32. doi: 10.1242/jcs.077388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 200.Choi CK, Vicentemanzanares M, Zareno J, Whitmore LA, Mogilner A, Horwitz AR. Actin and α-actinin orchestrate the assembly and maturation of nascent adhesions in a myosin II motor-independent manner. Nature cell biology. 2008;10:1039–50. doi: 10.1038/ncb1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 201.Babaei B, Davarian A, Lee SL, Pryse KM, Mcconnaughey WB, Elson EL, et al. Remodeling by fibroblasts alters the rate-dependent mechanical properties of collagen. Acta biomaterialia. 2016;37:28–37. doi: 10.1016/j.actbio.2016.03.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 202.Babaei B, Davarian A, Pryse KM, Elson EL, Genin GM. Efficient and optimized identification of generalized Maxwell viscoelastic relaxation spectra. Journal of the mechanical behavior of biomedical materials. 2015;55:32. doi: 10.1016/j.jmbbm.2015.10.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 203.Pryse KM, Nekouzadeh A, Genin GM, Elson EL, Zahalak GI. Incremental Mechanics of Collagen Gels: New Experiments and a New Viscoelastic Model. Annals of Biomedical Engineering. 2003;31:1287–96. doi: 10.1114/1.1615571. [DOI] [PubMed] [Google Scholar]
- 204.Chan MW, Flee C. Force-induced myofibroblast differentiation through collagen receptors is dependent on mammalian diaphanous (mDia) Journal of Biological Chemistry. 2010;285:9273–81. doi: 10.1074/jbc.M109.075218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 205.Provenzano PP, Inman DR, Eliceiri KW, Keely PJ. Matrix density-induced mechanoregulation of breast cell phenotype, signaling and gene expression through a FAK-ERK linkage. Oncogene. 2009;28:4326–43. doi: 10.1038/onc.2009.299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 206.Ihalainen TO, Aires L, Herzog FA, Schwartlander R, Moeller J, Vogel V. Differential basal-to-apical accessibility of lamin A/C epitopes in the nuclear lamina regulated by changes in cytoskeletal tension. Nature materials. 2015;14:1252–61. doi: 10.1038/nmat4389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 207.Fedorchak GR, Kaminski A, Lammerding J. Cellular mechanosensing: getting to the nucleus of it all. Progress in Biophysics & Molecular Biology. 2014;115:76–92. doi: 10.1016/j.pbiomolbio.2014.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 208.Horton ER, Byron A, Askari JA, Ng DH, Millon-Frémillon A, Robertson J, et al. Definition of a consensus integrin adhesome and its dynamics during adhesion complex assembly and disassembly. Nature cell biology. 2015;17:1577. doi: 10.1038/ncb3257. [DOI] [PMC free article] [PubMed] [Google Scholar]