Abstract
The temperature dependence of biological processes has been studied at the levels of individual biochemical reactions and organism physiology (e.g. basal metabolic rates) but has not been examined at the metabolic network level. Here, we used a systems biology approach to characterize the temperature dependence of the human red blood cell (RBC) metabolic network between 4 and 37 °C through absolutely quantified exo- and endometabolomics data. We used an Arrhenius-type model (Q10) to describe how the rate of a biochemical process changes with every 10 °C change in temperature. Multivariate statistical analysis of the metabolomics data revealed that the same metabolic network-level trends previously reported for RBCs at 4 °C were conserved but accelerated with increasing temperature. We calculated a median Q10 coefficient of 2.89 ± 1.03, within the expected range of 2–3 for biological processes, for 48 individual metabolite concentrations. We then integrated these metabolomics measurements into a cell-scale metabolic model to study pathway usage, calculating a median Q10 coefficient of 2.73 ± 0.75 for 35 reaction fluxes. The relative fluxes through glycolysis and nucleotide metabolism pathways were consistent across the studied temperature range despite the non-uniform distributions of Q10 coefficients of individual metabolites and reaction fluxes. Together, these results indicate that the rate of change of network-level responses to temperature differences in RBC metabolism is consistent between 4 and 37 °C. More broadly, we provide a baseline characterization of a biochemical network given no transcriptional or translational regulation that can be used to explore the temperature dependence of metabolism.
Keywords: computational biology, erythrocyte, metabolism, metabolomics, systems biology
Introduction
The rate of biological processes increases with increasing temperature. The dependence of biochemical rates on temperature has been studied since the late 19th century using an Arrhenius-type approach (1–6). The metric used for evaluating such temperature dependence is the temperature coefficient (Q10 coefficient).2 If Q10 = 2 for a given process, then the rate of that process increases by a factor of 2 for every 10 °C increase in temperature. The Q10 can be calculated from the slope of a rate versus temperature plot, which is approximately linear over the biologically relevant temperature range of 0–40 °C (7). Individual enzymes have different Q10 coefficients that are generally expected to be in the 2–3 range (3, 4, 6).
Temperature dependence at the physiological level is determined using phenomenological measurements (such as growth rate) to study overall physiological changes (5, 7–10). Changes at the physiological level depend on more than changes in the underlying individual biochemical reaction rates (11, 12). For instance, various regulatory mechanisms (e.g. transcriptional, post-translational, and allosteric) determine how cells respond to temperature shock (13). The existence of extra layers of regulation complicates the effects of temperature change on the biochemical network. Biology is inherently multiscale, and the gap between observing the temperature dependence at the scale of an individual reaction and at the physiological level can be addressed through methods of systems biology (14).
Red blood cells (RBCs) represent an ideal cell type to study the temperature dependence of network-level metabolic biochemistry because of the absence of a nucleus and genetic material. This absence results in a lack of complicated transcriptional or translational regulation on metabolic enzyme activity. Allosteric and other regulation of enzymatic reaction rates is still present in RBCs, representing enzyme kinetic mechanisms and thus direct biochemical functions.
In this study, we investigated the temperature dependence of metabolism in the RBC at the network level by examining the rate of change of metabolite concentrations and metabolic reactions rates. We measured exo- and endometabolomics profiles in human RBCs stored at four different temperatures that span the range between the ex vivo (storage) and in vivo (body) temperatures: 4, 13, 22, and 37 °C. We regressed the concentration profile of each metabolite across the measured temperature range to calculate its Q10 value. We integrated these measurements with a cell-scale network reconstruction of RBC metabolism (15) that contains 216 metabolites (43% of which are measurable by quantitative metabolomic profiling) to calculate Q10 coefficients for reaction fluxes and to observe pathway usage. By examining metabolite profiles in the context of a cell-scale metabolic model, we were able to assess temperature dependence on a network level, thus bridging the gap between studies at the reaction and physiological levels.
Results
Measurement of the temperature dependence of RBC metabolism ex vivo
RBCs were collected using standard collection procedures and stored in SAGM medium (16) at 4, 13, 22, and 37 °C. Starting 1 day after RBC collection (taken as time 0 in figures), metabolomic measurements were made in biological triplicate over time at each temperature (Fig. 1A). The data set was composed of 97 metabolites. In addition, standard blood bank quality control and assurance measurements (e.g. hemolysis and pH) were made at multiple time points over 21 (4, 13, and 22 °C) and 7 days (37 °C); all measured profiles are presented in supplemental Figs. S6–S16 and Data S1.
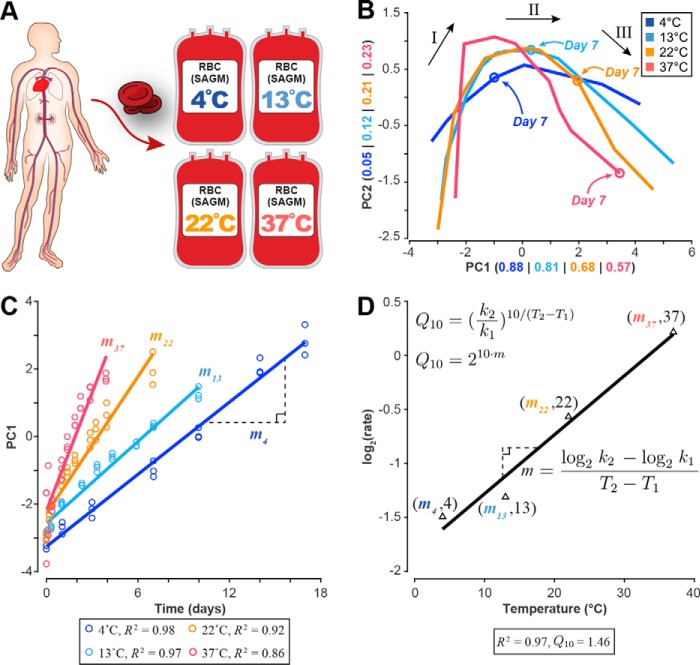
Figure 1.
Data generation and analysis workflow. A, human red blood cells were collected; stored in SAGM medium at 4, 13, 22, and 37 °C; and metabolically profiled across multiple time points. B, PCA of the eight extracellular biomarkers (same loading coefficients applied to data at each temperature). Overlaying these plots on the same axes shows that the shape of the three-phase metabolic decay is conserved but accelerated with increasing temperature as evidenced by the location of the day 7 time point. See supplemental Fig. S1 for a more detailed PCA plot at each temperature. The numbers in parentheses represent the amount of variance explained by each component. Black arrows and roman numerals label the three metabolic shifts that occur over the storage period. C, the first principal component was plotted against the time vector at each temperature to determine the relative storage time at each temperature. Linear regression was used to estimate the rate of change, showing strong correlation between PC1 and time at each temperature. D, these rates of change were then used to estimate the change in metabolic rate for every 10 °C (Q10) from an Arrhenius-type log2(rate) versus temperature plot.
As part of the baseline characterization, we observed the same metabolic changes that have previously been reported in the literature for RBC storage at 4 °C. We observed the same previously documented accumulation of lactate, 5-oxoproline, and hypoxanthine (17–19) and the depletion of AMP and the phosphoglycerate pool (17, 19). We measured the same high levels of intracellular malate previously reported in SAGM at 4 °C (19). A complete discussion of the raw metabolomics data is presented in the supplemental information and Figs. S2 and S3.
To determine temperature dependence, we first needed to determine how relative storage time scaled across temperature (Food and Drug Administration regulations set the maximum storage time for RBCs at 42 days). To determine a network-level Q10, we used multivariate statistical analysis on the metabolomics data to assess the impact of temperature changes on systemic metabolism. The network-level Q10 was used to determine the time points that represented the same metabolic phase at each temperature. Once these time periods were defined, we calculated Q10 coefficients for each measured metabolite using linear regression. The metabolomics data were then integrated into a mechanistic cell-scale model to calculate the rate of each reaction (i.e. the flux) in the network at each temperature; these calculated reaction rates were used to determine Q10 coefficients for reactions and to assess pathway usage across temperature.
Network-level temperature dependence
Following published reports for RBC storage at 4 °C (17, 19, 20), principal component analysis (PCA) was performed to obtain a global characterization of the data set. PCA is a multivariate statistical method that reduces the dimensionality of a complex data set by calculating the relative contribution of each measurement to the overall variability observed in the data. For each temperature, we performed PCA (Fig. 1B) on the time-series concentration profiles of eight recently identified extracellular metabolites (adenine, glucose, hypoxanthine, lactate, malate, nicotinamide, 5-oxoproline, and xanthine) that robustly represent the RBC metabolome under storage conditions (20). These metabolites serve as qualitative biomarkers for the age of stored RBCs and have been shown to also be good quantitative predictors for other systemic metabolite concentrations (21, 22). To make an accurate comparison across temperatures, the same loading coefficients were applied to the data at each temperature (see “Experimental procedures” for full details).
PCA revealed the same metabolic “shifts” that have been previously observed at 4 °C (17, 19). These shifts separate three distinct metabolic states that can be reliably determined from the profiles of the biomarkers (20). During storage at 4 °C, the two shifts in the PCA plot occur approximately at days 10 and 17. Here, these same metabolic states were observed to be conserved but notably accelerated with temperature as evidenced by the location of the day 7 time point at each temperature (Fig. 1B and supplemental Fig. S1). We identified the duration of the first metabolic state at each temperature. We then used these time points to determine the starting and ending points for the linear regression that would be used to calculate individual metabolite and reaction Q10 coefficients.
The first principal component at each temperature was highly correlated with time (Fig. 1C), yielding a “network-level” Q10 of 1.46 (R2 = 0.97) that describes how the system proceeds in storage time. The third metabolic state at 4 °C is primarily characterized by a general loss of function as the RBC undergoes severe morphological changes (23, 24), often leading to complications for transfusion patients (25, 26). Thus, we only used measurements from the first two metabolic states to calculate the network-level Q10. These results show an overall three-state metabolic decay that is observed to accelerate with increased temperature.
Metabolite-level temperature dependence
To determine the temperature dependence of individual metabolites, we used the data from the first metabolic state at each temperature (identified from the PCA results in Fig. 1B). We made this choice because the data are believed to be the most accurate as the cells are still intact and metabolism is functioning the closest to its normal physiological state. We linearly regressed the concentration profile of each metabolite at each temperature and used these rates to calculate a Q10 value (Fig. 1, C and D). Not all metabolite profiles could be accurately fit with a linear curve during the first state; to account for this, we did not include metabolites with an R2 < 0.50. Q10 coefficients for the 48 metabolites whose profiles could be estimated well with a linear fit are reported in Table 1. The calculated Q10 coefficients span 1.28 (extracellular 5-oxoproline) to 5.89 (intracellular hypoxanthine).
Table 1.
Q10 coefficients for extracellular (exo) and intracellular (endo) metabolites
| Metabolite | Q10 | R2 |
|---|---|---|
| 5-Oxoprolinea (exo) | 1.28 | 0.69 |
| l-Glycerate (endo) | 1.84 | 0.52 |
| S-Adenosylmethioninamine (endo) | 1.94 | 0.83 |
| l-Glutamate (endo) | 2.01 | 0.94 |
| cis-Aconitate (endo) | 2.06 | 0.91 |
| l-Glutamate (exo) | 2.15 | 0.99 |
| l-Aspartate (endo) | 2.18 | 0.73 |
| Nicotinamidea (exo) | 2.19 | 0.91 |
| Mannitol (exo) | 2.22 | 0.86 |
| Uridine (exo) | 2.27 | 0.94 |
| Citrate (exo) | 2.32 | 0.99 |
| l-Glutamine (endo) | 2.34 | 0.90 |
| Reduced Glutathione (exo) | 2.39 | 0.99 |
| Choline (endo) | 2.41 | 0.85 |
| GMP (endo) | 2.42 | 0.97 |
| 5-Oxoproline (endo) | 2.56 | 0.98 |
| Lactate (endo) | 2.61 | 0.98 |
| l-Acetylcarnitine (endo) | 2.62 | 0.72 |
| Xanthine (endo) | 2.65 | 0.84 |
| cis-Aconitate (exo) | 2.75 | 0.91 |
| Phosphorylcholine (endo) | 2.75 | 0.89 |
| Lactatea (exo) | 2.78 | 0.99 |
| Uridine (endo) | 2.79 | 0.96 |
| Glucosea (exo) | 2.81 | 0.98 |
| AMP (endo) | 2.96 | 0.79 |
| Adeninea (exo) | 2.98 | 0.93 |
| l-Serine (exo) | 2.99 | 0.99 |
| S-Adenosylhomocysteine (endo) | 3.01 | 0.83 |
| Malate (endo) | 3.02 | 0.97 |
| Oxidized glutathione (endo) | 3.03 | 0.95 |
| l-Carnitine (exo) | 3.04 | 0.97 |
| 5-Methylthioadenosine (endo) | 3.07 | 0.73 |
| Adenine (endo) | 3.17 | 0.95 |
| Glucose 6-phosphate (endo) | 3.19 | 0.97 |
| l-Glutamine (exo) | 3.23 | 0.99 |
| l-Phenylalanine (exo) | 3.33 | 0.75 |
| IMP (endo) | 3.45 | 1.00 |
| l-Lysine (exo) | 3.46 | 0.96 |
| Chloride ion (exo) | 3.94 | 0.99 |
| ATP (endo) | 3.95 | 0.92 |
| l-Histidine (exo) | 4.07 | 0.89 |
| ADP (endo) | 4.48 | 0.84 |
| 6-Phosphogluconate (endo) | 4.84 | 0.79 |
| Oxidized glutathione (exo) | 4.99 | 0.95 |
| Malatea (exo) | 5.05 | 0.99 |
| l-Lysine (endo) | 5.18 | 0.97 |
| Reduced glutathione (endo) | 5.61 | 0.96 |
| Hypoxanthine (endo) | 5.89 | 0.95 |
a Previously reported biomarker (20).
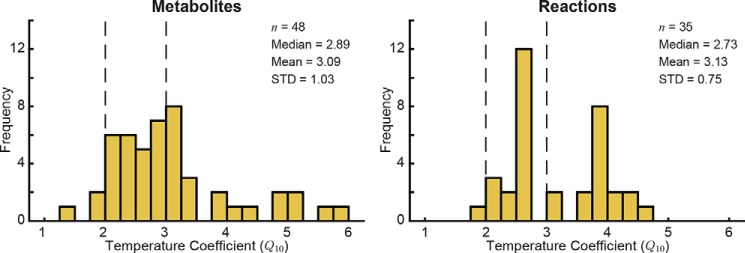
The calculated metabolite Q10 coefficients generally fall in the expected range of 2–3 for biochemical reactions (3, 4, 6) with a median of 2.89 (Fig. 2). The standard deviation of the metabolite Q10 coefficients was 1.03, indicating that although the distribution was centered in the expected range for biological measurements the temperature scaling was not uniform across the network. Interestingly, the biomarker pools that have been shown to robustly define the metabolic decay process (20) represented almost the full range of calculated Q10 coefficients from 1.28 (5-Oxoproline) to 5.05 (malate); extracellular xanthine and hypoxanthine did not have calculated Q10 coefficients due to the R2 cutoff. Several metabolite Q10 coefficients fell below 2.00 or above 3.00, including extracellular 5-oxoporline (1.28), ATP (3.95), ADP (4.48), and extracellular malate (5.05).
Figure 2.
Distribution of Q10 coefficients for metabolites and reactions. Q10 coefficients for metabolites were calculated based on the observed change in metabolite concentration across temperature. The vertical dashed lines at Q10 = 2 and Q10 = 3 represent the typical estimated range of Q10 coefficients for biological processes. STD, standard deviation.
Reaction-level temperature dependence
Next, we investigated the temperature dependence of biochemical reactions in the metabolic network. Previous studies have investigated the temperature dependence of individual reactions (1–6), but our goal was to use systems biology approaches to determine the temperature dependence of all reactions in the network together. To this end, we used a mechanistic cell-scale model of the RBC (15) to calculate the flux state of the network (i.e. the flux through each reaction in the system). The flux through a reaction (a rate with units of mmol/h) was calculated at each temperature; these values were then used to calculate a Q10 for each reaction using the same procedure shown in Fig. 1D. We tailored the model to the physiology at each temperature by integrating the metabolomics measurements for the first metabolic state into the model according to Bordbar et al. (27). See “Experimental procedures” for full details on flux modeling and metabolomics integration.
Model simulations yielded flux states for each temperature. We excluded transporters and reactions that carried flux at fewer than three temperatures to ensure the accuracy of the Q10 calculations. The calculated Q10 coefficients for 35 reactions are shown in Table 2 (only fits with R2 ≥ 0.50 were included in analysis). The distribution of reaction Q10 coefficients (Fig. 2) was tighter than that of the metabolite Q10 coefficients (standard deviation of 0.75 for reactions versus 1.03 for metabolites) but was still centered in the expected 2–3 range (median of 2.73). Several reactions in nucleotide metabolism and glutathione metabolism had Q10 coefficients above 3.5.
Table 2.
Q10 coefficients for reaction fluxes
Reaction and metabolite abbreviations are BiGG database identifiers. GGCT, glutamyl cyclotransferase; GLUCYS, γ-glutamylcysteine synthetase; GTHS, glutathione synthase; GLNS, glutamine synthetase; ADK1 , adenylase kinase; PPA, inorganic diphosphatase; PGK, phosphoglycerate kinase; ENO , enolase; PGM, phosphoglycerate mutase; ADA, adenosine deaminase; PYK, pyruvate kinase; HEX1, hexokinase; AMPDA, adenosine monophosphate deaminase; GAPD, glyceraldehyde-3-phosphate dehydrogenase; PFK , phosphofructokinase; FBA, fructose-bisphosphate aldolase; TPI, triose-phosphate isomerase; PGI, glucose-6-phosphate isomerase; PEPCK, phosphoenolpyruvate carboxylase; NDPK1, nucleoside-diphosphate kinase (ATP:GDP); NTD11, 5′-nucleotidase (IMP); NTD7, 5′-nucleotidase (AMP); PRPPS, phosphoribosylpyrophosphate synthetase; PDE1, 3′,5′-cyclic-nucleotide phosphodiesterase; ADNCYC, adenylate cyclase; DPGase, diphosphoglycerate phosphatase; GLUN, glutaminase; GUAPRT, guanine phosphoribosyltransferase; NTD9, 5′-nucleotidase (GMP); PUNP3, purine-nucleoside phosphorylase (guanosine); PPM, phosphopentomutase; PUNP5, purine-nucleoside phosphorylase (inosine); OPAHir, 5-oxoproline amidohydrolase (ATP-hydrolyzing); P C, pyruvate carboxylase ; HXPRT, hypoxanthine phosphoribosyltransferase; g lucys , γ-l-glutamyl-l-cysteine; 5 oxpro , 5-oxoproline; gthrd, reduced glutathione; 3pg, 3-phospho-d-glycerate; 13dpg, 3-phospho-d-glyceroyl phosphate; 2pg, 2-phospho-d-glycerate; pep, phosphoenolpyruvate; adn, adenosine; ins, inosine; pyr, pyruvate; g6p, d-glucose 6-phosphate; imp, inositate; g3p, glyceraldehyde 3-phosphate; f6p, d-fructose 6-phosphate; fdp, d-fructose 1,6-bisphosphate; dhap, dihydroxyacetone phosphate; oaa, oxaloacetate; r5p, α-d-ribose 5-phosphate; prpp, 5-phospho-α-d-ribose 1-diphosphate; 23dpg, 2,3-disphospho-d-glycerate; gua, guanine; gsn, guanosine; r1p, α-d-ribose 1-phosphate; hxan, hypoxanthine.
| Reaction | Q10 | R2 | Formula |
|---|---|---|---|
| GGCT | 1.98 | 0.93 | glucys → 5oxpro + cys-L |
| GLUCYS | 2.06 | 0.93 | atp + cys-L + glu-L → adp + glucys + h + pi |
| GTHS | 2.21 | 0.93 | atp + glucys + gly → adp + gthrd + h + pi |
| GLNS | 2.23 | 0.91 | atp + glu-L + nh4 → adp + gln-L + h + pi |
| ADK1 | 2.29 | 0.91 | amp + atp ⇆ 2 adp |
| PPA | 2.40 | 0.94 | h2o + ppi → h + 2 pi |
| PGK | 2.53 | 0.95 | 3pg + atp ⇆ 13dpg + adp |
| ENO | 2.57 | 0.95 | 2pg ⇆ h2o + pep |
| PGM | 2.57 | 0.95 | 2pg ⇆ 3pg |
| ADA | 2.58 | 0.99 | adn + h2o + h → ins + nh4 |
| PYK | 2.59 | 0.95 | adp + h + pep → atp + pyr |
| HEX1 | 2.60 | 0.95 | atp + glc-D → adp + g6p + h |
| AMPDA | 2.62 | 0.99 | amp + h2o + h → imp + nh4 |
| GAPD | 2.63 | 0.95 | g3p + nad + pi ⇆ 13dpg + h + nadh |
| PFK | 2.65 | 0.96 | atp + f6p → adp + fdp + h |
| FBA | 2.65 | 0.96 | fdp ⇆ dhap + g3p |
| TPI | 2.65 | 0.96 | dhap ⇆ g3p |
| PGI | 2.72 | 0.96 | g6p ⇆ f6p |
| PEPCK | 3.04 | 0.93 | gtp + oaa → co2 + gdp + pep |
| NDPK1 | 3.04 | 0.93 | atp + gdp ⇆ adp + gtp |
| NTD11 | 3.60 | 0.91 | h2o + imp → ins + pi |
| NTD7 | 3.70 | 0.91 | amp + h2o → adn + pi |
| PRPPS | 3.78 | 0.93 | atp + r5p ⇆ amp + h + prpp |
| PDE1 | 3.79 | 0.91 | camp + h2o → amp + h |
| ADNCYC | 3.79 | 0.91 | atp → camp + ppi |
| DPGase | 3.79 | 0.91 | 23dpg + h2o → 3pg + pi |
| GLUN | 3.79 | 0.91 | gln-L + h2o → glu-L + nh4 |
| GUAPRT | 3.81 | 0.91 | gua + prpp → gmp + ppi |
| NTD9 | 3.81 | 0.91 | gmp + h2o → gsn + pi |
| PUNP3 | 3.81 | 0.91 | gsn + pi ⇆ gua + r1p |
| PPM | 4.04 | 0.95 | r1p ⇆ r5p |
| PUNP5 | 4.16 | 0.96 | ins + pi ⇆ hxan + r1p |
| OPAHir | 4.26 | 0.92 | 5oxpro + atp + 2 h2o → adp + glu-L + h + pi |
| PC | 4.34 | 0.94 | atp + hco3 + pyr → adp + h + oaa + pi |
| HXPRT | 4.54 | 0.96 | hxan + prpp → imp + ppi |
Pathway usage across temperature
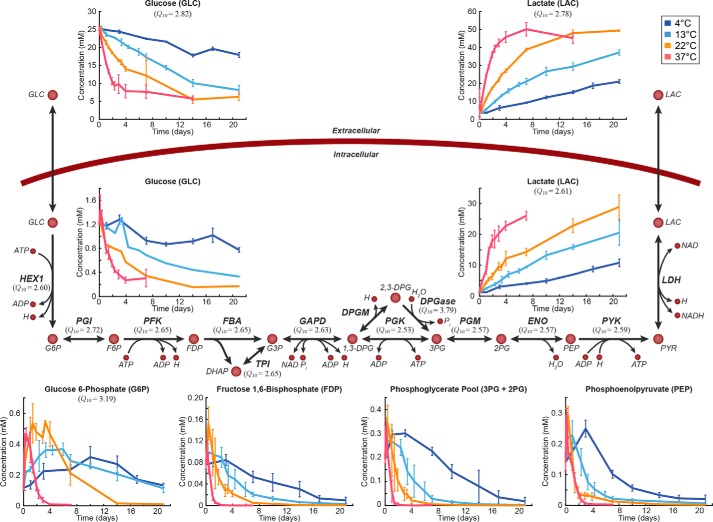
We then examined pathway usage across the 33 °C temperature range studied. Each reaction in RBC reconstruction has previously been assigned to one of 18 different metabolic subsystems (15). We first investigated whether the reactions in any of these pathways shared a similar dependence on temperature (i.e. pathways in which reactions had similar Q10 coefficients). We performed a pairwise comparison of the Euclidean distance between Q10 coefficients of reactions from a given subsystem (n reactions) versus 100,000 random permutations of n reactions from all calculated Q10 coefficients. The reactions in glycolysis (n = 12) and nucleotide metabolism (n = 7) both showed statistically significantly smaller distances between Q10 coefficients than would be expected due to random chance (p < 7e−5 and p < 0.047, respectively). Notably, these two metabolic subsystems contain reactions that interact with several of the storage age biomarkers (glucose, lactate, hypoxanthine, and xanthine). In particular, the temperature dependence of the glycolytic reactions is dictated by glucose, the major input to that linear pathway (Fig. 3).
Figure 3.
Metabolic map of glycolysis. Day 0 here is taken to be 1 day after the beginning of the storage period. Q10 coefficients are provided for those metabolites and reactions that could be calculated. Error bars represent the range of measured data for each time point (line indicates mean). All abbreviations are from the BiGG database. G6P, glucose 6-phosphate; F6P, fructose 6-phosphate; FDP, fructose 1,6-bisphosphate; DHAP, dihydroxyacetone phosphate; G3P, glyceraldehyde 3-phosphate; 1,3-DPG, 3-phospho-d-glyceroyl phosphate; 3PG, 3-phospho-d-glycerate; 2PG, 2-phospho-d-glycerate; PEP, phosphoenolpyruvate; PYR, pyruvate; LAC, l-lactate; HEX1, hexokinase; PGI, glucose-6-phosphate isomerase; PFK, phosphofructokinase; FBA, fructose-bisphosphate aldolase; GAPD, glyceraldehyde-3-phosphate dehydrogenase; DPGM, diphosphoglyceromutase; PGK, pyruvate kinase; DPGase, diphosphoglycerate phosphatase; PGM, phosphoglycerate mutase; ENO, enolase; LDH, lactate dehydrogenase.
Although the enrichment of a given pathway for similar Q10 coefficients depends on the reaction fluxes, this analysis does not directly measure whether the flux states between two temperatures were similar. To investigate the conservation of pathway usage across temperature, we normalized the data at each temperature to glucose uptake and calculated the percent distance between the flux states (i.e. the flux through each reaction) at 13, 22, and 37 °C and the flux state at 4 °C. Reactions that were unused at every temperature were excluded (n = 61). Of the remaining 166 reactions, 33 (19.9%) had less than 50% difference at each of the three higher temperatures. All of the glycolytic reactions for which Q10 coefficients were calculated (Fig. 3) were present in this subset of reactions.
Organizational structure of the network
To this point, we have investigated how the metabolomics measurements could be used to determine the temperature dependence of individual metabolites and reactions and of the network. When we integrated the metabolomics measurements into the cell-scale model, the network structure at each temperature changed due to the accumulation and/or depletion of metabolites. These results, however, do not provide any explanation as to why we observe certain Q10 coefficients for certain reactions. To answer this question, we studied the organizational structure of the network in terms of the coupling of certain reaction fluxes. Two reaction fluxes are said to be “flux-coupled” if the ratio of one to the other is constant (28); the flux coupling of a network is a property inherent to its topology. A set of coupled reactions is simply the linking of coupled reactions into a single pathway.
To determine whether the coupling of the network changed with temperature, we defined the coupling characteristic of a network to be the mean of the coupled reaction sets. We compared the base network structure of the RBC metabolic network with that of each temperature, revealing that the coupling characteristic of the network decreased ∼5–10% at each temperature. This result prompted us to ask whether this decoupling was more or less than would be expected due to random chance. We ran a permutation test, determining that the decoupling of the networks observed with a change in temperature was significantly less than would be expected due to random chance (p < 6e−3; see “Experimental procedures” for details on the generation of random networks and the permutation test). Thus, the RBC metabolic network is robust against changes in temperature over the measured 33 °C range.
Discussion
The temperature dependence of biological processes is of fundamental interest. Q10 coefficients have been used to characterize the temperature dependence of individual biochemical reactions and of organism-level behavior. Although these studies have yielded valuable insights, there is a gap between studying temperature dependence at the biochemical and physiological levels (1–10). Systems biology principles can be used to move past the individual reaction level and assess temperature dependence on the network level, effectively bridging the gap between the previous work on temperature dependence at the reaction and physiological levels. In this study, we used deep-coverage metabolomics of human red blood cells in storage to investigate the temperature dependence of network-level biochemistry. We chose a range of temperatures that ranges from the storage temperature of RBCs (4 °C) to body temperature (37 °C). By studying temperatures in this range, we provide baseline data with no transcriptional or translational regulation that can be used to begin to understand the temperature dependence of metabolism in broader contexts. Specifically, these data address the “passive” control that temperature has over network fluxes and metabolites in a system that has most of central carbon metabolism but is not growing. The results obtained here have several primary implications.
First, we determined that although the rate of change for each metabolite and reaction increased with increasing temperature the network-level response was dampened (i.e. lower Q10). This behavior is to be expected because of the difference in response times between individual reactions and a pathway. Notably, the scaling of metabolite and reaction temperature dependence was not observed to be uniform across the network (with high variability in Q10 coefficients). The fact that these network-level behaviors are conserved is a surprising result because certain enzyme inactivations might be expected to be qualitatively disruptive of network behavior at various temperatures. The observed behavior indicates that individual metabolite and reaction Q10 coefficients vary dramatically to preserve global network characteristics. This variability was particularly notable for the storage age biomarkers (20), an interesting result because of their ability to define the qualitative trend of the entire network. Overall, such variability can be expected due to the thermodynamics and kinetics associated with biochemical and enzymatic reactions. Approximately half of the calculated temperature coefficients fell in the 2–3 range (Fig. 2), which is generally accepted as the typical estimate for biological systems (3, 4, 6). Several of the metabolites (e.g. malate, hypoxanthine, and glutathione) and reactions (several glutathione synthesis and nucleotide metabolism reactions) that we calculated to have high Q10 coefficients are relatively disconnected from the rest of the network and thus may not be as affected.
Second, the pathway analyses indicate that even without transcriptional or translational regulation RBCs maintain consistent flux through glycolysis and nucleotide metabolism across temperature. The storage age biomarkers in glycolysis (glucose and lactate) represent the primary exchanges for the RBC metabolic network. The preservation of these exchanges indicates that sustaining these reactions is inherent to the network topology and necessary to maintain physiological functions. The change in pathway usage across the rest of the network is dependent upon kinetics and thermodynamics, properties that are subject to change over a 33 °C temperature range.
Third, it is important to be aware that the temperature dependences calculated here are based on ex vivo measurements, not single-enzyme in vitro assays. Such an assay would inherently be absent from any regulatory or network influences. Our results, although also generated in the absence of transcriptional or translational regulatory effects, suggest that the organizational structure of the network influences the temperature dependence of individual enzymes. Thus, we would not expect the systemic Q10 coefficients calculated here to correlate with previously reported in vitro values. For example, previous studies have reported Q10 coefficients for pyruvate kinase (PYK) in the range of 3.3–4.2 for fish (5), 1.4–1.9 for bats (29), and 1.66–1.69 for turtles (30); we calculated a systemic Q10 coefficient of 2.59 for PYK. The use of a cell-scale model to calculate the flux coupling of various reactions in the metabolic network provides an unambiguous explanation for why sets of reactions in the network have similar Q10 coefficients despite variation of individual Q10 coefficients. Additionally, the flux coupling results suggest that the ex vivo Q10 coefficients calculated here would be different from in vitro Q10 coefficients and from each other because the network structure intrinsically constrains the temperature dependence of certain reactions. The networks at the measured temperatures displayed no significant loss of flux coupling compared with the base model, suggesting that the structural characteristics of the RBC network are robust despite the accumulation or depletion of intermediate metabolites.
We have described the temperature dependence of a human metabolic network over a temperature range of 33 °C, from 4 °C (the Food and Drug Administration-defined RBC storage temperature for transfusion) to 37 °C (the in vivo temperature). Although the RBC represents a simple cellular system, the lack of complex regulatory motifs allows for a direct interrogation of the systems biochemistry underlying metabolism. The use of systems biology methods empowered us to assess the temperature dependence of an ex vivo metabolic system at the network level, helping to understand the relationship between the structure and function of the RBC metabolic network.
Experimental procedures
Experimental methods
RBC unit preparation, data measurements, and metabolomics analyses were performed as previously reported (19, 31). Metabolomics measurements were made over 21 (4, 13, and 22 °C) and 7 days (37 °C).
In brief, the metabolomics analysis was performed using ultraperformance liquid chromatography (UPLC) (ACQUITY, Waters) coupled with a quadrupole/time-of-flight mass spectrometer (SYNAPT G2, Waters). Chromatographic separation was achieved by working in hydrophilic interaction liquid chromatography mode using an ACQUITY amide column (1.7 μm, 2.1 × 150 mm) (Waters).
All RBC samples were analyzed three times: once in positive ionization mode using acidic chromatographic condition and twice in negative ionization mode using both acidic and basic chromatographic conditions. During acidic conditions, mobile phase A was 100% ACN, and mobile phase B was 100% H2O, both containing 0.1% formic acid. The following elution gradient was used during acidic condition: 0 min 99% A, 7 min 30% A, 7.1 min 99% A, 10 min 99% A. Basic conditions used ACN, 10 mm sodium bicarbonate (95:5) as mobile phase A and ACN, 10 mm sodium bicarbonate (5:95) as mobile phase B. During basic conditions, the following elution gradient was used: 0 min 99% A, 6 min 30% A, 6.5 min 99% A, 10 min 99% A.
In all conditions, the flow rate was set at 0.4 ml/min, column temperature was set at 45 °C, and injection volume was 3.5 μl. The mass spectrometer was operated using a 1.5-kV capillary voltage, 30-V sampling cone, and 5-V extraction cone. The cone and the desolvation gas flow were 50 and 800 liters/h, respectively. The source and desolvation gas temperatures were 120 and 500 °C, respectively. MS spectra were acquired in centroid mode from m/z 50 to 1,000 using a scan time of 0.3 s. Leucine enkephalin (2 ng/μl) was used as lock mass (m/z 556.2771 and 554.2615 in positive and negative experiments, respectively).
Identification of unexpected metabolites was achieved by integration, alignment, and conversion of MS data points into exact mass retention time pairs (MarkerLynx, v4.1, Waters). The identity of the unexpected metabolites was established by verifying peak retention time, accurate mass measurements, and tandem mass spectrometry against our in-house database and online databases, including HMDB (32) and METLIN (33). TargetLynx (v4.1, Waters) was used to integrate chromatograms of targeted metabolites. Extracted ion chromatograms were extracted using a 0.02-mDa window centered on the expected m/z for each targeted compound. Quantitation was performed by external calibration with reference standards. Details regarding the quantitative analysis (including the linear range and limit of detection) are reported in supplemental Tables S1 and S2. See the supplemental information for additional details
Multivariate statistical analysis
PCA has previously shown three distinct metabolic shifts occurring over the 42-day storage period for RBCs at 4 °C: days 1–10, days 10–17, and days 17–42 (17, 19, 20). In the data presented in this study, RBCs were stored at 4 °C for 21 days; to ensure that all three shifts were captured in full, we used the metabolomics data from Bordbar et al. (19) to calculate the weightings for the principal components. PCA was performed on the Z-scores of the eight extracellular biomarkers (20): adenine, glucose, hypoxanthine, lactate, malate, nicotinamide, 5-oxoproline, and xanthine. These weights were then used to transform the data presented here so that a more representative comparison could be made across all temperatures. The components were rotated in the transformed space such that the day 0 measurement appears in the lower left corner of the plot.
Calculation of temperature coefficients
Each measurement was plotted against time to find the rate of change. The rate of change was calculated through simple linear regression according to Equation 1,
| (Eq. 1) |
where ŷ is the calculated response, β0 is the y-intercept, β1 is the regression coefficient (i.e. the slope), and ϵ is the error (Fig. 1C). To determine the goodness of fit, the coefficient of determination (R2) was calculated using Equation 2,
| (Eq. 2) |
where ŷ is the calculated value of y and ȳ is the mean of y. Once a rate was obtained for each measurement, Q10 was calculated from the slope of the log2(rate) versus temperature plot (Fig. 1D). This procedure is outlined in the following text.
The definition of Q10 is on the Arrhenius equation (34), which states that the rate of a process (k) is exponentially related to the temperature of that process,
| (Eq. 3) |
where k represents the rate of the process, A is a constant factor that represents the frequency of molecular collision, Ea is the activation energy, R is the gas constant, and T is the temperature of the process (35). The temperature coefficient is empirically defined as the ratio of the rates of two processes (6, 11, 34, 36–38),
| (Eq. 4) |
where k1 and k2 represent the rates of two processes and T1 and T2 represent the temperature at which these processes occur. This relationship is the slope of a plot of log2(rate) versus temperature (Fig. 1D). Using linear regression, the slope of the log2(rate) versus temperature plots was calculated for each measurement and used to calculate the Q10 value from Equation 5,
| (Eq. 5) |
where m is defined as follows.
| (Eq. 6) |
Metabolites whose R2 values were less than 0.50 were excluded in the analysis. This cutoff was determined based on the distribution of R2 values (supplemental Fig. S5); our goal was to maximize the amount of data captured while simultaneously minimizing the inclusion of noisy or poorly fit data. We used the same procedure for calculating the reaction Q10 coefficients. We only included reactions that carried flux in at least three of the temperatures; transport reactions and reactions whose R2 was less than 0.50 were excluded in the analysis. This cutoff was determined based on the distribution of R2 values (supplemental Fig. S5); our goal was to maximize the amount of data captured while simultaneously minimizing the inclusion of noisy or poorly fit data. For reactions, we extended this cutoff to be based on the p value of the F statistic for the linear regression fit of the log2(rate) versus temperature plot; only those reactions whose p value was less than 0.05 were included. The R2 for the reactions whose p values were less than 0.05 was greater than 0.80 for all reactions (i.e. no reactions were excluded based on the R2 value from its linearly regressed fit).
Flux modeling
We used a modified version of the erythrocyte metabolic reconstruction iAB-RBC-283 (15), which was previously used for building personalized kinetic models (39). We integrated the metabolite concentrations into this model to predict the flux state of the network at each temperature using non-steady-state flux balance analysis (27). 2,3-DPG has previously been determined to be one of the more important metabolites in RBC physiology but was not measured here. To obtain the most accurate model of the entire network, we used existing metabolomics data (19) to predict the concentration profile of 2,3-DPG using the profiles of the eight biomarkers as input according to the workflow described in Yurkovich et al. (21).
Flux coupling
We used F2C2 (40) to calculate the flux coupling of the metabolic networks. When the metabolomics data are integrated into the metabolic model, the structure of the network is altered through the addition of source and sink reactions (27). To construct random networks, we needed to ensure that the models were feasible and mimicked the models created using the measured data. Therefore, we randomly chose nodes in the base RBC model that were “measured” as either accumulation (source) or depletion (sink); we used the measured data to determine 1) the number of randomly “measured” nodes, 2) the distribution of intracellular versus extracellular nodes, 3) the distribution of sources versus sinks, and 4) the bounds for the added sources and sinks.
The permutation test compared the difference in the flux coupling characteristic between the base network and the networks at the measured temperatures with the flux coupling characteristic between the base model and 1,000 randomly generated networks (supplemental Fig. S4). The p value was determined to be the fraction of random networks whose difference in the flux coupling characteristic was less than or equal to that of the measured temperature networks.
Author contributions
B. O. P. conceived the study. G. P., O. R., O. E. S., and K. W. generated the data. S. B., S. P., and S. G. operationalized the study. J. T. Y., D. C. Z., A. B., and L. Y. analyzed the results. J. T. Y., D. C. Z., L. Y., J. T. B., and B. O. P. wrote the manuscript. All authors revised and approved the final manuscript.
Supplementary Material
Acknowledgments
We thank Ke Chen, Bin Du, and Nathan Mih for assistance in performing calculations for the thermodynamic properties and thermostability of enzymes.
This work was supported by European Research Council Grant ERC-232816; United States Department of Energy Grant DE-SC0008701 and NHLBI, National Institutes of Health Grant R43HL123074. The authors declare that they have no conflicts of interest with the contents of this article. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
This article contains supplemental information, Data S1, Figs. S1–S16, and Tables S1 and S2.
- Q10
- temperature coefficient
- PCA
- principal component analysis
- SAGM
- saline-adenine-glucose-mannitol
- PYK
- pyruvate kinase
- ACN
- acetonitrile
- 2,3-DPG
- 2,3-diphosphoglycerate.
References
- 1. van't Hoff J. H., Cohen E., and Ewan T. (1896) Studies in Chemical Dynamics, pp. 130–136, Frederick Muller and Co., Amsterdam [Google Scholar]
- 2. Kavanau J. L. (1950) Enzyme kinetics and the rate of biological processes. J. Gen. Physiol. 34, 193–209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Behradek J. (1930) Temperature coefficients in biology. Biol. Rev. Camb. Philos. Soc. 5, 30–58 [Google Scholar]
- 4. Elias M., Wieczorek G., Rosenne S., and Tawfik D. S. (2014) The universality of enzymatic rate-temperature dependency. Trends Biochem. Sci. 39, 1–7 [DOI] [PubMed] [Google Scholar]
- 5. Somero G. N., and Hochachka P. W. (1968) The effect of temperature on catalytic and regulatory functions of pyruvate kinases of the rainbow trout and the antarctic fish Trematomus bernacchii. Biochem. J 110, 395–400 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Hochachka P. W. (1991) Temperature: the ectothermy option, in Biochemistry and Molecular Biology of Fishes (Hochachka P. W., and Mommsen T. P., eds.) Vol. 1, pp. 313–322, Elsevier, Amsterdam [Google Scholar]
- 7. Gillooly J. F., Brown J. H., West G. B., Savage V. M., and Charnov E. L. (2001) Effects of size and temperature on metabolic rate. Science 293, 2248–2251 [DOI] [PubMed] [Google Scholar]
- 8. Burnside W. R., Erhardt E. B., Hammond S. T., and Brown J. H. (2014) Rates of biotic interactions scale predictably with temperature despite variation. Oikos 123, 1449–1456 [Google Scholar]
- 9. Kirschbaum M. U. (1995) The temperature dependence of soil organic matter decomposition, and the effect of global warming on soil organic C storage. Soil Biol. Biochem. 27, 753–760 [Google Scholar]
- 10. Criddle R. S., Hopkin M. S., McArthur E. D., and Hansen L. D. (1994) Plant distribution and the temperature coefficient of metabolism. Plant Cell Environ. 17, 233–243 [Google Scholar]
- 11. Chaui-Berlinck J. G., Monteiro L. H., Navas C. A., and Bicudo J. E. (2002) Temperature effects on energy metabolism: a dynamic system analysis. Proc. Biol. Sci. 269, 15–19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Clarke A., and Fraser K. P. (2004) Why does metabolism scale with temperature? Funct. Ecol. 18, 243–251 [Google Scholar]
- 13. Al-Fageeh M. B., and Smales C. M. (2006) Control and regulation of the cellular responses to cold shock: the responses in yeast and mammalian systems. Biochem. J. 397, 247–259 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Schulte P. M. (2015) The effects of temperature on aerobic metabolism: towards a mechanistic understanding of the responses of ectotherms to a changing environment. J. Exp. Biol. 218, 1856–1866 [DOI] [PubMed] [Google Scholar]
- 15. Bordbar A., Jamshidi N., and Palsson B. O. (2011) iAB-RBC-283: a proteomically derived knowledge-base of erythrocyte metabolism that can be used to simulate its physiological and patho-physiological states. BMC Syst. Biol. 5, 110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Högman C. F., Hedlund K., and Sahleström Y. (1981) Red cell preservation in protein-poor media. III. Protection against in vitro hemolysis. Vox Sang. 41, 274–281 [DOI] [PubMed] [Google Scholar]
- 17. D'Alessandro A., Nemkov T., Kelher M., West F. B., Schwindt R. K., Banerjee A., Moore E. E., Silliman C. C., and Hansen K. C. (2015) Routine storage of red blood cell (RBC) units in additive solution-3: a comprehensive investigation of the RBC metabolome. Transfusion 55, 1155–1168 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Roback J. D., Josephson C. D., Waller E. K., Newman J. L., Karatela S., Uppal K., Jones D. P., Zimring J. C., and Dumont L. J. (2014) Metabolomics of ADSOL (AS-1) red blood cell storage. Transfus. Med. Rev. 28, 41–55 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Bordbar A., Johansson P. I., Paglia G., Harrison S. J., Wichuk K., Magnusdottir M., Valgeirsdottir S., Gybel-Brask M., Ostrowski S. R., Palsson S., Rolfsson O., Sigurjónsson O. E., Hansen M. B., Gudmundsson S., and Palsson B. O. (2016) Identified metabolic signature for assessing red blood cell unit quality is associated with endothelial damage markers and clinical outcomes. Transfusion 56, 852–862 [DOI] [PubMed] [Google Scholar]
- 20. Paglia G., D'Alessandro A., Rolfsson Ó., Sigurjónsson Ó. E., Bordbar A., Palsson S., Nemkov T., Hansen K. C., Gudmundsson S., and Palsson B. O. (2016) Biomarkers defining the metabolic age of red blood cells during cold storage. Blood 128, e43–50 [DOI] [PubMed] [Google Scholar]
- 21. Yurkovich J. T., Yang L., and Palsson B. O. (2017) Biomarkers are used to predict quantitative metabolite concentration profiles in human red blood cells. PLoS Comput. Biol. 13, e1005424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Yurkovich J. T., Yang L., and Palsson B. O. (2017) Utilizing biomarkers to forecast quantitative metabolite concentration profiles in human red blood cells, in Proceedings of the 1st IEEE Conference on Control Technology and Applications, Kohala Coast, Hawaii, August 27–30, 2017, Abstr. TA3.4, Institute of Electrical and Electronics Engineers, New York, NY [Google Scholar]
- 23. D'Alessandro A., Kriebardis A. G., Rinalducci S., Antonelou M. H., Hansen K. C., Papassideri I. S., and Zolla L. (2015) An update on red blood cell storage lesions, as gleaned through biochemistry and omics technologies. Transfusion 55, 205–219 [DOI] [PubMed] [Google Scholar]
- 24. D'Alessandro A., and Seghatchian J. (2017) Hitchhiker's guide to the red cell storage galaxy: omics technologies and the quality issue. Transfus. Apher. Sci. 56, 248–253 [DOI] [PubMed] [Google Scholar]
- 25. Lee J. S., and Kim-Shapiro D. B. (2017) Stored blood: how old is too old? J. Clin. Investig. 127, 100–102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Rapido F., Brittenham G. M., Bandyopadhyay S., La Carpia F., L'Acqua C., McMahon D. J., Rebbaa A., Wojczyk B. S., Netterwald J., Wang H., Schwartz J., Eisenberger A., Soffing M., Yeh R., Divgi C., et al. (2017) Prolonged red cell storage before transfusion increases extravascular hemolysis. J. Clin. Investig. 127, 375–382 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Bordbar A., Yurkovich J. T., Paglia G., Rolfsson O., Sigurjónsson Ó. E., and Palsson B. O. (2017) Elucidating dynamic metabolic physiology through network integration of quantitative time-course metabolomics. Sci. Rep. 7, 46249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Burgard A. P., Nikolaev E. V., Schilling C. H., and Maranas C. D. (2004) Flux coupling analysis of genome-scale metabolic network reconstructions. Genome Res. 14, 301–312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Borgmann A. I., and Moon T. W. (1976) Enzymes of the normothermic and hibernating bat, Myotis lucifugus: temperature as a modulator of pyruvate kinase. J. Comp. Physiol. B 107, 185–199 [Google Scholar]
- 30. Southwood A. L., Darveau C. A., and Jones D. R. (2003) Metabolic and cardiovascular adjustments of juvenile green turtles to seasonal changes in temperature and photoperiod. J. Exp. Biol. 206, 4521–4531 [DOI] [PubMed] [Google Scholar]
- 31. Paglia G., Sigurjónsson Ó. E., Rolfsson Ó., Valgeirsdottir S., Hansen M. B., Brynjólfsson S., Gudmundsson S., and Palsson B. O. (2014) Comprehensive metabolomic study of platelets reveals the expression of discrete metabolic phenotypes during storage. Transfusion 54, 2911–2923 [DOI] [PubMed] [Google Scholar]
- 32. Wishart D. S., Jewison T., Guo A. C., Wilson M., Knox C., Liu Y., Djoumbou Y., Mandal R., Aziat F., Dong E., Bouatra S., Sinelnikov I., Arndt D., Xia J., Liu P., et al. (2013) HMDB 3.0—the human metabolome database in 2013. Nucleic Acids Res. 41, D801–D807 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Smith C. A., O'Maille G., Want E. J., Qin C., Trauger S. A., Brandon T. R., Custodio D. E., Abagyan R., and Siuzdak G. (2005) METLIN: a metabolite mass spectral database. Ther. Drug Monit. 27, 747–751 [DOI] [PubMed] [Google Scholar]
- 34. Hegarty T. W. (1973) Temperature coefficient (q10), seed germination and other biological processes. Nature 243, 305–306 [Google Scholar]
- 35. Laidler K. J. (1984) The development of the Arrhenius equation. J. Chem. Educ. 61, 494 [Google Scholar]
- 36. Sierra C. A. (2011) Temperature sensitivity of organic matter decomposition in the Arrhenius equation: some theoretical considerations. Biogeochemistry 108, 1–15 [Google Scholar]
- 37. Leifeld J., and Fuhrer J. (2005) The temperature response of CO2 production from bulk soils and soil fractions is related to soil organic matter quality. Biogeochemistry 75, 433–453 [Google Scholar]
- 38. Hardy R. N. (1979) Temperature and Animal Life (Studies in Biology), Hodder and Stoughton Ltd., London [Google Scholar]
- 39. Bordbar A., McCloskey D., Zielinski D. C., Sonnenschein N., Jamshidi N., and Palsson B. O. (2015) Personalized whole-cell kinetic models of metabolism for discovery in genomics and pharmacodynamics. Cell Syst. 1, 283–292 [DOI] [PubMed] [Google Scholar]
- 40. Larhlimi A., David L., Selbig J., and Bockmayr A. (2012) F2c2: a fast tool for the computation of flux coupling in genome-scale metabolic networks. BMC Bioinformatics 13, 57. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.