Abstract
We developed a method to evaluate variations in the PET imaging process in order to characterize the relative ability of static and dynamic metrics to measure breast cancer response to therapy in a clinical trial setting. We performed a virtual clinical trial by generating 540 independent and identically distributed PET imaging study realizations for each of 22 original dynamic fluorodeoxyglucose (18F-FDG) breast cancer patient studies pre- and post-therapy. Each noise realization accounted for known sources of uncertainty in the imaging process, such as biological variability and SUV uptake time. Four definitions of SUV were analyzed, which were SUVmax, SUVmean, SUVpeak, and SUV50%. We performed a ROC analysis on the resulting SUV and kinetic parameter uncertainty distributions to assess the impact of the variability on the measurement capabilities of each metric. The kinetic macro parameter, Ki, showed more variability than SUV (mean CV Ki = 17%, SUV = 13%), but Ki pre- and post-therapy distributions also showed increased separation compared to the SUV pre- and post-therapy distributions (mean normalized difference Ki = 0.54, SUV = 0.27). For the patients who did not show perfect separation between the pre- and post-therapy parameter uncertainty distributions (ROC AUC < 1), dynamic imaging outperformed SUV in distinguishing metabolic change in response to therapy, ranging from 12 to 14 of 16 patients over all SUV definitions and uptake time scenarios (p < 0.05). For the patient cohort in this study, which is comprised of non-high-grade ER+ tumors, Ki outperformed SUV in an ROC analysis of the parameter uncertainty distributions pre- and post-therapy. This methodology can be applied to different scenarios with the ability to inform the design of clinical trials using PET imaging.
Keywords: virtual clinical trial, PET imaging, dynamic imaging, therapy response, breast cancer, kinetic modeling, simulations
1. Introduction
Positron emission tomography (PET) imaging is a diagnostic tool that is used to quantify and verify the extent of disease (e.g. cancer staging) and is also used to monitor treatment response or measure disease progression. In this study, we focused on the application of PET imaging to assess response to therapy and its ability to measure change in radiotracer uptake. This ability depends upon a number of factors, including both the bias and uncertainty in the measurements pre- and post-therapy. Numerous sources of variability in the imaging process lead to uncertainties in image-derived metrics that are often large relative to the underlying signal. Some of the physiological and technical sources of uncertainty have been summarized in Thie (2004), Boellaard (2009), Adams et al (2010) and Kinahan and Fletcher (2010). These sources include dose and scanner calibrations, blood glucose level, inflammation, uptake time, and image reconstruction parameters. These variabilities in PET imaging can confound the classification of tumor status as response, stable disease, or progressive disease.
Both kinetic parameters and standardized uptake value (SUV) have been used to monitor response, although SUV is more common owing to its easier estimation (Freedman et al 2003, Muzi et al 2012). While simplified methods such as SUV are more clinically practical to assess treatment response, studies have found results and conclusions could differ from those derived from a full kinetic analysis using dynamic imaging data (Cheebsumon et al 2011, Muzi et al 2012). Static SUV measurements are subject to variability in uptake time, body habitus, administered dose measurements, and other factors (Mankoff et al 2006). Kinetic parameter estimates may be more robust against such variations, but estimating the parameters is also more complex, requiring an arterial input function and dynamic data acquisition. Further, the range of error can be higher for kinetic parameters than for SUV (Shields et al 2008). Under certain conditions it has been found that estimates of kinetic parameters can better distinguish response than SUVs (Römer et al 1998, Dimitrakopoulou-Strauss et al 2004), particularly for lower uptake tumors (Doot et al 2007).
Despite such studies comparing SUV and kinetic parameters, the inherent bias and variance of these parameter estimation processes and the impact on response assessment have not been fully characterized. Comparing the ability of these metrics to detect change in the true underlying biology depends on acquisition hardware, algorithmic data analysis, and clinical protocol parameters. Assessing the impact of these areas on image-based tasks can be time-consuming and difficult. Our solution to evaluate both SUV and kinetic parameter metrics was to use a virtual clinical trial (VCT) approach, which uses a series of linked simulations to evaluate the impact of steps in the entire imaging process on each metric (Moore et al 2012, Kurland et al 2013, 2016, Harrison et al 2014, Maidment 2014, Rashidnasab et al 2015, Wangerin et al 2015, 2017, Häggström et al 2016). We first defined ground truth based on data from prior patient studies. We then performed the forward model, which replicated the patient imaging process and included uncertainties that could be encountered in an actual clinical trial. Finally, we measured the SUVs and estimated the kinetic parameters and analyzed the ability of each metric to measure a change in radiotracer uptake in response to therapy. Table 1 provides a summary of acronyms and key variables used in this paper.
Table 1.
List of acronyms and key variables.
| AIF | Arterial input function |
| ASIM | Analytical PET simulation software |
| AUC | Area under the curve |
| CV | Coefficient of variation |
| ER | Estrogen receptor |
| FDG | Fluorodeoxyglucose |
| i.i.d. | Independent and identically distributed |
| K1 | Rate of transport from plasma into tissue |
| k2 | Rate of transport from tissue into plasma |
| k3 | Rate of metabolism of free precursor to metabolized product in tissue compartment |
| k4 | Rate of retrograde metabolism from metabolized product to free precursor in tissue compartment |
| Ki | Net metabolic flux |
| OSEM | Ordered subsets expectation maximization |
| PET | Positron emission tomography |
| PMOD | Pharmacokinetic modeling software |
| PR | Progesterone receptor |
| ROC | Receiver operating characteristic |
| ROI | Region of interest |
| SD | Standard deviation |
| SUV | Standardized uptake value |
| SUVmax | SUV using maximum pixel value in ROI |
| SUVmean | SUV using mean of pixel values in ROI |
| SUVpeak | SUV using mean value of pixels in 1 cc sphere centered on pixel with maximum value |
| SUV50% | SUV using mean value of pixels in ROI defined by a threshold of 50% of the maximum pixel value |
| TAC | Time activity curve |
| VCT | Virtual clinical trial |
2. Methods
An overview of the VCT process is shown in figure 1. We define a VCT as the following steps: (1) define ground truth, (2) forward model, and (3) estimate and analyze. Each main step has a series of sub-steps that are individual simulations and where uncertainties or parameter variations are taken into account. While the main steps will largely remain constant for all VCTs, the sub-steps will vary for different VCT studies. Table 2 lists the three main steps and sub-steps required for the VCT in this work, the parameter variations applied in each sub-step, and the resulting number of replicates. The steps and sub-steps are described in more detail in the following sections.
Figure 1.
Illustration of the virtual clinical trial process using results for patient 11 of 22, showing the three main categories ((a)–(c)) and the sub-steps in each category: (a) define ground truth: measured patient tumor and normal tissue TACs and patient-specific AIFs were input into a two-compartment model to estimate the kinetic parameters and generate model TACs. These data were defined as ground truth. (b) Forward model: uncertainties were added to K1 and the AIF, and a family of TACs was generated. Each TAC was input into the PET scanner simulation to generate sinograms, from which a time-course of images was reconstructed. This process was performed for both the tumor and normal tissues, and only the tumor data are shown. (c) Estimate and analyze: the static SUV at 60 min post-injection and dynamic SUVs were estimated from the tumors in the reconstructed images. Uptake time uncertainty was added to the static SUV to generate the final SUV uncertainty distributions pre- and post-therapy. The estimated dynamic SUVs were re-input into the kinetic model to generate the final Ki uncertainty distributions.
Table 2.
Summary of steps in the VCT process including parameters and the number of replicates.
| Steps | Sub-step | Parameters | Replicates |
|---|---|---|---|
| Define ground truth | Acquire patient data | Pre- and post-therapy | n = 22 patients, 44 scans |
| Estimate patient AIF and scale population AIF | Pre- and post-therapy | 44 TACs | |
| Estimate kinetic parameters | Pre- and post-therapy | 44 sets (Table 4) | |
|
| |||
| Forward model | Add biological variability | 9.0% CV added to K1, 7.5% CV to AIF AUC | 540/patient scan (23 760 total) |
| Generate synthetic TACs | 22 time points | 540/patient scan (23 760 total) | |
| Simulate sinograms | Poisson noise based on 140M counts at 60 min | 22 time points/patient scan, 36 noise realizations/phantom (14 520 total) | |
| Reconstruct images | 6 mm transaxial and 4 mm axial post-filters | 14 520 total | |
|
| |||
| Estimate and analyze | Add scanner variability | 5% CV | 540/patient scan (23 760 total) |
| Define static SUV regions of interest | 4 variations: max, mean, peak, 50% | 2160/patient scan (95 040 total) | |
| Add static SUV uptake time variability | Scenario 1: perfect Scenario 2: good Scenario 3: poor |
6480/patient scan (285 120 total) | |
| Add AIF measurement noise | Poisson noise based on counts per time bin | 60 time points/patient scan, 540 TACs/patient scan (1 425 600 total time points) | |
| Estimate kinetic parameters | 540/patient scan (23 760 total) | ||
| Calculate AUC from | 23 760 total for Ki | ||
| ROC curves | 285 120 total for SUV | ||
2.1. Define ground truth from patient data
2.1.1. Acquire patient data
Ground truth was defined using patient datasets consisting of 60 min fluorodeoxyglucose (18F-FDG) dynamic acquisitions of 22 patients with non-high-grade (grades 1 and 2), estrogen receptor positive (ER+) primary breast cancer pre- and post-therapy, as previously described (Wangerin et al 2015). Patient characteristics are summarized in table 3. The patient scans were performed on a GE Discovery STE PET/CT Scanner (GE Healthcare, Waukesha, WI). The dynamic data were acquired with frames of 16 × 5 s, 7 × 10 s, 5 × 30 s, 5 × 60 s, 5 × 180 s, 7 × 300 s. The data were reconstructed using 3D OSEM with 28 subsets, six iterations, and a 7 mm transaxial Gaussian post-filter. The image voxel size was 4.3 × 4.3 mm transaxially and 3.3 mm axially. The tumor and normal breast tissue regions-of-interest (ROIs) were 3 × 3 × 3 voxels (1.6 cc). The normal breast tissue ROI was placed in the most homogeneous portion in successive tissue in the contralateral breast. We note here that while partial volume effects, as described in Soret et al (2007), were present in the estimate of SUV, the tumors were not expected to significantly change in size between the pre- and post-therapy scans (average time = 20 d) when treated with hormonal therapy. Thus, partial volume correction methods were not evaluated.
Table 3.
Patient characteristics pre-therapy (n = 22).
| Mean value | Range | |
|---|---|---|
| Age (yr) | 61.7 | 51.6–80.0 |
| Weight (kg) | 80.9 | 43.6–141.8 |
| Injected dose (MBq) | 315 | 230–366 |
| Blood glucose (mg dL−1) | 101.5 | 82–125 |
| Tumor diameter (cm) | 1.6 | 0.6–3.7 |
| Biopsy PR (Allred score) | 5.9 | 0–8 |
| Ki-67 (% staining) | 27.3 | 3.9–70.8 |
| Tumor SUVmean at 60 min | 1.8 | 0.7–4.0 |
| Normal tissue SUVmean at 60 min | 0.4 | 0.1–0.7 |
2.1.2. Estimate patient AIF and scale population AIF
Patient-specific arterial input functions (AIF) were mathematically extracted from the dynamic time-course (O’Sullivan et al 2010, Huang and O’Sullivan 2014) and scaled using the activity concentration measured from a left ventricular ROI drawn over the heart. We then used these patient-specific AIFs to scale a population-averaged AIF based on the late measurements (30–60 min) of the image-derived AIF for each individual patient to generate new patient-specific AIFs. The population AIF was obtained from arterial blood sampling of 57 patients out to 2 h (Olshen and O’Sullivan 1997). We chose to use this population AIF for two reasons. First, the population AIF more accurately captured the peak activity and initial washout phase in the AIF, which were missing from the image-derived input functions due to poor timing resolution. Second, we required AIFs out to 2 h post-injection for the simulation of the TACs, as described in section 2.2.2.
2.1.3. Estimate kinetic parameter sets
A two-tissue compartment model of FDG uptake with irreversible trapping (Sokoloff et al 1977) in PMOD kinetic modeling software (PMOD Technologies Ltd, Zurich, Switzerland) (Burger and Buck 1997) was used to estimate the kinetic parameters. The vascular blood fraction, Vb, of tissue was fixed at 0.04 based on reported experimental measurements of human breast and normal tissues (Beaney et al 1984) and for consistency with a previous study that also showed that a two-fold change in Vb did not significantly change the estimated kinetic parameters (Tseng et al 2004). We assumed irreversible trapping, such that the dephosphorylation rate constant of FDG-6-phosphate, k4, is zero. This is supported by evidence that FDG becomes trapped in breast tumors with slow retrograde metabolism due to the low concentration of glucose-6-phosphatase, as is the case in most cancers (Weber 1977, Okazumi et al 1992). Other studies ranging out to 1 or 2 h post-injection also assumed FDG metabolism to be irreversible and k4 to be zero (Lucignani et al 1993, Wahl et al 1993, Hamberg et al 1994, Zasadny et al 2003). Additionally, we compared the Ki estimates from our model with those from a Patlak graphical analysis (Patlak et al 1983), which assumes that k4 is zero, and found the values to be nearly identical, as expected.
Example patient images are shown in figure 2. Measured tumor and normal tissue TACs with fitted model curves pre- and post-therapy are shown in figure 1(a). The model curves were generated by parameter estimation using non-linear least squares optimization fitting a model curve to the TACs. Statistics on the kinetic modeling parameter estimates for all patients are summarized in table 4.
Figure 2.
Reconstructed patient images (summed 30–60 min of dynamic data) pre- and post-therapy.
Table 4.
Descriptive statistics for estimated tumor kinetic parameters (n = 22 patients).
| Pre-therapy
|
Post-therapy
|
|||
|---|---|---|---|---|
| Mean ± SD | Range | Mean ± SD | Range | |
| K1 (ml/g/min) | 0.043 ± 0.024 | 0.008–0.083 | 0.035 ± 0.020 | 0.005–0.084 |
| k2 (min−1) | 0.144 ± 0.086 | 0.039–0.448 | 0.119 ± 0.059 | 0.033–0.268 |
| k3 (min−1) | 0.020 ± 0.015 | 0.004–0.062 | 0.013 ± 0.007 | 0.001–0.030 |
| Ki | 0.005 ± 0.003 | 0.0006–0.013 | 0.003 ± 0.002 | 0.0005–0.008 |
2.2. Forward model data generation and image reconstruction
2.2.1. Add biological variability
For forward modeling of the simulated TACs, we used the patient-specific AIFs obtained from scaling a population-averaged AIF, as described in section 2.1.2. We added biological variability to these AIFs, as the AIF reflects the time-course of the FDG through the arterial plasma. We added variability based on the findings of Weber et al (1999), who investigated the variability of SUV and kinetic measures for repeat PET scans and found the coefficient of variation (CV) of the kinetic parameter, K1, and area under the AIF to be 9% and 7.5%, respectively.
Ideally, noise would be added to Ki, the net metabolic flux that is defined as Ki = (K1 · k3)/(k2 + k3), but because the estimates of k2 and k3 are correlated, we chose to add biological variability using the parameter K1, which describes the rate of FDG exchange from the blood into the tissue compartment. We added noise to K1 by randomly sampling from a normal distribution with a CV of 9%.
We added noise to the AIF by modifying its peak and shape. A three-exponential decay model (Feng et al 1993) was first fit to the AIF. Noise was added to each parameter of the AIF model by sampling from a normal distribution with a mean and standard deviation defined from the population. Random variation of six parameters resulted in AIFs that were unrealistic, so three constraints were enforced; any point in the new AIF could not deviate more than 15% from the original AIF, the curve must be monotonically decreasing, and the area under the AIF must be within the lower and upper limits defined by a CV of 7.5%.
We generated 540 TAC noise realizations with added biological variability for each pre- and post-therapy patient study. We chose this sample size to both limit computation time and provide 90% confidence that the sample standard deviation of the resulting parameter distributions would be within 10% of the population standard deviation. The tumor K1 uncertainty distributions and AIF noise realizations are shown in figure 1(b) for patient 11.
2.2.2. Generate synthetic time activity curves
The patient-specific estimated kinetic parameters with K1 uncertainty distributions and noisy AIF curves were input into the two-tissue compartment model to generate simulated tumor and normal tissue TACs out to 2 h post-injection for each patient pre- and post-therapy. We generated the TACs out to 2 h to allow for uncertainty in the SUV uptake time. Only 60 min of data were used in the kinetic analysis.
2.2.3. Simulate sinograms
The simulated tumor and normal tissue TACs were sampled at 22 time points, matching the timing of the dynamic imaging used in the original image acquisition. The tumor and normal tissue FDG activities were used to define the signal to background ratio of each tumor as a function of time. Considering 540 noise realizations, 22 time points, and 22 patients pre- and post-therapy, over 500 000 sinograms needed to be generated and then reconstructed. To make this task more tractable, we designed a test phantom with 36 spheres, where each sphere represented one noise realization. Therefore, only 15 phantoms were needed to generate the noise realizations for one time point for one patient, reducing the number of simulated sinograms to 14 520. The impacts of varying tumor size or heterogeneity were not parameters in this study, so a uniform 20 mm sphere size was used for all patients. An example of an axial slice with six spheres is shown in figure 1(b) for four dynamic time points.
ASIM, an analytical PET simulator (Comtat et al 1999), was used to generate noise-free sinogram data from each input phantom based on a GE Discovery STE PET/CT scanner. Poisson noise was added to each noise-free sinogram based on the number of prompt coincidence events in the acquired patient data for each time bin as a function of time post-injection. The number of events in each time bin was dependent on the time bin duration, the amount of activity in the field of view, and radiotracer decay. We simulated 172 million acquired prompt events at 60 min post-injection during a 5 min duration time frame, which was based on the average injected dose over all patients of 300 MBq. The prompt events were assumed to have a trues:scatter:randoms ratio of 1:1:0.35 (Harrison et al 2014).
2.2.4. Reconstruct images
Images were reconstructed using OSEM with 32 subsets and two iterations, and they were post-filtered with a Gaussian kernel having 6 mm and 4 mm full-width-at-half-maximum in the transaxial and axial directions, respectively. The image voxel size was 4.3 × 4.3 × 3.3 mm3, which gives a reconstructed resolution of 5–6 mm (Kinahan et al 2006). Reconstructed images for four dynamic imaging frames are shown in figure 1(b). The noise decreased with time due to increasing number of detected events, and the signal to background ratio increased due to increasing tracer uptake over time.
2.3. Estimate and analyze
2.3.1. Estimate time activity curves
The reconstructed images for each patient comprised of 540 independent and identically distributed (i.i.d.) noise realizations for each dynamic patient scan pre- and post-therapy. We used four methods to extract the SUV from both tumor and normal tissue regions in static 5 min scans at 60 min post-injection; the maximum pixel value in the ROI (SUVmax), the average SUV of a 1.6 cc ROI (3 × 3 × 3 voxels) (SUVmean), the average of a 1 cc spherical ROI centered over the hottest pixel (SUVpeak), and the average SUV over a region created by a 50% threshold of the maximum pixel value (SUV50%). For the kinetic parameter analysis, the SUVmean definition was used to generate TACs using each series of simulated dynamic images for tumor and normal tissue.
To account for additional uncertainties in scanner calibrations, an additional 5% CV was added to all estimates by randomly sampling from a normal distribution, based on measurements of variability for a carefully calibrated scanner over one month (Lockhart et al 2011). The same CV was added to all time points in one TAC. Estimated TACs from all SUV definitions are shown in figure 1(c).
2.3.2. Estimate SUV and kinetic parameters
The final source of uncertainty added to the static SUV measurement was uptake time, which is the time between radiotracer injection and imaging. Although the nominal uptake time is 60 min (Boellaard et al 2010), clinical workflow can result in the scan being performed earlier or later. Three different uptake time scenarios were used, as shown in figure 1(c). Scenario 1 was perfect uptake time for a clinical protocol of imaging 60 min post-injection. Scenarios 2 and 3 reflect rigorous and less rigorous adherence to the clinical protocol, respectively (Kurland et al 2016), and they are plotted for 1000 samples. For each of the three scenarios, SUVs were re-estimated for all of the 540 image realizations for each patient pre- and post-therapy.
Before re-estimating the kinetic parameter estimates, Poisson-distributed measurement noise was added to the scaled population-averaged AIF based on the activity in the each time bin (Graham 1997). The kinetic parameters were re-estimated by inputting these AIFs and TACs into the kinetic model. The overall FDG flux constant, Ki, was calculated for each TAC replicate for each patient.
2.3.3. Perform ROC curve analysis
The SUV and Ki distributions for each patient pre- and post-therapy were used to generate receiver operating characteristic (ROC) curves. Each SUV definition and uptake time scenario combination comprised of 540 measurements, and Ki comprised of 540 estimates. Since we had known ground truth and a large number of data points (e.g. figure 1(c)), we were able to calculate the ROC results by simply recording the true-positive and false-positive fractions for a series of threshold values for both SUV and Ki. The area under the curve (AUC) for each ROC curve was calculated using trapezoidal numerical integration.
3. Results
We compared the SUV and Ki quantitative measurements pre- and post-therapy. A bootstrapping analysis, similar to that performed in Wangerin et al (2015), was performed individually for each patient using the 540 noise realizations, which provided uncertainty distributions pre- and post-therapy for each metric. From these distributions, we calculated the standard deviation, mean, confidence interval of the mean, mean difference between pre- and post-therapy distributions, and statistical significance of the difference between SUV and Ki.
We first evaluated the standard deviations of the pre- and post-therapy AUC distributions as well as the mean difference between them. The results for SUV and Ki are compared in figure 3. For each patient, the CV (averaged between pre- and post-therapy distributions) is plotted versus normalized mean difference. In comparison to SUV, Ki showed higher variability and also a greater mean difference between pre- and post-therapy distributions. The average CV across patients for AUC SUV was 13% over all ROI definitions and uptake time scenarios compared to 17% for AUC Ki. The average CV across patients for AUC SUV differed by just 1.3% for the different ROI definitions and uptake time scenarios. The average pre- and post-therapy normalized mean difference for AUC Ki was 0.54 compared to 0.27 for AUC SUV.
Figure 3.
SUV and Ki CV versus normalized mean difference between pre- and post-therapy distributions. The CV for each patient data point is the average between pre- and post-therapy distributions. The lines connect the corresponding SUV and Ki metrics for each patient.
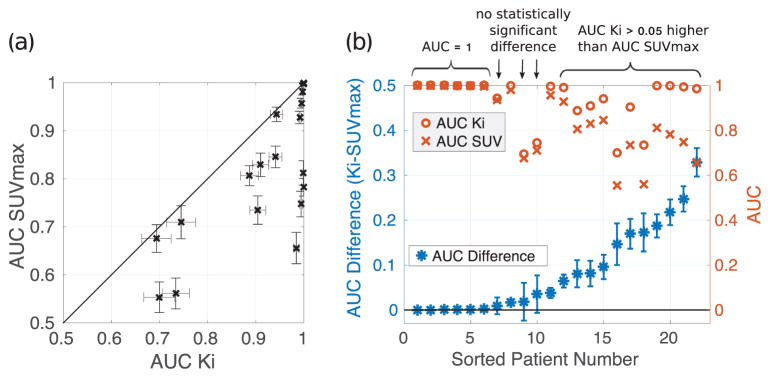
We then compared the AUC SUVmax for uptake time scenario 2 to AUC Ki. Figure 4(a) plots AUC SUVmax versus AUC Ki, where the error bars repesent the 95% confidence intervals and the line of identity separates which method better detected change between pre- and post-therapy radiotracer uptake. Figure 4(b) plots the difference between Ki and SUVmax along with the confidence interval and absolute AUC values. An AUC difference with error bars that do not cross below zero indicates statistically significant higher Ki performance. Six patients (27%) had perfect separation between pre- and post-therapy measures of both SUVmax and Ki (AUC =1). Ki outperformed SUVmax in measuring change in tumor FDG uptake between pre- and post-therapy for the majority of the remaining patients (14/16 (88%), p< 0.05). Eleven of these patients showed an AUC improvement greater than 0.05 for Ki compared to SUVmax. For three patients, there was no statistically significant difference in AUC (p> 0.05).
Figure 4.
(a) Correlation plot of AUC SUVmax for uptake time scenario 2 versus AUC Ki, showing the benefit of Ki over SUVmax in measuring change in response to therapy. (b) The difference between AUC Ki and AUC SUVmax for uptake time scenario 2 is sorted by increasing difference and plotted with 95% confidence intervals on the left-hand ordinate. The corresponding absolute AUC values of the two metrics are plotted on the right-hand ordinate.
We compared the AUCs between Ki and SUVmax for the three uptake time scenarios (figure 5(a)) and between Ki and all four definitions of SUV for uptake time scenario 2 (figure 5(b)). While the uptake time uncertainty impacted AUC SUVmax, the resulting differences in AUC were small compared to the differences with AUC Ki, shown in figure 5(a). The impact of SUV definition and uptake time in comparison to Ki is shown in table 5, which shows the number of patients whose AUC Ki or AUC SUV was at least 0.05 or 0.01 greater than the other metric. Ki outperformed SUV for all cases, with a range of 9–13 patients benefitting when using an AUC difference cutoff of 0.05. In contrast, SUV outperformed Ki for only one or two patients when using a cutoff of 0.05 or 0.01, respectively. While the SUV definition impacted the performance of SUV relative to Ki, the uptake time had almost no impact; the number of patients did not change except for one case of SUVmax.
Figure 5.
Comparison of AUCs for (a) Ki and SUVmax for the three uptake time scenarios and (b) Ki and the four SUV definitions for uptake time scenario 2. Patients are sorted by increasing AUC difference between Ki and SUVmax for both plots. The error bar represents the confidence interval.
Table 5.
The number of patients for whom the AUC of Ki or SUV was statistically significantly greater by at least 0.05 or (0.01).
| AUC Ki >AUC SUV
|
AUC SUV >AUC Ki
|
|||||
|---|---|---|---|---|---|---|
| Scenario 1 | Scenario 2 | Scenario 3 | Scenario 1 | Scenario 2 | Scenario 3 | |
| SUVmax | 11 (14) | 11 (13) | 11 (13) | 0 (0) | 0 (0) | 0 (0) |
| SUVmean | 10 (14) | 10 (14) | 10 (14) | 0 (1) | 0 (1) | 0 (1) |
| SUVpeak | 13 (14) | 13 (14) | 13 (14) | 0 (0) | 0 (0) | 0 (0) |
| SUV50% | 9 (12) | 9 (12) | 9 (12) | 1 (2) | 1 (2) | 1 (2) |
The differences in AUC for the different SUV definitions on a patient-by-patient basis were more significant, as shown in figure 5(b). However, we applied a Bonferroni correction across all patients and found that none of the SUV methods were statistically significantly different from each other. It is known that the Bonferroni correction is conservative and favors the null hypothesis, thus a more detailed analysis that takes into account correlations might find a statistically significantly difference.
4. Discussion
We developed a VCT methodology that links together a chain of models and simulations at each step in the PET imaging and analysis process. A VCT is grounded on data from prior patient studies. Different sources of variability, which could be encountered in an actual clinical trial, are taken into account to estimate the overall bias and variance. The uncertainties include patient protocol, scanner design, image reconstruction, and image analysis methods. The VCT approach does not predict the results of a specific prospective clinical trial, as that will depend on the therapy, disease, patient population, and many others trial-specific factors. Instead, a VCT starts with assumptions of ground truth and then estimates the ability of a single or multi-center trial using imaging to detect or measure a given change. We define a VCT as the following steps: (1) define ground truth, (2) forward model, and (3) estimate and analyze.
We have previously used the VCT approach to estimate the impact of variations in PET scanner sensitivity and reconstruction algorithms on SUV variability and the ability of SUV to measure change (Harrison et al 2014), impact of reconstruction algorithm on detectability (Wangerin et al 2017), impact of FDG uptake time on lesion detectability (Wangerin et al 2015), and impact on needed sample size in multicenter clinical trials (Kurland et al 2013, 2016). A similar method has also been used to assess novel breast screening modalities, such as digital breast tomosynthesis (Maidment 2014, Rashidnasab et al 2015) and chest radiographs (Moore et al 2012). The general framework is study-independent, but the specific modules can change depending on the given problem. For example, this study used a very similar framework to that used in Wangerin et al (2015), which evaluated the impact of imaging time post-injection on SUV.
Through VCTs, we can improve our understanding of any parameter of interest and inform the design of prospective clinical trials, with the goal to improve the success rate, reduce the cost of clinical development, and more quickly translate imaging advancements into the clinic. In this work, we performed a VCT to compare the performance of static and dynamic PET measures while evaluating the impact of known sources of uncertainty in the imaging process in comparison to ground truth. These uncertainties included biological variability, arterial input function measurement uncertainty, scanner calibration variability, quantum noise, image noise correlations, SUV definition, and uptake time uncertainty for SUV. By identifying the dominant sources of uncertainty in the measurements, steps could be taken to reduce the uncertainties and improve measurement capabilities.
While it is most realistic to conduct a VCT based on patient data, patient data lacks ground truth information. Therefore, we assumed the measured patient TACs pre- and post-therapy to be ground truth, from which we defined our baseline SUV measurements and Ki estimates pre- and post-therapy for this VCT study. We then simulated the patient imaging process, accounting for all uncertainties in the imaging process that impacted each metric. We used an ROC analysis to compare how well each metric could measure the original change in radiotracer uptake between pre- and post-therapy imaging. Outcome information was unavailable for this patient cohort, so we could not evaluate the prognostic or predictive value of either metric in correctly classifying responders versus non-responders. Instead, we focused on characterizing the measurement variability.
We found the CV of Ki to be higher than that for SUV (figure 3). Because kinetic parameters are estimated from a time-course of images, where the images immediately following radiotracer injection suffer from low count rates in the field of view, the kinetic parameter estimates are less robust and subject to increased variability compared to the measurement of SUV from a single image at a later time point. Our findings agree with those of Shields et al (2008), who reported that the uncertainty in kinetic measurements was higher than that seen with SUV for patients who underwent test-retest studies with fluorothymidine (18F-FLT). Unfortunately, test-retest studies for dynamic imaging using FDG are scarce. However, there are many studies regarding SUV, and the average CV of 13% found in this study is in line with reports in the literature. Weber et al (1999) found test–retest SUV uncertainty to be 9%, Vanderhoek et al (2012) found an intratumor and population average SUVpeak CV to be 14% and 17%, respectively, Minn et al (1995) found the mean difference in SUVlean and Ki for repeat scans to be 10% each, and Kinahan et al (2010) consulted many previous studies and found the estimated variability of SUVmax to be 10% in a test–retest scenario but at least 15% in practice. The slightly lower CV in this study could be due to a conservative estimate of scanner calibration uncertainty as well as exclusion of body habitus, dose measurement error, and differences in scatter correction methods.
For the majority of patients in this study, Ki was superior to SUV as measured by the ROC AUC (figure 4). Although the variability of Ki was higher than SUV, the AUC considers the trade-offs of both the separation of and variability in the pre- and post-therapy measurement uncertainty distributions; the increased separation in the Ki distributions outweighed the higher CV. Of note, this patient cohort included non-high-grade ER+ breast cancer, which tends to have modest FDG uptake (Fusselman 1995, Graham 1997). Doot et al (2007) found Ki to be superior to SUV in lower uptake tumors, and our findings are consistent with the results of this prior study. With dynamic imaging, we could discern smaller changes in lesion uptake, which is related to the ability of the kinetic parameters to estimate the rate of phosphorylated FDG (FDG-6-phosphate) at low uptake. In contrast, a large fraction of the SUV measurement includes free FDG in the vascular and tissue spaces, which is not related to tumor metabolism.
It is known that differences in SUV definition and uptake time variability can confound study results (Wahl et al 2009, Kinahan et al 2010). We investigated both uncertainties in this work and found SUV definition to have a greater impact than uptake time uncertainty (figure 5). The impact of uptake time largely depends on the shape of the time activity curves pre- and post-therapy, particularly around the standard imaging time of 60 min. Because the uptake curves for this patient cohort were relatively flat, the impact of uptake time on the calculated AUC was low and did not change the relative performance of Ki over SUV (table 5). For a different patient cohort with increasing FDG uptake at 60 min, uptake time jitter could have a larger impact on the performance of SUV relative to Ki. Uptake time jitter, however, is not a factor in dynamic imaging. Kinetic parameter analysis, which is based on the shape of the TAC, is also insensitive to scanner calibration errors.
Other factors that impact SUV include number of iterations and the static imaging duration (number of events). If more OSEM iterations had been performed, we would expect the bias to decrease and the variance to increase. In Harrison et al (2014), changing the scan duration increased the image noise as was expected. However, changing the number of events by a factor of four, for example, had negligible impact on the bias and variance of the estimated parameters, such as SUVmax, and their ability to detect change in response to therapy. Similar results on bias and variance versus scan time were shown in Doot et al (2010). Additionally, Poisson noise contributed only a small part of the total SUV uncertainty in this study. Therefore, we do not anticipate that the AUC results in this study would be significantly different by changing these factors.
Tumors were simulated as uniform spheres, as investigation of impact of ROI definition was beyond the scope of this work. More realistic tumors are often amorphous and heterogeneous, which could introduce more variability based on the ROI selection, thus increasing the variability of the SUV and kinetic parameter estimates. However, it is has been found that factors contributing to bias and variability cancel when looking at changes in response to therapy, provided partial volume effect is not a concern, as noted in Vriens et al (2010).
We did not consider the impact of blood glucose level of SUV. The amount of FDG uptake in the tumor will decrease with increasing blood glucose level and correspondingly lower SUV and Ki values, as described in Lindholm et al (1993). Blood glucose levels could be elevated as result of chemotherapy, which has been reported to cause glucose intolerance (Hickish et al 2009). They reported a maximum blood glucose level of 8 mmol l−1, which is beyond the acceptable limit for FDG PET imaging as recommended in Boellaard et al (2010). A significantly high blood glucose level post-therapy could result in artificially low FDG uptake in the tumor and thus cause a false positive assessment of response. However, measuring the blood glucose level prior to imaging is required, and the patient scan must be rescheduled if the blood glucose is beyond the limit.
We added uncertainty to the imaging process such that the resulting parameters varied around a certain pre- and post-therapy mean, or plausible definition of ground truth. The AIF was used in the definition of ground truth, after which the impact of uncertainties in the imaging process was investigated. Therefore, using the population-based AIF versus another patient-specific AIF did not add extra bias or variability to the study. Further, while we did take into account the possibility that the input function could change due to therapy by using a different patient AIF pre- and post-therapy in the simulation, further changes in AIF were beyond the scope of this work, as they will depend on disease, therapy, and individual response. However, this should not change our conclusions as the estimated parameters in the kinetic modeling take changes in the AIF into account.
We did not explore if there was a correlation in the performance of SUV or Ki in measuring therapeutic response to tumor pathology. We also did not have clinical outcomes such as tumor response or progression or patient survival to further evaluate the predictive value of change in SUV or Ki in response to therapy. Previous studies have found a correlation between pre-therapy SUV or Ki and tumor pathology, such as tumor grade and Ki-67 (Buck et al 2002, Shimoda et al 2007, Koo et al 2015), and the results of other studies have suggested that dynamic analysis may provide superior information in assessing patient response (Dimitrakopoulou-Strauss et al 2004, Mankoff et al 2006, Shields et al 2008). These previous studies included a range of tumor phenotypes, and the tumors in this patient cohort (non-high grade and ER+) were very similar, which was likely the reason that we found Ki to almost unanimously outperform SUV. It is anticipated that there would be a distinction between the performance of SUV and Ki metrics for different tumor characteristics if there had been a wider range of tumor phenotpyes and pre-therapy FDG uptake. A future VCT study could explore the linking of PET parameter changes to the biology of the tumor and patient outcomes to evaluate which metric has better prognostic value. This versatile VCT methodology could also be readily employed to assess the impact of factors not considered here. With slight modifications we could, for instance, determine the impact of image resolution or injected dose on the classification tasks discussed above.
5. Conclusions
A VCT was conducted to compare the ability of static SUV versus dynamic PET imaging to measure response to breast cancer therapy. For this patient cohort, we found that Ki showed a superior ROC performance compared to SUV, suggesting that kinetic analysis, which accounts for the metabolic state of the FDG in the tissue, may better detect or enable earlier assessment of response to therapy. This approach could be extended to evaluate the impact of other sources of variability on the imaging process where there is access to prior patient data.
Acknowledgments
The authors would like to acknowledge Darrin Byrd for helpful discussions and Dan Hippe for his guidance on the statistical analyses. This work was supported by NIH grant numbers CA146456, CA148131, CA72064, CA42045, CA138293, and Susan G Komen Foundation KG100258.
References
- Adams MC, Turkington TG, Wilson JM, Wong TZ. A systematic review of the factors affecting accuracy of SUV measurements. AJR Am J Roentgenol. 2010;195:310–20. doi: 10.2214/AJR.10.4923. [DOI] [PubMed] [Google Scholar]
- Beaney RP, Lammertsma AA, Jones T, McKenzie CG, Halnan KE. Positron emission tomography for in vivo measurement of regional blood flow, oxygen utilisation, and blood volume in patients with breast carcinoma. Lancet. 1984;1:131–4. doi: 10.1016/s0140-6736(84)90063-1. [DOI] [PubMed] [Google Scholar]
- Boellaard R. Standards for PET image acquisition and quantitative data analysis. J Nucl Med. 2009;50:11S–20S. doi: 10.2967/jnumed.108.057182. [DOI] [PubMed] [Google Scholar]
- Boellaard R, et al. FDG PET and PET/CT: EANM procedure guidelines for tumour PET imaging: version 1.0. Eur J Nucl Med Mol Imaging. 2010;37:181–200. doi: 10.1007/s00259-009-1297-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buck A, Schirrmeister H, Kühn T, Shen C, Kalker T, Kotzerke J, Dankerl A, Glatting G, Reske S, Mattfeldt T. FDG uptake in breast cancer: correlation with biological and clinical prognostic parameters. Eur J Nucl Med Mol Imaging. 2002;29:1317–23. doi: 10.1007/s00259-002-0880-8. [DOI] [PubMed] [Google Scholar]
- Burger C, Buck A. Requirements and implementation of a flexible kinetic modeling tool. J Nucl Med. 1997;38:1818–23. [PubMed] [Google Scholar]
- Cheebsumon P, Velasquez LM, Hoekstra CJ, Hayes W, Kloet RW, Hoetjes NJ, Smit EF, Hoekstra OS, Lammertsma AA, Boellaard R. Measuring response to therapy using FDG PET: semi-quantitative and full kinetic analysis. Eur J Nucl Med Mol Imaging. 2011;38:832–842. doi: 10.1007/s00259-010-1705-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comtat C, Kinahan PE, Defrise M, Michel C, Lartizien C, Townsend DW. Simulating wholebody PET scanning with rapid analytical methods. IEEE Nuclear Science Symp Conf Record. 1999;3:1260–4. [Google Scholar]
- Dimitrakopoulou-Strauss A, Strauss LG, Burger C, Rühl A, Irngartinger G, Stremmel W, Rudi J. Prognostic aspects of 18F-FDG PET kinetics in patients with metastatic colorectal carcinoma receiving FOLFOX chemotherapy. J Nucl Med. 2004;45:1480–7. [PubMed] [Google Scholar]
- Doot RK, Dunnwald LK, Schubert EK, Muzi M, Peterson LM, Kinahan PE, Kurland BF, Mankoff DA. Dynamic and static approaches to quantifying 18F-FDG uptake for measuring cancer response to therapy, including the effect of granulocyte CSF. J Nucl Med. 2007;48:920–25. doi: 10.2967/jnumed.106.037382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doot RK, Scheuermann JS, Christian PE, Karp JS, Kinahan PE. Instrumentation factors affecting variance and bias of quantifying tracer uptake with PET/CT. Med Phys. 2010;37:6035–46. doi: 10.1118/1.3499298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedman NM, Sundaram SK, Kurdziel K, Carrasquillo JA, Whatley M, Carson JM, Sellers D, Libutti SK, Yang JC, Bacharach SL. Comparison of SUV and Patlak slope for monitoring of cancer therapy using serial PET scans. Eur J Nucl Med Mol Imaging. 2003;30:46–53. doi: 10.1007/s00259-002-0981-4. [DOI] [PubMed] [Google Scholar]
- Fusselman DDD, Cutler PD, Katzenellenbogen JA, Welch MJ. Positron tomographic assessment of estrogen receptors in breast cancer: Comparison with FDG-PET and in vitro receptor assays. J Nucl Med. 1995;36:1766–74. [PubMed] [Google Scholar]
- Graham MM. Physiologic smoothing of blood time-activity curves for PET data analysis. J Nucl Med. 1997;38:1161–8. [PubMed] [Google Scholar]
- Häggström I, Beattie BJ, Schmidtlein CR. Dynamic PET simulator via tomographic emission projection for kinetic modeling and parametric image studies. Med Phys. 2016;43:3104. doi: 10.1118/1.4950883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamberg LM, Hunter GJ, Alpert NM, Choi NC, Babich JW, Fischman AJ. The dose uptake ratio as an index of glucose metabolism: useful parameter or oversimplification. J Nucl Med. 1994;35:1308–12. [PubMed] [Google Scholar]
- Harrison RL, Elston BF, Doot RK, Lewellen TK, Mankoff DA, Kinahan PE. A virtual clinical trial of FDG-PET imaging of breast cancer: effect of variability on response assessment. Transl Oncol. 2014;7:138–46. doi: 10.1593/tlo.13847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hickish T, Astras G, Thomas P, Penfold S, Purandare L, Hickish TF, Kerr D. Glucose intolerance during adjuvant chemotherapy for breast cancer. J Natl Cancer Inst. 2009;101:537. doi: 10.1093/jnci/djp025. [DOI] [PubMed] [Google Scholar]
- Huang J, O’Sullivan F. An analysis of whole body tracer kinetics in dynamic PET studies with application to image-based blood input function extraction. IEEE Trans Med Imaging. 2014;33:1093–108. doi: 10.1109/TMI.2014.2305113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinahan PE, Fletcher JW. Positron emission tomography-computed tomography standardized uptake values in clinical practice and assessing response to therapy. Semin Ultrasound CT MR. 2010;31:496–505. doi: 10.1053/j.sult.2010.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kinahan PE, Vesselle H, Williams J, Stearns CW, Schmitz R, Alessio AM, Macdonald L, Mawlawi O, Turkington T, Lewellen T. Performance evaluation of an integrated PET/CT scanner: discovery STE. J Nucl Med. 2006;47:392P. [Google Scholar]
- Koo HR, Park JS, Kang KW, Han W, Park IA, Moon WK. Correlation between 18F-FDG uptake on PET/CT and prognostic factors in triple-negative breast cancer. Eur Radiol. 2015;25:3314–21. doi: 10.1007/s00330-015-3734-z. [DOI] [PubMed] [Google Scholar]
- Kurland BF, Doot RK, Linden HM, Mankoff DA, Kinahan PE. Multicenter trials using 18F-fluorodeoxyglucose (FDG) PET to predict chemotherapy response: effects of differential measurement error and bias on power calculations for unselected and enrichment designs. Clin Trials. 2013;10:886–95. doi: 10.1177/1740774513506618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurland BF, Muzi M, Peterson LM, Doot RK, Wangerin KA, Mankoff DA, Linden HM, Kinahan PE. Multicenter clinical trials using 18F-FDG PET to measure early response to oncologic therapy: effects of injection-to-acquisition time variability on required sample size. J Nucl Med. 2016;57:226–30. doi: 10.2967/jnumed.115.162289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lindholm P, Minn H, Leskinen-Kallio S, Bergman J, Ruotsalainen U, Joensuu H. Influence of the blood glucose concentration on FDG uptake in cancer—a PET study. J Nucl Med. 1993;34:1–6. [PubMed] [Google Scholar]
- Lockhart CM, MacDonald LR, Alessio AM, McDougald WA, Doot RK, Kinahan PE. Quantifying and reducing the effect of calibration error on variability of PET/CT standardized uptake value measurements. J Nucl Med. 2011;52:218–24. doi: 10.2967/jnumed.110.083865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lucignani G, Schmidt KC, Moresco RM, Striano G, Colombo F, Sokoloff L, Fazio F. Measurement of regional cerebral glucose utilization with fluorine-18-FDG and PET in heterogeneous tissues: theoretical considerations and practical procedure. J Nucl Med. 1993;34:360–9. [PubMed] [Google Scholar]
- Maidment ADA. Virtual clinical trials for the assessment of novel breast screening modalities. Int Workshop on Digital Mammography 2014 [Google Scholar]
- Mankoff D, Muzi M, Zaidi H. Quantitative analysis in nuclear oncologic imaging. In: Zaidi H, editor. Quantitative Analysis in Nuclear Medicine Imaging. New York: Springer; 2006. pp. 446–7. [Google Scholar]
- Minn H, Zasadny KR, Quint LE, Wahl RL. Lung cancer: reproducibility of quantitative measurements for evaluating 2-[F-18]-fluoro-2-deoxy-D-glucose uptake at PET. Radiology. 1995;196:167–73. doi: 10.1148/radiology.196.1.7784562. [DOI] [PubMed] [Google Scholar]
- Moore CS, Avery G, Balcam S, Needler L, Swift A, Beavis AW, Saunderson JR. Use of a digitally reconstructed radiograph-based computer simulation for the optimisation of chest radiographic techniques for computed radiography imaging systems. Br J Radiol. 2012;85:e630–9. doi: 10.1259/bjr/47377285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muzi M, O’Sullivan F, Mankoff DA, Doot RK, Pierce LA, Kurland BF, Linden HM, Kinahan PE. Quantitative assessment of dynamic PET imaging data in cancer imaging. Magn Reson Imaging. 2012;30:1203–15. doi: 10.1016/j.mri.2012.05.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okazumi S, Isono K, Enomoto K, Kikuchi T, Ozaki M, Yamamoto H, Hayashi H, Asano T, Ryu M. Evaluation of liver tumors using fluorine-18-fluorodeoxyglucose PET: characterization of tumor and assessment of effect of treatment. J Nucl Med. 1992;33:333–9. [PubMed] [Google Scholar]
- Olshen AB, O’Sullivan F. Camouflaged deconvolution with application to blood curve modeling in FDG PET studies. J Am Stat Assoc. 1997;92:1293–303. [Google Scholar]
- O’Sullivan F, Kirrane J, Muzi M, O’Sullivan JN, Spence AM, Mankoff DA, Krohn KA. Kinetic quantitation of cerebral PET-FDG studies without concurrent blood sampling: statistical recovery of the arterial input function. IEEE Trans Med Imaging. 2010;29:610–24. doi: 10.1109/TMI.2009.2029096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Patlak CS, Blasberg RG, Fenstermacher JD. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. J Cereb Blood Flow Metab. 1983;3:1–7. doi: 10.1038/jcbfm.1983.1. [DOI] [PubMed] [Google Scholar]
- Rashidnasab A, Elangovan P, Mackenzie A, Dance DR, Young KC, Bosmans H, Wells K. Virtual clinical trials using inserted pathology in clinical images: investigation of assumptions for local glandularity and noise. Proc SPIE. 2015:94122D1–6. [Google Scholar]
- Römer W, Hanauske AR, Ziegler S, Thödtmann R, Weber W, Fuchs C, Enne W, Herz M, Nerl C, Garbrecht M, Schwaiger M. Positron emission tomography in non-Hodgkin’s lymphoma: assessment of chemotherapy with fluorodeoxyglucose. Blood. 1998;91:4464–71. [PubMed] [Google Scholar]
- Shields AF, Lawhorn-Crews JM, Briston DA, Zalzala S, Gadgeel S, Douglas KA, Mangner TJ, Heilbrun LK, Muzik O. Analysis and reproducibility of 3-Deoxy-3-[18F] Fluorothymidine positron emission tomography imaging in patients with non small cell lung cancer. Clin Cancer Res. 2008;14:4463–8. doi: 10.1158/1078-0432.CCR-07-5243. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimoda W, Hayashi M, Murakami K, Oyama T, Sunagawa M. The relationship between FDG uptake in PET scans and biological behavior in breast cancer. Br Cancer. 2007;14:260–8. doi: 10.2325/jbcs.14.260. [DOI] [PubMed] [Google Scholar]
- Sokoloff L, Reivich M, Kennedy C, Des Rosiers MH, Patlak CS, Pettigrew KD, Sakurada O, Shinohara M. The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino rat. J Neurochem. 1977;28:897–916. doi: 10.1111/j.1471-4159.1977.tb10649.x. [DOI] [PubMed] [Google Scholar]
- Soret M, Bacharach SL, Buvat I. Partial-volume effect in PET tumor imaging. J Nucl Med. 2007;48:932–45. doi: 10.2967/jnumed.106.035774. [DOI] [PubMed] [Google Scholar]
- Thie JA. Understanding the standardized uptake value, its methods, and implications for usage. J Nucl Med. 2004;45:1431–4. [PubMed] [Google Scholar]
- Tseng J, Dunnwald LK, Schubert EK, Link JM, Minoshima S, Muzi M, Mankoff DA. 18F-FDG kinetics in locally advanced breast cancer: correlation with tumor blood flow and changes in response to neoadjuvant chemotherapy. J Nucl Med. 2004;45:1829–37. [PubMed] [Google Scholar]
- Vanderhoek M, Perlman SB, Jeraj R. Impact of the definition of peak standardized uptake value on quantification of treatment response. J Nucl Med. 2012;53:4–11. doi: 10.2967/jnumed.111.093443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vriens D, Visser EP, de Geus-Oei LF, Oyen WJ. Methodological considerations in quantification of oncological FDG PET studies. Eur J Nucl Med Mol. 2010;37:1408–25. doi: 10.1007/s00259-009-1306-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wahl RL, Zasadny K, Helvie M, Hutchins GD, Weber B, Cody R. Metabolic monitoring of breast cancer chemohormonotherapy using positron emission tomography: initial evaluation. J Clin Oncol. 1993;11:2101–11. doi: 10.1200/JCO.1993.11.11.2101. [DOI] [PubMed] [Google Scholar]
- Wahl RL, Jacene H, Kasamon Y, Lodge MA. From RECIST to PERCIST: evolving considerations for PET response criteria in solid tumors. J Nucl Med. 2009;50:122S–50S. doi: 10.2967/jnumed.108.057307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wangerin KA, Ahn S, Wollenweber S, Ross SG, Kinahan PE, Manjeshwar RM. Evaluation of lesion detectability in PET when using a convergent penalized likelihood image reconstruction method. J Med Imaging. 2017;4:011002. doi: 10.1117/1.JMI.4.1.011002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wangerin KA, Muzi M, Peterson LM, Linden HM, Novakova A, O’Sullivan F, Kurland BF, Mankoff DA, Kinahan PE. Effect of 18F-FDG uptake time on lesion detectability in PET imaging of early stage breast cancer. Tomography. 2015;1:53–60. doi: 10.18383/j.tom.2015.00151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber G. Enzymology of cancer cells (second of two parts) N Engl J Med. 1977;296:541–51. doi: 10.1056/NEJM197703102961005. [DOI] [PubMed] [Google Scholar]
- Weber WA, Ziegler SI, Thödtmann R, Hanauske AR, Schwaiger M. Reproducibility of metabolic measurements in malignant tumors using FDG PET. J Nucl Med. 1999;40:1771–7. [PubMed] [Google Scholar]
- Zasadny KR, Tatsumi M, Wahl RL. FDG metabolism and uptake versus blood flow in women with untreated primary breast cancers. Eur J Nucl Med Mol Imaging. 2003;30:274–80. doi: 10.1007/s00259-002-1022-z. [DOI] [PubMed] [Google Scholar]