Constant pH Molecular Dynamics Reveals pH-modulated Binding of Two Small-Molecule BACE1 Inhibitors

Abstract

Targeting BACE1 with small-molecule inhibitors offers a promising route for treatment of Alzheimer’s disease. However, the intricate pH dependence of BACE1 function and inhibitor efficacy has posed major challenges for structure-based drug design. Here we investigate two, structurally similar BACE1 inhibitors that have dramatically different binding affinity and inhibitory activity using continuous constant pH molecular dynamics (CpHMD). At high pH, both inhibitors are stably bound to BACE1, however, within the enzyme active pH range, only the iminopyrimidinone-based inhibitor remains bound, while the aminothiazine-based inhibitor becomes partially dissociated following the loss of hydrogen bonding with the active site and change of the 10s loop conformation. The drastically lower affinity of the second inhibitor is due to the protonation of a catalytic aspartate and the lack of a propyne tail. This work demonstrates that CpHMD can be used for screening pH-dependent binding profiles of small-molecule inhibitors, providing a new tool for structure-based drug design and optimization.

β-secretase (BACE1), a leading therapeutic target for treating Alzheimer’s disease (AD), is one of the two aspartic proteases that cleave the amyloid precursor protein to produce the β-amyloid peptide (Aβ). Subsequent oligomerization and fibrillation of Aβ lead to neuritic plaques which are linked to the onset of AD. ¹ Since the discovery of BACE1 over a decade ago, hundreds of inhibitors have been developed, however, none have passed the FDA required clinical trial process and entered the market. ² The first generation of designed inhibitors are peptide-like transition-state analogs, which demonstrated excellent in vitro binding affinity for BACE1, however, high molecular weight, polarity and flexibility as well as numerous hydrogen bond donors and acceptors reduce their ability to penetrate the blood-brain barrier (BBB) to reach the central nervous system where BACE1 resides. ³ Therefore, in more recent years, small-molecule inhibitors have emerged as a promising route for treatment and prevention of AD. ³

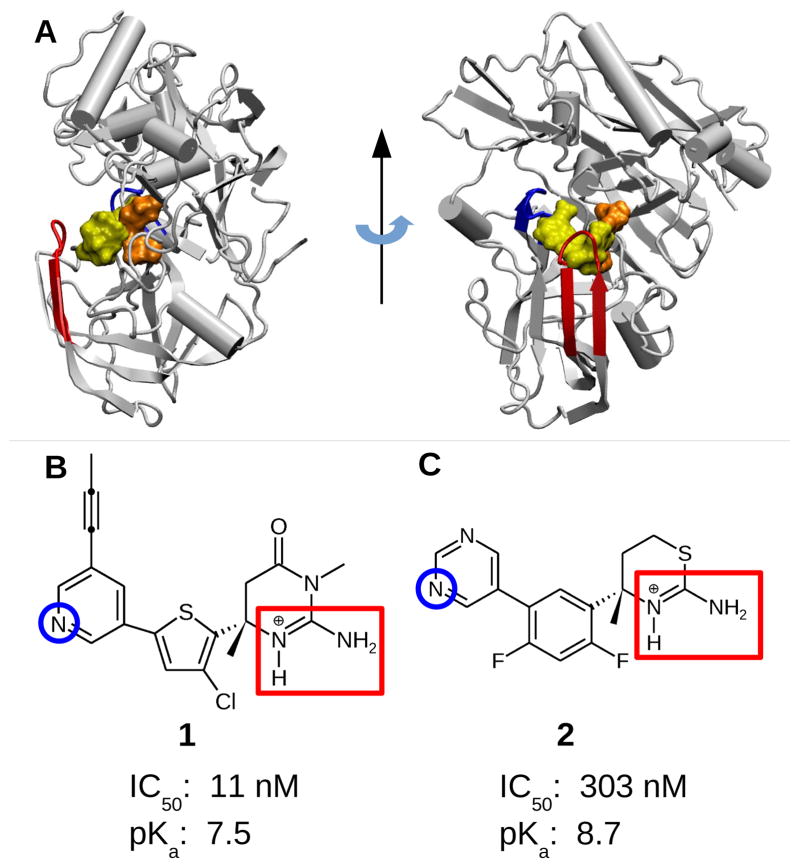
BACE1 is a monomeric protein localized in the acidic endosome and trans-Golgi apparatus. ² The catalytic domain of BACE1 contains a catalytic dyad, Asp32 and Asp228, which respectively act as a generalized acid and base to catalyze peptide hydrolysis.⁴ Three key regions in the structure of BACE1 must be considered when designing inhibitors (Figure 1A). First, the aspartic dyad directly interacts with inhibitors via hydrogen bonds and/or salt bridges. Generally, peptidomimetic compounds contain a hydroxyl group that forms a hydrogen bond with the active site, while small-molecule inhibitors contain a basic amine site with a pK_a greater than 6 that forms a salt bridge/hydrogen bond with one of the catalytic aspartates. Second, the flap, a β-hairpin loop spanning residues Tyr68 to Glu77, lies directly over the catalytic dyad and can open and close at room temperature to allow substrate and inhibitor access to the active site. ^3,5 Finally, the 10s loop, a β-hairpin loop with Ser10 at the tip, can adopt an “up” or “down” conformation, modulating the accessibility of an additional binding pocket, which further impacts the inhibitor effectiveness.⁶

Figure 1.

Structures of BACE1 and the two small-molecule inhibitors. A. BACE1 in complex with inhibitor 1 (PDB ID 4FRS ⁷). The inhibitor, catalytic dyad, flap, and 10s loop are shown in yellow, orange, red, and blue, respectively. B. Iminopyrimidinone-based inhibitor 1 discovered by Merck (MK8698). ⁷ C. Aminothiazine-based inhibitor 2 discovered by Eli Lilly (LY2811376). ⁸ The two endo- and exocyclic amines on the ABM are highlighted by a red rectangle. The nitrogen on the pyridine/pyrimidine ring (titratable in the simulations) is indicated by a blue circle. Experimental cell IC₅₀ values for 1 and 2 are taken from ref 7 and ref 8, respectively. Experimental pK_a’s refer to those of the endocyclic amine group of the ABM: 1 is taken from ref ⁷, while 2 was obtained by capillary electrophoresis experiments (see Methods and Protocols).

Recently, heterocycles that contain a basic amine site, positively charged in the enzyme active pH range ⁹ to engage the negatively charged aspartyl dyad, have emerged as a leading scaffold for designing potent, selective BACE1 inhibitors. ³ These heterocycles are often referred to as the aspartyl binding motif (ABM). However, determining the optimal pK _a of the basic amine has been a formidable task. While very high basicity (pK _a>9) increases the likelihood of the salt-bridge formation with the aspartyl dyad, it decreases brain permeability and thus lowers in vivo efficacy. ^10,11 Conversely, inhibitors with low basicity (pK _a~5.5), although more able to cross the BBB, are not active under mildly acidic conditions (such as pH 6.5). ¹²

In this work we investigate two potent drug-like BACE1 inhibitors. Inhibitor 1 ⁷ closely resembles the Merck inhibitor MK8931 currently under phase 2/3 clinical trial, ² while inhibitor 2 was discovered by Eli Lilly and tested in preclinical animal models and humans but discontinued due to retinal toxicity. ⁸ Recently, structure-based optimization has been applied to 2 by Pfizer in an effort to reduce toxicity. ^13,14 Both inhibitors occupy the same binding pockets and more importantly, they contain a six-membered ABM that forms bidentate hydrogen bond interactions with the catalytic dyad via the endo- and exocyclic amines (Figure 2A and 2B). Note that, with the pK _a’s of 7.5 and 8.7 for 1 and 2, respectively (Figure 1B and 1C), the endocyclic amines are charged in the BACE1 active pH range. ^9,15 Interestingly, despite having similar structure and nearly identical binding modes, the in vitro binding affinity and in vivo inhibitory activity of the two inhibitors are dramatically different. The IC₅₀ values of 2 is 30 fold higher than 1 (Figure 1B and 1C). Curiously, however, the pK _a of 2 is 1.2 units higher than that of 1, which, according to the current consensus based on chemical intuition,^12,3 should make 2 a stronger binder. Thus, there is no intuitive explanation for the significantly lower affinity of 2.

Figure 2.

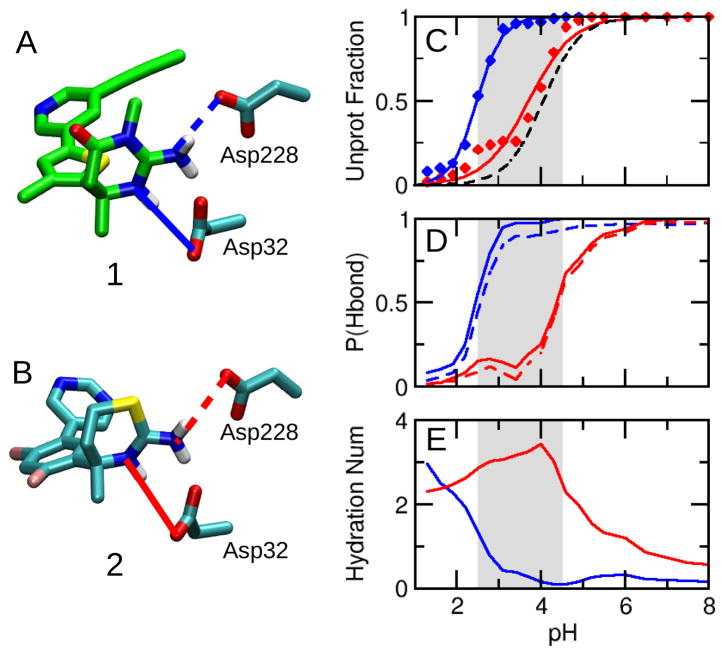
Titration of the BACE1 catalytic dyad affects the interaction with inhibitor. A and B. Inhibitors 1 and 2 interacting with the catalytic dyad. The solid and dashed lines depict hydrogen bonds with Asp32 and Asp228, respectively. C. Unprotonated fractions of Asp32 at different pH. Simulations of BACE1 complexed with 1 and 2 are shown in blue and red, respectively. The curves are the best fits to the Hill equation. The black dashed curve represents the apo BACE1 simulation. The simulated active pH range of apo BACE1 is indicated by the grey area. ⁵ D. pH-dependent occupancy of the hydrogen bonds with Asp32 (solid) and Asp228 (dashed). A hydrogen bond was considered to be present if the heavy atom donor-acceptor distance was below 3.5 Å and the acceptor-donor-H angle was less than 30°. E. pH-dependent hydration number of Asp32. Hydration number refers to the number of water molecules within the first solvation shell, defined as any water oxygen within 3.5 Å of the carboxylate oxygens of Asp.

To explore the interactions of the two inhibitors with BACE1 in the enzyme active pH range, we performed constant pH molecular dynamics (pHMD) simulations starting from the crystal structures of BACE1 complexed with 1 and 2 (PDB ID 4FRS ⁷ and 4YBI ⁸, respectively). Previous pHMD simulations and Born approximation methods have been utilized to predict shifts in the BACE1 catalytic dyad pK _a with neutral peptide-like inhibitors, while this work considers charged small molecules that change protonation state as a function of pH. ^16,17,5,18 Based on discrete ^19,20,21,22 or continuous variables ^23,24,25 to represent protonation states, pHMD enables ionizable sites of proteins and/or other solutes to simultaneously change protonation states in response to conformational dynamics at a specified solution pH, thus extending the commonly simulated NPT or NVT ensemble to include a constant pH condition. Here we employed continuous constant pH molecular dynamics (CpHMD)^23,24 with a hybrid-solvent scheme and pH replica-exchange. ²⁶ The hybrid-solvent CpHMD method makes use of accurate conformational sampling in explicit solvent and efficient calculation of solvation free energies with the generalized Born implicit-solvent model. ²⁶ Combined with the pH replica-exchange sampling protocol, ²⁶ it offers accurate pK _a convergence on the order of 1 ns per pH replica, ²⁶ in particular for interior sites of proteins that are notoriously challenging to predict with static structure-based electrostatics methods. ^27,28 A benchmark study showed that hybrid-solvent CpHMD can predict the pK _a’s of enzyme catalytic sites with a correct order and accuracy of about 1 pH unit. ²⁶ Most recently, we applied hybrid-solvent CpHMD to study the apo form of BACE1, revealing a pH-dependent population shift between three conformational states that gives rise to the bell-shaped pH profile of the enzymatic activity. In this work, we demonstrate that subtle differences in the titration behavior of the BACE1-inhibitor complex can lead to drastically different binding behavior within the enzyme active pH range. Such knowledge has been lacking although it is crucial for the design and optimization of BACE1 inhibitors.

BACE1 functions within a narrow pH range (3.5–5.5) ^9,15 and hydrolyzes peptide bonds via a general acid-base mechanism. ³ The experimentally determined pK _a’s of the acidic and basic components of the catalytic dyad are 5.2 and 3.5, respectively. ⁴ Therefore, within the BACE1 active pH range, the catalytic dyad is likely to be in the monoprotonated state. Our previous simulation of apo BACE1 using the hybrid-solvent CpHMD gave the calculated pK _a of 4.1 for Asp32 and 1.9 for Asp228, about one pH unit below the experimentally determined values.⁵ Accordingly, the simulated pH range of BACE1 where the catalytic dyad is in the monoprotonated state is 2.5–4.5 in the simulation. To account for the systematic deviation, we will adopt the simulated active pH range in the remainder of the discussion. Importantly, adoption of the simulated active pH range instead of the experimentally determined active pH range does not impact the results. The simulated active pH range is used as a guide for the simulated pH condition that likely represents the active form of BACE1.

We first consider the protonation states of Asp32 and Asp228. The active site of BACE1 is mostly hydrophobic and no charged or titratable residues are with 8 Å of the dyad, therefore, shifts in the catalytic dyad pK _a’s are predominately effected by the positive charge of the inhibitors. When BACE1 is bound to a basic inhibitor, the pK _a of Asp32 is expected to shift down as the hydrogen bond/salt bridge with the positively charged endocyclic amine stabilizes the charged state. This is indeed the case when BACE1 is bound with 1: the pK _a of Asp32 is lowered significantly from the apo-state value of 4.1 to 2.5 (Figure 2C, blue). However, binding with 2 produces a negligible pK _a shift: the pK _a is lowered only by 0.4 unit to 3.7 (Figure 2C, red). Thus, in the active pH range, Asp32 becomes deprotonated in the presence of 1; however, it remains partially protonated in the presence of 2. In contrast to Asp32, neither inhibitor significantly impacts the titration behavior of Asp228: the pK _a’s are 2.3 and 2.0 in the presence of 1 and 2, respectively (Table S1). Thus, Asp228 remains completely deprotonated in the active pH range. This indicates that the hydrogen bond between Asp228 and the neutral exocyclic amine group of the two inhibitors has approximately the same strength.

Next, we examine the most important BACE1-inhibitor interactions, i.e., the hydrogen bonds between the catalytic aspartates and the endo- and exocyclic amine groups on the ABM. Above the active pH range, both inhibitors form stable hydrogen bonds with the aspartyl dyad, as evident from the high percentage of hydrogen bond occupancy (Figure 2D). The hydrogen bond between the endocyclic amine group and Asp32 is particularly strong, as it is also a salt bridge due to the charge on both groups. However, within the active pH range, the occupancy of the hydrogen bonds between 2 and the aspartate dyad decreases sharply as pH is lowered (Figure 2D, red). In contrast, the hydrogen bonds between 1 and the catalytic dyad remain almost completely intact within the active pH range (Figure 2D, blue). Interestingly, the shape of the pH-dependent hydrogen bond occupancy is nearly identical as the pH-dependent unprotonated fraction of Asp32 in the active pH range. Note, Asp228 is always deprotonated in this pH range. Thus, the data suggests that, in the presence of 2, Asp32 becomes protonated in the active pH range, destabilizing the hydrogen bond with the inhibitor. As expected, the hydrogen bond occupancy is correlated with the hydration number of the active site. Within the active pH range, breakage of the hydrogen bond between 2 and Asp32 leads to entrance of water molecules to the active site (Figure 2E, red). In contrast, when BACE1 is complexed with 1, the active site remains dry in the entire active pH range (Figure 2E, blue).

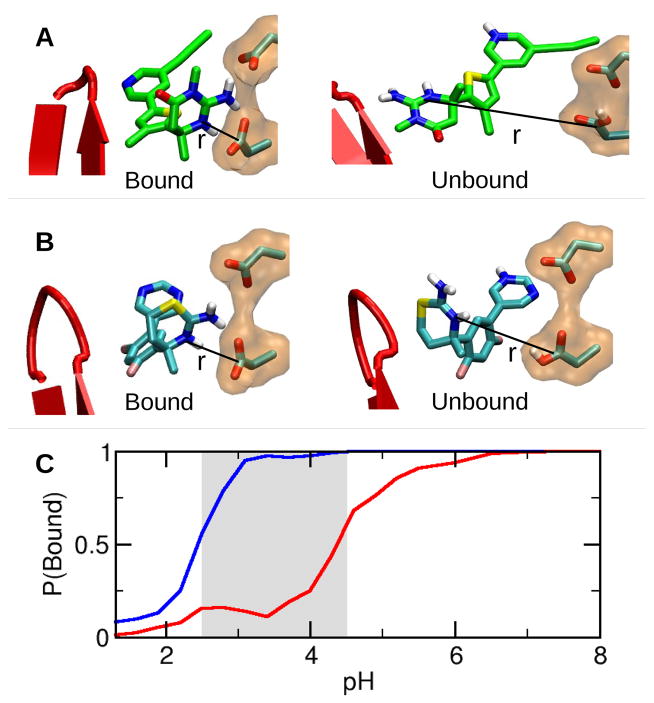
The breakage of the hydrogen bonds and entrance of water into the active site is an indication of dissociation of inhibitor 2 from BACE1. To quantify the degree of dissociation, we calculated the fraction of bound configurations as a function of pH. A bound configuration is considered formed when the distance between the endocyclic nitrogen of the ABM and the carbonyl carbon of Asp32 is less than 4 Å. Above the active pH range, both inhibitors are largely bound (Figure 3A and 3C). However, in the active pH range, only 1 remains bound, while the fraction of bound configurations in the presence of 2 sharply decreases as pH is decreased. At the most active pH (3.5) of BACE1, less than 25% of 2 is bound (Figure 3B and 3C). The pH-induced dissociation of 2 is a consequence of the protonation of Asp32 and offers an explanation for the significantly reduced binding affinity and activity of 2 when measured under the most active pH condition of the enzyme. ^7,8 We note that, since dissociation of the inhibitor occurs on a longer time scale compared to our limited simulation length, the fraction of unbound configurations shown in Figure 3C is likely not quantitative. However, a quantitative prediction of binding affinity is not in the scope of the current work as the simulation length required for absolute convergence of the entire ensemble of unbound configurations is prohibitively expensive. Rather, our focus here is to provide a method for screening pH-dependent binding profiles of small-molecule inhibitors. Importantly, within the 18 ns of simulation, individual replicas undergo unbinding and binding events as they walk through pH space, this would likely be missed by performing conventional MD simulations with fixed protonation states.

Figure 3.

pH-dependent binding of each inhibitor to BACE1. A. A bound configuration of 2 with BACE1. B. An unbound configuration of 2 with BACE1. C. Population of the bound configurations as a function of pH. The simulations in the presence of 1 and 2 are shown in blue and red, respectively.

Examination of the ABM suggests two possible factors contributing to the different protonation behavior of Asp32 in the presence of 1 and 2. First, the presence of the exocyclic methyl group in the ABM of 1 provides steric hindrance for water to access the active site, thus stabilizing the hydrogen bonds between the endo- and exocyclic amine groups and Asp32 (Figure 2A, blue line) and making the deprotonated state of Asp32 favorable. Second, the partial negative charge (−0.33) of the sulfur atom on the ABM of 2 (6 Å from Asp32, Figure 2B) makes the deprotonation of Asp32 unfavorable. In contrast, at the same position in the ABM of 1, the methyl amine group is nearly neutral (+0.02) with a positive partial charge on the methyl group (+0.11). Thus, despite the fact that inhibitor 1 is less basic (measured pK _a of 7.5) than 2 (measured pK _a of 8.7), the pK _a of Asp32 is shifted lower in the presence of 1, which makes the catalytic dyad di-deprotonated in the active pH range and enhances the electrostatic attraction with the positively charged inhibitor. Notably, neither inhibitor interacts with other charged or titratable residue in both the bound and unbound configurations.

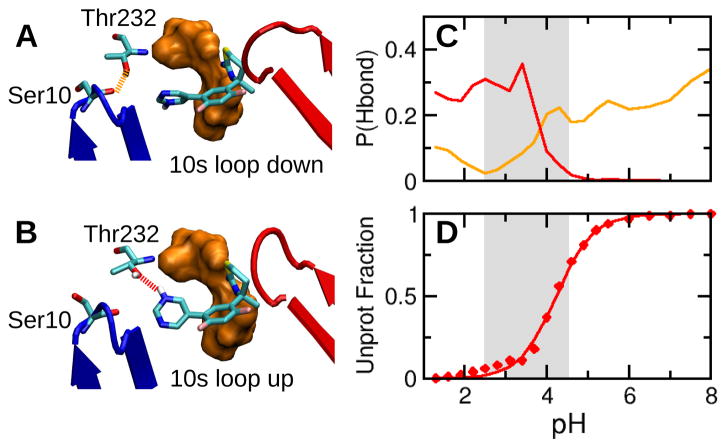
Finally, we test a hypothesis that correlates the position of the 10s loop with inhibitor efficacy. Surveys of inhibitor-bound BACE1 crystal structures showed that the 10s loop adopts either “up” or “down” conformation.⁶ In the 10s-down conformation, Ser10 can form a hydrogen bond with Thr232 (Figure 4A), while in the 10s-up conformation, Ser10 is distant from Thr232 (Figure 4B). Based on a series of tertiary carbinamine derived compounds, McGaughey et al. hypothesized that inhibitors that form favorable interactions with Thr232 may disrupt the hydrogen bond between Thr232 and Ser10, effectively locking the 10s loop in the up configuration and increasing the binding interactions.⁶

Figure 4.

Inhibitor 2 competes with the 10s loop for the interaction with Thr232. A. Binding mode of 2 at high pH. The 10s loop and flap are shown in blue and red, respectively. Ser10 forms a hydrogen bond with Thr232, and the 10s loop is down. B. Binding mode of 2 at low pH. A hydrogen bond is formed between Thr232 and the pyrimidine nitrogen of 2, and the 10s loop is up. C. pH-dependent hydrogen bond occupancy. The hydrogen bond between Thr232 (hydroxyl) and Ser10 (backbone carbonyl) is shown in orange, while that between Thr232 (hydroxyl) and the pyrimidine nitrogen of 2 is shown in red. D. Unprotonated fraction of the pyrimidine nitrogen of 2 at different pH. The solid curve is the best fit to the Hill equation.

To test this hypothesis, we calculated the hydrogen bond occupancy of Thr232 with Ser10 and the inhibitors. In the simulation of BACE1 complexed with 1, the pyridine ring of the inhibitor can not reach Thr232 due to the steric hindrance by the alkyne tail and does not modulate the 10s conformation. In contrast, in the simulation of BACE1 complexed with 2, the lack of alkyne group allows its pyrimidine ring to approach Thr232 in a pH-dependent manner. Above the enzyme active pH range, Thr232 can form a hydrogen bond with Ser10 (about 25%) but not with 2 (Figure 4C), and 10s loop is mostly down, consistent with the X-ray crystal structure, which was obtained at pH 7.4 (PDB ID 4YBI). Interestingly, as pH decreases in the active pH range, the hydrogen bond occupancy for Ser10 sharply decreases, whereas that for the inhibitor sharply increases until it plateaus at around pH 3.5, corresponding to the most active pH of BACE1 (Figure 4C). The formation of the latter hydrogen bond can be attributed to the protonation of the pyrimidine nitrogen (Figure 4D), enabling it to donate a hydrogen to Thr232 effectively locking the 10s loop in the up configuration (Figure 4B). Thus, together with the earlier analysis showing that 2 becomes partially detached from BACE1 in the active pH range, these data support the hypothesis that inhibitors that compete with Ser10 to form a hydrogen bond with Thr232 decrease binding interactions with the catalytic dyad.

In summary, constant pH molecular dynamics simulations revealed that, despite having a similar structure and nearly identical binding modes, inhibitors 1 and 2 exhibit different pH-dependent interactions with BACE1. Within the enzyme active pH range, 2 shows disrupted hydrogen bonds with the catalytic dyad in favor of hydrogen bond with Thr232. The former is due to the protonation of Asp32, which decreases the attraction to the charged aminothiazine ring. The hydrogen bonding with Thr232 is due to the lack of a propyne tail (present in 1), which allows the pyrimidine ring to move closer and donate a hydrogen from the protonated amine effectively forcing the 10s loop to the up position. Together, these changes lead to a significantly lowered binding affinity of 2 in the BACE1 active pH range, consistent with the drastically higher IC₅₀ value.

Our work demonstrates how mutual interactions between BACE1 and inhibitors result in subtle changes in the protonation states which in turn alters the binding interactions and strength. Thus, obtaining a detailed knowledge of the pH-dependent conformational dynamics and protonation-state changes of protein-small molecule complexes is crucial for designing potent, selective inhibitors of BACE1 and other enzymes that contain titratable catalytic sites and function over a narrow pH range. CpHMD can be used for illuminating pH-dependent dynamic details and screening pH profiles of small-molecule binding, thus providing a unique new tool for structure-based drug design and optimization.

METHODS AND PROTOCOLS

Continuous constant pH molecular dynamics (CpHMD) simulations ^23,24 with a hybrid-solvent scheme and pH replica-exchange protocol ²⁶ were performed on BACE1 in complex with inhibitors 1 and 2 starting from the respective crystal structures (PDB ID 4FRS ⁷ and 4YBI ⁸) using CHARMM (version C37b). ²⁹ The CHARMM22/CMAP all-atom force field ^30,31 was used to represent BACE1, while the force field parameters for the inhibitors were obtained in house following the protocol of CHARMM General Force Field (CGenFF) ³². Each system was simulated using 20 pH replicas in the pH range 1.3–8. Each BACE1 complex was simulated for 26 ns per replica under NPT conditions, resulting in a total simulation time of 520 ns. The last 18 ns per replica (360 ns in total) were used for analysis. Other simulation parameters and setting were identical to those in our previous work ⁵. The titratable sites include all Asp, Glu and His residues on the protein and the amine group on the pyridine/pyrimidine ring of the inhibitor (see Table S1 for all calculated pK_a’s). The model pK_a’s for Asp, Glu and His are 4.0, 4.4, and 6.5, respectively, ²⁶ while those for inhibitor 1 and 2 are 2.9 and 3.7, respectively. The latter pK_a’s were estimated using the program MoKa. ³³ The pK_a measurements for the inhibitors were conducted using capillary electrophoresis experiment following the protocol from ref. ³⁴