Proton-Coupled Conformational Allostery Modulates the Inhibitor Selectivity for β-secretase

Abstract

Many important pharmaceutical targets, such as aspartyl proteases and kinases, exhibit pH-dependent dynamics, functions and inhibition. Accurate prediction of their binding free energies is challenging because current computational techniques neglect the effects of pH. Here we combine free energy perturbation calculations with continuous constant pH molecular dynamics to explore the selectivity of a small-molecule inhibitor for β-secretase (BACE1), an important drug target for Alzheimer’s disease. The calculations predicted identical affinity for BACE1 and the closely-related cathepsin D at high pH; however, at pH 4.6 the inhibitor is selective for BACE1 by 1.3 kcal/mol, in excellent agreement with experiment. Surprisingly, the pH-dependent selectivity can be attributed to the protonation of His45, which allosterically modulates a loop–inhibitor interaction. Allosteric regulation induced by proton binding is likely common in biology; considering such allosteric sites could lead to exciting new opportunities in drug design.

The β-site amyloid precursor protein cleavage enzyme (β-secretase or BACE1) is a major drug target for treating Alzheimer’s disease. ¹ BACE1 belongs to the broad aspartyl protease family; therefore selectivity is a major challenge in designing efficacious inhibitors. In particular, cathepsin D (CatD) shares a similar structure with BACE1 (Figure 1), and its inhibition was linked to retinal toxicity. ^2,3 In recent years, computational drug design methods using free energy perturbation (FEP) based free energy calculations have enjoyed success for some target systems.^4–7 Given the clinical significance of BACE1, using these methods to help design selective inhibitors seems an attractive idea; however, current FEP-based methods neglect the effects of pH and protonation-state changes and given that BACE1 exhibits significant pH dependence in conformational dynamics ⁸ and substrate/inhibitor binding, ^9–12 it is unclear how these methods will perform. In addition to BACE1, many drug targets are pH sensitive. For example, activation of kinases depends on protonation-state changes,¹³ and small-molecule binding to kinases involves titratable residues. ¹⁴ Thus, developing a protocol that can accurately account for pH effects and protonation-state changes in free-energy calculations is highly desirable.

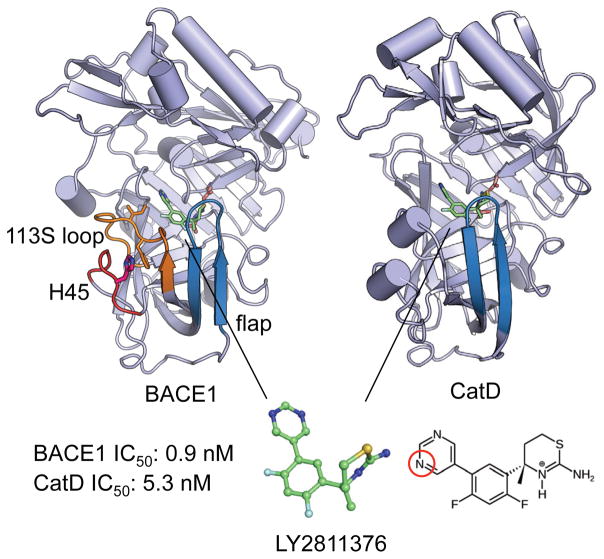
Figure 1. Structures of BACE1 and CatD bound to the inhibitor LY2811376.

In both structures, the catalytic dyad and inhibitor are drawn as sticks, while the flap is colored blue. In BACE1, the 113S loop¹⁸ and the loop that contains His45 are colored orange and red, respectively. The sidechains of His45, Phe109 and Ile110 are shown. In the inhibitor, nitrogen, fluorine and sulfur atoms are shown in blue, cyan and yellow, respectively. The endocyclic nitrogen on the aminothiazine ring carried a +1 charge, while a pyrimidine nitrogen (circled in red) was titratable in the simulation pH range. The coordinates for the BACE1 complex were taken from the X-ray crystal structure with PDB ID 4YBI;² the coordinates for the CatD complex were taken from our previous work. ¹² The listed IC₅₀ values (at pH 4.6) were obtained by Pfizer³ and correspond to a selectivity of 6 fold or a binding free energy difference of 1.0 kcal/mol.

Prompted by the above challenge, we applied a protocol that combines the FEP-based double decoupling scheme with continuous constant pH molecular dynamics (CpHMD)^15,16 and the Wyman linkage equation¹⁷ to the calculation of the binding free energies of BACE1 and CatD to a small-molecule inhibitor LY2811376.² We aimed to test if such a protocol can accurately predict the pH-dependent binding free energies and inhibitor selectivity, which would be useful in structure-based drug design for important pharmaceutical targets, such as aspartyl proteases and kinases. The results suggest that the pH-dependent contributions are responsible for the experimentally observed selectivity of LY2811376 for BACE1 relative to CatD. Surprisingly, the major contribution comes from an allosteric histidine in BACE1, which favors the charged state upon inhibitor binding and thereby increasing the binding affinity.

We first performed FEP-based double decoupling calculations to obtain the absolute binding free energies of BACE1 and CatD at a reference pH, i.e., the pH corresponding to a chosen set of protonation states for the titratable residues in both protein and inhibitor. The N- and C-terminal groups of the protein were acetylated and amidated, respectively. Asp, Glu, Lys and Arg were kept charged, and Cys and Tyr were kept neutral in both proteins. His was kept charged in BACE1 and neutral in CatD (see explanation in Methods and Protocols). The inhibitor carried a positive charge (or singly protonated, Fig. 1 bottom). These conditions represent the high pH states (more discussion in Methods and Protocols). Note, this protocol contrasts with a hypothetical free energy calculation at the experimental pH (IC50 measurements were conducted at pH 4.6), ³ where defining the protonation states would be difficult due to likely titration of Asp/Glu and possibly His.

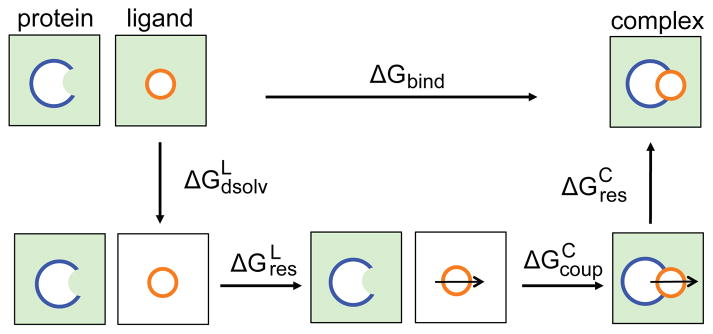
In the double decoupling scheme,^6,19–21 the protein-ligand binding free energy is a sum of four contributions in the thermodynamic cycle (Figure 2): the desolvation free energy of the ligand ( $\mathrm{\Delta }{G}_{\text{dsolv}}^{\mathrm{L}}$); the free energy of restraining the ligand to the binding pose in vacuum ( $\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{L}}$); the free energy of coupling the restrained ligand to the protein in water ( $\mathrm{\Delta }{G}_{\text{coup}}^{\mathrm{C}}$); and the free energy of releasing the restraints on the bound ligand in the complex ( $\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{C}}$). Except for $\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{L}}$, which was calculated using an analytic formula, ²⁰ each contribution was calculated with FEP (detailed protocol in SI). Interestingly, the calculated ΔG(pH^ref) are nearly identical for BACE1 and CatD, -12.1±0.4 and -12.2±0.5 kcal/mol, respectively, comparable to the free energies of BACE1 binding to other inhibitors, ⁷ and suggesting that the inhibitor has no selectivity towards the desired target BACE1. Examination of the individual contributions to the binding free energy (Table 1) shows that the largest contributions come from desolvating the ligand and coupling the ligand into the bound complex. The difference in the coupling free energies of BACE1 and CatD nearly cancels the difference in the restraining free energies.

Figure 2.

Thermodynamic cycle used in the double decoupling scheme.^6,19–21

Table 1.

Absolute binding free energies of BACE1 and CatD^a

ΔG (kcal/mol)	BACE1	CatD
$\mathrm{\Delta }{G}_{\text{dsolv}}^{\mathrm{L}}$	47.5±0.3	47.5±0.3
$\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{L}}$	16.4	15.5
$\mathrm{\Delta }{G}_{\text{coup}}^{\mathrm{C}}$	−73.7±0.2	−70.0±0.3
$\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{C}}$	−3.7±0.1	−6.7±0.3
ΔGfinite–size	1.3	1.4
ΔG(pHref)	−12.1±0.4	−12.2±0.5
ΔG(pH 4.6)	−13.8±0.4	−12.5±0.5

^aΔG(ref) refers to that calculated using the fixed-protonation- state free energy calculations. Individual free energy contributions are explained in the main text. ΔG_{finite–size} represents the correction to the electrostatic energy calculated with particle mesh Ewald under periodic boundary conditions for charged systems.²² No error bars are given for $\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{L}}$ and ΔG_{finite–size}, as they were calculated analytically. The error bar of ΔG(pH 4.6) was estimated by combining the errors in ΔG(pH^ref) and the pH-dependent corrections. As to the latter, the free energy errors due to titration of His45 (0.24) and His145 (0.09) were used for BACE1, and the inhibitor titratable site (0.16) was used for CatD.

The Wyman linkage relation describes the thermodynamic response of a macromolecular system to an external variable, such as pH. ¹⁷ In short, the derivative of the binding free energy with respect to pH is proportional to the binding-induced change in the total charge (Q) of the protein-ligand system,

$$\partial \mathrm{\Delta }G/\partial \text{pH}=2.303RT\mathrm{\Delta }Q.$$ (1)

Since Q at different pH can be calculated from pK_a’s, Eq. 1 can be written in the integrated form as, ^23–28

$$\mathrm{\Delta }G(\text{pH})-\mathrm{\Delta }G({\text{pH}}^{\text{ref}})=-RT\sum _i^{\mathrm{N}}ln\frac{1+{10}^{{\text{pK}}_i^{\text{holo}}-\text{pH}}}{1+{10}^{{\text{pK}}_i^{\text{apo}}-\text{pH}}}·\frac{1+{10}^{{\text{pK}}_i^{\text{apo}}-{\text{pH}}^{\text{ref}}}}{1+{10}^{{\text{pK}}_i^{\text{holo}}-{\text{pH}}^{\text{ref}}}}.$$ (2)

where i is the index for titratable sites, ΔG(pH^ref) is the binding free energy at a reference pH, e.g., the one calculated with the double decoupling scheme. ${\text{pK}}_i^{\text{apo}}$ and ${\text{pK}}_i^{\text{holo}}$ refer to the pK_a’s in the apo and holo states, respectively. It follows that only residues having a pK_a in the relevant pH range and an appreciable pK_a shift upon binding (difference between the holo and apo pK_a’s) make significant contributions to the pH dependence of ΔG.

To calculate ΔG(pH), we first examined the pK_a shifts obtained from the hybrid-solvent CpHMD simulations. ^11,12 For both BACE1 and CatD systems, except for the catalytic aspartic acids and inhibitor titratable site, most residues display small pK_a shifts with absolute values below 0.2 units (Fig. 3a) and block standard errors of 0–0.2 units (Table S1 and S2). To account for the statistical uncertainty, the contributions with an absolute pK_a shift below 0.4 or below twice the block standard error were excluded from the calculation of ΔG(pH). Contributions with pK_a’s that could not be reliably determined were also excluded. Note, these pK_a’s are all below 4 and therefore do not affect the relevant pH range 4 to 8.

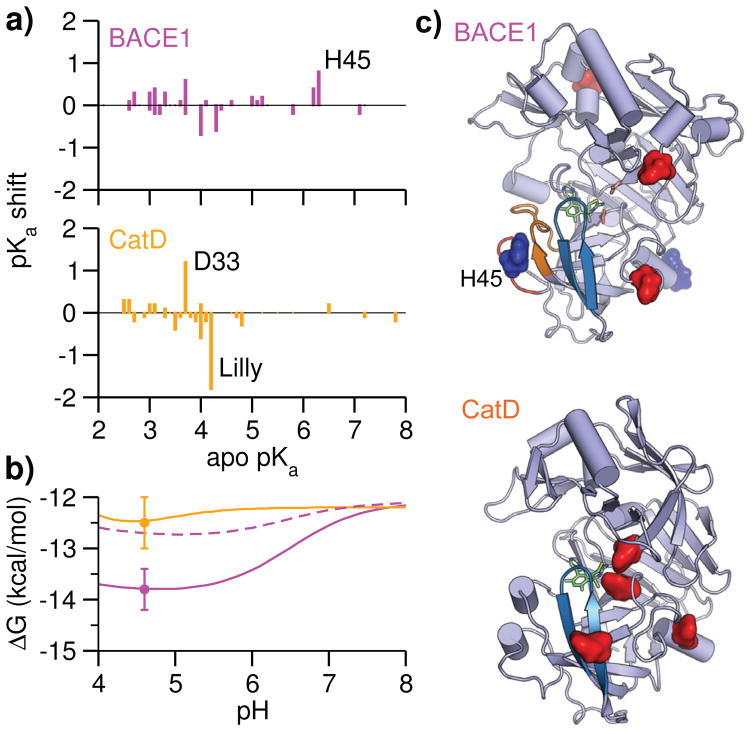
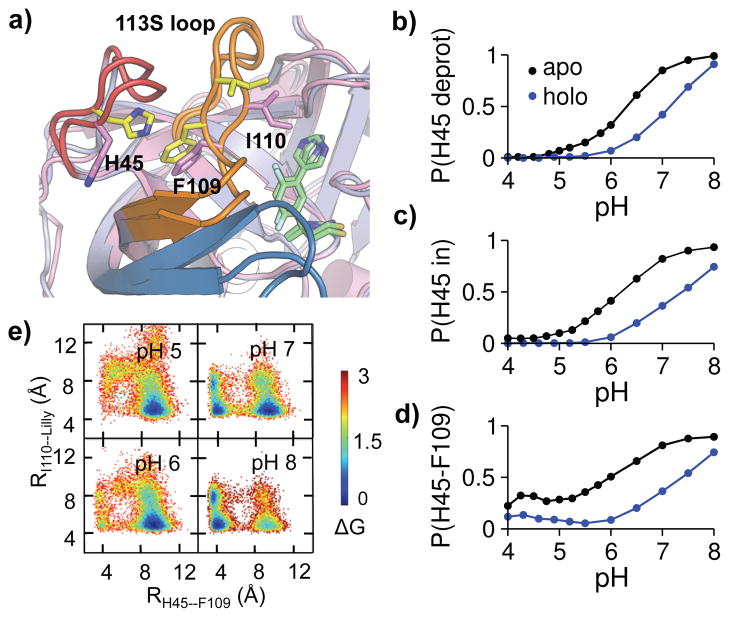
Figure 3. Inhibitor selectivity for BACE1 relative to CatD is pH dependent.

a) Calculated pK_a shifts vs. apo pK_a’s for BACE1 and CatD. The pK_a shift is defined as pK_a ^holo - pK_a ^apo. The block standard errors (BSE) for pK_a shifts are mostly below 0.2 units (Table S1 and S2). b) pH-dependent absolute binding free energies of BACE1 (solid magenta, without the His45 contribution is shown in dashed magenta) and CatD (orange). ΔG at pH 8 (reference pH) was calculated with the double decoupling scheme (Table 1), while the pH dependence was calculated with Eq. 2 using apo and holo pK_a’s of BACE1 (Table S1) and CatD (Table S2). The error bars are shown for ΔG at pH 4.6 (see Table 1). Considering that several acidic pK_a’s could not be reliably determined, (Table S1 and S2), the pH profile below 4 is not shown. c) Spatial view of residues contributing to the pH-dependent binding free energies of BACE1 and CatD. Asp/Glu are colored red and His sidechains are colored blue.

Remarkably, the calculated ΔG for BACE1 decreases by 1.7 kcal/mol, from -12.1 kcal/mol at pH 8 (the reference pH) to a minimum of -13.8 kcal/mol in the pH range 4.5–5, while ΔG for CatD decreases by only 0.3 kcal/mol, from -12.2 kcal/mol at pH 8 to a minimum of -12.5 kcal/mol around pH 4.5 (Fig. 3b). At pH 4.6, the experimental condition for IC50 measurements ³ and the optimum pH for BACE1 activity, ^9,10 ΔG for BACE1 is 1.3 kcal/mol lower than CatD (Table 1), in excellent agreement with the estimate of 1.0 kcal/mol based on the relative IC50 values. ³ Thus, the inhibitor selectivity for BACE1 relative to CatD is pH dependent. The pH-dependent increase of the BACE1 binding affinity to the Lilly compound is consistent with the observation that BACE1–OM99 binding (a peptide inhibitor) becomes stronger as pH is lowered to 4. ¹⁰

To understand the differences in the pH-dependent binding free energies of BACE1 and CatD, we examine the residue-specific contributions. For BACE1, the inhibitor titratable site and five residues far from the binding interface (Fig. 3c) experience significant binding-induced pK_a shifts, thus contributing to the pH-dependent binding free energy (Fig. 4a). Two histidine contributions stabilize the binding as pH is lowered from 8. His45 makes the largest contribution by shifting the pK_a from 6.1 in the apo to 7 in the holo state, which stabilizes the bound complex by 1.0±0.24 kcal/mol as pH decreases from 8 to 5 (Fig. 4a, red, no change below pH 5). Importantly, if the contribution of His45 was neglected, there would be nearly no difference between ΔG of BACE1 and CatD at the experimental pH 4.6 (Fig 3b, dashed curve). Thus, the contribution from His45 is crucial to predicting the inhibitor selectivity. Interestingly, His145 also contributes to the affinity increase as pH is lowered from 8. By undergoing a pK_a shift from 6.2 to 6.7, it stabilizes the bound complex by 0.65 kcal/mol at pH 4.6 compared to 8 (Fig. 4a, blue). We note that three acidic residues have pK_a shifts of 0.4–0.5 units, but their apo pK_a’s are below 4 and as such they only affect ΔG below pH 4 (Fig. 4a).

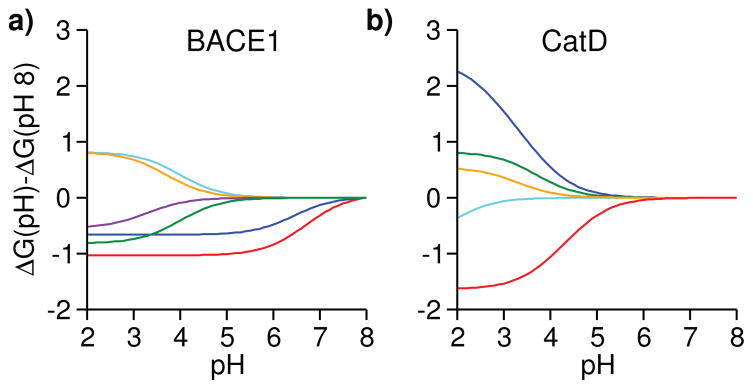
Figure 4. Residue-specific contributions to the pH-dependent binding free energies of BACE1 and CatD.

ΔG at pH 8 is used as a reference. a) Contributions from His45 and His145 to the BACE1 binding free energy are shown in red and blue, respectively. Contributions from Asp130, Asp223, Asp363 and the inhibitor titratable site are shown in cyan, orange, purple and green, respectively. The block standard error for His45 pK_a shift is 0.18, which corresponds to a binding free energy error of 0.24 kcal/mol. (b) Contributions from the inhibitor titratable site and catalytic Asp33 to the CatD binding free energy are shown in red and blue, respectively. Contributions from Asp75, Asp152 and Asp231 are shown in green, cyan and orange, respectively.

In contrast to BACE1, only acidic residues and no His contribute to ΔG(pH) of CatD. The largest contribution comes from the catalytic Asp33 (pK_a downshift of 1.8 units) followed by the inhibitor titratable site (pK_a upshift of 1.2 units). As pH is lowered from 8 to 4.6, the former contributes 0.19 kcal/mol towards destabilization, while the latter contributes 0.58 kcal/mol towards stabilization of the bound complex (Fig. 4b, red and blue). Thus, the pH profile of CatD binding is relatively flat in the pH range 4 to 8 (Fig. 4b). Note, the other three contributions only affect the pH region below 4.

What is the origin of the pK_a shift for His45 and how does it induce pH-dependent protein-ligand binding? Large pK_a shifts of residues near the binding interface have been previously reported in the literature ^{8,11,27,29,30} and can be trivially understood. For example, the catalytic Asp and the inhibitor titratable group in both BACE1 and CatD exhibit sizable pK_a shifts (Table S1 and S2) due to electrostatic interactions with the charged inhibitor. However, the pK_a shift of His45 is puzzling, since it is located on a loop that does not contact the inhibitor and the closest heavy-atom distance between His45 and the inhibitor is about 11 Å in the crystal structure. The existence of long-range coupling between protein/ligand binding and receptor protonation through a conformational mechanism has been previously hypothesized by Alexov and later Onufriev based on the Poisson-Boltzmann calculations. ^25,30–32 The pK_a shift of His45 in BACE1 binding is reminiscent of an experimentally known case: a distal residue His164 in plasmepsin II (another aspartyl protease) shifts its pK_a from 6 to 7.5 upon pepstatin binding. ^31,33

Analysis of the apo and holo trajectories of BACE1 at different pH conditions revealed that the protonation equilibrium of His45 is shifted towards the charged state (i.e., pK_a upshift) through a ligand-induced conformational allostery. Conversely, charging His45 (lowering pH) increases the protein-ligand binding affinity. Specifically, proton titration of His45 is coupled to a pH-dependent χ₁ rotation and consequently the contact formation with Phe109 on the 113S loop (Fig. 5a–d). At low pH, His45 is protonated (charged) and rotated out to solvent and does not interact with Phe109. At high pH, His45 is deprotonated (neutral) and rotated in to form a contact with Phe109. At intermediate pH, His45 samples both charged/out and neutral/in states. In the presence of the inhibitor, the protonation equilibrium of His45 is shifted to a higher pH (Fig. 5b, red), and so are the pH profiles of His45 rotation and interaction with Phe109 (Fig. 5c and d, red), indicating that while charged His45 is favored, the His-in state and His45–F109 interaction are disfavored.

Figure 5. Protonation of His45 is coupled to the BACE1-inhibitor binding affinity change through conformational allostery.

a) Overlaid snapshots showing two dominant conformations: His45 in/His45–Phe109 contact (yellow), His45 out/I110–inhibitor contact (magenta). b) Probability of His45 deprotonation at different pH. c) Probability of His45-in rotation at different pH. His45 in is defined by χ₁ > 140° or χ₁ < −140°. d) Probability of His45–Phe109 contact formation at different pH. Based on the probability distribution of the His45–Phe109 distance, a contact is considered present when the distance is below 6 Å (Fig. S1). e) Free energy surface as a function of His45 (CE1)–Phe109 (CB) and Ile110 (CD)–inhibitor (C23) distances in holo BACE1 at different pH. For b-d, the apo and holo states are shown in black and blue, respectively.

Part of the binding affinity of the inhibitor comes from a hydrophobic contact with Ile110 on the 113S loop, which is also present in other BACE1-inhibitor complexes¹⁸ but not in CatD binding (based on our data). Strikingly, this contact is weakened by the interaction between His45 and Phe109, as evidenced by the correlation between the His45–Phe109 and I110-Lilly distances in the free energy surface (FES) (Fig. 5e). At low pH (5 and 6), the FES displays a single minimum in the lower right corner, indicating that while the H45–Phe109 interaction is absent (His45 out), Ile110 maintains a hydrophobic contact with the inhibitor. At high pH (8), the FES displays two minima, indicating that while the H45–Phe109 interaction is present (His45 in), the Ile110–inhibitor contact can form and break. At intermediate pH (7), the above two minima remain in the FES, and the lower right minimum seen in the FES of pH 5 and 6 reappears, indicating that the probability for the Ile110–inhibitor contact is increased compared to high pH (8). Thus, the BACE1–inhibitor affinity is strengthened with the breakage of the His45–Phe109 interaction, which in turn favors charged His45 and the rotation out to solvent.

In summary, we tested a protocol that combines CpHMD with FEP-based calculations to account for pH effects in protein-ligand binding. This protocol offers significant advantages compared to the alternative approach which directly employs constant pH MD in the alchemical calculations: the errors due to the free energy calculations and pH-dependent corrections are separable; and the computational cost is smaller. Additionally, CpHMD can uncover proton-coupled allosteric events, such as the one found in this study. We note that in principle, pH-dependent free energy corrections can be obtained using any pK_a calculation method; however, static-structure based Poisson-Boltzmann or empirical methods are very sensitive to the structure and therefore have a higher chance of generating false positives, i.e., many large pK_a shifts upon binding.³⁰ This is however not the case with CpHMD, which explicitly accounts for conformational relaxation and consequently has a lower level of “noise”. For example, most pK_a shifts for BACE1 and CatD inhibitor binding (and other protein systems, unpublished work by Shen and coworkers) are very small (below 0.2 units). Furthermore, error cancellation in the pK_a shifts removes a large part of the systematic errors, although errors due to the solvent model and force field still remain, which manifest most notably in the desolvation penalty and electrostatic interactions in the buried environment. ^8,15 Another caveat of the present work lies in the limited sampling time of the CpHMD simulations, which resulted in an insufficient conformational relaxation for a handful of residues that are deeply buried, involved in salt bridges, or undergo coupled titration. Fortunately, potential contributions from these residues can be neglected, as their pK_a’s are below 4 and as such would not affect the pH range of interest (4–8).

We demonstrated that the new protocol can improve the prediction of inhibitor selectivity, which is a challenging task in structure-based drug design, especially for aspartyl proteases and kinases, where off-targets are highly similar in overall structure and binding site. Our data revealed that it is the difference in the pH-dependent binding free energy, which gives rise to the inhibitor selectivity for BACE1 by 1.3 kcal/mol, matching the experimental estimate of 1.0 kcal/mol.³ Although this level of agreement might be fortuitous, it is encouraging and underscores the significance of including pH in the free energy calculations of protein-ligand binding.

Surprisingly, our data revealed that the pH dependence of BACE1 binding is mainly due to the protonation of a distal residue His45 in BACE1, and despite the large pK_a shifts of the catalytic residue and inhibitor titratable site, CatD binding is relatively independent of pH. The latter is reminiscent of HIV-1 protease, which shows a large pK_a shift of the aspartyl dyad upon inhibitor binding but no pH dependence in the measured binding affinity. ²⁹ Previous computational studies of possibly pH-dependent protein-ligand binding have focused on titratable sites directly involved in binding;^12,27,29 our findings demonstrate that to quantitatively predict the pH-dependent binding free energy, the pK_a shifts of all titratable sites need to be considered.

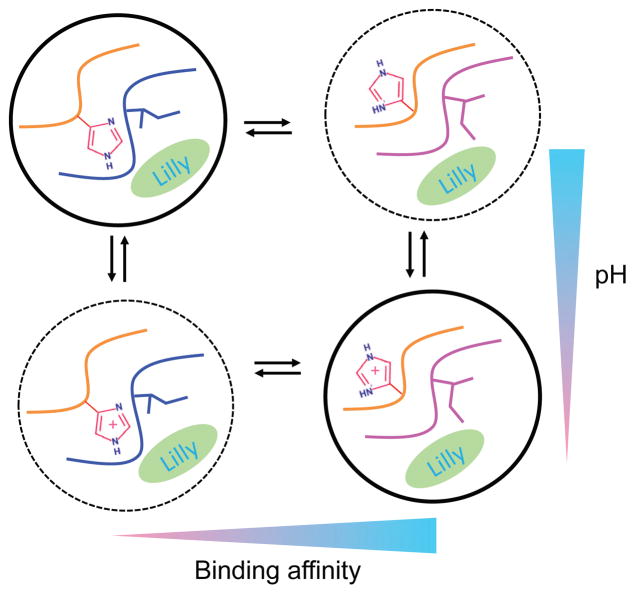
Perhaps the most surprising finding of the present work is how His45 protonation modulates inhibitor binding. Our data showed a thermodynamic linkage between His45 protonation and inhibitor binding through a nonintuitive allosteric mechanism. Protonation of His45 induces a local conformational event, a χ₁ rotation, which is propagated through the movement of the 113S loop to affect BACE1- inhibitor binding (Fig. 6). Conversely, inhibitor binding perturbs the 113S loop, which is propagated to affect the sidechain rotation of His45, resulting in a shift in the protonation equilibrium. Thus, our finding adds a new dimension to the allosteric regulation framework³⁴ and confirms a long-standing hypothesis based on the pioneering work of Alexov^31,32 and later Onufriev and coworkers ^25,30 using Poisson-Boltzmann calculations. The proposed mechanism can be experimentally verified by testing whether mutating His45 to a charged amino acid such as Lys would increase the binding affinity of BACE1. His45 is not conserved in BACE1 related proteases; thus, we hypothesize that an allosteric molecule which disrupts the His45–Phe108 interaction would increase the inhibitor selectivity. Our finding regarding His45 is not an exception. Experiment demonstrated that plasmepsin II binding to pepstatin resulted in a 1.5-unit increase in the pK_a of the remote His164. ^31,33 Thus, pK_a perturbation of distal histidines due to ligand binding may be more common than previously thought, and it is highly relevant, given that the model pK_a of histidine is near the physiological pH. We suggest that proton-coupled allosteric control is likely common in biology and may present exciting new opportunities in structure-based drug design.

Figure 6. Schematic view of the protonation-coupled conformational allostery in BACE1.

Protonation equilibria are shown vertically, while conformational changes are shown horizontally. Dominant states are indicated by circles with solid lines. His45, Ile110 and the inhibitor are explicitly shown. The loop that has His45 and the 113S loop that has Ile110 are also displayed.

Methods and Protocols

We followed the double decoupling scheme of Boresch et al. ²⁰ (Figure 2) to calculate the absolute binding free energies of BACE1 and CatD to the inhibitor LY2811376^11,12 at the reference pH (pH 8). The free energy perturbation (FEP) method was used to compute $\mathrm{\Delta }{G}_{\text{dsolv}}^{\mathrm{L}},\mathrm{\Delta }{G}_{\text{coup}}^{\mathrm{C}}$, and $\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{C}}$. The analytic approach developed by Boresch et al. ²⁰ was used to estimate $\mathrm{\Delta }{G}_{\text{res}}^{\mathrm{L}}$. All FEP calculations were set up with the VMD visualization program³⁵ and performed with the NAMD molecular dynamics engine.³⁶ The proteins were modeled with the CHARMM22/CMAP force field, ^37,38 and the inhibitor LY2811376 was modeled with the force field obtained previously by us. ^11,12 The FEP protocols made use of 14–31 λ windows, and each window was run for 1 ns.

The protein-ligand systems were built as in our previous work. ^11,12 In all the above calculations, Asp and Glu sidechains as well as the inhibitor were fixed in the charged state (the inhibitor titratable site is neutral). ^11,12 For BACE1, His sidechains were fixed in the neutral state, which, when considering the calculated pK_a’s (Table S1), corresponds to pH ~9.5 and higher. However, since there are no pK_a shifts above pH 7, ΔG is the same as pH 8. CatD is known to undergo a large conformational transition, which relocates the N-terminal residues to the active site at high pH.³⁹ Although this transition may not occur in the limited simulation time, to avoid potential structural deviation, histidine sidechains were fixed in the charged state, which, when considering the calculated pK_a’s (Table S2), corresponds to pH ~6. However, since there are no pK_a shifts above pH 6, ΔG^bind is the same as pH 8.

The pK_a’s of the apo and holo forms of BACE1 and CatD were taken from the previous hybrid-solvent continuous constant pH MD (CpHMD) simulations. ^8,11,12 In these simulations, the Asp, Glu and His sidechains as well as the inhibitor pyrimidin nitrogen (Fig. 1, circled red) were allowed to titrate, while Cys and Tyr were kept neutral and Lys and Arg were kept charged. Cys, Tyr, Lys and Arg have model pK_a’s above ~9⁴⁰ and structural analysis does not indicate pK_a downshifts to the interested pH range (i.e., below pH 8). The apo BACE1 was simulated with 24 pH replicas in the pH range 1–8; in the production run, each replica was sampled for 21 ns. The holo BACE1 was simulated with 20 pH replicas in the pH range 1.3–8; in the production run, each replica was sampled for 26 ns. The apo and holo CatD were simulated with 24 pH replicas in the pH range 1–8; in the production run, each replica was sampled for 31 and 36 ns, respectively. More details see. ^8,11,12