Towards enhanced and interpretable clustering/classification in integrative genomics

Abstract

High-throughput technologies have led to large collections of different types of biological data that provide unprecedented opportunities to unravel molecular heterogeneity of biological processes. Nevertheless, how to jointly explore data from multiple sources into a holistic, biologically meaningful interpretation remains challenging. In this work, we propose a scalable and tuning-free preprocessing framework, Heterogeneity Rescaling Pursuit (Hetero-RP), which weighs important features more highly than less important ones in accord with implicitly existing auxiliary knowledge. Finally, we demonstrate effectiveness of Hetero-RP in diverse clustering and classification applications. More importantly, Hetero-RP offers an interpretation of feature importance, shedding light on the driving forces of the underlying biology. In metagenomic contig binning, Hetero-RP automatically weighs abundance and composition profiles according to the varying number of samples, resulting in markedly improved performance of contig binning. In RNA-binding protein (RBP) binding site prediction, Hetero-RP not only improves the prediction performance measured by the area under the receiver operating characteristic curves (AUC), but also uncovers the evidence supported by independent studies, including the distribution of the binding sites of IGF2BP and PUM2, the binding competition between hnRNPC and U2AF2, and the intron–exon boundary of U2AF2 [availability: https://github.com/younglululu/Hetero-RP].

INTRODUCTION

Rapidly evolving high-throughput technologies have enabled biologists to progressively collect large amounts of genomic data with unprecedented diversity and high resolution. For example, The Cancer Genome Atlas (TCGA) project and Encyclopedia of DNA Elements (ENCODE) project have provided open access to genomic, transcriptomic and epigenomic information from a diverse group of samples. Potential data include, but not limited to, genome and protein sequences (1), single nucleotide variants (SNV) (2) and gene ontologies (3). Integrative analysis of such a wealth of heterogeneous data has motivated growing interests, giving rise to enhanced reliability of novel discoveries and improved understanding towards molecular heterogeneity of biological processes. Thus far, integrative analyses are carried out in pervasive clustering and classification studies. The former captures underlying patterns of the data and groups them into biologically interpretable groups, such as metagenomic contig binning (4). And the latter infers general properties of the data from a few annotated examples, such as RNA-binding protein (RBP) binding site prediction (5).

One common idea of integrating different types of data is to concatenate the feature vectors representing the data, as illustrated in Figure 1(A). Despite its simplicity, due to the unbalanced scales, data with a large number of features tend to have larger influence on the final outcome than others. One potential remedy is to normalize the data inversely proportional to its corresponding feature size, however, meaningful features from larger data may be diluted and become even weaker than unwanted features from smaller data. Another common practice of data integration projects multiple data types onto the same latent feature space (7). However, different data sources usually exhibit some unique features that are not shared by others, thus the enforcement of a joint space can potentially miss essential complementary information from the different data sources. In general, despite extensive studies, integrative studies pose significant challenges.

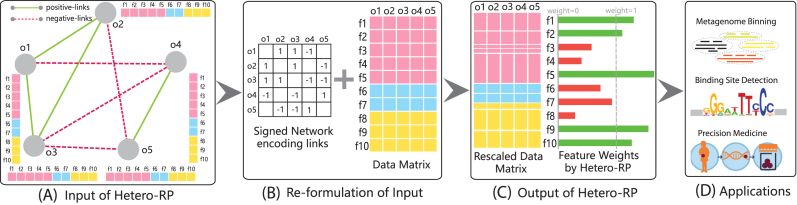
Figure 1.

Illustration of Hetero-RP on a toy example. (A) Each object o₁, ⋅⋅⋅, o₅ is represented by its corresponding feature vector, containing features indexed from f₁ to f₁₀, with colors indicating different data sources. ‘positive-links’ and ‘negative-links’ are in green solid line and red dash line, respectively. (B) The input to Hetero-RP contains two parts, the data matrix based on the concatenated feature vectors and the signed graph encoding both ‘positive-links’ and ‘negative-links’. (C) Hetero-RP rescales each dimension of features, but keeps the overall scale fixed. (D) The applications of Hetero-RP widely cover both clustering and classification domains.

In this paper, we introduce Heterogeneity Rescaling Pursuit (Hetero-RP), a scalable and tuning-free preprocessing framework for integrative genomic studies, to rescale features from multiple data sources so that important features are weighted more highly than less important ones. The rationale to determine the weights of different features is based on the implicitly existing auxiliary knowledge related to the problem of interest. We demonstrate the effectiveness of Hetero-RP in two clustering and classification applications: metagenomic contig binning and RBP binding site prediction. The objective of metagenomic contig binning is to cluster contigs in metagenomic samples so that contigs from the same genome are binned together. Additionally, two contigs may map to the same reference genome or there are multiple paired-end reads linking the two contigs. To utilize the auxiliary information on contig pairs, we introduce the concept of ‘positive-links’ between pairs of contigs supported by strong evidence of being binned together. Adversely, two contigs mapped to phylogenetically distant genomes are most unlikely to belong to the same bin. Thus we introduce the concept of ‘negative-links’ between pairs of contigs not belonging to the same bin. With a plethora of such auxiliary information available, we determine the weights of the different features. Similarly, the objective of RBP binding site prediction aims to predict whether RBPs bind to specific nucleotide positions of target RNA or not. With the existence of class labels provided by the training data, two nucleotide positions may share the same labels or different labels. To utilize the auxiliary information on label information, we introduce ‘positive-links’ between pairwise nucleotide positions indicating those sharing the same class label from the training data, and ‘negative-links’ otherwise. In addition, the auxiliary knowledge not only implicitly exists for exploration, but can be acquired actively and interactively as well. With human aid, interactive annotation gathered from experts can further promote the performance in both clustering (8) and classification (9).

Hetero-RP aims to seek better weights of features that match up with the auxiliary knowledge containing ‘positive-links’ and ‘negative-links’, particularly tailored for heterogeneous data from multiple sources. Unlike conventional feature selection, Hetero-RP makes no assumptions of feature independence (10–12). Likewise, Hetero-RP does not enforce the majority of features to be ‘irrelevant’, instead it assumes that the fraction of features without unit weight is small. These interpretable weights enable us to characterize the driving forces of the underlying biology.

We demonstrate the effectiveness of Hetero-RP using metagenomic contig binning and RBP binding sites prediction as examples. In metagenomic contig binning, Hetero-RP automatically weighs abundance and composition profiles according to the varying number of samples, resulting in markedly improved performance of contig binning on both simulated and real datasets. In RBP binding site prediction, a combination of Hetero-RP with state-of-the-art methods improves the prediction performance measured by the area under the receiver operating characteristic curves (AUC) substantially in 28 out of 31 real datasets by an average of 5.9%. Better still, the interpretable feature importance learned by Hetero-RP uncovers the evidence supported by independent studies, including the distribution of the binding sites of IGF2BP and PUM2, the binding competition between hnRNPC and U2AF2, and the intron–exon boundary of U2AF2.

MATERIALS AND METHODS

Let 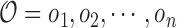be the set of n objects that possibly indicate metagenomic contigs for binning, RBP interaction sites for prediction, etc. Each object is represented by a feature vector, for features from a single data source or concatenation of multiple data sources. Mathematically, each data source i with feature dimensionality p_i on the same set of n objects is represented by a data matrix 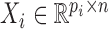. When the number of data sources m > 1, we stack them together by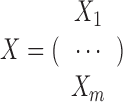. 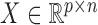is the stacked data matrix illustrated in Figure 1(B) and p≜p₁ + p₂ + ⋅⋅⋅ + p_m, where p₁, p₂, ⋅⋅⋅, p_m are the feature dimensionality of each data source, respectively. Then the feature vector of o_i is denoted as X_{· i}, for i = 1, 2, ⋅⋅⋅, n.

We encode ‘positive-links’ and ‘negative-links’ by an undirected signed graph 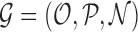, where 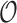is the set of objects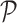, and and 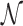consist of ‘positive-links’ and ‘negative-links’, respectively. 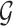can be represented by an adjacency matrix 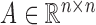, where A_ij = 1 if there is a ‘positive-link’ between o_i and o_j, A_ij = −1 if there is a ‘negative-link’ between o_i and o_j, and A_ij = 0 otherwise. With these notations, Hetero-RP aims to find a p-dimensional vector W = [w₁, w₂, ⋅⋅⋅, w_p] for overall p features, so as to minimize the inconsistency between the signed graph and the feature-wise rescaled data matrix diag(W)X where diag( · ) diagonalizes the vector into a diagonal matrix.

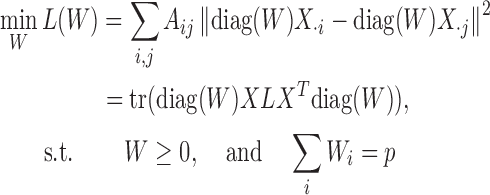(1)

where L = D − A denotes the 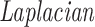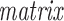(13) of adjacency matrix A and D indicates the diagonal matrix whose d_ii entry equals the sum of the i-row (or column due to symmetry) of A. In the above formulation, inconsistency decreases when object pairs joined by positive-links are pulled closer after data matrix is rescaled. To avoid trivial solutions, we enforce W to be nonnegative and conserved in sum, i.e. ∑_iW_i = p, as shown in Figure 1(C).

Unlike conventional feature selection that assumes most features are irrelevant, Hetero-RP assumes the majority of features are useful. Among those useful features, only a subset of them are more or less informative (weight ≠ 1) whereas the rest are neutral (weight =1). In comparison, conventional feature selection treats features either relevant (weight =1) or irrelevant (weight =0). To examine whether the assumption of Hetero-RP holds, for the clustering scenario, the dip test (14) can be used to check if each feature is multi-modal. If not, that feature is regarded uninformative and thus excluded. For the classification task, univariate metrics such as t-test can also be applied to score each feature and the resulting p-values are obtained. Features whose p-values exceed a certain threshold are not considered as well. The assumption of Hetero-RP naturally leads to the regularization of ΔW = W − 1, the deviation from unit weight. Thus, Equation (1) changes to the following quadratic programming problem:

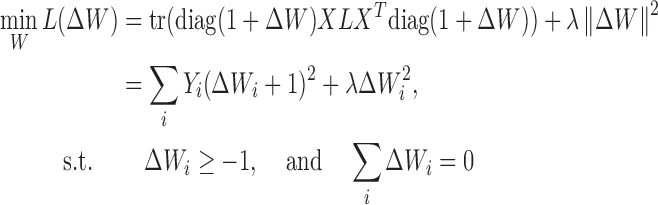(2)

where the parameter λ > 0 shrinks weight towards unit and towards each other. And Y is the diagonal vector of XLX, i.e., Y_i = (XLX)_ii, for i = 1, 2, ⋅⋅⋅, n. Note that when ‘negative-links’ are available, Y may no longer remain nonnegative. To keep convexity of Equation (2) for easy optimization, a common practice chooses Y_i = max (0, (XLX)_ii), for i = 1, 2, ⋅⋅⋅, n.

Parameter choice for λ

Hetero-RP selects the parameter λ in Equation (2) automatically (15) by carrying out the following two steps iteratively until convergence:

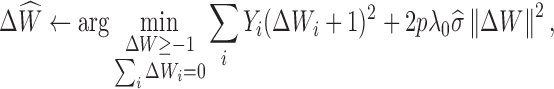(3a)

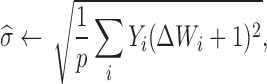(3b)

where λ₀ is chosen according to the suggestion of (16) and has also been used in (17). In particular, λ₀ = B/(p − 1 + B²)^1/2, where B = tq(1 − p^1/2/(2rlog r), p − 1) with tq(α, d) the αth quantile of a t-distribution with d degrees of freedom, and r represents the rank of L (see supplementary material for more details).

Insufficient auxiliary knowledge

When ‘positive-links’ and ‘negative-links’ are sparse, Equation (2) may suffer from ‘overfitting’, unable to provide expected weight reliably. Therefore, we utilize auxiliary knowledge along with the original data matrix X. Specifically, we consider a k-nearest neighbor network containing n vertices where each vertex i corresponds to X_{· i}, the i-th column of X and k is chosen as 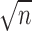. For each vertex i, i = 1, 2, ⋅⋅⋅, n, if vertex j belongs to the k-nearest neighbors of vertex i, then vertex i and vertex j are connected by edge with weight 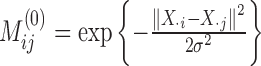, where σ can be chosen as 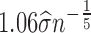and 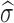is the standard deviation of X (18). We let 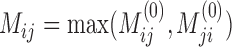for symmetry. Finally, we use the combined adjacency matrix A + γM, where the parameter γ > 0 controls the trade-off between intrinsic data structure and auxiliary knowledge. To balance the contribution from A and M, γ is chosen as γ = tr((A)^TM)/((A)^TA), the minimizer of 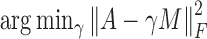, where 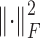indicates the sum of squared error.

RESULTS

Application to clustering: metagenomic contig binning

The next-generation sequencing technologies (NGS) enable biologists to sequence microbial communities from environmental samples directly. Contig binning is a process to group assembled sequence fragments, also known as contigs, into operational taxonomic units (OTUs), in which contigs in the same bin belong to closely related genomes (19). Most available methods rely on the integrated usage of abundance profiles across multiple metagenomic samples and tetra-mer composition profiles of contig sequences (4,20–23).

In brief, binning utilizes two types of data, p₁-dimensional relative abundance profiles X₁, and p₂-dimensional composition profiles X₂, where p₁ is the dimension of abundance profiles and p₂ is the number of distinct tetranucleotides. In addition, the co-alignment of contig pairs and paired-end reads linkage are considered as the auxiliary knowledge that potentially contribute to the binning performance (4).

We compared our previously proposed method, COCACOLA (4), with or without using Hetero-RP. The COCACOLA used in this paper is an upgraded version, which takes a non-linear transformation of the input features by spectral embedding (24) (see supplementary material for more details). To guarantee a fair comparison, the bin number is fixed as the estimation from single-copy genes (22). We not only showed the improvement of COCACOLA after incorporating Hetero-RP as preprocessing, but also compared the improved performance against three state-of-the-art methodologically distinct methods: CONCOCT (20), MaxBin (22) and MetaBAT (23).

We evaluated the gain from Hetero-RP based on both simulated and real datasets. The simulated ‘species’ dataset consists of 101 distinct species across 96 samples (20), with more than 3% sequence differences. Overall n = 37 628 contigs of length at least 1kbps were assembled for binning. The binning result is evaluated by the Adjusted Rand Index (ARI), an overall measure taking both precision and recall into account (see supplementary material for definition). The real ‘MetaHIT’ dataset contains 264 different samples from the MetaHIT consortium (25) (SRA:ERP000108), with a total of 192 673 assembled contigs of length at least 1 kbps remaining for binning. Unlike simulated dataset, the true labels are inaccessible in real dataset. Instead, we applied CheckM (26) to estimate the approximate precision (by the percentage of genes absent from different genomes) and completeness (by the percentage of expected single-copy genes that are binned).

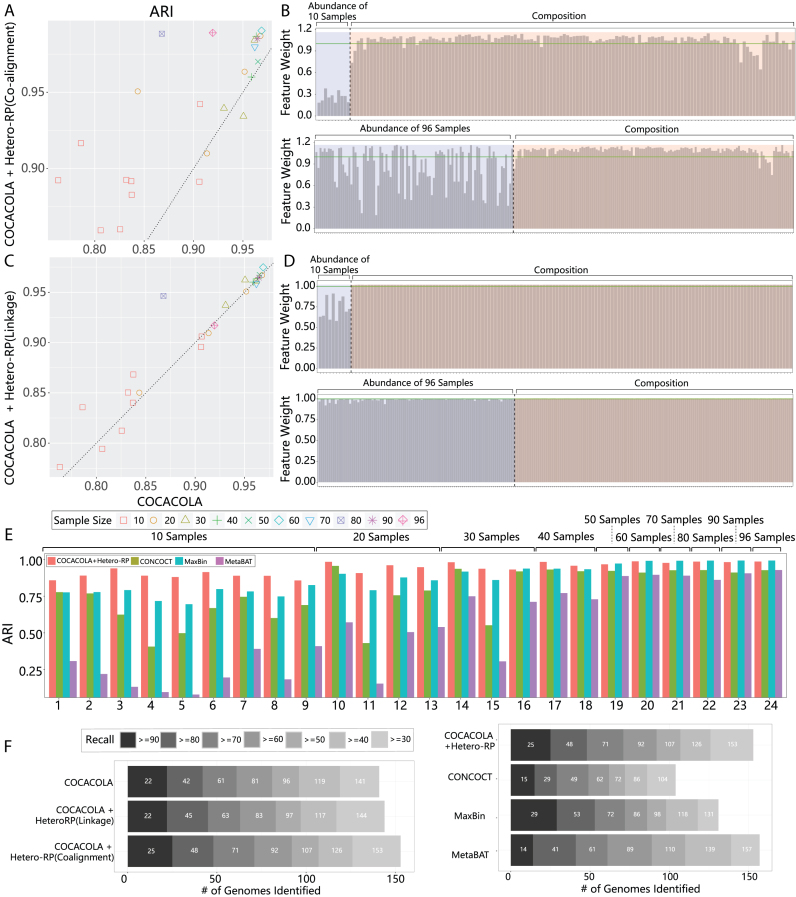
For the simulated ‘species’ dataset, to assess the gain of Hetero-RP thoroughly, we further sub-sampled the data of size varying from 10 to 90, with a step size of 10. To avoid duplicate contributions from multiple replicates, the numbers of replicates are 9, 4, 3, 2, 1, 1, 1, 1, 1, respectively. When using co-alignment as auxiliary knowledge, as shown in Figure 2(A), the ARI is improved in 20 cases by an average of 5.9% and decreased in two cases by an average of 1.7%. We also scrutinized the weight obtained by Hetero-RP on two randomly picked cases of sample size 10 and 96, respectively. As illustrated in Figure 2(B), the average weight of abundance profiles are 0.26 and 0.87 when sample sizes are 10 and 96, respectively. That is, Hetero-RP prefers to scale down the abundance profiles when sample size is small, consistent with the observation that binning performs better when the sample size increases (4,20) (see supplementary material for more details). When using paired-end reads linkage as auxiliary knowledge, as depicted in Figure 2(C), the ARI is improved in 9 cases by an average of 2.9% and decreased in three cases by an average of 1.4%. The improvement is less prominent than co-alignment because the positive-links set of co-alignment is ∼1800x larger than the set of linkage. The inferior performance is also revealed by the weight obtained by Hetero-RP. As shown in Figure 2(D), the abundance profiles are not sufficiently scaled down by an average of 0.74 when sample size is 10, and the weight has an average of 0.99, almost diminished when sample size is 96. We next compared COCACOLA with Hetero-RP using co-alignment against CONCOCT, MaxBin, and MetaBAT. As illustrated in Figure 2(E), Hetero-RP performs well in a majority of the cases, achieving better precision-recall tradeoff, especially when sample sizes are small.

Figure 2.

Incorporating Hetero-RP in metagenomic contig binning. (A) COCACOLA with Hetero-RP applied to the simulated ‘species’ dataset with multiple sub-sampling replicates, evaluated by Adjusted Rand Index (ARI). The auxiliary knowledge consider the co-alignment of contig pairs. (B) The feature weight of two randomly picked samples of size 10 and 96 using co-alignment. The blue shadow on the left side of the dashed line indicates the scales of abundance profile, whereas the red shadow on the right side of the dashed line indicates the scales of composition profile. The green horizontal line indicates the scales of 1. (C) The auxiliary knowledge consider the paired-end reads linkages. (D) The feature weight of two randomly picked samples of size 10 and 96 using linkage. (E) COCACOLA with Hetero-RP using co-alignment is compared against CONCOCT, MaxBin, and MetaBAT using ARI. The improvement is more prominent in small size cases such as 10 and 20. (F) Application to the real ‘MetaHIT’ dataset. The evaluation is based upon the recovery of genome bins at every completeness threshold. The number of recovered genome bins (X-axis) by each method (Y-axis) in different completeness threshold (gray scale) with precision >80%, calculated by the lack of contamination using CheckM.

For the real ‘MetaHIT’ dataset, we focused on the identification of genome bins having >80% precision (the lack of contamination) and >30% recall (completeness). As shown in Figure 2(F), Hetero-RP contributes to more or equivalent genome bins at every completeness threshold. Because co-alignment outperforms linkage consistently, we compared COCACOLA with Hetero-RP using co-alignment against CONCOCT, MaxBin and MetaBAT. We observe that for the recovery of a genome bin with >90% completeness, MaxBin dominates other methods. In particular, MaxBin recovers 29 genome bins in comparison to 25 by COCACOLA with Hetero-RP, 15 by CONCOCT and 14 by MetaBAT, respectively. Nevertheless, MaxBin does not perform well for genome bins with <70% completeness. COCACOLA with Hetero-RP consistently recovers more genome bins than CONCOCT at every completeness threshold. It recovers more high quality genome bins with ≥60% completeness than MetaBAT. We conclude that in the experiment involving real metagenomic contigs, COCACOLA with Hetero-RP still performs well.

Application to classification: RBP binding site prediction

We next incorporated Hetero-RP as a preprocessing step to predict whether RNA-binding proteins (RBP) bind to specific nucleotide positions of target RNA, as RBPs are of vital importance in the control of gene expression. Current state-of-the-art methods utilize the combination of multiple data sources including tetranucleotides, secondary structure, region type, CLIP co-binding and Gene Ontology (GO) terms (5).

For a given RBP, a predictive model is built based upon n training nucleotide positions indicating whether each position is a binding side or not. For each nucleotide position, the neighboring [−50, 50] positions are considered in five types of data. Specifically, the tetranucleotide composition X₁ has p₁ dimensions where p₁ = 256 × 101 = 25 856; the probabilistic scores of secondary structure X₂ computed by RNAfold (27) has p₂ dimensions where p₂ = 101; the region type X₃ is has five presence/absence indicators for intron, exon, 5′-UTR, 3′-UTR and ORF, with dimensionality p₃ = 5 × 101 = 505; the co-binding proteins cDNA counts X₄ involve other 30 RBP experiments, with dimensionality up to 30 × 101 = 3 030; and the GO annotations X₅ has p₅ = 39 560 GO term markers indicating the position within known genes having that annotation (see supplementary material for more detailed descriptions). In addition, the auxiliary knowledge is considered as whether pairwise nucleotide positions share the same labels or different labels.

We evaluated Hetero-RP based on 31 published CLIP experiments, with 19 distinct RBPs with one or multiple experimental replicates (5). These RBPs involve a variety of functionalities such as splicing (ELAVL1, FUS, hnRNPs, TDP-43, U2AF2 etc.) and processing of 3′-UTR (Ago, IGF2BP etc.). For each individual experiment, up to 20 000 identified crosslinking sites split into training and test sets as positive samples, whereas sites within non-interacting genes as negatives. The prediction performance measured by the area under the receiver operating characteristic curves (AUC).

We first compared the state-of-the-art method, iONMF (5), with or without using Hetero-RP. iONMF relies on orthogonality-regularized nonnegative matrix factorization, not only outperforming other state-of-the-art methods GraphProt (28) and RNAContext (29) but also discovering class-specific RNA binding patterns (see supplementary material for more details). In particular, we applied Hetero-RP to the training set, and obtained the corresponding weight. The same weights were applied to both training and test sets afterwards. We not only showed the improvement of iONMF after incorporating Hetero-RP as preprocessing, but also compared the improved performance against GraphProt and RNAContext. Meanwhile, we also compared Hetero-RP against three popular feature selection methods: Correlation-based Feature Selection (CFS) (30), Fast Correlation-Based Filter (FCBF) (31), and Sparse Logistic Regression (SLR) (32) (see supplementary material for definitions).

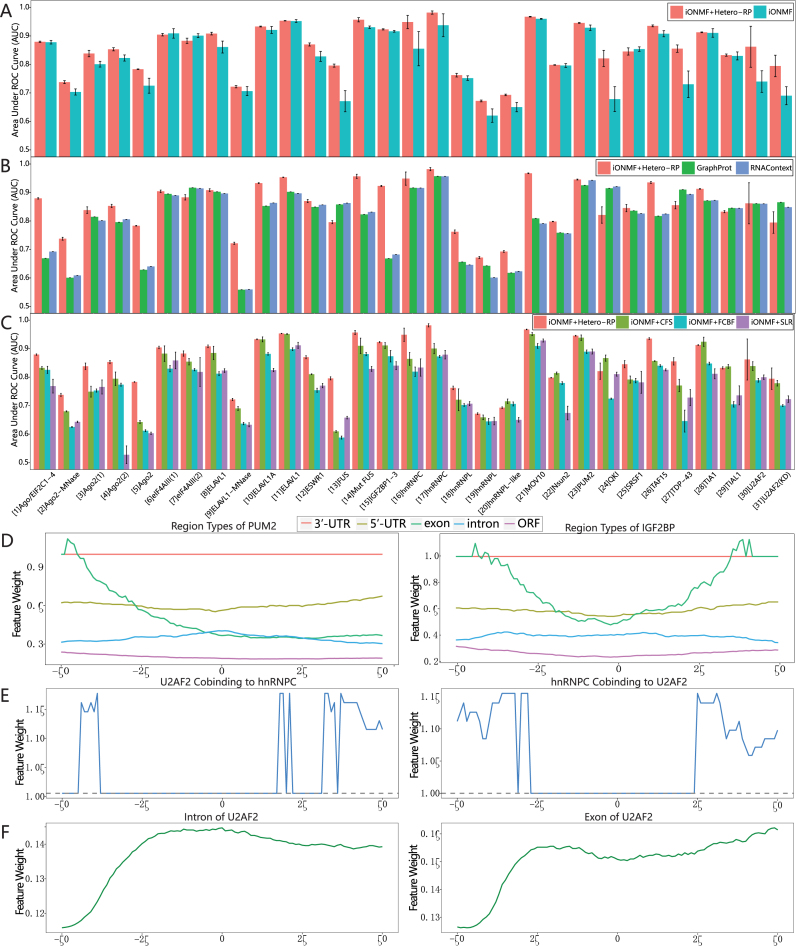
We ran iONMF 20 times with different random seeds. For each round, the random seed was fixed for both training and testing stages regardless of whether Hetero-RP is used. As shown in Figure 3(A), in 28 out of 31 cases, Hetero-RP substantially improves the performance of the already state-of-the-art method by an average increase of 5.9%. In the remaining cases, Hetero-RP shows negligibly worse performance by an average decrease of 1.2%. It is notable that QKI achieves a 21.1% improvement by Hetero-RP, with the AUC score increasing from 0.678 to 0.821. Furthermore, Hetero-RP facilitates more robust prediction by decreasing the standard deviation by an average of 45.9%. We next compared the improved performance of iONMF against state-of-the-art methods. As illustrated in Figure 3(B), iONMF with Hetero-RP outperforms GraphProt and RNAContext in 25 out of 31 cases by an average increase of 11.1% and 11.0%, respectively. In remaining six cases, Hetero-RP is outperformed by an average of 6.2% and 5.7%, respectively. After that, we compared Hetero-RP with three different types of feature selection methods. As shown in Figure 3(C), Hetero-RP outperforms CFS, FCBF, and SLR in 26, 30 and 31 out of 31 cases by an average increase of 6.7%, 12.0% and 12.9%, respectively. In comparison, Hetero-RP merely shows worse performance by an average decrease of 2.4% and 1.9% in the remaining cases for CFS and FCBF, respectively.

Figure 3.

Incorporating Hetero-RP in RBP binding sites prediction. (A) iONMF with or without Hetero-RP is applied to 31 published CLIP experiments. The positive-links and negative-links sets are constructed according to the labels of the nucleotide positions in the training set. The performance is evaluated by the area under the receiver operating characteristic curve (AUC). (B) Hetero-RP is compared against state-of-the-art methods. (C) Hetero-RP is compared against popular feature selection methods. (D–F) Interpretations of the scales obtained by Hetero-RP. (D) The 3′-UTR region type of PUM2 and IGF2BP has the largest weights, consistent with the fact that the binding sites of both IGF2BP and PUM2 are distributed across 3′-UTRs. (E) The mutual co-binding of hnRNPC and U2AF2 has large weights and this observation agrees with the fact that hnRNPC interacts with the same positions as U2AF2. Moreover, the weights are even larger at the upstream and downstream, supporting the evidence of direct competition between the two. (F) The intron and exon region types of U2AF2 start to scale up at ∼30 nucleotides upstream from the binding site, where the reported intron–exon boundary is located.

We scrutinized the weights obtained by Hetero-RP (see supplementary material for more details). As shown in Figure 3(D), 3′-UTR region types turn out to be the most informative features across the upstream and downstream of the crosslinking sites for RBP such as IGF2BP and PUM2. In contrast, intron, 5′-UTR, and ORF region types are scaled down. This observation agrees with the fact that the binding sites of both IGF2BP and PUM2 are distributed across 3′-UTRs (33). In addition, both IGF2BP and PUM2 are mainly cytoplasmic and their binding sites are mainly located in exons (33), which is also captured by Hetero-RP. Specifically, exon features across the upstream of the crosslinking sites are scaled up for both IGF2BP and PUM2, and the downstream are also enriched for IGF2BP.

It has been reported that hnRNPC interacts with the same positions as U2AF2 (5), consistent with the weights revealed in Figure 3(E), which is either scaled up or unchanged across the upstream and downstream of the crosslinking sites. The underlying rationale is that binding of the hnRNPC or U2AF2 serves as the indirect evidence of binding of the counterpart. Meanwhile, there is evidence supporting the direct competition between the two (34), implied by the fact that the weights of positions around [−25, 25] relative to the binding site is lower than the upstream and downstream.

Finally, U2AF2 is a splicing factor that predominantly crosslinks to the 3′ splice site (34). It has also been reported that the intron–exon boundary is at ∼30 nucleotides upstream from the binding site (5), exactly where the weights of both intron and exon region types start to increase steeply, as depicted in Figure 3(F).

DISCUSSION

Hetero-RP provides a general data preprocessing framework for integrative genomic studies. By utilizing implicitly existing auxiliary knowledge, Hetero-RP introduces a scalable algorithm to weigh important features more highly than less important ones. At the same time, efforts have been made to avoid overfitting by regularization and incorporating intrinsic structure from data per se. From practitioners’ perspective, Hetero-RP is tuning-free without tedious cross-validation for tuning parameters.

We demonstrate the effectiveness of Hetero-RP in both clustering and classification domains, from metagenomic contig binning to RBP binding site prediction, showing the wide applicability of our framework. More importantly, Hetero-RP not only plays the role as a ‘black box’, but also leads to interpretability of feature importance, offering insights into better biological understanding.

We also notice the potential improvement of Hetero-RP for future investigation:

1. The ‘positive-links’ and ‘negative-links’ chosen as auxiliary knowledge are assumed to be generic so that they remain invariant to all situations. Nevertheless, such generic assumption may be limited when auxiliary knowledge vary with different situations. That is, a specific ‘positive-link’ or ‘negative-link’ may take place in certain situation while not in others. For example, individual RBP binding activities may change along with different cell types, environmental conditions, or biological systems. Therefore, modeling condition-specific auxiliary knowledge is needed to adaptively learn feature weights that exhibit condition-specific behavior. Moreover, once having obtained feature weights learned from auxiliary knowledge in some conditions, how and to what extent to reuse such results to help boost the performance given auxiliary knowledge in other conditions is also needed.

2. More general form of auxiliary knowledge, such as the relative comparison in the form of ‘A is closer to B than A is to C’, can be considered. The relative comparison is pervasive and ubiquitous in many scenarios. For example, the relative comparison encodes a phylogenetic tree containing the interspecies relationships among the microbial organisms. To be specific, two genomes sharing the same genus taxonomic level are more likely to belong to the same OTU than those in different levels (35). Actually, the positive-links and negative-links are special cases of relative comparison, that is, an positive-link pair is closer than any random pair which in turn is closer than a negative-link pair.

3. Hetero-RP measures the features against auxiliary knowledge implicitly in Euclidean distance, which may not hold well for all sources of data. We can potentially employ Kernel Principal Component Analysis (36) to project the original data into a new data matrix with the nonlinear features induced by the kernel, and then use the resulting data matrix as the input to Hetero-RP. This procedure is referred to as ‘KPCA trick’, which is theoretically sound (37).

4. The quadratic programming form of Hetero-RP is not computationally optimal, and faster solvers such as ADMM (38) can be applied.

In summary, Hetero-RP can serve as a foundational preprocessing tool for integrative genomic studies. With the advent of high-throughput technologies, researchers are exposed to ‘Big Data’ in biology and medicine. Though integrative studies are increasingly common, facilitating better understanding towards biological mechanisms, the optimal integration of diverse heterogeneous massive data still needs to be explored. We expect Hetero-RP to motivate a rich set of applications in integrative genomic studies and ‘Big Data’ practices.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

National Science Foundation (NSF) [DMS-1518001, OCE-1136818]; National Institutes of Health [R01GM120624]; Gordon and Betty Moore Foundation Marine Microbiology Initiative [GBMF3779]; Simons Foundation. Funding for open access charge: NSF [DMS-1518001].

Conflict of interest statement. None declared.