Two-Dimensional Sound Localization in Cochlear Implantees

Introduction

Cochlear implants (CIs) have become an effective tool in the treatment of profound hearing impairment and deafness. Compared with monaural stimulation, bilateral stimulation provides improvements in speech perception in noise (e.g., Schleich, Nopp & D'Haese, 2004) and horizontal-plane sound localization (e.g., van Hoesel & Tyler, 2003; Nopp, Schleich & D'Haese, 2004). The auditory system uses binaural cues to localize sounds in the horizontal plane (e.g., Macpherson & Middlebrooks, 2002), and these cues, in the form of interaural level differences and interaural time differences, can be used in electric stimulation to some extent (e.g., Laback, Pok, Baumgartner, Deutsch & Schmid, 2004; Grantham, Ashmead, Ricketts, Haynes & Labadie, 2008). In contrast, vertical-plane sound localization and front-back discrimination rely on the spectral coloration or timbre of the incoming sounds (Carlile & Pralong, 1994; Perrett & Noble, 1997; Middlebrooks, 1999). The ability of CI users to localize sounds in vertical planes has not yet been investigated in CI listeners.

The position-dependent filtering of sounds introduced by the pinna, head, and torso can be described by head-related transfer functions (HRTFs; Blauert, 1974; Shaw, 1974; Møller, Sørensen, Hammershøi & Jensen, 1995). In normal-hearing (NH) listeners, it has been shown that subject-dependent HRTFs with frequencies between 4 and 16 kHz are important for vertical-plane localization (Morimoto & Aokata, 1984; Wightman & Kistler, 1997; Langendijk & Bronkhorst, 2002). Compared with NH listeners, CI listeners have a smaller number of frequency channels and poorer frequency selectivity because of a broad spread of excitation along the cochlea (Shannon, 1983bb; Cohen, Richardson, Saunders & Cowan, 2003). In addition, in current clinical CI systems, the microphone is usually located behind the ear (BtE), is often omnidirectional, and the upper frequency range of the sound processing is limited to approximately 10 kHz. These limitations in CI hearing result in a substantial alteration of the position-dependent filtering (particularly from the pinna), and the alterations are expected to impair the localization in the vertical planes.

On the other hand, for low-pass-filtered sounds (cut-off frequency of 3 kHz), Algazi, Avendano & Duda (2001) showed that listeners were able to localize sounds in vertical planes when the sound source was located away from the median plane. They attributed the elevation-dependent changes in the HRTFs to changes in the reflections from the torso and shoulders. These results indicate that the absence of high-frequency pinna cues does not necessarily rule out the ability to localize sounds in vertical planes. Hence, it may be possible that CI listeners are able to use their BtE-HRTFs to discriminate front from back to a certain extent.

The aim of this study was to investigate two-dimensional sound localization in CI listeners. In particular, we asked whether CI listeners are able to localize sources in vertical planes using their clinical speech processors. In addition, the results for CI listeners were compared with those for NH listeners, who were tested in the study by Majdak et al. (2010) using the same experimental methodology as in this study.

Experiment 1

Materials and Methods

Subjects

Five postlingually-deafened CI listeners participated in the experiments; the age range was 23 to 70 years. The subjects had excellent speech understanding in quiet. They were implanted bilaterally with the C40+ implant system (MED-EL Corporation, Austria), with the exception that subject CI24 was implanted at the right ear with a PULSAR CI 100 that was driven in the C40+-compatibility mode. Clinical data of the listeners are provided in Table 1.

Table 1.

Clinical data and stimulation levels of the CI listeners. The stimulation level is given in dB re: hearing level (dB re: HL) and in percentage of the dynamic range (%DR). The first value shows the level used in experiment 1 and the second value shows the level used in experiment 2. NA, not available.

Subject	Etiology	Age at implantation		Deafness duration		Bilateral electric stimulation experience (yr)	Age at testing (yr)	Dynamic range (dB)	Stimulation level (dB re HL;%DR)
		Left (yr)	Right (yr)	Left (yr)	Right (yr)
CI1	Meningitis	14	14	0.5	0.1	9	23	N.A. >35	35 dB; N.A. 25 dB; <71%
CI3	Meningitis	21	21	0.2	0.2	3.5	24	N.A. N.A.	15 dB 15 dB
CI8	Osteogenesis imperfekta	41	39	3	12	3	44	N.A. >38	50 dB; N.A. 35 dB; <87%
CI24	Progressive	48.5	49	2	2.5	2	51	38 38	27 dB; 71% 27 dB; 71%
CI52	Morbus Menière	68	63	0.5	1.5	2	70	31 38	20 dB; 65% 20 dB; 65%

Apparatus

The virtual acoustic stimuli were presented via auxiliary inputs of the speech processors (Tempo+, MED-EL Corporation) in a semi-anechoic room. The everyday clinical settings of each listener were used, except that the automatic gain control (AGC) of the speech processors was omitted.¹ The settings were the standard clinical settings for Tempo+ processors: monopolar stimulation with 26.7-µs biphasic pulses, 12 electrodes each activated at a pulse rate of 1515 pps, and a frequency range from 200 to 8500 Hz. Minor exceptions were that CI3 had a 31-µs pulse duration at electrodes 6 to 8 in the left ear, CI24 had a 24.2-µs pulse duration at all electrodes in the right ear, and CI3 had 1456 pps in the left ear. A potentially important exception was that CI1 used a frequency range from 300 Hz to 5500 Hz. This discrepancy was deliberately not corrected because of our aim to test the listeners' performance with everyday clinical settings and because of potential learning effects that may confound our results. Stimuli were generated using a computer and output via a digital audio interface (ADI-8, RME) with a 48-kHz sampling rate. A virtual visual environment was presented via a head-mounted display (HMD; 3-Scope, Trivisio). It provided two screens with a field of view of 32° x 24° (horizontal x vertical dimensions). The virtual visual environment was presented binocularly with the same picture for both eyes. A tracking sensor (Flock of Birds, Ascension) was mounted on the top of the listeners' head, which captured the position and orientation of the head in real time. A second tracking sensor was mounted on a manual pointer. The tracking data were used for the 3-D graphic rendering and response acquisition. More details about the apparatus are provided in the study by Majdak et al. (2010).

HRTF measurement

BtE-HRTFs were measured for each listener. Twenty-two loudspeakers (custom-made boxes with VIFA 10 BGS as drivers) were mounted on a vertical circular arc at fixed elevations from -30° to 80°, with a 10° spacing between 70° and 80° and 5° spacing elsewhere. The listener was seated at the center point of the circular arc on a computer-controlled rotating chair. The distance between the center point and each speaker was 1.2 m. The listener wore two BtE processors (customized Tempo+, MED-EL). The microphone output signals were directly recorded via amplifiers (FP-MP1, RDL) by the digital audio interface.

For the spatial setup and system identification, we used the same procedure as in the study by Majdak et al. (2010). A 1729-msec exponential frequency sweep from 50 to 20 kHz was used to measure each HRTF. To speed up the measurements, for each azimuth, the multiple exponential sweep method was used (Majdak, Balazs & Laback, 2007). In the interaural horizontal plane¹, the HRTFs were measured with 2.5° spacing within the azimuthal range of ± 45° and with 5° spacing otherwise. With this rule, the other measurement positions were distributed with a constant spatial angle, i.e., the horizontal spacing increased with the elevation. In total, HRTFs for 1550 positions within the full 360° horizontal span were measured for each listener. During the HRTF measurement, the vertical arc was fixed, and the different azimuths were achieved by rotating the listener on the chair. Also, the head position and orientation were monitored with the same tracker as used in the experiments. The measurement procedure lasted for approximately 20 minutes. The acoustic influence of the equipment was removed by equalizing the HRTFs with the transfer functions of the equipment. The equipment transfer functions were derived from the reference measurements in which the processor microphones were placed at the center point of the circular arc, and the measurements were performed for all loudspeakers.

The directional transfer functions (DTFs) were calculated using a method similar to the procedure described in the study of Middlebrooks (1999). The magnitude of the common transfer function (CTF) was calculated by averaging the log-amplitude spectra of all HRTFs for each individual listener. The phase spectrum of the CTF was set to the minimum phase corresponding to the amplitude spectrum. The DTFs were the result of filtering HRTFs with the inverse complex CTF. Finally, the impulse responses of all DTFs were windowed with an asymmetric Tukey window (fade-in of 0.5 msecs and fade-out of 1 msec) to a 5.33-msec duration.

Stimuli

To specify the spatial position of the acoustic targets, the horizontal-polar coordinate system was used (Middlebrooks, 1999). The acoustic targets were uniformly distributed on the surface of a virtual sphere, with the listener in the center of this sphere. The positions of the acoustic targets during the experiment were random. The lateral target angle ranged from -90° to 90°. The polar target angle ranged from -30° (front, below eye-level) to 210° (rear, below eye-level).

The stimuli were Gaussian white noises with a 500-msec duration, which were filtered with the subject-specific DTFs. Before filtering, the position of the target was discretized to the grid of available DTFs. The filtered signals were temporally windowed using a Tukey window with a 10-msec fade.

The level of stimuli was defined relative to the individual hearing threshold, i.e., dB re: hearing threshold. The thresholds were estimated in a manual up-down procedure using a target positioned at azimuth and an elevation of 0°. The estimated hearing threshold defined 0 dB for each subject, and all following levels are relative to the individual hearing threshold. In NH listeners, Vliegen & Van Opstal (2004) showed that levels between 40 and 50 dB yield a good localization performance in the vertical dimension. Even though it is not appropriate to map 1:1 from NH to CI listeners, we also attempted to use 50 dB. On the one hand, CI listeners have often smaller electric dynamic ranges than NH listeners. On the other hand, speech processors use a compressive mapping to adapt the dynamic range of the acoustic signals to the smaller dynamic range of the electric currents. The input dynamic range is more than 55 dB in Tempo+ processors with deactivated AGCs (Stöbich, Zierhofer & Hochmair, 1999; Spahr & Dorman, 2005). Nevertheless, we expected individual differences that could originate from the individual level-compression functions in the stimulation strategy of the speech processors. Having no indications for a better choice than 50 dB, we started with 50 dB and asked each subject if this level yielded comfortable loudness.

For CI8, the level of 50 dB yielded a comfortable loudness. After finishing experiment 1 (one day of testing), the listener reported that this level had become uncomfortably loud, and 35 dB was perceived as comfortably loud. Thus, we reduced the level to 35 dB in experiment 2; however, we could not repeat the experiment 1 at the lower level because of the limited availability of that listener.

For CI24, the level of 50 dB yielded a comfortable loudness, and experiment 1 could be performed without any problems. However, at the beginning of experiment 2, CI24 reported 50 dB as being uncomfortably loud. We roughly estimated the dynamic range and levels larger than 37 dB were uncomfortably loud, whereas levels around 27 dB yielded a comfortable loudness. We repeated experiment 1 and performed experiment 2 at the level of 27 dB.

For CI1, the level of 50 dB yielded an uncomfortable loudness, whereas the level of 35 dB yielded a comfortable loudness. Thus, we used 35 dB in experiment 1. At the beginning of experiment 2, the listener reported 35 dB as being uncomfortable loud. We roughly estimated the dynamic range and levels larger than 35 dB were uncomfortably loud, while levels around 25 dB yielded a comfortable loudness. Thus, we used 25 dB in experiment 2. Unfortunately, we could not repeat experiment 1 at the lower level.

For CI3 and CI52, the levels of 15 dB and 20 dB yielded a comfortable loudness, respectively, and these level were used in both experiments.

All the levels are summarized in Table 1. In addition, the level of the stimuli was randomly roved for each presentation within the range of ± 2.5 dB to reduce the possibility of localizing spatial positions based on broadband level.

Procedure

The listeners were immersed in a spherical virtual visual environment (for more details, see Majdak et al., 2010). They held a pointer in their right hand. The projection of the pointer direction on the sphere's surface, calculated based on the position and orientation of the tracker sensors, was recorded as the perceived target position. The pointer was visualized whenever it was in the listeners' field of view.

Before the main tests, listeners performed a procedural training. The aim was to train subjects to point accurately to targets in the main experiment. The procedural training was a simplified game in the first-person perspective, where listeners had to find and point at a visual target, and click within a limited time period. This training was continued until 95% of the targets were found with a root-mean-square (RMS) angular error smaller than 2°. This performance was reached within a few hundred trials.

In the main experiment, at the beginning of each trial, the listeners were asked to align themselves with the reference position and click a button. Then, the stimulus was presented. During the presentation, the listeners were instructed not to move. The listeners were asked to point to the perceived stimulus location and click the button again. This response was recorded for the data analysis. Then, a visual target in the form of a red rotating cube was shown at the position of the acoustic target. In cases where the target was outside of the field of view, an arrow pointed towards its position. The listeners were asked to find and point at the target, and click the button. At this point in the procedure, the listeners had both heard the acoustic target and seen the visualization of its position. To stress the link between visual and acoustic location, the listeners were asked to return to the reference position and listen to the same acoustic target once more. During this second acoustic presentation, the visual target remained on. Then, while the target was still visualized, the listeners had to point at the target and click the button again.

The tests were performed in blocks; each block consisted of 50 acoustic targets and lasted for approximately 30 minutes. Within a block, the targets were sampled randomly with replacement from the 1550 possible spatial positions. Each subject was tested for eight blocks, resulting in responses for 400 trials for each listener. Before collecting the data, the subjects were trained using the same procedure as during the test for at least 100 trials.

Data analysis

The errors were calculated by subtracting the target angles from the response angles. After the conventions of Heffner & Heffner (2005), we distinguish between the localization accuracy, which represents the systematic error as measured by the bias, and the localization precision, which represents the blur or consistency of the localization ability. In the lateral dimension, the lateral bias was calculated from the signed mean of the lateral errors. The lateral absolute bias was also calculated by collapsing the absolute value of the lateral biases across the left and right sides. Finally, the lateral localization precision error was calculated from the standard deviation of the lateral errors.

In the polar dimension, the quadrant errors were analyzed to represent the number of confusions between the front and back hemifields (Middlebrooks, 1999). We used the quadrant error rate metric (in %), which is the percentage of responses where the absolute weighted polar error exceeded 45°. Note that our weighting of the polar errors is different to that used in the study by Middlebrooks (1999). The weighted polar error was calculated by weighting the polar error with w=0.5⋅cos (2⋅α)+0.5, where α is the lateral angle of the corresponding target. For targets in the median plane (α=0°), w=1 and the polar error must exceed ± 45° to be considered a quadrant error. For targets at α=±45°, because of the weighting (w<1), the polar error must exceed ± 90° to be considered a quadrant error. For targets at α=±60°, no quadrant errors were recorded because the polar error must exceed ± 180° to be considered a quadrant error. Circular statistics (Batschelet, 1981) were used to analyze the accuracy and precision in the polar dimension (Montello, Richardson, Hegarty & Provenza, 1999). The bias in the polar dimension is represented by the circular mean of the polar errors. Because the polar bias is highly correlated with the quadrant error, the polar bias was calculated for the data without quadrant errors. Similarly, the precision in the polar dimension is represented by the circular SD of the weighted polar errors calculated for the data without quadrant errors. For more details on the metrics used in this study see the study by Majdak et al. (2010).

Comparison with NH listeners is based on data from Majdak et al. (2010) where we tested sound localization in five NH listeners under conditions comparable with this study. In that study, listeners were presented virtual acoustic stimuli via headphones. In contrast to this study, HRTFs were measured at the entrance of the blocked ear canal in the study by Majdak et al. (2010). Otherwise, the studies were identical.

For the position-dependent analysis in the lateral dimension, the localization ability was investigated separately for the front and back hemifields, and for three different lateral position ranges per side, resulting in 12 lateral position ranges in total. The data separation for the two hemifields was done on the basis of the polar response angle. The different lateral positions were analyzed by grouping target positions. For the right hemifield, the groups were: 0° to -20°, -20° to -40°, and -40° to -90°. For the left hemifield, the groups were: 0° to 20°, 20° to 40°, and 40° to 90°. These groups contained approximately the same number of tested positions. For the position-dependent analysis of the quadrant errors, the data were analyzed in four groups resulting from the combination of two elevations (eye-level and top) and two hemifields (front and rear). The elevation “eye-level” included all targets with elevations between -30° and +30°. The elevation “top” included all targets with elevations between +30° and +90°. For targets in the median plane, this corresponds to ± 30°-groups at polar angles centered around 0°, 60°, 120°, and 180°. In contrast to the quadrant errors where the data were separated on the basis of the elevation angle, the data for the polar bias and polar precision error were separated on the basis of the target polar angle. The four position groups were -30° to +30°, 30° to 90°, 90° to 150°, and 150° to 210°.

For comparisons with previous studies, other metrics are provided. The lateral absolute error (Nopp et al., 2004; the absolute difference between the response and target angles averaged over all positions) and the RMS error (Middlebrooks, 1999; the square root of the average of the squared differences between the response and target angles) represent a combined measure of bias and precision. The lateral precision error for central targets (Nopp et al., 2004; includes only targets within ± 20°) allows an estimate of the precision near the median plane. The lateral and polar correlation coefficients represent the correlation of the response and target angles in the lateral and polar dimensions, respectively (Algazi et al., 2001). The level-response correlation coefficient shows the correlation between the broadband level of the acoustic target and the polar response angle. The front-back confusion rate was defined as the percentage of hemifield confusions for targets near the median plane, that is within the lateral range of ± 30° (Makous & Middlebrooks, 1990); however, targets near to the frontal plane, which are within the polar angle range of 60° to 120°, were removed from the calculations (Carlile, Leong & Hyams, 1997). This metric directly reflects the percentage of front-back confusions; however, it is restricted to a very small region of the hemifield. The chance rate for this metric was 50%, and the binomial-distribution probability test was used to test whether this metric was significantly different from chance.

Results

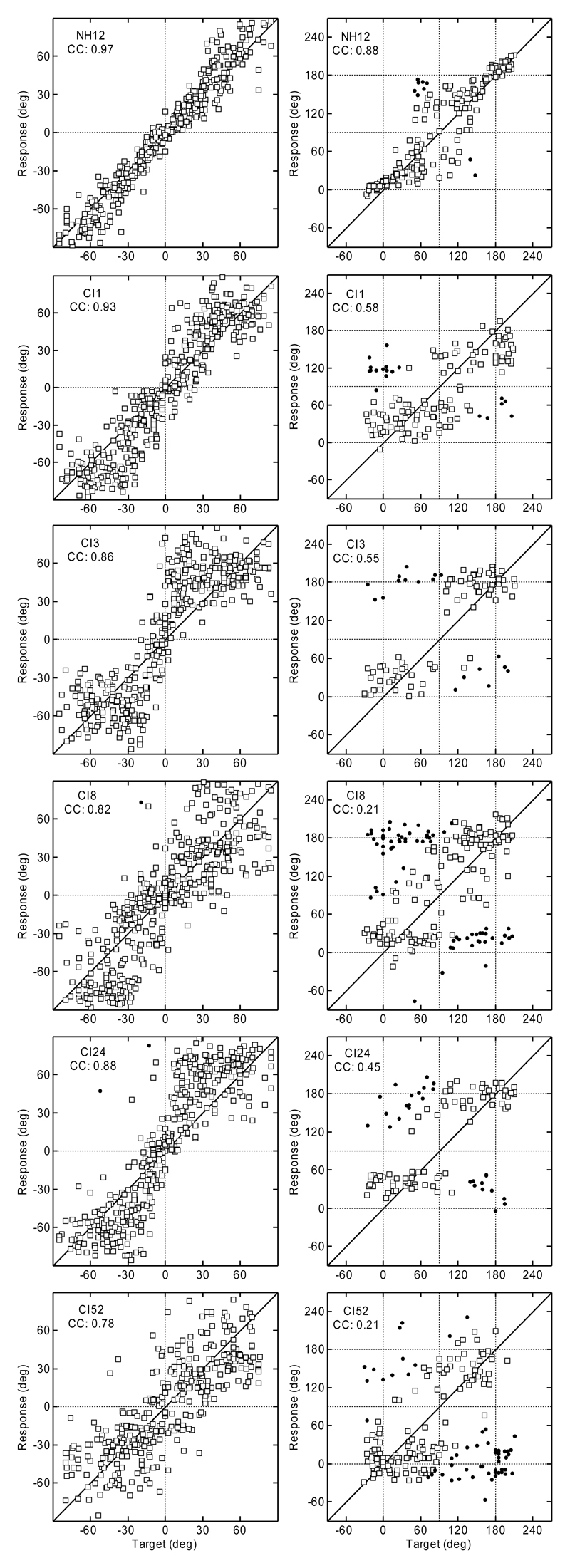
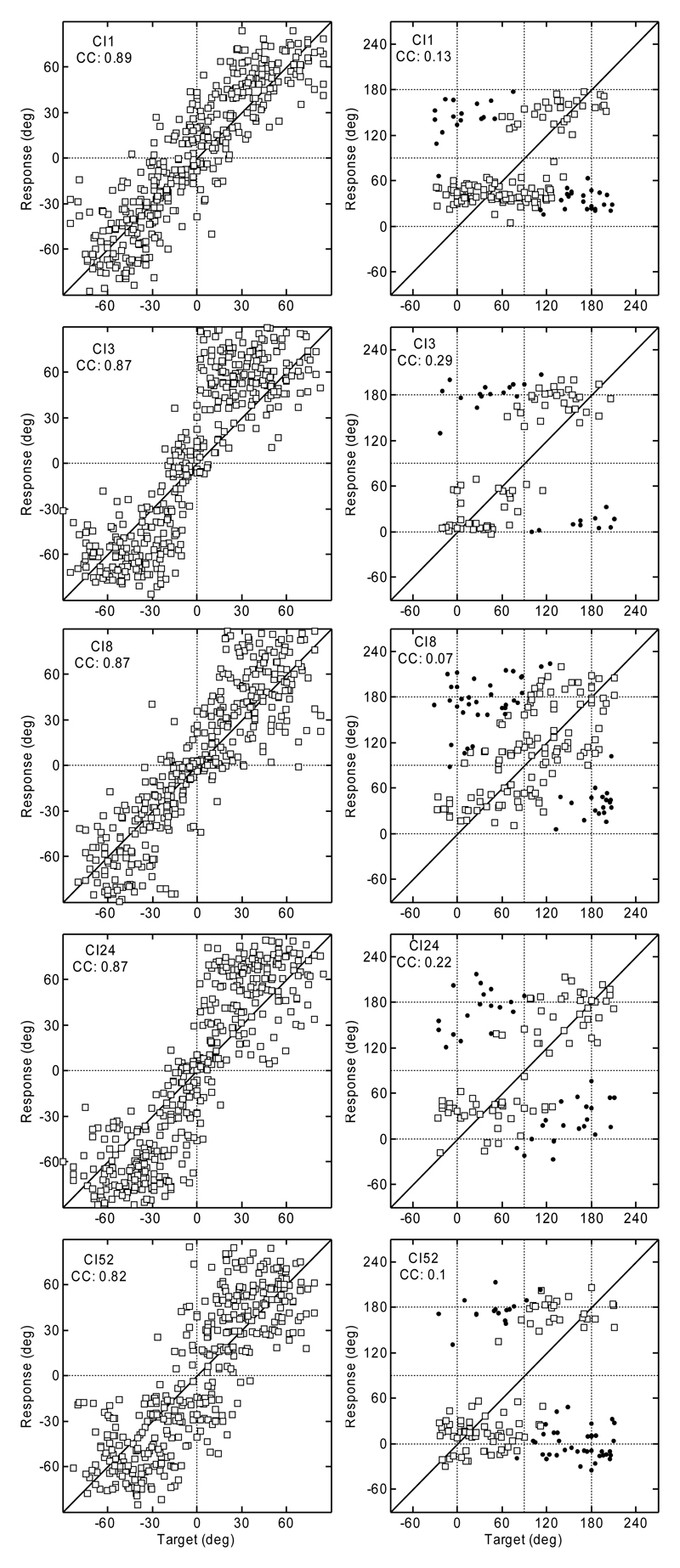
Figure 1 shows the results of experiment 1. The data for a typical NH listener from the study by Majdak et al. (2010) are shown in the top row, and the data for the CI listeners are shown below. The target angles are shown on the horizontal axis, and the response angles are shown on the vertical axis of each panel. For the polar dimension, the results are shown for targets with lateral angles within ± 30° only. Responses that resulted in absolute polar errors >90° are plotted as filled circles. All other responses are plotted as open squares.

Fig. 1.

Top row: Localization results for a typical NH listener from the study by Majdak et al. (2010). Lower rows: Results for CI listeners from experiment 1. Lateral results are plotted in the left column and the polar results in the right. Polar results outside the lateral range of 30° are not shown. Filled circles: Responses with errors outside the 90° range. CC, correlation coefficient between responses and targets.

Figure 1 clearly shows the differences in the response patterns for individual listeners. In the lateral dimension, CI1 could localize stimuli to the correct side and had the smallest response spread of the tested CI listeners. However, compared to the NH listeners, CI1 clearly showed a poorer ability to indicate the exact lateral position. Responses for CI8 and CI52 showed a larger response spread than the responses for CI1, including several left-right confusions, especially for the central positions. CI3 and CI24 showed a different response pattern: having very few left-right confusions, they appear to guess the correct position within each lateral quadrant.

In the polar dimension, there are also noticeable individual response patterns for the CI listeners. Compared with other CI listeners, CI1 seems to be most able to estimate the polar position of the target, because the responses are distributed nearer the diagonal line than for the other CI listeners. However, the spread of the responses was larger than that for NH listeners. The response patterns of CI8 and CI52 appear as if they were guessing the polar position with a slight preference for responding to the eye-level elevations. CI3 and CI24 responded mostly at the eye-level for the rear targets and around elevations of 30° for the front targets – both listeners clearly avoided more elevated positions. Compared with the NH listeners, the results for our CI listeners show dramatically worse localization performance.

Individual and group performance metrics averaged over all positions are provided in Table 2. The averages for the NH listeners are based on the data from Majdak et al. (2010). These results are discussed in the next section.

Table 2.

Average results from experiment 1

Metric	CI					CI	NH
	CI1	CI3	CI8	CI24	CI52	Average	Average
Lateral bias (deg)	-2.2	4.2	-3.2	4.4	-0.9	0.5 ± 3.6	-0.0 ± 2.4
Lateral precision error (deg; C = 33)	17.7	23.4	25.8	22.8	24.5	22.8 ± 3.1	13.6 ± 2.1
Lateral target-response correlation coefficient	0.92***	0.86***	0.82***	0.88***	0.78***	0.85***	0.95***
Absolute lateral bias (deg; C = 12)	7.7	9.7	3.2	12.4	5.9	7.8 ± 3.5	4.3 ± 0.8
Lateral precision error ±20° (deg; C = 27)	16.9	23.2	22.2	23.9	25.7	25.7 ± 3.3	11.0 ± 3.2
Absolute lateral error (deg; C = 29)	15.2	20.2	20.6	20.4	20.1	19.3 ± 2.3	11.2 ± 1.6
Lateral RMS error (deg; C = 27)	16.5	20.3	21.8	20.5	24.5	20.7 ± 2.9	12.4 ± 2.2
Quadrant error (%; C = 49%)	30.0	26.1	48.0	33.3	47.2	36.9 ± 10.1	17.1 ± 5.6
Polar bias (deg)	-3.0	11.9	9.3	2.0	-10.6	1.9 ± 9.1	0.1 ± 5.9
Polar precision error (deg; C = 31)	30.4	28.5	29.3	28.3	28.8	29.0 ± 0.8	21.9 ± 2.4
Polar target-response correlation coefficient	0.56***	0.55***	0.21**	0.45***	0.21**	0.34***	0.72***
Front-back confusions (%(N); C = 50%)	13.0***(89)	20.3***(64)	34.0**(85)	25.3***(79)	45.0(98)	29.1***(395)	12.8***(539)
Level-response correlation coefficient	-0.39***	-0.48***	-0.22**	-0.44***	-0.35***	-0.33***	-0.07*

See Methods section for details on the metrics; Individual listener data = means across all positions; Average = mean ± SD across the listeners; C = chance rate; N = number of responses considered in the calculations; NH = data calculated basing on results from Majdak, Goupell & Laback (2010);

*, **, and *** Level of significance (0.05, 0.01, and 0.001, respectively)

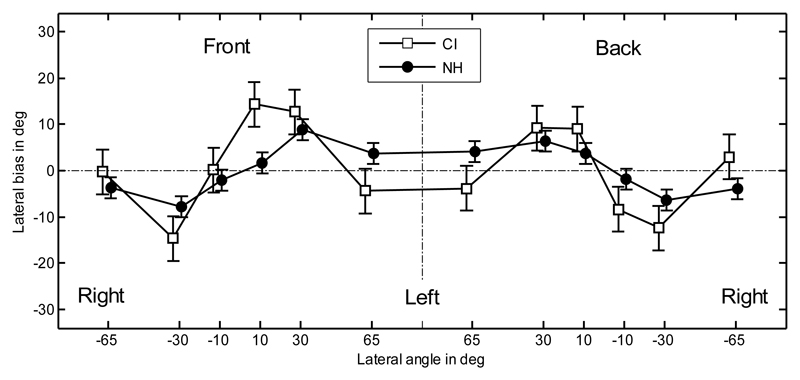
For the position-dependent performance, the results for the metrics were averaged over listeners. The lateral bias for the CI and NH listeners is shown in Figure 2. The data on the left central vertical dash-dotted line represent responses to the front hemifield and on the right to the rear. A repeated-measures (RM) analysis of variance (ANOVA), with factors hemifield and position, was performed on the lateral bias. The effect of position was significant [F(5,44) = 8.17; p < 0.0001], and subsequent Tukey-Kramer post-hoc tests showed a significantly different bias (p < 0.05) between positions +30° and -30°. The effect of the hemifield was not significant [F(1,44) = 0.47; p = 0.50]. Because of the symmetry across left and right sides, the comparison between NH and CI listeners was performed on the absolute bias. An ANOVA with factor listener group showed a significantly higher absolute bias for CI listeners (10.3°)¹ than for NH listeners (5.6°) [F(1,118) = 15.9; p = 0.0001].

Fig. 2.

Lateral bias. Error bars show the standard errors calculated separately for CI and NH listeners. The vertical dashed-dotted line separates the front and rear hemifields. Positive bias indicates responses toward the left.

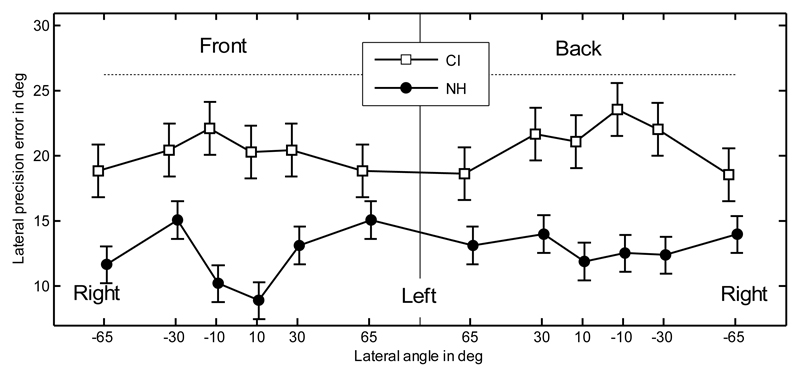
The lateral precision error is shown in Figure 3. The horizontal dotted line shows chance rate when the correct side is known. In other words, it is the precision error when listeners' responses were replaced by random responses uniformly distributed within the correct side. The precision errors for CI listeners (20.6°) were significantly higher than for NH listeners (12.7°; ANOVA with factor listener group; [F(1,118) = 101; p < 0.0001]). The CI listeners' precision errors showed no significant effects of hemifield or position (RM ANOVA on CI data with factors hemifield [F(1,44) = 0.43; p = 0.51] and position [F(5,44) = 1.21; p = 0.32]). This is in contrast to the results for NH listeners, which showed lower precision errors for both more central targets and targets located in the front (Majdak et al., 2010).

Fig. 3.

Lateral precision error. Error bars show the standard errors calculated separately for CI and NH listeners. The horizontal dotted line shows the precision error for random responses.

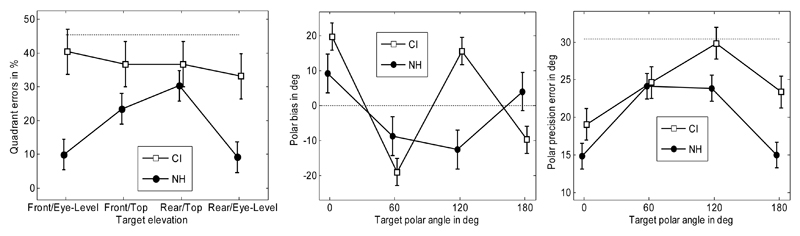
The quadrant error rate is shown in the left panel of Figure 4. In this figure, the dotted lines represent the errors when the listeners' responses were replaced by random polar angle responses uniformly distributed between -30° and 210°. There was a significant difference between the results for CI listeners (36.7%) and NH listeners (18.2%) [ANOVA with factor listener group; F(1,38) = 16.0; p = 0.0003]. While the CI data showed no effect of elevation and hemifield [RM ANOVA with factors hemifield and elevation; F(1,12) < 0.29; p > 0.60 for all], the NH listeners showed significant differences between the eye-level and top elevations (Majdak et al., 2010).

Fig. 4.

Quadrant error rate (left panel), polar bias (middle panel), and precision error (right panel). Horizontal dotted lines show the errors for random responses. Error bars show the standard errors. The positive polar bias indicates very high and very low responses for the front and back targets, respectively.

The polar bias is shown in the middle panel of Figure 4. Because of the coordinate system used, note that a positive polar bias indicates responses higher in elevation than the targets for the frontal targets and responses lower in elevation than the targets for the rear targets. There was no significant difference between the results for CI and NH listeners [ANOVA with factor listener group; F(1,38) = 0.57; p = 0.45]. For the CI listeners, the effect of position was significant [RM ANOVA with the factor position; F(3,12) = 23.5; p < 0.0001]. Tukey-Kramer post-hoc tests showed a significant difference (p < 0.05) between the positions 0° and 60°, which means that subjects systematically overestimated the eye-level and underestimated the top positions. This can be interpreted as pointing at one elevation of 45° in the front, regardless of the actual elevation of the targets. Similarly, the difference between 120° and 180° was significant (p < 0.05), showing a similar response pattern for the rear targets.

The polar precision error is shown in the right panel of Figure 4. There was a significant difference between the results for CI and NH listeners [ANOVA with factor listener group; F(1,38) = 9.42; p = 0.0039]. For the CI listeners, the effect of the position was significant [RM ANOVA with the factor position; F(3,12) = 4.46; p = 0.025], showing a lower precision error for the eye-level targets (21.2°) compared to the elevated targets (27.2°).

Discussion

Horizontal plane

Our results show large inter-individual differences in localization performance. Subject CI24 could correctly determine the correct side for most of the trials, but guessed the location within the hemifield [the absolute bias (12.4°) was at chance performance (approximately 12°)]. CI3 could better localize targets within the hemifield [lower absolute bias (9.7°)]. Showing a different pattern, CI8 and CI52 seem to be able to lateralize sounds with a constant accuracy over the horizontal plane [small absolute bias (CI8: 3.2°; CI52: 5.9°)]. However, the responses of CI8 were relatively scattered [large precision error (26.2°) and small correlation coefficient (0.82)]. Also, the responses of CI52 were relatively scattered (large precision error (24.5°) and small correlation coefficient (0.78)]. CI1 showed the best performance among the CI listeners [CI1: smallest precision error (17.7°), the largest correlation coefficient (0.92), and an average absolute bias (7.7°)]. However, even the best CI listener, CI1, performed worse than the NH listener group [NH group: smaller precision error (13.6°), larger correlation coefficient (0.95), and smaller absolute bias (4.3°)].

On average, our CI listeners showed no substantial bias (0.5°, SD = 3.6°), indicating a lack of preference for one of the sides. This is consistent with the results of Nopp et al. (2004) who showed that CI listeners demonstrate a small lateral bias when they are provided with a bilateral CI system. This also seems to be in agreement with the results of Gantz et al. (2002) who reported correct identification (percent correct scores >95%) of loudspeakers placed at either -45° or +45° in front of the CI listeners when CIs were tested bilaterally. The small lateral bias of our CI listeners further indicates that they had a consistent bilateral acoustic-to-electric mapping of the stimuli in terms of thresholds, maximum comfortable levels, and level-to-current mapping (but not AGC as the AGC was bypassed).

Seeber, Baumann & Fastl (2004) tested free-field sound localization in bilateral CI listeners for targets positioned within a ± 50°-range at the front. Their correlation coefficients for four listeners were: 0.97, 0.75, 0.72, and 0.53. Their best listener was better than our best listener (CI1, 0.92), and their worst listener was worse than our worst listener (CI52, 0.78). This indicates that localization results are highly variable among the CI listeners population, and our results should be considered only as case studies. Seeber et al. (2004) also reported absolute errors, which were in the range of 6.2° and 19.5°. Our absolute errors were substantially larger, which were in the range of 15.2° and 20.6°. One explanation for these performance differences may be because of the larger span of positions (± 180°) in our study (see below).

Nopp et al. (2004) tested 20 CI listeners on sound direction identification in the frontal horizontal plane using a span of ± 90°. They reported a bias of 3.5° (SD = 5.7°), which is similar to our bias of (0.5°, SD = 3.6°). They also reported a precision error (their variability s) of 28.9°, which is a little larger than our precision error (22.8°). With respect to their variability, one-third of their 20 listeners performed at chance. In our study, none of our listeners showed precision errors near the chance rate; however, the large RMS error of CI52 (24.5°) may indicate guessing for one of five subjects. Nopp et al. (2004) also reported the metric d (19.1°), which is similar to our absolute error (19.3°). In summary, their listeners showed similar localization performance to that of our listeners. Grantham, Ashmead, Ricketts, Labadie & Haynes (2007) tested 22 CI listeners on horizontal-plane localization using a loudspeaker span of ± 90°, and they reported the constant error of 25.5° (SD = 9.4°). This metric is similar to our absolute lateral error, which was 19.3° (SD = 2.3°).

van Hoesel, Ramsden & Odriscoll (2002) reported data on sound-direction identification of one CI listener using 11 loudspeakers spanning the frontal horizontal plane. The listener showed an absolute bias of 8.1°, an RMS error of 15.1°, and a precision error (their SD) of 13.1°. All these results indicate a comparable performance with that of our best listener CI1 (absolute bias of 7.7°, RMS error of 16.5°, and precision error of 17.7°). van Hoesel & Tyler (2003) reported RMS errors of sound-direction identification in five CI listeners. The average error was 9.8° (SD = 1.3°), showing excellent performance when compared with the chance rate of their experiment (26.8°). In our study, the RMS error was 20.7° (SD = 2.9°), which shows that our listeners were closer to chance performance (approximately 27°). This may be an effect of a different span of target positions, which was ± 55° in the study by van Hoesel & Tyler (2003) and ± 180° in our study. Accordingly, van Hoesel (2004) reported RMS errors of approximately 6° for a smaller span (± 29°) and RMS errors (approximately 22°) compared with our study (20.7°) for a larger span (± 90°).

The above comparisons show that our listeners performed similar to listeners from studies with a comparable lateral position span. Studies with a smaller position span reported a better localization performance. A similar conclusion has already been derived in Grantham et al. (2007), who discussed the effect of position span. Hence, in future inter-study comparisons, the position span should always be taken into account.

The data from Majdak et al. (2010) showed that NH listeners had a better precision for central targets (11.0°) compared with the precision when all targets are considered (13.6°). Our CI listeners in our study did not show a significant effect of position on lateral precision error. Nopp et al. (2004) also reported that the precision did not change when only the central positions were considered in the analysis, which strengthens our finding about position-independent lateral precision in CI listeners. Of course, it also could be that the large variance of the bias contributes to the lack of significance in our data.

Vertical plane

The localization performance in the polar dimension was much worse than that in the lateral dimension. Averaged over CI listeners, the quadrant error rate was near chance, the precision error was at chance, and the polar target-response correlation coefficient was low (0.34). However, there was a large amount of inter-individual variability, and even though these observations can be found in most of the individual results, it seems like that not all subjects were guessing the position in the vertical dimension. CI8 and CI52 showed quadrant error rates in the range of chance and very small correlation coefficients; however, CI8 had an idea about the hemifield of the central targets located at eye-level as supported by the front-back confusion rate (34%) being significantly lower than chance (50%). For CI52, both the quadrant error rate (47.2%) and the front-back confusion rate (45%) being almost at chance, indicate that CI52 could not localize in the vertical dimension. The other three CI listeners showed much smaller quadrant error rates, which were, however, higher than those for NH listeners. Interestingly, CI1 showed a front-back confusion rate (12.3%) similar to that of NH listeners (10.7%). This indicates that for the restricted target area of ± 30° in horizontal and vertical dimensions for this analysis, this listener identified the correct hemifield almost as well as a typical NH listener! However, the polar precision error (30.4°) of CI1 was in the range of chance (30.9°; for compared with NH listeners: 21.4°), which shows that within the correct quadrant, this listener was simply guessing.

Two interesting observations can be made from the position-dependent analysis. First, in CI listeners, the quadrant error rates were constant across the positions, whereas in NH listeners, they were larger for the top positions. This may be a ceiling effect because the quadrant error rates were near the chance for the CI listeners. Second, the bias significantly fluctuated over the elevations; the top positions were localized too low, whereas the eye-level positions were localized too high. Such a pattern may result from constantly pointing to the same elevation, yielding a bimodal response distribution as a function of the polar angle: just front or back. For example, for the rear targets, CI3 responded mostly at the eye-level despite the elevation of the actual target (see Fig. 1). Note that our listeners were instructed to respond uniformly across all elevations if they were uncertain about the target location. However, it seems reasonable to assume that our listeners mostly responded at a constant polar angle when they were guessing the elevation. In NH listeners, the bias did not fluctuate and the responses were not bimodally distributed.

General

The results of this experiment indicate that compared to NH listeners, individual CI listeners were very poor at localizing sounds in the vertical plane, although they performed better than chance levels in discriminating front from back. A few hypotheses may explain these findings.

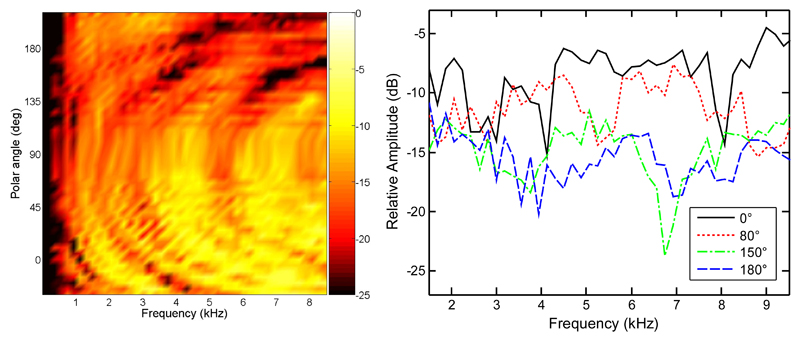
First, it may be that the CI listeners, using frequencies up to 8.5 kHz and 12 frequency channels, may have used the spectral tilt across the channels to estimate the correct hemifield of the target. Figure 5 shows the amplitude spectra of the left BtE-HRTF for CI3 in the median plane. In the right panel, the spectra are shown for four selected positions: front eye-level (0°), front top (80°), rear elevated (150°), and rear eye-level (180°). The spectra for the rear positions clearly show a larger tilt than the spectra for the front positions. The differences in the spectral tilt as a function of the polar angle might have been used by CI3 to resolve front-back confusions. Those differences are evident also for lower frequencies (4 kHz in Fig. 5, right panel). This fact may explain why CI1, who had an even more limited frequency range (300 to 5500 Hz), could perform better than chance. Using the spectral tilt as a cue, it should theoretically be possible to resolve front-back confusions with a very limited number of spectral channels. Results from studies on NH listeners show that only a few parameters are required to sufficiently represent spectral cues for vertical-plane sound localization (Kulkarni & Colburn, 1998; Langendijk & Bronkhorst, 2002; Iida, Motokuni, Itagaki & Morimoto, 2007; Goupell, Majdak & Laback, 2010). In the recent study, Goupell et al. (2010) directly investigated the impact of the number of spectral channels on vertical-plane sound localization in NH listeners. They found that nine spectral channels were sufficient to provide decent vertical-plane localization performance. In that study, the stimuli were Gaussian-envelope-tone trains, which provide discrete number of spectral channels and a pulsatile timing structure, mimicking the pulsatile stimulation in electric hearing. This supports the possibility that CI listeners in our study, having access to only 12 physical spectral channels, are able to use the spectral tilt.

Fig. 5.

Amplitude spectra of BtE-HRTFs for the left ear of CI3 in the median plane. The right panel shows data for selected positions from the left panel. Polar angles of 0°, 80°, 150°, and 180° represent positions at front eye-level, front top, rear elevated, and rear eye-level, respectively.

Second, it seems that the localization performance may have been affected by the stimulation levels because the level varied among listeners. Our attempt of using the level of 50 dB re: hearing threshold for all subjects was based on findings from acoustic-hearing studies. However, we could not achieve it, mainly because of between-listener differences in the dynamic range. Adapting the levels on an individual basis, we ended up with levels which are roughly comparable across subjects when expressed as percentage in the individual dynamic range. However, the issue seems to be more complicated because the loudness perception changed over time: As observed for CI8 and CI24, for experiment 1, 50 dB was not too loud, but for experiment 2, it was too loud. Interestingly, for CI24, we repeated experiment 1 with the lower levels and the performance did not change substantially. ¹ It seems like the larger levels neither affected the binaural nor the spatial spectral cues for this listener.

Third, it may be that the relative broadband level of the stimuli helped CI listeners identify the correct hemifield of the target. Because of the acoustic shadow of the speech processor, listeners may have associated the louder sounds to the front and the quieter sounds to the back. This effect is wellknown in NH listeners, where the acoustic shadow of the pinna results in broadband level reduction for sounds located in the back. However, sound localization based on broadband levels is only possible with the a priori knowledge of the source level. In many realistic situations, this is seldom possible, and an analysis of the spectral profile, not broadband level is required. In our experiment, we intended to reduce the contribution of the level to the vertical-plane localization by roving the level in the range of ± 2.5 dB. For NH listeners from the study by Majdak et al. (2010), this level roving seemed to be sufficient, because the correlation of the polar response angles and the broadband free-field-stimulus level were very low (-0.07), indicating that the level was not the primary localization cue. However, for CI listeners, there was a higher level-response correlation (-0.33). Because of the many differences between acoustic and electric hearing, the amount of level roving may have a different impact on the performance in the two hearing modes. Hence, it may be that the roving range of ± 2.5 dB was too small, and the CI listeners used the level as the primary localization cue. To test this hypothesis, we repeated the experiment with a larger level-roving range.

Experiment 2

In this experiment, it was hypothesized that the broadband level was the primary vertical-plane localization cue for the CI listeners. The level roving was increased from ± 2.5 dB to ± 5 dB. If the level was the primary cue in experiment 1, by using a larger roving range, the correlation between target and response angle should decrease, whereas the correlation between level and response angle should remain constant or increase. If the spectral profile was the primary cue, then the larger roving range should not affect the localization performance and the correlations. Assuming that listeners use binaural cues for sound localization in the horizontal plane (Macpherson & Middlebrooks, 2002) and the larger level roving does not affect these cues, the lateral target-response correlation should remain constant.

Methods

The range of the level roving was increased to ± 5 dB. For CI1 and CI8, the overall level had to be reduced compared with experiment 1. All levels are shown in Table 1. All other conditions were the same as those in experiment 1.

Results and Discussion

The results are shown in Figure 6. Based on these results, the corresponding metrics have been calculated, and they are shown in the two right-most columns of Table 2.

Fig. 6.

Localization results from experiment 2 (larger level roving). All other conventions are as in Figure 1.

The results for the lateral dimension did not substantially change. On average, the listeners showed a similar lateral target-response correlation (0.86) compared with that from experiment 1 (0.85) and a similar precision error (23.4°) compared with that from experiment 1 (22.8°). This indicates that the larger level roving did not have a substantial effect on the binaural cues.

The results for the polar dimension show a substantial deterioration of the localization performance compared with experiment 1. The quadrant error rates increased for all except one subject (CI52); the exception seems to be a ceiling effect. On average, the quadrant error rate increased from 36.9% to 40.5%. The front-back confusion rate increased from 29.1% to 36.9%, remaining lower than chance performance (50%). For the front-back confusions, CI52 was again an exception, showing less confusions in experiment 2 (38.8%) than in experiment 1 (45.0%). The polar precision errors, which were almost at chance in experiment 1, did not substantially change. Thus, with the larger level-roving range, CI listeners essentially guessed the sound location in the vertical planes.

The level-response correlation (-0.34) was similar to that from experiment 1 (-0.33). This indicates that the listeners used the broadband level in a similar manner as in experiment 1. The polar target-response correlation (0.16) decreased compared to that from experiment 1 (0.34). This indicates that the relative weight of the broadband level remained constant, whereas the relative weight of other cues like spectral profile decreased.

General Discussion and Conclusions

The larger front-back confusion rate combined with the larger level-roving range indicates that the broadband level was the most salient cue for vertical-plane localization in this study. There are at least two explanations why our five tested CI listeners might not have used spectral cues like NH listeners would have, and relied more on the overall level for vertical-plane sound localization. First, our listeners might have been insensitive to the weak spectral cues introduced by the BtE-HRTFs. Providing stronger elevation-dependent spectral cues by using in-ear microphones may ameliorate the problem encountered with BtE-HRTFs. Second, the varying stimulus level may have further reduced the salience of spectral cues. The electric dynamic range is smaller than the acoustic dynamic range (Shannon, 1983a; Chatterjee & Shannon, 1998) and can vary across electrodes, resulting in electrode-specific loudness-growth functions (e.g., Fu & Shannon, 1998). Electrode-specific level mapping, which theoretically allows to match the loudness-growth functions, is an essential property of clinical stimulation strategies. However, in the clinical fitting, the loudness-growth functions are not always exactly determined. If the level mapping does not match the loudness-growth function, the variation of the stimulus level may lead to spectral distortions. This may have reduced the salience of spectral cues and in turn the localization performance of our subjects.

The results with the small level roving (experiment 1) seem to indicate that our best listener, CI1, may have had some access to spatial spectral cues to resolve front-back confusion. Nevertheless, this listener's results with the larger level roving in experiment 2 show that the broadband level cue was clearly the most salient cue for the vertical-plane localization. This is consistent with the findings of Goupell, Laback, Majdak & Baumgartner (2008) who reported that CI listeners could not identify different spectral features when level roving was included. It is also possible that our CI users are able to use spectral cues when tested with static levels, and we underestimated localization performance by attempting to include level roving.

One should consider the relevance of our findings for more realistic situations where the sound spectrum is not constant and the broadband levels vary by more than our ±5 dB level roving. It is not unlikely that our “artificial” testing conditions overestimated the real-life localization performance of our listeners. On the other hand, it is known from studies on NH listeners that head movements help to resolve front-back confusions (e.g., Perrett & Noble, 1997). Thus, even with degraded spectral localization cues, CI users may be able to resolve the front-back confusions by turning their head and using the binaural cues. However, given their large lateral precision error of 23°, relatively large head movements would be required to resolve the confusions. Moreover, head movements help minimally for short-duration sounds and for elevation perception. Thus, providing better access to both binaural and spectral localization cues seems to be important for future CI systems.

Table 3.

Average results from experiment 2 (larger level roving)

Metric	CI					CI
	CI1	CI3	CI8	CI24	CI52	Average
Lateral bias (deg)	4.5	6.1	1.1	-2.30	-1.8	1.5 ± 3.7
Lateral precision error (deg; C = 33)	20.4	23.5	22.2	24.3	26.6	23.4 ± 2.3
Lateral target-response correlation coefficient	0.89***	0.87***	0.87***	0.87***	0.82***	0.86***
Absolute lateral bias (deg; C = 12)	4.5	13.5	4.2	13.3	2.8	7.7 ± 5.3
Lateral precision error ±20° (deg; C = 27)	20.8	24.4	19.6	27.3	32.4	24.9 ± 5.2
Absolute lateral error (deg; C = 29)	16.6	21.9	17.3	22.6	21.5	20.0 ± 2.8
Lateral RMS error (deg; C = 28)	20.1	20.6	18.2	20.9	24.0	20.8 ± 2.1
Quadrant error (%; C = 48%)	35.0	33.5	53.7	39.4	40.8	40.5 ± 8
Polar bias (deg)	4.6	4.0	7.4	1.5	-1.6	3.2 ± 3.4
Polar precision error (deg; C = 31)	32.8	32.6	27.1	29.3	30.4	30.4 ± 2.4
Polar target-response correlation coefficient	0,13	0.29**	0,07	0.22*	0,1	0.16***
Front-back confusions (%(N); C = 50%)	38.0*(92)	29.6**(54)	36.9*(65)	38.9*(72)	38.8***(80)	36.9***(363)
Level-response correlation coefficient	-0.28***	-0.55***	-0.29***	-0.12	-0.52***	-0.34***

All conventions as in Tab. 2.