Mortality under plausible interventions on antiretroviral treatment and depression in HIV-infected women: an application of the parametric g-formula

Abstract

Purpose

Among HIV-infected persons, antiretroviral therapy (ART) and depression are strongly associated with mortality. We estimated reductions in 5-year mortality in Women’s Interagency HIV Study (WIHS) participants under plausible hypothetical increases in ART initiation and reductions in depression (CES-D score≥16).

Methods

We followed 885 ART-naïve WIHS participants for 5 years from their first study visit after April 1998 to death or censoring. We used the parametric extended g-formula to estimate cumulative mortality under the natural course (NC) and alternative exposure distributions.

Results

Baseline prevalence of depression was 52% and 62% initiated ART by 5 years. Compared to mortality under NC (13.2%), immediate ART and elimination of 36% or 67% of depressive episodes were associated with risk differences (RD) of −5.2% (95% CI: −7.7%, −2.6%) and −5.7 (95% CI: −8.7, −2.7). Compared to immediate ART and NC for depression, additionally eliminating 67% of depressive episodes was associated with RD = −1.6 (95% CI: −3.9, 0.8). Compared to 5-year mortality under NC for ART and elimination of 67% of depression, also initiating ART immediately was associated with RD = −2.6 (95% CI: −5.0, −0.3).

Conclusions

Increasing ART initiation and reducing depression were associated with moderate reductions in 5-year mortality among HIV-infected women.

INTRODUCTION

Antiretroviral therapy (ART) has reduced immunodeficiency-associated morbidity and mortality in persons infected with HIV (1, 2), exposing the importance of managing comorbid conditions. Depression is two to four times more common in HIV-infected persons than in the general population (3). Untreated depression is associated with lower probabilities of ART initiation and ART adherence (4, 5). Furthermore, depression is associated with faster progression of HIV disease (6) and AIDS-related and non-AIDS-related mortality (7), even after adjusting for ART use and adherence. ART and depression may interact biologically or psychosocially (3). It is necessary to consider ART and depression changes together to explore this interaction (8, 9).

A recent analysis by Todd et al. in the Women’s Interagency HIV Study (WIHS) was one of the first to explicitly consider joint effects (10) of ART and depressive symptoms (8). In that study, the relative hazard (HR) of mortality associated with depressive symptoms was similar to the HR associated with no ART (8). Todd et al. contrasted mortality hazards under four extreme counterfactual exposure distributions: 1) everyone initiates ART immediately and never has depressive symptoms; 2) everyone initiates ART immediately and always has depressive symptoms; 3) everyone delays ART initiation indefinitely (i.e., never initiates ART) and never has depressive symptoms; and 4) everyone delays ART initiation indefinitely and always has depressive symptoms.

Our goal in the present analysis was to extend this prior work by estimating 5-year, all-cause mortality under several less extreme, hypothetical interventions to jointly increase ART uptake and reduce depressive symptoms, compared to the natural course (i.e., the 5-year mortality under the observed exposure distributions) (11). This type of contrast has been called a “generalized intervention contrast” (12).

Hypothetical interventions

We estimated effects of two sets of hypothetical interventions on 5-year mortality. First, we imposed no direct intervention on ART initiation (ART initiation was allowed to be affected indirectly through interventions on depression) and simultaneously either: 1) eliminated depressive symptoms with probability 36% at a given visit when a woman would have reported being depressed if all interventions were discontinued right before that visit (the natural value of depression) (13); 2) eliminated depressive symptoms with probability 67% at a given visit when a woman would have reported her natural value of depression as depressed; or 3) eliminated 100% of depressive symptoms for all women at all visits. Next, set ART initiation to be immediate for all women and simultaneous reduction of either 0% (no direct intervention on depression), 36%, 67% or 100% in the probability of depressive symptoms at a given, for woman-visits when the natural value of depression would have been depressed. All interventions assumed no loss to follow-up.

Reductions of 36% and 67% in depressive symptoms generally correspond to the reductions in depression seen among outpatients with non-psychotic major depressive disorder in the Sequenced Treatment Alternatives to Relieve Depression (STAR*D) trial (see Discussion). Thirty-six percent of participants experienced depressive symptom elimination following first-line depression treatment and 67% experienced symptom elimination after switching or augmenting treatment if their current regimen was not working (14).

METHODS

Study population

A full description of the WIHS cohort, recruitment, study enrollment, and study procedures is provided elsewhere (15, 16). Briefly, between 1994 and 2015, the WIHS enrolled 4982 women in ten sites across the US, of whom approximately 3 in 4 were HIV seropositive at enrollment. Women attended semiannual follow-up visits, at which time detailed measurements on HIV disease history and progression, medications, laboratory results and behavioral characteristics, were collected. Institutional review boards at each site approved the WIHS, and this analysis was approved by the institutional review board of the University of North Carolina.

We took 1 April 1998 to be the start of the modern ART era and eligibility for this analysis. HIV-seropositive, ART-naïve WIHS participants with detectable viral load at their earliest WIHS visit on or after 1 April 1998 (defined as baseline for this analysis) were included. Thus study sample was a mix of women enrolled in the first wave of WIHS who remained ART-naïve through April 1998 and women who were ART-naïve when they enrolled in the second (2001/2002) or third (2011/2012) wave of WIHS recruitment. Of 3,567 seropositive WIHS participants, 928 were ART-naïve at their first visit during the analytic period. We excluded 43 (5%) who did not have at least one depression measure, one CD4 cell count and one HIV RNA viral load determination within one year of baseline. The final study population included 885 participants.

Mortality Ascertainment

Mortality for women enrolled in the WIHS is obtained from clinic sources, follow-up with family members for participants lost to follow-up, and regular matches against the National Death Index.

Statistical analysis

We followed women from their first eligible WIHS visit on or after 1 April 1998 until first of death, loss to follow-up (defined as 12 months since the most recent WIHS visit), or administrative censoring at five years follow-up or site-specific administrative end of follow-up (most recent check for deaths in the National Death Index; 31 December 2010 for 12% of women and 31 December 2012 for 88%). Time-fixed baseline covariates included: race (black or other); age in years; current smoking; and at-risk drinking (>7 drinks/week) (17). Time-varying covariates included CD4 cell count (cells/μL), HIV viral load (log₁₀ copies/mL) and illicit drug use (any use of crack, cocaine, heroin, amphetamines, or other drugs, excluding marijuana, since the last visit). Women reported whether they had initiated ART since their last visit, where ART was defined as ≥3 antiretroviral medications, one of which was a protease inhibitor, a non-nucleoside reverse transcriptase inhibitor, abacavir, tenofovir, an integrase inhibitor (e.g., raltegravir) or an entry inhibitor (e.g., Maraviroc or enfuvirtide) (18). Presence of depressive symptoms was defined as a score of ≥16 on the Center for Epidemiological Studies Depression scale [CES-D], measured at each visit (19). The CES-D has been shown to have reasonably high sensitivity (95%) and specificity (70%) among low income women (20); positive predictive value of the CES-D should be high in the WIHS where prevalence of depression is high.

We used the parametric g-formula and the parametric extended g-formula to estimate 5-year cumulative mortality under several scenarios (21, 22). In instances where confounders also serve as mediators, in contrast to standard methods, g-methods remain unbiased (23, 24); for the current research question, CD4 cell count and viral load are confounders and mediators of the effect of ART, and illicit drug use may be a confounder and mediator of the effect of depressive symptoms. We employed the parametric extended g-formula (11, 23) because it allows estimation of the effects of hypothetical exposure distributions that may depend on the natural value of exposure. The trade-off for increased flexibility of the parametric g-formula is increased assumptions about correct joint-model fit. As an informal check on the plausibility of the modeling assumptions required in the parametric g-formula, we compared results from the g-formula with results from a marginal structural model, for always/never exposure distributions for ART and depression (static deterministic regimes). Because the parametric g-formula and marginal structural models rely on different modeling assumptions, agreement between the two results increases confidence in model specification (25). The marginal structural model we fit for comparison modeled joint effects on 5-year mortality of always versus never having depressive symptoms and immediately versus never initiating ART. The denominator of the weights for ART were estimated using logistic models for the probability of ART initiation conditional on time since baseline, black race, age, illicit drug use reported at baseline, baseline smoking, baseline heavy drinking, baseline CD4 cell count, baseline viral load, and 6-months’ lagged depressive symptoms, CD4 cell count, and detectable viral load. The denominator for the weights for depression were estimated using logistic models for the probability of depressive symptoms, stratified by 6-months’ lagged history of depressive symptoms, conditional on time since baseline, black race, age, illicit drug use reported at baseline, baseline smoking, baseline heavy drinking, baseline CD4 cell count, baseline viral load, ART initiation, and 6-months’ lagged CD4 cell count, and detectable viral load. Both sets of weights were stabilized by time since baseline; inverse probability of depression weights were also stabilized by ART initiation. Censoring weights were conditional on the same set of confounders as both treatment weights, as well as prior ART initiation, prior depression, and a product term for the two exposures. All continuous variables were modeled with restricted cubic splines with knots at the 5^th, 35^th, 65^th and 95^th percentile of their distribution (26). The final weights were the product of the ART, depression, and censoring weights.

A formal description of methods for the parametric extended g-formula appears in the appendix. Descriptions of the parametric g-formula and parametric extended g-formula have been published elsewhere (11, 21, 22, 27–29). Briefly, we first fit parametric (pooled logistic or linear) models in the following order for: 1) reporting recent illicit drug use at visit j = 1 … J conditional all time-fixed covariates and time-varying covariates at visit j − 1 (see table 1) including an interaction term between depression and ART (note: this and subsequent models were also implicitly conditional on survival and retention in the cohort until visit j); 2) undetectable HIV RNA viral load (<200 copies/mL) at visit j, conditional on time-fixed covariates, time-varying covariates other than illicit drug use at visit j − 1, and illicit drug use at visit j; 3) CD4 cell count at visit j, conditional on time-fixed covariates, time-varying covariates other than illicit drug use and viral load at visit j − 1, and illicit drug use and detectable viral load at visit j; 4) depressive symptoms at visit j (exposure), conditional on time-fixed covariates, ART initiation prior to j, and time-varying covariates at visit j; 5) ART initiation in the interval from j to j +1 (exposure), conditional on time-fixed covariates, time-varying covariates at visit j, and not yet having initiated ART; 6) remaining uncensored until visit j + 1, conditional on time-fixed covariates, time-varying covariates at visit j, and ART initiation in the interval starting with j; and 7) death before visit j + 1 (outcome), conditional on time-fixed covariates, time-varying covariates at visit j, and ART initiation in the interval starting with j. We saved parameter estimates from each model for use in the Monte Carlo simulation. We explored alternative orderings of modeling time-varying covariates (27) and saw little change in final estimates.

TABLE 1.

Characteristics of 885 Women’s Interagency HIV Study (WIHS) participants who were ART-naïve at baseline and followed for up to 5 years

	WIHS participants at baseline N=885	Person-years of follow-upa N=3377
Black raceb	571 (65)	2193 (64)
Age, yearsc	38 (32, 45)	40 (34, 46)
Baseline past or current smokingb	658 (74)	2591 (75)
Baseline heavy drinking (>7 drinks/week)b	121 (14)	420 (12)
Illicit drug use in past 6 monthsb,d	199 (22)	614 (18)
Most recent CD4 cell countc	441 (273, 649)	433 (277, 623)
Most recent log10 viral loadc	3.5 (2.7, 4.3)	3.3 (2.3, 4.2)
Current depressive symptomsb,e	457 (52)	1639 (48)
CES-D scorec	16 (7, 27)	15 (6, 25)

Abbreviations: ART, antiretroviral treatment; CES-D, Center for Epidemiological Studies Depression scale; HIV, human immunodeficiency virus

^aFor time-updated covariates, N (%) and Median (IQR) are summaries of the covariate across all person-years of follow-up

^bN (%)

^cMedian (IQR)

^dParticipant reported use of crack, cocaine, heroin, methadone, methamphetamine, or other drug use (excluding marijuana) since the previous visit

^eDefined as CES-D≥16

We used Monte Carlo simulation to estimate cumulative mortality curves approximated by the joint distribution of the models above. We sampled WIHS participants at baseline with replacement 50,000 times, discarding follow-up data. We simulated follow-up data for each of the 50,000 resamples based on the parameters estimated from the models above to estimate the natural course. Inability to recapture the observed distributions of time-varying covariates or cumulative incidence of the outcome imply model misspecification. Thus, we compared observed and natural course cumulative incidence curves for ART initiation, drop-out and mortality, and mean variable values over time for CD4 cell count, viral suppression, illicit drug use and depression. We did a further check of model specification by setting covariate values for ART initiation and depression (in addition to removing all drop-out) to estimate cumulative incidence of mortality under exposure distributions corresponding to immediately/never initiating ART and always/never having depressive symptoms for comparison with marginal structural model effect estimates (8). Finally, we estimated cumulative mortality curves under interventions by first predicting the natural value of depression at visit j (that is, the value of depression that would have been observed if the intervention were discontinued right before j) and then modifying the probability of depression at visit j + 1 if the woman was depressed at visit j (13).

We estimated the standard error of estimates from the standard deviation from 200 bootstrap resamples (30). Unrestricted random samples were drawn with replacement from the study sample. Models described above were fit and Monte Carlo simulation was run within each bootstrap resample. All analyses were carried out using SAS 9.3 (SAS Institute Inc., Cary, NC).

RESULTS

Of 885 women in the WIHS who met inclusion criteria and had complete data, 65% were black, 74% reported ever smoking, 14% reported at-risk drinking and 22% reported recent illicit drug use. Median age was 38 years (interquartile range [IQR]: 32, 45). Median CD4 cell count and viral load were 441 cells/μL (IQR: 273, 649) and 3.5 log₁₀ copies/mL (IQR: 2.7, 4.3), respectively. Over half of participants had prevalent depressive symptoms at the first visit (52%). Median CES-D score was 16 (IQR: 7, 27) (Table 1).

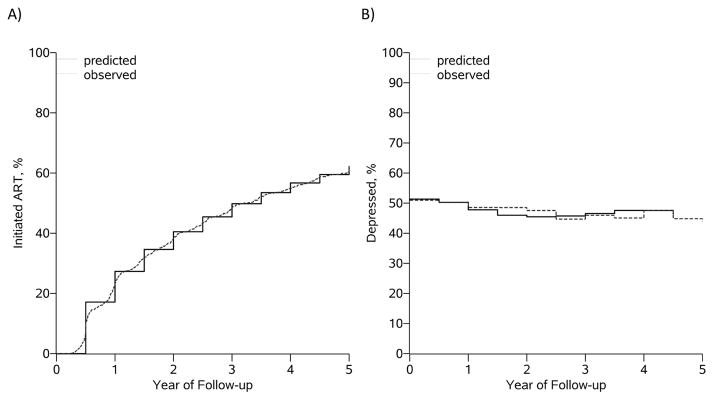
During 3,377 person-years of follow-up, 191 patients were lost to follow-up, and 92 patients died. Overall, 5-year mortality risk was 12.6% (95% CI: 10.1%, 15.1%). Cumulative incidence of ART initiation by 5 years was 62% (Figure 1). Prevalence of depressive symptoms was steady across the study period, around 45% (Figure 1). We were able to recapture the observed data with the parametric g-formula for all modeled covariates, exposures and outcome.

Figure 1.

Natural history (observed) and natural course (modeled/predicted) for (A) ART initiation and (B) prevalence of depression

Using the parametric g-formula, we estimated that, compared to never initiating ART and always being depressed, never initiating ART and never being depressed was associated with a 5-year mortality risk difference of −12.3 (95% CI: −19.7, 4.9), immediately initiating ART and always being depressed was associated with a 5-year mortality risk difference of −10.8 (95% CI: −18.7, −2.9), and immediately initiating ART and never being depressed was associated with a 5-year mortality risk difference of −16.0 (95% CI: − 23.2, −8.9) (Table 2).

TABLE 2.

Exposure effects of ART and depression on 5-year risk of mortality estimated among 885 ART-naïve women enrolled in the Women’s Interagency HIV Study (WIHS)

	Parametric g-formula
	5-year Mortality Risk	Risk Difference	Risk Ratio	Hazard Ratio
No ART, always depressive symptoms	23.2 (16.9, 29.4)	0.	1.	1.
No ART, never depressive symptoms	10.9 (6.5, 15.2)	−12.3 (−19.7, −4.9)	0.47 (0.37, 0.59)	0.50 (0.28, 0.89)
Immediate ART, always depressive symptoms	12.4 (6.7, 18.0)	−10.8 (−18.7, −2.9)	0.53 (0.40, 0.71)	0.44 (0.24, 0.75)
Immediate ART, never depressive symptoms	7.1 (3.8, 10.5)	−16.0 (−23.2, −8.9)	0.31 (0.26, 0.37)	0.28 (0.15, 0.52)
No ART	18.6 (14.0, 23.1)	0.	1.	1.
Immediate ART	9.0 (6.3, 11.8)	−9.6 (−14.9, −4.3)	0.49 (0.33, 0.72)	0.46 (0.30, 0.71)
Always depressive symptoms	16.4 (12.5, 20.3)	0.	1.	1.
Never depressive symptoms	9.4 (6.3, 12.6)	−7.0 (−12.0, −2.0)	0.57 (0.38, 0.87)	0.55 (0.35, 0.86)
	Inverse probability weighted marginal structural model
No ART, always depressive symptoms	25.0 (9.6, 40.4)	0.	1.	1.
No ART, never depressive symptoms	12.1 (5.1, 19.2)	−12.8 (−29.8, 4.2)	0.49 (0.21, 1.13)	0.45 (0.19, 1.05)
Immediate ART, always depressive symptoms	11.1 (5.8, 16.3)	−13.9 (−29.8, 2.0)	0.44 (0.21, 0.92)	0.39 (0.17, 0.89)
Immediate ART, never depressive symptoms	4.7 (2.0, 7.5)	−20.2 (−36.0, −4.4)	0.19 (0.08, 0.45)	0.17 (0.07, 0.42)
No ART	17.5 (11.7, 23.3)	0.	1.	1.
Immediate ART	8.2 (5.4, 11.1)	−9.3 (−15.6, −2.9)	0.47 (0.29, 0.76)	0.45 (027, 0.74)
Always depressive symptoms	17.7 (12.7, 22.6)	0.	1.	1.
Never depressive symptoms	8.4 (5.1, 11.7)	−9.3 (−15.5, −3.0)	0.48 (0.28, 0.80)	0.46 (0.27, 0.78)

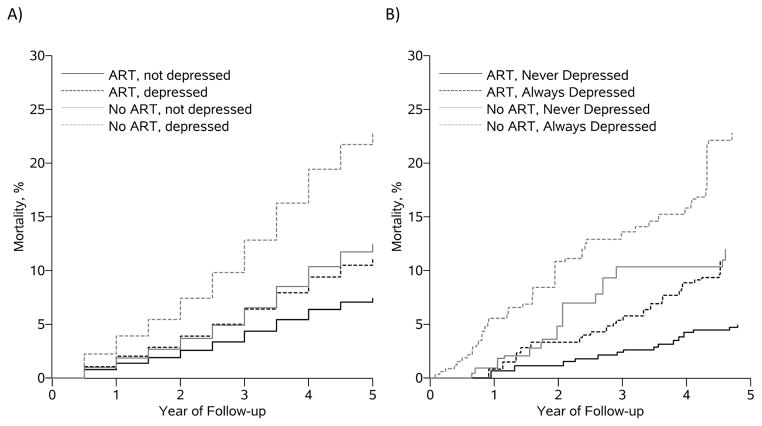
When we estimated the same exposure contrasts using a joint marginal structural model all estimates were slightly larger (Table 2). Cumulative mortality curves for each of the four always/never exposure effects from the parametric g-formula and marginal structural models coincide at 5 years, but there are some differences in predicted mortality associated with the treatment policy never initiate ART/never be depressed (Figure 2).

Figure 2.

Cumulative mortality curves from (A) the parametric g-formula and (B) inverse probability weighted marginal structural model under intervention regimens: 1) immediately initiate ART and never be depressed; 2) immediately initiate ART and always be depressed; 3) never initiate ART and never be depressed; and 4) always initiate ART and always be depressed

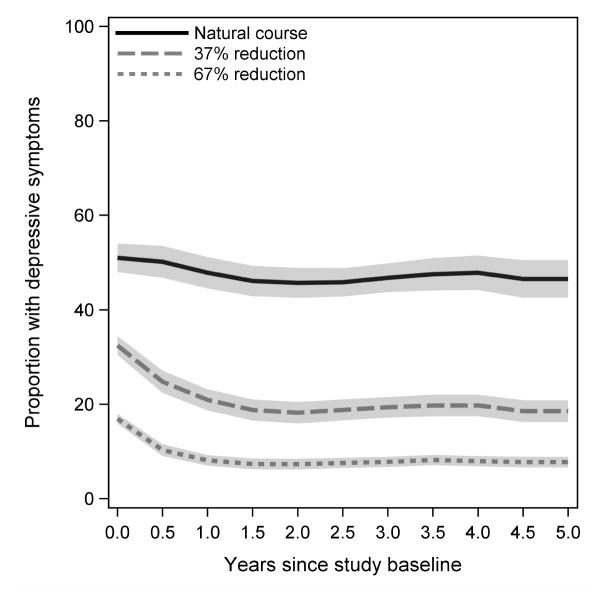
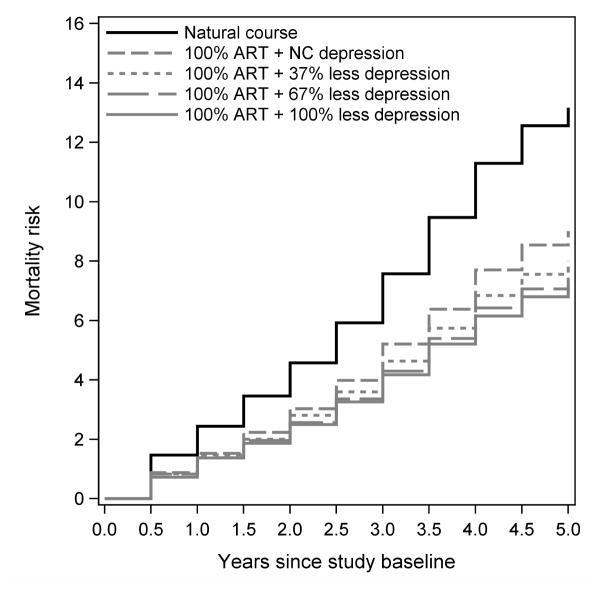
Generalized intervention contrasts were attenuated compared to exposure effects (Table 3). If depressive symptoms were treated with 36%, 67%, or 100% probability of elimination at the next visit (Figure 3) and if ART initiation was immediate, associated 5-year mortality risk differences were −4.2 (95% CI: −6.3, −2.0), −5.2 (95% CI: −7.7, −2.6), and −6.0 (95% CI: −9.4, −2.6), respectively. Compared to only intervening to reduce depression by 67% at the next visit, also intervening to initiate everyone on ART immediately was associated with risk difference of −2.6 (95% CI: −5.0, −0.3). Compared to only intervening to initiate everyone on ART, also reducing depressive symptoms by 67% at the next visit would further reduce 5-year mortality by −1.6 (95% CI: −3.9, 0.8). For completeness, we present cumulative incidence functions for modeled interventions in Figure 4 and risk differences, risk ratios and hazard ratios in Table 3.

TABLE 3.

Generalized effect of several plausible interventions on antiretroviral treatment and depression (CES-D score≥16) on 5-year risk of mortality among 885 ART-naïve women enrolled in the Women’s Interagency HIV Study (WIHS)

	Parametric g-formula
	5-year Mortality Risk	Risk Difference	Risk Ratio	Hazard Ratio
Natural course	13.2 (10.6, 15.9)	0.	1.	1.
Natural course for ART and…
…reduce depression 36% at next visit	11.4 (8.9, 14.0)	−1.8 (−3.4, −0.2)	0.87 (0.76, 0.99)	0.86 (0.74, 0.99)
…reduce depression 67% at next visit	10.1 (7.2, 12.9)	−3.1 (−5.4, −0.9)	0.76 (0.62, 0.94)	0.75 (0.60, 0.94)
…eliminate all depression	9.4 (6.3, 12.6)	−3.7 (−6.5, −1.0)	0.72 (0.54, 0.95)	0.70 (0.52, 0.94)
Immediate ART and…
…natural course for depression	9.0 (6.3, 11.8)	−4.2 (−6.3, −2.0)	0.68 (0.55, 0.86)	0.67 (0.53, 0.85)
…reduce depression 36% at next visit	8.0 (5.3, 10.7)	−5.2 (−7.7, −2.6)	0.61 (0.45, 0.81)	0.59 (0.44, 0.80)
…reduce depression 67% at next visit	7.4 (4.4, 10.5)	−5.7 (−8.7, −2.7)	0.57 (0.39, 0.82)	0.55 (0.37, 0.81)
…eliminate all depression	7.1 (3.7, 10.5)	−6.0 (−9.4, −2.6)	0.54 (0.34, 0.86)	0.53 (0.33, 0.85)
Immediate ART and reduce depression 67% at next visit versus…
…natural course for ART and reduce depression 67% at next visit (ref)		−2.6 (−5.0, −0.3)	0.74 (0.54, 1.01)	0.73 (0.53, 1.01)
…immediate ART and natural course for depression (ref)		−1.6 (−3.9, 0.8)	0.83 (0.60, 1.1)	0.82 (0.59, 1.14)

Abbreviations: ART, antiretroviral treatment; CES-D, Center for Epidemiological Studies Depression scale; HIV, human immunodeficiency virus

FIGURE 3.

Prevalence of depressive symptoms (CES-D score ≥16) under the natural course and various interventions to reduce the probability of depressive symptoms at the next visit given depressive symptoms at a given visit. Shaded areas indicate pointwise 95% confidence intervals.

Figure 4.

Cumulative mortality curves from the parametric g-formula for the natural course (no intervention) and interventions that would treat everyone with ART immediately and treat depressive symptoms with success rates of 34%, 67%, and 100%

DISCUSSION

We used Robins’ parametric g-formula (21, 22) to substantiate the strong association between constant exposure to depressive symptoms and long-term delay of ART initiation and higher mortality estimated with a marginal structural model (8). However, contrasts of mortality under various reductions in depression symptoms and increases in ART compared with mortality under the natural course provide more realistic, generalizable (12) estimates of the effect that interventions might produce. Mortality reductions attainable with immediate ART initiation in contemporary HIV-infected cohorts may be even less because ART use is more common (and fewer people have not yet started ART under the natural course). Mortality reductions associated with depression treatment, assuming ART initiation was immediate for all women, were modest; in particular, there was arguably not a meaningful difference between a reduction in episodes of depression of 37% or 67%. This may be due to sub-additive causal interactions between the two exposures or it may be due to the relatively minor differences in depression prevalence under the two hypothetical interventions (figure 3). However, our results indicated that improving ART coverage and reducing depressive symptoms were both associated with clinically meaningful mortality reductions that were similar in magnitude, and reducing depressive symptoms reduced mortality (marginally) even in the presence of 100% ART coverage.

ART use has an undisputed direct effect (not through depression) on mortality (2, 31), and it is possible that it also has a weak indirect effect on mortality by reducing depressive symptoms (32). In addition the indirect effects of depression on mortality through HIV progression and treatment, depression may have a direct effect (not through HIV) on mortality. Depression in HIV-infected adults has also been linked with higher non-AIDS-related mortality, including mortality due to liver disease, drug overdose, violence (homicide/suicide/accident), and non-AIDS-related malignancy (7). Because of these interactions between depression and ART use, a major strength of our analysis was our consideration of them jointly.

A set of assumptions sufficient for a causal interpretation of our results includes conditional exchangeability (13, 24), treatment version irrelevance (33), positivity (22, 34), correct model specification (24), no measurement error (35), and no interference (36). We frame the limitations of this analysis in terms of potential violations of these assumptions. Perhaps most significant is that depression treatment was not collected during part of the study period, and the format in which it was collected was inconsistent across time; thus we focused our analysis on depressive symptoms rather than depression treatment. This decision could result in violations of several assumptions. First, women who were never depressed may be meaningfully different from formerly depressed women whose depressive symptoms are eliminated, violating the exchangeability assumption. However, HIV-infected women receiving treatment for depression (specifically serotonin reuptake inhibitors) had ART adherence and laboratory value trajectories similar to non-depressed women (5). Furthermore, while we are fairly confident that key confounders of the effect of ART on mortality are measured, it is less plausible that we accounted for all possible confounders of the effect of depression on mortality; time-varying smoking, risky sexual behaviors, and engagement in medical care are just some possible confounders whose influence should be explored in future analyses. Second, because we did not model a specific intervention on depression, assuming treatment version irrelevance is more problematic. Acknowledging this limitation, we chose to model reductions in depression that coincided with effects seen in the STAR*D trial (14). If women with depressive symptoms were already receiving depression treatment and were resistant to treatment, first-line depression treatment may be less effective for an unidentifiable subgroup of the cohort. However, less than 20% of HIV-infected women with prevalent depression are estimated to be receiving any depressive treatment (37), and thus depressive symptoms are likely indicative of untreated depression. Our modeled intervention did not exactly correspond to the STAR*D trial result in that the probability of remission found per individual in the STAR*D trial was applied to each depressive episode in our analysis, and thus the overall individual probability of remission of depressive symptoms over a 5-year period in our cohort was higher than was found in the trial (figure 3). As a consequence, our results may be overly optimistic about the reduction in mortality attainable by treating depression in this population. Alternatively, we could have assigned each woman a latent probability of having depression that was responsive to treatment, but such an approach has not been implemented nor formalized before. Third, because we modeled the effect of a change in depressive symptoms rather than modeling the effect of a specific intervention on clinical depression, if CES-D were a poor indicator of the presence of clinical depression, we may have misclassified women as eligible for intervention when they were not. However, to the first point, the CES-D has been shown to have high sensitivity (95%) and specificity (70%) for clinical depression among low income women (20). Finally, we believe that in this analysis, there is little potential for violations of the assumptions of positivity and no interference.

One strength of our analysis was our decision to fit both a marginal structural model and the parametric g-formula for comparisons of always/never having depressive symptoms and no/immediate ART initiation (static deterministic treatment regimes). We did not check our findings from the parametric extended g-formula (in which the intervention depends on the natural value of exposure) against a comparable marginal structural model (22), which would be computationally more complicated. Fitting either a marginal structural model or using g-computation should arguably be standard operating procedure when employing the parametric g-formula to triangulate toward the truth (22, 25, 27). The parametric g-formula assumes correct model specification for the outcome and all time-varying covariates; in contrast, marginal structural models rely on correct specification of the model(s) for exposure and (possibly) censoring. If results from alternate estimators disagree, this is an indication that at least one assumption of at least one of the estimators is violated. Using double robust methods or an alternate study design [e.g., instrumental variable methods (38, 39) or structural nested models (40)] may give clues as to which estimator is biased.

We chose to estimate joint effects of ART and depression given their high potential to interact in determining mortality. We report a generalized impact contrast, which is arguably more useful to policy makers than exposure effects. While intervention effects associated with realistic interventions on ART and depressive symptoms were attenuated compared to exposure effects, they were still clinically significant. Our results provide further evidence supporting immediate ART initiation for persons with HIV, and some evidence that depression screening and treatment may provide marginal additional benefit for prevention of all-cause mortality.

LIST OF ABBREVIATIONS

AIDS

Acquired Immunodeficiency Syndrome

ART

Antiretroviral therapy

CES-D

Center for Epidemiological Studies Depression scale

HIV

Human Immunodeficiency Virus

HR

Hazard ratio

STAR*D

Sequenced Treatment Alternatives to Relieve Depression (trial)

WIHS

Women’s Interagency HIV Study

APPENDIX

We follow the convention of denoting random variables with uppercase letters and possible realizations of those random variables with lowercase letters. Let i = 1, …, N index WIHS participants, and let j = 1, …, J denote completed months of follow-up. For participant i, let Y_ij be an indicator of death in month j; let C_ij be an indicator of censoring (having gone 12 months since the last study visit) in month j; let A_ij be an indicator of antiretroviral therapy (ART) in month j; let D_ij be an indicator of depression in month j; and finally, let Z_ij be a vector of time-fixed and time-varying covariates that confound the effect of A on Y or that confound the effect of D on Y, in month j. By design, A_i(−1) = Y_i0 = C_i0 = 0, since we restricted to persons who were ART naïve and alive and at risk for death at baseline. By definition, if Y_ik = 1 then Y_i(k+1) = 1, and if C_ik = 1 then C_i(k+1) = 1. Also, because we analyzed the data using an intent-to-treat approach for initiation of ART, if A_ik = 1 then A_i(k+1) = 1 by definition.

The cumulative incidence of death observed in the WIHS by month j + 1 (the natural course) (25) can be written:

$$F(j)=\sum _{{\overline{a}}_j}\sum _{{\overline{d}}_j}\sum _{{\overline{\mathit{z}}}_j}\sum _{k=0}^j\left\{\begin{array}{l}P\left(Y_{k+1}=1\mid {\overline{\mathit{Z}}}_k={\overline{\mathit{z}}}_k,{\overline{D}}_k={\overline{d}}_k,{\overline{A}}_k={\overline{a}}_k,{\overline{Y}}_k={\overline{C}}_{k+1}=0\right)\times \\ \prod _{m=0}^k\left[\begin{array}{l}P\left(A_m=a_m\mid {\overline{\mathit{Z}}}_m={\overline{\mathit{z}}}_m,{\overline{D}}_m={\overline{d}}_m,{\overline{A}}_{m-1}={\overline{a}}_{m-1},{\overline{Y}}_m={\overline{C}}_m=0\right)\times \\ P\left(D_m=d_m\mid {\overline{\mathit{Z}}}_m={\overline{\mathit{z}}}_m,{\overline{D}}_{m-1}={\overline{d}}_{m-1},{\overline{A}}_{m-1}={\overline{a}}_{m-1},{\overline{Y}}_m={\overline{C}}_m=0\right)\times \\ f({\mathit{Z}}_m\mid {\overline{\mathit{Z}}}_{m-1},{\overline{D}}_{m-1},{\overline{A}}_{m-1},{\overline{Y}}_m={\overline{C}}_m=0)\times \\ P\left(Y_m=0\mid {\overline{\mathit{Z}}}_{m-1}={\overline{\mathit{z}}}_{m-1},{\overline{D}}_{m-1}={\overline{d}}_{m-1},{\overline{A}}_{m-1}={\overline{a}}_{m-1},{\overline{Y}}_{m-1}={\overline{C}}_m=0\right)\end{array}\right]\end{array}\right\}$$

where P(·|·) is the conditional probability evaluated at the observed covariates values for a given participant; f(·|·) is the conditional density function; and F(j)is the cumulative incidence function of death evaluated at time j. We assumed that censoring was not informative of subsequent outcome, exposure or covariates, given measured covariate and exposure history.

Many typical epidemiologic analyses estimate exposure effects. That is, they ask the question, “what would be the difference in the incidence of death in the study sample had everyone initiated ART immediately and no one been depressed ever, versus had no one initiated ART and everyone always been depressed?” To answer that question, we would estimate the cumulative incidence of death under a deterministic intervention g of the form:

$$F^g(j)=\sum _{{\overline{\mathit{z}}}_j}\sum _{k=0}^j\left\{\begin{array}{l}P\left(Y_{k+1}=1\mid {\overline{\mathit{Z}}}_k={\overline{\mathit{z}}}_k,{\overline{D}}_k^g={\overline{d}}_k^g,{\overline{A}}_k^g={\overline{a}}_k^g,{\overline{Y}}_k={\overline{C}}_{k+1}=0\right)\times \\ \prod _{m=0}^k\left[\begin{array}{l}1\times \\ 1\times \\ f\left({\mathit{Z}}_m\mid {\overline{\mathit{Z}}}_{m-1},{\overline{D}}_{m-1}^g,{\overline{A}}_{m-1}^g,{\overline{Y}}_m={\overline{C}}_m=0\right)\times \\ P\left(Y_m=0\mid {\overline{\mathit{Z}}}_{m-1}={\overline{\mathit{z}}}_{m-1},{\overline{D}}_{m-1}^g={\overline{d}}_{m-1}^g,{\overline{A}}_{m-1}^g={\overline{a}}_{m-1}^g,{\overline{Y}}_{m-1}={\overline{C}}_m=0\right)\end{array}\right]\end{array}\right\}$$

We use g to indicate interventions on a and d, g, = (g_a, g_d). Note that here we compare mortality under exposure regimens ${\overline{a}}_j^g=(1,\dots ,1)$ and ${\overline{d}}_j^g=(0,\dots ,0)$ (always treated and never depressed) versus ${\overline{a}}_j^g=(0,\dots ,0)$ and ${\overline{d}}_j^g=(1,\dots ,1)$ (never treated and always depressed), for example. Ensuring no loss to follow-up, that is, intervening to set c̄_j = (0,…,0), is a component of both regimens.

In this paper, we aimed to estimate an intervention effect (21). That is, we asked the question, “what would be the difference in the incidence of death in the study sample had we intervened to get all women initiated on ART immediately, treated depression with effectiveness T% for all women with depressive symptoms, and had no one been lost to follow-up, versus the incidence of death in the absence of any intervention?” This is a contrast of mortality under the natural course F(j) compared to a contrast of mortality under an intervention g of the form:

$$F^g(j)=\sum _{{\overline{d}}_j}\sum _{{\overline{\mathit{z}}}_j}\sum _{k=0}^j\left\{\begin{array}{l}P\left(Y_{k+1}=1\mid {\overline{\mathit{Z}}}_k={\overline{\mathit{z}}}_k,{\overline{D}}_k^g={\overline{d}}_k^g,{\overline{A}}_k^g={\overline{a}}_k^g,{\overline{Y}}_k={\overline{C}}_{k+1}=0\right)\times \\ \prod _{m=0}^k\left[\begin{array}{l}1\times \\ P^g\left(D_m^g=d_m^g\mid D_m^{\ast }=d_m^{\ast },{\overline{\mathit{Z}}}_m={\overline{\mathit{z}}}_m,{\overline{D}}_{m-1}^g={\overline{d}}_{m-1}^g,{\overline{A}}_{m-1}^g={\overline{a}}_{m-1}^g,{\overline{Y}}_m={\overline{C}}_m=0\right)\times \\ P^{\mathit{obs}}\left(D_m^{\ast }=d_m^{\ast }\mid {\overline{\mathit{Z}}}_m={\overline{\mathit{z}}}_m,{\overline{D}}_{m-1}^g={\overline{d}}_{m-1}^g,{\overline{A}}_{m-1}^g={\overline{a}}_{m-1}^g,{\overline{Y}}_m={\overline{C}}_m=0\right)\times \\ f({\mathit{Z}}_m\mid {\overline{\mathit{Z}}}_{m-1},{\overline{D}}_{m-1}^g,{\overline{A}}_{m-1}^g,{\overline{Y}}_m={\overline{C}}_m=0)\times \\ P\left(Y_m=0\mid {\overline{\mathit{Z}}}_{m-1}={\overline{\mathit{z}}}_{m-1},{\overline{D}}_{m-1}^g={\overline{d}}_{m-1}^g,{\overline{A}}_{m-1}^g={\overline{a}}_{m-1}^g,{\overline{Y}}_{m-1}={\overline{C}}_m=0\right)\end{array}\right]\end{array}\right\}$$

The intervention depends on the natural value of depression at time k, which is defined as the value of depression that would have been observed if the intervention were discontinued right before k (13). We denote the natural value of depression at time k as $D_k^{\ast }$. $a_m^g$ is set according to exposure regimens ${\overline{a}}_j^{1,g_d}=(1,\dots ,1)$ and ${\overline{a}}_j^{0,g_d}=(0,\dots ,0)$, and $d_m^g$ is set according to exposure regimens:

If $d_m^{\ast }=0$, then

$$P^g(D_m^g=d_m^g\mid D_m^{\ast }=d_m^{\ast },{\overline{\mathit{Z}}}_m={\overline{\mathit{z}}}_m,{\overline{D}}_{m-1}^g={\overline{d}}_{m-1}^g,{\overline{A}}_{m-1}^g={\overline{a}}_{m-1}^g,{\overline{Y}}_m={\overline{C}}_m=0)=\{\begin{array}{ll}1,\hfill & \text{if}{d}_m^g=0\hfill \\ 0,\hfill & \text{if}{d}_m^g=1\hfill \end{array}$$

And if $d_m^{\ast }=1$, then

$$P^g(D_m^g=d_m^g\mid D_m^{\ast }=d_m^{\ast },{\overline{\mathit{Z}}}_m={\overline{\mathit{z}}}_m,{\overline{D}}_{m-1}^g={\overline{d}}_{m-1}^g,{\overline{A}}_{m-1}^g={\overline{a}}_{m-1}^g,{\overline{Y}}_m={\overline{C}}_m=0)=\{\begin{array}{ccc}(1-T^g/100)& ,& \text{if}{d}_m^g=1\\ T^g/100& ,& \text{if}{d}_m^g=0\end{array}$$

By definition $d_{-1}^g=d_{-1}=0$. The intervention specified above is equivalent to: “Initiate everyone on ART immediately, and among those who are depressed (assuming any intervention on depression were discontinued right before depression was measured), treat them all with T% probability of remitting depressive symptoms.” Individuals who are treated for depression are not prevented from relapsing and experiencing depressive symptoms at a future visit.