Distinct in vivo target occupancy by bivalent‐ and induced‐fit‐like binding drugs

Abstract

Background and Purpose

Optimal drug therapy often requires long‐lasting target occupancy While this attribute was usually linked to the drug's pharmacokinetic properties, the dissociation rate is now increasingly recognized to contribute as well. Nearly all the earlier pharmacokinetic‐pharmacodynamic (PK‐PD) simulations encompassed single‐step binding drugs and focused on k_off. However, ‘micro’‐PK mechanisms and more complex binding mechanisms like bivalent‐ and induced‐fit binding may contribute as well. Corresponding binding models are presently explored.

Experimental Approach

We compared the 24 h in vivo occupancy over time profiles of prototype bivalent‐ and induced‐fit‐like binding drugs (A and B) after one or repeated daily dosings, both without and with rebinding. Special attention was focused on the effect of each of the microscopic rate constants on the occupancy profiles and on the metrics to represent those profiles.

Key Results

Although both models can be represented by the same mathematical formulation, drugs A and B display quite different occupancy profiles, even though they have the same potency. These differences can be attributed to the different effects of their microscopic rate constants on their composite k_off and also on their susceptibility to experience rebinding. This also affects how the occupancy profiles of bivalent‐ and induced‐fit‐like binders progress when repeating the dosings and by changing the dosage.

Conclusions and Implications

Closer attention should be paid to more complex binding models in PK‐PD simulations. This may help pharmacologists and medicinal chemists to improve the translation of in vitro kinetic measurements from preclinical screening programmes into clinical efficiency.

Abbreviations

PK

pharmacokinetics

PD

pharmacodynamics

Introduction

In the past, pharmacodynamic (PD) screening studies were essentially aimed at optimizing the efficacy and potency/affinity (K _D) of drug candidates. Their pharmacokinetic (PK) properties were traditionally held responsible for the duration of their pharmacological effect until the seminal articles by Swinney (2004), and Copeland et al. (2006) disclosed that binding kinetics also played an important role. The subsequent review articles essentially focused on long‐lasting target occupancy (or a long ‘residence time’; Copeland, 2010) and the implications thereof for the successful treatment of pathological conditions (see Tummino and Copeland, 2008; Zhang and Monsma, 2009; Lu and Tonge, 2010; Swinney and Anthony, 2011; Núñez et al., 2012; Copeland, 2016).

In compliance with the principle of Occam's razor, drug‐target (L–R) interactions are often represented as a single‐step, reversible, bimolecular mechanism. However, additional steps are likely to be necessary to yield a long residence time and high affinity (Vauquelin et al., 2015). In this respect, spectroscopic and molecular modelling approaches reveal that an initial bimolecular complex might go through many subsequent states, via small conformational adjustments (Garvey, 2010; Copeland, 2011; Dror et al., 2011). For simplicity, this is usually reduced to two steps, as in the ‘conformational selection’ and ‘induced‐fit’ binding mechanisms. As shown in Figure 1A, they form part of a thermodynamic cycle and allow the final complex, R′L (where the conformation of R′ differs from R), to be accessed by initial binding to either free R′ or R. Here, we will only focus on the ‘induced fit’ mechanism, as this is regarded to govern the binding of most of the drugs with high clinical efficacy (Copeland, 2010, 2011). A long residence time and high affinity (often also denoted as avidity) can also be achieved without a conformational change by the ‘bivalent binding’ model that accounts for the binding of immunoglobulins as well as of smaller bivalent constructs (Holliger and Hudson, 2005; Rudnick and Adams, 2009; Kroll et al., 2013; Vauquelin and Charlton, 2013; Waring et al., 2016). In the thermodynamic cycle presented in Figure 1A, each of the drug's pharmacophores can bind first and it is the pathway or lane with the fastest bidirectional transit between the initial and final, fully bound state that is most often selected (Vauquelin, 2013). The equations that govern induced‐fit binding (Figure 1B) also apply to such pathways but, from the microkinetic point of view, a distinction should be made regarding the ways in which a long residence time may be achieved. While this property of a long residence time stems primarily from the stability of R′L, i.e., a low k₄, for induced‐fit binding (Tummino and Copeland, 2008; Copeland, 2010), it also stems from the ability of a partly bound RL complex to quickly reach the fully bound R′L state, for bivalent binding (Plückthun and Pack, 1997; Kramer and Karpen, 1998; Vauquelin, 2013; Vauquelin and Charlton, 2013). This allows R′L to re‐form many times before the antibody or drug fully dissociates (i.e. a high k₃/k₂ ratio).

Figure 1.

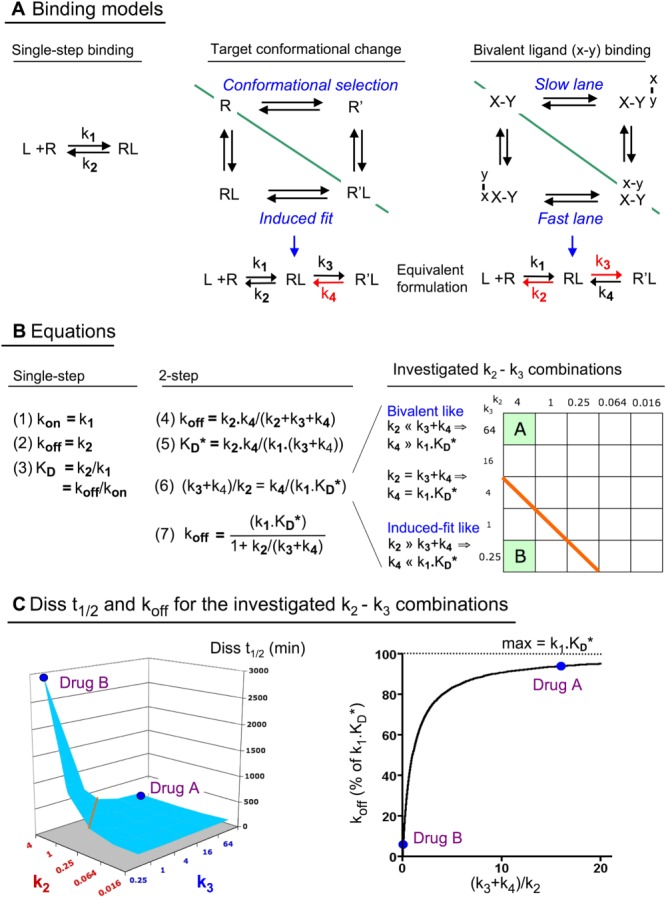
Binding models (Panel A) and equations (Panel B) that are brought into play and consequent differentiation between the in vitro k_off (Panel C) of the bivalent‐ and the induced‐fit‐like binding Drugs A and B. (A) Schematic representation of the drug‐target ‘L–R’ binding models that are analysed in the text. Left side: single‐step bimolecular binding process that obeys the law of mass‐action. Right side: thermodynamic cycles offer the most complete description of the present two‐step binding models (Vauquelin, 2015). In the first one, a conformational change of the target may take place either before (i.e. the ‘conformational selection’ model) or after binding of the drug (i.e. the ‘induced‐fit’ model) (Strickland et al., 1975; Copeland, 2011). For a bivalent drug, both of its pharmacophores, ‘x’ and ‘y’, bind to their respective sites, ‘X’ and ‘Y’, at the target according to the law of mass‐action (Plückthun and Pack, 1997; Kramer and Karpen, 1998; Vauquelin and Charlton, 2013). Those thermodynamic cycles can be split in two lanes (green dividing line), and it is the lane with the fastest bidirectional transit between the initial and final state that is mostly selected (Vauquelin, 2013). In particular, the overall k_off of bivalent drugs corresponds to the sum of the k_off's of each of those lanes, that is, twice the k_off of each lane for a homobivalent drug and close to the highest k_off for a heterobivalent drug. This distinction also offers a rationale for why the induced fit mechanism is most often chosen for enzyme inhibitors and receptor antagonists (Tummino and Copeland, 2008; Copeland, 2011; Guo et al., 2014). In particular, a conformational change is considered to be rate‐limiting and to be slower for the free target than for the drug‐associated target. According to the induced‐fit mechanism, slow dissociation and high affinity rely on the stability of R′L (i.e. a low reverse isomerisation rate constant, k₄, in red). On the other hand, slow dissociation and high affinity of a bivalent drug is based on the premise that, when only one of its pharmacophores (either ‘x’ or ‘y’) is bound, the local concentration of the other pharmacophore near its cognate site is fixed and very high. This fixed value allows each lane to be represented in the same way as the induced‐fit process since the second association step can be represented by a composite first‐order rate constant similar to k₃ (Vauquelin, 2013; Vauquelin et al., 2015). Moreover, because of the high local concentration, freshly dissociated pharmacophores will experience swift (re)binding to their site as long as the other pharmacophore is still bound. Thus, the repeated toggling between the partly and fully bound complexes (i.e. a scenario that is favoured by a high k₃/k₂ ratio, in red) is responsible for the slow dissociation and high affinity of bivalent drugs. (B) The presented equations that apply to the models shown in Panel A. Equation 4: k_off is the macroscopic first‐order dissociation rate constant (Neubig et al., 2003). Equation 5: K _D* is the macroscopic/pseudo affinity constant; it equals [L] when the occupancy (i.e. [RL] + [R′L]) is half maximal at equilibrium (Vauquelin et al., 2016). Equation 6 is an alternative formulation of Equation 5; it emphasizes the equivalence of the (k₃ + k₄)/k₂ and k₄/(k₁.K _D*) ratios. Their value allows bivalent‐like binders (>1 with Drug A as prototype) to be distinguished from induced‐fit‐like binders (<1 with Drug B as prototype) in the grid (also referred to as two‐dimensional ‘kinetic space’) that embraces the full set of investigated k₂–k₃ combinations at the right side of the panel. There, the microscopic rate constants k₂ and k₃ are given in min⁻¹, and the orange diagonal line separates the distinct categories. Equation 7 combines Equations 4 and 5. Binding parameters are provided in Section 2 and in Supporting Information Table S1. Please note that, since k₃ >> k₄, Equations 5 to 7 can be simplified for Drugs A and B since the contribution of [RL] to their binding is negligible. (C) Left side: the dissociation t _1/2 values (i.e. Diss t _1/2 = 0.69/k_off) of the full set of investigated k₂–k₃ combinations are enumerated in Supporting Information Table S1 and also graphically represented in the 3D plot. Right side: Equation 7 allows k_off to be represented by a hyperbolic function with k₁.K _D* as the upper limit. The k_off of a one‐step binding drug always equals k₁.K _D*. The k_off of Drug A and other bivalent‐like binders is only moderately (i.e. up to twofold) less than k₁.K _D*. For Drug B and other induced‐fit‐like binders, k_off cannot exceed k₄, which, by being less than k₁.K _D*, now represents the ‘kinetic bottleneck’ of the dissociation process (see Panel B). Hence, the k_off of such drugs can be appreciably less than k₁.K _D*.

There is still a reluctance to integrate the ‘residence time’ concept in lead optimization programmes (Walkup et al., 2015; Zhang, 2015). First, confusion is nurtured by claims about the benefit of a high association rate constant, k_on, to clinical therapy (Yin et al., 2013; Schoop and Dey, 2015). One of those benefits, a faster onset of the clinical effect, should be viewed with caution as it does not apply to the most pertinent comparative ‘constant C_max/K _D’ dosing paradigm. Unfortunately, this dosing paradigm, in which the dose of each drug has to vary according to its affinity, has hitherto only been adopted for some of the PK‐PD simulations (see Gabrielsson et al., 2009; Vauquelin, 2010, 2016a; Dahl and Akerud, 2013; de Witte et al., 2016). Furthermore, Dahl and Akerud (2013) pointed out that, contrary to the prevalent opinion that a drug has to dissociate slower than its PK‐elimination in order to prolong its clinical action (Vauquelin and Van Liefde, 2006; Tummino and Copeland, 2008; Lu and Tonge, 2010; Dahl and Akerud, 2013), candesartan, tiotropium and many other drugs actually dissociate faster. It is of note that this opinion did not take account of ‘micro’‐PK mechanisms that are able to extend the duration of a drug's action (Sykes et al., 2014; Vauquelin, 2015). These include drug partitioning into the membrane (Anderson, 1993; Johnson, 2001), internalization of drug‐target complexes (Irannejad et al., 2013; Hottersall et al., 2016) and the ability of freshly dissociated drug molecules to re‐bind before drifting away from their targets (Goldstein and Dembo, 1995; Coombs and Goldstein, 2004; Vauquelin and Charlton, 2010). This last mechanism is favoured in confined biological spaces and it considerably prolongs the ‘overall’ residence time of drugs in vitro (Fierens et al., 1999), as well as ex vivo (Perry et al., 1980). Simulations also suggest that it permits the clinical action of ‘borderline’ drugs to outlast the expectations that are based only on their PK‐elimination (Vauquelin, 2010, 2015, 2016b).

Drug rebinding is also favoured by a high k_on, and recent PK‐PD simulations according to the constant C_max/K _D dosing paradigm revealed that this mechanism allows an increase in k_on to affect the in vivo occupancy over time profile of a drug in the same way as a decrease in k_off (Vauquelin, 2016a). Interestingly, the same observation was also made when the PK‐PD simulations incorporated ‘target‐mediated drug disposition’, instead of rebinding (de Witte et al., 2016). It is important to note that both studies only dealt with the simple, one‐step binding mechanism. In view of the growing interest in more complex mechanisms, we have here repeated such PK‐PD simulations for two‐step binding drugs with special focus on those with a high k₃/k₂ ratio (epitomized by Drug A) and with a low k₄ (epitomized by Drug B). While such a distinction, based on microscopic parameters, is necessary for the sake of PK‐PD modelling, it does not strictly reflect the actual molecular mechanisms of induced‐fit and bivalent binding (see the Discussion section). To call attention to this point, we will further denote drugs with a high k₃/k₂ ratio as bivalent‐like and those with a low k₄ as induced‐fit‐like.

In summary, we have found that Drugs A and B displayed quite distinct occupancy profiles, even though they had the same potency. This difference stems from the different effects of the microscopic rate constants, not only on their k_off, but also on their susceptibility to experience rebinding. Also, their occupancy profiles progress differently with repeated dosings and by changing the dosage. Our findings show that closer attention should be paid to such more elaborate binding mechanisms in PK‐PD modelling studies.

Methods

Drug A stands as a prototype of drugs that bind according to a bivalent‐like model (i.e. with k₂ << k₃) and Drug B stands as a prototype of drugs that bind according to induced‐fit‐like model (i.e. with k₂ >> k₃) (Figure 1A). Both models can be described by the same equations, shown in Figure 1B (Vauquelin, 2013; Vauquelin et al., 2015). The ‘microscopic’ rate constants of the individual steps are as follows: k₁ (in M⁻¹·min⁻¹), k₂ (in min⁻¹), k₃ (in min⁻¹) and k₄ (in min⁻¹) (Neubig et al., 2003). The difference in Gibbs‐free energy between the ground state R and the final R′L state is the same for Drugs A and B as well as for the additional drugs that are examined in Figure 2 and in Supporting Information Table S1 and Figure S2. To this end, their (k₂.k₄)/(k₁.k₃) ratio is arbitrarily set to 4.10⁻⁹ M, and k₁ is also kept constant at 1.10⁶ M⁻¹·min⁻¹, as in Vauquelin et al. (2016). The binding properties are then only controlled by k₂ and k₃ (because k₄ = 4.10⁻³.k₃/k₂·min⁻¹). Each of the microscopic rate constants will also be changed individually (i.e. increasing k₁ or k₃ or decreasing k₂ or k₄ 10‐fold) to investigate the effects on their dissociation rate, and on their in vivo occupancy over time profile (see below). For Drugs A and B, the corresponding ‘variants’ do remain within the same category as the parent drugs. They are referred to by the suffix −k_1H, −k_2L, −k_3H or −k_4L (e.g. A‐k_2L refers to Drug A with 10‐fold lower k₂).

Figure 2.

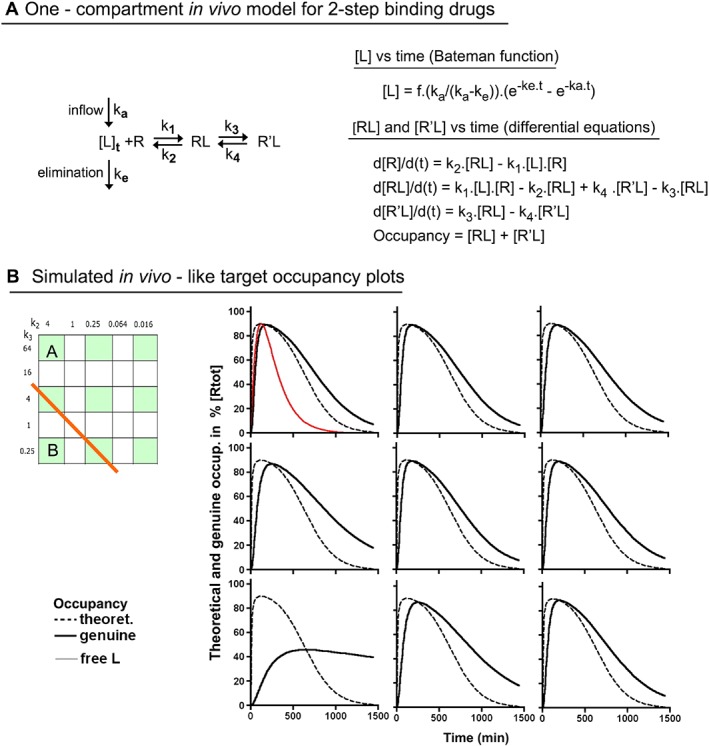
Simulated occupancy over time plots after a single in vivo dosing of nine two‐step binding Drugs (including Drugs A and B) according to the constant [L_max]/K _D* ratio paradigm. (A) The simulations are based on the one‐compartment in vivo body model in where first‐order rate constants k_a and k_e correspond to the inflow/input and the elimination/clearance of the drug respectively. The Bateman function (Garret, 1994) defines how the concentration of free drug, [L], near the target evolves with time (see Chapter 2). The differential equations at the right side describe the time (t)‐dependent changes in each mode of target occupancy after dosing. To this end, the equations are consecutively solved over very small time intervals till the desired time point is attained, as previously described (Vauquelin et al., 2001). (B) Comparison of the occupancy (i.e. [RL] + [R′L]) profiles of the nine highlighted drugs in the grid at the left. The Bateman function was adjusted for all to yield 90% maximal occupancy in case of instant equilibrium. To facilitate comparison, [L] (in red) is normalized to reach the same apex (all alike, therefore only shown for Drug A). Broken black lines account for the occupancy in case of instant equilibrium and solid black lines account for the actual drugs. The occupancy half‐life (Occ t _1/2) values are provided in Section E of Supporting Information Table S1.

Simulated association and dissociation curves of all the examined drugs and variants can `be adequately fitted by mono‐exponential association and decay paradigms respectively (data not shown). The associated ‘macroscopic’ dissociation rate constants, k_off (Neubig et al., 2003), closely fit with the theoretical values that can be calculated via Equation 4 in Figure 1B (Supporting Information Table S1 for more drugs). The concentration of a drug at which half of the targets are occupied at equilibrium (where both RL and R′L participate) is denoted here as K _D* (to keep same terminology as in Tummino and Copeland, 2008). K _D* acts as a ‘macroscopic’/pseudo affinity constant and is related to the microscopic rate constants as stipulated by Equation 5 in Figure 1B. Drugs A and B have the same K _D*, and their variants also have the same 10‐fold lower K _D*.

Living organisms are ‘open systems’ where, after each dosing, the concentration of free drug near the target, [L], first increases and then declines. In the simplest ‘one compartment’ body model, this bell‐shaped pattern can be described by the Bateman function (Garret, 1994), that is,

$$\left[\mathrm{L}\right]=\mathrm{f}.\left({\mathrm{k}}_{\mathrm{a}}/\left({\mathrm{k}}_{\mathrm{a}}-{\mathrm{k}}_{\mathrm{e}}\right)\right).\left({\mathrm{e}}^{-\mathrm{ke}.\mathrm{t}}-{\mathrm{e}}^{-\mathrm{ka}.\mathrm{t}}\right)$$

The first‐order rate constants for the inflow, k_a, and the elimination/clearance of the drug, k_e, remain the same throughout this study (i.e. 0.0115 and 0.00575 min⁻¹, for t _1/2 = 60 and 120 min, respectively). The same values were also utilized in Vauquelin (2016a). Likewise, the parameter, ‘f’ (which accounts for the drug's dose, bioavailability and volume of distribution), was set to obtain a [L_max]/K _D* ratio (where [L_max] is the maximal concentration of free drug near the target, also denoted as C_max in PK) that allows 90% of the targets to be occupied under instant equilibrium conditions (i.e. [L_max]/K _D* = 9) for Figures 2, 3, 4 and also to allow 98.9% occupancy (i.e. [L_max]/K _D* = 90) for Figure 5. Of note is that the present dosing paradigm is the most relevant one from the clinical perspective (Dahl and Akerud, 2013). It also allows any change of k₁ to be compensated for by the dosing so that the occupancy profile is not affected (Vauquelin, 2016a).

Figure 3.

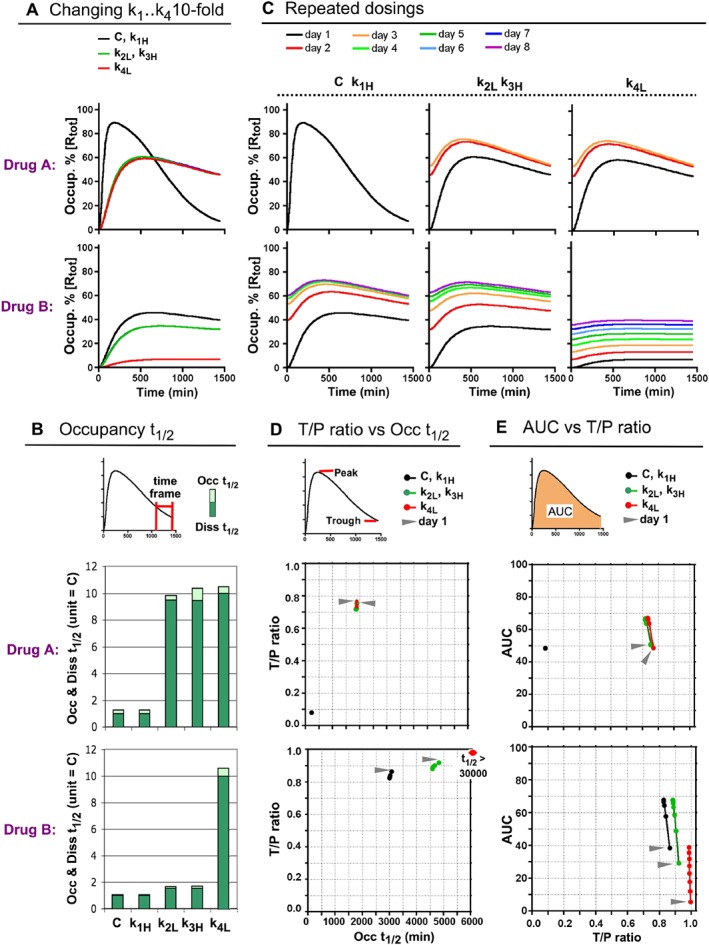
Effect of altering the individual microscopic rate constants of Drugs A and B on their in vivo occupancy profile after a single dose (A and B) and repeated daily dosings (C to E). (A) Simulated occupancy over time plots of the parent Drugs A and B (black line, here used as control) and their ‘variants’ with 10‐fold increased k₁ or k₃ or decreased k₂ or k₄ (denoted with the suffix −k_1H, −k_3H, −k_2L and −k_4L, respectively). The plots overlap for the parent drugs and their −k_1H variants and also for the −k_2L and −k_3H variants. (B) Effect of a 10‐fold change of the microscopic rate constants on the Diss t _1/2 and Occ t _1/2 values. Curves are shown in Panel A. The Diss t _1/2 values of the parent drugs, ‘C’, are assigned as unity to better appreciate this effect. Occ t _1/2 values account for the decline in occupancy during the 1050–1440 min post‐dosing interval for all except for the very slow dissociating B‐k_4L variant for which a 1050–2880 min interval was chosen due to the late manifestation of its peak occupancy (Supporting Information Figure S3). Those time frames are also adopted for the further Occ t _1/2 determinations. (C) Effect of up to eight repeated daily dosings on the target occupancy over time plots by Drugs A (top) and B (bottom) and their variants. After each dosing, [L] is adapted to include the free drug that remained 24 h after the previous dosing. If the occupancy profile no longer changes after a given day, then the curves after that colour‐coded day are not shown. (D) For the same drugs as in Panel C: trough‐to‐peak, T/P, ratios (please see top of the panel for definition) are plotted versus the Occ t _1/2 values (abscissa). Data (dots) for the first dosing of each drug are pointed to by an arrow and are linked to the data for subsequent dosings (only shown when they differ sufficiently from those of the previous day). Overall, the data closely tally with a bi‐exponential paradigm (Supporting Information Figure S4). (E) AUC versus T/P ratios (abscissa) of the same drugs. AUCs account for the 24 h post‐dosing target occupancy and are expressed as % of the theoretical maximum, that is, for continuous full occupancy.

Figure 4.

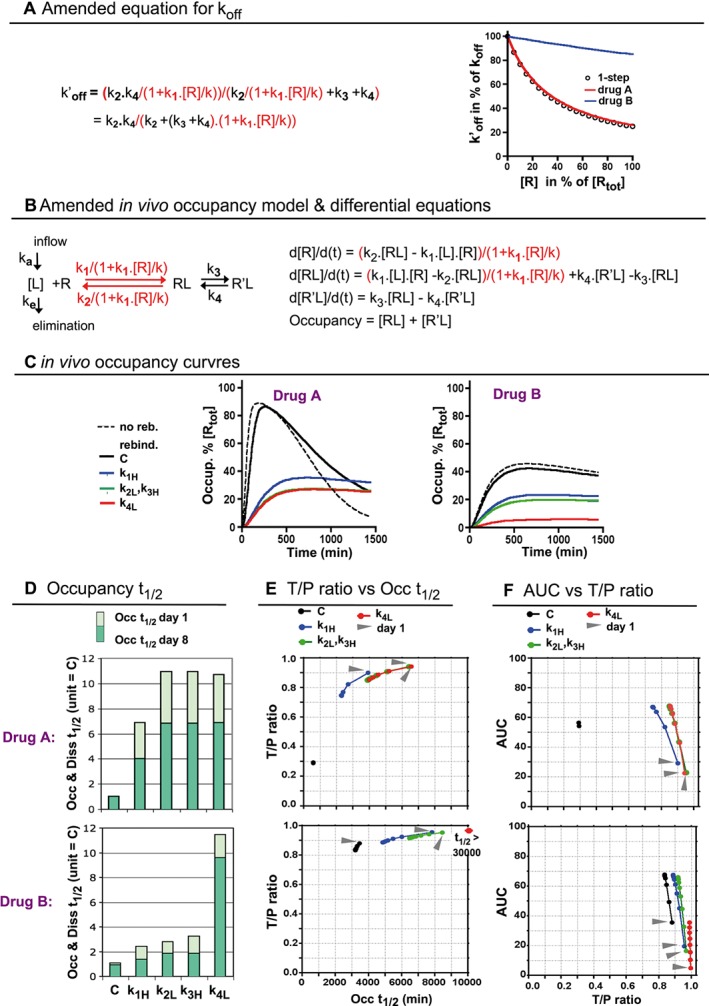
Effect of rebinding on the k_off (A) and on the in vivo target occupancy profile (B) of Drugs A, B and their variants after one (C) and repeated daily dosings (D to F). (A) Left side: to incorporate limited diffusion‐related rebinding, k₁ and k₂ are replaced by the first‐order ‘effective’ forward‐ and reverse rate coefficients (in red, more explicit information is provided in Methods). The ‘rebinding factor’, k₁.[R_tot]/k, constitutes a convenient metric for the firmness of rebinding and is set to 3 for all the drugs with k₁ = 1.10⁶ M⁻¹·min⁻¹ and to 30 for the −k_1H variants. Right side: the amended k_off (now denoted as k′_off) decreases when [R] increases. This effect is equal for Drug A and for drugs that bind in a single step (open circles) but less marked for Drug B. (B) Left side: a similarly amended (in red) representation of the one‐compartment in vivo body model that was shown Figure 2A. Right side: the differential equations that describe the time‐dependent changes in each mode of target occupancy after dosing are amended accordingly. (C) In vivo occupancy over time plots after a single dosing with Drugs A, B and their variants in the presence of rebinding (similar representation as in Figure 3A). Dotted lines refer to Drugs A and B in the absence of rebinding. Please note that the curves for the −k_1H variants are now comparable to those of the −k_2L and −k_3H variants. (D) Effect of a 10‐fold change of the microscopic rate constants on the Occ t _1/2 values at day 1 and at day 8 in the presence of rebinding. The Occ t _1/2 values of the parent drugs at day 1, C, are assigned as unity. Values are obtained as for Figure 3B. In the presence of rebinding, those values are comsiderably lower after several dosings. (E) T/P ratios are plotted versus the Occ t _1/2 values (abscissa) of after one or more dosings with the drugs shown in Panel D. Same type of representation as in Figure 3D. Both parameters can also be related to one another by a bi‐exponential paradigm (Supporting Information Figure S4). (F) For the same drugs, AUCs are plotted versus the T/P ratios (abscissa) such as in Figure 3E.

Figure 5.

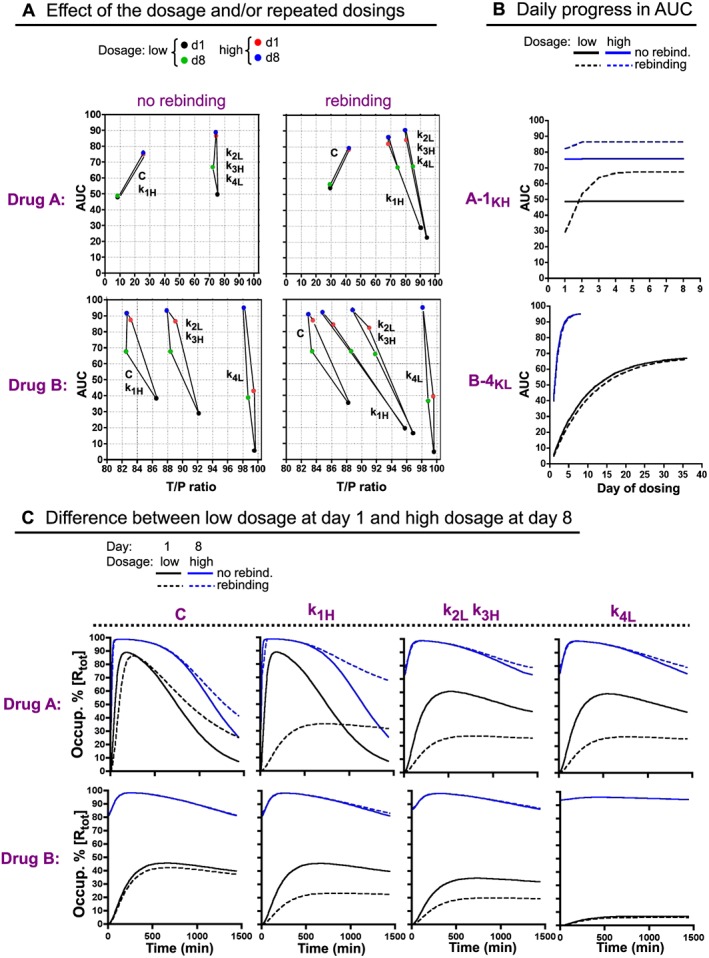
Effect of the dosage and/or repeated dosings on the in vivo occupancy profile of Drugs A, B and their variants, without and with rebinding. (A) Effect of a 10‐fold higher dose (allowing 98.9% maximal occupancy instead of the earlier 90% in case of instant equilibrium) and/or eight daily dosings on the T/P ratio and AUC of Drugs A, B (denoted as ‘C’) and their variants. Left side: without rebinding. Right side: with rebinding. The parameters are defined such as in Figure 3D, E. (B) Differences in the effect of a 10‐fold higher dosage and/or rebinding on the AUCs of two selected variants: A‐k_1H (top) and B‐k_4L (bottom). The AUCs are shown after each successive dosing (numbered in the abscissa). (C) Comparison of the in vivo occupancy over time profiles after one dosing with the low dose and after eight dosings with the high dose with Drugs A, B (denoted as ‘C’) and their variants, without and with rebinding.

Schematic representations of and differential equations for the processes that were taken into account for simulating in vivo target occupancy after each dosing are shown in Figures 2A (without rebinding) and 4B (with rebinding). For those simulations, the differential equations that govern the changes of each mode of target occupancy were consecutively solved in parallel over very small time intervals (Vauquelin et al., 2001). Several parameters were used as metrics of the occupancy versus time profile, that is, the occupancy half‐life, Occ t _1/2, to estimate the rate by which the occupancy declines at the end of the post‐dosing period; the trough to peak occupancy ratio, T/P ratio (where through occupancy is measured 24 h after dosing), to express how constant the occupancy of the target remains between two consecutive dosings and, finally, the AUC corresponding to the average occupancy of the target over the 24 h post‐dosing period.

Explicit information about the incorporation of hindered diffusion‐related rebinding in the equations has already been provided elsewhere (Vauquelin and Charlton, 2010; Vauquelin, 2016a). In short, k₁ has to be replaced by the ‘effective’ forward rate coefficient (k_f = k₁/(1 + k₁.[R]/k) and k₂ by the ‘effective’ reverse rate coefficient (k_r = k₂/(1 + k₁.[R]/k) (Figure 4A, B). The parameter, ‘k’, depends on the free drug's diffusion rate and on the geometric characteristics of the target's and target clustering (Coombs and Goldstein, 2004; Vauquelin and Charlton, 2010). The k₁.[R]/k product, which constitutes a metric for the firmness of rebinding at each level of target occupancy, is maximal when all the targets are free. The corresponding ‘rebinding factor’, k₁.[R_tot]/k, was set to 3 for k₁ = 1.10⁶ M⁻¹·min⁻¹ and to 30 for all the −k_1H variants. The pertinence of the chosen values for the different parameters has been addressed previously (Vauquelin, 2016a).

Nomenclature of targets and ligands

Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY (Southan et al., 2016), and are permanently archived in the Concise Guide to PHARMACOLOGY 2015/16 (Alexander et al., 2015).

Results

Distinction between bivalent‐ and induced‐fit‐like binders

The model (Figure 1A) and equations (4 and 5 in Figure 1B) that are dedicated to genuine induced‐fit binding also apply to bivalent drugs or ligands (Vauquelin et al., 2015, 2016). In both scenarios, the equations allow long residence to be achieved, albeit by different means. More explicit information is provided in the legend of the figure. Drug A and the other drugs for which k₂ < k_3, i.e. all those that reside above the orange dividing line in the grid (‘kinetic landscape’) on the right side of Figure 1B, do bind according to a bivalent‐like mechanism. Simulated dissociation experiments reveal that the ‘macroscopic’ k_off of Drug A is close to its calculated k₁.K _D* product (Diss t _1/2 = 0.69/k_off = 184 vs. 172 min, Table 1). In general, the k_off values vary little among all the bivalent‐like binders (Figure 1C, left panel), and the individual values are also close to the corresponding k₁.K _D* products (Supporting Information Table S1). In this respect, Equation 6 in Figure 1B, which is an alternative formulation of Equation 5, highlights the equivalence between the (k₃ + k₄)/k₂ and k₄/(k₁.K _D*) ratios. This implies that k₄ exceeds k₁.K _D* when k₂ < k₃ or, in other words, that the k₁.K _D* product represents the rate‐limiting factor for the dissociation of the bivalent‐like binders.

Table 1.

Binding constants and parameters for Drugs A and B. The difference in Gibbs‐free energy between the ground state R and the final R′L state of both drugs is equal, and the corresponding thermodynamic K _D (i.e. (k₂.k₄)/(k₁.k₃)) is set to 4 × 10⁻⁹ M, as in 2016. k₁ = 1.10⁶ M⁻¹·min⁻¹ and k₂ = 4 min⁻¹ for both; k₂ = 64 min⁻¹ for Drug A and 0.24 min⁻¹ for Drug B; k₄ = (K _D.k₁.k₃)/k₂. The first step is only governed by k₁ and k₂. The ‘macroscopic’ dissociation rate constant, k_off, can be calculated by using Equation 4 or 6 in Figure 1B. The ‘macroscopic’ affinity constant, K _D*, represents the concentration of free ligand, [L], at which the occupancy of the target is half maximal at equilibrium and is calculated by using Equation 5 in Figure 1B. As k₄ << k₃, K _D* can be set equal to K _D

	First step	Drug A	Drug B
K D* (nM)	4000	4	4
koff (min−1)	4	3.76·10−3	2.35·10−4
k1.K D* (min−1)	4	4.00·10−3	4.00·10−3
k4 (min−1)	‐	6.40·10−2	2.50·10−4

In contrast, the simulated dissociation‐based k_off of Drug B is well below its k₁.K _D* product (Figure 1C, right panel) and, in fact, rather close to k₄ (Diss t _1/2 = 2983 vs. 2760 min, Table 1). This stems from the fact that k₄ < k₁.K _D* when k₂ > k₃ (Figure 1B), so that it is now k₄ that acts as the rate‐limiting factor for its dissociation. Hence, Drug B qualifies as an induced‐fit‐like binder. The same extrapolation also applies to the other drugs that reside below the orange dividing line in the grid of Figure 1B (Supporting Information Table S1). In thermodynamic terms, their extra slow dissociation stems from the high‐energy barrier that R′L must overcome to revert to RL (Copeland, 2011).

The k₂/k₃ ratios have also been used to distinguish bivalent‐fit from induced‐fit‐like binders in another context (Strickland et al. 1975). Indeed, a very effective method of identifying induced‐fit‐like binding is to perform association experiments with multiple concentrations of L and by plotting the k_obs (i.e. the pseudo‐first order association rate constant) of each as a function of [L] (Strickland et al. 1975; Tummino and Copeland, 2008). Such plots are linear with k_obs = k_off + k_on.[L] for one‐step binding drugs but hyperbolic for induced‐fit‐like binders such as Drug B (denoted as ‘F’ in Figure 4A of Vauquelin et al., 2016). This precludes the utilization of k_on as a simple second‐order rate constant. An even more elaborate equation applies to define the k_obs versus [L] plot when k₂ < k₃, such as for the presently defined bivalent‐like binders (Strickland et al. 1975). In this respect, such plots have been shown to be quasi‐linear for Drug A (denoted as ‘A’ Figure 4A of Vauquelin et al., 2016). The slope is close to the input k₁, i.e. 0.94 10⁶ M⁻¹·min⁻¹, which agrees with the present observation that the k_off of Drug A is close to its calculated k₁.K _D*. Accordingly, while k_on equals k₁ for one‐step binding drugs (Figure 1B), it is close – but not equal – to k₁ for bivalent‐like binders.

Temporal evolution of target occupancy after a single in vivo dosing

The simulated occupancy profiles are based on a one‐compartment in vivo body model (Figure 2A) where the free drug concentration, [L], increases and then decreases rather swiftly. While its peak level permits 90% of the targets to be occupied under theoretical instant equilibrium conditions, only little remains at the end of the 24 h post‐dosing period. Figure 2B compares the corresponding occupancy profiles of the nine drugs that are shown (in green) in the grid on the left. The profiles of Drug A and the other bivalent‐like binders are closely alike. When compared to instant equilibrium binding, their peak occupancy is only slightly lower and the subsequent decline is only moderately delayed. These profiles are barely discernible from those of one‐step binding drugs with the same k₁ and K _D* (not shown). This tallies with the fact that the k_off of the bivalent‐like binders is only slightly less than k₁.K _D*, that is, the k_off of the single‐step binders (Figure 1C, Table 1). Yet, even though Drug B has the same k₁ and K _D* as Drug A, its peak occupancy is perceptibly more depressed and its occupancy also declines much more slowly afterwards (Figure 2B). This difference can be entirely attributed to the slower dissociation of Drug B, especially since its occupancy profile is identical to that of a single‐step binder with the same low k_off (data not shown). This suggests that the effect of k₂, k₃ and k₄ on the in vivo occupancy profile of the investigated drugs reflects their relative contributions to the composite k_off.

Effect of each microscopic rate constant and of repeated dosings

As there is a growing interest among medicinal chemists in bivalent‐ and induced‐fit‐like binders, we next explored the effects of a 10‐fold increase of k₁ or k₃ or decrease of k₂ or k₄ on the in vivo occupancy profile of Drugs A and B. The resulting variants (with suffix −k_1H, −k_2L, −k_3H or −k_4L) have closely the same 10‐fold lower K _D*. They also remain within the same category as the parent drugs. Similar to the one‐step model (Vauquelin, 2016a), changing k₁ does not affect their occupancy profile as it is compensated for by an opposite change of [L]. However, changing the other microscopic rate constants may give dissimilar occupancy profiles. On the one hand, the −k_2L, −k_3H and −k_4L variants of Drug A exhibit the same depressed profile (Figure 3A), and their Diss t _1/2 increases alike (Figure 3B, dark green bars). The same observations also apply the other bivalent binders (Supporting Information Figure S2). On the other hand, the occupancy profile of B‐k_4L is appreciably more depressed when compared to the cognate k_2L and k_3H variants. This stems from the lesser influence of k₂ and k₃ on its Diss t _1/2 (Figure 3B, dark green bars). Interestingly, the profiles of the k_2L and k_3H variants of the same drug always overlap (Figure 3A). Hence, it is the k₃/k₂ ratio (or in other words the destiny of RL) that prevails over the individual rate constants.

Diss t _1/2 values can be easily determined when total drug and target concentrations remain steady with time, as in assays carried out in vitro (Vauquelin, 2012; Guo et al., 2014; Cusack et al., 2015; de Witte et al., 2015; Meyer‐Almes, 2015). However, this condition is not met in vivo where drug concentrations fluctuate over time (Copeland, 2016). Despite this, the in vivo occupancy is often found to decline exponentially (de Witte et al., 2016), so that its rate can be specified by a first‐order constant, here referred to as Occupancy (Occ) t _1/2. Supporting Information Figure S3A shows that, although the Occ t _1/2 values always exceed the input Diss t _1/2, this excess can be kept to a minimal level, i.e. <10, for the widest range of drugs when the occupancy data are collected late, for instance, during the 1050–1440 min post‐dosing interval, as adopted in the present work (Figure 3B and Supporting Information Figure S2). Note that this excess will remain higher for rather fast and extremely slow dissociating drugs like B‐k_4L. This can at least in part be ascribed to the late appearance of peak occupancy (Supporting Information Figure S3B) and is presently minimized by collecting data for a more extended period (i.e. 1050–2880 min for B‐k_4L in Figures 3B and 4D).

The simulations in Figure 3C extend this exploration to study the effects of repeated daily dosings. As already shown for the one‐step model (Vauquelin, 2016a), peak occupancy is already maximal at day 1 for the fastest dissociating Drug A. When the Diss t _1/2 gradually increases, peak occupancy first significantly increases on day 2 only, then also on day 3 and so on. This increase will settle most slowly for Drug B and its variants because of their slower dissociation. For B‐k_4L, this will take about 1 month (see below). Figure 3D compares the trough to peak occupancy, T/P, ratios of the different drugs with their Occ t _1/2 values. Those ratios are used in clinical pharmacology to parameterize how constant the occupancy remains between consecutive dosings. Contrary to the peak occupancies, the Occ t _1/2 values and the T/P ratios are only minimally changed by the consecutive dosings (Figure 3D). The T/P ratio of Drug A is appreciably lower than for Drug B and all the −k_2L, −k_3H and −k_4L variants. As further illustrated in Supporting Information Figure S4, these observations comply with an exponential T/P ratio – Occ t _1/2 relationship. The AUC is also an important parameter in clinical pharmacology, because it represents the averaged occupancy after each dosing. Figure 3E shows that the AUCs behave quite similarly to the peak occupancies. Except for Drug A, the AUCs rise most early on and then less and less. Interestingly, the same ceiling level (i.e. about 70% of the theoretical limit, corresponding to continuous full target occupancy) will be reached, usually within 8 days but only after more than 1 month for B‐k_4L (Figure 5B). Taken together, while repeated dosings produce gradual increase of the AUC of slow‐dissociating drugs, their T/P ratios are scarcely changed.

Effects of rebinding

Next, we explored the occupancy profiles in a subcellular location where the diffusion of free drug is hindered and/or the targets are clustered. Based on the consideration that rebinding only affects the initial binding step, k_off was amended by replacing k₁ and k₂ by the corresponding rate coefficients (now referred to as k′_off, Figure 4A). More explicit information is provided in Vauquelin (2016a) and in the Methods section. k′_off is not constant; it is maximal when all the targets are free and gradually increases till k_off when the occupancy increases (Figure 4A). Interestingly, it is only for Drug A that the k′_off/k_off ratio versus [R] plot overlaps with those of one‐step binding drugs. Also, while the maximal k′_off/k_off ratio is 0.33 for the former (i.e. corresponding to a threefold slower k′_off when all the targets are free), it remains much closer to 1 for Drug B.

The simulated in vivo occupancy profiles are based on the combination of a one‐compartment body model and rebinding (Figure 4B). To better appreciate the effects of rebinding, the ‘rebinding factor’ was purposefully kept small so that the profiles of the parent drugs are only moderately affected. Nevertheless, the occupancy of Drug A already declines significantly more slowly, i.e. Occ t _1/2 = 571 vs. 230 min without rebinding (Figure 4C). On the other hand, the Occ t _1/2 of Drug B changes less (i.e. 3440 vs. 3090 min). This tallies with the lesser effect of rebinding on its k′_off (Figure 4A). Changing k₂, k₃ and k₄ affects the occupancy profile and Occ t _1/2 of Drugs A and B in the same way as without rebinding (please compare Figure 4C, D with Figure 3A, B). However, increasing k₁ now produces nearly the same effect as changing k₂ and k₃, that is, nearly the same effect as changing k₄ for Drug A and a much less marked effect as changing k₄ for Drug B (Figure 4C, D).

Figure 4D also compares the Occ t _1/2 values after eight consecutive daily dosings (dark green bars), and Figure 4E shows how these values evolve from day to day. Interestingly, and in contrast to the situation without rebinding, the Occ t _1/2 of all the variants decline day after day, even by up to 50% at day 8 for some of them. This can be largely attributed to the lesser impact of rebinding when the occupancy increases (Figure 4A). Indeed, this drop is also observed for the k_1H variant whose Occ t _1/2 is only responsive to changing the firmness of rebinding (Vauquelin, 2016a). Second, this drop is more pronounced early on and also coincides with the increase in AUC (Figure 4F). Third, no such drop is observed for Drug A, whose occupancy is already nearly maximal at day 1 (Figure 4C). Finally, the Occ t _1/2 values do not drop below those in absence of rebinding (please compare Figure 4E with 3D). Finally, Figure 4E also points out that the daily fall in Occ t _1/2 goes along with a decline of the T/P ratio. Based on more drugs and variants, Supporting Information Figure S4 illustrates that the T/P ratio–Occ t _1/2 relationship is still exponential in the presence of rebinding.

Comparing Figures 4F and 3E reveals that rebinding triggers a further initial drop in the AUC of all the variants. However, subsequent dosings allow a gradual increase of AUC until almost the same ceiling level is attained. While 8 days suffice for most of the variants, it will take here again about 1 month for B‐k_4L (Figure 5B). The close match between the ceiling levels in the absence and presence of rebinding (i.e. 70% of the maximum) may seem surprising. but it can be related to the decreasing impact of rebinding at high occupancy.

Taken together, rebinding allows increasing k₁ to boost the Occ t _1/2 and T/P ratio of Drug A almost as effectively as decreasing k₂ or increasing k₃. However, this effect will gradually fade after repeated dosings and this characteristic also prevents rebinding from modifying the ceiling AUCs.

Effects of dosage

Increasing the dosage boosts the AUC of a drug (Vauquelin, 2016a). This is also illustrated in Figure 5A, which compares the effects of a 10‐fold higher dosage on the T/P ratio and the AUC of Drugs A, B and their variants, both in the absence and presence of rebinding. For all, a single dosing with the high dosage already yields appreciably higher AUC (red dots) than after as many as eight, daily dosings with the low dosage (green dots).

Except for Drug A, repeated dosings with this high dosage yield the highest AUCs, now even exceeding 90% of the theoretical maximum (blue dots). This combined effect is most prominent for B‐k_4L; its AUC of about 95% is now even the highest of all. Figure 5B compares how the AUCs of the quite dissimilar A‐k_1H and B‐k_4L variants progress with repeated dosings with the low and the high dosage. At the high dosage, their ceiling AUC is not only higher but also attained sooner. This pattern is especially marked for B‐k_4L. Figure 5A also shows that, as shown for repeated dosings (green dots), increasing the dosage decreases the T/P ratio for all the drugs (except for Drug A), especially in the presence of rebinding. Of note is that B‐k_4L is the least affected. Here again, the T/P ratios and the Occ t _1/2 values can be correlated by an exponential paradigm (Supporting Information Figure S4).

To provide a more evocative representation of the above considerations, Figure 5C compares the occupancy profiles of Drugs A, B and their variants after the two most extreme dosing regimens, that is, a single dosing with the low dosage and eight dosings with the high dosage. The second regimen allows peak occupancy to appear earlier on and also to be higher; it even nears the theoretical maximum for all the drugs, both with and without rebinding. Also, while the first regimen allows rebinding to clearly depress peak occupancy of many variants, this attribute is now completely lost for the latter regimen. The combined effect of a high dosage and repeated dosings is especially dramatic for B‐k_4L, which now displays the highest and least variable occupancy level of all.

Discussion

A long residence time is increasingly recognized to be a key attribute of many marketed drugs, and ‘micro’‐PK and ‐PD mechanisms have been proposed to contribute to this outcome (Copeland, 2010, 2011; Sykes et al., 2014; Swinney et al., 2015; Vauquelin, 2015, 2016b). Here, we focus on limited diffusion‐ related rebinding for the PK contribution and on bivalent‐like (Drug A) and induced‐fit like binding (Drug B) for the PD contributions (Figure 1). Although the latter mechanisms can be represented by the same mathematical formulation (Vauquelin et al., 2015, 2016), Drugs A and B differ markedly with regard to the effects of their microscopic rate constants on their composite k_off and on the firmness of rebinding. This has also interesting repercussions on how their occupancy profiles progress with repeated dosings and by changing the dosage.

The occupancy profile of a one‐step binding drug only depends on its dissociation rate when the dosing complies with the clinically most relevant constant C_max/K _D ratio paradigm (Dahl and Akerud, 2013; Vauquelin, 2016a). We here show that, under the same dosing conditions, the occupancy profile of Drug B is more depressed than for Drug A (Figure 2B), even though both have the same k₁ and K _D*. This stems from the much slower dissociation of Drug B and can be explained by the differing contribution of the microscopic rate constants (k₂, k₃ and k₄) to the composite k_off of both drugs. A rapid ‘toggle switch’ between the partly bound RL and fully bound R′L states (i.e. k₃ > k₂) shapes the dissociation of Drug A. The k₁.K _D* product acts as the ‘kinetic bottleneck’ for its dissociation, and changing k₂, k₃ and k₄ individually has equal effect on this product, on the dissociation rate and on the occupancy profile (Figure 3A, B). In contrast, the dissociation of Drug B is shaped by the high‐energy barrier that R′L has to overcome to revert to RL. Its k₄ is lower than k₁.K _D* and now acts as the ‘kinetic bottleneck’. As k₂ and k₃ can only act on k₁.K _D*, they affect the occupancy profile much less than k₄. This is clearly illustrated by the lower peak occupancy and its slower subsequent decline for the B‐k_4L variant (i.e. Drug B with 10‐fold lower k₄), than for the corresponding B‐k_2L and B‐k_3L variants (Figure 3A, B).

In this respect, it is of note that a distinction based on a high k₃/k₂ ratio versus a low k₄ should not be strictly associated with the actual molecular mechanisms of induced‐fit and bivalent binding, in particular when it comes to distinguishing mono‐ from bi‐valency. Indeed, it is potentially also possible for monovalent agonists to have a greater probability of inducing receptor activation than dissociating (i.e. k₃ > k₂) and that each activation is brief. In the same context, some bivalent drugs could have greater probability of dissociating than forming the fully bound complex, but that once it forms, it could be very stable. To call attention to this point, we have referred to Drug A (and its analogues) as bivalent‐like and to Drug B, as induced‐fit‐like.

Binding kinetics may prolong the clinical action of a drug if its dissociation is slower than its PK‐elimination (Vauquelin and Van Liefde, 2006; Dahl and Akerud, 2013). Because rebinding is able to prolong the occupancy, this may help ‘borderline’ drugs such as candesartan to act longer than predicted by this rule (Swinney et al., 2015). Although k₁ cannot affect the occupancy profile by itself, under the present dosing paradigm (Dahl and Akerud, 2013), it is able to control the firmness of rebinding. This allows k₁ to influence the occupancy profile of single‐step binding drug, quite like k₂ (Vauquelin, 2016a). The present study extends this aptitude to bivalent‐like binders such as Drug A; that is, the occupancy profile of the A‐k_1H is now quite comparable to that of the other three variants in the presence of rebinding (Figure 4C, D). In contrast, increasing k₁ has only a limited effect on the occupancy profile of Drug B. The rationale behind this difference is that this profile is only significantly changed by k₄, which is not affected by rebinding. However, it is doubtful whether the low sensitivity of induced‐fit‐like binders to rebinding really matters as, at equal K _D*, they inherently already dissociate much more slowly. An additional matter to consider is that the firmness of rebinding, and hence also effects of a high k₁ on this variable, is no longer pronounced at high target occupancy (Figure 4A). It is thus pertinent to consider the utility of changing the k₁ of a drug candidate in light of its binding mechanism, the location of its targets and whether a constant‐near maximal target occupancy is required.

While Diss t _1/2 values are of increasing interest in drug screening programmes, AUCs and T/P ratios are important parameters in clinical pharmacology. To better compare the Diss t _1/2 values with the occupancy profiles, we parameterized how fast the occupancy declined at the end of the post‐dosing period. The resulting Occ t _1/2 values agree reasonably well with the input Diss t _1/2 values when the dosage is relatively low, i.e., when C_max/K _D = 9. Also, the T/P ratio–Occ t _1/2 relationship can be represented by a quite stable exponential paradigm, unaffected by the presence of rebinding, the duration of the treatment and the dosage (Supporting Information Figure S4).

The benefit of increasing a drug's Diss t _1/2 and/or the firmness of rebinding often comes at the expense of a depressed peak occupancy and AUC. This can be remedied by repeated daily dosings (Figures 3E and 4F), but it may take quite a while before the AUC of very slowly dissociating drugs reaches a ceiling level (Figure 5B). Nevertheless, the ceiling AUCs remained still despairingly low for all the presently investigated drugs at the standard dosage. Among the different approaches to remedy this deficiency, we have here focused on a 10‐fold higher dosage. This procedure already boosts the AUC of all the drugs after the first dose, and it also allows the ceiling AUCs to be notably higher and even to be attained faster. In this respect, it is remarkable that, while the AUC of the B‐k_4L variant is the lowest of all after a single dosing with the standard dosage, increasing the dose allows its ceiling AUC to become the highest of all and also to be attained after only a few days (Figure 5B). Hence, a high dose of a very slowly dissociating drug is the best regimen, if the goal is to rapidly obtain high and steady occupancy of the target, as necessary for certain therapeutic indications (Copeland, 2010; Núñez et al., 2012).

In summary, the present study explores the in vivo occupancy profile of two‐step binding drugs. The simulations show that, because of the different effects of the microscopic rate constants on their dissociation rate and on their reactions to rebinding, bivalent and induced‐fit‐like binders with equal potency, display quite different occupancy profiles. The latter dissociate appreciably more slowly and are also less sensitive to rebinding. This implies that some of the conclusions that are based on PK‐PD simulations with one‐step binding drugs (de Witte et al., 2016; Vauquelin, 2016a), such as a positive impact of a high k_on (and the derived high affinity) on the occupancy profile in confined spaces or compartments, are only of limited effect in the case of induced‐fit‐like binders. Whereas nearly all the previous PK‐PD modelling studies dealt with the simplest binding mode, the present findings demonstrate that closer attention should also be paid to more complex mechanisms.

Author contributions

G.V. contributed to study design, simulations, writing and artwork.

Conflict of interest

The author declares no conflicts of interest.

Declaration of transparency and scientific rigour

This Declaration acknowledges that this paper adheres to the principles for transparent reporting and scientific rigour of preclinical research recommended by funding agencies, publishers and other organisations engaged with supporting research.

Supporting information

Table S1 Binding constants and parameters for an extended range of two‐step binding drugs.

Figure S2 Effect of changing the microscopic rate constants on the Diss t_1/2 and in vivo Occ t_1/2 values for an extended range of drugs.

Figure S3 Mechanisms that are accountable for elevated Occ t_1/2/Diss t_1/2 ratios.

Figure S4 Relationship between T/P ratios and Occ t_1/2 values: effect of rebinding and dosage.

Vauquelin, G. (2017) Distinct in vivo target occupancy by bivalent‐ and induced‐fit‐like binding drugs. British Journal of Pharmacology, 174: 4233–4246. doi: 10.1111/bph.13989.