Brain network dynamics are hierarchically organized in time

Significance

We address the important question of the temporal organization of large-scale brain networks, finding that the spontaneous transitions between networks of interacting brain areas are predictable. More specifically, the network activity is highly organized into a hierarchy of two distinct metastates, such that transitions are more probable within, than between, metastates. One of these metastates represents higher order cognition, and the other represents the sensorimotor systems. Furthermore, the time spent in each metastate is subject-specific, is heritable, and relates to behavior. Although evidence of non–random-state transitions has been found at the microscale, this finding at the whole-brain level, together with its relation to behavior, has wide implications regarding the cognitive role of large-scale resting-state networks.

Abstract

The brain recruits neuronal populations in a temporally coordinated manner in task and at rest. However, the extent to which large-scale networks exhibit their own organized temporal dynamics is unclear. We use an approach designed to find repeating network patterns in whole-brain resting fMRI data, where networks are defined as graphs of interacting brain areas. We find that the transitions between networks are nonrandom, with certain networks more likely to occur after others. Further, this nonrandom sequencing is itself hierarchically organized, revealing two distinct sets of networks, or metastates, that the brain has a tendency to cycle within. One metastate is associated with sensory and motor regions, and the other involves areas related to higher order cognition. Moreover, we find that the proportion of time that a subject spends in each brain network and metastate is a consistent subject-specific measure, is heritable, and shows a significant relationship with cognitive traits.

Resting brain activity is far from random and has been shown to organize into a number of large-scale networks with characteristic spatial architectures (1–3). It is also known that many of the networks of activity found in the resting brain are also observed in tasks (4). However, despite evidence at the microscale that the brain deploys populations of neurons in a temporally coordinated manner both in tasks (5) and at rest (6), relatively little is known about the temporal organization of large-scale resting-state networks. This has been limited to evidence of, for example, anticorrelations between certain networks (7), long-range temporal dependencies (8), and time-varying modularity (9, 10). Nonrandom transitions have also been found between brain states defined as electroencephalographic microstates (11), attractors in metastable systems (12), or local minima in energy landscape analysis (13). In this work, we hypothesize that there must exist more specific patterns of temporal organization than have been described so far, and propose that these transitions are not only nonequiprobable but are themselves organized in a hierarchical manner.

To study the temporal organization of the brain’s large-scale network dynamics, we used a method designed to discover networks that repeat over time (referred to as brain states). Importantly, we define networks as probability distributions representing graphs, with not only distinct patterns of activation but, crucially, also distinct patterns of functional connectivity. This approach has access to temporal scales as fast as the data modality allows and overcomes the statistical limitations of the sliding windows technique when applied to the analysis of brain dynamics (14–17). Applying this method to whole-brain resting-state fMRI data from 820 subjects from the Human Connectome Project (HCP) (18) reveals a clear temporal organization. We find that transitions between different brain networks do not occur in complete randomness; instead, certain networks are much more likely to follow others in time. Further, this nonrandom sequencing of brain networks is itself hierarchically organized, and strikingly reveals two sets of brain networks, or metastates, that the brain has a tendency to cycle within, with sporadic cycling between them. One metastate is associated with sensorimotor and perceptual (visual and auditory) regions. The other involves areas related to higher order cognition, including regions of the default mode network (DMN), language, and extensive prefrontal areas.

We also examine the most basic temporal characteristic of these brain networks, or states, which is their occupancy. Occupancy is defined as the proportion of time that each subject spends in each brain state. Notably, these occupancies show a strongly dominant mode of variation over subjects that corresponds to the same two metastates that were apparent in the sequencing of brain networks. We then demonstrate that the proportion of time spent in each metastate is very subject-specific and significantly heritable. Not only can we predict the metastate occupancy in a new session using the occupancy from previous sessions but we can also significantly predict the occupancy using behavioral information of the subject. In particular, more occupancy of the cognitive metastate tends to relate to positive traits, particularly to cognitive performance and satisfaction. We analyze the relation of the metastates’ distribution to sleep and motion, concluding that the high-level temporal dynamics are not an artifactual result of these factors.

In summary, this study highlights the hierarchically organized temporal nature of resting-state networks of interacting brain areas, characterizing its properties in a large cohort of subjects and relating its cross-subject variability to behavior and heritability.

Results

Dynamic Switching Between Brain Networks Is Not Random.

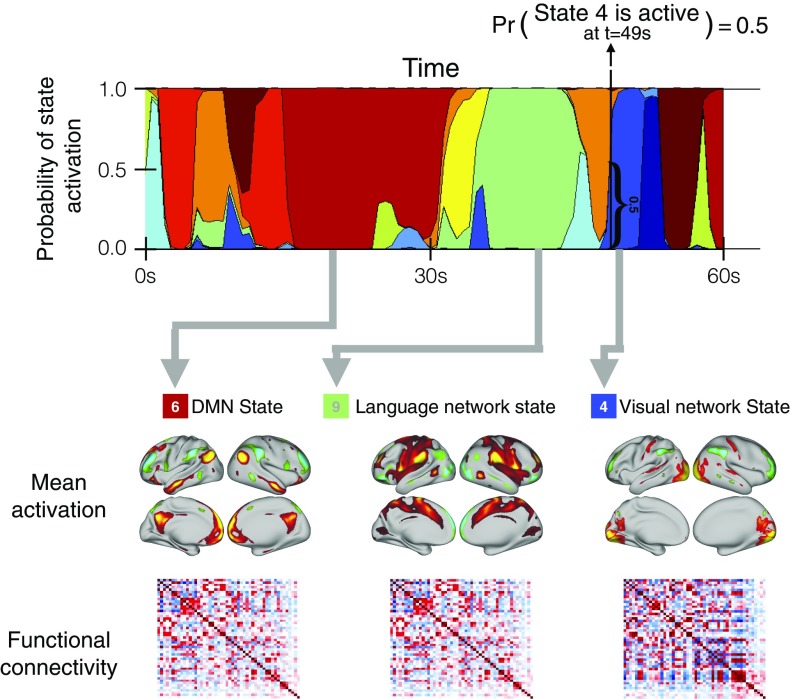
We used resting-state fMRI data from 820 subjects in the HCP (18). Data across the multiple subjects were temporally concatenated, resulting in a single group data matrix from which a hidden Markov model (HMM) with 12 states was inferred (Methods). The HMM states represent unique brain networks of distinct activity and functional connectivity (where functional connectivity is defined as Pearson correlation over time between brain areas) that repeat at different points in time (19, 20). Other approaches (typically based on sliding windows estimations and subsequent clustering) have been proposed to find repeating states (21); the HMM, however, offers a probabilistic (generative) model that, through a single process of Bayesian inference (Methods), models the time series in a self-contained manner. Here, whereas the states are estimated at the group level, each subject has a characteristic state time course that indicates the points in time at which that state is active. Fig. 1 shows an illustrative 1-min section of the state time course for one example subject. Mean activation maps are shown for three of the 12 inferred states, along with their corresponding functional connectivity matrices. The mean activity maps for all states are shown in Fig. S1.

Fig. 1.

HMM estimates a number of brain networks (or states) that are common to all subjects, together with a specific state time course for each subject indicating when each state is active. The states are characterized by their mean activation and functional connectivity matrix. (Top) Sixty-second section of the state time course for one example subject. Pr, probability. (Bottom) Mean activation maps (projected from 50D ICA space to brain space) for three of the 12 inferred states, along with their corresponding functional connectivity matrices.

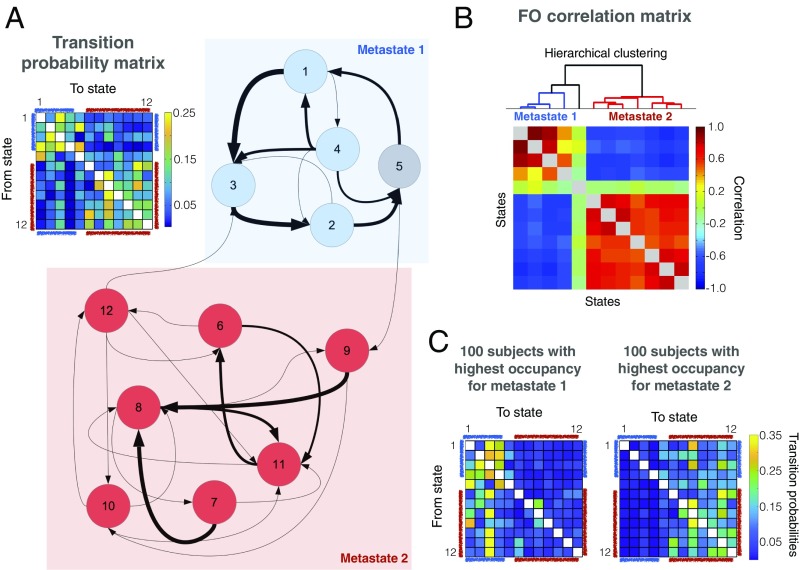
We used the temporal structure of the inferred brain states to reveal that the temporal organization of brain activity is, while stochastic, not completely random. In particular, we examined the HMM’s estimate of the transition probability matrix, which specifies the probability of transitioning from any state to another (mathematical details are provided in Methods). Fig. 2A shows the estimated transition probabilities in two different formats: a matrix and a graph, where nodes represent states and arrow thickness represents (thresholded) state transition probability. Community discovery analysis using the transition probability matrix as an input (22) reveals two sets of states or metastates (colored blue and red in Fig. 2A), indicating that the brain tends to cycle between brain networks within a metastate, with less frequent transitions between them (the average number of metastate switches is ∼30 per scanning session, and 96% of the sessions have at least one switch). To gain confidence in the result, we performed bootstrapped subject resampling (1,000 draws of 820 subjects with repetition) and applied the community discovery algorithm (22) on each bootstrap sample separately. We obtained the exact same separation in all bootstrap samples, confirming that the separation between these sets is highly significant. Further, it was found that the probability of transition between states heavily depends on how similar the brain networks in those states are (estimated using the correlation between the brain state functional connectivity matrices) but very little on the correlation between the brain state activation patterns, suggesting that changes at the level of connectivity are smoother than changes at the level of absolute activation (Fig. S2).

Fig. 2.

Transitions between brain networks are not random, giving rise to two very distinct sets of states, which are referred to as metastates. (A) Transition probability matrix (Top Left) indicates the probability of transitioning from any state to another, showing that some transitions are much more likely than others. This is apparent when shown in graph format (Top Right and Bottom), where the nodes represent brain states and the thickness of the arrows represents the state transition probability (transitions were thresholded for readability). (B) FO matrix, which contains the total time spent in each state per subject, exhibits exceptionally strong correlations between states across subjects. Even more strongly than the transition probability matrix, these correlations indicate a clear hierarchical metastate structure. Hierarchical clustering (illustrated above the FO correlation matrix) confirms this result. (C) Transition probability matrix for the 100 subjects with the highest occupancy for metastate 1 and the 100 subjects with the highest occupancy for metastate 2.

Time Spent Visiting Distinct Brain Networks Is Not Random.

Another summary measure of the temporal characteristics of the states, or brain networks, is the proportion of time spent visiting each state. This is referred to as the fractional occupancy (FO) for each state and for each subject. This allows us to examine the FO correlations for each pair of states across subjects; that is, if matrix R refers to the FO for all subjects, such that R_i,k is the proportion of time spent by subject i in state k, then the (number of states by number of states) FO correlation matrix C has elements C_k,l = corr (R_.,k, R_.,l), where R_.,k represents the column vector of R that corresponds to state k. Fig. 2B illustrates the result of correlating the FO of each pair of states across subjects and performing hierarchical clustering (using Ward’s algorithm) on the resulting correlation matrix. This analysis reveals between-state correlations that are extremely high (with absolute values over 0.5 and often close to 1.0), indicating an exceptionally clear hierarchical organization of the brain dynamics, with the states divided into two sets, or metastates, corresponding to those in Fig. 2A. More explicitly, here, the metastates correspond to sets of states whose FOs are strongly correlated across subjects (red blocks in Fig. 2B); conversely, the between-metastate FO correlations are negative (blue areas in Fig. 2B). State 5, which was included in one of the metastates by the previous community detection analysis (Fig. 2A), is, however, uncorrelated to the rest of the states in terms of its FO. This state, with a relatively strong correlation with motion (Fig. S5A) and a much higher signal variance for all regions than the rest of the states (Fig. S5C), may well be related to head movements, and is thus left out of subsequent analyses. As we show in Supporting Information (Fig. S3), the metastate organization in the FO correlation matrix can largely be explained by between-subject differences of the Markovian dynamics encoded in the transition probability matrix. To illustrate the extent to which transition probabilities (although estimated in the HMM at the group level) can vary across subjects, we recalculated the transition probability matrix for the 100 subjects with the highest occupancy for metastate 1 and the 100 subjects with the highest occupancy for metastate 2. These are shown in Fig. 2C, depicting much larger transition probabilities from metastate 2 to metastate 1 in the first group, and the opposite in the second group.

The Emerging Metastates Have Distinctive Spatial Features.

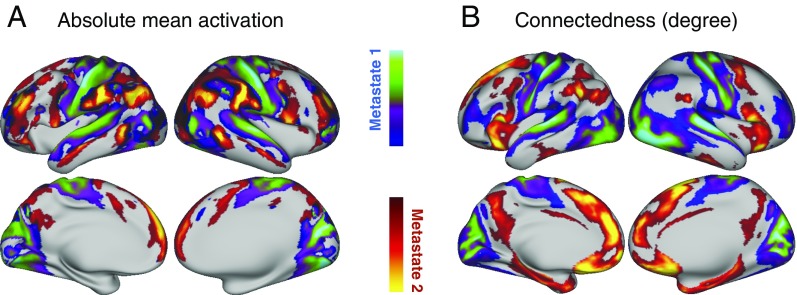
Fig. 3A shows, for each metastate, a spatial map of the average absolute amplitude within the metastate. Regions with high values in these maps can be interpreted as having brain activity that deviates substantially from their average activity levels during the time the metastate is active. Fig. 3B shows a spatial map of the functional connectedness (or degree) of each brain area, computed as the sum of the absolute value of functional connectivity with the rest of the brain. Both the amplitude and connectivity reflect a clear functional distinction between the first metastate, composed of sensory (somatic, visual, and auditory) and motor regions, and the second metastate, covering higher order cognitive regions that include the DMN, language, and prefrontal areas. The correlation between the absolute amplitude and the connectedness maps is significantly positive (r = 0.52, P < 0.001).

Fig. 3.

Two metastates contain distinctive functional areas. Whereas the first metastate is associated with sensory (somatic, visual, and auditory) and motor regions, the second metastate involves areas related to higher order cognition (including regions of the DMN, language, and extensive prefrontal areas). This is apparent in both the activation level and connectivity. (A) In the first case, we look at the average absolute amplitude of each region within the metastate, which can be interpreted as a measure of the amount of deviation from average activity levels. (B) In the second case, we compute the connectedness, or degree, defined as the sum of functional connectivity of each region with the rest of the brain.

Time Spent Visiting Brain Networks and Metastate Predicts Behavioral Traits.

If the temporal organization of the brain network dynamics is functionally relevant, then it should link to behavior. We next assessed how strongly the time spent (i.e., FO) in the states or metastates can be predicted by subject-specific behavioral traits. Motion, sex, age, body mass index, and a measure of surface registration differences (using the surface-warping Jacobian obtained from the multimodal surface matching process and taking the mean of the absolute logarithm of the area ratio images) were regressed out as confounds from all of the considered variables (FO and traits). Furthermore, we discarded the 10% of subjects with the highest measures of motion. Then, using (Bayesian) partial least squares combined with permutation testing (23), the relationship between FO and behavioral traits was found to be statistically significant (P = 0.003; Methods).

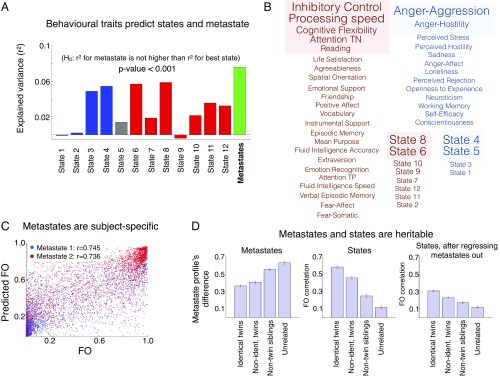
We then questioned whether the metastates’ FO would be better predicted by the behavioral traits than by the individual states’ FO, as this would show that the metastates are behaviorally relevant above and beyond the underlying brain states. Fig. 4A shows the explained variance of each state’s FO, predicted using cross-validation (Methods), along with the explained variance of the metastate profile, defined as the FO of the cognitive metastate minus the FO of the sensorimotor/perceptual metastate. This analysis illustrates that the prediction for the metastate is higher than any of the single states separately (P < 0.001), suggesting that the metastates are not only subject-specific but also relevant to behavior.

Fig. 4.

Brain network dynamics and the metastate profile are subject-specific, relate to behavior, and are heritable. (A) Using behavioral traits (well-being, intelligence, and personality) as regressors, we can significantly predict the states’ FO and (even more accurately) the metastate profile. H₀, null hypothesis. (B) Metastate profile separates “positive” from “negative” traits, which correlate to the metastate profile with the opposite signs; the statistical significance of this correlation is highlighted (variables correlate when they have the same color and anticorrelate otherwise), and the font size corresponds to the magnitude of the correlation. TN, true negatives; TP, true positives. (C) FO of the metastates for a given session can be accurately predicted for each subject using information from the other sessions, suggesting that the metastate profile is a very specific subject fingerprint. (D) Metastate (Left) and state (Middle) distributions are strongly heritable; the state distribution is heritable (but to a lesser extent) if we regress out the metastate information (Right). Non-ident., nonidentical.

Next, to assess the individual significance of each variable (either FO or trait), we use canonical correlation analysis (24). Motion, sex, age, body mass index, and registration differences (discussed above) were again regressed out as confounds from all of the considered variables (FO and traits). We then looked at the individual correlation of each behavioral trait or each state’s FO against the opposite canonical covariate (i.e., the canonical covariate of the state FO was used for the behavioral traits, and vice versa; Methods). Fig. 4B shows the behavioral traits and brain states separated into two groups according to the sign of the correlation, where the four colored boxes (red and blue) indicate statistical significance (permutation testing, significance level of 0.05). As observed, there is a tendency of the positive traits to correlate with the FO of the higher order cognitive metastate.

Time Spent in Each Metastate Is a Subject-Specific, Heritable Measure.

Given that we have seen that the proportion of time spent in each metastate is associated with behavioral traits (Fig. 4 A and B), we could also expect them to be very subject-specific measures. To assess this, we performed cross-validated predictions of the FO for each session, either for the states or the metastates, as a function of the FO of the other three sessions for the same subject. Fig. 4C shows that, despite the fact that the subjects were scanned on different days, the metastate FOs are consistent across sessions and can be reliably predicted.

It has been recently reported that functional connectivity within and across large-scale brain networks has a heritable component (25, 26). Here, we found that both the states’ FO and the metastates’ FO are also highly heritable. The dataset contains twin structure, including a combination of nonidentical twins and nontwin siblings. That allowed us to compare whether related subjects had a more similar metastate profile than nonrelated subjects. For each pair of subjects, we computed the absolute difference of their metastate profile values, gathering a distribution of differences for each type of familial relation. Fig. 4D (Left) shows that identical twins, followed by nonidentical twins and then nontwin siblings, all have a closer metastate profile than unrelated individuals. We also calculated the correlation of the state FO (a vector of 12 elements per subject) for each pair of individuals. Fig. 4D (Middle) reveals a huge difference between unrelated pairs of subjects and pairs of subjects that are twins or even nontwin siblings. We then questioned whether these differences in the state FO were solely due to the differences in the metastate profile. To answer this, we regressed the metastate profile out of the FO and repeated the analysis. Fig. 4D (Right) indicates that whereas many of the differences were actually due to the heritability of the metastate profile, the specific states’ FO contains further information that is also heritable.

Are the Metastates Related to Motion and/or Sleep?

One possible concern about the cognitive interpretation of the metastates is whether they are driven by motion. However, the correlation between head motion (measured as the session average) and the metastate profile is relatively low (r = 0.05) in comparison to other subject measures (Fig. S4A). Also, the correlation between motion and the metastate profile is very low in comparison to the individual state correlations (Fig. S4B). In particular, state 5 [the one associated with the highest signal variance (Fig. S4C)] has the highest correlation with motion in absolute value, followed by state 6, which corresponds to the DMN and anticorrelates with motion significantly. Furthermore, if we regress motion out of the FO matrix and then repeat the calculation of the correlation between the states’ FO across subjects (as in Fig. 2B), the two metastates (and the unrelated state 5) are still evident (Fig. S4D). Therefore, although there seems to be a certain influence of motion on the individual states, the metastate distribution appears to be relatively free of motion confounds.

If we consider the metastates to represent a high-level state of cognition, then it is important to consider how the metastates relate to macrostates such as sleep. As reported by Tagliazucchi and Laufs (27), many subjects transit from wakefulness to sleep stages N1 and N2 during the first 10 min of the resting-state session, and that is certainly a major cause of genuine neural activity change over time. Moreover, if we divide the 15-min sessions into four blocks, the occurrence of the metastates varies significantly between the four blocks, with an increase in the occurrence of the sensorimotor/perceptual metastate as the session progresses (Fig. S5A).

Hence, do the sensorimotor/perceptual and cognitive metastates simply represent sleep and wakefulness, respectively? Although it is possible that the sensorimotor/perceptual metastate is higher in states of drowsiness and sleep (given Fig. S5A and the results from ref. 27), we argue that there is more information in the metastates than just sleep, and that both metastates coexist in pure wakefulness. First, the HCP resting-state protocol corresponds to subjects having their eyes open with fixation, which reduces the probability of falling asleep. Second, the amount of time spent, on average, in the sensorimotor/perceptual metastate during the first minute of scanning (when sleep is highly unlikely) is around 20 s (Fig. S5B). Third, if we look at the state dwell times of the metastates (after removing metastate visits shorter than 4 s to rule out noisy artifactual transitions), Fig. S5C shows that most of the transitions are too short to capture sleep or wakefulness periods (e.g., around 50% of the metastate visits are shorter than 15 s even when ignoring the shortest visits). Finally, if the metastates are primarily capturing sleep versus wakefulness, we might expect the metastate profile to correlate highly with the Pittsburgh Sleep Quality Index (PSQI) score provided within the HCP set of variables, which essentially measures the quality and pattern of sleep of the subjects. The PSQI is, however, uncorrelated to the metastate profile (r = −0.0056). Fig. S5D shows that this correlation is lower in absolute value than the majority of the behavioral variables considered in this study. Also, as illustrated in Fig. S5E, this correlation is lower than most of the states when considered separately. Altogether, our results suggest that the metastate organization goes beyond separating wakefulness and sleep, and arguably represents a more general and ubiquitous temporal pattern in spontaneous brain activity.

Discussion

Robust patterns of synchronized activity can be measured in the brain in both task and rest. The spatial organization of these patterns at rest has been studied well. In this study, we focus on the temporal organization of the dynamics of the resting-state networks, and discover a temporal hierarchy in which brain networks are organized into two distinct sets, or metastates. These metastates have a clear functional separation (cognitive versus sensorimotor/perceptual) that is consistent across subjects, relates to behavior, is heritable, and is reproducible (Supporting Information and Fig. S6). Although other work has reported hierarchical aspects of the fMRI resting-state networks (28–30), these analyses assume the existence of a hierarchy in the first place, whereas the HMM neither imposes nor encourages it; that is, if a hierarchical structure arises from the HMM results, then this is purely driven by the structure in the data. More importantly, whereas previous work extracts the hierarchical structure from the zero-lag correlations of the [voxels’ or independent component analysis (ICA) components’] time series, we are here referring to the hierarchical structure of the network dynamics. This hierarchy manifests in two ways: first, in the hierarchical structure of the transition probability matrix (i.e., the hierarchy emerges not from correlations but from transitions) and, second, in the FO correlation across subjects [i.e., it is not the correlation of the time series within subjects but the correlation between the (subject-specific) averaged state probabilities (of which the FO is an estimation) across subjects].

These results can be related to current theoretical perspectives on cognition. First, the hierarchy of brain networks (in the form of the metastates) and, more generally, the nonrandom transitions between the states naturally imply that current and previous brain states can constrain future states in task-free conditions. This relates to, and can potentially complement, current results on the persistence of activity in specific areas of the brain (31) to the whole brain. Second, there is some overlap between the metastates and the two extremes of the principal axis of structural connectivity variation estimated by Margulies et al. (32), which is based on a mathematical decomposition of the structural connectivity elicited from the same 820 subjects used in this study. This coincidence of structural and functional hierarchies is meaningful from a theoretical perspective and deserves further investigation, perhaps also at other hierarchical levels. Third, from an evolutionary psychology perspective, it is interesting to observe that FO of the higher order cognition metastate is, in general, positively correlated with positive traits, and so may indicate an adaptive value of intrinsically generated mental states (33).

Leveraging the common framework provided by the HMM to integrate different data modalities, future work will aim to investigate whether or not the same hierarchical structure and metastates can also be found in electrophysiological data such as magnetoencephalography and electroencephalography. To this end, we will use an observation model specifically tailored to this type of data (34).

Alternative Representations of the Data.

It is worth noting that we are not claiming the HMM to be the ground truth or to explain all aspects of the data, but to offer a useful perspective on the data. Other models and techniques such as multivariate autoregressive modeling (35) or lag-based activity propagation approaches (36, 37) offer their own complementary and useful descriptions of the dynamics in the data. In this work, the HMM has been able to reveal a strong hierarchical structure in the data, represented by metastates. While it is possible that the same (or related) phenomena might be detected using other approaches, it is unclear how this would be achieved in practice. An advantage of the HMM over other techniques is that the HMM explicitly parametrizes time-dependent information (in the form of the state time courses), such that it can be more easily used to access network dynamics [e.g., in task responses (20)]. In Supporting Information, we explore the relationship between the HMM and both the multivariate autoregressive model and lag-based activity propagation analysis in more detail.

Data Stationarity.

The HMM assumes that, within each state, the data are drawn from a single given HMM observation model, which is defined by a single set of parameters. Although more general statistical definitions of stationarity exist (38), we here refer to stationarity with respect to the observation model used by the HMM, which, in this case, is a multivariate Gaussian distribution. In other words, we refer to data as being nonstationary when they have a time-varying mean and/or covariance within a given session. Now, the facts that (i) the HMM needs more than one state to model the data and does not collapse into a single state and (ii) multiple states are inferred with significantly different observation model parameters suggest that the data are nonstationary in this sense. Further evidence supporting nonstationary can be gathered from the synthetic data used in Supporting Information (Using the HMM to Assess Nonstationarity).

In relation to this question, recent studies have reasonably questioned whether observed changes in dynamical functional connectivity in resting-state fMRI are due to genuine brain transitions or, rather, are mostly explained by sampling variability (14–17). However, these valid concerns are specific to techniques that measure dynamic function connectivity using sliding windows. The HMM, however, can bypass the problem of sampling variability by using, for each state, the entire set of subjects to provide an estimation of functional connectivity (SI Methods). The amount of data used to infer the network characteristics for each brain state is thus orders of magnitude larger (on average, 820 subjects × four sessions × 1,200 time points per session, divided by 12 states) than that which a sliding window can possibly encompass, especially given the size of the dataset used in this study. At the same time, and unlike long sliding windows, the model is able to capture quick changes in brain activity.

Conclusion

Altogether, our approach reveals an intriguing property in the resting-state temporal dynamics: The brain transitions between networks in a manner that is stochastic yet not completely random. More specifically, there is a hierarchical organization of the brain networks into two major metastates, whose functional attributes are well separated, such that one metastate covers regions that correspond to the sensorimotor systems and perception, whereas the other relates to high cognitive functions. The evidence of temporal organization of large-scale network states in the resting brain adds to previous evidence at the microscale in both task (5) and rest (6), suggesting that this is a general characteristic of activity in human cognition that exists at a wide range of spatiotemporal scales. This perspective, and the methods used to provide it, paves the way for future investigations into the cognitive role of the temporal dependency of brain network states (e.g., in short-term memory and learning). Further, it contributes to the important debate about the feasibility of assessing dynamic functional connectivity in resting-state fMRI by showing the relation of our estimations to behavior and heritability.

Methods

Data and Preprocessing.

We used resting-state fMRI data from Ν = 820 subjects from the HCP, which provides the required ethics and consent needed for study and dissemination, such that no further institutional review board (IRB) approval is required. These are all subjects with complete resting fMRI data from the 900-subject public data release, all healthy adults (aged 22–35 y, 453 females) scanned on a 3-T Siemens connectome-Skyra. For each subject, four 15-min runs of fMRI time series data with a temporal resolution of 0.73 s and a spatial resolution of 2-mm isotropic were available. The preprocessing pipeline followed the technique of Smith et al. (18, 39), and thus will be described only briefly here. Spatial preprocessing was applied using the procedure described by Glasser et al. 40. After structured artifact removal using ICA followed by FMRIB's ICA-based X-noisefier (FIX) from the FMRIB Software Library (FSL) (41), which removed more than 99% of the artifactual ICA components in the dataset, we used group spatial ICA to obtain a “parcellation” of 50 components that covers both the cortical surfaces and the subcortical areas. We did not use global signal regression. Then, we used this parcellation to project the fMRI data into 50D time series. Such time series (size: number of participants × number of scans × number of time points × number of ICA components = 820 × 4 × 1,200 × 50) were finally standardized so that, for each scan, subject, and ICA component, the data have a mean of 0 and SD of 1.

Hidden Markov Modeling.

The HMM assumes that the time series data can be described using a sequence of a finite number of states. Each state is here represented by a multivariate Gaussian distribution, which is described by the mean and covariance. The HMM is inferred using the (publicly available) HMM-MAR (multivariate autoregressive) toolbox, which provides estimates of the parameters of the state distributions, the (group-level) transition probability matrix, and the probabilities of each state to be active at each time point (20, 42). The FOs are computed as the aggregations of these probabilities for each subject. Full details are provided in SI Methods.

Estimation and Statistical Testing On the Metastates.

The presence of the metastates were investigated in two different ways. First, the Louvain community detection algorithm (22) was used on the transition probability matrix. This method aims to find communities or nodes (here, metastates) in a graph (here, a directed, weighted graph representing the transition probability matrix), such that the connectivity between the nodes (here, states) within a community is strong with respect to the connectivity across communities. Second, we looked at the structure of the correlation matrix of the FOs, which contains the correlation for each pair of states’ FO across subjects. Full details of this and the statistical testing with behavior and heritability are provided in SI Methods.