Significance
Subcortical structures play a critical role in brain functions such as sensory perception, memory, emotion, and consciousness. There are limited options for assessing neuronal dynamics within subcortical structures in humans. Magnetoencephalography and electroencephalography can measure electromagnetic fields generated by subcortical activity. But localizing the sources of these fields is very difficult, because the fields generated by subcortical structures are small and cannot be distinguished from distributed cortical activity. We show that cortical and subcortical fields can be distinguished if the cortical sources are sparse. We then describe an algorithm that uses sparsity in a hierarchical fashion to jointly localize cortical and subcortical sources. Our work offers alternative perspectives and tools for assessing subcortical brain dynamics in humans.
Keywords: MEG, EEG, subcortical structures, source localization, sparsity
Abstract
Subcortical structures play a critical role in brain function. However, options for assessing electrophysiological activity in these structures are limited. Electromagnetic fields generated by neuronal activity in subcortical structures can be recorded noninvasively, using magnetoencephalography (MEG) and electroencephalography (EEG). However, these subcortical signals are much weaker than those generated by cortical activity. In addition, we show here that it is difficult to resolve subcortical sources because distributed cortical activity can explain the MEG and EEG patterns generated by deep sources. We then demonstrate that if the cortical activity is spatially sparse, both cortical and subcortical sources can be resolved with M/EEG. Building on this insight, we develop a hierarchical sparse inverse solution for M/EEG. We assess the performance of this algorithm on realistic simulations and auditory evoked response data, and show that thalamic and brainstem sources can be correctly estimated in the presence of cortical activity. Our work provides alternative perspectives and tools for characterizing electrophysiological activity in subcortical structures in the human brain.
Deep brain structures play important roles in brain function. For example, brainstem and thalamic relay nuclei have a central role in sensory processing (1, 2). Thalamocortical and hippocampal oscillations govern states of sleep, arousal, and anesthesia (3–8). Striatal regions are crucial for movement planning, while limbic structures like the hippocampus and amygdala drive memory, emotion, and learning (9–13). Altered signaling within the thalamus, striatum, hippocampus, and amygdala underlies pathologies such as autism, dementia, and depression (14). Much of our understanding of subcortical function comes from lesion studies and invasive electrophysiological recordings in animal models. Improved tools to characterize subcortical activity in humans would make it possible to analyze interactions between subcortical structures and other brain areas and could be used to better understand how subcortical activity relates to perception, cognition, behavior, and associated disorders.
At present, techniques for characterizing deep brain dynamics are limited. Invasive electrophysiological recordings (15) in humans are generally limited to regions that need to be monitored for clinical purposes. Functional magnetic resonance imaging (fMRI) can noninvasively measure deep brain activity with a spatial resolution of up to , but cannot record fast signals or oscillations. Magnetoencephalography (MEG) and electroencephalography (EEG) noninvasively measure fields generated by neural currents with millisecond-scale temporal resolution (16), and M/EEG source estimation (17) is widely used to spatially resolve neural dynamics to within in the cerebral cortex (18–21). However, it remains an open question whether M/EEG can be used to estimate neural currents in deep brain structures.
The anatomy of deep brain structures poses significant challenges for source estimation with M/EEG. Subcortical structures produce smaller scalp M/EEG signals because subcortical structures are farther from the scalp than cortical structures. In addition, neurons in subcortical structures can have a closed-field geometry that further weakens the fields observed at a distance (22). A second, perhaps more fundamental problem is that subcortical structures are enclosed by the cortical mantle. Thus, measurements arising from activity within deep brain structures can potentially be explained by a surrogate distribution of currents on the cortical surface. This implies that it would be very difficult to estimate subcortical activity when cortical activity is occurring simultaneously.
Clearly, if the scalp M/EEG signals generated by subcortical structures are too small to measure, it is not possible to estimate subcortical sources. But in many cases, subcortical sources do generate measurable scalp signals, and in these cases it might be possible to estimate those sources, if only their fields could be distinguished from those generated by cortical sources. In many neuroscience studies, salient cortical activity can be restricted to a set of well-circumscribed areas (23, 24). We introduce the hypothesis that if the cortical generators are sparse in this sense, it might be possible to uniquely recover both the cortical and subcortical sources.
In this paper, we analyze M/EEG field patterns generated by cortical and subcortical sources and assess the extent to which sparse cortical and subcortical sources can be distinguished. We then introduce a hierarchical sparse estimation algorithm to illustrate how we can capitalize on these concepts to characterize both cortical and subcortical activity. We demonstrate the algorithm’s performance on simulated and experimental M/EEG data containing both cortical and subcortical activity.
Theory
Neural Sources and M/EEG Fields.
Primary neural currents (25), usually modeled with an ensemble of current dipoles, generate M/EEG fields ,
| [1] |
where is the gain matrix determined by the quasistatic approximation of Maxwell’s equations, contains the amplitudes of the current dipole sources, is the noise, is the number of sensors, is the number of sources, and is the number of time points measured. To simplify notation, we assume that the data, the gain matrix, and the noise in Eq. 1 have been whitened to account for the spatial covariance of the actual observation noise (26), so that is Gaussian with zero mean and identity covariance matrix . When , we use notations and in lieu of and .
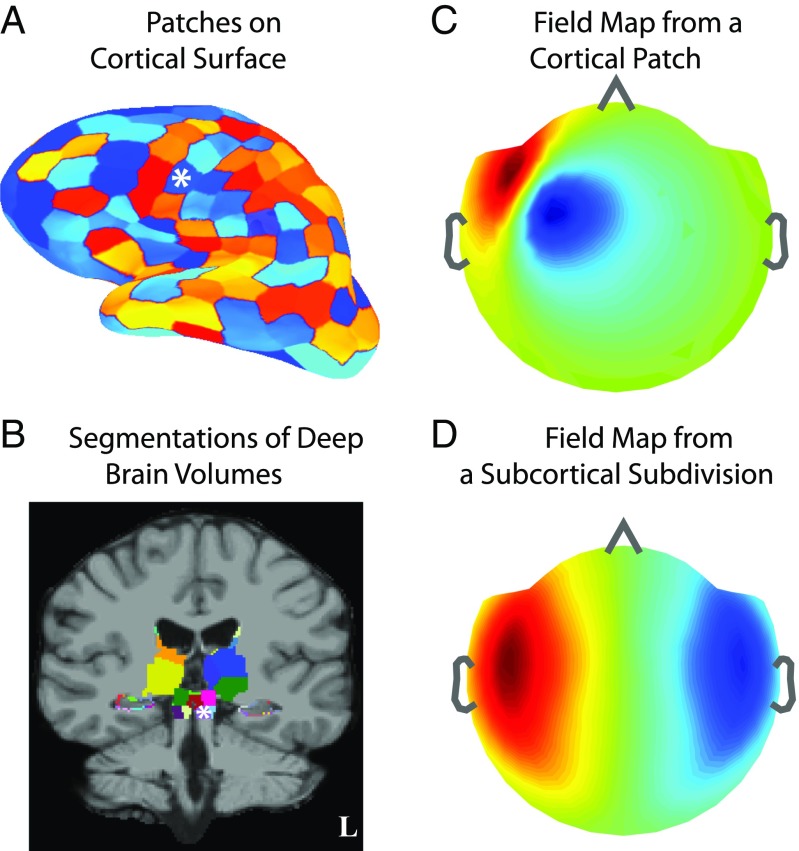
We use high-resolution structural MRIs from healthy volunteers to delineate cortical surfaces and subcortical anatomic regions to define the locations and orientations of the elementary dipole sources (Materials and Methods). We place sources on cortical surfaces and in subcortical volumes and cluster proximal groups of dipoles into surface patches or volume subdivisions sized to homogenize signal strengths (Materials and Methods; Fig. 1 A and B; and SI Appendix, section SI I and Fig. S1). The resulting set of patches and subdivisions, together called divisions, constitutes the distributed brain source space.
Fig. 1.
Illustration of source spaces and field patterns. (A) Cortical source space comprising patches (sized ) on the gray–white matter surface interface. (B) Subcortical source space comprising volume subdivisions (sized ) in the caudate, putamen, amygdala, thalamus, brainstem, and surface patches (sized ) on hippocampus. (A and B) The set of cortical and subcortical divisions forms the full distributed source space. (C and D) Example of noiseless MEG field pattern arising from activity in a frontotemporal cortical patch and a brainstem subdivision, respectively (white asterisks in A and B). Inflated surfaces and field maps have a left–right convention opposite to the MRI views. (C vs. D) Cortical fields tend to have more focal spatial patterns, while subcortical fields tend to be more distributed.
We can then group the columns of and rows of according to these divisions and rewrite Eq. 1 as
| [2] |
where and denote the gain matrix and source currents within the th division, respectively. We compute for each division in and decompose it into a set of eigenmodes (Materials and Methods). We denote gain matrices and source currents for a set of divisions by , respectively. Fig. 1 C and D illustrates field patterns for one cortical and one subcortical division.
Fields Generated by Subcortical Sources Can Be Explained by Currents on the Cortex.
To analyze distinctions between subcortical and cortical fields, we investigated the extent to which MEG field patterns arising from subcortical currents can be explained by cortical surrogates.
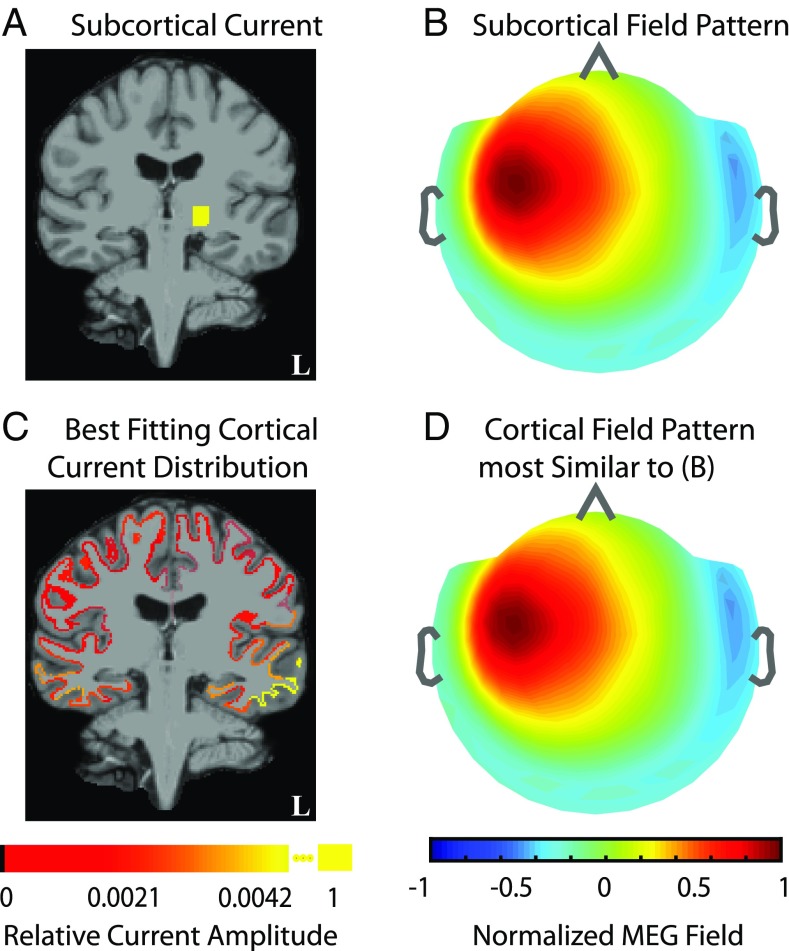
We simulated field pattern corresponding to unit current in the VPL thalamus (Fig. 2 A and B) and assessed whether could be explained by some distribution of cortical source currents. Specifically, we fitted the subcortical field pattern with cortical sources; i.e., we computed the cortical minimum-norm estimate to explain . We found that the resulting currents are small and broadly distributed across several cortical patches (Fig. 2C). Further, the goodness of fit between the field pattern for the cortical estimate (Fig. 2D) and was , showing that can be explained by some combination of sources in the full dense cortical space.
Fig. 2.
Fields generated by subcortical sources can be explained by currents on the cortex. (A and B) Example of unit source current in left ventroposterolateral (VPL) thalamus (sized ) and the corresponding noiseless MEG field pattern. (C and D) Distribution of currents on cortical surface patches (sized ) that reproduce the MEG field pattern generated by the subcortical source. C and D show the fitted cortical currents and MEG field pattern. The source current plots in A vs. C are the resultant currents from dipoles within a subdivision. The field maps in B and D are normalized. The fitted cortical field pattern is indistinguishable from the simulated subcortical pattern. This analysis illustrates how a subcortically generated field can be explained by some distribution of cortical currents.
Analysis of Forward Solutions.
To generalize the above result, we used principal angles (27, 28) to characterize the relationship between the cortical and subcortical field patterns. Principal angles quantify the correlation between linear subspaces, in this case the space spanned by MEG fields arising from sources in different cortical and subcortical regions. For the example in Fig. 2, the maximum principal angle between subspaces spanned by the subcortical and cortical gain matrices was . Further, the maximum principal angle between any subcortical gain matrix and the cortical gain matrix was . We conclude that the presence of the full cortical source space makes it impossible to unambiguously estimate currents in simultaneously active subcortical sources.
Sparsity Makes It Possible to Distinguish Fields from Subcortical and Cortical Sources.
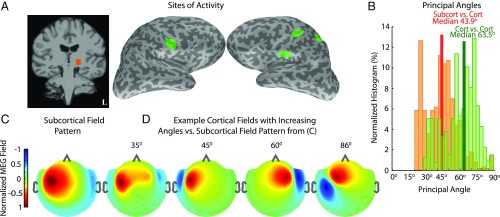
We next studied the extent of subspace correlation when subcortical sources are active together with only a small subset of cortex. As an example, we examined the scenario of median-nerve somatosensory stimulation, which elicits activity in ventroposterolateral (VPL) thalamus, primary and secondary sensory cortices (S1, S2), and posterior parietal cortex (PPC) (29), and analyzed forward solutions for a source space encompassing these brain areas (Fig. 3A).
Fig. 3.
Sparsity makes it possible to distinguish fields from subcortical and cortical sources. (A) Sources of activity derived from stimulation of the right median nerve: left VPL thalamus, primary and secondary somatosensory areas (S1, bilateral S2), and posterior parietal cortex (PPC). (B) Normalized histogram of principal angles, which quantify the correlation between fields arising from all representative combinations of activity within this neurophysiological source space. The orange histogram shows the distribution of subcortical vs. cortical angles, while the green histogram shows the distribution of cortico-cortical angles. (C) MEG field pattern resulting from activity in VPL thalamus. (D) Representative fields from example cortical source sets, whose gain matrices have the indicated principal angles with the subcortical gain matrix, that best fit the subcortical field pattern in C. All field map color scales are normalized to emphasize the spatial patterns. The spatial profiles of the cortical and subcortical MEG field patterns are distinct, even for a principal angle of , and substantially so for principal angles >45°. These distinctions suggest the feasibility of resolving simultaneous subcortical and cortical activity.
Specifically, we considered all possible configurations of subcortical and cortical currents in these divisions, computed principal angles between the subcortical and cortical gain matrices corresponding to each possible configuration (Materials and Methods), and plotted the distribution of angles (Fig. 3B). A large proportion of the principal angles are high (median ), indicating that many different configurations of activity within the sparse cortical and subcortical divisions can be distinguished from one another. We also computed principal angles for all mutually exclusive configurations of activity within the cortical divisions in Fig. 3A and found comparable principal angles (median ). Therefore, in principle, the problem of distinguishing subcortical sources from sparse cortical sources is similar in difficulty to that of distinguishing sparse cortical sources from one another. We also illustrate typical subcortical and cortical field patterns (Materials and Methods) for source current configurations corresponding to the various angles in this distribution (Fig. 3 C and D). Subcortical and cortical field patterns with principal angles as low as are clearly distinguishable.
This example represents a conservative scenario, but illustrates an approach for characterizing the extent to which subcortical sources can be resolved for any given cortical source distribution. We also found similar trends for other more general cases (SI Appendix, section SI II and Figs. S2 and S3). These results lead us to conclude that spatial sparsity constraints can enable distinctions between cortical and subcortical field patterns. Based on this analysis, we introduce and test an inverse algorithm that uses a sparse cortical representation to achieve localization of simultaneous subcortical and cortical activity.
Inverse Algorithm
Electromagnetic Inverse Problem.
The electromagnetic inverse problem is to estimate source currents underlying M/EEG data , given forward gain matrix for divisions distributed across the brain. This inverse problem is commonly solved using the linear minimum-norm estimator (MNE),
| [3] |
where is an estimate of , and the MNE estimator is a function of . The performance of can be assessed using the resolution matrix
| [4] |
The ideal corresponds to a which exactly recovers the current locations and amplitudes, in the absence of noise (30). In practice, source estimates are biased and more extended than the true sources. This nonideal behavior can be analyzed using the spatial dispersion (SD) and dipole localization error (DLE) metrics (31) (Materials and Methods), which indicate how far the inverse solution for a given source spreads from the actual source location. We analyze the performance of the MNE on the subcortical and cortical source estimation problems and describe our proposed inverse algorithm.
Estimation Performance—Distributed Cortical and Subcortical Sources.
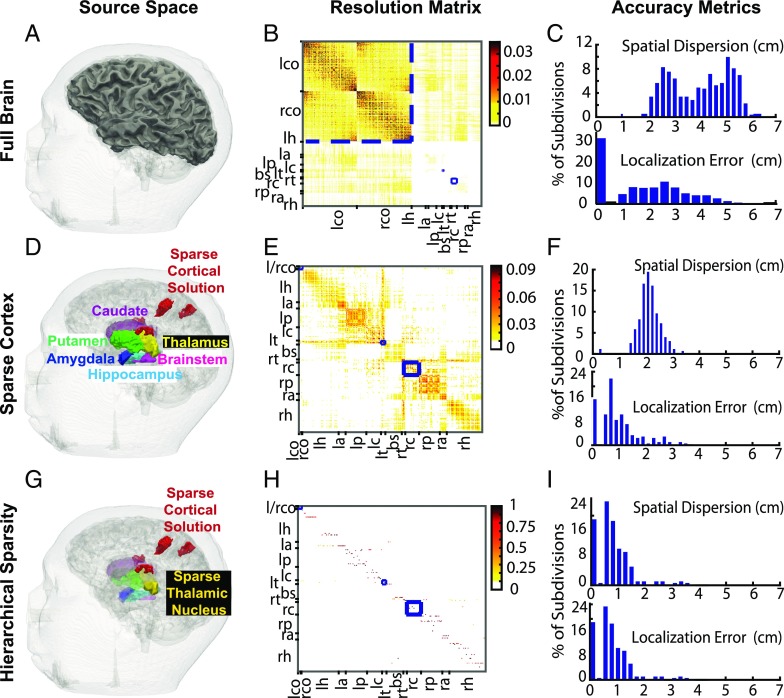
We first considered the problem of estimating neural currents in a set of divisions distributed across both cortical and subcortical structures in the brain (Fig. 4A). Fig. 4B shows the MNE resolution matrix . We found that estimates for the cortical sources concentrate around the diagonal (Fig. 4B, upper left), implying good resolution for cortical sources. On the other hand, estimates for subcortical sources have low amplitudes on the diagonal and instead spread to cortical sources (Fig. 4B, upper right and lower left). Fig. 4C shows the distribution of SD and DLE across all divisions. The median SD is (close to the radius of the human brain), and the median DLE is . The cortical DLE is ∼ and the subcortical DLE is in the 2- to 3-cm range. These findings are consistent with our principal angle analyses (Fig. 2).
Fig. 4.
An analysis of how sparsity and hierarchy influence subcortical source estimation. (A) Illustration of all brain divisions considered. (B) Minimum-norm estimator (MNE) resolution matrix for the source space in A. (C) Summary dispersion and error metrics for the resolution matrix in B. Cortical estimates concentrate around the diagonal (low localization error), whereas subcortical estimates spread significantly to the cortex (high spatial dispersion). (D) A reduced space composed of sparse cortical regions that generate somatosensory evoked potentials combined with all subcortical volumes. (E and F) MNE resolution matrix and associated performance metrics for the reduced source space in D. The sparse subset of the cortical source space allows subcortical activity to be estimated, albeit with significant spread to nondiagonal regions. (G) Final sparse cortical and subcortical source regions identified using an inverse solution employing sparsity constraints. The faded subcortical regions show the hierarchically reduced subcortical source space, while the foreground subcortical regions show estimated sources in the thalamus. (H and I) Empirical resolution matrix (one active source per column) and associated performance metrics for the sparse solution. Estimates mostly concentrate on and around the diagonal for both cortical and subcortical sources. B, E, and H show left/right (l/r) cortex (l/rco), hippocampus (r/lh), amygdala (r/la), putamen (r/lp), caudate (r/lc), thalamus (r/lt), and brainstem (bs). All resolution matrices order sources based on physical proximity. Therefore, when sources are estimated accurately, the resolution matrix has a diagonal appearance. The blue boxes are used to delineate the position of the cortical, left thalamic, and right caudate sources in the resolution matrices. The changes in the color-scale range highlight the 3−10× increase in recovered source amplitude when sparse estimation is applied across progressively refined hierarchies. Overall, hierarchical sparsity enables focal spatial resolution with minimal dispersion (or point spread) for inverse solutions incorporating both cortical and subcortical sources.
Estimation Performance—Sparse Cortical and Distributed Subcortical Sources.
Earlier we found the principal angles improve when only sparse subsets of cortical sources are active alongside deep sources (Fig. 3). Therefore, we assessed whether the resolution of the MNE inverse solution improves similarly. We considered the somatosensory stimulation example from Fig. 3 and constructed a composite source space comprising the sparse cortical divisions in Fig. 3A alongside all subcortical divisions (Fig. 4D). Fig. 4E shows the MNE resolution matrix . We see that the estimates for subcortical sources do not spread significantly to the cortex (Fig. 4E, low values for upper right and lower left). However, the estimates for subcortical sources tend to spread across the subcortical source space (Fig. 4E, lower right, off-diagonal portions). Fig. 4F shows the resolution error metrics across all divisions in . The median SD is , and the median DLE is . This is an improvement from the previous case, but still not as accurate as needed to resolve many subcortical sources. Given a sparse cortical source space as a starting point, we anticipate that it might be possible to use a subsequent sparse estimation step to reduce spread among subcortical sources.
Estimation Performance—Sparse Cortical and Sparse Subcortical Sources.
Sparse estimation procedures based on -norm minimization, projection pursuit, and/or Bayesian theory are effective at pruning out spurious features, while identifying relevant sparse features in noisy high-dimensional problems (32–35). We have recently shown that subspace pursuit can accurately estimate multiple sparse cortical sources underlying MEG data (36). Thus, we assessed whether a similar subspace pursuit algorithm could reduce the spread among spurious subcortical sources and enable improved resolution for subcortical source estimates.
We continue with our analysis of the resolution matrix in the composite source space (Fig. 4G, faded background), this time with subspace pursuit. Since the subspace pursuit algorithm is nonlinear, a closed-form resolution matrix in the sense of Eq. 4 does not exist; thus the performance of subspace pursuit must be characterized empirically instead. To this end, we simulated unit currents in each division within , one at a time, to generate corresponding noiseless field patterns . Then, for each , we performed subspace pursuit and constructed an empirical resolution matrix (Materials and Methods). The resulting matrix, shown in Fig. 4H, has a near-diagonal structure for the majority of cortical and subcortical sources. Moreover, Fig. 4I shows SD and DLE, across all divisions in . The median SD and DLE are the same and equal to . This is a substantial improvement over previous solutions that do not use sparsity constraints (Fig. 4H vs. Fig. 4 C and E).
Hierarchical Subspace-Pursuit Inverse Algorithm.
The above results suggest that it is possible to resolve both cortical and subcortical sources by applying sparsity in both domains. In previous work, we developed a sparse estimation algorithm for cortical divisions (36), in which sets of cortical divisions were nested in successively finer resolutions (i.e., smaller patches or divisions), and subspace pursuit was applied to derive sparse estimates in successively finer resolutions, which formed a hierarchy from coarse to fine resolution. We therefore intuited that subcortical sources could be viewed as an additional, ultimate step in this hierarchical refinement process, achieved by adding a set of subcortical divisions to the final set of sparse cortical sources and applying subspace pursuit.
Inverse Algorithm.
Inputs: Data , distributed gain matrix , and target sparsity level .
Notation: Denote the distributed cortical and subcortical source spaces as , respectively. Denote as the set of brain divisions whose estimated neural currents best explain data .
-
1.
Do subspace pursuit on the distributed cortical source space : .
-
2.
Construct in a finer subdivision of cortical patches.
-
3.
Repeat subspace pursuit on the coarse-to-fine hierarchy of cortical source spaces : .
-
4.
Construct the composite space of sparse cortical sources and distributed subcortical sources: .
-
5.
Repeat subspace pursuit on the composite sparse space : , where 1.
Outputs: Cortical and subcortical source locations ; and the estimated time courses of neural currents at these locations .
Subspace pursuit (steps 1, 3, and 5).
For a source space comprising a subset of brain divisions with gain matrices , subspace pursuit (SP) estimates the locations and time courses of neural currents to explain data series :
| [5] |
The pursuit procedure finds a sparse subset of dictionary that best explains data , computes residuals remaining to be explained, and iterates to find new relatively uncorrelated subsets of that best explain these residuals, until all matching subsets of are found (34–36) (SI Appendix, section SI III).
Hierarchical construction (steps 2 and 4).
We first apply SP on a distributed cortical source space to identify the subset of cortical divisions that best explain the measured fields. Then, to improve accuracy of this sparse subset of cortical sources, we perform SP across a coarse-to-fine hierarchy of cortical source spaces (36) (SI Appendix, Fig. S4). Subsequently, we construct a composite space of the sparse cortical source estimates and distributed subcortical sources and use SP on this composite sparse space to identify the subset of subcortical and cortical sources that best explain the data. This process of using sparse estimation across increasingly refined hierarchies enables systematic reduction of the distributed source space and the gain matrix: pruning out sources not important for explaining the data, implicitly decorrelating the columns of the gain matrix, and concentrating estimates into subsets of the brain whose neural currents best explain the data. Overall, given data , distributed gain matrix , and target sparsity level , the hierarchical SP algorithm identifies the sparse subset that specifies locations for both cortical and subcortical sources and estimates the time courses of neural currents at those locations.
Data Examples
We illustrate the performance of the algorithm by analyzing noisy evoked response simulations and experimental data. First, we preprocess the measurements and estimate the noise covariance matrix . Next, we use the MRI data to construct the distributed source space, i.e., brain divisions , and compute the forward solutions . Then, we use the hierarchical SP inverse algorithm to estimate the locations and time courses of sources that best explain the M/EEG data. We perform all data analyses at the individual subject level. We specify the target sparsity level for SP empirically, based on a conservative approximation of the expected number of active divisions. We maintain across the cortical hierarchies and increase it by a factor of for the final hierarchy, i.e., the composite hybrid source space comprising sparse cortical sources and distributed subcortical sources. Estimates displayed in this section are obtained at the final hierarchy level . We note that specifies the number of eigenmodes included in the sparse solution and that currents from a given patch or subdivision may be represented by more than one eigenmode. As a result, the number of subdivisions seen on the topographical maps may be less than .
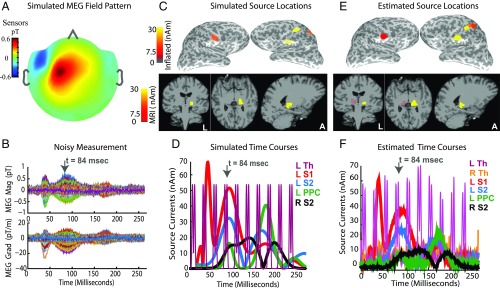
Somatosensory Evoked Simulations.
We simulated MEG evoked responses mimicking those elicited by electrical stimulation of the right median nerve at the wrist. Fig. 5 A and B illustrates the spatial and temporal features of simulated fields in the sensor space. The simulated fields include additive Gaussian noise, with a signal-to-noise ratio (SNR) of , similar to resting eyes-open recordings. Fig. 5 C and D display the spatial and temporal patterns of simulated currents in the source space. Specifically, the evoked responses comprise early currents in the left somatosensory region of thalamus (L Som Th), followed by currents in the left primary somatosensory cortex (L S1, near the postcentral gyrus), and later currents in the left PPC (L PPC) and bilateral secondary somatosensory cortices (L/R S2). The simulated thalamic current time course has a periodic on/off pattern up to poststimulus. This pattern was chosen to assess source estimation performance for the challenging case of phasic, temporally overlapping subcortical and cortical activity. We note that the MEG fields arising from thalamic source currents (e.g., in Fig. 5B) lie below the observation noise and are significantly smaller than those arising from cortical currents (e.g., in Fig. 5B).
Fig. 5.
Sparse hierarchical estimates recover simulated somatosensory responses. (A and B) Spatial distribution and time courses (one color per channel) of simulated MEG fields in sensor space. (C and D) Spatial distribution and time courses of simulated source currents in source space. Inflated views show sources located in somatosensory (S1, S2) and parietal (PPC) cortices. MRI views show thalamic source locations. The sagittal section passes through the left thalamus. The somatosensory thalamus (Th) is activated in a periodic on/off pattern. (D vs. B) While the cortical source currents contribute large-amplitude MEG signals, fields due to thalamic sources are not visible above the simulated noise. (E and F) Spatial distribution and time courses of estimated source currents in the source space. All topographical snapshots are at (top gray arrows in time-course plots), the color scales and slice locations are the same in C–E, and all source currents are plotted in terms of the resultant magnitudes across dipoles within each region in the key. (E and F vs. C and D) Estimated source locations and time courses closely match the simulated ground truth. The thalamic source estimate follows the true phasic on/off pattern. Although there is a stray source estimate in right thalamus, it is weak and relatively constant over time. In SI Appendix, Figs. S6 and S7 compare the performance of our algorithm to alternatives that do not use sparsity and hierarchy.
For source estimation, we used a source space different from that used for the simulation, to recreate a scenario closer to what might occur in practice, in which the true generating sources and the source space parcellation might not correspond. We set the sparsity level to and for the cortical and hybrid hierarchies, respectively. The procedure refines source current estimates across cortical hierarchies (SI Appendix, Fig. S5) and culminates in the final hybrid hierarchy . The final spatial distributions and time courses of estimated source currents (Fig. 5 E and F) closely resemble those of the simulated ground truth (Fig. 5 C and D) for both cortical and subcortical sources. The estimated left thalamic time course in Fig. 5F matches the simulation in shape and phase and further is not contaminated by leakage from cortical sources.
Further, we found that our algorithm offers significant gains in performance compared with other methods that do not use principles of sparsity and hierarchy (SI Appendix, Figs. S6 and S7). We conclude that both sparsity and hierarchy are necessary to accurately resolve locations and time courses of the thalamic source currents (SI Appendix, Fig. S6). Further, using sparsity in a hierarchical fashion helps recover the true distribution of mean source activity across anatomic regions (SI Appendix, Fig. S7).
Auditory Evoked Response Experiments.
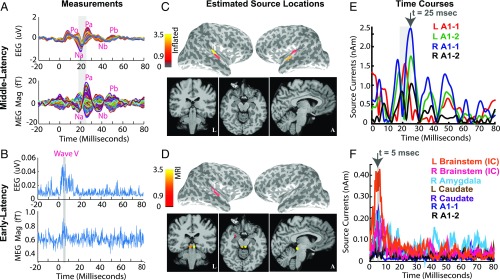
We recorded auditory evoked responses elicited by binaural stimulation with a train of clicks (37, 38) during the resting eyes-open condition simultaneously with MEG and EEG. Auditory responses comprise distinct M/EEG peaks at established latencies corresponding to a progression of activity from the cochlea, through the inferior colliculus in the brainstem, to the auditory cortex (37), and thus serve as a suitable test case for validating a subcortical source estimation algorithm.
The M/EEG evoked responses are shown in Fig. 6 A and B. We see early auditory brainstem response (ABR) peaks in both EEG and MEG at and , a low-amplitude Po feature in the EEG at , and prominent midlatency response (MLR) peaks Na-Pa in MEG and EEG channels at poststimulus. The ABR peaks are consistent with the brainstem wave V known to arise from the inferior colliculus (IC), the Po feature marks the end of brainstem components, and the Na-Pa peaks correspond to cortical responses known to arise in the auditory cortex (37).
Fig. 6.
Cortical and subcortical source estimates for evoked auditory responses. Stimulus-locked average auditory evoked responses were recorded from a healthy volunteer presented with a broadband click train stimulus. Time courses are averages across epochs filtered between 500 Hz and 1,625 Hz for the auditory brainstem response (ABR), and between 30 Hz and 300 Hz for the middle latency response (MLR). (A) MLR time courses displayed across channels, one color per channel. Red labels denote common peaks occurring at the expected poststimulus latencies. The Na and Pa peaks (shaded gray section) are particularly prominent. (B) ABR time courses rectified and averaged across channels. The shaded gray section marks the 5.0- to 6.5-ms period poststimulus, when peaks consistent with ABR wave V appear in the recordings. (C and E) Sparse cortical estimates for middle-latency recordings (: snapshots at (top black arrow, E). The activity is localized to the Heschl’s gyrus and superior temporal gyrus, consistent with auditory cortical processing. The source time courses from these areas have peaks consistent with the Na and Pa peaks in the scalp recordings in A. (D and F) Sparse hierarchical estimates for early-latency recordings (, obtained using a source space comprised of sparse subsets of cortex in C and the distributed subcortical space. The spatial plots display the source activity at (top black arrow, F). The activity is localized primarily to the inferior colliculus. A weak stray source is also seen in right amygdala. The brainstem source time courses show peaks consistent with the ABR wave V peaks in B. The color scales and slice locations are maintained for topographical snapshots across C and D, and all source currents are resultant magnitudes across dipoles within each region in the key. The color scales in C and D have units nAm and , respectively. Overall, our sparse hierarchical algorithm recovers cortical and subcortical sources consistent with the auditory stimuli presented. SI Appendix, Fig. S10 compares the performance of our algorithm to alternatives that do not use sparsity and hierarchy.
We performed hierarchical SP and set sparsity levels to and for the cortical and hybrid hierarchies, respectively. Fig. 6 C and E shows localization of the 18- to 25-ms Na-Pa MLR peaks to bilateral auditory cortices and the associated time courses. The auditory areas compose the reduced cortical source space, which, along with the distributed subcortical sources, forms the hybrid source space for estimation of deep sources underlying the ABR data. Fig. 6 D and F illustrates the localization of the wave V ABR peaks to bilateral ICs. Although the recorded wave V peaks do not have very high SNR, the source time course at the IC peaks at and drops off after , as expected. Consistent results in another subject are shown in (SI Appendix, Fig. S9). We compared performance to algorithms that do not use sparsity and hierarchy (SI Appendix, Fig. S10) and found that hierarchical SP is necessary to estimate specific subcortical sources even for filtered recordings containing temporally separated early latency responses.
Discussion
The extent to which subcortical activity can be estimated from M/EEG measurements has been a controversial subject. Our key finding is that the M/EEG fields from subcortical sources can be distinguished from those generated by the cortex when the underlying cortical activity is sparse, i.e., limited to a subset of cortical regions. In this scenario, the problem of distinguishing subcortical from cortical sources has a similar level of ambiguity to that of resolving different cortical sources. To demonstrate how this insight might be practically applied, we developed a sparse hierarchical algorithm to estimate both sparse cortical and subcortical sources.
It is known that deep and superficial sources exhibit different M/EEG field patterns (39), but the degree to which this information could be used to resolve multiple distributed subcortical and cortical sources has remained unclear. Analyses of cortical and subcortical field patterns assuming that entire structures can be simultaneously active have provided evidence for substantial correlation (40), consistent with our Fig. 2. However, we reasoned that it would be unlikely to observe synchronous activity, the major determinant of MEG/EEG (41), simultaneously within the entirety of cortex and any given subcortical structure. Thus, we analyzed sparse subdivisions of cortical and subcortical structures and found clear distinctions in the ensuing field patterns (Fig. 3). Although previous work and the data presented here show that cortical and subcortical sources cannot, in general, be unambiguously resolved, we found that if the distribution of cortical and subcortical sources is sparse, the problem becomes tractable.
These observations motivated us to create a hierarchical SP inverse algorithm to find the set of sparse cortical and subcortical sources that best explain the M/EEG data. Our analyses of various source estimators (Fig. 4) showed that our algorithm has a performance superior to alternatives for the subcortical structures and similar to existing approaches for the cortical structures (36, 42–45).
If the locations of activity in cortical and subcortical structures are known, and each active area can be modeled with an equivalent current dipole, linear least squares can be used to estimate source current time courses (46, 47). However, fitting the locations of multiple dipolar sources usually requires tailored and often interactively guided fitting strategies. Our approach, on the other hand, automatically finds the constellation of sources in a variety of conditions, including those where the source activities may overlap in time. Further, instead of isolated current dipoles we use concise distributed dipole representations within relevant subcortical anatomical subdivisions. Other methods, such as magnetic field tomography (48) and the linearly constrained minimum-variance beamformer (49, 50), that have been applied to locate deep sources implicitly, use some of the principles we formalize here. Our analyses on simulated and experimental data show that algorithms using both sparsity and hierarchy can resolve simultaneously active cortical and subcortical sources under realistic low SNR conditions (Figs. 5 and 6).
Our algorithm relies on being able to specify, at least approximately, the sparsity level for the cortical and subcortical sources. This parameter can be set based on domain knowledge of the number of expected sources. In this work, we chose conservative values for exceeding the true or expected level of sparsity and found that the algorithm performed well. In cases where prior domain knowledge does not reasonably exist, formal model selection methods such as cross-validation could be used to choose . Several recent publications have proposed sparsity-based algorithms for M/EEG cortical source estimation (20, 21, 36, 51–61). These and other methods (62) might also be applied in a hierarchical fashion to estimate both cortical and subcortical sources. Further, techniques using distributed sparse representations and dynamical sparsity constraints could be used to estimate subcortical sources in conditions involving more extended areas of cortex (63, 64).
Our analysis implies that sparsity is not merely an assumption, but rather a crucial requirement for cortical and subcortical sources to be jointly estimated. The key question to answer is the extent to which the cortical fields can be distinguished from those of potential subcortical sources. Since the cortical areas that participate will vary according to the task, fulfillment of this requirement must be evaluated on case-by-case basis. Notably, even in complex cognitive tasks such as picture naming (23) and viewing or mimicking of lip forms (24), salient activity can be limited to a small number of regions. In each of these regions the source may be focal (well represented by a dipole) or extended (a cortical patch). The methods we have presented in this paper illustrate one approach for characterizing the extent to which subcortical activity can be recovered using M/EEG.
Materials and Methods
MRI and M/EEG Acquisition.
We acquired MRI and M/EEG data from four healthy subjects aged . All subjects provided written informed consent. All studies were approved by the Human Research Committee at Massachusetts General Hospital. Data from one subject were used for the principal angles analysis and simulations. We recorded auditory evoked fields in three other subjects. In one subject, technical problems made the data unusable. For each subject, we obtained T1-weighted structural MRI, a -channel MEG, and a -electrode EEG recording (SI Appendix, section SI I).
Source Space Construction.
We used FreeSurfer to reconstruct neocortical and hippocampal surfaces and segment subcortical volumes from the MRI (65–67). We placed dipoles with orientations normal to the triangulated surface mesh for neocortex and hippocampus at the gray–white matter interface, with spacing. We placed triplets of orthogonal dipoles in subcortical volumes covering the thalamus, putamen, caudate, brainstem (midbrain), and amygdala, at voxel spacing. To reduce the dimensionality of the source space, we grouped neighboring cortical dipoles into “patches” (68–70). We grouped neighboring subcortical dipoles into “subdivisions” sized to produce signals with similar amplitudes to the cortical patches (SI Appendix, section SI I). For cortical patches with an average area of , this sizing procedure resulted in subcortical subdivisions with volumes ranging from 175- to 1,800- (Fig. 1B). Regions with higher current density have finer divisions (higher resolution) than those with low current density (e.g., divisions in striatum vs. divisions in thalamus).
Forward Solutions.
We derived a three-compartment boundary-element model from the MRI data and numerically computed forward solutions using the MNE software package (68, 69). To account for the different sensor types, units, and noise levels in the M/EEG measurements, we whitened the gain matrices, using an estimate of the observation noise covariance matrix (69). For MEG simulation studies, we set the noise covariance matrix to be similar to typical resting eyes-open recordings, , where and . For M/EEG experimental studies, we estimated noise covariance matrices from the resting eyes-open data. To account for differences in current strength across brain divisions, we scaled gain matrices for each division by the regional current strengths (71) (SI Appendix, section SI I). We constructed the reduced-dimensionality M/EEG gain matrices for each division , using a singular value decomposition, retaining components to capture of the total spectral energy (36, 70).
Analysis of Forward Solutions.
We simulated the field pattern for a division by activating the most significant eigenmode of with a unit current. We assessed the degree to which the field pattern could be explained by some distribution of currents in a region ) by fitting to , using the regularized minimum-norm criterion. We computed , setting the regularization parameter to . We then quantified the goodness of fit between the best-fitting field patterns, and the original pattern , as . For visualization of the fields, we dewhitened and mapped it to a virtual grid of magnetometers distributed evenly across the Elekta helmet (72).
We used principal angles (27, 28) to quantify the correlation between putative field patterns arising from currents in two nonoverlapping regions: and . We define a configuration of currents in a collection of patches or subdivisions as a combination of eigenmodes from those patches or subdivisions. Any putative field pattern arising from a configuration of currents in is defined by some subset of the eigenmodes of the gain matrix . If comprises eigenmodes, there are subsets of eigenmodes collectively corresponding to all possible current configurations within . Similarly, for region , the gain matrix comprises eigenmodes, and there are subsets of eigenmodes collectively corresponding to all possible current configurations within . The degree to which a field pattern arising from any current configuration in can be explained by a field pattern arising from any current configuration in is specified by the set of principal angles between each subset of and each subset in . We computed the set of principal angles across all combinations of subsets of and .
The principal angles analysis does not account for the gains of the eigenmodes. To ensure that the principal angles histogram is not biased toward smaller eigenmodes, we confined the histogram to include only those subsets of and that contained the largest eigenmodes from each patch or subdivision. To illustrate how the principal angles correspond to field patterns with varying levels of similarity, we selected a representative combination of eigenmodes and having angles , , , and ; generated the field ; projected (minimum -norm) to ; and plotted the most similar to .
Analysis of Resolution Matrices for Inverse Solutions.
We used the resolution matrix to assess performance of the minimum -norm (MNE) and SP inverse solutions. The MNE solution for the distributed source space , with prewhitened gain matrix , is . We specified the prior source covariance so that , set (72), and computed the MNE resolution matrix (30). We used a similar process to compute the MNE resolution matrix . The SP estimates for the source space , with prewhitened gain matrix , were obtained using the procedure in SI Appendix, section SI III. We characterized the SP resolution matrix empirically. We simulated unit currents in the most significant eigenmode of each brain division and used the gain matrix to generate the noiseless (prewhitened) MEG fields . We then used SP to estimate the source location and computed the source current , using a least-squares fit of to . The estimated and together specify the locations and magnitudes of the nonzero elements of the empirical resolution matrix . As , only the element of column of is nonzero. In the resolution matrices, we ordered the sources according to their physical proximity to each other. Therefore, when sources are estimated accurately, the resolution matrix has a diagonal appearance. We used the resolution matrices and to compute the spatial dispersion and the dipole localization error , where and is the distance between centroids of divisions and (31).
Source Estimation Algorithm.
At each hierarchy level, we performed source estimation using the SP algorithm in ref. 36, modified to use relaxed mutual coherence thresholds. The mutual coherence thresholds were set equal to the mean-max correlation among gain matrices from neighborhoods of brain divisions under consideration. Our relaxed mutual coherence thresholds adapt to changing levels of gain matrix correlation across hierarchy levels, giving correlation thresholds in the range. Additional details are in SI Appendix, section SI III, Table S2, and Fig. S4.
Somatosensory Evoked Response Simulations.
We simulated activity in five regions of interest: a volume in the left somatosensory thalamus including the ventral posterior area and four - to surface patches in primary and secondary somatosensory cortices and the posterior parietal area. The simulated cortical current time courses were Gabor atoms of the form , where , , and denote the amplitude, delay, and width of the evoked component and were set based on previous studies (15, 36, 58). The simulated thalamic current time course consisted of repetitions of with , , duration , and repetition period . We simulated currents over a time range of , with sampling rate. We calculated the MEG signals using the MRI-based forward model and added white Gaussian observation noise with mean zero and variance specified to achieve a SNR of .
Auditory Evoked Response Recordings.
We recorded M/EEG simultaneously while presenting binaural broadband click trains ( duration, intensity, interstimulus interval, click rate) as subjects rested with eyes open (38, 73). We preprocessed the data, performed stimulus-locked averaging to compute the ABR and the MLR, estimated observation noise covariances using the filtered baseline recordings (38) (SI Appendix, Fig. S8), whitened the filtered MEG and EEG data using their respective noise covariances, and used both MEG and EEG for source estimation. Further details are in SI Appendix, section SI IV.
Materials Availability.
All code and data from this paper are shared online on our MNE website: martinos.org/mne.
Supplementary Material
Acknowledgments
We acknowledge data collection assistance from Samantha Huang, Stephanie Rossi, and Tommi Raij; helpful discussions on source space construction with Koen Van Leemput, Imam Aganj, Doug Greve, and Bruce Fischl; and helpful discussions on canonical correlations and sparsity with Demba Ba and Emery N. Brown. This work was supported by NIH Grants P41-EB015896, 5R01EB022889, and 5R01-EB009048, NIH Grant 1S10RR031599-01 (to M.S.H.), and NIH Grant DP2-OD006454 (to P.L.P.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1705414114/-/DCSupplemental.
References
- 1.Jones EG. The thalamic matrix and thalamocortical synchrony. Trends Neurosci. 2001;24:595–601. doi: 10.1016/s0166-2236(00)01922-6. [DOI] [PubMed] [Google Scholar]
- 2.Jones EG. Thalamic circuitry and thalamocortical synchrony. Philos Trans R Soc Lond B Biol Sci. 2002;357:1659–1673. doi: 10.1098/rstb.2002.1168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Steriade M, McCormick DA, Sejnowski TJ. Thalamocortical oscillations in the sleeping and aroused brain. Science. 1993;262:679–685. doi: 10.1126/science.8235588. [DOI] [PubMed] [Google Scholar]
- 4.Buzsaki G. Theta oscillations in the hippocampus. Neuron. 2016;33:325–340. doi: 10.1016/s0896-6273(02)00586-x. [DOI] [PubMed] [Google Scholar]
- 5.Ching S, Cimenser A, Purdon PL, Brown EN, Kopell NJ. Thalamocortical model for a propofol-induced alpha-rhythm associated with loss of consciousness. Proc Natl Acad Sci USA. 2010;107:22665–22670. doi: 10.1073/pnas.1017069108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Steriade M, Contreras D, Amzica F, Timofeev I. Synchronization of fast (30-40 hz) spontaneous oscillations in intrathalamic and thalamocortical networks. J Neurosci. 1996;16:2788–2808. doi: 10.1523/JNEUROSCI.16-08-02788.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Crunelli V, Hughes SW. The slow rhythm of non-REM sleep: A dialogue between three cardinal oscillators. Nat Neurosci. 2010;13:9–17. doi: 10.1038/nn.2445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Hughes SW, Crunelli V. Thalamic mechanisms of EEG alpha rhythms and their pathological implications. Neuroscientist. 2005;11:357–372. doi: 10.1177/1073858405277450. [DOI] [PubMed] [Google Scholar]
- 9.Graybiel AM. The basal ganglia. Curr Biol. 2000;10:509–511. [Google Scholar]
- 10.Alexander GE, DeLong MR, Strick PL. Parallel organization of functionally segregated circuits linking basal ganglia and cortex. Annu Rev Neurosci. 1986;9:357–381. doi: 10.1146/annurev.ne.09.030186.002041. [DOI] [PubMed] [Google Scholar]
- 11.Haber SN. The primate basal ganglia: Parallel and integrative networks. J Chem Neuroanat. 2003;26:317–330. doi: 10.1016/j.jchemneu.2003.10.003. [DOI] [PubMed] [Google Scholar]
- 12.Phelps EA, LeDoux JE. Contributions of the amygdala to emotion processing: From animal models to human behavior. Neuron. 2005;48:175–187. doi: 10.1016/j.neuron.2005.09.025. [DOI] [PubMed] [Google Scholar]
- 13.Douglas RJ, Pribram KH. Learning and limbic lesions. Neuropsychologia. 1966;4:197–220. [Google Scholar]
- 14.Blumenfeld H. Neuroanatomy Through Clinical Cases. 2nd Ed Sinauer; Sunderland, MA: 2010. [Google Scholar]
- 15.Schomer DL, da Silva FL, editors. Electroencephalography: Basic Principles, Clinical Applications and Related Fields. 6th Ed. Lippincott Williams & Wilkins; Philadelphia: 2010. pp. 669–724. [Google Scholar]
- 16.Hämäläinen MS. Magnetoencephalography - theory, instrumentation, and applications to noninvasive studies of the working human brain. Rev Mod Phys. 1993;65:413–505. [Google Scholar]
- 17.Baillet S, Mosher JC, Leahy RM. Electromagnetic brain mapping. IEEE Signal Process Mag. 2001;18:14–30. [Google Scholar]
- 18.Dale A, Sereno M. Improved localization of cortical activity by combining EEG and MEG with MRI cortical surface reconstruction: A linear approach. J Cogn Neurosci. 1993;5:162–176. doi: 10.1162/jocn.1993.5.2.162. [DOI] [PubMed] [Google Scholar]
- 19.Dale AM, et al. Dynamic statistical parametric mapping: Combining fMRI and MEG for high-resolution imaging of cortical activity. Neuron. 2000;26:55–67. doi: 10.1016/s0896-6273(00)81138-1. [DOI] [PubMed] [Google Scholar]
- 20.Ou W, Hämäläinen MS, Golland P. A distributed spatio-temporal EEG/MEG inverse solver. Neuroimage. 2009;44:932–946. doi: 10.1016/j.neuroimage.2008.05.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Gramfort A, Strohmeier D, Haueisen J, Hämäläinen MS, Kowalski M. Time-frequency mixed-norm estimates: Sparse M/EEG imaging with non-stationary source activations. Neuroimage. 2013;70:410–422. doi: 10.1016/j.neuroimage.2012.12.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Attal Y, Schwartz D. Assessment of subcortical source localization using deep brain activity imaging model with minimum norm operators: An MEG study. PLoS One. 2013;8:e59856. doi: 10.1371/journal.pone.0059856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Salmelin R, Hari R, Lounasmaa OV, Sams M. Dynamics of brain activation during picture naming. Nature. 1994;368:463–465. doi: 10.1038/368463a0. [DOI] [PubMed] [Google Scholar]
- 24.Nishitani N, Hari R. Viewing lip forms: Cortical dynamics. Neuron. 2002;36:1211–1220. doi: 10.1016/s0896-6273(02)01089-9. [DOI] [PubMed] [Google Scholar]
- 25.Hari R, Ilmoniemi R. Cerebral magnetic fields. Crit Rev Biomed Eng. 1986;14:93–126. [PubMed] [Google Scholar]
- 26.Engemann D, Gramfort A. Automated model selection in covariance estimation and spatial whitening of MEG and EEG signals. Neuroimage. 2015;108:328–342. doi: 10.1016/j.neuroimage.2014.12.040. [DOI] [PubMed] [Google Scholar]
- 27.Bjorck A, Golub GH. Numerical methods for computing angles between linear subspaces. Math Comput. 1973;27:579–594. [Google Scholar]
- 28.Knyazev AV, Argentati ME. Principal angles between subspaces in an A-based scalar product: Algorithms and perturbation estimates. SIAM J Sci Comput. 2002;23:2008–2040. [Google Scholar]
- 29.Forss N, et al. Activation of the human posterior parietal cortex by median nerve stimulation. Exp Brain Res. 1994;99:309–315. doi: 10.1007/BF00239597. [DOI] [PubMed] [Google Scholar]
- 30.Liu AK, Belliveau JW, Dale AM. Spatiotemporal imaging of human brain activity using functional MRI constrained magnetoencephalography data: Monte Carlo simulations. Proc Natl Acad Sci USA. 1998;95:8945–8950. doi: 10.1073/pnas.95.15.8945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Molins A, Stufflebeam SM, Brown EN, Hämäläinen MS. Quantification of the benefit from integrating MEG and EEG data in minimum L2-norm estimation. Neuroimage. 2008;42:1069–1077. doi: 10.1016/j.neuroimage.2008.05.064. [DOI] [PubMed] [Google Scholar]
- 32.Friedman JH, Tukey J. A projection pursuit algorithm for exploratory data analysis. IEEE Trans Comput. 1973;23:881–890. [Google Scholar]
- 33.Huber P. Projection pursuit. Ann Stat. 1985;13:435–475. [Google Scholar]
- 34.Needell D, Tropp JA. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples. Appl Comput Harmonic Anal. 2009;26:301–321. [Google Scholar]
- 35.Dai W, Milenkovic O. Subspace pursuit for compressive sensing signal reconstruction. IEEE Trans Inform Theor. 2009;55:2230–2249. [Google Scholar]
- 36.Babadi B, et al. A subspace pursuit-based iterative greedy hierarchical solution to the neuromagnetic inverse problem. NeuroImage. 2014;87:427–443. doi: 10.1016/j.neuroimage.2013.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pockett S. Anesthesia and the electrophysiology of auditory consciousness. Conscious Cognit. 1999;61:45–61. doi: 10.1006/ccog.1998.0373. [DOI] [PubMed] [Google Scholar]
- 38.Parkkonen L, Fujiki N, Makela JP. Sources of auditory brainstem responses revisited: Contribution by magnetoencephalography. Hum Brain Mapp. 2009;30:1772–1782. doi: 10.1002/hbm.20788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Williamson S, Kaufman L. Biomagnetism. J Magnetism Magn Mater. 1981;22:129–201. [Google Scholar]
- 40.Attal Y, et al. Modeling and detecting deep brain activity with MEG & EEG. Proc Annu Int Conf IEEE Eng Med Biol Soc. 2007;2007:4937–4940. doi: 10.1109/IEMBS.2007.4353448. [DOI] [PubMed] [Google Scholar]
- 41.Hämäläinen M, Hari R. Toga AW, Mazziotta JC. Brain Mapping, The Methods. Academic; San Diego: 2002. [Google Scholar]
- 42.Nunez PL. Neocortical Dynamics and Human EEG Rhythms. 1st Ed Oxford Univ Press; New York: 1995. [Google Scholar]
- 43.Mosher JC, Spencer ME, Leahy RM, Lewis PS. Error bounds for EEG and MEG dipole source localization. Electroencephalogr Clin Neurophysiol. 1993;86:303–321. doi: 10.1016/0013-4694(93)90043-u. [DOI] [PubMed] [Google Scholar]
- 44.Sekihara K, Sahani M, Nagarajan SS. Localization bias and spatial resolution of adaptive and non-adaptive spatial filters for MEG source reconstruction. Neuroimage. 2005;25:1056–1067. doi: 10.1016/j.neuroimage.2004.11.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nunez PL, Srinivasan R. Electric Fields of the Brain: The Neurophysics of EEG. 2nd Ed Oxford Univ Press; New York: 2006. [Google Scholar]
- 46.Tesche CD. Non-invasive imaging of neuronal population dynamics in human thalamus. Brain Res. 1996;729:253–258. [PubMed] [Google Scholar]
- 47.Tesche CD. Non-invasive detection of ongoing neuronal population activity in normal human hippocampus. Brain Res. 1997;749:53–60. doi: 10.1016/s0006-8993(96)01286-3. [DOI] [PubMed] [Google Scholar]
- 48.Ioannides AA, et al. Magnetic field tomography of cortical and deep processes: Examples of ‘real-time mapping’ of averaged and single trial MEG signals. Int J Psychophysiol. 1995;20:161–175. doi: 10.1016/0167-8760(95)00031-3. [DOI] [PubMed] [Google Scholar]
- 49.Kensuke Sekihara SSN. Adaptive Spatial Filters for Electromagnetic Brain Imaging. Springer; Berlin: 2008. [Google Scholar]
- 50.Crespo-Garcia M, et al. Slow-theta power decreases during item-place encoding predict spatial accuracy of subsequent context recall. Neuroimage. 2016;142:533–543. doi: 10.1016/j.neuroimage.2016.08.021. [DOI] [PubMed] [Google Scholar]
- 51.Gorodnitsky I, George J, Rao B. Neuromagnetic source imaging with FOCUSS: A recursive weighted minimum norm algorithm. Electroencephalogr Clin Neurophysiol. 1995;95:231–251. doi: 10.1016/0013-4694(95)00107-a. [DOI] [PubMed] [Google Scholar]
- 52.Mosher JC, Leahy RM. Recursive music: A framework for EEG and MEG source localization. IEEE Trans Biomed Eng. 1998;45:1342–1354. doi: 10.1109/10.725331. [DOI] [PubMed] [Google Scholar]
- 53.Uutela K, Hämäläinen M, Somersalo E. Visualization of magnetoencephalographic data using minimum current estimates. Neuroimage. 1999;10:173–180. doi: 10.1006/nimg.1999.0454. [DOI] [PubMed] [Google Scholar]
- 54.Durka PJ, Matysiak A, Montes EM, Sosa PV, Blinowska KJ. Multichannel matching pursuit and EEG inverse solutions. J Neurosci Methods. 2005;148:49–59. doi: 10.1016/j.jneumeth.2005.04.001. [DOI] [PubMed] [Google Scholar]
- 55.Friston K, et al. Multiple sparse priors for the M/EEG inverse problem. NeuroImage. 2008;39:1104–1120. doi: 10.1016/j.neuroimage.2007.09.048. [DOI] [PubMed] [Google Scholar]
- 56.Vega-Hernandez M, Martinez-Montes E, Sanchez-Bornot J, Lage-Castellanos A, Valdes-Sosa P. Penalized least squares methods for solving the EEG inverse problem. Stat Sin. 2008;18:1535–1551. [Google Scholar]
- 57.Wipf DP, Owen JP, Attias HT, Sekihara K, Nagarajan SS. Robust Bayesian estimation of the location, orientation, and time course of multiple correlated neural sources using MEG. Neuroimage. 2010;49:641–55. doi: 10.1016/j.neuroimage.2009.06.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Gramfort A, Strohmeier D, Haueisen J, Hamalainen MS, Kowalski M. Functional brain imaging with M/EEG using structured sparsity in time-frequency dictionaries. Proc Conf Inf Process Med Imaging. 2011;22:600–611. doi: 10.1007/978-3-642-22092-0_49. [DOI] [PubMed] [Google Scholar]
- 59.Gramfort A, Kowalski M, Hämäläinen MS. Mixed-norm estimates for the M/EEG inverse problem using accelerated gradient methods. Phys Med Biol. 2012;57:1937–1961. doi: 10.1088/0031-9155/57/7/1937. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Valdes-Sosa P, Vega-Hernandez M, Sanchez-Bornot JM, Martinez-Montes E, Bobes MA. EEG source imaging with spatio-temporal tomographic nonnegative independent component analysis. Hum Brain Mapp. 2009;30:1898–1910. doi: 10.1002/hbm.20784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Vega-Hernandez M, Martinez-Montes E, Sanchez-Bornot J, Lage-Castellanos A, Valdes-Sosa PA. Penalized least squares methods for solving the EEG inverse problem. Stat Sin. 2008;18:1535–1551. [Google Scholar]
- 62.Trujillo-Barreto NJ, Aubert-Vazquez E, Valdes-Sosa PA. Bayesian model averaging in EEG/MEG imaging. NeuroImage. 2004;21:1300–1319. doi: 10.1016/j.neuroimage.2003.11.008. [DOI] [PubMed] [Google Scholar]
- 63.Babadi B, Kalouptsidis N, Tarokh V. SPARLS: The sparse RLS algorithm. IEEE Trans Signal Process. 2010;58:4013–4025. [Google Scholar]
- 64.Mileounis G, Babadi B, Kalouptsidis N, Tarokh V. An adaptive greedy algorithm with application to nonlinear communications. IEEE Trans Signal Process. 2010;58:2998–3007. [Google Scholar]
- 65.Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. Segmentation and surface reconstruction. NeuroImage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- 66.Fischl B, Sereno MI, Dale AM. Cortical surface-based analysis: II. Inflation, flattening, and a surface-based coordinate system. NeuroImage. 1999;9:195–207. doi: 10.1006/nimg.1998.0396. [DOI] [PubMed] [Google Scholar]
- 67.Fischl B, et al. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- 68.Hämäläinen MS, Sarvas J. Realistic conductivity geometry model of the human head for interpretation of neuromagnetic data. IEEE Trans Biomed Eng. 1989;36:165–171. doi: 10.1109/10.16463. [DOI] [PubMed] [Google Scholar]
- 69.Gramfort A, et al. MNE software for processing MEG and EEG data. NeuroImage. 2014;86:446–460. doi: 10.1016/j.neuroimage.2013.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Limpiti T, Van Veen BD, Wakai RT. Cortical patch basis model for spatially extended neural activity. IEEE Trans Biomed Eng. 2006;53:1740–1754. doi: 10.1109/TBME.2006.873743. [DOI] [PubMed] [Google Scholar]
- 71.Attal Y, Maess B, Friederici A, David O, De C. Head models and dynamic causal modeling of subcortical activity using magnetoencephalographic/electroencephalographic data. Rev Neurosci. 2012;23:85–95. doi: 10.1515/rns.2011.056. [DOI] [PubMed] [Google Scholar]
- 72.Hämäläinen MS, Ilmoniemi RJ. Interpreting magnetic fields of the brain: Minimum norm estimates. Med Biol Eng Comput. 1994;32:35–42. doi: 10.1007/BF02512476. [DOI] [PubMed] [Google Scholar]
- 73.Makela JP, Hamalainen MS, Hari R, McEvoy L. Whole-head mapping of middle-latency auditory evoked magnetic fields. Electroencephalogr Clin Neurophysiol. 1994;92:414–421. doi: 10.1016/0168-5597(94)90018-3. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.