Significance
Using a self-propelled Voronoi model of epithelia known to predict a liquid–solid transition, we examine the interplay between cell motility and cell shape, tuned by cortex contractility and cell–cell adhesion, in controlling the mechanical properties of tissue. Our work provides a unifying framework for existing, seemingly distinct notions of stress in tissues and relates stresses to material properties. In particular, we show that the temporal correlation function of shear stresses can be used to define an effective tissue viscosity that diverges at the liquid–solid transition. This finding suggests a unique way of analyzing traction force microscopy data that may provide information on tissue rheology.
Keywords: cell stress, cell shape, vertex model, self-propelled, phase transition
Abstract
Collective cell migration is a highly regulated process involved in wound healing, cancer metastasis, and morphogenesis. Mechanical interactions among cells provide an important regulatory mechanism to coordinate such collective motion. Using a self-propelled Voronoi (SPV) model that links cell mechanics to cell shape and cell motility, we formulate a generalized mechanical inference method to obtain the spatiotemporal distribution of cellular stresses from measured traction forces in motile tissues and show that such traction-based stresses match those calculated from instantaneous cell shapes. We additionally use stress information to characterize the rheological properties of the tissue. We identify a motility-induced swim stress that adds to the interaction stress to determine the global contractility or extensibility of epithelia. We further show that the temporal correlation of the interaction shear stress determines an effective viscosity of the tissue that diverges at the liquid–solid transition, suggesting the possibility of extracting rheological information directly from traction data.
It is now broadly recognized that the transmission of mechanical forces can be as important as genetics and biochemistry in regulating tissue organization in many developmental processes, including embryogenesis, morphogenesis, wound healing, and cancer metastasis (1–12). To make quantitative predictions for large-scale cell remodeling in tissues, we must understand their material properties, such as stiffness and viscosity, as well as the forces that build up inside them, characterized by local pressures and stresses. Motivated by experiments highlighting the slow glassy dynamics of dense epithelia, work by us and others has suggested that monolayers of motile cells may form glassy or jammed states and that a relatively small change of parameters may trigger a change from an elastic response to a state with fluid-like behavior (13–15). This liquid–solid transition is tuned by the interplay of cell–cell adhesion and cortex contractility, manifested in cellular shape, and by cell motility. This suggestion has been verified experimentally in specific cell types (16), indicating that the paradigm of tissues as active materials may be a useful way of organizing experimental data and classifying large-scale tissue behavior in terms of a few effective parameters.
In contrast, quantifying stresses and pressures in active, motile tissues is largely an open problem. One possible reason is that there are different definitions of stresses and pressures that arise naturally in different experiments and simulations, and it is not immediately clear how they are related to one another or under which conditions each definition applies. For example, traction force microscopy (TFM) is a powerful tool that probes the dynamic forces cells exert onto soft substrates by measuring the substrate deformations (10, 11, 17–19). In some experiments, intercellular stresses are extracted from the traction forces, using finite-element analysis under the condition that traction forces are balanced by cellular interactions. The resulting stress maps reveal a highly dynamical and heterogeneous mechanical landscape, characterized by large spatial and temporal fluctuations in both normal and shear stresses (6, 10, 11, 18, 20). A key assumption used in the TFM approach to infer stresses from tractions is that the cell layer can be described as a continuum linear elastic material (18).
A second important set of mechanical inference methods also predicts cellular stresses, but in static tissues. These methods rely on advances in imaging techniques that provide a spatially resolved view of tissue development during morphogenesis, with visualization of the cell boundaries of 2D cell sheets (21–25). Assuming mechanical equilibrium, one can then infer the tensions along cell edges and pressures within each cell from the cell configurations. This method provides a spatial distribution of intercellular stresses and directly couples mechanics to morphology, but it does not capture temporal stress fluctuations arising from the nonequilibrium nature of the tissue. It has been used successfully to characterize cell morphology in the development of the Drosophila wing disk (23, 26), where cellular rearrangements are slow on the timescales of interest, demonstrating that the analysis of cell shapes can provide fundamental insight on the mechanical state of tissues in developmental processes.
A third line of research has focused on the homeostatic pressure that tissues exert on their containers or surroundings. The homeostatic pressure has been proposed as a quantitative measure of the metastatic potential of a tumor (27, 28). It is defined as the force per unit area that a confined tissue would exert on a moving piston permeable to fluid, and hence it represents an active osmotic cellular pressure. The existing literature has focused on the contribution to the homeostatic pressure from tissue growth due to cell division and death, but in general other active processes, such as cell motility and contractility, will also contribute to the forces exerted by living tissues on confining walls. A related body of work has investigated the pressures generated by motile particles, such as active colloids. In these highly nonequilibrium systems that break time-reversal symmetry, there is a contribution to the total pressure called the swim pressure generated entirely by persistent motility (29–31).
So far, there is no unifying theory for these seemingly distinct notions of pressure and stress or their relationship to material properties. In this paper, we show that a recently proposed self-propelled Voronoi (SPV) model of epithelia (Fig. 1) (15) provides a natural framework for unifying these ideas. One of the benefits of the SPV model is that it explicitly accounts for the forces that motile cells exert on the substrate. This allows us to develop a generalized mechanical inference method to infer cellular stresses from traction forces and to show that these match the stresses calculated from instantaneous cell shape, relating TFM data and mechanical inference techniques in motile tissues. Additionally, our method provides absolute values for junctional tensions and pressure differences. This is in contrast to equilibrium mechanical inference, which yields only relative forces (21, 23).
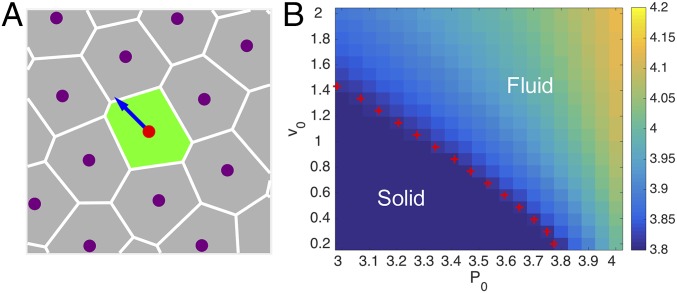
Fig. 1.
(A) Illustration of the SPV model, where cells are represented by polygons obtained via a Voronoi tessellation of initially random cell positions, with a self-propulsion force applied at each cell position. (B) Phase diagram in the plane based on the value of the shape parameter (color scale), with the phase boundary (red crosses) determined by .
There are two additive contributions to the mechanical stress that describe the forces transmitted in a material across a bulk plane. The first one represents the flux of propulsive forces through a bulk plane carried by particles that move across it. The second one describes the flux of interaction forces across a bulk plane. We demonstrate that the generalized mechanical inference measurements probe the latter, which we denote interaction stresses. The former, which we denote the tissue swim stress, approximates the contribution from cell motility to the osmotic pressure generated by cells immersed in a momentum-conserving solvent on a semipermeable piston and hence to the tissue homeostatic pressure. The tensorial sum of the swim stress and the interaction stress is the total stress. The normal component of the total stress determines whether a tissue will tend to exert extensile or contractile forces on its environment, which is an important consideration in wound healing and cancer tumorigenesis.
An obvious open question, then, is how these stresses vary as a function of material properties. We find that the normal component of the interaction stress is contractile in both the solid and the liquid due to the contractility of the actomyosin cortex, although much more weakly so in the liquid state. In contrast, the normal component of the motility-induced swim stress is always extensile, corresponding to a positive swim pressure, although its magnitude depends on the phase: In a solid the swim pressure is negligible, while in the fluid it can be significant. This can result in a change in sign of the total mean stress: Indeed, we find it is always contractile in the solid state but becomes extensile deep in the liquid state when cell motility exceeds actomyosin contractility.
Because the transition from contractile to extensile does not coincide with the fluid to solid transition, it is natural to ask whether the stress displays any signatures of the fluid–solid transition. We develop a definition for the effective viscosity of the tissue that can be extracted from the temporal correlation of the interaction shear stress and find that it diverges as the tissue transits from the liquid state to the solid state. Importantly, this theoretical prediction suggests that TFM combined with mechanical inference can provide rheological information about the tissue and could be tested by a new analysis of experimental data.
Results and Discussion
SPV Model.
The SPV model describes an epithelium as a network of polygons. Each cell is endowed with a position vector , and cell shape is defined by the Voronoi tessellation of all cell positions (Fig. 1), which has been shown to provide a good representation of some real epithelia, such as the blastoderm of the red flour beetle Tribolium castaneum and the fruit fly Drosophila melanogaster (32). Like for vertex models, tissue forces are obtained from an effective energy functional for cells, given by (7, 15, 26, 33, 34)
| [1] |
with and the cross-sectional area and perimeter of the th cell, respectively. The first term in Eq. 1 arises from incompressibility of the layer in three dimensions and its resistance to height fluctuations, with a preferred cross-sectional area. The second term represents the competition between cortical tensions from the actomyosin network at the apical surface and cell–cell adhesions from adhesive complexes at intercellular junctions (26), with a preferred perimeter resulting from this competition. We simulate cells in a square box of area , with the average cell area and with periodic boundary conditions. The system is initialized with a set of random cell positions, independently drawn from a uniform distribution. Throughout the simulations, we set unless otherwise noted, and .
Each Voronoi cell is additionally endowed with a constant self-propulsion speed along the direction of polarization describing cell motility. The dynamics of each Voronoi cell are governed by
| [2] |
where is the force on cell and is the mobility. The direction of cell polarization is randomized by orientational noise of rate , with and . The timescale controls the persistence of single-cell dynamics. As in self-propelled particle (SPP) models, an isolated cell performs a persistent random walk with a long-time translational diffusivity (29, 35, 36). After each time step, a new Voronoi tessellation is generated based on the updated cell positions. The cell shapes are determined in the process and the exchange of cell neighbors occurs naturally through topological transitions (13).
We showed in ref. 15 that the SPV model exhibits a transition from a solid-like state to a fluid-like state upon increasing the single-cell motility , the persistence time , or the cell shape parameter that characterizes the competition between cell–cell adhesion and cortical tension. The phase diagram in the plane is reproduced in Fig. 1B. The transition is identified by setting the shape index to the value , where denotes the average over all cells. It was shown in ref. 15 that the transition line located by coincides with the one based on the vanishing of the effective diffusivity obtained from the cellular mean-square displacement. Note that for fixed system size and cell number , the preferred cell area does not affect the interaction forces or cellular shapes. Hence the solid–fluid transition is insensitive to , as shown analytically in SI Text. The preferred area only shifts the total pressure of the tissue by a constant.
Developing and Validating Traction-Based Mechanical Inference.
It is well established that in a model tissue described by the energy Eq. 1 , the mechanical state of cell is characterized by a local stress tensor given by (21, 23, 37)
| [3a] |
| [3b] |
where is the hydrostatic cellular pressure and is the cell-edge tension, with . Here we use Roman indexes to label cells and to label vertices, while Greek indexes denote Cartesian components. The summation in Eq. 3a runs over all edges of cell , and is the edge vector joining vertices and when the perimeter of cell is traversed clockwise, as shown in Fig. S1A. The factor of in the second term on the right-hand side of Eq. 3a is due to the fact that each edge is shared by two cells. We have used the convention that the cellular stress is positive when the cell is contractile and negative when the cell is extensile. Contractile stress means that if the cell is cut off from its neighbors, it tends to contract, consistent with the contractility of the actomyosin network within the cell.
Note that in a vertex model the interaction stress as defined in Eq. 3a is indeed the stress acting on the tissue boundary. This is, however, not the case for the Voronoi model because the Voronoi construction introduces constraints not present in the vertex model. We have verified that the differences are small (SI Text) and in the following use Eq. 3a as a good approximation for the Voronoi model.
Our goal is to obtain the distribution of cellular stresses in a layer of motile cells, where cellular configurations do not minimize the tissue energy, but are governed by the dynamics described by Eq. 2. In this case, as discussed in the Introduction, the local cellular stress can be written as the sum of contributions from interactions and propulsive forces as
| [4] |
where, following recent work on active colloids (29, 30),
| [5] |
describes the flux of propulsive force across a boundary, calculated from a virial expression. The negative sign in Eq. 5 ensures that the swim stress follows the same convention as the interaction stress, i.e., is positive for contractile stress and negative for extensile stress. The swim stress is proportional to the cell motility and vanishes for nonmotile cells. The contribution is still given by Eq. 3a, but depends implicitly on cell motility through the instantaneous values of and that are determined not by energy minimization, but by the system dynamics governed by Eq. 2. From the local stresses one can then obtain the total mean stress in the tissue as (SI Text) , with
| [6] |
In simulations where the energy functional is known, it is simple to directly extract the instantaneous pressures and tensions from cell shapes to calculate the interaction contribution . The definitions, Eq. 3b, give
| [7] |
where is the cell–cell interface that separates cells and . Both and are obtained at every time step of the simulation and implicitly depend on cell motility, parameterized by speed and persistence . This method directly infers the interaction stress from instantaneous cell shape fluctuations through Eq. 3a, yielding what we call shape-based stresses. While easily implemented numerically, this method is of limited use in experiments where the energy functional is not known and likely more complicated.
For this reason we develop a new mechanical inference method for motile monolayers that attempts to approximate the interaction stresses using only information that is accessible in experiments. Specifically, the proposed traction-based mechanical inference infers tensions and pressures from segmented images of cell boundaries and traction forces obtained by TFM. In the SPV model, we define the traction force at each vertex as the gradient of the tissue energy with respect to the vertex position , which balances the interaction force . Equilibrium mechanical inference methods express the interaction force at each vertex in terms of cellular pressures and edge tensions and the measured geometry of the cellular network (Eqs. S6–S8). Pressures and edge tensions are then obtained by inverting the equations . For a nonequilibrium epithelial layer of motile cells we invert the force balance equations
| [8] |
where the edge tensions have been written as the sum of cortical tensions of adjacent cells (Eq. S7), reducing the number of independent unknowns. The interaction contribution to the local cellular stresses is then calculated using Eq. 3a. A constraint counting yields force balance equations for variables, rendering the system overdetermined, which requires the implementation of a least-squares minimization for the mechanical inference (SI Text).
The equations developed thus far require knowledge of the tractions at each vertex, which is again not realistic in experiments. Therefore, we have developed and implemented a coarse-grained version of this approach that uses experimentally accessible traction forces averaged over a square grid, with a grid spacing of the order of a cell diameter. Pressures and tensions are then calculated by inverting the force balance equation at the center of each grid element,
| [9] |
An outline of the coarse-graining procedure is given in SI Text. We refer to stresses inferred from Eq. 9 as traction-based stresses. We emphasize that the traction-based stress from mechanical inference is generally different from the intercellular stress obtained with monolayer stress microscopy (MSM), which rests upon the assumption that the tissue is an isotropic, homogeneous, and linearly elastic material (18). The mechanical inference does not make such assumptions and is compatible with any epithelia whose cell–cell interactions can be decomposed into tensions at cell junctions and pressures within cell bodies. Examples include Drosophila ectoderm (9) and mesoderm (25), Drosophila wing disk (26), and Madin–Darby canine kidney (MDCK) epithelium (12).
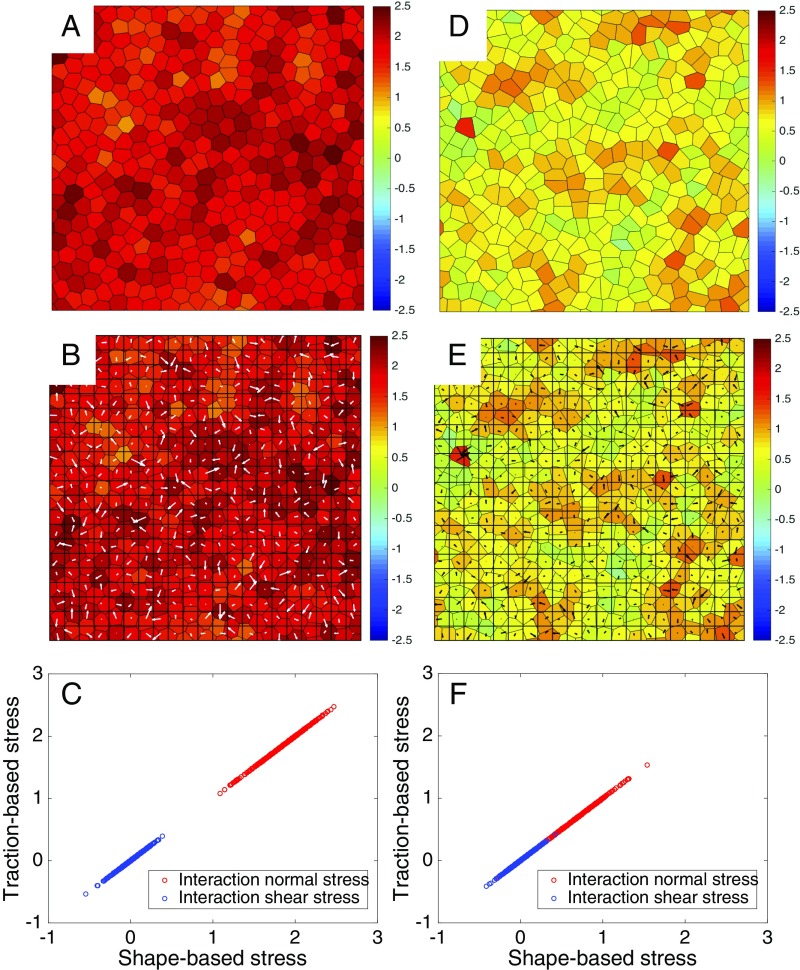
Within the framework of the SPV model, we have validated the coarse-grained method by showing that the resulting traction-based stresses agree with the shape-based stresses computed exactly from the simulations (Fig. 2 C and F).
Fig. 2.
Comparison of shape-based and coarse-grained traction-based stress. (A–C) Solid state at , . (D–F) Liquid state at , . (A and D) Interaction normal stress calculated from the instantaneous cell shapes obtained from Eqs. 3a and 7. Red denotes positive (contractile) stress and blue negative (extensile) stress. (B and E) Interaction normal stress calculated using the coarse-grained traction-based mechanical inference by inverting Eq. 9 and using Eq. 3a. The arrows denote the traction forces. (C and F) The coarse-grained traction-based mechanical inference is validated by plotting the traction-based stress against the shape-based stress in the solid (C) and in the liquid (F) state. The data are for cells in a square box of side with and with periodic boundary condition.
Stress Characterizes Rheological Properties of the Tissue.
To study the mechanical properties of motile confluent tissues, we simulate a confluent cell layer with periodic boundary conditions, using the SPV model. By examining the temporal correlations of the mean stress in the tissue, as defined in Eq. 6, we show that the tissue displays distinct mechanical properties in the liquid and the solid states. Thus, mechanical measurements such as those provided by TFM can be used to characterize the rheological properties of the tissue.
The stress tensor is symmetric and has three independent components in two dimensions. Both the mean and local stress components are most usefully expressed in terms of normal stress , shear stress , and normal stress difference , with
| [10] |
Each of the interaction and swim contributions can similarly be split in normal, shear, and normal difference components. Below we focus on normal and shear stresses. TFM probes the forces exchanged between tissue and substrate, which by force balance are determined entirely by intercellular forces and hence by interaction stresses. In contrast, the swim components of stress and pressure cannot be probed in TFM, but contribute to the pressure that the tissue would exert laterally on a confining piston. As we show below, the swim contribution dominates the pressure in the liquid state.
Using the expression for the local stress obtained from cell shapes, the mean interaction normal stress of the tissue can be expressed entirely in terms of area and perimeter fluctuations in a virial-like form (SI Text)
| [11] |
The first term represents the interaction contribution from the pressures within the cells. The second term is the contribution from the competition between actomyosin contractility and cell–cell adhesion that controls the cortical tensions. In our simulation, the cellular pressure is suppressed by setting and the normal stress comes mainly from the cortical tensions. Eq. 11 then provides a way for extracting mechanical information directly from cell shape based on snapshots of segmented cell images.
Normal stresses are contractile in the solid phase and may become extensile deep in the liquid phase.
We show in Fig. 2 snapshots of the local interaction normal stress in the solid state (A–C) and in the liquid state (D–F). In both the solid and the liquid the interaction normal stress is on average contractile (red), with relatively weaker spatial fluctuations, but much larger mean value in the solid, where contractile cortical tension exceeds cell–cell adhesion.
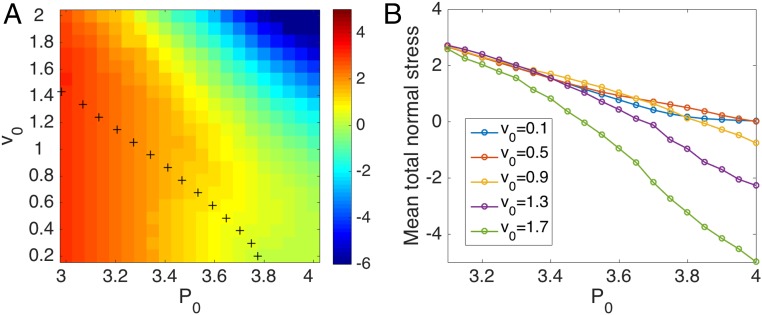
Fig. 3 displays the total mean normal stress (the separate contributions from interaction and swim stress are shown in Fig. S2) across the solid–liquid transition. The color map shows that the total normal stress is contractile in the solid and across the transition line (Fig. 3A, black crosses), but changes sign and becomes extensile deep in the liquid. While the interaction stress is always positive due to cell contractility and consistent with experimental observations (1–3, 38, the change in sign of the total stress is due to the swim stress that is zero in the solid and always negative in the liquid (Fig. S2), indicating that motility induces extensile stresses, tending to stretch the tissue. The total normal stress is analogous to the stress on a wall confining an active Brownian colloidal fluid (29, 30). We speculate that its change in sign could lead to an expansion of the tissue if released from confinement due to substrate patterning or to surrounding tissue and may contribute to epithelia expansion in wound-healing assays. In our model confinement is provided by the periodic boundary conditions.
Fig. 3.
Mean total normal stress. (A) Heat map of the mean total normal stress of the tissue in the plane. The black crosses outline the solid–liquid phase boundary determined by . Red indicates contractile stress and blue extensile stress. (B) Mean total normal stress as a function of at various , showing a change in sign deep in the liquid state ( cells for and with periodic boundary condition).
The tissue effective shear viscosity diverges at the liquid–solid transition.
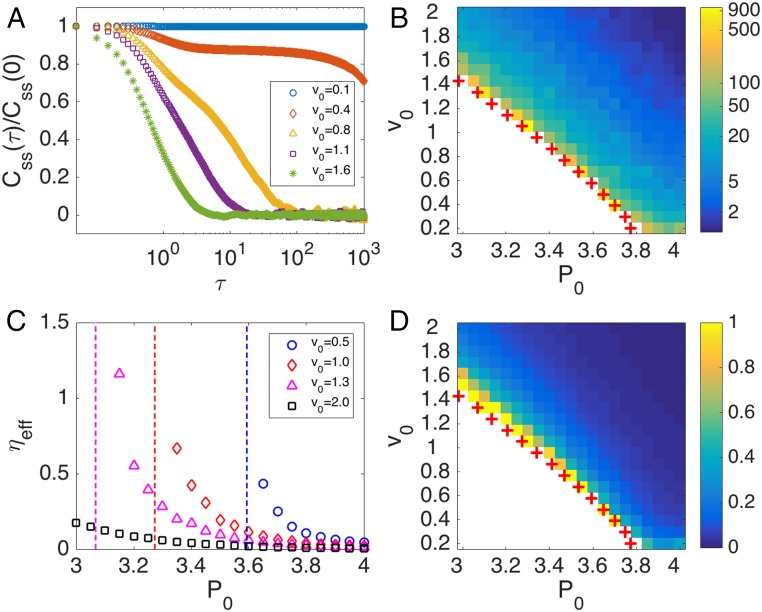
While the local shear stress averages to zero in both the liquid and the solid states, its temporal correlations provide a distinctive rheological metric for distinguishing the liquid from the solid and identifying the transition. The time autocorrelation function of the interaction shear stress,
| [12] |
where denotes the average over the length of the simulation, is shown in Fig. 4A for various across the liquid–solid transition. Shear stress correlations decay in the liquid state and slow down as the transition is approached from the liquid side, becoming frozen in the solid. To quantify this we have defined the correlation time as the time when the correlation has decreased below 1% of its initial value. This correlation time shown in Fig. 4B diverges at the liquid–solid phase transition, suggesting that shear stress autocorrelations can provide a robust metric for the transition. Our work therefore suggests that TFM combined with mechanical inference can provide a tool for the measurement of tissue rheology. Correlating such measurements with cell shape data will provide a stringent test for our theory. Finally, in the liquid state we define an effective viscosity , using a Green–Kubo-type relation by integrating the correlation function over the duration of the correlation time (41, 42),
| [13] |
where we have used the ideal gas effective temperature so that has dimensions of a shear viscosity in two dimensions. Of course the Green–Kubo relation is based on the existence of a fluctuation–dissipation theorem, which does not hold in active systems. For small values of the persistence time , however, the orientational noise in the SPV becomes uncorrelated in time and can be mapped onto thermal noise at an effective temperature . In this limit we expect to indeed play the role of a shear viscosity. Remarkably, the effective viscosity shown in Fig. 4 C and D grows as the tissue approaches the solid state from the liquid side and diverges at the transition. The effective viscosity quickly approaches zero deep in the liquid phase, suggesting that the system behaves as a gas of uncorrelated cells in this region.
Fig. 4.
Time autocorrelation of interaction shear stress and effective tissue viscosity. (A) Time autocorrelation function of the mean interaction shear stress for at various . (B and D) Heat maps of the correlation time (B) and of the effective viscosity (D). The red crosses denote the liquid–solid phase transition boundary determined by . The white region corresponds to regions where correlation time and effective viscosity diverge. Note that these regions largely coincide with the solid regime. (C) The effective viscosity as a function of at various . The dashed lines correspond to the critical where the liquid–solid phase transition occurs. All results are for cells, , and with periodic boundary condition.
Discussion and Conclusions
Using the SPV model we have formulated a unifying framework for quantifying the contributions from cell shape fluctuations and cell motility to mechanical stresses in an epithelial tissue. Cell shape fluctuations from actomyosin contractility and cell–cell adhesion control the interaction stress, while cell motility determines the swim stress that is generically present in all self-propelled systems (29, 30).
Unlike monolayer stress microscopy that computes interaction stress from traction forces by assuming the tissue to be a continuum linear elastic material (18), the traction-based mechanical inference method developed here incorporates spatial and temporal deformations of the tissue due to actomyosin contractility and cell–cell adhesion and can be generalized to account for cell division, apoptosis, and nematic/polar order of the tissue. In contrast to equilibrium mechanical inference techniques (21, 23), our approach does not require cells to be in or close to static mechanical balance, and it also provides the absolute scale of the junctional tensions and pressure differences. This can for instance be important for testing hypotheses involving mechanosensitive biomolecules. Experimentally, our method provides unique ways to extract intercellular interaction stresses from existing traction force data and segmented cell images.
The swim stress, on the other hand, cannot be measured using TFM as it represents the flux of propulsive forces across a bulk plane in the tissue. It contributes to the homeostatic pressure at the lateral boundary of the tissue. The sum of the swim stress and the interaction stress approximates the total stress at the tissue boundary, which is generally contractile but can become extensile when the tissue is deep in the liquid state and cell motility exceeds actomyosin contractility. The exact location of the transition from contractile to extensile depends on the average cellular pressure, which we fix by setting the average cell area to the preferred area, as discussed in SI Text. This change in sign may be observable in wound-healing assays where the transition from contractile to extensile behavior can result in tissue expansion upon removal of confinement by neighboring tissue.
We have extracted an effective tissue viscosity from the temporal correlation of the interaction shear stress. The correlation time and effective viscosity display a slowing down and arrest at the transition to the solid, thus serving as a direct probe of tissue rheology. Moreover, we observed a similar behavior for the temporal correlations of traction forces as demonstrated in SI Text. Therefore, our work suggests that TFM measurement (11) combined with mechanical inference could provide information on tissue rheology. To our knowledge, this has not been attempted yet on experimental data.
Our work sets the stage for examining the feedback between cell activity and tissue mechanics that is apparent in many tissue-level phenomena. Recent work has shown that mechanical stresses influence cell proliferation in tumor spheroids (28) and regulate cell growth in the developing Drosophila wing (43). Regulation of cell motility, as in contact inhibition of locomotion, has been proposed to explain stress patterns during collective cell migration (44). TFM has revealed the tendency of cells to move along the direction of minimal shear stress, a phenomenon termed “plithotaxis” (11). Our model provides a unifying framework for quantifying the relative roles of various cell properties, such as shape, motility, and growth, on the mechanics of the tissue.
Supplementary Material
Acknowledgments
We thank Daniel Sussman for valuable discussions. This work was supported by the Simons Foundation through Targeted Grant Award 342354 (to M.C.M. and M.C.) and Investigator Award 446222 (to M.L.M., M.C., and M.M.) in the Mathematical Modeling of Living Systems; by the National Science Foundation (NSF) through Awards DMR-1305184 (to M.C.M. and X.Y.), DMR-1609208 (to M.C.M.), DMR-1352184 (to M.L.M. and D.B.), and the Integrative Graduate Education and Research Traineeship (IGERT) Grant DGE-1068780 (to M.C.M. and M.C.); by the NIH through Grant R01GM117598-02 (to M.L.M.); and by the computational resources provided by Syracuse University and through NSF Grant ACI-1541396. All authors acknowledge support from the Syracuse University Soft Matter Program.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1705921114/-/DCSupplemental.
References
- 1.Lecuit T, Lenne PF. Cell surface mechanics and the control of cell shape, tissue patterns and morphogenesis. Nat Mol Cell Biol. 2007;8:633–644. doi: 10.1038/nrm2222. [DOI] [PubMed] [Google Scholar]
- 2.Heisenberg CP, Bellaiche Y. Forces in tissue morphogenesis and patterning. Cell. 2013;153:948–962. doi: 10.1016/j.cell.2013.05.008. [DOI] [PubMed] [Google Scholar]
- 3.Murrell M, Oakes PW, Lenz M, Gardel ML. Forcing cells into shape: The mechanics of actomyosin contractility. Nat Rev Mol Cell Biol. 2015;16:486–498. doi: 10.1038/nrm4012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Etournay R, et al. Interplay of cell dynamics and epithelial tension during morphogenesis of the drosophila pupal wing. eLife. 2015;4:e07090. doi: 10.7554/eLife.07090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Shraiman BI. Mechanical feedback as a possible regulator of tissue growth. Proc Natl Acad Sci USA. 2005;102:3318–3323. doi: 10.1073/pnas.0404782102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Serra-Picamal X, et al. Mechanical waves during tissue expansion. Nat Phys. 2012;8:628–634. [Google Scholar]
- 7.Staple DB, et al. Mechanics and remodelling of cell packings in epithelia. Eur Phys J E Soft Matter. 2010;33:117–127. doi: 10.1140/epje/i2010-10677-0. [DOI] [PubMed] [Google Scholar]
- 8.Guillot C, Lecuit T. Mechanics of epithelial tissue homeostasis and morphogenesis. Science. 2013;340:1185–1189. doi: 10.1126/science.1235249. [DOI] [PubMed] [Google Scholar]
- 9.Rauzi M, Verant P, Lecuit T, Lenne PF. Nature and anisotropy of cortical forces orienting drosophila tissue morphogenesis. Nat Cell Biol. 2008;10:1401–1410. doi: 10.1038/ncb1798. [DOI] [PubMed] [Google Scholar]
- 10.Trepat X, et al. Physical forces during collective cell migration. Nat Phys. 2009;5:426–430. [Google Scholar]
- 11.Tambe DT, et al. Collective cell guidance by cooperative intercellular forces. Nat Mater. 2011;10:469–475. doi: 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Puliafito A, et al. Collective and single cell behavior in epithelial contact inhibition. Proc Natl Acad Sci USA. 2012;109:739–744. doi: 10.1073/pnas.1007809109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bi D, Lopez JH, Schwarz JM, Manning ML. Energy barriers and cell migration in densely packed tissues. Soft Matter. 2014;10:1885–1890. doi: 10.1039/c3sm52893f. [DOI] [PubMed] [Google Scholar]
- 14.Bi D, Lopez JH, Schwarz JM, Manning ML. A density-independent rigidity transition in biological tissues. Nat Phys. 2015;11:1074–1079. [Google Scholar]
- 15.Bi D, Yang X, Marchetti MC, Manning ML. Motility-driven glass and jamming transitions in biological tissues. Phys Rev X. 2016;6:021011. doi: 10.1103/PhysRevX.6.021011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Park JA, et al. Unjamming and cell shape in the asthmatic airway epithelium. Nat Mater. 2015;14:1040–1048. doi: 10.1038/nmat4357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Soiné JRD, et al. Model-based traction force microscopy reveals differential tension in cellular actin bundles. PLoS Comput Biol. 2014;11:e1004076. doi: 10.1371/journal.pcbi.1004076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tambe DT, et al. Monolayer stress microscopy: Limitations, artifacts, and accuracy of recovered intercellular stresses. PLoS One. 2013;8:e55172. doi: 10.1371/journal.pone.0055172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Zimmermann J, et al. Intercellular stress reconstitution from traction force data. Biophys J. 2014;107:548–554. doi: 10.1016/j.bpj.2014.06.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kim JH, et al. Propulsion and navigation within the advancing monolayer sheet. Nat Mater. 2013;12:856–863. doi: 10.1038/nmat3689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ishihara S, Sugimura K. Bayesian inference of force dynamics during morphogenesis. J Theor Biol. 2012;313:201–211. doi: 10.1016/j.jtbi.2012.08.017. [DOI] [PubMed] [Google Scholar]
- 22.Nier V, et al. Inference of internal stress in a cell monolayer. Biophys J. 2016;110:1625–1635. doi: 10.1016/j.bpj.2016.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chiou KK, Hufnagel L, Shraiman BI. Mechanical stress inference for two dimensional cell arrays. PLoS Comput Biol. 2012;8:e1002512. doi: 10.1371/journal.pcbi.1002512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Noll N, Mani M, Heemskerk I, Streichan S, Shraiman BI. 2015. Active tension network model of epithelial mechanics. arXiv:1508.00623. [DOI] [PMC free article] [PubMed]
- 25.Brodland GW, et al. Video force microscopy reveals the mechanics of ventral furrow invagination in Drosophila. Proc Natl Acad Sci USA. 2010;107:22111–22116. doi: 10.1073/pnas.1006591107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Farhadifar R, Roper JC, Aigouy B, Eaton S, Julicher F. The influence of cell mechanics, cell-cell interactions, and proliferation on epithelial packing. Curr Biol. 2007;17:2095–2104. doi: 10.1016/j.cub.2007.11.049. [DOI] [PubMed] [Google Scholar]
- 27.Basan M, Risler T, Joanny JF, Sastre-Garau X, Prost J. Homeostatic competition drives tumor growth and metastasis nucleation. HFSP J. 2009;3:265–272. doi: 10.2976/1.3086732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Montel F, et al. Stress clamp experiments on multicellular tumor spheroids. Phys Rev Lett. 2011;107:188102. doi: 10.1103/PhysRevLett.107.188102. [DOI] [PubMed] [Google Scholar]
- 29.Yang X, Manning ML, Marchetti MC. Aggregation and segregation of confined active particles. Soft Matter. 2014;10:6477–6484. doi: 10.1039/c4sm00927d. [DOI] [PubMed] [Google Scholar]
- 30.Takatori SC, Yan W, Brady JF. Swim pressure: Stress generation in active matter. Phys Rev Lett. 2014;113:028103. doi: 10.1103/PhysRevLett.113.028103. [DOI] [PubMed] [Google Scholar]
- 31.Solon AP, et al. Pressure is not a state function for generic active fluids. Nat Phys. 2015;11:673–678. [Google Scholar]
- 32.Vazquez-Faci T, van Drongelen R, van der Zee M, Idema T. 2017. Mechanics of epithelial tissue formation in early insect embryos. arXiv:1705.06205. [DOI] [PubMed]
- 33.Barton DL, Henkes S, Weijer CJ, Sknepnek R. Active vertex model for cell-resolution description of epithelial tissue mechanics. PLoS Comput Biol. 2016;13:e1005569. doi: 10.1371/journal.pcbi.1005569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Su T, Lan G. 2016. Overcrowding drives the unjamming transition of gap-free monolayers. arXiv:1610.04254.
- 35.Henkes S, Fily Y, Marchetti MC. Active jamming: Self-propelled soft particles at high density. Phys Rev E. 2011;84:040301. doi: 10.1103/PhysRevE.84.040301. [DOI] [PubMed] [Google Scholar]
- 36.Fily Y, Marchetti MC. Athermal phase separation of self-propelled particles with no alignment. Phys Rev Lett. 2012;108:235702. doi: 10.1103/PhysRevLett.108.235702. [DOI] [PubMed] [Google Scholar]
- 37.Nestor-Bergmann A, Goddard G, Woolner S, Jensen O. 2016. A vertex-based model relating cell shape and mechanical stress in an epithelium. arXiv:1611.04744.
- 38.Bambardekar K, Clement R, Blanc O, Chardes C, Lenne PF. Direct laser manipulation reveals the mechanics of cell contacts in vivo. Proc Natl Acad Sci USA. 2015;112:1416–1421. doi: 10.1073/pnas.1418732112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rauzzi M, Lenne PF, Lecuit T. Planar polarized actomyosin contractile flows control epithelial junction remodelling. Nature. 2010;23:1110–1114. doi: 10.1038/nature09566. [DOI] [PubMed] [Google Scholar]
- 40.Kasza KE, Farrell DL, Zallen JA. Spatiotemporal control of epithelial remodeling by regulated myosin phosphorylation. Proc Natl Acad Sci USA. 2014;111:11732–11737. doi: 10.1073/pnas.1400520111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Hansen JP, McDonald I. Theory of Simple Liquids. 3rd Ed Academic; Cambridge, MA: 2006. [Google Scholar]
- 42.Levashov VA, Morris JR, Egami T. Viscosity, shearwaves, and atomic-level stress-stress correlations. Phys Rev Lett. 2011;106:115703. doi: 10.1103/PhysRevLett.106.115703. [DOI] [PubMed] [Google Scholar]
- 43.Pan Y, Heemskerk I, Ibar C, Shraiman BI, Irvine KD. Differential growth triggers mechanical feedback that elevates hippo signaling. Proc Natl Acad Sci USA. 2016;113:E6974–E6983. doi: 10.1073/pnas.1615012113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Zimmermann J, Camley BA, Rappel WJ, Levine H. Contact inhibition of locomotion determines cell-cell and cell-substrate forces in tissues. Proc Natl Acad Sci USA. 2016;113:2660–2665. doi: 10.1073/pnas.1522330113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. MathWorks (2017) Matlab R2017b documentation: Moore-Penrose pseudoinverse. https://www.mathworks.com/help/matlab/ref/pinv.html. Accessed November 7, 2017.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.