Frequent nonallelic gene conversion on the human lineage and its effect on the divergence of gene duplicates

Significance

Nonallelic gene conversion (NAGC) is a driver of more than 20 diseases. It is also thought to drive the “concerted evolution” of gene duplicates because it acts to eliminate any differences that accumulate between them. Despite its importance, the parameters that govern NAGC are not well characterized. We developed statistical tools to study NAGC and its consequences for human gene duplicates. We find that the baseline rate of NAGC in humans is 20 times faster than the point mutation rate. Despite this high rate, NAGC has a surprisingly small effect on the average sequence divergence of human duplicates—and concerted evolution is not as pervasive as previously thought.

Abstract

Gene conversion is the copying of a genetic sequence from a “donor” region to an “acceptor.” In nonallelic gene conversion (NAGC), the donor and the acceptor are at distinct genetic loci. Despite the role NAGC plays in various genetic diseases and the concerted evolution of gene families, the parameters that govern NAGC are not well characterized. Here, we survey duplicate gene families and identify converted tracts in 46% of them. These conversions reflect a large GC bias of NAGC. We develop a sequence evolution model that leverages substantially more information in duplicate sequences than used by previous methods and use it to estimate the parameters that govern NAGC in humans: a mean converted tract length of 250 bp and a probability of $2.5\times {10}^{-7}$ per generation for a nucleotide to be converted (an order of magnitude higher than the point mutation rate). Despite this high baseline rate, we show that NAGC slows down as duplicate sequences diverge—until an eventual “escape” of the sequences from its influence. As a result, NAGC has a small average effect on the sequence divergence of duplicates. This work improves our understanding of the NAGC mechanism and the role that it plays in the evolution of gene duplicates.

As a result of recombination, distinct alleles that originate from the two homologous chromosomes may end up on the two strands of the same chromosome. This mismatch (“heteroduplex”) is then repaired by synthesizing a DNA segment to overwrite the sequence on one strand, using the other strand as a template. This process is called gene conversion.

Although gene conversion is not an error but rather a natural part of recombination, it can result in the nonreciprocal transfer of alleles from one sequence to another, and can therefore be thought of as a “copy and paste” mutation. Gene conversion typically occurs between allelic regions (allelic gene conversion, AGC) (1). However, nonallelic gene conversion (NAGC) between distinct genetic loci can also occur when paralogous sequences are accidentally aligned during recombination because they are highly similar (2)—as is often the case with young tandem gene duplicates (3).

NAGC is implicated as a driver of over 20 diseases (2, 4, 5). The transfer of alleles between tandemly duplicated genes—or pseudogenes—can cause nonsynonymous mutations (6, 7), frameshifting (8), or aberrant splicing (9)—resulting in functional impairment of the acceptor gene. A recent study showed that alleles introduced by NAGC are found in 1% of genes associated with inherited diseases (5).

NAGC is also considered to be a dominant force restricting the evolution of gene duplicates (10–12). It was noticed half a century ago that duplicated genes can be highly similar within one species, even when they differ greatly from their orthologs in other species (13–16). This phenomenon has been termed “concerted evolution” (17). NAGC is an immediate suspect for driving concerted evolution, because it homogenizes paralogous sequences by reversing differences that accumulate through other mutational mechanisms (10, 13, 14, 18). Another possible driver of concerted evolution is natural selection. Both purifying and positive selection may restrict sequence evolution to be similar in paralogs (3, 11, 19–24). Importantly, if NAGC is indeed slowing down sequence divergence, it puts in question the fidelity of molecular clocks for gene duplicates (3, 25). To develop expectations for sequence and function evolution in duplicates, we must characterize NAGC and its interplay with other mutations.

In attempting to link NAGC mutations to sequence evolution, we need to know two key parameters: (i) the rate of NAGC and (ii) the converted tract length. These parameters have been mostly probed in nonhuman organisms with mutation accumulation experiments limited to single genes—typically, artificially inserted DNA sequences (26, 27). The mean tract length has been estimated fairly consistently across organisms and experiments to be a few hundred base pairs (28). However, estimates of the rate of NAGC vary by as much as eight orders of magnitude (26, 29–32)—presumably due to key determinants of the rate that vary across experiments, such as genomic location, sequence similarity of the duplicate sequences and the distance between them, and experimental variability (27, 33). Alternatively, evolutionary-based approaches (19, 34) tend to be less variable: NAGC has been estimated to be 10 to 100 times faster than point mutation in Saccharomyces cerevisiae (35), Drosophila melanogaster (36, 37), and human (19, 38–40). These estimates are typically based on single loci (but see refs. 41, 42). Recent family studies (43–45) have estimated the rate of AGC to be $5.9\times {10}^{-6}$ per base pair per generation. This is likely an upper bound on the rate of NAGC, since NAGC requires a misalignment of homologous chromosomes during recombination, while AGC does not.

Here, we estimate the parameters governing NAGC with a sequence evolution model. Our method is not based on direct empirical observations, but it leverages substantially more information than previous experimental and computational methods: We use data from a large set of segmental duplicates in multiple species, and exploit information from a long evolutionary history. We estimate that the rate of NAGC in newborn duplicates is an order of magnitude higher than the point mutation rate in humans. Surprisingly, we show that this high rate does not necessarily imply that NAGC distorts the molecular clock.

Results

To investigate NAGC in duplicate sequences across primates, we used a set of gene duplicate pairs in humans that we had assembled previously (46). We focused on young pairs where we estimate that the duplication occurred after the human–mouse split, and identified their orthologs in the reference genomes of chimpanzee, gorilla, orangutan, macaque, and mouse. We required that each gene pair have both orthologs in at least one nonhuman primate and exactly one ortholog in mouse. Since our inference methods implicitly assume neutral sequence evolution, we focused our analysis on intronic sequence at least $50$ bp away from intron–exon junctions. After applying these filters, our data consisted of $\mathrm{97,055}$ bp of sequence in $169$ intronic regions from $75$ gene families (SI Appendix).

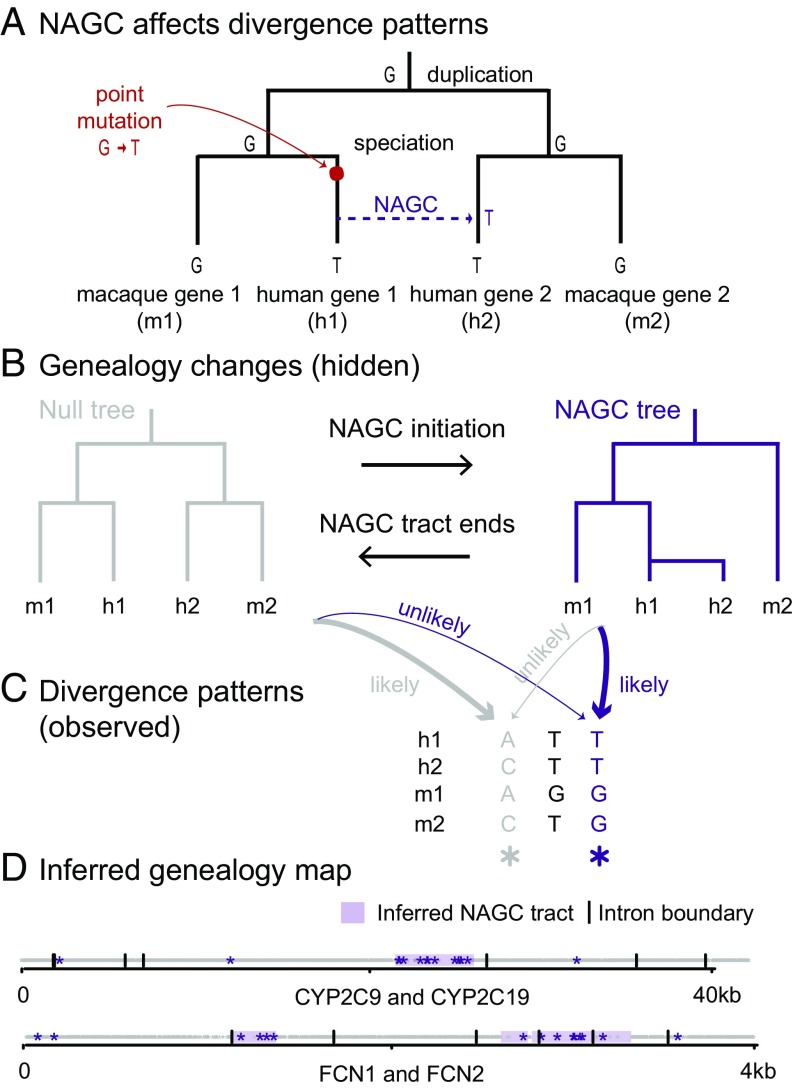
We examined divergence patterns (the partition of alleles in gene copies across primates) in these gene families. We noticed that some divergence patterns are rare and clustered in specific regions. We hypothesized that NAGC might be driving this clustering. To illustrate this, consider a family of two duplicates in human and macaque which resulted from a duplication followed by a speciation event—as illustrated in Fig. 1B (“Null tree”). Under this genealogy, we expect certain divergence patterns across the four genes to occur more frequently than others. For example, the gray sites in Fig. 1C can be parsimoniously explained by one substitution under the null genealogy. They should therefore be much more common than purple sites, as purple sites require at least two mutations. However, if we consider sites in which an NAGC event occurred after speciation (Fig. 1A and “NAGC tree” in Fig. 1B), our expectation for divergence patterns changes: Now, purple sites are much more likely than gray sites.

Fig. 1.

NAGC alters divergence patterns. (A) NAGC can drive otherwise rare divergence patterns, like the sharing of alleles between paralogs but not orthologs. (B) An example of a local change in genealogy, caused by NAGC. (C) Examples of divergence patterns in a small multigene family. Some divergence patterns—such as the one highlighted in purple—were both rare and spatially clustered. We hypothesized that underlying these changes are local changes in genealogy, caused by NAGC. (D) Genealogy map (null genealogy marked by white, NAGC marked by purple tracts) inferred by our HMM based on observed divergence patterns (stars). Two different gene families are shown. For simplicity, only the most informative patterns (purple and gray sites, as exemplified in C) are plotted.

Mapping Recent NAGC Events.

We developed a Hidden Markov Model (HMM) which exploits the fact that observed local changes in divergence patterns may point to hidden local changes in the genealogy of a gene family (Fig. 1 B and C). In our model, genealogy switches occur along the sequence at some rate; the likelihood of a given divergence pattern at a site then depends only on its own genealogy and nucleotide substitution rates. Our method is similar to others that are based on incongruency of inferred genealogies along a sequence (47–49), but it is model-based and robust to substitution rate variation across genes (SI Appendix).

We applied the HMM to a subset of the gene families that we described above: families of four genes consisting of two duplicates in human and a nonhuman primate. Since the HMM assumes that the duplication preceded the speciation, we required that the overall intronic divergence patterns support this genealogy, using the software MrBayes (50). This requirement decreased the number of gene families considered to 39.

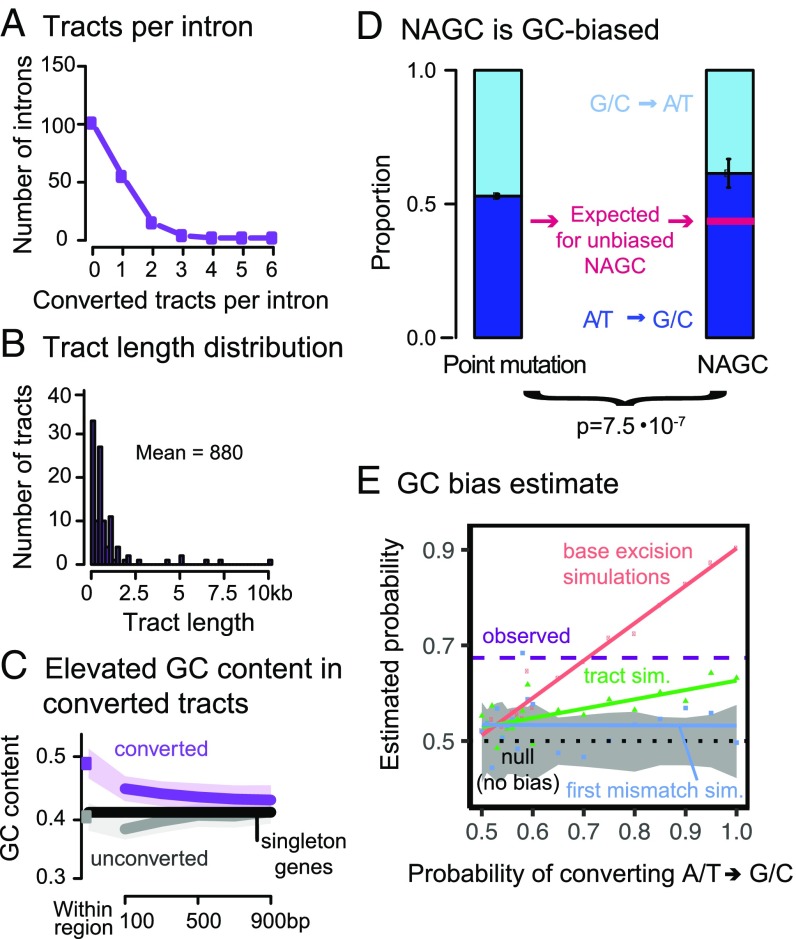
Applying our HMM, we identified putatively converted tracts in $18/39$ (46%) of the gene families, affecting 25.8% of the intronic sequence (Fig. 2A; see complete list of identified tracts in Datasets S1–S4). Previous studies estimate that only several percent of the sequence is affected by NAGC, but the definition of “affected sequence” statistic is arguably method-dependendent and therefore not directly comparable (41, 51, 52). Fig. 1D shows an example of the maximum likelihood genealogy maps for two gene families. The average length of the detected converted tracts is 880 bp (Fig. 2B). As previously discussed for other methods (27), this is likely an overestimate of the mean tract length of NAGC, because some identified NAGC tracts result from multiple NAGC events occurring in close proximity (SI Appendix, Fig. S2).

Fig. 2.

Properties of HMM-inferred converted tracts. (A) Number of tracts per intron. (B) Tract length distribution. (C) The purple dot shows the average GC content in converted regions. The gray dot shows the average for random unconverted regions, matched in length and within the same gene as the converted regions. The lines show GC content for symmetric 200 bp bins centered at the respective regions (excluding the focal tract). Shaded regions show 95% confidence intervals. The black line shows the intronic average for human genes with no identified paralogs. (D) In purple sites (Fig. 1C) that are most likely to be a direct result of NAGC (right bar), AT$\to$GC substitutions are significantly more common than GC$\to$AT substitutions. The left bar shows the estimated proportion of AT$\to$GC substitutions through point mutations and AGC in unconverted regions, which we used to derive the expected proportion for unbiased NAGC (pink line) after accounting for their different GC contents. Error bars show two standard errors around the point estimates. (E) Point estimate of GC bias. The dashed purple line shows the estimated probability of resolving a GC/AT heteroduplex in favor of the G/C allele. The color dots show simulation results under three different mechanistic models of biased gene conversion. The solid colored lines show linear fits. The gray-shaded area is a 95% binomial confidence interval for the “tract” model with no GC bias.

When an AT/GC heteroduplex DNA arises during AGC, it is preferentially repaired toward GC alleles (53, 54). We sought to examine whether the same bias can be observed for NAGC (53, 55–57). We found that converted regions have a high GC content (percentage of bases that are either guanine or cytosine): $48.9\%$, compared with $39.6\%$ in matched unconverted regions ($p=4\times {10}^{-5}$, two-sided t test; Fig. 2C). This base composition difference has been previously observed for histone paralogs (55). However, the difference could be a driver and/or a result of NAGC. To test whether NAGC preferentially repairs AT/GC heteroduplexes toward GC, we focused on sites that carry the strongest evidence of nucleotide substitution by NAGC—these are the sites with the “purple” divergence pattern as before (Fig. 1C). Using a parsimony consideration, we inferred the directionality of such substitutions involving both weak (A/T) and strong (G/C) nucleotides. We found that $61\%$ of these changes were weak to strong changes, compared with an expectation of $44\%$ through point mutation differences and GC-biased AGC alone (exact binomial test $p=7.5\times {10}^{-7}$, and see SI Appendix and Fig. 2D). We estimate that this observed difference corresponds to a probability of $67.3\%$ in favor of strong alleles when correcting strong/weak heteroduplexes. Our estimate agrees with the GC bias estimated for AGC (43, 44). Among several possible repair mechanisms that could underlie biased gene conversion that we consider in a simulation study (58, 59), the most likely to underlie such a large bias is the base excision repair mechanism—in which the choice of strand to repair is independent for each heteroduplex (SI Appendix and Fig. 2E). Conversely, it has been shown that the dominant driver of GC bias in yeast acts over long tracts (like the mismatch repair mechanism) (58). This could suggest that different mechanisms drive GC bias in different species (as also suggested by ref. 59).

The power of our HMM is likely limited to recent conversions, where local divergence patterns show clear disagreement with the global intron-wide patterns; it is therefore applicable only in cases where NAGC is not so pervasive that it would have a global effect on divergence patterns (28, 60). Next, we describe a method that allowed us to estimate NAGC parameters without making this implicit assumption.

NAGC Is an Order of Magnitude Faster than Point Mutation.

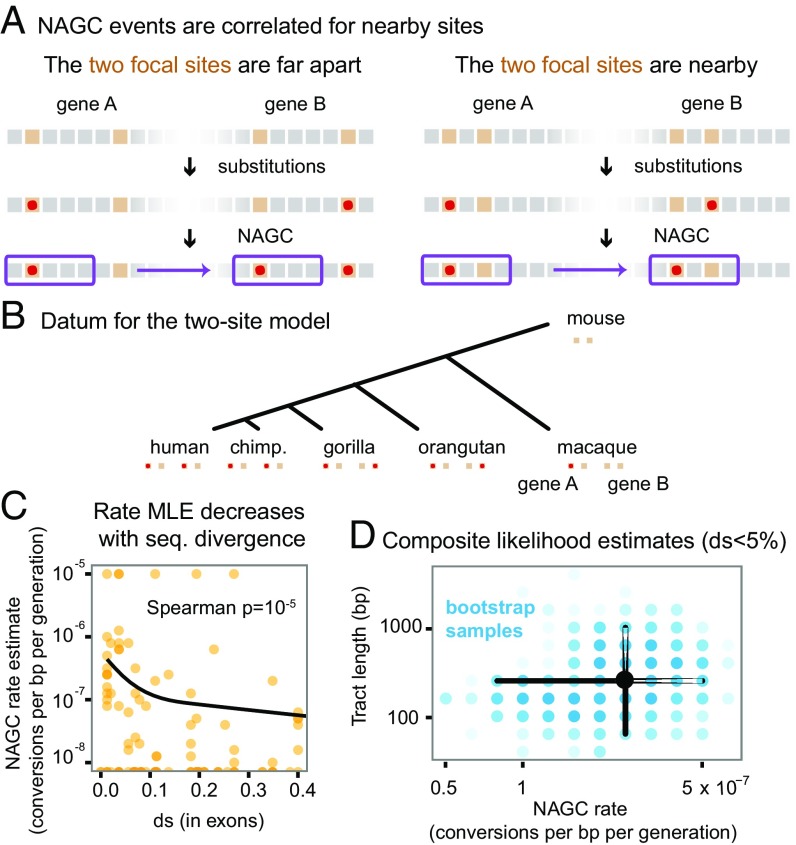
To estimate the rate and the tract length distribution of NAGC, we developed a two-site model of sequence evolution with point mutation and NAGC (Methods). This model is inspired by the rationale that guided Hudson (61) and McVean et al. (62) in estimating recombination rates: While computing the full likelihood of a sequence evolving through both point mutation and NAGC is intractable, we were able to model the likelihood of the observed divergence between paralogs at a pair of nucleotides at a time. In short, mutation acts to increase—while NAGC acts to decrease—sequence divergence between paralogs. When the two sites under consideration are close by (with respect to the NAGC mean tract length), NAGC events affecting one site are likely to incorporate the other (Fig. 3A). Our model makes no prior assumptions on the frequency of NAGC: Unlike the tract detection method, multiple hits are accounted for in the likelihood of the two-site model.

Fig. 3.

Estimation of NAGC parameters. (A) The two-site sequence evolution model exploits the correlated effect of NAGC on nearby sites (near with respect to the mean tract length). In this illustration, orange squares represent focal sites. Point substitutions are shown by the red points, and a converted tract is shown by the purple rectangle. (B) Illustration of a single datum on which we compute the full likelihood, composed of two sites in two duplicates across multiple species (except for the mouse outgroup for which only one ortholog exists). (C) MLE rate estimates for each intron (orange points). MLEs of zero are plotted at the bottom. The solid line shows a natural cubic spline fit. The rate decreases with sequence divergence ($ds$). We therefore only use lowly diverged genes ($ds\le 5\%$) to get point estimates of the baseline rate. (D) Composite likelihood estimates. The black point is centered at our point estimates for $ds\le 5\%$ genes. The blue points show 1,000 nonparametric bootstrap estimates, where the intensity of each point corresponds to the number of bootstrap samples. The corresponding $95\%$ marginal confidence intervals are shown by black lines.

For each pair of sites in each intron in our data, we computed the likelihood of the observed alleles in all available species, over a grid of NAGC rate and mean tract length values (Fig. 3B and SI Appendix). We then obtained maximum composite likelihood estimates (MLE) over all pairs of sites (ignoring the dependence between pairs).

We first estimated MLEs for each intron separately, and matched these estimates with $ds$ (16) in exons of the respective gene. We found that NAGC rate estimates decrease as $ds$ increases (Spearman $p=1\times {10}^{-5}$, Fig. 3C). This trend is likely due to a slowdown in NAGC rate, or its complete stop, as the duplicates diverge in sequence. Since our model assumes a constant NAGC rate, we concluded that the model would be most applicable to lowly diverged genes and therefore limited our parameter estimation to introns with $ds<5\%$.

We define NAGC rate as the probability that a random nucleotide is converted per base pair per generation. We estimate this rate to be $2.5\times {10}^{-7}$ ($[0.8\times {10}^{-7},5.0\times {10}^{-7}]$ 95% nonparametric bootstrap CI, Fig. 3D). This estimate accords with previous estimates based on smaller sample sizes using polymorphism data (19, 27) and is an order of magnitude slower than the AGC rate (43, 44). We simultaneously estimated a mean NAGC tract length of $250$ bp ($[\mathrm{63,1,000}]$ nonparametric bootstrap CI)—consistent with estimates for AGC (43, 63) and with a metaanalysis of many NAGC mutation accumulation experiments and NAGC-driven diseases (27).

Live Fast, Stay Young? The Effect of NAGC on Neutral Sequence Divergence.

We next consider the implications of our results on the divergence dynamics of paralogs post duplication. In light of the high rate we infer, the question arises: If the divergence of paralogous sequences through point mutation is much slower than the elimination of divergence by NAGC (64, 65), should we expect gene duplicates never to diverge in sequence?

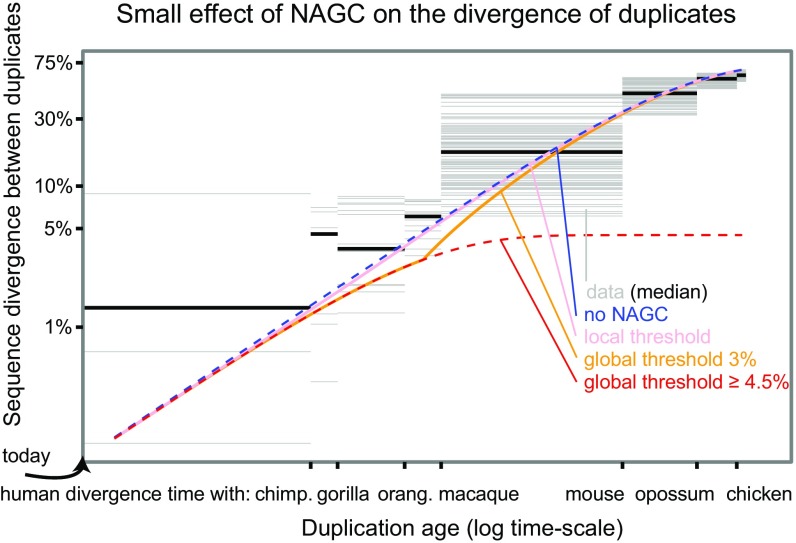
We considered several models of sequence divergence (SI Appendix). First, we considered a model where NAGC acts at the constant rate that we estimated throughout the duplicates’ evolution (“continuous NAGC”). In this case, divergence is expected to plateau around $4.5\%$, and concerted evolution continues for a long time [red line in Fig. 4; in practice, there will eventually be an “escape” through a chance rapid accumulation of multiple mutations (11, 66)]. However, NAGC is hypothesized to be contingent on high sequence similarity between paralogs.

Fig. 4.

The effect of NAGC on the divergence of duplicates. The figure shows both data from human paralogs and theoretical predictions of different NAGC models. The blue line shows the expected divergence in the absence of NAGC and the red line shows the expected divergence with NAGC acting continuously. The pink, orange, and red lines show the expected divergence for models in which NAGC initiation is contingent on sequence similarity between the paralogs. The gray horizontal bars correspond to human duplicate pairs. The duplication time for each pair is inferred by examining the nonhuman species that carry orthologs for both of the human paralogs. The y axis shows the synonymous sequence dissimilarity between the two human paralogs.

We therefore considered two alternative models of NAGC dynamics: first, a model in which NAGC acts only while the sequence divergence between the paralogs is below some threshold (“global threshold”); second, a model in which the initiation of NAGC at a site is contingent on perfect sequence homology at a short 400-bp flanking region upstream from the site [“local threshold”, (2, 27, 67)]. The local threshold model yielded a similar average trajectory to that in the absence of NAGC. A global threshold of as low as $4.5\%$ may lead to an extended period of concerted evolution as in the continuous NAGC model. A global threshold of $<4.5\%$ results in a different trajectory. For example, with a global threshold of 3%, duplicates born at the time of the primates’ most recent common ancestor would diverge at 3.9% of their sequence, compared with 5.7% in the absence of NAGC (Fig. 4 and SI Appendix, Figs. S10–S12 show trajectories for other rates and threshold values).

Lastly, we asked what these results mean for the validity of molecular clocks for gene duplicates. We examined the explanatory power of these different theoretical models for synonymous divergence in human duplicates. We wished to obtain an estimate of the age of duplication that is independent of $ds$ between the human duplicates; we therefore used the extent of sharing of both paralogs in different species as a measure of the duplication time. For example, if a duplicate pair was found in human, gorilla, and orangutan—but only one ortholog was found in macaque—we estimated that the duplication occurred at the time interval between the human–macaque split and the human–orangutan split. Except for the continuous NAGC model (or global threshold $\ge$4.5%), all models displayed similar broad agreement with the data (Fig. 4).

The small effect of NAGC on divergence levels is intuitive in retrospect: For identical sequences, NAGC has no effect. Once differences start to accumulate, there is only a small window of opportunity for NAGC to act before the paralogous sequences escape from its hold. This suggests that neutral sequence divergence (e.g., ds) may be an appropriate molecular clock even in the presence of NAGC (as also suggested by refs. 41, 46, and 68).

Discussion

In this work, we identify recently converted regions in humans and other primates, and estimate the parameters that govern NAGC. Previously, it has been somewhat ambiguous whether concerted evolution observations were due to natural selection, abundant NAGC, or a combination of the two (3, 22, 23). Today, equipped with genomic data, we can revisit the pervasiveness of concerted evolution; the data in Fig. 4 suggest that, in humans, duplicates’ divergence levels are roughly as expected from the accumulation of point mutations alone. When we plugged in our estimates for NAGC rate, most mechanistic models of NAGC also predicted a small effect on neutral sequence divergence. This result suggests that neutral sequence divergence may be an appropriate molecular clock even in the presence of NAGC.

One important topic left for future investigation is the variation of NAGC parameters. Our model assumes constant action of NAGC through time and across the genome to get a robust estimate of the mean parameters. However, substantial variation likely exists across gene pairs due to factors such as recombination rate, sequence context, physical distance between paralogs (SI Appendix, Fig. S9), and sequence similarity. These factors can also have very different distributions in pervasive, highly homologous sequences other than segmental gene duplicates. For example, long terminal repeats comprise several percent of the genome, and experience pervasive NAGC (69).

Our estimates for the parameters that govern the mutational mechanism alone could guide future studies of other forces shaping the evolution of gene duplicates, such as natural selection. Together with contemporary efforts to measure the effects of genomic factors on gene conversion, our results may clarify the potential of NAGC to drive disease, improve the dating of molecular events, and further our understanding of the evolution of gene duplicates.

Methods

Gene Families Data.

To investigate NAGC in duplicate sequences, we used a set of 1,444 reciprocal best-matched protein-coding gene pairs in the human reference genome that we had assembled previously (46) using the human reference genome (build 37). We focused on young pairs consistent with a duplication after the human–mouse split, and identified their orthologs in the reference genomes of chimpanzee, gorilla, orangutan, macaque, and mouse (Table S1). We focused our analysis on intronic sequences at least $50$ bp away from intron–exon junctions. For each of the two inference tasks, we applied additional method-specific filters (SI Appendix)–leaving us with 75 gene families for parameter estimation and 39 gene families for inference of converted tracts.

Two-Site Model Transition Matrix.

We consider the evolution of two biallelic sites in two duplicate genes as a discrete homogeneous Markov Process. We describe these four sites with a four-bit vector (“state vector”). The state $l_A{l}_B{r}_A{r}_B\in {\{0,1\}}^4$ corresponds to allele $l_A$ at the “left” site in copy A, allele $l_B$ at the left site in copy B, allele $r_A$ at the “right” site in copy A, and allele $r_B$ at the right site in copy B. The labels 0 and 1 are defined with respect to each site separately—the state $0000$ does not mean that the left and right sites necessarily have the same allele. We first derive the (per generation) transition probability matrix. There are two possible events that may result in a transition: point mutations which occur at a rate of $\mu =1.2\times {10}^{-8}$ per site per generation (64) and NAGC. The probability of a site being converted per generation is $c$. We consider these mutational events to be rare and ignore terms of the order $O({\mu }^2)$, $O(c^2)$, and $O(\mu c)$. For example, consider the per-generation transition probability from 0110 to 0100, for two sites that are $d$ bp apart. This transition can happen either through point mutation at the right site of copy A or by NAGC from copy B to copy A involving the right site but not the left. The transition probability is therefore

$$P(0110\to 0100)=\mu /3+c(1-g(d))+O({\mu }^2)+O(c^2)+O(\mu c),$$

where $g(d)$ is the probability of a conversion event including one of the sites given that it includes the other. Similarly, we can derive the full transition probability matrix $𝐏$ (SI Appendix). We note that our parameterization ignores possible mutations to (third and fourth) unobserved alleles.

We next derive $g(d)$. Following previous work (28), we model the tract length as geometrically distributed with mean $\lambda$. It follows that the probability of a conversion including one site conditional on it includes the other is

$$g_{init}(d)={\left(1-\frac{1}{\lambda }\right)}^d,$$

by the memorylessness of the geometric distribution. In SI Appendix, we show that recombination (with a breakpoint between the two sites) has a negligible effect on $g_{init}$.

Lastly, we turn to compute transition probabilities along evolutionary timescales. Each datum consists of state vectors (corresponding to two biallelic sites in two paralogs) encoding the alleles in the human reference genome and one to four other primate reference genomes. The mouse two-bit state (two sites in one gene) will only be used to set a prior on the root of the tree (SI Appendix). We assume a constant tree—namely, a fixed topology and constant edge lengths $\{t_{ij}\}$ as defined in SI Appendix, Fig. S5. We used estimates for primate split times from ref. 70, and assumed a constant generation time of 25 y. Each node corresponds to a state. We assume that—for both mutation types—substitution occurs at a rate equal to the corresponding mutation rate. Therefore, the transition probability matrix ${𝐏}_{(\mathrm{𝐞𝐝𝐠𝐞}\mathrm{𝐢𝐣})}^{\ast }$ for the edge between node i and node j is

$${𝐏}_{(\mathrm{𝐞𝐝𝐠𝐞}\mathrm{𝐢𝐣})}^{*}={𝐏}^{t_{ij}}.$$