Significance
Molecular springs, constituted by nanoporous materials immersed in a nonwetting liquid, are compact, economical, and efficient means of storing energy, owing to their enormous surface area. Surface energy is accumulated during liquid intrusion inside the pores and released by decreasing liquid pressure and thus triggering confined cavitation. State-of-the-art atomistic simulations shed light on the intrusion and extrusion of water in hydrophobic nanopores, revealing conspicuous deviations from macroscopic theories, which include accelerated cavitation, increased intrusion pressure, and reversible intrusion and extrusion processes. Understanding these nanoscale phenomena is the key to a better design of molecular springs as it allows relating the characteristics of the materials to the overall properties of the devices, e.g., their operational pressure and efficiency.
Keywords: molecular springs, molecular dynamics, hysteresis, rare event methods, hydrophobic nanoporous materials
Abstract
Heterogeneous systems composed of hydrophobic nanoporous materials and water are capable, depending on their characteristics, of efficiently dissipating (dampers) or storing (“molecular springs”) energy. However, it is difficult to predict their properties based on macroscopic theories—classical capillarity for intrusion and classical nucleation theory (CNT) for extrusion—because of the peculiar behavior of water in extreme confinement. Here we use advanced molecular dynamics techniques to shed light on these nonclassical effects, which are often difficult to investigate directly via experiments, owing to the reduced dimensions of the pores. The string method in collective variables is used to simulate, without artifacts, the microscopic mechanism of water intrusion and extrusion in the pores, which are thermally activated, rare events. Simulations reveal three important nonclassical effects: the nucleation free-energy barriers are reduced eightfold compared with CNT, the intrusion pressure is increased due to nanoscale confinement, and the intrusion/extrusion hysteresis is practically suppressed for pores with diameters below 1.2 nm. The frequency and size dependence of hysteresis exposed by the present simulations explains several experimental results on nanoporous materials. Understanding physical phenomena peculiar to nanoconfined water paves the way for a better design of nanoporous materials for energy applications; for instance, by decreasing the size of the nanopores alone, it is possible to change their behavior from dampers to molecular springs.
Hydrophobic nanoporous materials immersed in water offer a unique opportunity to store (“molecular springs”), transform, or dissipate (dampers) energy (1–7). By increasing the hydrostatic pressure, water is forced to wet the hydrophobic pores, thus accumulating surface energy. This storage mechanism is very effective and compact thanks to the enormous surface area per unit mass characterizing nanoporous materials and the high surface tension of water. On the other hand, when the pressure is lowered, water is expelled from the pores, and (part of) the stored energy is released (3). Hysteresis between these intrusion and extrusion processes can be significant, especially when the pore diameter is several nanometers (5, 8); the related energy dissipation due to the distinct mechanisms of water intrusion and confined vapor nucleation makes these materials efficient vibration dampers, which are weakly frequency-dependent.
The performance of the molecular springs and dampers described above hinges on the peculiar phase behavior of water in extreme confinement. The two relevant phenomena are the intrusion of liquid water inside the pores and its extrusion due to the nucleation of a vapor phase within them (cavitation); the conditions at which these transitions happen strongly depend on the size and on the chemical composition of the confining material. For instance, the vapor phase cannot be restored at positive pressure in alumina membranes with pore diameters of nm to nm (9), in hydrophilic channels (10), or in some kind of zeolites (3), precluding their use in energy applications. The intrusion pressure of water in pores of several nanometers is still well described by the macroscopic Kelvin–Laplace equation (9, 11); however, for smaller nanopores, significant deviations from this law are expected due to various nanoscale effects (12, 13). On the other hand, the nucleation of a vapor cavity is typically a thermally activated event which happens only at very negative pressures: ca. MPa in bulk, ultrapure water (14). However, hydrophobic confinement dramatically accelerates cavitation (15), making it possible to observe liquid extrusion even at positive pressures (13, 16–18). This is the case for hydrophobic nanopores (5, 6) in which cavitation was observed for pressures larger than MPa with nucleation rates of ca. Hz (see also ref. 7). In summary, the intrusion/extrusion pressure hysteresis defines both the applicability and the efficiency of a given heterogeneous system: as small as possible hysteresis for energy storage, and pronounced hysteresis for energy dissipation. Combined with the ability of molecular springs to operate under unprecedented frequencies, hysteresis vs. compression–decompression speed dependence becomes critically important for practical use. This work offers a microscopic understanding of the physics of intrusion, extrusion, and hysteresis in hydrophobic nanopores, thus paving the way for the design of molecular springs by tuning their physical and chemical properties.
Both intrusion and extrusion in nanopores are difficult to characterize in detail via experiments; theoretical and simulation studies are the tool of choice for understanding the microscopic aspects of these processes and interpreting the global quantities that can actually be measured. For instance, typical experiments are able to measure nucleation rates at different thermodynamic conditions (pressure and temperature) and in different confining geometries. Since nucleation rates depend exponentially on thermodynamic properties, cavitation experiments have been used as exponentially sensitive probes for elusive quantities, such as line tension (5) and curvature corrections to surface tension (19). However, a nucleation theory is needed to interpret the experimental (or simulation) results, i.e., to relate the nucleation rates to the quantities to be measured. Typically this connection is done via the classical nucleation theory (20, 21) (CNT) or extensions thereof able to deal with confined nucleation (4). However, issues may arise due to the path discontinuity observed in CNT in confined geometries (4, 5, 22). This flaw can be ascribed to the use of a single order parameter defined in terms of the volume of the new phase which is implicit in CNT (23) (see also refs. 24 and 25). Even more importantly, many nanoscale effects which become crucial in such extreme confinement are neglected in CNT: fluctuations, diffusion of the interface, line tension, curvature dependence of surface tensions, etc. Here these limitations are overcome by using molecular dynamics (MD) in combination with a specialized technique that is able to tackle rare events and to reveal the intrusion and nucleation mechanisms.
At variance with previous atomistic simulations focusing, e.g., on the hydrophobic effect (16, 26–33), here we use the string method in collective variables (CVs) (34), which allows us to describe the nucleation process in terms of the density field, avoiding the limitations of a single order parameter. This approach gives access to the detailed nucleation mechanism, i.e., a sequence of snapshots of the density field along the transition, and to the complete free-energy profile for nucleation. This information is crucial (i) for comparing with macroscopic (4) or density functional theories (35) and (ii) for identifying nonclassical effects on nucleation such as the contribution of line terms. We use the TIP4P/2005 (36) model of water which captures relevant properties of liquid water close to ambient conditions, most importantly the surface tension (37). Concerning the solid, a variety of materials is considered in experiments and applications, including silicates (5, 8, 38–42), zeolites (3, 43, 44), and metal–organic frameworks (7, 45, 46); here, rather than reproducing the detailed structure of a specific material (47), we focus on the phenomena which are generic of nanoconfined water by simulating a nanopore excavated from a simple hydrophobic crystalline material. Nanopores of diameters ranging from mesopores ( nm) to micropores ( and nm) are addressed.
In summary, hydrophobic nanoporous materials show promise both for technological applications and as powerful probes of physical quantities at the nanoscale. However, the missing piece for understanding and controlling these phenomena is a detailed microscopic description of water behavior in extreme hydrophobic confinement. Here we provide, via MD, a comprehensive picture of water intrusion and extrusion in hydrophobic nanopores, revealing three conspicuous nanoscale effects: a reduced nucleation barrier due to line effects, a significant increase of the intrusion pressure compared with the macroscopic Kelvin–Laplace prediction, and a sharp reduction of the intrusion/extrusion hysteresis in micropores with diameters below nm. Simulations show that hysteresis increases with frequency and decreases with the pore size, in agreement with experimental results on a variety of nanoporous materials. A simple interpretation of these behaviors in kinetic and geometric terms is proposed.
Results
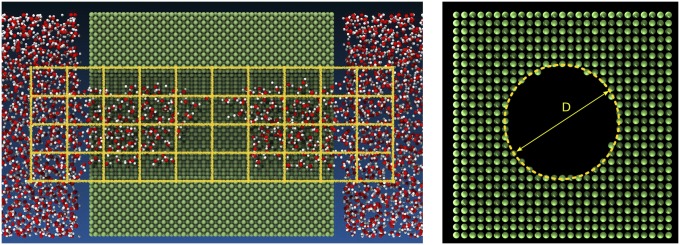
The main system we simulate consists of a single cylindrical nanopore of finite extent excavated from a hydrophobic matrix immersed in TIP4P/2005 water (36) (Fig. 1). The characteristics of the pore are chosen to capture the salient features of hydrophobic mesopores, e.g., MCM-41 (Mobil Composition of Matter 41) reported in the literature (5). The solid–oxygen interactions are of the Lennard-Jones type, described by the pair potential , where and set the characteristic energy and range of the interaction, respectively, is the distance between two particles, and modulates the attractive tail to render the desired Young contact angle . A nanopore with a diameter nm is excavated from the bulk crystalline material, which is characterized by [as computed from independent simulations of a drop on a planar substrate (Fig. S1)]. At the simulated conditions, K and , where is the two-phase bulk coexistence pressure, the TIP4P/2005 water model has a surface tension of N/m very close to the experimental value of N/m (37). (Since, for the present phenomena, it is the deviation from the coexistence pressure that matters and since, for water at K, MPa, we will often refer to simply as “pressure”; this word choice also reflects the fact that the only experimental control parameter is the liquid pressure.)
Fig. 1.
System used in the atomistic string calculations; it comprises a nanopore excavated from a hydrophobic Lennard-Jones crystal and ca. TIP4P/2005 molecules. (Left) The coarse-grained density field of water is computed on a grid of cubic cells with the sides measuring ca. Å (yellow lines). Further details on the simulations and on the string method are found in Supporting Information. (Right) Definition of the pore diameter adopted here, based on the center of the last wall atoms.
The string method in CVs (34), when combined with MD, allows identification of the most probable transition path in high-dimensional, rough free-energy landscapes (see, e.g., ref. 48). CVs are convenient descriptors of the state of the system in macroscopic terms; for wetting and nucleation, a natural CV is the coarse-grained density field (Fig. 1) which, at the same time, avoids the artifacts due to considering a single CV (qualitative and quantitative deviations from the actual path and free energy, typically detectable as jumps and discontinuities; see the discussion in refs. 23 and 25 and Fig. S2) and allows making a direct contact with density functional theory and with CNT (cf. refs. 49 and 50). Other methods, such as umbrella sampling (51) or temperature-accelerated MD (52), involve the direct reconstruction of the free-energy landscape, followed by a search for the most probable path; since the simulation time scales exponentially with the dimension of the landscape (53), these approaches become impracticable for the current CV.
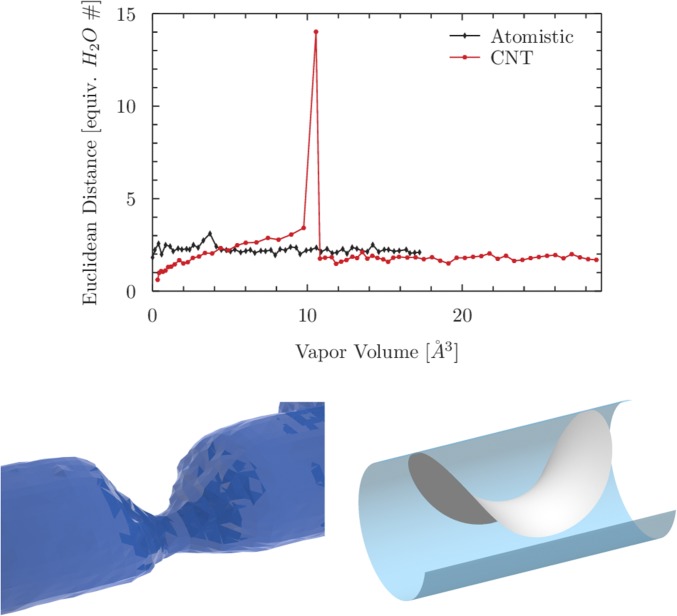
The path identified by the string method is reported in Fig. 2 and in Movie S1; this is the most probable sequence of densities for the nucleation of a vapor bubble and for the opposite process of water intrusion. (Since, in the string method, as in CNT, the thermally activated event is assumed to happen quasistatically, the sequence of densities in Fig. 2 is the same for both forward and backward processes. Based on symmetry arguments, one could conceive that a symmetric path is followed during the intrusion process; this path, however, is connected with a higher free-energy barrier, as suggested by the dot-dashed lines in Fig. S2.) Each density field is computed from a (restrained) MD simulation (34) and thus contains the complete atomistic information. Starting from the fully wet configuration, it is seen that the vapor bubble initially forms on a wall and gradually expands along the pore walls. The bubble is nonaxisymmetric and, in the first phase, it takes up a shape that minimizes surface free energy, i.e., with constant mean curvature. However, as its size approaches that of the pore, the bubble becomes more elongated toward the opposite wall, with a shape similar to a wedge. The small capillary neck then breaks, promoting the formation of a pore-spanning vapor bubble. This configuration corresponds to the transition state (TS), i.e., the free-energy maximum of the activated process which defines the free-energy barrier and the activated kinetics. The two newly formed menisci rapidly become axisymmetric and proceed toward the pore ends. In the final equilibrium configuration, the two menisci are pinned at the two ends of the pore.
Fig. 2.
Most probable path for the extrusion process computed via the string method in CVs (see also Movie S1). For visualization purposes, the Gibbs dividing surface corresponding to the isosurface is shown. Under the assumption that the process is quasistatic, the most probable intrusion process is obtained by inverting the direction of the arrows.
Fig. 3 compares the characteristics of the paths obtained via the string method and CNT (4). In particular, in order to give a quantitative indicator of the regularity of the path, the distance between two successive density configurations (identified by the bubble volumes and , respectively) is compared for the string and CNT paths. It is seen that, while the string method yields a continuous process, CNT, like other approaches based on a single CV, has a significant density jump in correspondence of the TS. As a consequence of this discontinuity, which is physically impossible for a continuous nucleation process, the predictions for the TS (Fig. 3) and for the free-energy barriers depart from the string one (Fig. S2). The main conceptual difference between the two approaches is that the string seeks the most probable path in the density space, while CNT-like approaches minimize surface energy independently for each configuration along the path, i.e., the CNT path consists of a sequence of minimal surfaces enclosing a prescribed bubble volume (Fig. S3). In the first and last stages of extrusion, the two paths are very similar; the corresponding interfaces are in the shape of a hyperbolic saddle delimiting a nonaxisymmetric bubble and two axisymmetric menisci, respectively (Fig. 2). Since, in CNT, the path is a juxtaposition of these two morphologies, the TS occurs where the hyperbolic saddle cannot be accommodated anymore within the pore (4). At this point, there is a discontinuous jump to the two-menisci morphology, which is reflected in a jump in the free energy (Fig. S2). The atomistic string method, instead, yields intermediate morphologies between the two limiting ones, allowing for a continuous transition dynamics and free energy. As a consequence, the bubble morphologies at the TS are significantly different (Fig. 3). As will be discussed in Discussion, it is crucial for a nucleation theory to correctly capture the shape of the bubble at the TS and the related free energy, because these features determine the free-energy barriers and the kinetics of the process.
Fig. 3.
(Upper) Distance between consecutive density configurations along the discretized path for the atomistic string (black) and for the CNT path (red). The CNT results are obtained via Surface Evolver (65) calculations similar to those in refs. 4 and 5 (Figs. S2 and S3). Note that the final volume is different in the two cases due to excluded volume effects in the atomistic simulations. (Lower) The TS configurations in the (Left) atomistic and (Right) CNT cases.
The string method also gives access to the free energy along the nucleation process (see, e.g., ref. 23 for additional details), which is shown in Fig. 4 as a function of the bubble volume . The free-energy profile is formed by two different regions: The first (I) is related to cavitation and spans, approximately, from the fully wet state up to the free-energy maximum (TS); the second (II) goes from the TS to the evaporated state. In the cavitation region, the free energy gently grows and is characterized by a downward concavity; the maximum is also smooth and is within a few from the other points, where is the Boltzmann constant. Closely following the TS, the free energy has a linear trend, which corresponds to the formation of the two axisymmetric menisci. At two-phase bulk coexistence ( K and ), the evaporated state at Å3 is the thermodynamically stable one, i.e., the absolute minimum.
Fig. 4.
Free-energy profiles at K and obtained via the atomistic string (blue symbols), via modified CNT (dashed orange line), and via modified CNT with terms proportional to the triple line and using an effective contact angle (green line). The two regions related to cavitation of the critical bubble (I) and to the sliding of two symmetric menisci (II) are indicated. “Modified CNT” free-energy profiles are obtained relaxing its third assumption, i.e., using the path calculated from the string isosurfaces shown in Fig. 2. Nanoscale effects are further added by considering an effective “line tension” (i.e., a term proportional to the triple line) N and an effective contact angle in Eq. 2. Additional comparisons with standard CNT and variations thereof are shown in Fig. S2.
Discussion
The results of the atomistic string calculations—the path in Fig. 2 and the free-energy profile in Fig. 4—contain detailed microscopic information on the thermodynamics and kinetics of the intrusion and extrusion processes of water in hydrophobic nanoporous materials. In this section, we compare them with CNT predictions and with additional in silico experiments on microporous materials with and nm, identifying three important nonclassical effects: (i) reduced cavitation free-energy barrier due to line effects, leading to an accelerated extrusion of water; (ii) increased intrusion pressure due to extreme hydrophobic confinement; and (iii) hysteresis suppression in the intrusion/extrusion isotherms for microporous materials with nm.
Although these results are obtained for a somewhat idealized pore, the physical effects described are fairly general and explain experimental results for a broad class of nanoporous materials as demonstrated by Figs. 5 and 6.
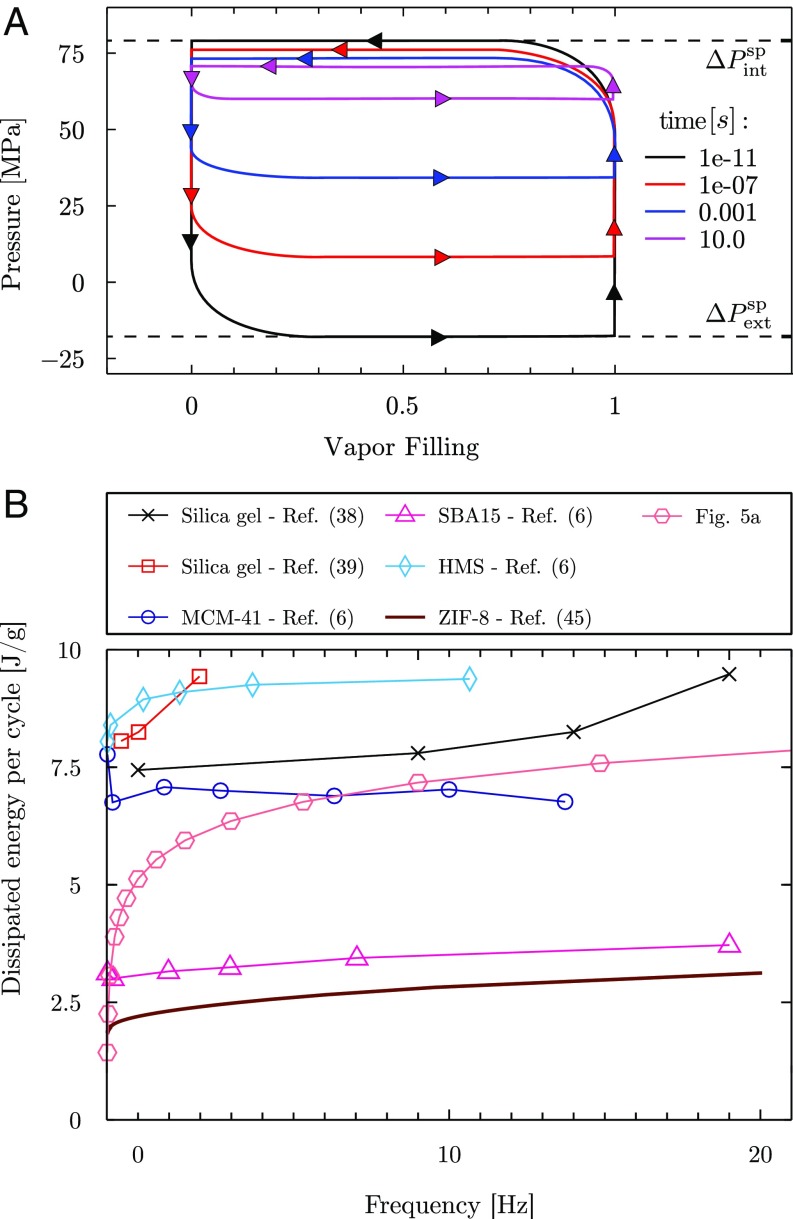
Fig. 5.
(A) Hysteresis cycle for a thought intrusion/extrusion experiment on the -nm pore; the pressure is varied between the intrusion value and the extrusion one, (black lines). The plot is constructed by adding a term to the atomistic free-energy profile at in Fig. 4 and by computing the spinodal pressures; the compressibility of the liquid and of the pore walls is not taken into account, resulting in a rectangular cycle (only the values of the pressure at the plateaus are actually computed; rounded angles help visualization). On the axis, the bubble volume is normalized with the maximum value such that it ranges from (fully wet pore) to (vapor bubble occupying the nanopore). The pressures at which intrusion (top plateau) and extrusion (lower plateau) happen for fixed experimental times are computed inverting Eq. 1 to obtain the intrusion and extrusion barriers corresponding to the prescribed (colored lines). (B) Energy dissipated per cycle as a function of the frequency, from refs. 6, 38, 39, and 45 and from A. Experimental data, which are available over a limited range of frequencies, were originally given in different units, which required estimates of the porosity (38, 39) or interpolation of and (45). We remark that experiments are performed on different materials, temperatures, and, for some of them (38), refers to the entire device.
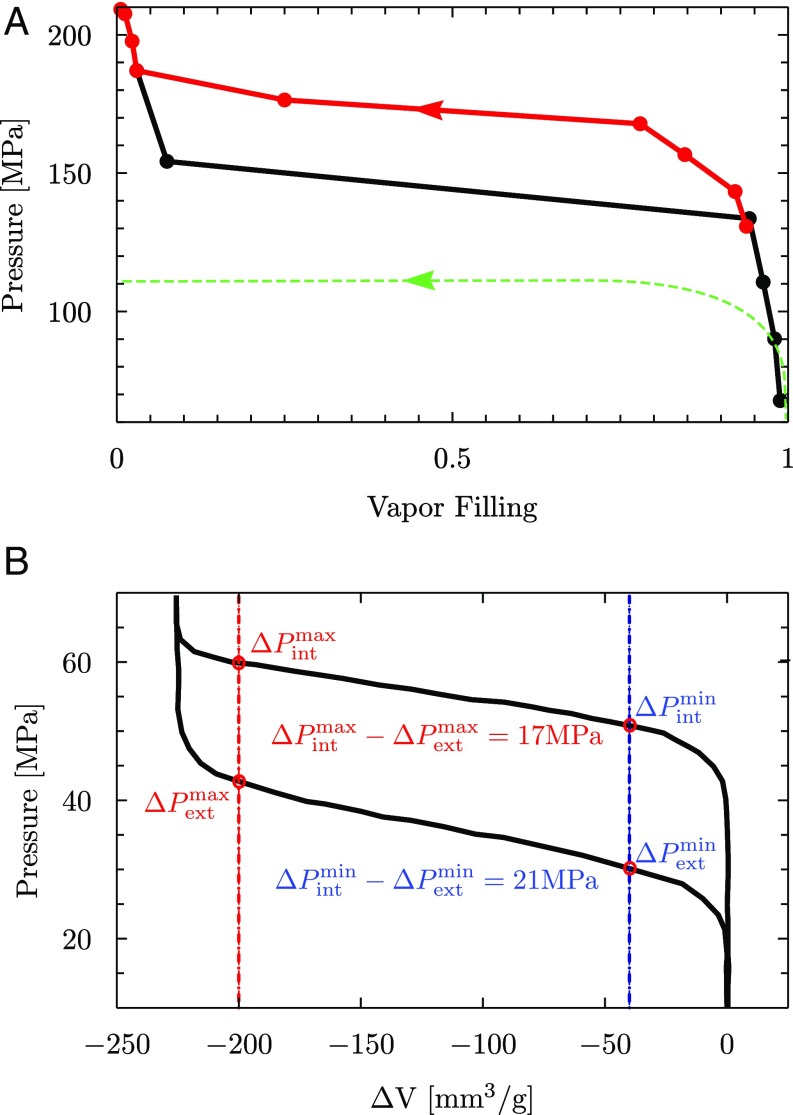
Fig. 6.
(A) Intrusion/extrusion cycle for a nanopore with nm showing reduced hysteresis. The black and red curves are computed from an in silico experiment in which the pressure is changed in steps of MPa and allowed to stabilize for at least ns; the average value of vapor filling is obtained by discarding the initial steps in which pressure is varied. The dashed green line is an illustration of the same experiment as predicted by classical theories: The intrusion pressure calculated via Eq. 3 yields MPa. The classical extrusion spinodal pressure because the related macroscopic barrier never vanishes: The “classical” intrusion/extrusion cycle is actually not closed for finite pressures. (B) Intrusion and extrusion cycle for MCM-41 from ref. 4. The intrusion and extrusion pressures for the largest and smallest pore diameters are indicated as and , respectively, showing a decrease in the hysteresis with the size of the nanopores.
Concerning cavitation, it is useful to briefly introduce the kinetics of thermally activated events and CNT to put the discussion in a clear theoretical framework. The average time which one has to wait for a sufficiently large thermal fluctuation to overcome the free-energy barrier is given by (21)
| [1] |
where is the free-energy barrier of the thermally activated event and is a prefactor setting its timescale; it can be conservatively assumed to be an atomic timescale s (5). With this estimate for and with the value for the extrusion barrier in Fig. 4, , Eq. 1 yields ns, which explains the observation of “spontaneous” extrusion within the duration of the experiment of ref. 5.
Typical experiments on hydrophobic nanoporous materials consist of intrusion/extrusion cycles obtained by increasing and then decreasing the liquid pressure over a broad range. The duration of such experiments, typically above s (6), is much longer than the atomistic time required to relax the system to the local minimum; it is therefore possible to interpret such experiments in terms of a quasistatic process in which the system relaxes to the local minimum of the free energy at the current pressure (54). Starting from the string data of Fig. 4, which are at , we construct a similar thought experiment, for which one needs the free-energy minima and the free-energy barriers at different pressures. This information can be reliably obtained by adding the term to the free-energy profile of Fig. 4 (22, 49, 55–57); this procedure effectively tilts the free-energy profile. From these profiles at , the minima for each pressure (related to the fully wet and evaporated state) are easily identified, which coincide with the vertical lines in Fig. 5A. These states exist as long as there is a free-energy barrier separating them from the other state; the intrusion and extrusion barriers disappear at the spinodal pressures and , respectively (horizontal black lines in Fig. 5A; the meaning of the other lines with different colors will be explained in the next paragraph). The intrusion and extrusion curves of the thought experiments on the – plane are constructed by joining the black horizontal and vertical lines counterclockwise (Fig. 5A), which reflects the fact that experiments are usually started at low pressures in the evaporated state, and then the pressure is increased (vertical line at vapor filling ) until there is a sudden transition to the fully wet state (horizontal line at ). The extrusion phase consists in decreasing the pressure from this point (vertical line at vapor filling ) until is reached and the cycle closes. The thought intrusion/extrusion cycle of Fig. 5A shows that, for nm, there is a large hysteresis loop between MPa and MPa.
The intrusion/extrusion cycle represented by the black curve of Fig. 5A is a limit one, in which the transitions from the evaporated state to the fully wet one and vice versa happen at the spinodals and . This implies that the cycle must be performed in a time comparable to the microscopic timescale of the spinodal transition, which is of the order of the prefactor in Eq. 1. To facilitate the connection with experiments that take a (longer) fixed time, e.g., those in which a frequency is imposed by a moving piston (6, 38, 39, 45, 58), we consider an intrusion/extrusion cycle with generic duration . For such a case, the observed intrusion and extrusion phenomena can be described by Eq. 1; inverting yields the intrusion and extrusion barriers corresponding to the pressures and at which the experimental system is expected to experience intrusion or extrusion, respectively (Fig. 4). Based on these calculations, Fig. 5A shows that the intrusion/extrusion curves are expected to exhibit a decrease of hysteresis with increasing duration of the experiment (decreasing frequency): e.g., for s, MPa and MPa. This behavior reflects the fact that, while the spinodals correspond to the maximum and minimum pressures at which a metastable state can exist, at finite times, one moves toward the thermodynamic limit in which the system is always found in the thermodynamically stable state and a single curve for intrusion and extrusion exists. While both the intrusion and extrusion processes are, in principle, thermally activated (see figure 4.4 of ref. 45 referring to the microporous ZIF-8, Zeolitic Imidazolate Framework 8), for the considered mesopore, the free-energy barrier for extrusion is less sensitive to pressure changes (Fig. S4), which explains why significant changes of are caused by varying the duration of the experiment while is (almost) constant. This asymmetry is physically related to the fact that, due to the minuscule volume of the critical bubble, the extrusion barrier is dominated by surface terms while the intrusion barrier sensitively depends on the pressure due to the larger vapor volumes connected to the evaporated state (Eq. 2). This trend is consistent with the experiments of refs. 5 and 6 in which nm pores are considered.
The time-varying hysteresis loops reported in Fig. 5A have important repercussions on applications: The dissipated energy per cycle—the area within the hysteresis loop—depends on the applied frequency; in particular, damping becomes more effective at higher frequencies. Fig. 5B compares the simulation results with experimental data available in the literature, for a variety of nanoporous materials [silica gel (38, 39), MCM-41, SBA15 (Santa Barbara Amorphous 15), and HMS (Hexagonal Mesoporous Silica) (6), and ZIF-8 (45)]. The theoretical prediction based on Eq. 1 is that , which captures the reported experimental trends. Since, however, the frequencies explored in experiments are usually within a limited range, the weakly time-dependent can often be considered constant.
To connect the experimental values of the extrusion time with the various contributions to the free-energy barrier in Eq. 1, a nucleation theory is needed (for instance, in ref. 5, this procedure is used for estimating the line tension of water). The standard one is CNT and extensions thereof, all of which are based on three main assumptions: (i) The interfaces between phases are sharp and bulk properties valid up to the dividing surface; (ii) the process happens quasistatically; and (iii) the order parameter for the transition is the bubble volume (23). It is worth remarking that the third assumption gives rise to the discontinuous behavior shown in Fig. 3 and Fig. S2. For sharp-interface models, like CNT, the excess free energy for forming a (confined) bubble of volume is
| [2] |
where is the liquid–vapor (LV) surface tension, and are the areas of the LV and solid–vapor interfaces, respectively, and is the Young contact angle.
Equipped with Eq. 2, we now attempt to relax the third assumption of CNT. For this purpose, we extract the geometrical parameters in Eq. 2 from the atomistic path shown in Fig. 2; the missing thermodynamic parameters (, , and ) are measured via independent MD simulations. By plugging these quantities into Eq. 2, it is possible to compute the sharp-interface free energy of the bubble configurations belonging to the correct path and compare them directly with the atomistic results. Summarizing, this modified CNT estimate is consistent with assumptions i and ii of CNT but eliminates the third assumption, using the “correct,” most probable transition path. Fig. 4 reports the CNT estimate of the free energy via Eq. 2 (orange line), which can be compared against the one computed directly via atomistic calculations (blue symbols). Since the two free energies are calculated along the same path, it is possible to identify precisely which effects are nonclassical, i.e., deviate from assumptions i and ii of the CNT and are due to genuine nanoscale effects.
The first prominent nonclassical effect, which is observed in region I, is a significant reduction of the free-energy barrier of the atomistic case compared with the CNT prediction. This phenomenon has been reported in experiments, in which nucleation kinetics was found to be much faster than expected from CNT (5). Eq. 1 allows interpretation of this accelerated kinetics as a reduction of the free-energy barriers; in ref. 5, a term proportional to the length of the triple line, , was added to Eq. 2, with a negative line tension . From the simulated path, we are able to compute (Fig. S5) and verify directly this hypothesis. Due to the intricate contact of the asymmetric bubble with the pore walls, varies dramatically and reaches its maximum in region I, while it remains constant in region II in which two identical menisci slide along the pore. Fig. 4 shows that, by adding the term to Eq. 2 with a value N, the barrier decreases to the actual value of (green line). This value of is about one-half of the experimental estimate reported in ref. 5 for MCM-41, with the same negative sign. Given the different transition paths used for computing and the inevitable differences between the simulated system and the experiments, this accord is actually surprising. What is even more interesting is that an energy term proportional to the triple line length added to Eq. 2 not only matches the value of the barrier but also collapses the full sharp-interface free-energy profile on the atomistic one in region I. [The value of computed above should be taken as an effective line tension, since there exist several nanoscale terms scaling with the length of the triple line (59, 60); furthermore, the initial bubbles are comparable in size to the width of the interface, which suggests, for the future, further investigations on the robustness of this extension of the CNT to the nanoscale.]
The second important nonclassical effect concerns the intrusion pressure , i.e., the pressure at which the intrusion free-energy barrier vanishes. The macroscopic estimate for is given by the Kelvin–Laplace equation,
| [3] |
where and are the LS and the vapor–solid surface tensions, respectively, and the last equality is obtained by multiplying and dividing by to obtain the usual form with the Young contact angle . Eq. 3 yields MPa, which is lower than the atomistic one ( MPa, computed from Fig. 5). Based on the first equality in Eq. 3, the increase of in the nanopore can be interpreted in terms of variations of and . On one hand, the short-range repulsion at the walls decreases the volume available to liquid water, effectively decreasing in Eq. 3 (Fig. S6). On the other hand, the difference between the liquid–solid and vapor–solid surface tensions may depart from its macroscopic value due to the confined environment and to the different crystalline planes exposed within the excavated pore. It can be shown that is determined by the slope of the free-energy profile in region II of Fig. 4 (55). This linear trend in the free-energy profile results from the substitution of the vapor–solid interface with the liquid–solid one, which happens with the two symmetric menisci sliding along the pore without changing their shape. As a consequence, there is no appreciable variation in the free energy associated with the LV interface term in Eq. 2. The intrusion pressure is determined by and by —quantities that are affected by the extreme confinement—but does not depend significantly on .
We further test how scales with the dimension of the pore, by simulating intrusion in smaller pores with nm and nm (Fig. S7). It is important, at these scales, to remark that the diameter is defined as the distance between the centers of two wall atoms across the nanopore (Fig. 1). With this convention, is always greater than the Kelvin–Laplace prediction. Careful analysis of the liquid density and of the wall potential within the pores underscores an increasing departure of both quantities from the case of a flat wall as the pore diameter approaches the nanometer (Fig. S6). While the bulk density is attained at the center of the pore with the largest diameter, wall layering dominates in the interior of the pores for the smaller diameters: Bulk liquid properties cannot be recovered. In particular, for nm, the wall potential inside the pore is more attractive, resulting in an increased density peak of the first layer and a decreased density at the center of the pore, due to excluded volume effects.
The fact that it is more difficult to intrude liquid within nanopores has important consequences for porosimetry, which often relies on the measurement of for a nonwetting liquid such as mercury (61, 62). The use of the Kelvin–Laplace law to obtain the diameter implies that such measurements yield smaller values than the actual ones, with larger errors for smaller pores: The porosimetry results would be , , and nm for the pores here considered (provided that the macroscopic contact angle is used in Eq. 3), which actually correspond to , , and nm, respectively. If, instead, the diameter is known from independent measurements or from the crystalline structure of the material, one can ponder whether the contact angle can be extracted from . Since this quantity is determined by the slope (55) of the free-energy profile in region II of Fig. 4, one readily sees that the effective value of the contact angle that must be used in Eq. 3 to fit the atomistic data (, green line) differs for the macroscopic value used in the modified CNT (, orange line). These results underscore the fact that nanoscale measurements of or do not coincide with their precise definition based on the atomic positions: These are effective quantities which lump together different nanoscale effects. Similar intricacies concerning the determination of these quantities by interpreting porosimetry data via the Kelvin–Laplace law Eq. 3 were already pointed out in ref. 63 for the case of vapor adsorption.
The third nonclassical effect is concerned with the amplitude of the hysteresis cycles and therefore with the energy dissipated in an intrusion and extrusion cycle; for pores with nm, J. This value, multiplied by the typical number of pores per gram, ca. [obtained dividing the porous volume of MCM-41 (6) by the volume of the simulated pore], yields a remarkable dissipation capacity on the order of J/g, which is comparable to the experimental values in Fig. 6B. While, for realizing dampers, it is technologically advantageous to maximize , for energy storage applications (molecular springs), the aim is that of minimizing the dissipated energy exploiting in full the high intrinsic efficiency of mechanical energy storage (3, 7, 40, 41, 43, 46).
To understand which physical parameters determine the behavior of a nanoporous material as a damper or as a spring, we simulated an intrusion/extrusion experiment on a much smaller nanopore with nm which is excavated from the same bulk material (). Results plotted in Fig. 6A show that the pore diameter has a critical effect on the reversibility of the intrusion/extrusion cycle [see also ref. 30], dramatically decreasing hysteresis down to, at most, MPa. This figure refers to microscopic timescales; hysteresis is expected to vanish for experimentally relevant durations of ca. s (Fig. 5A). This is the third nonclassical effect, which deviates from CNT in which the extrusion barrier never completely vanishes and is never achieved (Fig. 6A and refs. 15, 22). Extrusion is facilitated in micropores due to the combination of excluded volume effects at the center of the pore (Fig. S7) and decreased size of the critical confined bubble. These two effects lower the extrusion free-energy barrier below a few , allowing the recovery of the capillary vapor at large positive pressures, ca. MPa, within the molecular time of our simulations ( ns). For micropores, these processes do not show the typical signature of thermally activated events, and extrusion happens as soon as the pressure is lowered.
Since, in MD, pores of different diameters can be excavated from the same material, it was possible to disentangle the size effect from that of the chemistry, which is difficult to achieve in experiments, which often imply changing the chemical structure of the material to achieve extreme confinement. However, indirect experimental evidence of this behavior can be deduced from model nanoporous materials such as MCM-41 in which (i) the pores are independent and perfectly cylindrical and (ii) the diameter has some degree of polidispersity (64). Owing to this pore size distribution, and vary by more than MPa during the intrusion and extrusion phases (the pseudoplateaus in Fig. 6B); assuming that the largest values (lowest) of and correspond to the smallest (largest) pores, Fig. 6B shows that pressure hysteresis continuously decreases from MPa to MPa when the pore diameter is decreased, consistent with the hysteresis reduction seen in the atomistic results of Figs. 5A and 6B.
These results suggest that, in order to obtain molecular springs, one of the physical parameters that can be varied is the pore size, with smaller diameters corresponding to lower hysteresis. At the same time, however, the -nm pore is characterized by a large intrusion pressure, ca. MPa. Given the opposite trends, a tradeoff between low dissipation and low intrusion pressure (which renders the nanoporous materials compatible with operational pressure conditions) must be made when designing actual materials.
Conclusions
Hydrophobic nanoporous materials have an enormous potential in energy applications but, at the same time, challenge the current knowledge on the phase behavior of water in extreme confinement. The present MD simulations of hydrophobic nanopores immersed in TIP4P/2005 water have revealed three conspicuous nanoscale effects in the intrusion and extrusion processes. The first is the acceleration of the nucleation process beyond the predictions of CNT; the reduction of nucleation free-energy barriers causes extrusion to occur at much larger pressures, even positive ones. We have been able to relate this effect to energetic terms proportional to the length of the triple line. The second effect is the increase of the intrusion pressure as compared to the macroscopic Kelvin–Laplace law, which can be ascribed to the extreme confinement of water inside the nanopore. The third effect we investigated concerns the role of the pore size when the matrix is made of the same material: As the pore diameter is decreased, hysteresis in the intrusion/extrusion curves decreases. Interestingly, by changing the diameter alone, it is possible to tune a nanoporous material from a highly dissipative one to a reversible means of storing energy: For microporous materials with nm, hysteresis practically disappears and the nanoporous material is ideally suited as a molecular spring. The present simulations provide a microscopic interpretation for several experimental results, including the frequency (6, 38, 39, 45, 58) and size dependence (4) of intrusion/extrusion hysteresis, porosimetry measurements, and the determination of line tension.
Supplementary Material
Acknowledgments
We thank Emanuele Lisi for help with the Surface Evolver calculations. The research leading to these results received funding from the European Research Council (ERC) under the European Union’s Seventh Framework Program (FP7/2007–2013)/ERC Grant Agreement 339446. We acknowledge PRACE (Partnership for Advanced Computing in Europe) for awarding us access to Fermi and Marconi at CINECA (Consorzio Interuniversitario del Nord-Est per il Calcolo Automatico), Italy.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission. C.D. is a guest editor invited by the Editorial Board.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1714796114/-/DCSupplemental.
References
- 1.Eroshenko V. Effect of heat exchange on filling of lyophobic pores and capillaries with liquid. Colloid J USSR. 1988;49:769–773. [Google Scholar]
- 2.Fadeev AY, Eroshenko VA. Study of penetration of water into hydrophobized porous silicas. J Colloid Interf Sci. 1997;187:275–282. doi: 10.1006/jcis.1996.4495. [DOI] [PubMed] [Google Scholar]
- 3.Eroshenko V, Regis R-C, Soulard M, Patarin J. Energetics: A new field of applications for hydrophobic zeolites. J Am Chem Soc. 2001;123:8129–8130. doi: 10.1021/ja011011a. [DOI] [PubMed] [Google Scholar]
- 4.Lefevre B, et al. Intrusion and extrusion of water in hydrophobic mesopores. J Chem Phys. 2004;120:4927–4938. doi: 10.1063/1.1643728. [DOI] [PubMed] [Google Scholar]
- 5.Guillemot L, Biben T, Galarneau A, Vigier G, Charlaix É. Activated drying in hydrophobic nanopores and the line tension of water. Proc Natl Acad Sci USA. 2012;109:19557–19562. doi: 10.1073/pnas.1207658109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Guillemot L, Galarneau A, Vigier G, Abensur T, Charlaix É. New device to measure dynamic intrusion/extrusion cycles of lyophobic heterogeneous systems. Rev Sci Instrum. 2012;83:105105. doi: 10.1063/1.4754631. [DOI] [PubMed] [Google Scholar]
- 7.Grosu Y, et al. A highly stable nonhysteretic Cu2 (tebpz) MOF+ water molecular spring. ChemPhysChem. 2016;17:3359–3364. doi: 10.1002/cphc.201600567. [DOI] [PubMed] [Google Scholar]
- 8.Grosu Y, Ievtushenko O, Eroshenko V, Nedelec J-M, Grolier J. Water intrusion/extrusion in hydrophobized mesoporous silica gel in a wide temperature range: Capillarity, bubble nucleation and line tension effects. Colloids Surf A Physicochem Eng Asp. 2014;441:549–555. [Google Scholar]
- 9.Smirnov S, Vlassiouk I, Takmakov P, Rios F. Water confinement in hydrophobic nanopores. Pressure-induced wetting and drying. ACS Nano. 2010;4:5069–5075. doi: 10.1021/nn101080k. [DOI] [PubMed] [Google Scholar]
- 10.Duan C, Karnik R, Lu M-C, Majumdar A. Evaporation-induced cavitation in nanofluidic channels. Proc Natl Acad Sci USA. 2012;109:3688–3693. doi: 10.1073/pnas.1014075109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rouquerol J, Rouquerol F, Llewellyn P, Maurin G, Sing KS. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications. Academic; New York: 2013. [Google Scholar]
- 12.Helmy R, Kazakevich Y, Ni C, Fadeev AY. Wetting in hydrophobic nanochannels: A challenge of classical capillarity. J Am Chem Soc. 2005;127:12446–12447. doi: 10.1021/ja053267c. [DOI] [PubMed] [Google Scholar]
- 13.Giacomello A, Schimmele L, Dietrich S, Tasinkevych M. Perpetual superhydrophobicity. Soft Matter. 2016;12:8927–8934. doi: 10.1039/c6sm01727d. [DOI] [PubMed] [Google Scholar]
- 14.Azouzi MEM, Ramboz C, Lenain J-F, Caupin F. A coherent picture of water at extreme negative pressure. Nat Phys. 2013;9:38–41. [Google Scholar]
- 15.Giacomello A, Chinappi M, Meloni S, Casciola CM. Geometry as a catalyst: How vapor cavities nucleate from defects. Langmuir. 2013;29:14873–14884. doi: 10.1021/la403733a. [DOI] [PubMed] [Google Scholar]
- 16.Bérard D, Attard P, Patey G. Cavitation of a Lennard-Jones fluid between hard walls, and the possible relevance to the attraction measured between hydrophobic surfaces. J Chem Phys. 1993;98:7236–7244. [Google Scholar]
- 17.Lum K, Chandler D, Weeks JD. Hydrophobicity at small and large length scales. J Phys Chem B. 1999;103:4570–4577. [Google Scholar]
- 18.Sharma S, Debenedetti PG. Free energy barriers to evaporation of water in hydrophobic confinement. J Phys Chem B. 2012;116:13282–13289. doi: 10.1021/jp308362h. [DOI] [PubMed] [Google Scholar]
- 19.Bruot N, Caupin F. Curvature dependence of the liquid-vapor surface tension beyond the Tolman approximation. Phys Rev Lett. 2016;116:056102. doi: 10.1103/PhysRevLett.116.056102. [DOI] [PubMed] [Google Scholar]
- 20.Skripov VP. Metastable Liquids. Halsted; New York: 1972. [Google Scholar]
- 21.Debenedetti PG. Metastable Liquids: Concepts and Principles. Princeton Univ Press; Princeton: 1996. [Google Scholar]
- 22.Amabili M, Lisi E, Giacomello A, Casciola C. Wetting and cavitation pathways on nanodecorated surfaces. Soft Matter. 2016;12:3046–3055. doi: 10.1039/c5sm02794b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Meloni S, Giacomello A, Casciola CM. Theoretical aspects of vapor/gas nucleation at structured surfaces. J Chem Phys. 2016;145:211802. doi: 10.1063/1.4964395. [DOI] [PubMed] [Google Scholar]
- 24.Bolhuis PG, Chandler D, Dellago C, Geissler PL. Transition path sampling: Throwing ropes over rough mountain passes, in the dark. Annu Rev Phys Chem. 2002;53:291–318. doi: 10.1146/annurev.physchem.53.082301.113146. [DOI] [PubMed] [Google Scholar]
- 25.Giacomello A, Meloni S, Müller M, Casciola CM. Mechanism of the Cassie-Wenzel transition via the atomistic and continuum string methods. J Chem Phys. 2015;142:104701. doi: 10.1063/1.4913839. [DOI] [PubMed] [Google Scholar]
- 26.Lum K, Luzar A. Pathway to surface-induced phase transition of a confined fluid. Phys Rev E. 1997;56:R6283–R6286. [Google Scholar]
- 27.Bolhuis PG, Chandler D. Transition path sampling of cavitation between molecular scale solvophobic surfaces. J Chem Phys. 2000;113:8154–8160. [Google Scholar]
- 28.Leung K, Luzar A, Bratko D. Dynamics of capillary drying in water. Phys Rev Lett. 2003;90:065502. doi: 10.1103/PhysRevLett.90.065502. [DOI] [PubMed] [Google Scholar]
- 29.Luzar A. Activation barrier scaling for the spontaneous evaporation of confined water. J Phys Chem B. 2004;108:19859–19866. [Google Scholar]
- 30.Coasne B, Galarneau A, Di Renzo F, Pellenq R. Intrusion and retraction of fluids in nanopores: Effect of morphological heterogeneity. J Phys Chem C. 2009;113:1953–1962. [Google Scholar]
- 31.Sharma S, Debenedetti PG. Evaporation rate of water in hydrophobic confinement. Proc Natl Acad Sci USA. 2012;109:4365–4370. doi: 10.1073/pnas.1116167109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Remsing RC, et al. Pathways to dewetting in hydrophobic confinement. Proc Natl Acad Sci USA. 2015;112:8181–8186. doi: 10.1073/pnas.1503302112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Altabet YE, Haji-Akbari A, Debenedetti PG. Effect of material flexibility on the thermodynamics and kinetics of hydrophobically induced evaporation of water. Proc Natl Acad Sci USA. 2017;114:E2548–E2555. doi: 10.1073/pnas.1620335114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Maragliano L, Fischer A, Vanden-Eijnden E, Ciccotti G. String method in collective variables: Minimum free energy paths and isocommittor surfaces. J Chem Phys. 2006;125:024106–024106. doi: 10.1063/1.2212942. [DOI] [PubMed] [Google Scholar]
- 35.Husowitz B, Talanquer V. Nucleation in cylindrical capillaries. J Chem Phys. 2004;121:8021–8028. doi: 10.1063/1.1795133. [DOI] [PubMed] [Google Scholar]
- 36.Abascal JL, Vega C. A general purpose model for the condensed phases of water: TIP4P/2005. J Chem Phys. 2005;123:234505. doi: 10.1063/1.2121687. [DOI] [PubMed] [Google Scholar]
- 37.Vega C, De Miguel E. Surface tension of the most popular models of water by using the test-area simulation method. J Chem Phys. 2007;126:154707. doi: 10.1063/1.2715577. [DOI] [PubMed] [Google Scholar]
- 38.Eroshenko V. 2000. US Patent 6,052,992.
- 39.Eroshenko V, Piatiletov I, Coiffard L, Stoudenets V. A new paradigm of mechanical energy dissipation. Part 2: Experimental investigation and effectiveness of a novel car damper. Proc Inst Mech Eng D. 2007;221:301–312. [Google Scholar]
- 40.Trzpit M, Soulard M, Patarin J. The pure silica Chabazite: A high volume molecular spring at low pressure for energy storage. Chem Lett. 2007;36:980–981. [Google Scholar]
- 41.Trzpit M, et al. Pure silica Chabazite molecular spring: A structural study on water intrusion- extrusion processes. J Phys Chem B. 2008;112:7257–7266. doi: 10.1021/jp711889k. [DOI] [PubMed] [Google Scholar]
- 42.Gallo P, Rovere M, Chen S-H. Dynamic crossover in supercooled confined water: Understanding bulk properties through confinement. J Phys Chem Lett. 2010;1:729–733. [Google Scholar]
- 43.Eroshenko V, Regis R-C, Soulard M, Patarin J. The heterogeneous systems ‘water-hydrophobic zeolites’: New molecular springs. C R Phys. 2002;3:111–119. [Google Scholar]
- 44.Michelin-Jamois M, Picard C, Vigier G, Charlaix E. Giant osmotic pressure in the forced wetting of hydrophobic nanopores. Phys Rev Lett. 2015;115:036101. doi: 10.1103/PhysRevLett.115.036101. [DOI] [PubMed] [Google Scholar]
- 45.Michelin-Jamois M. 2014. PhD thesis (Institut National des Sciences Appliquées, Lyon)
- 46.Grosu Y, Renaudin G, Eroshenko V, Nedelec J-M, Grolier J-P. Synergetic effect of temperature and pressure on energetic and structural characteristics of ZIF-8+ water molecular spring. Nanoscale. 2015;7:8803–8810. doi: 10.1039/c5nr01340b. [DOI] [PubMed] [Google Scholar]
- 47.Bushuev YG, Sastre G, de Julian-Ortiz JV, Gálvez J. Water–hydrophobic zeolite systems. J Phys Chem C. 2012;116:24916–24929. [Google Scholar]
- 48.Miller TF, Vanden-Eijnden E, Chandler D. Solvent coarse-graining and the string method applied to the hydrophobic collapse of a hydrated chain. Proc Natl Acad Sci USA. 2007;104:14559–14564. doi: 10.1073/pnas.0705830104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Giacomello A, Schimmele L, Dietrich S. Wetting hysteresis induced by nanodefects. Proc Natl Acad Sci USA. 2016;113:E262–E271. doi: 10.1073/pnas.1513942113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Amabili M, Giacomello A, Meloni S, Casciola C. Collapse of superhydrophobicity on nanopillared surfaces. Phy Rev Fluids. 2017;2:034202. [Google Scholar]
- 51.Torrie GM, Valleau JP. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J Comp Phys. 1977;23:187–199. [Google Scholar]
- 52.Maragliano L, Vanden-Eijnden E. A temperature accelerated method for sampling free energy and determining reaction pathways in rare events simulations. Chem Phys Lett. 2006;426:168–175. [Google Scholar]
- 53.Laio A, Rodriguez-Fortea A, Gervasio FL, Ceccarelli M, Parrinello M. Assessing the accuracy of metadynamics. J Phys Chem B. 2005;109:6714–6721. doi: 10.1021/jp045424k. [DOI] [PubMed] [Google Scholar]
- 54.Amabili M, Giacomello A, Meloni S, Casciola CM. Intrusion and extrusion of a liquid on nanostructured surfaces. J Phys Condens Matt. 2016;29:014003. doi: 10.1088/0953-8984/29/1/014003. [DOI] [PubMed] [Google Scholar]
- 55.Giacomello A, Chinappi M, Meloni S, Casciola CM. Metastable wetting on superhydrophobic surfaces: Continuum and atomistic views of the Cassie-Baxter–Wenzel transition. Phys Rev Lett. 2012;109:226102. doi: 10.1103/PhysRevLett.109.226102. [DOI] [PubMed] [Google Scholar]
- 56.Prakash S, Xi E, Patel AJ. Spontaneous recovery of superhydrophobicity on nanotextured surfaces. Proc Natl Acad Sci USA. 2016;113:5508–5513. doi: 10.1073/pnas.1521753113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Panter JR, Kusumaatmaja H. The impact of surface geometry, cavitation, and condensation on wetting transitions: Posts and reentrant structures. J Phys Condens Matter. 2017;29:084001. doi: 10.1088/1361-648X/aa5380. [DOI] [PubMed] [Google Scholar]
- 58.Iwatsubo T, Suciu CV, Ikenagao M, Yaguchio K. Dynamic characteristics of a new damping element based on surface extension principle in nanopore. J Sound Vib. 2007;308:579–590. [Google Scholar]
- 59.Schimmele L, Napiórkowski M, Dietrich S. Conceptual aspects of line tensions. J Chem Phys. 2007;127:164715. doi: 10.1063/1.2799990. [DOI] [PubMed] [Google Scholar]
- 60.Schimmele L, Dietrich S. Line tension and the shape of nanodroplets. Eur Phys J E. 2009;30:427–430. doi: 10.1140/epje/i2009-10542-3. [DOI] [PubMed] [Google Scholar]
- 61.Rouquerol J, et al. Recommendations for the characterization of porous solids (technical report) Pure Appl Chem. 1994;66:1739–1758. [Google Scholar]
- 62.Giesche H. Mercury porosimetry: A general (practical) overview. Part Part Syst Character. 2006;23:9–19. [Google Scholar]
- 63.Ball PC, Evans R. Temperature dependence of gas adsorption on a mesoporous solid: Capillary criticality and hysteresis. Langmuir. 1989;5:714–723. [Google Scholar]
- 64.Neimark AV, Ravikovitch PI, Grün M, Schüth F, Unger KK. Pore size analysis of MCM-41 type adsorbents by means of nitrogen and argon adsorption. J Colloid Interface Sci. 1998;207:159–169. doi: 10.1006/jcis.1998.5748. [DOI] [PubMed] [Google Scholar]
- 65.Brakke KA. The surface evolver. Exp Math. 1992;1:141–165. [Google Scholar]
- 66.Plimpton S. Fast parallel algorithms for short-range molecular dynamics. J Comp Phys. 1995;117:1–19. [Google Scholar]
- 67.Ryckaert J-P, Ciccotti G, Berendsen HJ. Numerical integration of the Cartesian equations of motion of a system with constraints: Molecular dynamics of n-alkanes. J Comp Phys. 1977;23:327–341. [Google Scholar]
- 68.Martyna GJ, Klein ML, Tuckerman M. Nosé–Hoover chains: The canonical ensemble via continuous dynamics. J Chem Phys. 1992;97:2635–2643. [Google Scholar]
- 69.E W, Ren W, Vanden-Eijnden E. Simplified and improved string method for computing the minimum energy paths in barrier-crossing events. J Chem Phys. 2007;126:164103. doi: 10.1063/1.2720838. [DOI] [PubMed] [Google Scholar]
- 70.Lorensen WE, Cline HE. Proceedings of the 14th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’87. Vol 21. Assoc Comput Machinery; New York: 1987. pp. 163–169. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.