Chasing the open-state structure of pentameric ligand-gated ion channels

Members of the pentameric ligand-gated ion channel family have been crystallized in different conformations, including one in which the transmembrane pore is surprisingly wide. Gonzalez-Gutierrez et al. show that the open-channel conformation of animal members is more similar to the models with narrow pores.

Abstract

Remarkable advances have been made toward the structural characterization of ion channels in the last two decades. However, the unambiguous assignment of well-defined functional states to the obtained structural models has proved challenging. In the case of the superfamily of nicotinic-receptor channels (also referred to as pentameric ligand-gated ion channels [pLGICs]), for example, two different types of model of the open-channel conformation have been proposed on the basis of structures solved to resolutions better than 4.0 Å. At the level of the transmembrane pore, the open-state models of the proton-gated pLGIC from Gloeobacter violaceus (GLIC) and the invertebrate glutamate-gated Cl^– channel (GluCl) are very similar to each other, but that of the glycine receptor (GlyR) is considerably wider. Indeed, the mean distances between the axis of ion permeation and the Cα atoms at the narrowest constriction of the pore (position −2′) differ by ∼2 Å in these two classes of model, a large difference when it comes to understanding the physicochemical bases of ion conduction and charge selectivity. Here, we take advantage of the extreme open-channel stabilizing effect of mutations at pore-facing position 9′. We find that the I9′A mutation slows down entry into desensitization of GLIC to the extent that macroscopic currents decay only slightly by the end of pH 4.5 solution applications to the extracellular side for several minutes. We crystallize (at pH 4.5) two variants of GLIC carrying this mutation and solve their structures to resolutions of 3.12 Å and 3.36 Å. Furthermore, we perform all-atom molecular dynamics simulations of ion permeation and picrotoxinin block, using the different open-channel structural models. On the basis of these results, we favor the notion that the open-channel structure of pLGICs from animals is much closer to that of the narrow models (of GLIC and GluCl) than it is to that of the GlyR.

Introduction

It may be argued that the ultimate goal of structural biology as applied to ion channels is to provide a picture of what the protein looks like in its different physiologically relevant conformational states. Although by no means the “whole story,” it seems that little could be done without this information if we wish to understand the physicochemical bases of ion-channel function. Remarkable advances have been made toward the structural characterization of ion channels in the last two decades. However, the assignment of well-defined functional states to the obtained structural models—a crucial aspect of the entire endeavor—has proved more elusive than anticipated and is often a matter of controversy.

Undoubtedly, the problem arises because protein structure cannot typically be studied under the same conditions that are used to study protein function. For example, whereas the functional properties of an ion channel are usually assessed in the context of a phospholipid membrane at room temperature, structure is frequently determined in detergent micelles at cryogenic temperatures, often under the constraints imposed by a crystal lattice. Furthermore, whereas the functional effect of channel-activating stimuli is often assessed under nonequilibrium conditions (say, right after the application of a ligand-concentration jump), the effect of such stimuli on structure is—with only rare exceptions (e.g., Unwin and Fujiyoshi, 2012)—studied at much longer times, too long to be reached during electrophysiological recordings, once the conformational equilibrium has presumably been attained. Thus, in the face of such disconnect between structural and functional studies, some authors choose to predict the functional state of structural models on the basis of electrophysiological observations, whereas others make a judgment simply on the basis of what the structures look like, irrespective of functional considerations. In our view, both approaches have their own limitations, and we can imagine situations in which both may lead to wrong conclusions.

One aspect of channel function that benefits greatly from structural information is ion permeation. In the particular case of the pentameric ligand-gated ion channels (pLGICs), for example, decades of electrophysiological experiments—starting with, say, the seminal work of Imoto and coworkers (Imoto et al., 1988) and Galzi and coworkers (Galzi et al., 1992)—have led to a fairly sophisticated understanding of the determinants of single-channel conductance (Cymes and Grosman, 2012) and charge selectivity (Cymes and Grosman, 2016), and it seems to us that little can be advanced at this point by simply adding more electrophysiological observations. In our opinion, further knowledge will emerge from the application of molecular simulations, and for these to have any realistic meaning, an appropriate model of the open-channel structure must be used.

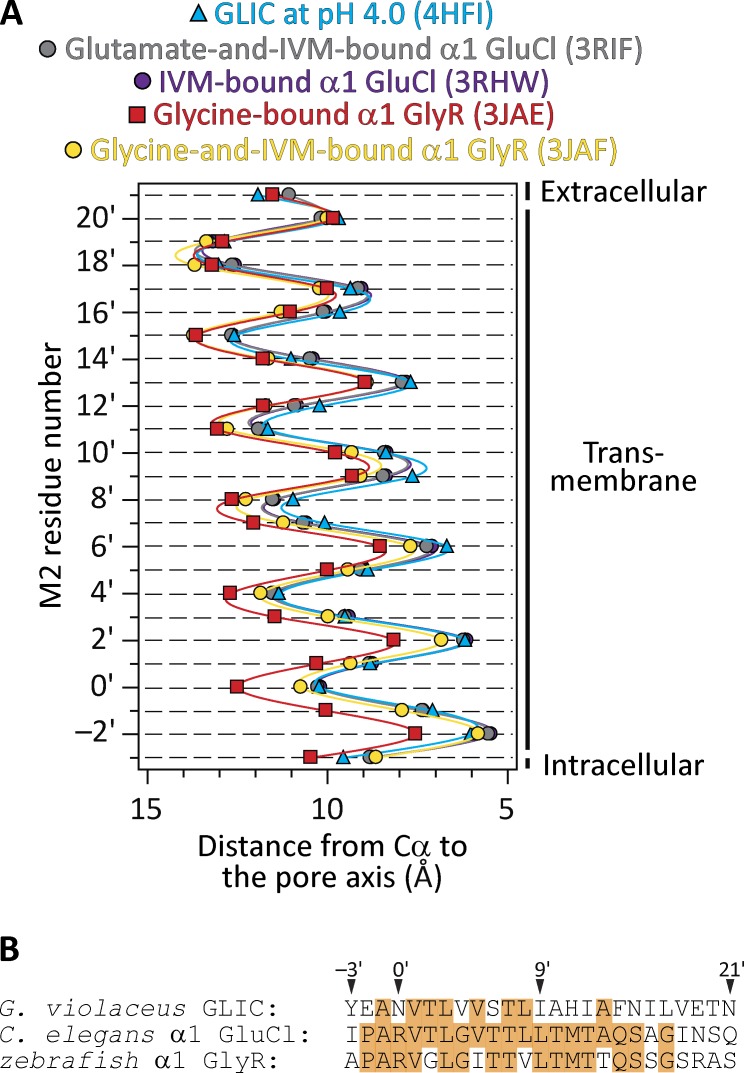
Models of the open-channel conformation of pLGICs (at resolutions better than 4.0 Å) have been proposed for the bacterial ligand-gated ion channel from Gloeobacter violaceus at pH 4.0 (GLIC; Protein Data Bank [PDB] ID code 4HFI; resolution, 2.4 Å; x-ray crystallography; Sauguet et al., 2013), the Caenorhabditis elegans α1 glutamate-gated Cl^– channel (α1 GluCl) bound to glutamate and ivermectin (PDB ID code 3RIF; 3.35 Å; x-ray crystallography; Hibbs and Gouaux, 2011), the C. elegans α1 GluCl bound to ivermectin alone (PDB ID code 3RHW; 3.26 Å; x-ray crystallography; Hibbs and Gouaux, 2011), and the zebrafish α1 glycine receptor (α1 GlyR) bound to glycine (PDB ID code 3JAE; 3.9 Å; single-particle electron cryomicroscopy; Du et al., 2015). A comparison of these structures reveals that, at the level of the transmembrane pore—and disregarding the side chains, which differ among members of the superfamily—the models of GLIC and GluCl are very similar to each other, whereas the model of the glycine-bound GlyR is considerably wider, especially at the intracellular end (Fig. 1). The mean distances between the axis of ion permeation and the Cα atoms at the narrowest constriction of the pore (position −2′) differ by ∼2 Å in these two classes of model. This difference in size is particularly relevant for studies of ion permeation because the channel’s charge-selectivity filter is formed precisely by this constriction and because the filter’s diameter is expected to affect conductance and selectivity. The assignment of these four structural models to the open-channel conformation was made, essentially, on the basis of pore size. Indeed, in all four cases, the transmembrane-pore lumen was deemed to be wide enough for hydrated or partially dehydrated monovalent ions to go through. However, when functional considerations are also taken into account to guide the interpretation of the data, a conflict arises because GLIC at pH 4.0, for example, desensitizes nearly completely in a matter of a few seconds (Gonzalez-Gutierrez and Grosman, 2010) and the α1 GlyR fully bound to glycine does so in a matter of a few minutes (e.g., Papke et al., 2011; Papke and Grosman, 2014)—of course, when embedded in a cell membrane. Needless to say, this is orders of magnitude faster than the kinetics of crystal growth.

Figure 1.

Different open-channel models. (A) Distances between the axis of ion permeation and the Cα atoms for residues in the pore-lining M2 α-helices of five different structural models of pLGICs (mean ± SE of all subunits; error bars smaller than the symbols were omitted). IVM, ivermectin. Solid lines are cubic-spline interpolations. The two GluCl profiles are nearly indistinguishable from each other. A comparison of pore dimensions including the side chains (as could be obtained using HOLE [Smart et al., 1996], for example) seems unwarranted here because the different models correspond to members of the superfamily with different amino acid sequences. The lumen of the pore is to the right of the plot. (B) Alignment of M2 α-helix sequences of the three pLGICs compared in A. Identical residues are indicated with an orange background.

Perhaps adding more confusion, a model of the zebrafish α1 GlyR bound to both glycine and ivermectin has also been recently generated (PDB ID code 3JAF; 3.8 Å; single-particle electron cryomicroscopy; Du et al., 2015). As shown in Fig. 1 A, the Cα profile of this model’s second transmembrane segment (M2) α-helices relative to the pore axis lies somewhere in between those of the narrower open-channel pores of GLIC and GluCl on the one hand, and the wider open-channel pore of the GlyR bound to glycine alone on the other. However, at the level of the most intracellular turn of M2 (that is, where the charge-selectivity filter is), the model of the GlyR bound to both glycine and ivermectin is much closer to the narrower models than it is to the wider one.

In an attempt to make sense out of this multiplicity of open-channel models, the narrower-pore conformation has recently been reclassified as a “partially open or desensitized-like” state (Du et al., 2015). It is unclear, however, how one would reconcile such a partially open conformation with what is known about these channels because sojourns in open-channel low-conductance states are rare and very short-lived in single-channel recordings from pLGICs (e.g., Auerbach and Sachs, 1983; Mangin et al., 2003). Also, it is unclear how the properties of a desensitized-like conformation would differ from those of a genuine desensitized conformation.

In hopes of shedding some light on this confusing situation, we crystallized two variants of GLIC (at pH 4.5) carrying the highly open-channel stabilizing isoleucine-to-alanine mutation at position 9′—in the middle of M2—and solved their structures. Furthermore, we performed all-atom molecular dynamics (MD) simulations of ion permeation and picrotoxinin block using the different structural models of pLGICs proposed to represent the open-channel conformation. On the basis of these results, we favor the idea that the open-channel structure of pLGICs—with the likely exception of the ligand-gated ion channel from Erwinia chrysanthemi (ELIC), which seems to form atypically wide pores (Gonzalez-Gutierrez and Grosman, 2015)—is much closer to the structural models of GLIC at pH ∼4.0, GluCl bound to ivermectin, GluCl bound to glutamate and ivermectin, and the GlyR bound to glycine and ivermectin (that is, the narrower models) than it is to the model of the GlyR bound to glycine alone.

Materials and methods

Electrophysiology, cell surface expression, and x-ray crystallography

Macroscopic currents from WT and mutant GLIC channels transiently expressed in HEK-293 cells were recorded at ∼22°C (Axopatch 200B amplifier; Molecular Devices; bandwidth: DC–5 kHz) using fast-perfused outside-out patches of membrane (solution-exchange time_10–90% < 150 µs) or fast-perfused whole cells (solution-exchange time_10–90% < 1.0 ms). In both the outside-out and whole-cell patch-clamp configurations, the membrane potential was held at −80 mV (negative inside the cell), and rapid pH jumps were achieved by the switching of two solutions (differing only in the proton concentration and pH-buffering molecule) flowing from either barrel of a piece of theta-type capillary glass mounted on a piezo-electric device (Burleigh-LSS-3100; Thorlabs; discontinued). In these two configurations, the patch-pipette solution consisted of (in mM) 110 KF, 40 KCl, 1.0 CaCl₂, 11 EGTA, and 10 HEPES/KOH, pH 7.4, whereas the solutions flowing through the barrels of the theta-type tubing consisted of (mM) 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, and—depending on the pH—10 acetic-acid/KOH (pH 4.5), 10 HEPES/KOH (pH 7.4), or 10 TABS/KOH (pH 9.0). Single-channel currents from the rat α1 GlyR (isoform b; accession no. P07727-2) transiently expressed in HEK-293 cells were recorded in the cell-attached configuration at ∼22°C (Axopatch 200B amplifier; Molecular Devices). These recordings were digitized at 100 kHz, filtered (cascaded f_c ≅ 23 kHz), and idealized (using the SKM algorithm in QuB; Qin, 2004) to estimate the open-channel current amplitude at different voltages. In this configuration, the pipette solution consisted of (in mM) 142 KCl, 5.4 NaCl, and 10 HEPES/KOH, pH 7.4. To bring the membrane potential of the cells close to zero, the cells were bathed in a high-K⁺ solution consisting of (in mM) 142 KCl, 5.4 NaCl, 1.8 CaCl₂, 1.7 MgCl₂, and 10 HEPES/KOH, pH 7.4.

The level of expression of GLIC WT and mutants on the plasma membrane of transfected HEK-293 cells was estimated by immunochemical detection of a human-influenza hemagglutinin tag (HA-tag) appended to the C-terminus of each construct. Immunochemical detection was performed using an anti–HA-tag high-affinity antibody from rat (clone 3F10; Roche) and an anti–rat IgG–horseradish peroxidase conjugate (Sigma-Aldrich). Chemiluminescence was detected using the ECL Plus kit (GE Healthcare) and a microplate reader (FLUOstar Omega; BMG Labtech) with background counts subtracted from each measurement. Total protein concentration was estimated using the Bradford assay. cDNAs coding HA-tagged channels were transfected only for the purpose of surface-expression determination. For electrophysiology and x-ray crystallography, cDNAs coding the HA-tag–less counterparts of these constructs were used instead.

Overexpression, purification, crystallization, and structure determination of GLIC mutants were performed as described previously (Gonzalez-Gutierrez et al., 2013).

Simulation-system preparation

Four structural models of pLGICs were studied computationally in this work: (1) GLIC C27S + K33C + I9′A + N21′C at pH 4.5 (this work); (2) GLIC Y27′A at pH 4.0 (PDB ID code 4LMK; Gonzalez-Gutierrez et al., 2013); (3) zebrafish α1 GlyR bound to glycine (PDB ID code 3JAE; Du et al., 2015); and (4) zebrafish α1 GlyR bound to both glycine and ivermectin (PDB ID code 3JAF; Du et al., 2015). For both GLIC and the GlyR, only the transmembrane portion of the protein—extending from the beginning of M1 (Phe 195 in GLIC, and Gln 235 in the GlyR) to the last residue of each subunit (Phe 317 in GLIC, and Val 364 in the GlyR)—was simulated. In the case of the structural model of the α1 GlyR bound to glycine alone, M3–M4-linker residues 327 and 328 (which are missing from the PDB file) were not included in the model. The side chains at position 21′ of GLIC in the C27S + K33C + I9′A + N21′C mutant and position 27′ in the Y27′A mutant were modeled as their WT counterparts using the psfgen module in VMD (Humphrey et al., 1996). CHARMM ACE and CT2 patches were added to the N-terminal and C-terminal residues, respectively, to avoid introducing artificial charges.

The simulated transmembrane-domain fragments of GLIC and zebrafish GlyR contain several naturally occurring ionizable residues. In the absence of experimental information about their side-chain pK_a values, acidic residues were assumed to be negatively charged, histidines were assumed to be neutral, and arginines and lysines were assumed to be positively charged. Little is known about the effect of positive or negative transmembrane charges on the single-channel conductance of GLIC or the GlyR, but data on the muscle nicotinic acetylcholine receptor (AChR; Cymes et al., 2005; Cymes and Grosman, 2008, 2012, 2015) allow us to predict that only the protonation states of ionizable side chains at the intracellular end of M2 (namely, the glutamate at position −2′ of GLIC and the arginine at position 0′ of the GlyR) have a major effect on the rate of ion conduction. It should be noted that the pH of the intracellular solution is typically held at neutral during electrophysiological recordings from these two channels.

The two models of GLIC were embedded in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE) membranes, whereas the two models of the α1 GlyR were embedded in 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) membranes using a new protocol (see Membrane-patch preparation, below). Each prepared membrane patch was combined with the corresponding membrane protein, and water and ions were added subsequently (150 mM KCl for GLIC and 150 mM NaCl for the GlyR). Protein side-chain rotamers were optimized using SCWRL4 (Krivov et al., 2009).

To generate the expanded and partially expanded versions of the model of the GlyR bound to glycine and ivermectin, we applied grid-steered MD simulations (Wells et al., 2007) to the cryo-EM model (PDB ID code 3JAF). The system was prepared using the same protocol as for all other systems with 500 mM NaCl. The system was simulated for 400 ps to relax the lipid tails with protein-heavy atoms and lipid-phosphorus atoms harmonically restrained with a force constant of 1.0 kcal mol^–1 Å^–2. This was followed by a 5-ns simulation with only protein-backbone heavy atoms restrained (k = 1.0 kcal mol^–1 Å^–2). After these two steps, grid-steered MD simulations were performed for 1 ns. A potential-energy grid was imposed upon the Cα atoms of residues 266–270 (M2 positions −2′ through 2′) with a grid-scaling factor of 2 or 3. The Cα atoms of other protein residues with α-helical secondary structure were restrained (k = 0.1 kcal mol^–1 Å^–2). In addition, the secondary structure (backbone hydrogen bonds, angles, and dihedrals) of all α-helical regions was restrained (k = 20 kcal mol^–1 Å^–2 for bonds, 20 kcal mol^–1 deg^–2 for angles, and 200 kcal mol^–1 for dihedrals). Furthermore, a symmetry restraint (Chan et al., 2011) was applied to all Cα atoms in the α-helical regions (k = 2 kcal mol^–1 Å^–2) to maintain the fivefold symmetry of the system. The potential energy on the grid was highest at the origin, and it decreased radially (with a slope of 1 kcal mol^–1 Å^–1) along the x and y dimensions while remaining constant along the z dimension.

In their original PDB files, some of the side chains of the two GlyR models were modeled as methyl groups even when the corresponding amino acids were not alanine (Du et al., 2015). Here, we constructed these side chains as their WT counterparts using the psfgen module in VMD (Humphrey et al., 1996). The final size of each system was 150–160 Å × 150–160 Å × 95–100 Å with ∼200,000–220,000 atoms.

Membrane-patch preparation

A 3-Å–resolution simulated density map was generated using the VMD MDFF plugin (Humphrey et al., 1996; Trabuco et al., 2008; Singharoy et al., 2016) for each structural model. After superimposing this map with a lipid bilayer, any phospholipid with at least one atom inside the high-density region (> 0.8) or inside the central hollow region (that is, in the pore lumen) was removed. Each membrane patch was simulated at 100 mM ionic strength using implicit solvent (ε_r = 80). The cutoff for Born radii was 14 Å, 16 Å for nonbonded interactions, and switching-function took effect at 15 Å. The pair-list cutoff radius was 17 Å. The time step was 1 fs with long-range electrostatic forces computed every 4 steps, and short-range nonbonded interactions updated every 2 steps. The Langevin thermostat was used to maintain the temperature at 310 K with a damping coefficient of 1.0 ps^–1 and hydrogen atoms excluded from the temperature bath. Grid force (Wells et al., 2007) was applied to the heavy atoms of the phospholipids, which were repelled by the 3-Å–resolution simulated density map. The pseudo-charges of the phospholipid atoms were set at 1 elementary charge. Phospholipid molecules that were 60 Å away from the center of the channel were restrained to their starting positions by a harmonic potential with a force constant of 1.0 kcal mol^–1 Å^–2. We found this procedure necessary to maintain the shape of the membrane edges because applying periodic-boundary conditions in implicit-solvent simulations is not fully supported in NAMD (Nelson et al., 1996; Kalé et al., 1999; Phillips et al., 2005). Each system was energy-minimized for 1,000 steps and then equilibrated for 50 ps. The last frame of these membrane-preparation trajectories was used to generate the fully solvated protein–membrane systems.

Molecular dynamics simulations

MD simulations were performed with a constant pressure–temperature (NPT) ensemble at 310 K and 101,325 Pa. Each solvated protein–membrane system was first energy-minimized for 500 steps followed by 400 ps of lipid-tail relaxation. During this step, the lipid-phosphorus atoms and the protein heavy atoms were harmonically restrained with a force constant of 1.0 kcal mol^–1 Å^–2. Then, each system was simulated with only protein-backbone heavy atoms restrained. Throughout these simulations, the root mean-square deviation (RMSD) calculated for all protein-backbone heavy atoms (using the initial conformation as the reference) remained below 0.41 Å for all simulated systems. Bonds involving hydrogen atoms were constrained using the SETTLE algorithm (Miyamoto and Kollman, 1992). The time step was set at 2.0 fs with long-range electrostatic forces computed every 2 steps, and short-range nonbonded interactions calculated every step. The Langevin thermostat was used to maintain the temperature with a damping coefficient of 1.0 ps^–1. The pressure control along each dimension was decoupled. The ratio between the length and width of the membrane plane was kept constant. Nosé-Hoover Langevin piston pressure control was used (Martyna et al., 1994; Feller et al., 1995) with an oscillation period of 100 fs and a damping time of 50 fs. All simulations were performed using NAMD 2 (Nelson et al., 1996; Kalé et al., 1999; Phillips et al., 2005) using the CHARMM36 force field (with the August 2014 update) for both protein (Best et al., 2012) and lipids (Klauda et al., 2010). This version of the force field includes a correction for the van der Waals interactions between Na⁺ and oxygen atoms occurring in protein carboxylate groups and in lipid carboxylate, carboxylate-ester, and phosphate-ester groups (Venable et al., 2013).

Some of the simulations probed the effect of picrotoxinin (C₁₅H₁₆O₆) on the number of ion crossings through the GlyR. To this end, the toxin structure was taken from PDB ID code 3RI5 (a structural model of the picrotoxinin-bound α1 GluCl channel; Hibbs and Gouaux, 2011) and placed into the structural models of the glycine-bound GlyR (PDB ID code 3JAE) and the glycine-and-ivermectin–bound GlyR (PDB ID code 3JAF) upon GluCl–GlyR pairwise alignment using the Cα atoms of their respective transmembrane domains. The force field parameters for picrotoxinin were obtained from CGenFF (Vanommeslaeghe and MacKerell, 2012; Vanommeslaeghe et al., 2012). No restraints were applied to the toxin during the simulations.

All pore-radius profiles were calculated using HOLE (Smart et al., 1996) with parameter file simple.rad.

Online supplemental material

Fig. S1 shows representative size-exclusion chromatography profiles of WT GLIC and the C27S + K33C + I9′A + N21′C mutant. Fig. S2 shows ion trajectories corresponding to an MD simulation of ion permeation through the structural model of the disulfide-reduced GLIC C27S + K33C + I9′A + N21′C mutant at −500 mV along with the mean pore-radius profile of the protein during the simulation. Fig. S3 shows mean pore-radius profiles of two picrotoxinin-bound models of the α1 GlyR during MD simulations of ion permeation. Table S1 shows data collection and refinement statistics corresponding to the x-ray crystal structures of GLIC E−2′I + I9′A and the disulfide-reduced GLIC C27S + K33C + I9′A + N21′C mutants.

Results

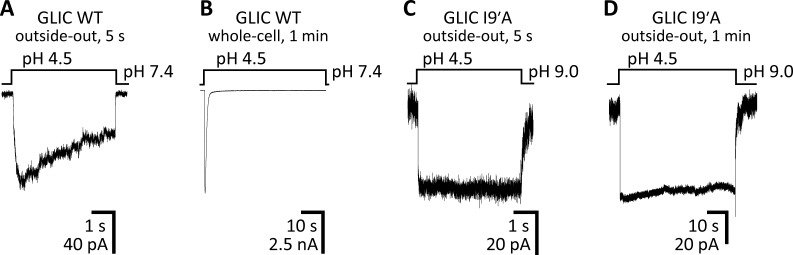
In an effort to obtain direct structural information about the open-channel conformation of pLGICs, we set out to crystallize an open-channel–stabilized mutant of the bacterial orthologue GLIC. We chose to work on GLIC because we have recently found its gating and pore-blocking properties to mimic those of pLGICs from animals more closely than do the gating and blocking properties of the, also bacterial, ELIC channel—the open-channel properties of ELIC are consistent with a much wider pore instead (Gonzalez-Gutierrez and Grosman, 2015). Moreover, unlike ELIC, GLIC has been found to crystallize in a variety of conformations (Bocquet et al., 2009; Hilf and Dutzler, 2009; Prevost et al., 2012; Gonzalez-Gutierrez et al., 2013; Sauguet et al., 2014; Basak et al., 2017), some (at least) of which are expected to have physiological relevance. For example, we have crystallized GLIC in what is likely to be the fully bound (that is, fully protonated) closed-channel conformation (Gonzalez-Gutierrez et al., 2013), whereas others have crystallized its deprotonated counterpart (Sauguet et al., 2014); here, we are interested in the fully protonated open-channel conformation. In an attempt to bias the closed $\rightleftharpoons$ open $\rightleftharpoons$ desensitized equilibrium strongly toward the open conformation—despite the eventually unfavorable energetic effects of detergent solubilization and crystal-lattice formation—we decided to engineer an extreme gain-of-function mutation: the isoleucine-to-alanine mutation at position 9′ of M2. In GLIC, this mutation manifests electrophysiologically in essentially the same way as it does when engineered in animal pLGICs: the deactivation time constant becomes slower than the WT’s by a factor of >150 (Gonzalez-Gutierrez and Grosman, 2015), and desensitization upon exposure to pH 4.5 extracellular solution becomes so slow that little decline of the current can be observed during 1-min applications (Fig. 2; see also Gonzalez-Gutierrez et al., 2012). Although we could not record clear single-channel currents from this mutant—which would have allowed a more unambiguous characterization of its functional properties—the displayed macroscopic behavior was consistent with the channel having a much-increased closed $\rightleftharpoons$ open equilibrium constant and a much-reduced open $\rightleftharpoons$ desensitized equilibrium constant (both at pH 4.5) just as has been found to be the case for the well-characterized 9′-position mutants of the fully liganded muscle AChR (Filatov and White, 1995; Labarca et al., 1995; Cymes et al., 2002) and the α7 AChR (Revah et al., 1991). A direct consequence of this stabilization of the open-channel conformation relative to the closed- and desensitized-channel conformations is a leftward shift of the open-probability–agonist-concentration relationship. In the particular case of the proton-gated GLIC, this phenomenon likely explains the increased mutant-channel activity at pH 7.4, a concentration of protons that is too low to appreciably activate the WT. It is precisely to reduce this increased background activity of the I9′A mutant that, for some of our recordings, we raised the pH of the “ligand-free” solution to 9.0.

Figure 2.

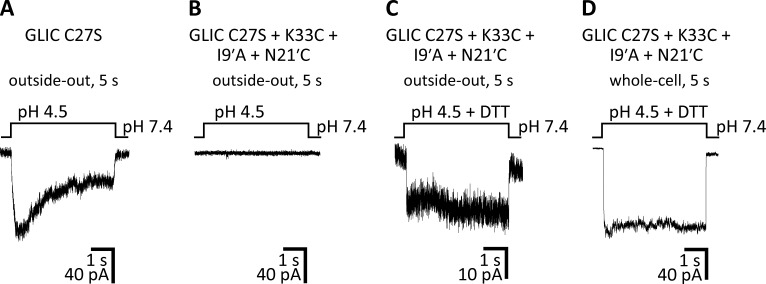
The gain-of-function effect of the I9′A mutation on GLIC. (A–D) Macroscopic-current responses of WT GLIC (A and B) and the I9′A mutant (C and D) to 5-s or 1-min pulses of pH 4.5 extracellular solution. The displayed traces are representative recordings obtained in the outside-out or whole-cell configuration at −80 mV.

Structures of open-channel–stabilized mutants

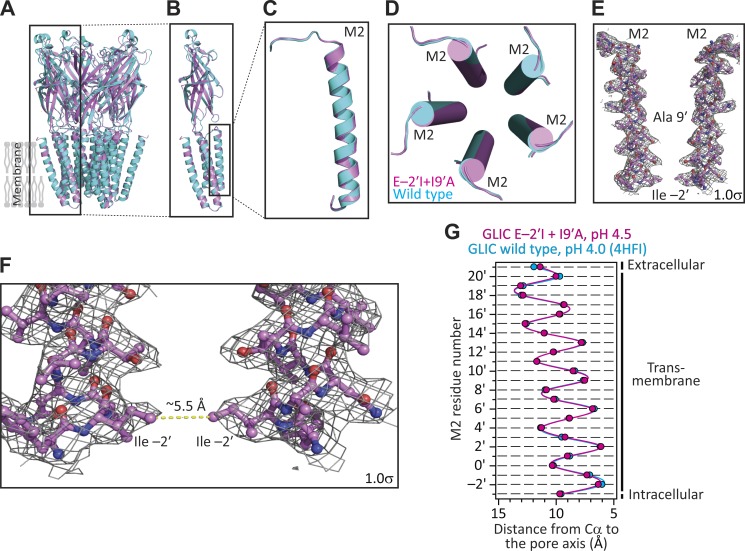
BL21-Gold (DE3) Escherichia coli cells (Agilent Technologies) transformed with the I9′A mutant of GLIC failed to grow, likely because of the toxic effect of the increased channel activity at the neutral pH (∼7.15) of the culture medium (Terrific broth; Invitrogen). Because lowering the medium’s proton concentration to pH 9.0 did not recover cell growth, we decided to further engineer the I9′A construct. First, we mutated the glutamate at position −2′ of M2 to the bulkier and nonionizable isoleucine. From single-channel functional studies that unambiguously reported on the open-channel conformation, we found that position −2′ lines the narrowest constriction of the transmembrane pore of the muscle AChR (Cymes et al., 2005). Assuming that the same is the case for GLIC, we surmised that replacing a pore-facing acidic side chain in a cation-selective channel with a neutral and bulkier side chain would lower the single-channel conductance. In turn, this would allow the transformed E. coli cells to grow, even if the channel’s open probability at neutral pH were high. Both expectations were borne out: channel currents could not be recorded from HEK-293 cells transfected with cDNA coding the E−2′I + I9′A double mutant (Fig. 3, A and B), despite WT-like expression on the plasma membrane (Fig. 3 C), and the transformed E. coli cells grew well and expressed typical amounts of recombinant protein. We crystallized this construct at pH 4.5 and solved its structure to a resolution of 3.12 Å (Table S1). A comparison to the structural model obtained for WT GLIC at pH 4.0 (PDB ID code 4HFI) revealed that the two structures are, essentially, indistinguishable at the level of the Cα atoms of the five pore-lining M2 α-helices (Fig. 4). Analysis of the mutant’s model pore-radius profile (estimated using HOLE; Smart et al., 1996) indicated that the narrowest constriction of the pore (∼2.0 Å in diameter) occurs at the level of the engineered isoleucine side chains.

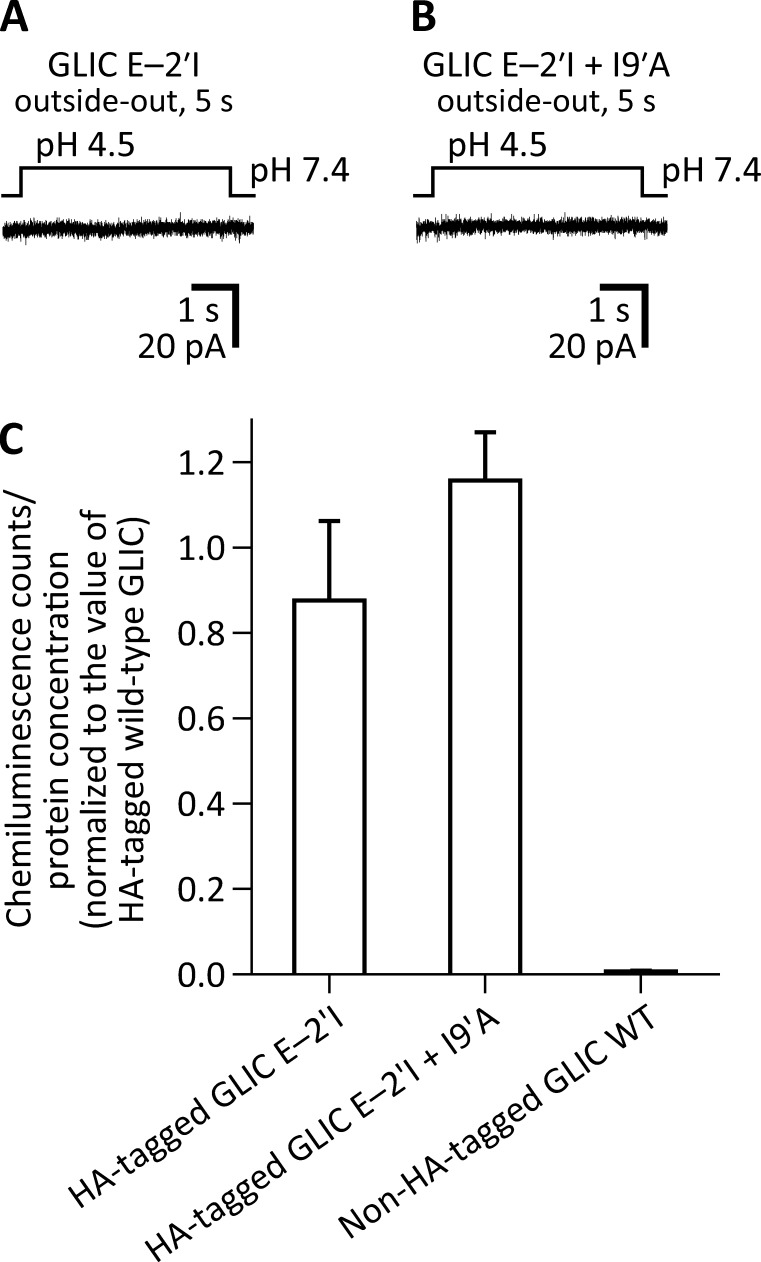
Figure 3.

The E−2′I mutation suppresses the gain-of-function effect of the I9′A mutation on GLIC. Macroscopic-current responses of the E−2′I (A) and E−2′I + I9′A (B) mutants to 5-s pulses of pH 4.5 extracellular solution. The displayed traces are representative recordings obtained in the outside-out configuration at −80 mV. (C) Expression of GLIC mutants on the plasma membrane of HEK-293 cells. The presence of GLIC on the cell surface was detected immunochemically using a HA-tag appended to the C-terminal end of each tested construct. Values of chemiluminescence counts divided by protein concentration were normalized to those obtained for the HA-tagged WT GLIC for each individual experiment (n = 3). The mean and standard error of these normalized values were calculated and plotted for each construct.

Figure 4.

X-ray crystal structure of GLIC E−2′I + I9′A at pH 4.5. (A–D) Structural alignment of the models of GLIC E−2′I + I9′A at pH 4.5 (magenta) and GLIC WT at pH 4.0 (PDB ID code 4HFI; cyan). (E and F) M2 α-helices of two nonadjacent subunits of the double mutant. The approximate locations of the mutated side chains are indicated. Mesh representations show the 2F_o − F_c electron-density maps contoured at a level of 1.0σ. The narrowest constriction of this mutant’s pore occurs at the level of the engineered isoleucine side chains; its diameter (estimated using HOLE [Smart et al., 1996], and thus taking into account the atoms’ van der Waals radii) is ∼2.0 Å. (G) Cα profiles of the two structural models compared in (A–D). The five subunits of each model were averaged. Error bars (omitted if smaller than the symbols) are standard errors. Solid lines are cubic-spline interpolations. The lumen of the pore is to the right of the plot.

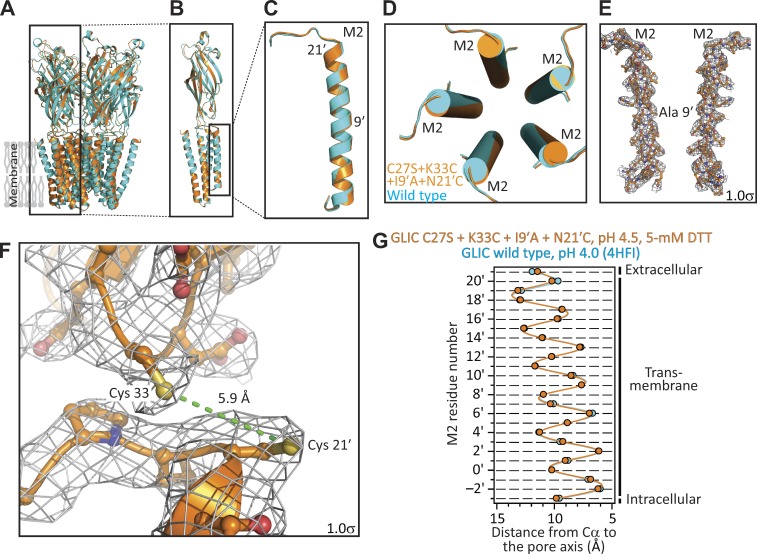
It may be argued that our failure to record currents from the E−2′I + I9′A double mutant—which we attributed to the channel’s much-reduced single-channel conductance—could instead reflect a loss-of-function effect of the E−2′I mutation on the closed $\rightleftharpoons$ open $\rightleftharpoons$ desensitized equilibrium that more than compensated for the gain-of-function effect of the I9′A mutation. If this were the case, the double mutant would not preferentially adopt the open-channel conformation at pH 4.5, but rather, the closed or the desensitized conformation. Because testing this hypothesis requires the electrophysiological characterization of the effect of the E−2′I mutation, and because no currents at all could be recorded from the E−2′I single mutant, either (Fig. 3 A), this possibility could not be ruled out. Therefore, we designed an alternative mutagenesis approach to countering the gain-of-function effect of the mutation at position 9′. We engineered a pair of cysteines—at positions 33 (in the extracellular-domain β1–β2 loop) and 21′ (at the extracellular end of M2)—whose oxidation to form an intrasubunit disulfide bond has been found to have a loss-of-function effect on the channel’s conformational equilibrium (Prevost et al., 2012). We speculated that, being a covalent modification, the open-channel–destabilizing effect of cysteine oxidation could offset the pronounced open-channel–stabilizing effect of the I9′A mutation, thus mitigating the toxicity of channel expression on E. coli growth. Importantly, once expressed and purified, the addition of reducing agents would relieve the covalent constraints, thus allowing the channel to occupy the open-channel conformation so strongly favored by the mutation at position 9′. These predictions were confirmed by our experiments: currents from this multiple mutant could be elicited only in the presence of 5 mM dithiothreitol (DTT), and the DTT-reduced channel displayed a much slower time course of desensitization (Fig. 5), much like the I9′A single mutant did (Fig. 2, C and D). Moreover, transformed E. coli cells grew well, and—although the amount of recombinant protein expressed was lower than in the case of the WT channel or the E−2′I + I9′A mutant, and the size-exclusion chromatography profile showed signs of lower pentameric stability in detergent (Fig. S1)—we succeeded in purifying this multiple mutant in enough quantities for structural determination. We crystallized this construct at pH 4.5 and in the presence of 5 mM DTT, and solved its structure to a resolution of 3.36 Å (Table S1). The distance between the side-chain sulfur atoms (∼5.9-Å) is consistent with the engineered cysteines being reduced (the sulfur–sulfur distance in a disulfide is ∼2.0 Å). Evidently, the large tendency of the I9′A mutation to keep the channel open at pH 4.5—and therefore, to keep residues 33 and 21' far apart—must have placed the engineered Cys33–Cys21′ disulfide bridge under mechanical strain at this pH. This added strain must have increased the disulfide's reduction potential (that is, its propensity to be reduced), which would explain the ability of DTT to split this disulfide even under the acidic conditions of our experiments (note that DTT’s oxidation potential decreases with proton concentration). A comparison of this structural model to that of WT GLIC at pH 4.0 (Fig. 6) and, indirectly, to that of the E−2′I + I9′A double mutant at pH 4.5 (Fig. 4), revealed that the three structures are, essentially, indistinguishable at the level of Cα atoms of the five pore-lining M2 α-helices.

Figure 5.

A disulfide bridge between cysteines engineered at positions 33 and 21′ suppresses the gain-of-function effect of the I9′A mutation on GLIC. (A–D) Macroscopic-current responses of the indicated constructs to 5-s pulses of pH 4.5 extracellular solution. The displayed traces are representative recordings obtained in the outside-out (A–C) or whole-cell (D) configuration at −80 mV. The cysteine at position 27—the only native cysteine of GLIC—was mutated to serine. The concentration of DTT was 5 mM. The traces in C and D are two examples of recordings from the same construct obtained on different cells. The recording in D was more heavily low-pass filtered than those in A–C.

Figure 6.

X-ray crystal structure of GLIC C27S + K33C + I9′A + N21′C, in the presence of 5 mM DTT, at pH 4.5. (A–D) Structural alignment of the models of GLIC C27S + K33C + I9′A + N21′C, in the presence of 5 mM DTT, at pH 4.5 (orange) and GLIC WT at pH 4.0 (PDB ID code 4HFI; cyan). (E) M2 α-helices of two nonadjacent subunits of the quadruple mutant. The approximate location of position 9′ is indicated. (F) Magnified view of the cysteines engineered at positions 33 (in the β1–β2 loop of the extracellular domain) and 21′ (at the extracellular end of M2). The ∼5.9-Å distance between the two side-chain sulfur atoms (in yellow) is consistent with the cysteines being reduced. In E and F, mesh representations show the 2F_o − F_c electron-density maps contoured at a level of 1.0σ. (G) Cα profiles of the two structural models compared in A–D. The five subunits of each model were averaged. Error bars (omitted if smaller than the symbols) are standard errors. Solid lines are cubic-spline interpolations. The lumen of the pore is to the right of the plot.

The desensitization time course of GLIC I9′A

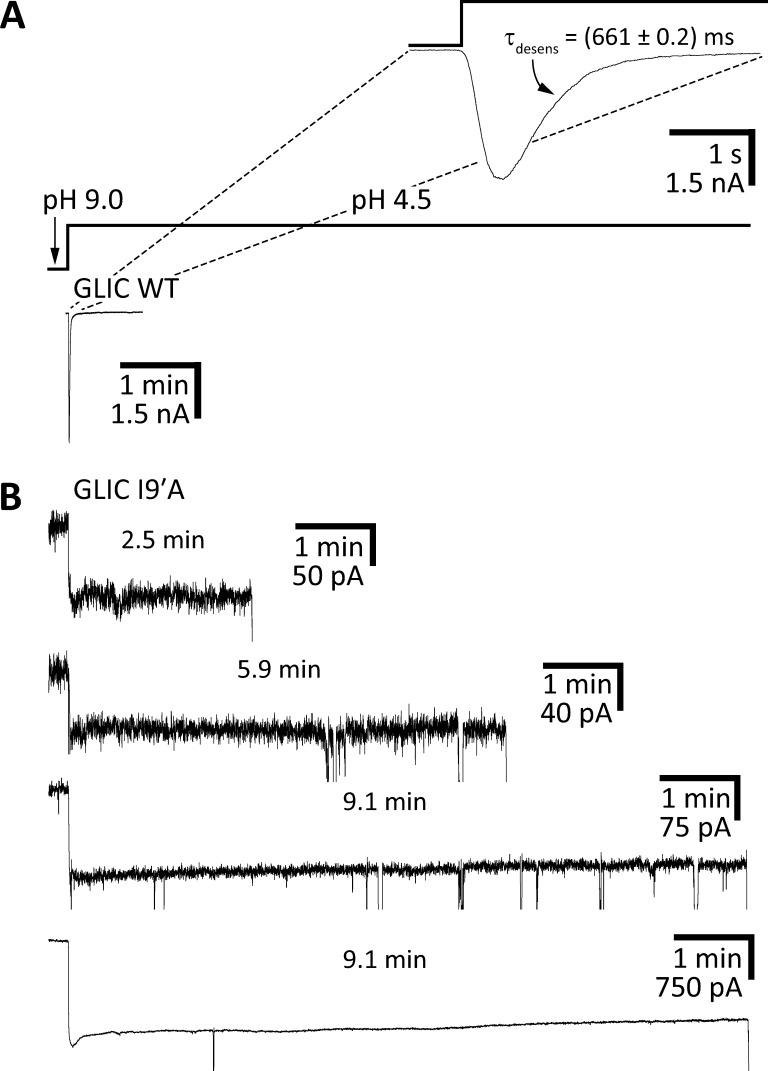
We realize that, in addition to the uncertainties associated with the presence or absence of a phospholipid membrane, one of the most obvious limitations of our approach is the vastly different time scales of the electrophysiological recordings and the crystallization process. Indeed, in the recordings from the I9′A mutant showing little desensitization (Fig. 2, C and D), the exposure to pH 4.5 solution was, at most, 1 min long, whereas it took several days at this pH for the crystals of the E−2′I + I9′A mutant (and several months for those of the C27S + K33C + I9′A + N21′C mutant) to grow. Thus, in an attempt to obtain more meaningful electrophysiological data, we recorded whole-cell currents upon stepping (rather than pulsing) the pH of the extracellular solution to 4.5. The recordings lasted as long as the patch-pipette–plasma-membrane seals did. In other words, the recordings terminated when the whole-cell seals, which were strongly destabilized upon prolonged exposure to pH 4.5, broke. We obtained a total of 12 recordings with pH 4.5 exposures longer than 1 min, and representative traces—including the two longest ones (both ∼9 min at pH 4.5)—are shown in Fig. 7. A comparison with the WT channel behavior under the same experimental conditions (Fig. 7 A) reveals that desensitization is greatly slowed down by the I9′A mutation. Moreover, the decay of the currents that is apparent in the traces (Fig. 7 B) should not be extrapolated to imply that the mutant desensitizes completely upon long-enough exposures to pH 4.5. As expected from the typically linear relationship between activation barriers and standard free-energy differences (ΔG°) of chemical reactions (Leffler and Grunwald, 1963) and conformational changes (Grosman et al., 2000), the much slower kinetics of entry into desensitization caused by the I9′A mutation are also likely to be accompanied by a destabilization of the desensitized state relative to the closed and open states. Such destabilization would result in a lower (perhaps much lower) occupancy of the desensitized state at equilibrium, and thus, in a nonzero value of the macroscopic currents elicited by saturating concentrations of agonist at long recording times.

Figure 7.

The desensitization time course of GLIC I9′A. Macroscopic-current responses of the indicated constructs upon stepping the pH of the extracellular solution from 9.0 to 4.5. The displayed traces are representative recordings obtained in the whole-cell configuration at −80 mV. (A) WT GLIC. In this recording, the current decayed to a zero-current level with a time-constant of ∼0.66 s. This means that it took only ∼3.0 s for the WT current to decay to ∼1% of its peak value. (B) GLIC I9′A. The brief downward current deflections reflect the instability of the membrane during prolonged exposure to pH 4.5; eventually, the seals broke, and the recordings ended. The duration of the pH 4.5 application before the seals broke is indicated for each I9′A trace. Evidently, desensitization is greatly slowed down by the mutation. The time scale is the same for all traces in A and B (with the exception of those in the inset of A).

Similarly long recordings from the C27S + K33C + I9′A + N21′C quadruple mutant could not be obtained; the seals were very unstable and the functional expression, as judged by the peak-current values, was typically low.

Computer simulations of ion conduction through GLIC

It could be said that our experimental evidence for a particular structure of the pore in the open-channel conformation is not any stronger than that supporting the much wider pore observed for the glycine-bound GlyR (PDB ID code 3JAE). Certainly, after all, both types of model resulted from the application of structural methods to detergent-solubilized pLGICs. Also, although the I9′A mutation favored the open-channel conformation of membrane-embedded GLIC at the pH at which the crystals grew (Fig. 7), the lack of a phospholipid membrane in the crystals, and the vastly different time scales of the electrophysiological observations and the crystallization process, made us wonder about the limitations of our results. Moreover, our own previous attempts to favor the open-channel conformation of the bacterial pLGIC ELIC, also using gain-of-function mutations, failed to change the channel’s conformation in crystals (Gonzalez-Gutierrez et al., 2012). To address these concerns, we decided to examine the different structural models of the open-channel conformation of pLGICs using all-atom molecular dynamics simulations of ion permeation and block.

We started by simulating ion permeation through the structural model of the double-cysteine + I9′A mutant of GLIC (Fig. 8). To make the system computationally more tractable, we simulated only the transmembrane domain of the pentamer—namely, the stretch between Phe 195 (at the N-terminus of M1) and Phe 317 (the most C-terminal residue) of each of the five subunits. To limit the drift of the simulated system away from the initial structure, we applied restraints to the protein-backbone heavy atoms throughout the simulations (for all simulated systems and all ion-permeation MD simulations performed in this work, the RMSD remained below 0.41 Å). We embedded this reduced model in a POPE membrane facing symmetrical 150 mM KCl solutions at 37°C. We chose to use K⁺ rather than Na⁺ because the experimentally estimated single-channel conductance of K⁺-carried currents is larger than that of Na⁺-carried currents in the cation-selective pLGICs (e.g., Elenes et al., 2009; Cymes and Grosman, 2012), and because we expected to record few cation crossings through GLIC at physiologically relevant membrane potentials. We chose POPE for these simulations because this phospholipid is a major component of Gram-negative bacterial membranes (Epand et al., 2007), whereas we typically use POPC bilayers for eukaryotic proteins (van Meer et al., 2008). Importantly, the fact that backbone atoms were restrained during our simulations of ion permeation (see Materials and methods) minimizes the impact of the particular choice of phospholipid on protein dynamics.

Figure 8.

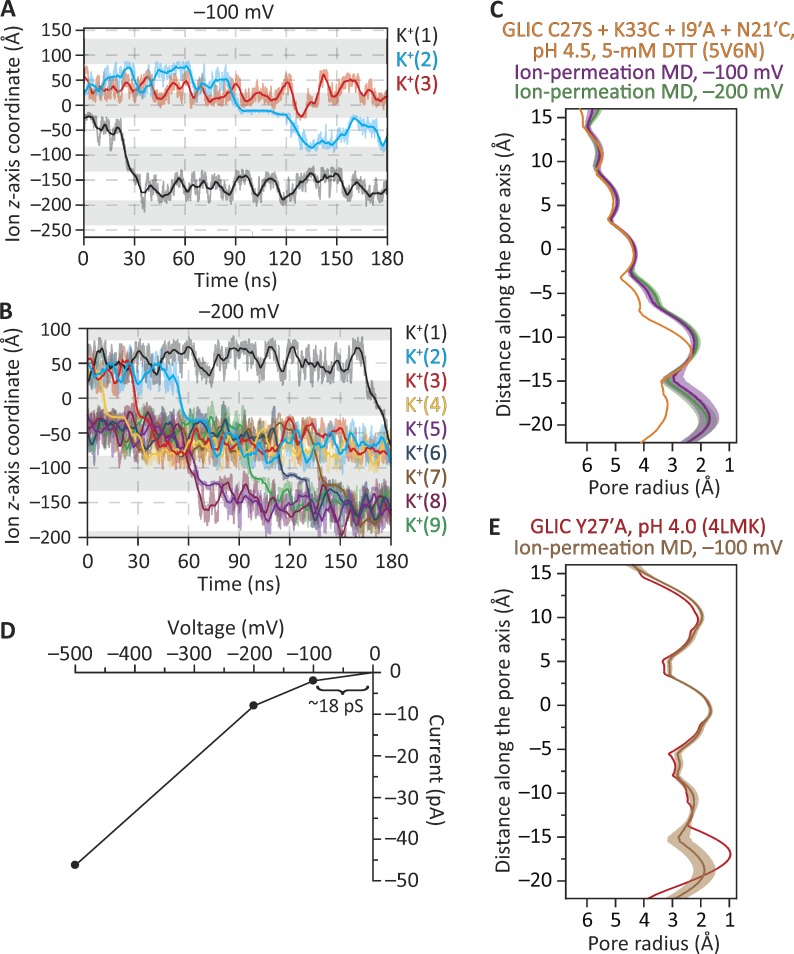
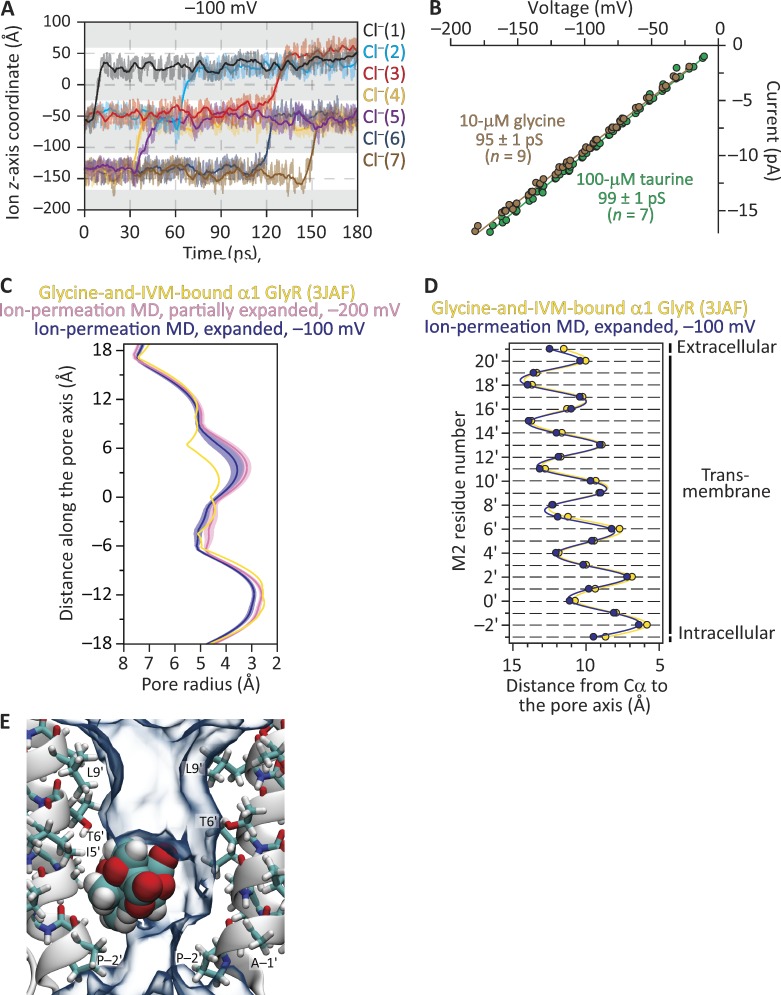
MD simulations of ion permeation through the structural model of the disulfide-reduced GLIC C27S + K33C + I9′A + N21′C mutant. The membrane was bathed by symmetrical 150 mM KCl, and the temperature was 37°C. (A) Ion trajectories at −100 mV. (B) Ion trajectories at −200 mV. In A and B, only the trajectories of ions that crossed the membrane are plotted. In these plots, gray areas indicate the regions occupied by the membrane in the periodic-simulation system, and downward transitions of the ion trajectories through these regions represent inward crossings. The darker lines are running averages of the data, which are displayed in a lighter shade. The length of the simulation box along the z-axis was 108 Å. (C) Pore-radius profiles (estimated using HOLE [Smart et al., 1996]) of structural models of the disulfide-reduced quadruple mutant. The profile of the crystal-structure model (PDB ID code 5V6N; this work) is compared with those computed during the ion-permeation MD simulations illustrated in A and B. (D) Current–voltage relationship from simulations performed at −100, −200, and −500 mV; ion trajectories at −500 mV, and the corresponding MD pore-radius profile, are shown in Fig. S2. (E) Pore-radius profiles of structural models of the closed-channel conformation. The profile of the crystal-structure model (PDB ID code 4LMK; Gonzalez-Gutierrez et al., 2013) is compared with that computed during an ion-permeation MD simulation at −100 mV. In C and E, ion-permeation-MD pore-radius profiles are mean profiles—displayed as the mean (darker lines) ± 1 SD (lighter shade)—calculated from the different frames of each simulation; the vertical axes extend, approximately, between M2 positions −3′ (bottom) and 21′ (top). Side-chain rotamers were optimized using SCWRL4 (Krivov et al., 2009) before the ion-permeation simulations were run.

At −100 mV (negative on the intracellular side) and in 180 ns of simulation, we observed 2 K⁺ and no Cl^– crossings (Fig. 8 A). Two cation crossings in the same direction (here, from the extracellular side to the intracellular side) in 180 ns represent an inward current of approximately −1.8 pA, and −1.8 pA at −100 mV under symmetrical salt concentrations across the membrane (such that, at zero voltage, the current is zero) correspond to a single-channel conductance of 18 pS (Fig. 8 D). Considering the short duration of the simulations, the low number of permeation events, and the fact that only the transmembrane domain of the channel was included in the simulations, a value of 18 pS compares favorably with the value of ∼9 pS estimated from single-channel currents recorded between −40 and −100 mV at room temperature with ∼150 mM Na⁺ on the extracellular side and ∼150 mM Cs⁺ on the intracellular side of outside-out patches (Sauguet et al., 2013). Furthermore, during this simulation at −100 mV, one K⁺ (labeled as K⁺[3] in Fig. 8 A) entered the pore from the extracellular side and moved all the way to its intracellular end before returning back to the extracellular solution. At more hyperpolarized potentials (for which there are no experimental counterparts), the number of K⁺ crossings in 180-ns simulations was 9 at −200 mV (Fig. 8, B and D), and 52 at −500 mV (Fig. 8 D and Fig. S2 A), all in the inward direction; no Cl^– crossings were observed. Thus, collectively, these results favor the idea that the structural models of GLIC generated here represent an ion-conductive conformation—probably the fully protonated open-channel conformation. Note, however, that the side-chain–rotamer optimization procedure that preceded the ion-permeation MD simulations (see Materials and methods), as well as the simulations themselves, led to a pore that is narrower than suggested by the (static) crystal-structure model (Fig. 8 C and Fig. S2 B); it is this narrower pore that supported the reported number of ion crossings. We also performed analogous simulations using a structural model of GLIC in a conformation that we have deemed to represent the fully protonated closed-channel state (PDB ID code 4LMK; Gonzalez-Gutierrez et al., 2013; Fig. 8 E); we observed no ion crossings in 180 ns at −100 mV.

Throughout these MD simulations, all five glutamate side chains of the charge-selectivity filter (at position −2′, in the particular case of GLIC) were kept deprotonated and free to sample all possible dihedral angle combinations. It may be argued that the probability of glutamate side chains being negatively charged decreases at the acidic pH that is used to open the channel. This point is of relevance in the context of our simulations because the number of negative charges at the pore’s narrowest constriction has a strong effect on the computed single-channel conductance (Cheng et al., 2010). However, it should be noted that position −2′ is at the intracellular end of the pore, and that the intracellular solution is typically kept at nearly neutral pH during electrophysiological recordings; it is the extracellular pH—not the intracellular one—that switches. This makes the prediction of protonation states much less straightforward not only because the pK_a values of these glutamate side chains are unknown in GLIC but also because the pH of the solution around them is less well defined under the asymmetrical extracellular–intracellular pH conditions used to activate the channel (Cymes and Grosman, 2015). Nevertheless, it is clear that the pH value that needs to be used to predict the protonation state of these intracellular glutamates is much closer to 7.0 than it is to 4.5. Regarding the freedom of these glutamate side chains to sample torsional space, we argue that we do not have experimental evidence for their conformations being restricted to a particular subset of rotamers as we do, instead, for the glutamates at position −1′ of the muscle AChR (Cymes and Grosman, 2012; Harpole and Grosman, 2014).

Computer simulations of ion conduction and block through the α1 GlyR

In single-channel recordings from the GlyR in the presence of picrotoxin (a mixture of picrotoxinin [C₁₅H₁₆O₆] and picrotin [C₁₅H₁₈O₇], two toxic plant compounds), open-channel intervals are shortened in a manner that is consistent with the phenomenon of ion-channel blockade by these organic molecules (e.g., Wang et al., 2006, 2007). We reasoned that we could use the current-blocking properties of picrotoxinin in MD simulations of ion permeation to help us identify which structural model is more likely to represent the open-channel conformation. The open-channel model is expected to be wide enough to let ions permeate, yet narrow enough for ion permeation to be completely blocked when bound to picrotoxinin. On the other hand, a nonconductive pore would be too narrow to pass currents even in the absence of picrotoxinin, whereas a model of an overly dilated pore would still pass currents in the presence of this molecule.

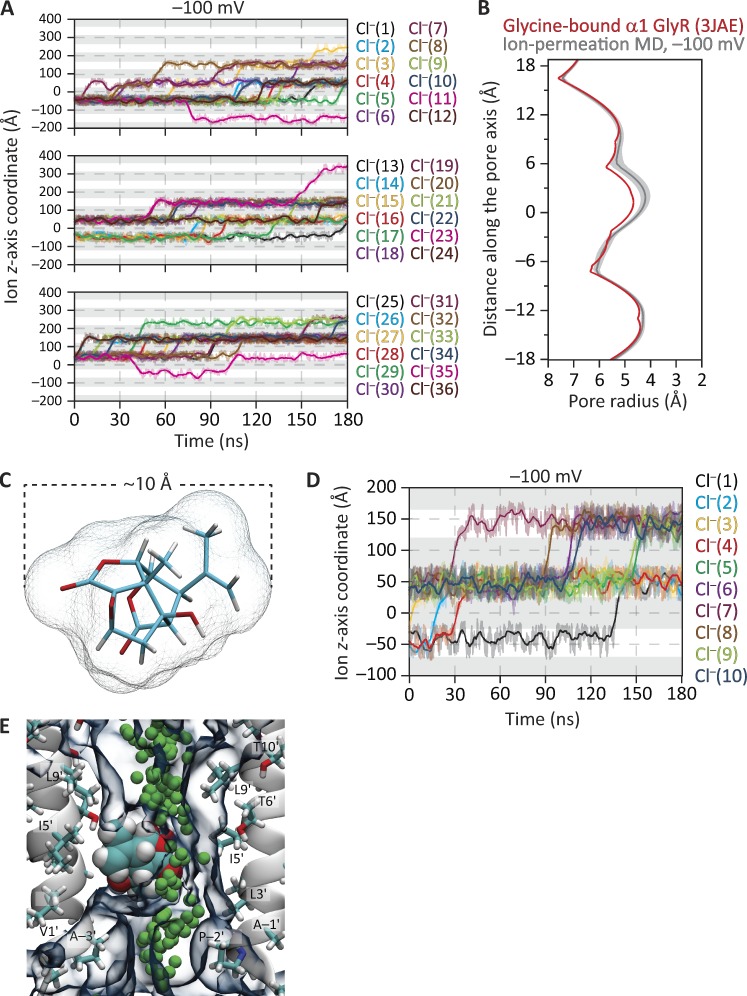
We started by simulating the model of the glycine-bound GlyR (PDB ID code 3JAE; Fig. 9). As was the case for GLIC, only the transmembrane domain of each subunit was included in the simulations (from Gln 235 to Val 364), and restraints were applied to the protein-backbone heavy atoms throughout the simulations. We embedded this reduced model in a POPC bilayer facing symmetrical 150 mM NaCl solutions at 37°C. At −100 mV and in 180 ns of simulation, we observed 25 Cl^– moving outward (i.e., from the intracellular to the extracellular side) once, 6 Cl^– moving outward twice, and 3 Cl^– moving outward three times, for a total of 46 outward crossings (Fig. 9, A and B). Also, during the simulation, one Cl^– moved inward once, and another Cl^– moved inward first and outward ∼50 ns later. Thus, the number of net Cl^– crossings in 180 ns at −100 mV was 45. Because no Na⁺ crossings were observed during the simulated time, this number of Cl^– outward crossings represents a single-channel conductance of ∼400 pS, whereas the experimentally observed value around −100 mV for the full-length α1 GlyR at room temperature is ∼95–100 pS. We then placed picrotoxinin (Fig. 9 C) in the pore of this GlyR model in such a way that the toxin adopted essentially the same pose and position as those inside the pore of the picrotoxinin-bound model of GluCl (PDB ID code 3RI5; Hibbs and Gouaux, 2011). Although the toxin decreased the simulated current, its blocking effect was far from complete. Indeed, 10 outward Cl^– crossings (and no Na⁺ crossings) were still recorded in 180 ns at −100 mV (Fig. 9, D and E; and Fig. S3 A), which corresponds to a single-channel conductance of ∼89 pS. Certainly, the lumen of the pore was wide enough for Cl^– to slip by the molecule of the tumbling toxin and traverse the pore. The diameter of this model’s pore at its narrowest constriction (including the side chains and disregarding the molecule of picrotoxinin) is ∼8.5 Å (Fig. 9 B and Fig. S3 A). The mean effective size of picrotoxinin during the simulation—calculated by subtracting the pore radius profile with the toxin from that without the toxin—was 5.7 Å in diameter.

Figure 9.

MD simulations of ion permeation and block through the structural model of the glycine-bound α1 GlyR. The membrane was bathed by symmetrical 150 mM NaCl, and the temperature was 37°C. (A) Ion trajectories at −100 mV. For clarity of display, the trajectories of the 36 Cl^– that crossed the membrane at least once in the simulated 180 ns were displayed in three separate panels. (B) Pore-radius profiles (estimated using HOLE [Smart et al., 1996]) of structural models of the glycine-bound GlyR. The profile of the cryo-EM-structure model (PDB ID code 3JAE) is compared with that computed during the ion-permeation MD simulation illustrated in A. The latter is the mean profile—displayed as the mean (darker lines) ± 1 SD (lighter shade)—calculated from the different frames of the simulation; the vertical axis extends, approximately, between M2 positions −3′ (bottom) and 21′ (top). Side-chain rotamers were optimized using SCWRL4 (Krivov et al., 2009) before the ion-permeation simulation was run. (C) Stick representation of the molecule of picrotoxinin (C₁₅H₁₆O₆); carbon atoms are cyan, oxygens are red, and hydrogens are white. The mesh representation shows the solvent-accessible surface of the toxin calculated using a 1.5-Å probe radius and with van der Waals radii taken from HOLE (Smart et al., 1996) parameter file simple.rad. (D) Ion trajectories at −100 mV computed for the glycine-bound GlyR model with a molecule of picrotoxinin placed in the pore. In A and D, only the trajectories of ions that crossed the membrane are plotted. In these plots, gray areas indicate the regions occupied by the membrane in the periodic-simulation system, and upward transitions of the ion trajectories through these regions represent outward crossings. The darker lines are running averages of the data, which are displayed in a lighter shade. The length of the simulation box along the z-axis was 95.5 Å. (E) Snapshot from the ion-permeation MD simulation of the 3JAE model at −100 mV with a molecule of picrotoxinin placed in the pore. The permeation trajectory of a Cl^– ion is shown as green spheres. The molecule of picrotoxinin is shown in van der Waals representation, and the 30% water-occupancy isosurface is shown as transparent shapes. For clarity, only two nonadjacent chains are shown.

We then simulated the model of the glycine-and-ivermectin–bound GlyR (PDB ID code 3JAF; Fig. 10). As was the case for the glycine-bound model, only the transmembrane domain of each subunit was included in the simulations (from Gln 235 to Val 364, with protein-backbone heavy-atom restraints applied), and this reduced model was embedded in a POPC bilayer facing symmetrical 150 mM NaCl solutions at 37°C. At −100 mV and in 240 ns of simulation, no ion crossings were observed despite the overall similarity between this model’s Cα profile and that of our open-channel model of GLIC (Figs. 1 and 6 G). Analysis of pore-radius profiles indicated that the side-chain-rotamer optimization procedure and the MD simulation itself had decreased the pore’s narrowest constriction from ∼5.0 Å (in diameter) in the cryo-EM structural model to a mean value of ∼4.4 Å during the simulation. Thus, suspecting that the narrowing of the pore’s constriction may have rendered this model nonconductive, we proceeded to expand the pore so as to recover, approximately, its original size. To this end, we applied an outward force to the five M2 α-helices using grid-steered MD (grid-scaling factor = 2; Wells et al., 2007). MD simulations of ion permeation through this new model in the presence of 500 mM NaCl yielded only one Cl^– outward crossing during 20 ns at −500 mV, and none during 40 ns at −200 mV; at its narrowest constriction, this model's mean diameter was ∼5.2 Å throughout the simulation. We then proceeded to expand the pore even more by applying a larger outward force to M2 (grid-scaling factor = 3). In ion-permeation MD simulations of this additional model at −100 mV and in the presence of 150 mM NaCl, we observed seven outward Cl^– crossings (and no Na⁺ crossings) in 180 ns (Fig. 10 A). This number of outward Cl^– crossings through this zebrafish GlyR model represents a single-channel conductance of ∼62 pS, which compares favorably with the experimentally estimated values of ∼95–100 pS for the (full-length) rat α1 GlyR in the cell-attached configuration with ∼150 mM Cl^– in the pipette solution (Fig. 10 B) and ∼80–88 pS for the homo-oligomeric-like GlyR of the zebrafish larva Mauthner cell in the outside-out configuration with nearly symmetrical ∼150 mM Cl^– (Legendre, 1997). At its narrowest constriction, this model's mean diameter was ∼5.8 Å throughout the simulation. The reasons why the model with an ∼5.2-Å narrowest constriction (the “partially expanded” model; Fig. 10 C) displayed such a low conductance in simulations are unclear. What is clear, however, is that the model with an ∼5.8-Å narrowest constriction (the “expanded” model; Fig. 10, C and D) is wider by only ∼0.6 Å, and that its computed single-channel conductance is comparable to the experimentally estimated value. Consistent with the notion that the expanded model represents an open-channel structure, no ion crossings were observed when picrotoxinin was placed in the pore and the system was simulated for 180 ns at −100 mV in the presence of 150 mM NaCl (Fig. 10 E and Fig. S3 B). During this simulation, the mean effective size of the tumbling toxin was 5.6 Å in diameter. Note that, at the level of backbone atoms, the cryo-EM 3JAF model of the GlyR, its expanded version, and the two models of I9′A GLIC at pH 4.5 presented here are all very similar to one another, especially toward the intracellular end of the transmembrane pore (Figs. 1 A, 4 G, 6 G, and 10 D).

Figure 10.

MD simulations of ion permeation and block through the structural model of the glycine-and-ivermectin–bound α1 GlyR. (A) Ion trajectories at −100 mV through an expanded version of the cryo-EM-structure model (PDB ID code 3JAF) obtained using grid-steered MD (Wells et al., 2007). The membrane was bathed by symmetrical 150 mM NaCl, and the temperature was 37°C. Only the trajectories of ions that crossed the membrane are plotted. Gray areas indicate the regions occupied by the membrane in the periodic-simulation system, and upward transitions of the ion trajectories through these regions represent outward crossings. The darker lines are running averages of the data, which are displayed in a lighter shade. The length of the simulation box along the z-axis was 84 Å. (B) Single-channel current–voltage relationships of the (full-length) rat α1 GlyR at ∼22°C. The recordings were obtained in the cell-attached patch-clamp configuration from transiently transfected HEK-293 cells. The pipette solution contained ∼150 mM Cl^–. Taurine is a partial agonist of the α1 GlyR, whereas glycine is a full agonist. (C) Pore-radius profiles (estimated using HOLE [Smart et al., 1996]) of structural models of the glycine-and-ivermectin–bound GlyR. The profile of the cryo-EM-structure model is compared with those computed during MD simulations of ion permeation through a partially expanded version and the expanded version of the 3JAF model. Ion-permeation-MD pore-radius profiles are mean profiles—displayed as the mean (darker lines) ± 1 SD (lighter shade)—calculated from the different frames of each simulation; the vertical axis extends, approximately, between M2 positions −3′ (bottom) and 21′ (top). Side-chain rotamers were optimized using SCWRL4 (Krivov et al., 2009) before the ion-permeation simulations were run. IVM, ivermectin. (D) Cα profiles of the cryo-EM-structure model and the expanded version. For clarity, the Cα profile of the partially expanded model was omitted; it lies somewhere in between those displayed. In the case of the expanded 3JAF model, the profile was calculated for a randomly chosen frame of the ion-permeation MD simulation. The five subunits of each model were averaged. Error bars (omitted if smaller than the symbols) are standard errors. Solid lines are cubic-spline interpolations. The lumen of the pore is to the right of the plot. (E) Snapshot from the ion-permeation MD simulation of the expanded model at −100 mV with a molecule of picrotoxinin placed in the pore. No ion crossings were recorded through this system. The molecule of picrotoxinin is shown in van der Waals representation, and the 30% water-occupancy isosurface is shown as transparent shapes. For clarity, only two nonadjacent chains are shown.

The open-channel model of the Torpedo AChR

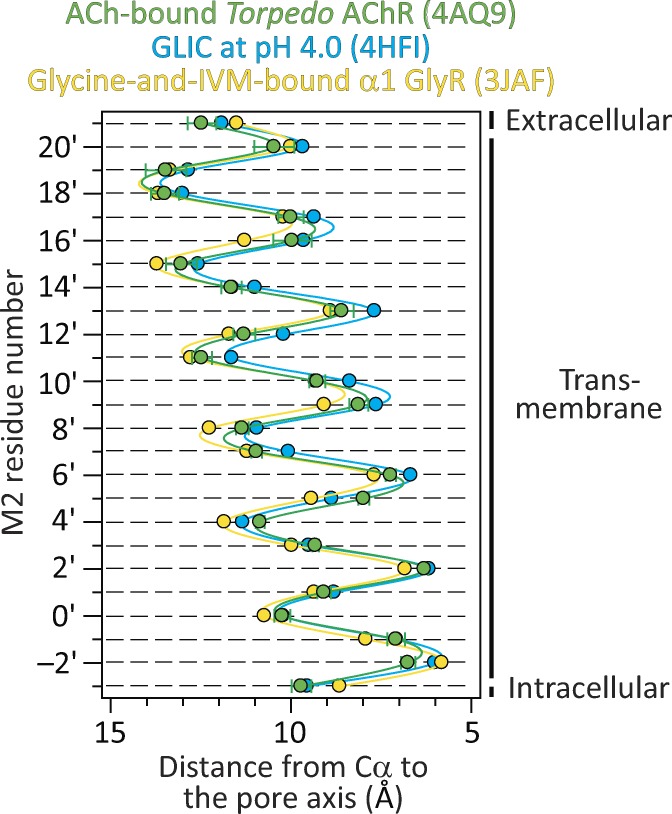
The muscle-type Torpedo AChR has also been imaged in a proposed open-channel conformation, in this case, using electron crystallography (PDB ID code 4AQ9; Unwin and Fujiyoshi, 2012). Although, at 6.2 Å, the resolution of this model was the lowest of all competing open-channel structures, it seems to us that the conditions used to favor the fully liganded open state were the most appropriate ones; in fact, they seem nearly ideal. Indeed, the channel remained embedded in its native plasma membrane, and it was exposed to a saturating concentration of ACh for only ∼10 ms before the tubular crystals were frozen. Such a 10-ms exposure to saturating ACh is long enough to open most of the channels in the sample, yet short enough to minimize entry into desensitization. Intriguingly, the Cα profile of the Torpedo AChR turned out to be very similar to those of the narrower-pore models along the entire length of the M2 α-helix (Fig. 11). Although, in this model, the amino-acid sequence of the AChR was mis-threaded at the level of M2 (Mnatsakanyan and Jansen, 2013), our comparison here involved only the positions of the Cα atoms—not the side chains—and thus, this limitation of the Torpedo AChR model becomes irrelevant in this particular context.

Figure 11.

The open-channel structural model of the Torpedo AChR in the context of other structures. Cα profiles of the indicated structural models. The five subunits of each model were averaged. Error bars (omitted if smaller than the symbols) are standard errors. Solid lines are cubic-spline interpolations. In the case of the Torpedo AChR, we applied a residue-numbering correction that accounts for the mis-threading of the amino-acid sequence in the original model (Mnatsakanyan and Jansen, 2013). The lumen of the pore is to the right of the plot.

Discussion

Nearly 20 years after the first x-ray crystal structure of a detergent-solubilized ion channel was unveiled (Doyle et al., 1998), it seems as though the ambitious goal of providing pictures of what these proteins look like in their different physiologically relevant conformational states has not been fully attained, yet. Although methods for engineering, overexpressing, purifying, crystallizing, and imaging ion channels have become increasingly powerful, the approaches followed to assign well-defined functional states to the obtained structural models have remained, for the most part, overly simplistic. Indeed, there seems to be no reason why one should expect that the lack of a membrane or the presence of a (rigid) crystal lattice have no effect on the conformational free-energy landscape of a membrane protein (e.g., Martinez et al., 2002; Fanucci et al., 2003a,b; Efremov et al., 2006; Hamouda et al., 2006; daCosta et al., 2009; Freed et al., 2010). Moreover, it seems that judging the conductive versus nonconductive nature of an ion-channel structural model solely on the basis of what the pore lumen looks like may be misleading because mechanisms more subtle than simple steric occlusion are also expected to gate the flow of ions in biological channels (Beckstein and Sansom, 2003, 2004).

It is with these caveats in mind that we set out to determine the structure of the open-channel conformation of fully liganded pLGICs. To decide between the “narrow-pore” and “wide-pore” competing models (Fig. 1), we crystallized a variant of the bacterial channel GLIC (at pH 4.5) bearing a mutation that markedly stabilizes the open state relative to the closed and desensitized states. Although the effect of this mutation on GLIC could not be assessed unequivocally at the single-channel level, the macroscopic currents were consistent with the well-characterized open-channel stabilizing effect of this mutation on the pLGICs from animals. The solved structures favor the notion that the model with a narrower pore is the one that more closely represents the open-channel conformation of animal pLGICs. The model of the GlyR bound to glycine, on the other hand, seems too dilated at the intracellular end of the transmembrane pore—that is, where the determinants of charge selectivity and single-channel conductance lie.

Aware, however, of the limitations of assigning a functional state to a structural model of a detergent-solubilized ion channel on the basis of its behavior when embedded in a membrane, we performed MD simulations of ion permeation and picrotoxinin block. These results pointed to the same conclusion as did our structural data: the narrower-pore models seem more likely to represent the open-channel conformation of animal pLGICs. If this functional assignment were correct, it would be unclear which end state of a pLGIC’s conformational free-energy landscape the wider-pore model corresponds to, and what its occupancy probability in vivo is. Certainly, there is no electrophysiological evidence for the existence of two (or more) open-channel conformations with widely different single-channel conductances in pLGICs. Although single-channel recordings from human (Lewis et al., 2003) and rat (Beato et al., 2004) α1 GlyR homomers heterologously expressed in HEK-293 cells often show more than a single high-occupancy open-channel current level, these are so closely spaced that it seems unlikely that they reflect the interconversion of pore structures as different as those represented by the glycine-bound and the glycine-and-ivermectin–bound GlyR models. Thus, although we cannot rule out the possibility that both conformations coexist in the membrane, it seems prudent to assume that one of them is much more populated than the other, and therefore, is more representative of the open state.

Whereas much effort has been devoted to optimize the biochemical steps leading to the preparation of membrane proteins suitable for x-ray crystallography or electron cryomicroscopy, comparatively little attention has been paid to the challenging problem of assigning functional states to structural models. In this paper, we aimed to contribute to this aspect of ion-channel structural biology in two different ways: (1) by engineering mutations with extreme effects on the relative stabilities of the different end states—in hopes of overcoming the eventually competing energetic effects of detergent solubilization and crystal-lattice formation; and (2) by performing computer simulations of ion permeation and block. We would like to emphasize, however, that we do not mean to imply that now we know what the open-channel conformation of pLGICs exactly looks like. Indeed, we are fully aware of the theoretical and practical limitations of computer simulations, and we realize that inferring the functional state of a detergent-solubilized membrane protein on the basis of its behavior in a membrane usually involves a great deal of speculation (Gonzalez-Gutierrez and Grosman, 2010; Parikh et al., 2011). Moreover, we would not find it surprising if the fine details of the open-channel structure differed among different pLGICs, even at the level of backbone atoms. In fact, within the class of narrower-pore models, the Cα profiles of GLIC and GluCl are very similar to each other, whereas that of the glycine-and-ivermectin–bound GlyR is clearly different toward the extracellular half (Fig. 1). However, what seems to be abundantly clear from our work is that narrower-pore models, as a group, are a much better starting point to understand ion permeation and other properties of the open-channel conformation of animal pLGICs than is the—much different—wider-pore model.

Undoubtedly, a more detailed understanding of a protein’s conformational free-energy landscape, the application of nonequilibrium approaches to imaging proteins, and the routine incorporation of computational tools such as those described here will help fill the vexing gap between the structural biology and electrophysiology of ion channels.