Reliability of functional magnetic resonance imaging activation during working memory in a multisite study: Clarification and implications for statistical power

To the Editors

We take this opportunity to clarify the meaning of the statistics reported in our study examining reliability of fMRI measures of brain activation during a working memory task (Forsyth et al., 2014) and to consider their implications for statistical power in single-site versus multisite designs.

In our report, we used a variance components framework and an application of generalizability theory (Shavelson and Webb, 1991) to probe the robustness of such measures in a multisite context. In our study, eight human subjects were scanned twice on successive days at each of eight sites. Given this design, the proportion of variance due to person from the variance components analysis (shown in Figure 5 in Forsyth et al., 2014) represents the reliability one can expect in a typical multisite study where each subject is scanned only once on the scanner available at the site in which they were recruited. We wish to make explicit that in applying generalizability theory, we estimated reliability by calculating generalizability and dependability coefficients (Shavelson and Webb, 1991) for a study design corresponding to the design of the full traveling subject study. Given this, these estimates reflect the reliability in relative and absolute measurement, respectively, that one can expect when every subject is scanned twice on each of eight different scanners. The corresponding generalizability and dependability coefficients (shown in Table 5 in Forsyth et al., 2014) were generally quite large, as would be expected when each subject’s measurement is based on the aggregation of sixteen scan sessions. Thus, the coefficients reported apply to the reliability of the measures from the reliability study itself, that is, for task-induced brain activations resulting from analysis of the eight traveling subjects’ fMRI data considered in aggregate across their sixteen scan sessions. Clearly, however, such a design is highly unlikely outside of a reliability study context, and so the reported generalizability and dependability coefficients are of limited applicability, a point that should have been made explicitly in the original paper. As shown in the table below, when using generalizability theory to model the reliability one can expect when a given subject is assessed on one occasion on a scanner drawn randomly from the set of all available scanners, the generalizability and dependability coefficients are more modest and, in the case of the dependability coefficients, identical to the percentages of variance attributable to person from the variance components analyses (as reported in Figure 5 of Forsyth et al., 2014). Indeed, under these assumptions, these two reliability formulations are mathematically equivalent.

Table.

G-coefficients and D-coefficients (Shavelson and Webb, 1991) providing estimates of relative and absolute measurement reliability, respectively, for a multisite study design in which each subject is studied on one occasion on a scanner drawn randomly from the set of all available scanners, as well as average within-site (test-retest) intraclass correlations in left and right hemisphere anterior cingulate cortex (ACC), dorsolateral prefrontal cortex (DLPFC), supplementary motor cortex (SM), insula (IN), inferior temporal cortex (IT), superior parietal cortex (SP), occipital cortex (OCC), thalamus (T), basal ganglia (BG), and cerebellum (C) for the correct trials versus rest contrast, and for medial frontal gyrus (MFG) and posterior cingulate cortex (PCC) for the rest versus correct trials contrast. Figures in parentheses represent 95% confidence intervals (Zhou et al., 2011).

Region	G-coefficients		D-coefficients		Within-site ICCs
	Left	Right	Left	Right	Left	Right
ACC1	0.19 (0, 0.43)	0.20 (0, 0.34)	0.17 (0, 0.38)	0.19 (0, 0.45)	0.19 (0, 0.25)	0.14 (0, 0.23)
DLPFC1	0.25 (0, 0.31)	0.00 (0, 0)	0.22 (0, 0.56)	0.00 (0, 0)	0.44 (0.07, 0.64)	0.08 (0, 0.08)
SM1	0.28 (0, 0.56)	0.20 (0, 0.45)	0.27 (0, 0.57)	0.20 (0, 0.45)	0.31 (0, 0.38)	0.18 (0, 0.28)
IN1	0.00 (0, 0)	0.17 (0, 0.22)	0.00 (0, 0)	0.15 (0, 0.39)	0.22 (0, 0.39)	0.18 (0, 0.31)
IT1	0.48 (0,16, 0.77)	0.31 (0.03, 0.61)	0.48 (0, 0.79)	0.30 (0, 59)	0.55 (0.16, 0.69)	0.36 (0.03, 0.52)
SP1	0.58 (0.26, 0.83)	0.37 (0.03, 0.60)	0.57 (0, 0.84)	0.37 (0, 0.64)	0.59 (0.01, 0.85)	0.42 (0, 0.67)
T1	0.12 (0, 0.27)	0.14 (0, 0.22)	0.12 (0, 0.30)	0.13 (0, 0.36)	0.18 (0, 0.27)	0.12 (0, 0.15)
BG1	0.04 (0, 0.04)	0.08 (0, 0.17)	0.04 (0, 0.04)	0.08 (0, 0.18)	0.12 (0, 0.16)	0.07 (0, 0.09)
C1	0.04 (0, 0.04)	0.03 (0, 0.03)	0.04 (0, 0.04)	0.03 (0, 0.03)	0.18 (0, 0.34)	0.15 (0, 0.29)
MFG2	0.22 (0, 0.49)		0.20 (0, 0.46)		0.27 (0, 0.44)
PCC2	0.29 (0, 0.48)		0.27 (0, 0.50)		0.40 (0, 0.58)

¹Task positive regions;

²Task negative regions

Shown explicitly, if ${\sigma }_p^2,{\sigma }_s^2$, and ${\sigma }_d^2$ correspond to the variance component estimates for the main effects of person, site, and day, respectively; ${\sigma }_{ps}^2,{\sigma }_{pd}^2$, and ${\sigma }_{sd}^2$ correspond to the variance component estimates for the two-way interactions between person and site, person and day, and site and day, respectively; and ${\sigma }_{\mathit{psd},e}^2$ corresponds to the variance component estimate for the residual due to the person x site x day interaction and random error, when the number of sites described by $n_s^{\prime }$ and the number of days described by $n_d^{\prime }$ in the D-coefficient equation are both set to one, as in the actual NAPLS study where subjects are scanned at one site on one day, (rather than eight and two, respectively, as in the traveling subject study design), the D-coefficients become equivalent to the proportion of variance due to subject divided by the proportion of variance due to all sources of measurement and error.

Equation 6.17, with expansion of one term as in Equation 6.4, from (Shavelson and Webb, 1991):

$$\varphi =\frac{{\sigma }_p^2}{({\sigma }_p^2+\frac{{\sigma }_s^2}{n_s^{\prime }}+\frac{{\sigma }_d^2}{n_d^{\prime }}+\frac{{\sigma }_{ps}^2}{n_s^{\prime }}+\frac{{\sigma }_{pd}^2}{n_d^{\prime }}+\frac{{\sigma }_{sd}^2}{n_s^{\prime }{n}_d^{\prime }}+\frac{{\sigma }_{\mathit{psd}.e}^2}{n_s^{\prime }{n}_d^{\prime }})}$$

Indeed, by varying the values for number of sites ( $n_s^{\prime }$) and number of scanning occasions or days ( $n_d^{\prime }$), one can use the variance components calculated in the travelling subjects study to estimate how the reliability of the fMRI measurements would change if each subject were scanned on a given number of scanners ( $n_s^{\prime }$) and/or across a given number of occasions or days ( $n_d^{\prime }$). In computing the coefficients reported in the table, the error terms are divided by one, to model the situation in which each subject is scanned once on a single scanner drawn randomly from the pool of available scanners.

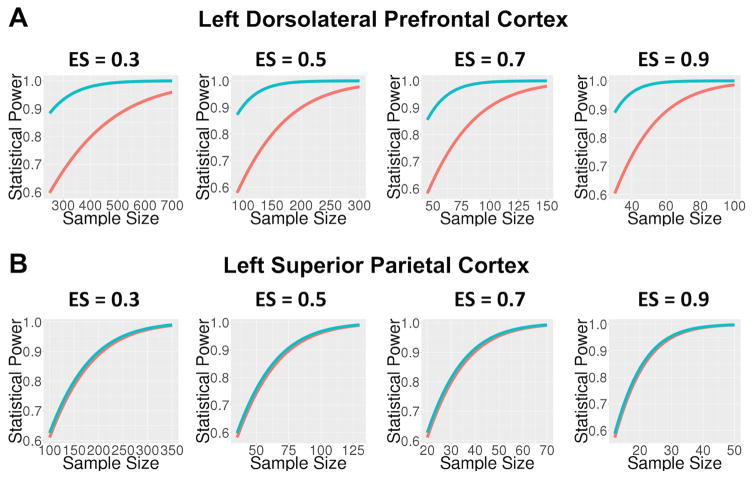
The practical implication of less than perfect reliability of measurement is attenuation of effect size and reduction of statistical power (Cohen, 1988). Multisite neuroimaging studies are an increasingly popular option for studying rare conditions, as they provide an efficient means to obtain sample sizes large enough to detect group differences. However, when utilizing multisite studies for this purpose, a key question is how much statistical power is sacrificed by the introduction of variance due to site-related factors when moving from a single site to a multisite study design, and what sample sizes are necessary to offset the reduction in power due to attenuation of measurement reliability. One way to answer this question is to compare the reliability of the person effect given a multisite design in which individuals are scanned once at a given scanner and data are pooled across sites, to the reliability of the person effect at individual sites, averaged across the sites that would be involved in the multisite design. Utilizing the reliability estimates for the single site versus multisite design, one can then estimate the sample sizes needed to achieve sufficient statistical power by correcting the effect size for measurement reliability (i.e., ES′ = ES × √r, where ES′ is the corrected effect size, ES is the effect size under the assumption of perfect measurement, and r is the estimated reliability of measurement; (Cohen, 1988)). As shown in the table below, for some ROIs, such as left dorsolateral prefrontal cortex (DLPFC), the average within-site intraclass correlation coefficients (i.e., representing single site reliability estimates for each of the eight NAPLS sites, averaged across sites) are larger than the corresponding multisite generalizability coefficients, but for other ROIs, such as left and right superior parietal cortex (SP), the difference in single versus multisite reliability is negligible. As shown in the figure, when accounting for differential reliability in left DPLFC, although higher levels of power are achieved with smaller sample sizes in the single-site compared with multisite context, multisite studies achieve acceptable levels of power (≥0.8) with moderate to large effect sizes (ES ≥0.5) beginning at sample sizes of approximately 125 subjects. These results accord well with the results reported in our original study analyzing single-session scans from 154 healthy subjects, each drawn from one of the eight scanning sites, which observed robust activation in key working memory nodes (e.g., DLPFC, SP, and anterior cingulate, supplementary motor, and inferior temporal cortices) whether using image-based-meta-analysis or mixed effects modeling with site as a covariate (Forsyth et al., 2014).

Figure.

Statistical power as a function of sample size across multiple effect sizes (Cohen’s d for one group all correct trials versus rest contrast) for left dorsolateral prefrontal cortex (A) and left superior parietal cortex (B). The red lines represent power for multisite studies while the blue lines represent power for single-site studies, with nominal effect sizes adjusted downward for observed reliabilities in the multisite and single-site contexts, respectively. For DLPFC, although higher levels of power are achieved with smaller sample sizes in the single-site compared with multisite context, multisite studies achieve acceptable levels of power (≥ 0.8) with moderate to large effect sizes (ES ≥ 0.5) beginning at sample sizes of approximately 125 subjects. For PC, where there is no difference between multisite versus single site reliability (and therefore the red and blue lines overlap), power is adequate to detect moderate to large effect sizes (ES ≥ 0.5) beginning at sample sizes of approximately 50 subjects in either the single or multi-side study context.

Whether the reliability coefficients for working memory-related activation reported here will generalize to other task designs or samples with demographic features different from those of the participants in this study is not known. It is also important to note that the 95% confidence intervals (Zhou et al., 2011) for these coefficients are quite wide, which is to be expected given the small sample size (N=8). Given this wide interval, the power estimates shown in the figure could be under or overestimated considerably; see (Doros and Lew, 2010) for an approach to power calculation that accounts for the confidence interval around the reliability estimate. Nevertheless, it is encouraging that although the observed estimates are consistent with modest reliability, the differences in the estimates for multisite versus single-site studies (and the corresponding trade-off in terms of power) are also modest, indicating that the multisite format is a relatively efficient means to increase the number of subjects included in fMRI studies.