Abstract
Magnetic resonance imaging (MRI) provides a powerful set of tools with which to investigate biological tissues noninvasively and in vivo. Tissues are heterogeneous in nature; an imaging voxel contains an ensemble of different cells and extracellular matrix components. A long-standing challenge has been to infer the content of and interactions among these microscopic tissue components within a macroscopic imaging voxel. Spatially resolved multidimensional relaxation–diffusion correlation (REDCO) spectroscopy holds the potential to deliver such microdynamic information. However, to date, vast data requirements have mostly relegated these type of measurements to nuclear magnetic resonance applications and prevented them from being widely and successfully used in conjunction with imaging. By using a novel data acquisition and processing strategy in this study, spatially resolved REDCO could be performed in reasonable scanning times with excellent prospects for clinical applications. This new MR imaging framework—which we term “magnetic resonance microdynamic imaging (MRMI)”—permits the simultaneous noninvasive and model-free quantification of multiple subcellular, cellular, and interstitial tissue microenvironments within a voxel. MRMI is demonstrated with a fixed spinal cord specimen, enabling the quantification of microscopic tissue components with unprecedented specificity. Tissue components, such as axons, neuronal and glial soma, and myelin were identified on the basis of their multispectral signature within individual imaging voxels. These tissue elements could then be composed into images and be correlated with immunohistochemistry findings. MRMI provides novel image contrasts of tissue components and a new family of microdynamic biomarkers that could lead to new diagnostic imaging approaches to probe biological tissue alterations accompanied by pathological or developmental changes.
Keywords: MRI, microdynamic, relaxation, diffusion, spectroscopy, glia, model-free, MADCO, relaxometry
1. Introduction
Diffusion magnetic resonance imaging (dMRI) provides a means to investigate biological tissue microstructure, organization, and architecture (Johansen-Berg and Behrens, 2013). These techniques are sensitive to features of the net displacement distribution of water molecules within the sample (Stejskal and Tanner, 1965), providing powerful tools to explore microscopic domains quantitatively (Price, 2009). In conjunction with tissue models, dMRI experiments can be used to infer macroscopic (Basser et al., 1994, 2000) and microscopic (Burcaw et al., 2015; Szczepankiewicz et al., 2015; Benjamini et al., 2016) structural features, on the basis of the type and scale of physical barriers that are present in heterogeneous biological tissue.
MRI can also be sensitized to features of the local chemical environment and various dynamic relaxation processes, known as longitudinal and transverse relaxation, characterized by relaxation times, T1 and T2, respectively. Methods have been developed that do not assign a single, average relaxation time to each voxel but rather measure the distribution of the relaxation times within the volume (Whittall and MacKay, 1989; Kleinberg and Horsfield, 1990). This approach provides a one-dimensional (1D) distribution of T1, T2 or the apparent diffusivity, D, and it therefore implies a multicomponental tissue structure. These methods are usually referred to as nuclear magnetic resonance (NMR) relaxometry and are mainly used to characterize soil, rock, soft matter porous media (Whittall and MacKay, 1989; Kleinberg and Horsfield, 1990; Fordham et al., 1995), and ex vivo biological tissue (Beaulieu et al., 1998; Peled et al., 1999; MacKay et al., 2006).
Combining multidimensional MR contrast mechanisms, e.g., D-T2, would provide novel and complementary information about dynamic molecular processes and microscopic physical and chemical environments within tissue. To date, these multidimensional relaxation–diffusion correlation (REDCO) spectroscopy experiments have been primarily relegated to applications involving NMR studies in homogeneous samples (Silva et al., 2002; Galvosas and Callaghan, 2010; Bernin and Topgaard, 2013; Song et al., 2016). However, apart from a few studies (Zhang and Blümich (2014); Tax et al. (2017); Kim et al. (2017)), these methods have not been widely used in MRI applications owing to the vast amount of scan time and acquired MR data required to reconstruct a single multidimensional spectrum.
A few studies have demonstrated integration of two-dimensional (2D) D-T2 or T1–T2 spectroscopy with imaging of biological tissue. Does and Gore resolved three components within a region of interest (ROI) in peripheral nerve using a T1–T2 correlation experiment that included 512 acquisitions (Does and Gore, 2002). A compressed sensing approach for reducing the data requirements for such a type of experiment was recently suggested and demonstrated on a spinal cord sample (Bai et al., 2015), in which an ROI-based analysis resulted in two peaks in the T1–T2 white matter (WM) spectrum. With that method, a maximal acceleration factor of 3.5 was achieved, reducing the number of acquisitions from 1,800 to 450, which is still infeasible for clinical MRI applications. A recent spatially resolved REDCO study reported one distinct D-T2 peak in the WM region and a different distinct peak in the gray matter (GM) region of a spinal cord specimen (Kim et al., 2017). These results, specifically the monocompartmental tissue structure in WM, contradict many previous studies (e.g., Ronen et al. (2006); Peled et al. (1999); MacKay et al. (2006)) and may be due to the very small number of acquisitions, 28, used to reconstruct the D-T2 spectra, or to the use of spatial regularization.
Data acquisition and processing strategies prevent spatially resolved REDCO spectroscopy to achieve its full potential, and particularly its expected high sensitivity and specificity to different microenvironments within biological tissue. To overcome this bottleneck we recently proposed the marginal distributions constrained optimization (MADCO) framework for accelerated multidimensional MRI (Benjamini and Basser, 2016). The concept in this approach is to use the more accessible 1D information (i.e., the marginal distributions) to enforce physical constraints on the multidimensional distribution, resulting in a dramatic reduction in the number of data samples required and a concomitant reduction in MRI acquisition times (Benjamini and Basser, 2016, 2017).
Most of the recent microstructure imaging methods proposed in the past decade (e.g., Assaf and Basser (2005); Alexander et al. (2010); Zhang et al. (2012)) also invoke parametric tissue models that are based on an assumed tissue microstructure and may not faithfully reflect the underlying “ground truth.” We therefore believe that the high level of complexity and variability of biological tissue requires a departure from this current trend of model-based MRI methods. Here, by using MADCO, we introduce a new MR imaging framework–which we term magnetic resonance microdynamic imaging (MRMI)—that permits the simultaneous noninvasive quantification of multiple cellular, interstitial, and subcellular tissue components within tissue. This unique information is obtained without imposing a priori tissue models, and in a clinically or biologically feasible time period. The term “microdynamic” captures both physical and chemical aspects of the multidimensional acquisition, and the way the suggested framework integrates this information to resolve microenvironments. While diffusion is indeed a dynamic process, the diffusion MR measurement in this study is not time dependent, and therefore provides only a snapshot in time regarding the physical microstructural environment. In contrast, the relaxation measurements are time dependent, and provide information that is directly related to molecular energy transfer, which is inherently dynamic. Although it can be used to investigate other types of biological tissue (e.g., muscle Harrison et al. (1995)), we chose to apply MRMI on a spinal cord specimen because its microstructure and organization are well known and highly ordered.
2. Materials and Methods
2.1. Specimen preparation
The animal used in this study was housed and treated at the Uniformed Services University of the Health Sciences (USUHS) according to national guidelines and institutional oversight. As part of standard necropsy for an unrelated study, a healthy adult male ferret was euthanized and underwent transcardial perfusion with ice-cold 0.1M phosphate buffered saline (PBS, pH 7.4, Quality Biological) followed by 4% paraformaldehyde (PFA, Santa Cruz Biotechnology, in PBS 0.1M pH 7.4) at USUHS, according to standard methods. For the present study, the spinal cord tissue was extracted by careful surgical dissection. A cervical portion of the spinal cord was then transferred to a PBS-filled container for 7 days to ensure any residual PFA was removed from the tissue. The sample was then immersed in perfluoropolyether (Fomblin LC/8, Solvay Solexis, Italy) and inserted into a 5 mm Shigemi tube (Shigemi Inc., Japan) with a glass plunger matched to the susceptibility of water. The tube was placed and oriented along the direction of the main magnetic field in a 5 mm birdcage radio frequency (RF) coil.
2.2. MRI data acquisition
MRI data were collected on a 7 T Bruker wide-bore vertical magnet with an AVANCE III MRI spectrometer equipped with a Micro2.5 microimaging probe and three GREAT60 gradient amplifiers, which have a nominal peak current of 60 A per channel. This configuration can produce a maximum nominal gradient strength of 24.65 mT/m/A along each of the three orthogonal directions. MRI data were acquired with an inversion recovery spin-echo diffusion-weighted (DW) echo planar imaging (IR–DWI–EPI) sequence, with an adiabatic 180° inversion pulse applied before the standard spin-echo DW sequence, and with a DWI–EPI sequence. The sample temperature was set at 16.8°C. For a DW experiment, the spin magnetization decays according to the diffusivity, D, due to the DW parameter, b. For a T1-weighted measurement, the spin magnetization returns to thermodynamic equilibrium, followed by an IR experiment with the inversion period, τ1, as the governing experimental parameter. Finally, the echo time, τ2, governs the decay due to T2.
The three 1D distributions of T1, T2, and D, were estimated, respectively, with the following data acquisition protocols: A 1D T1-weighted data set (b = 0, τ2 = 10.7 ms) with 12 logarithmically sampled τ1 values ranging from 20 to 3000 ms by using an IR–DWI–EPI sequence; a 1D T2-weighted data set (b = 0) with 20 logarithmically sampled τ2 values ranging from 10.7 to 150 ms by using a DWI–EPI sequence; and a 1D DW data set (τ2 = 10.7 ms) with 20 linearly sampled b-values ranging from 0 to 25068 s/mm2 by using a DWI–EPI sequence. In all DW acquisitions, the diffusion encoding direction was set perpendicular to the main axis of the spinal cord. Other acquisition parameters were diffusion gradient duration and separation of δ = 4 ms and Δ = 15 ms, respectively.
The three 2D distributions of D-T1, D-T2, and T1–T2, were estimated, respectively, with the following data acquisition protocols (in conjunction with the a priori obtained 1D distributions as constrains): A 2D D-T1-weighted data set with 12 sampled combinations of inversion times and b-values within the above 1D acquisition range by using an IR–DWI–EPI sequence; a 2D D-T2-weighted data set with 12 sampled combinations of echo times and b-values within the above 1D acquisition range by using an DWI–EPI sequence; a 2D T1–T2-weighted data set with 12 sampled combinations of inversion and echo times within the above 1D acquisition range by using an IR-EPI sequence.
For all types of acquisitions, TR = inversion time + 4 s. A single 2.5 mm axial slice with a matrix size of 64 × 64 and inplane resolution of 101×101 μm2, was acquired with 2 averages and 8 segments. Each image took 1 min to acquire, leading to 52 min for the 1D spectra and 36 min for the 2D spectra, for a total of 88 min. Signal-to-noise ratio (SNR) was defined as the ratio between the average signal intensity within a tissue ROI, and the standard deviation of the signal intensity within a background (i.e., no sample) ROI. The highest SNR image (i.e., the least amount of diffusion and relaxation decay, with b = 0 and τ2 = 10.7 ms) had an SNR of 80 and 103 for WM and GM, and the lowest SNR image had an SNR of 20 and 19.7 for WM and GM, respectively.
2.3. Immunohistochemistry
After completion of MRI scans, the ferret spinal cord was sent to FD Neurotechnologies Inc.(Columbia, MD) for histopathological staining. It was then cryoprotected with 0.1 M phosphate buffer (pH 7.4) containing 20% sucrose for 72 h. After rapid freezing in isopentane, pre-cooled to −70°C with dry ice, the frozen tissue was stored in a freezer at −80°C before sectioning. Serial sections (40 μm) were cut transversely through the spinal cord with a cryostat. Sections were then stained with FD cresyl violet solution (FD Neurotechnologies Inc., Columbia, MD). Other sections were processed with primary antibodies markers for astrocytes (Rat anti-GFAP antibody, 1:10000; Invitrogen, 13-0300), microglia (rabbit anti-Iba1 antibody, 1:2000;Wako, 019-19741), myelin oligodendrocyte glycoprotein (mouse anti-MOG antibody, 1:250; Sigma, SAB1406138), and pan-neurofilaments (rabbit anti-pan neurofilaments, 1:500; Biomol, NA1297), following standard procedures.
2.4. Microscopy and image processing
Whole spinal cord slides were scanned with a Hamamatsu Nanozoomer (Hamamatsu Photonics, Japan) at a magnification of 40, resulting in a 230 nm/pixel resolution. Images of all the stained slides were white balanced and converted to monochrome by using Image J (NIH, Bethesda, MD). Following standard practice (Fawcett and Scott, 1960), normalized image intensities, I, were converted to their corresponding optical density values according to
| (1) |
The MRI and immunohistochemistry (IHC) images were quantitatively compared by first subsampling the latter to match the MR image in-plane resolution. A voxelwise correlation was allowed across modalities by registering the MR images to the subsampled IHC optical density images. An affine transformation based on the Mattes mutual information metric was performed by using MATLAB’s Image Processing Toolbox (The Mathworks, Natick, MA).
2.5. MRI data processing
To obtain the 1D or higher dimensional distribution of a particular MR contrast or set of contrasts, one must numerically invert the Fredholm integral of the first kind, which is a classic ill-conditioned problem (McWhirter and Pike, 1978). The main implication is that the data inversion is inherently non-unique (Provencher, 1982; Whittall and MacKay, 1989), which may lead to spurious peaks and the split-up of wide peaks to multiple narrow peaks (“pearling”) in the reconstructed spectrum (Bernin and Topgaard, 2013). A standard approach to solving ill-conditioned problems is to regularize them. When the spectrum is expected to be smooth, ℓ2 regularization is appropriate (Fordham et al., 1995). While slightly distorted, a regularized problem has (by definition) a unique solution that depends smoothly on the data (Fordham et al., 1995). Furthermore, the solution to the regularized problem should be close to one of the infinity of feasible solutions of the original ill-conditioned problem. Although ℓ2 regularization helps address the pearling phenomenon, it may also artificially broaden intrinsically narrow peaks. Further detail can be found in Appendix A.
All MRI data were processed by using the MADCO framework (Benjamini and Basser, 2016). Briefly, all T1, T2, and D 1D data sets were processed by using well-established algorithms to determine the corresponding 1D distributions (Menon and Allen, 1991; Hansen, 1992; Fordham et al., 1995) in each image voxel. With the 1D distributions as constraints, the 2D data sets were then processed by using the MADCO framework (Benjamini and Basser, 2016), which extended widely used procedures (English et al., 1991; Venkataramanan et al., 2002; Song et al., 2002).
As detailed in Appendix A, the MR signal attenuation is modeled with a multiexponential function, which should capture the T1, T2, and D decay curves. In this study, a small portion of the data was inconsistent with this model. The T2 data contained such slight deviation from purely exponential behavior in 58 of the 968 voxels (less than 1.4% of the entire dataset), while the rest of the data did not. The abnormal voxels were concentrated around the central cerebrospinal fluid (CSF) canal. This deviation might have originated from background gradients induced by magnetic susceptibility differences between CSF and tissue in that particular region, which was shown to results in such nonexponential behavior (van Gelderen et al., 2012). Nevertheless, the 1D T2 spectra resulting from the nonexponential decay voxels had similar features compared to spectra obtained from their “normal appearing” neighboring voxels. The nonexponential signal decay did not result in significantly different T2 spectra, which implies that this abnormality did not affect the presented results.
All data processing was performed with in-house code written in MATLAB (The Mathworks, Natick, MA). To resolve the 2D spectra subject to the MADCO constraints we used CVX, a package for specifying and solving convex programs (Grant and Boyd, 2008; CVX Research, 2012).
2.6. Quantifying uncertainty in the spectra
The jackknife technique (Quenouille, 1949) was used to quantify the uncertainty in the estimated parameters in the following manner: first, the 1D T1, T2, and D, estimations were repeated with one data point being left out in each iteration, resulting in 20 spectra for T2 and D, and 12 for T1. Then, the 2D spectra, D-T2, T1–T2, and D-T1, were reconstructed using MADCO with the “leave-one-out” 1D spectra as constraints, resulting in 400 D-T2 spectra and 240 T1–T2 and D-T1 spectra. The high dimensionality of the spectra prevents direct visualization of the uncertainty, and we therefore adopted a previous approach (Prange and Song, 2009) that maps each spectrum into a single number or numbers whose uncertainty can then be visualized as histograms. We chose to focus on the tissue components apparent volume fractions, which were obtained by integration over the corresponding spectral peak (as described in more detail in section 3.5). Those apparent volume fractions were obtained from each of the leave-one-out spectra, and their standard deviation was used to indicate the uncertainty in their estimation. This process was repeated in each of the image voxels.
3. Results and Discussion
3.1. The MADCO framework
Reexamination of the relationships between the 1D and higher-dimension distributions (Benjamini and Basser, 2014) laid the groundwork for addressing the primary issue precluding multidimensional REDCO biological and clinical applications in conjunction with imaging. Briefly, one can regard the 2D REDCO spectrum as a joint probability distribution of two variables, each with its own 1D marginal distribution of the 2D spectrum. These 1D and 2D spectra are linked via well-known relationships from probability theory; this link is the basis of the MADCO framework for accelerated 2D spectroscopic MRI (Benjamini and Basser, 2016).
The children’s board game, Battleship (by Milton Bradley) is helpful in illustrating our approach. In this game, two players place toy ships somewhere on a discrete rectangular x-y grid representing a body of water. Neither player can see the location of the other player’s ships. The goal is to find all the opponent’s ships before he or she finds yours. Each player has to devise a search strategy to guess the location of the other player’s ships. A reasonable search strategy is for each player to choose random points within the grid from a uniform distribution, because players have no a priori information about the location of the opponent’s ships. Suppose we modify the rules of the game so that in the first two moves, each player can obtain additional information, specifically, (1D) projections of the mass distribution of their opponents’ ships along the y and x axes (i.e., columns and rows). The search strategy would be quite different: the information provided along each row and each column would provide powerful constraints that would enable a player to find most of the opponent’s ships within a few moves. This example can help us understand how to design experiments to detect and reconstruct multispectral peaks in a REDCO spectrum. It is often straightforward and experimentally fast to obtain a robust 1D projection of the 2D spectrum along each axis. We can then use these 1D marginal distributions to recover the entire 2D relaxation spectrum.
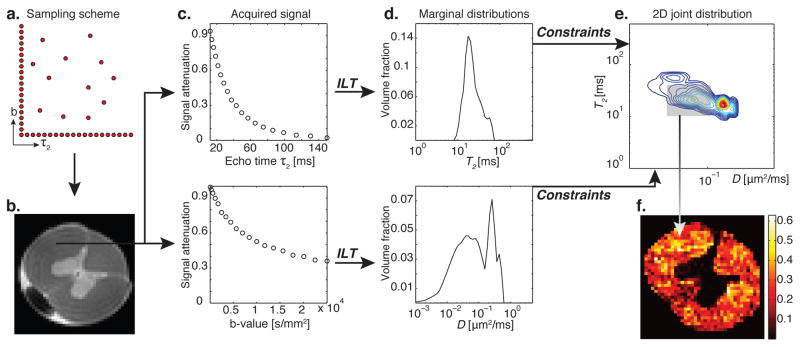
A 1D distribution of a particular MR contrast is obtained by encoding along the contrast’s corresponding 1D experimental parameter (e.g., for T2 distribution, we acquire data as a function of the experimental parameter, τ2, Fig. 1c). Similarly, 2D distributions of two correlated MR contrasts have conventionally required sampling over both corresponding experimental parameters, this time over a 2D rectangular grid, resulting in a quadratically longer acquisition. A schematic showing the principle of MADCO is given in Fig. 1. In this example, D-T2 REDCO distribution from a spinal cord WM region is reconstructed, and from it a quantitative tissue component image is obtained. A complete mathematical description and implementation of the framework are given in Appendix A.
Figure 1.
Schematic and principle of MADCO MRI with a D-T2 example. (a) Two-dimensional sampling scheme encoding T2 and D result in (b) a spinal cord image. A WM voxel is chosen, and the 1D T2 and D signal attenuations shown in (c), top to bottom, are used to evaluate their corresponding 1D marginal distributions by using an inverse Laplace transform (ILT) (Provencher, 1982; Whittall and MacKay, 1989), shown in (d). The 2D D-T2 spectrum can be obtained with MADCO by sampling only a dozen random data points (instead of sampling over the entire 2D parameter space). (e) The reduced 2D data are then transformed to 2D spectrum by using a 2D ILT, constrained by the a priori estimated marginal distributions. The peaks in the resulting 2D spectrum originate from different microenvironments within the given voxel (Peled et al., 1999; Does and Gore, 2002). After judicious assignment of peaks to their respective tissue components, integration over each peak results in the signal fraction of that component, which is assumed to be proportional to its volume fraction. (f) This process is repeated in every image voxel, resulting in spatially resolved quantitative images of the microdomain.
It is worth noting that the efficiency and acceleration of the MADCO framework increases with the number of dimensions. Assume N is the number of dimensions and M is the number of acquisitions required in each dimension; then 𝒪(MN) measurements are required to reconstruct the M-dimensional spectrum by using a conventional approach, while only 𝒪(N × M) measurements are required when MADCO is used. This relation leads to an acceleration factor of 𝒪(M(N−1)/N).
3.2. Identification of tissue microenvironments
Similar microanatomical components share common physical and chemical microenvironments, which can be differentiated on the basis of their various relaxation and diffusion properties by using MRI. We used MADCO to generate multidimensional relaxation–diffusion spectra with relatively few MR data, so that microdynamic REDCO can be performed voxel by voxel within an imaging volume in a preclinically feasible time period. To enable our assignment of the REDCO peaks to their correct corresponding tissue components we selected a cervical spinal cord specimen. It is part of the central nervous system (CNS), yet exhibits excellent segregation of GM and WM into distinct histological regions (Standring, 2015).
Before presentation of the results, it is worth noting that previous 1D and 2D NMR and MRI relaxometry studies of a variety of neural tissues were able to distinguish and isolate three microscopic components within the investigated volume: intracellular, extracellular, and myelin associated (Beaulieu et al., 1998; Peled et al., 1999; Does and Gore, 2002; MacKay et al., 2006). In the present study we show that MRMI delivers unprecedented specificity to cellular subpopulations. To unequivocally assign the multispectral peaks to tissue components we show that each of them possesses a unique joint distribution of T2, T1, and D values, which can be regarded as a multispectral signature. In this study we therefore reconstructed three 2D distributions from the spinal cord – D-T2, D-T1, and T1–T2 – to decipher the particular tissue origin of the peaks.
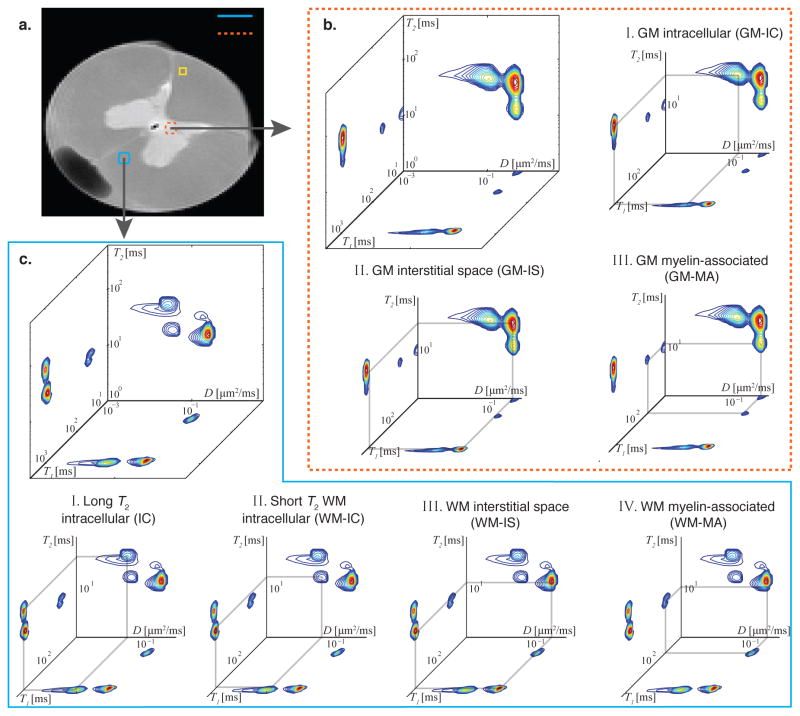
We first focus on a GM ROI in the spinal cord (Fig. 2a), whose REDCO spectra are shown and analyzed in Fig. 2b. There are almost no multicompartmental T1, T2, and D MRI studies with well-segregated GM tissue. However, given what is known about spinal cord anatomy, we can assume that GM is mainly composed of different cell types (i.e., neurons, glia), dendrites, a few mainly unmyelinated axons, and interstitial space (Standring, 2015). The GM intracellular (GM-IC) and GM interstitial (GM-IS) spaces are disentangled by their physical environment, reflected by the D dimension, whose peaks are shown in Figs. 2bI and II, respectively. Magnetization transfer (MT) between bulk water protons and nonaqueous protons (e.g., protons residing on proteins) was shown to be the source of short T1 components in the brain (Gochberg and Gore, 2007; Prantner et al., 2008). The third identified short T1 and T2 GM peak (Fig. 2bIII) was therefore assigned to a myelin-associated (GM-MA) component. This determination is also backed by previous studies, which found that the short T2 component, usually assigned to myelin water (Beaulieu et al., 1998; Mackay et al., 1994; Does and Gore, 2002; Bjarnason et al., 2005), is involved with large MT processes because of its close association with myelin bilayer proteins (MacKay et al., 2006). It is worth noting that dendrites in GM, which are expected to be randomly oriented, may contribute to the GM-IC, IC, and GM-IS components, depending on the angle of the dendrite relative to the diffusion gradient direction. Therefore, the dendrite microenvironment cannot be distinguished from the rest using a single diffusion gradient direction (for further discussion, see section 3.8).
Figure 2.
Spectra from GM and WM ROIs. (a) A high-resolution proton density MR image with the locations of representative ROIs: WM (blue box) and GM (red box) ROIs. After voxelwise analysis, the spectra in each of the GM and WM ROIs were averaged and are presented in (b) and (c), respectively. The different peaks are assigned to microscopic neuroanatomical components according to their D, T1, and T2 values. GM: I. Intracellular (GM-IC), II. GM interstitial space (GM-IS), and III. GM myelin-associated (GM-MA). WM: I. Long T2 intracellular (IC), II. Short T2 intracellular (WM-IC), III. WM interstitial space (WM-IS), and IV. WM myelin-associated (WM-MA).
The same types of spectra from a representative WM ROI (Fig. 2a) are shown and analyzed in Fig. 2c. Three peaks can be identified in each of the multidimensional spectra; however, four distinct microscopic components can be assigned from them. When only the physical environment, reflected by D, is considered, two domains can be identified: slow and fast apparent diffusion, in agreement with previous WM 1D studies (e.g., Ronen et al. (2006)). Similarly to GM, the slow and fast apparent diffusivity domains can be assigned to water residing in the intracellular and interstitial (labeled WM-IS) spaces, respectively. A more careful analysis of the D-T2 spectrum suggests two subpopulations of IC water, with long and short T2 values, whose peaks are shown in Figs. 2cI and II, respectively. While the long T2 IC component is readily visible in the WM spectra, nonnegligible spectral intensity in the peak location is also present in the GM D-T2 spectrum. Since both WM and GM share the long T2 IC component, we label it for the time being, as IC. The short T2 IC component is exclusive to WM, and therefore labeled WM-IC. It is worth noting that the intracellular space in WM is mainly comprised of axons and glial soma (Walhovd et al., 2014), and the ability to detect cellular subpopulations within WM is unique to MRMI. Assigning these components to specific microenvironments on the basis of their spatial arrangement within the spinal cord, along with the relevant assumptions, is discussed in the next sections. The fourth, short T1–T2 WM component (Fig. 2cIII) is identified as a WM myelin-associated (WM-MA) component, similar to the GM case.
3.3. Tissue components have a unique multispectral signature
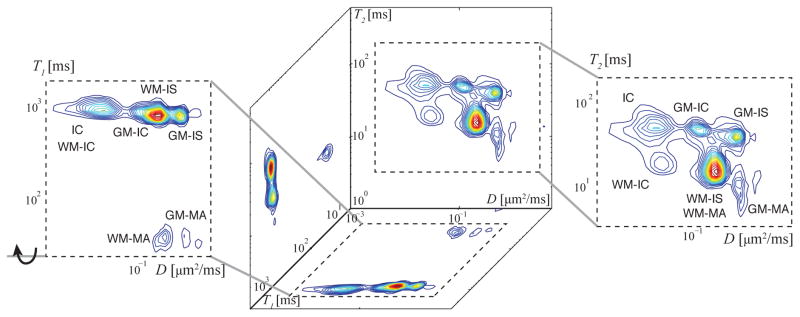
Apart from the spinal cord, such clear GM and WM separation is rare in other regions of the CNS. In most cases, a typical MRI brain voxel would contain a mixture of axons, neuronal soma, different types of glia, myelin, and interstitial spaces. One of the greatest challenges facing researchers using quantitative MRI methods is distinguishing between at least a subset of these components within an imaging voxel. The strength of microdynamic imaging in this context was demonstrated by analyzing a mixture of spectra from the above GM and WM ROIs (Fig. 2a). The resulting REDCO spectra are shown in Fig. 3. All of the identified WM and GM peaks possess a unique multispectral signature, thus allowing unequivocal assignments of these peaks to tissue components in the more challenging, and more realistic case, of mixed GM and WM.
Figure 3.
Microscopic compartmental analysis of a mixture of the representative GM and WM ROIs in Fig. 2a, which yield a gray–white matter “mixed volume.” To the right is the most informative D-T2 spectrum with four peaks, corresponding to four unique microscopic nervous components that can be unequivocally assigned (IC, WM-IC, GM-IC, and GM-IS). Having similar T2 and D values, the WM-IS, WM-MA, and GM-MA peaks are well separated by their T1 value, reflected in the D-T1 spectrum to the left. With this information, all seven peaks identified in Fig. 2 are accounted for.
Even in a mixed gray–white matter volume, the microdynamic information from the D-T2 and D-T1 spectra reveals the seven peaks identified in Fig. 2. The T1–T2 spectrum is the least informative of the three, not contributing any new information. However we retained this spectrum because it provides an internal experimental control, since it has to be consistent with the other two spectra. In addition, it may reveal distinct components in a different region of the CNS. It should be noted that discarding the T1–T2 measurement would reduce the number of acquisitions from 88 to 76.
3.4. Numerical representations of the tissue components
Mean values of the identified peaks are presented in Table 1. First, the weighted geometric mean of the T1, T2, and D of each component were derived according to the peaks’ intervals, which are also shown in the table. After that, the mean values from each of the components were again averaged across the spinal cord image according to their relative weights, which resulted in the global weighted mean and standard deviation (SD) that are shown in Table 1. Each component’s weighted global mean and SD of the apparent volume fraction (AVF) is also shown. Note that weighted AVFs do not, and should not, add up to 1.
Table 1.
Mean T1, T2, D, and AVF values of the identified peaks.
| Component | T1 [ms] | T2 [ms] | D [μm2/ms] | AVF | |||
|---|---|---|---|---|---|---|---|
| Mean†± SD | Interval | Mean†± SD | Interval | Mean†± SD | Interval | Mean†± SD | |
| WM-IC | 830 ± 44 | [42, 1700] | 20 ± 4.6 | [2.0, 34] | 0.051 ± 0.022 | [0.0040, 0.10] | 0.30 ± 0.11 |
| GM-IC | 900 ± 57 | [42, 1700] | 48 ± 7.5 | [38, 140] | 0.16 ± 0.037 | [0.11, 0.26] | 0.21 ± 0.12 |
| IC | 1010 ± 66 | [590, 1700] | 47 ± 11 | [34, 140] | 0.030 ± 0.018 | [0.0010, 0.10] | 0.29 ± 0.085 |
| WM-IS | 800 ± 74 | [420, 1700] | 13 ± 4.5 | [2.0, 30] | 0.23 ± 0.042 | [0.13, 0.37] | 0.39 ± 0.10 |
| GM-IS | 830 ± 76 | [420, 1500] | 37 ± 7.1 | [23, 110] | 0.45 ± 0.084 | [0.31, 1.5] | 0.32 ± 0.17 |
| WM-MA | 33 ± 6.3 | [13, 110] | 15 ± 4.1 | [2.0, 30] | 0.13 ± 0.046 | [0.010, 0.37] | 0.11 ± 0.027 |
| GM-MA | 31 ± 5.3 | [13, 81] | 32 ± 7.9 | [23, 110] | 0.49 ± 0.14 | [0.44, 1.5] | 0.075 ± 0.032 |
Global weighted mean averaged over the entire image.
Fig. 3 and Table 1 indicate a difference between the interstitial water of GM and WM. Although the term “interstitial” is somewhat ambiguous, the gray–white matter D-T2 spectrum suggests some important distinctions between WM- and GM-IS, in terms of their physical and chemical environments. The higher apparent diffusivity of the GM-IS reflects a less compact and ordered macroscopic tissue arrangement, compared with its WM counterpart, as expected. The faster relaxation in the WM-IS may be caused by a higher concentration of macromolecules, such as collagen and myelin, which are known to reduce the overall observed T2 (Sundaram et al., 1987; Beaulieu et al., 1998; Peled et al., 1999).
Another question that can be addressed from Table 1 is whether intracellular T2 is longer than its extracellular space counterpart. We suggest examining the different tissue regions, GM and WM, separately. In WM, our findings support previous studies, which have concluded the longer-lived T2 component corresponds to intracellular water (Peled et al., 1999; Wachowicz and Snyder, 2002; Dortch et al., 2010). In the present study, the WM description is a bit more complex because the tissue does not partition to only extra- and intracellular water, and the restricted diffusion component is divided into an additional two subpopulations. From Table 1, WM-IS, WM-IC, and IC have a global weighted mean T2 of 13, 20, and 47 ms, respectively, which is in agreement with the above-mentioned studies.
Very few studies have focused on quantifying T2 values of extra- and intracellular spaces in GM tissue. In the present study, the relevant GM components had average T2 values of 37, 48, and 47 ms, for the GM-IS, GM-IC, and IC, respectively (Table 1). These numbers indicate that similar to WM, the intracellular T2 is longer than the extracellular T2, although to a much lesser extent. These findings are partially backed by the work of Dortch et al. (2010), who could not distinguish between the intra- and extracellular components in the cortical and subcortical GM based on their T2. Contrary to our findings, Flint et al. (2012) investigated the spinal cord’s ventral horn (i.e., GM) using MR microscopy imaging, and showed a T2-weighted image with 6.25 μm isotropic resolution with hypointense neuronal cells, which may be interpreted as having reduced T2 compared with IS. However, two important issues prevent such a direct assertion: (a) IC hypointensity may be due to differences in proton density, i.e., proton density is lower in the IC compared with the IS, and therefore leads to lower signal. (b) Flint et al. (2012) have also reported that the IC diffusivity is about three times higher than that of the IS. Therefore, the presence of the imaging gradients could have resulted in unintentional diffusion-weighting in the T2-weighted images, which can be attributed to the IC hypointensity.
Intra- and extracellular fractions ratios can also be studied from these results. Previous brain extracellular space real-time iontophoresis studies determined that the volume fractions of the two intra- and extracellular water pools are about 0.8 and 0.2, respectively (Nicholson and Syková, 1998; Syková and Nicholson, 2008). We point back to Table 1, where such ratios can be obtained for the GM and WM regions. Ignoring the contribution of the MT-generated component, the ratios of the intra- and extracellular fractions are 0.61:0.39 and 0.60:0.40, in GM and WM, respectively. These ratios are not far from the established “ground truth” from the direct diffusion analysis by Nicholson and Syková (1998), especially considering the difference between the measuring techniques. It is worth noting that previous studies that used a biexponential diffusion model (Niendorf et al., 1996; Mulkern et al., 2000) have consistently found this ratio to be almost the opposite of what is expected.
As detailed above, MT, which can occur either by direct chemical exchange or by indirect dipole-mediated crossrelaxation, is the source of the short T1 peaks (WM- and GM-MA). From Table 1, these components have a T1 value of about 30 ms, while their T2 and D are similar to those of their respective IS components. With an effective diffusion period of 17 ms, which is not sufficient for complete MT-governed exchange, one would expect that the short T1 component would have two diffusivities in the D-T1 spectrum, corresponding to the diffusivities of the two exchanging pools. However, this is not the case and only one component was detected. We believe that the magnetization of this component originates from nonaqueous protons (Henkelman et al., 1993) and not water residing between or within the myelin sheaths. In that case, even if the MT process did not reach pseudo equilibrium during the diffusion period, the expected second peak in the D-T1 spectrum is undetectable due to its T2 (~ 10 μs), which is invisible when normal solution-state MRI techniques are used (Prantner et al., 2008).
3.5. Images of microscopic tissue components using MRMI
The REDCO spectrum is considered to be the joint probability density function of any two MR contrasts. Summing over a particular peak would therefore result in its signal fraction. It is generally assumed that the MR signal fraction is proportional to the proton’s volume fraction, thus giving the multispectral content physical meaning. We caution here that the relationship between the observed signal fraction and the actual volume fraction of the tissue component depends on many factors, such as the MR pulse sequence and MT efficiency (Prantner et al., 2008), and therefore the observed signal fraction is referred to here as the apparent volume fraction (AVF).
We now want to assign the different multispectral components in Fig. 3 to actual tissue microenvironments. The fact that each spinal cord image voxel has its own multispectral signature, containing information from the seven identified tissue components, helps us with the correct assignment. By summing over each of the identified distinct peaks, the AVFs of the seven tissue components are obtained in each voxel. The boundaries around the peaks (i.e., intervals) were determined based on the identified components in Fig. 2b, c, and are detailed in Table 1.
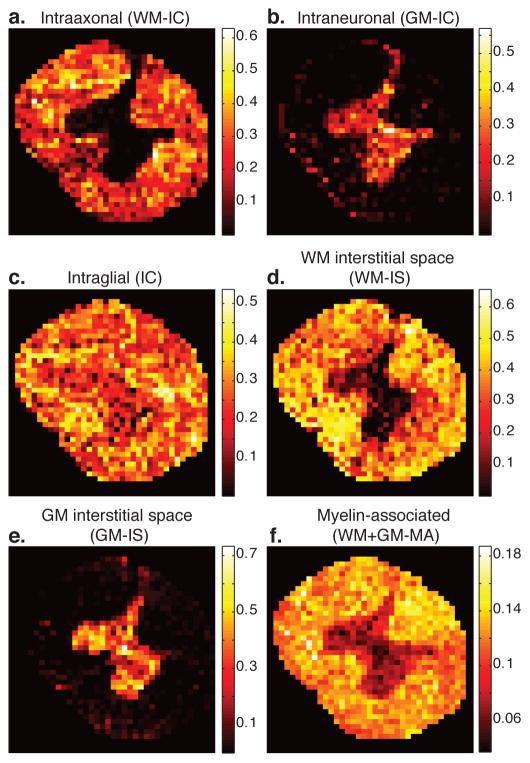
The AVF images of the nervous tissue components, shown in Fig. 4, exhibit unique contrasts. First, let us examine the spatial distribution of all the intracellular components we identified – WM-IC, GM-IC, and IC – and assign them to biological components:
Figure 4.
Generated quantitative images of the identified microscopic neuroanatomical tissue components. Image intensity reflects the AVF of the specific tissue component within each voxel. (a–c) The three identified intracellular tissue component images, WM-IC, GM-IC, and IC, corresponding to intraaxonal, intraneuronal, and intraglial AVF images, respectively. (d–e) Interstitial spaces, WM- and GM-IS AVF images. (f) Total content of myelin-associated components (GM and WM). Note that the AVFs are additive and normalized, and therefore sum to 1.
The WM-IC peak does not appear at all in the gray column voxelwise spectra (Fig. 4a). It has a weighted mean diffusivity value of 0.051 μm2/ms (Table 1), which is similar to previous findings in ex vivo WM (e.g., Avram et al. (2017)). It should be noted that very few axons, if any, are expected to reside in the cervical portion of the spinal cord GM, while a significant concentration of axons is expected in the WM(Standring, 2015). This microanatomical information would lead to an image with similar contrast as Fig. 4a, and we therefore suggest that the WM-IC component be assigned to intraaxonal water.
High spectral intensity of the GM-IC peak is mainly limited to the GM (Fig. 4b), and it has a geometric mean diffusivity value of 0.16 μm2/ms (Table 1), which may still be considered restricted (compared with the GM-IS diffusivity, for example). The gray column concentrates neuronal and glial soma and dendrites, with the former being physically larger (Rajkowska et al., 1998, 1999). The component’s high intensity in GM precludes it from originating from axonal water, and its relatively high diffusivity makes it improbable that it originates from glial soma. Therefore we assign the GM-IC component to the neuronal soma microenvironment (termed here intraneuronal).
The spectral intensity of the IC component peak is distributed in most areas of the spinal cord, with hyperintensity in certain regions of the WM (Fig. 4c). To assign this peak, it is worth noting that glia are present in all CNS regions, with higher concentration in WM (Snell, 2009; Azevedo et al., 2009), similar to the contrast in Fig. 4c. In addition, glia has a broad range of size (i.e., microglia and macroglia), while the IC peak spans a wide range of diffusivities, suggesting a broad size distribution (diffusivity range interval of [0.001, 0.10] μm2/ms, from Table 1). We therefore hypothesize that the IC peak originates from glial soma water (termed here intraglial).
As anticipated, WM-IS image intensity is mainly limited to WM (Fig. 4d) and is complementary to the GM-IS image, whose intensity is almost exclusively present in the gray column (Fig. 4e).
The total myelin-associated content (WM-MA + GM-MA) MRMI stain suggests a higher concentration in WM, but non negligible presence in the GM as well (Fig. 4f). This tissue component originates from MT between nonaqueous protons that reside on proteins and bulk water protons. Myelin-associated proteins, such as myelin basic protein (MBP) and myelin oligodendrocyte glycoprotein (MOG), are present in both myelin and in oligodendrocytes (Baumann and Pham-Dinh, 2001). While myelin is almost exclusively present in WM; oligodendrocytes are present in GM as well, which is consistent with the observed MA image contrast.
3.6. Stability and uncertainty
In light of the previously discussed non-uniqueness of the reconstructed 1D spectra, it is important to discuss their reliability, especially because MADCO uses them to constrain the 2D spectra estimation. Examination of the 1D projections from the 2D spectra in Fig. 2 reveals that all of the (1D) spectral peaks were previously reported in multiple publications: 1D diffusion spectrum with 2 peaks (e.g., Ronen et al. (2006)), 1D T2 spectrum with two or three peaks, depending on the tissue subregion (e.g., Dortch et al. (2010)), and 1D T1 spectrum with two peaks (e.g., Dortch et al. (2010)). The fact that the current 1D estimates are in agreement with the previous literature reduces the probability of the introduction of spurious peaks in the 2D spectra by using MADCO (i.e., applying the equality constraints). As additional evidence of the inversion stability, Fig. 5 shows the spatially varying spectra from four voxels within a WM ROI, indicated with a yellow rectangle on Fig. 2a. As can be seen, the distributions from single adjacent voxels demonstrate the robustness of the inversion. All three WM D-T2 components can be identified, with slight spectral intensity changes, across the ROI, highlighting the spatially varying nature of the estimated multidimensional spectroscopic signature across the heterogenous sample.
Figure 5.
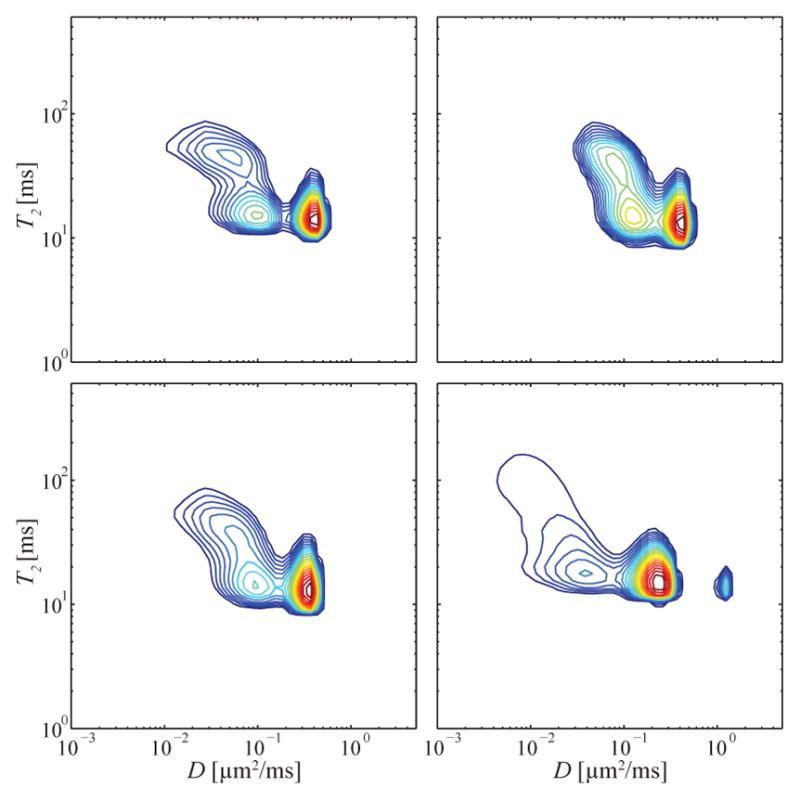
Spatially varying D-T2 spectra from a WM ROI, corresponding to the yellow box drawn on the anatomical image in Fig. 2a.
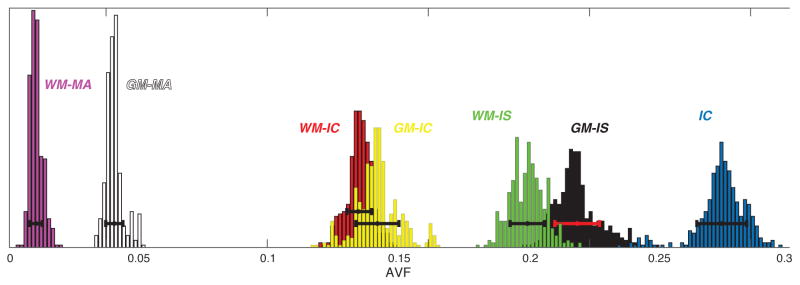
To quantify the uncertainty in the obtained 1D and 2D spectra, we used a jackknife approach (Quenouille, 1949), following a previously suggested method to reduce the resulting dimensionality (Prange and Song, 2009), as detailed in section 2.6. We obtained the spatially resolved AVFs of the tissue components from 880 2D spectra estimated from the resampled data. We report here their weighted means and SDs across the image: 0.30±0.015, 0.19±0.016, 0.28±0.016, 0.36±0.014, 0.3±0.020, 0.10 ± 0.0064, and 0.080 ± 0.0075, for the WM-IC, GM-IC, IC, WM-IS, GM-IS, WM-MA, and GM-MA, respectively. The SD of each AVF represents a quantified measure of its uncertainty. The SDs are under an order of magnitude smaller than the corresponding means, pointing to relative stability and low uncertainty. In addition, we presented in Fig. 6, as a representative example, the AVF histograms of the 7 components, along with their means and SDs, from the mix gray-white matter ROI spectra in Fig. 3.
Figure 6.
Histograms of the AVF values of the 7 tissue components computed from 880 2D spectra from the mix gray-white matter ROI in Fig. 3. The mean and SD for the histograms are indicated by the solid bars.
3.7. Consistency across modalities
Because of the rich and compelling nature of high-resolution IHC images, a quantitative comparison of IHC- and MRI-derived images would appear to be a natural control and validation step. However, fundamental differences between these two methodologies (detailed below) prevent IHC images from being used as “ground truth” for MRI-based findings. Nevertheless, it is consistency and not fidelity that we are testing for, given the artifacts and uncertainties present in both imaging modalities.
IHC findings were used to solidify the validity of the assignment of the multispectral signatures peaks to nervous tissue components. The same spinal cord specimen scanned with MRMI was subsequently studied with IHC, staining for astrocytes (GFAP), microglia (Iba1), neurofilaments (NF), myelin oligodendrocyte glycoprotein (MOG), and cell nuclei (cresyl violet). Further details and protocols are provided in the Materials and Methods section. Multi-variable linear regression was performed to assess consistency between the MRMI-derived nervous tissue component images and the relevant IHC-derived images after image registration. To visualize the fit of the dependent variable versus the other variables in the model we used the Frisch–Waugh–Lovell theorem (Frisch and Waugh, 1933; Lovell, 1963). Eight ROIs were selected, and MRMI voxels from each were correlated to IHC pixels. We divided this analysis into two sections, WM (axons and myelin) and cellular content (neurons and glia).
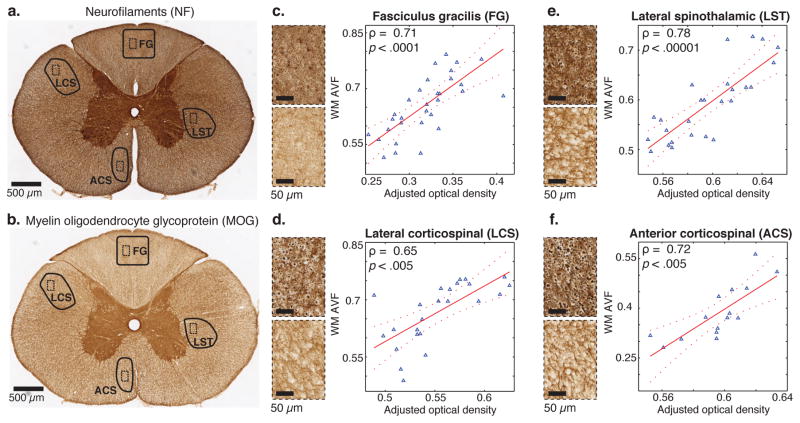
For WM, the multiple linear regression model included the NF and MOG IHC optical density images as independent variables, regressed onto a combined WM MRMI image, generated by adding the intraaxonal (WM-IC) and the total MA images. Although not exclusively specific to axons, NF optical density provides an indirect measure that should increase with axon density. The WM ROIs, fasciculus gracilis (FG), lateral corticospinal (LCS), lateral spinothalamic (LST), and anterior corticospinal (ACS) tracts, are marked on the IHC NF and MOG images of the entire spinal cord (Fig. 7a, b). Figs. 7c–f show the plots of the WM AVF obtained from REDCO versus the results of the adjusted multiple linear regression model, in the FG, LCS, LST, and ACS ROIs, respectively. Pearson’s correlation coefficients, ρ, of 0.71, 0.65, 0.78, and 0.72, with p < .0001, p < .005, p < .00001, and p < .005, in the FG, LCS, LST, and ACS ROIs, respectively, point to strong correlations with a high level of statistical significance.
Figure 7.
Correlations between various MRMI- and IHC-derived WM volume fractions. (a) Anti-NF IHC of the entire spinal cord slice with FG, LCS, ACS, and LST ROIs (solid lines) and magnified subregions within them (dashed lines). (b) Same for anti-MOG IHC. MRMI-based intraaxonal (WM-IC) and myelin-associated (MA) images were added to create a WM image in each ROI. After registration of IHC images to the MR image space, IHC images were resampled at MRI in-plane resolution, followed by multivariable regression with NF and MOG IHC images as predictor variables in a linear regression model. Scatter plots, along with the correlation coefficient (ρ) and the p-value for FG, LCS, LST, and ACS ROIs are shown in (c–f), respectively. The fitted model is the solid red line, and the dashed lines are the 95% confidence bounds.
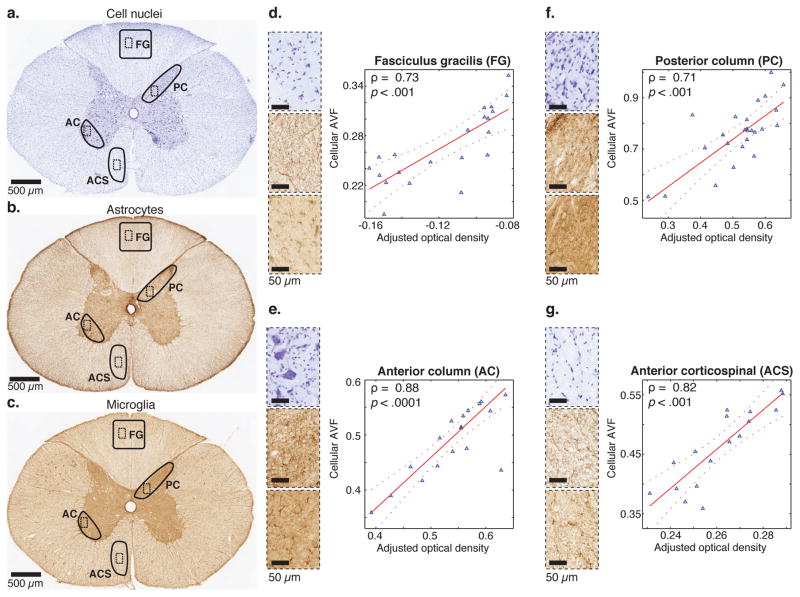
The cellular content is examined by correlating the MRMI-based combined GM-IC and IC image with the IHC findings. The multiple linear regression model included the optical densities of the cell nuclei (neurons and glia), astrocytes, and microglia IHC images as independent variables. For this analysis, we focused on the FG and ACS WM ROIs, and on the gray column in two regions, the posterior column (PC) and anterior column (AC). These ROIs are marked on the cell nuclei, astrocytes, and microglia histology images of the entire spinal cord (Fig. 8a–c). Fig. 8d–g show the plots of the cellular AVF obtained from MRMI against the adjusted multiple linear regression model in the FG, AC, PC, and ACS ROIs, respectively. Pearson’s correlation coefficients, ρ, of 0.73, 0.88, 0.71, and 0.82, with p < .001, p < .0001, p < .001, and p < .001, in the FG, AC, PC, and ACS ROIs, respectively, show strong correlations with a high level of statistical significance.
Figure 8.
Correlations between various MRMI- and IHC-derived cellular volume fractions. (a) Cresyl violet stain of the entire spinal cord slice with FG, AC, PC, and ACS ROIs (solid lines) and magnified subregions within them (dashed lines). (b) Same for anti-GFAP IHC. (c) Same for anti-Iba1 IHC. MRMI-based intraneuronal (GM-IC) and intraglial (IC) images were added to create a cellular content image in each ROI. After registration of IHC images to the MR image space, IHC images were resampled at MRI in-plane resolution, followed by multivariable regression with cresyl violet stain, GFAP, and Iba1 IHC images as predictor variables in a linear regression model. Scatter plots, along with the correlation coefficient (ρ) and the p-value for FG, AC, PC, and ACS ROIs are shown in (d–g), respectively. The fitted model is the solid red line, and the dashed lines are the 95% confidence bounds.
Although these results point to relatively strong correlation, it is important to bear in mind two major differences between MRI-based data and IHC. The first concerns the source of the signal. In MRI, the signal originates from protons and is proportional to their content. IHC contrast results from a chemical reaction (binding of an antibody to a specific protein), and the measured signal is an intensely colored product or a change in OD (Ramos-Vara, 2005). Water is generally used as a reporter molecule in MRI, while proteins are used in IHC, the former transmitting volumetric signal and the latter OD from the surface. The second difference relates to the physical state of the specimen. Even when imaging the same sample with both modalities, MRI scans the tissue in a completely hydrated state, without using any prior chemical processing (except fixation). Conversely, IHC microscopy requires multiple sample preparation steps, which are known to alter tissue microstructural features (Gusnard and Kirschner, 1977; Strausfeld, 1983).
3.8. Practical translational considerations
MRI is more time demanding from the perspective of data acquisition and scanning time than NMR because of the additional spatial encoding required. Although multidimensional MR is a powerful approach, these limitations have relegated its widespread use to non-MRI applications only. In vivo MRI measurements are generally limited in time – typically to 20 min for clinical scans, to 60 min for human neuroscience research, and up to 180 min for small animal imaging studies.
When a conventional 3 T clinical scanner with a 32-channel RF coil and a single-shot spin-echo DWEPI pulse sequence are used, acquisition of one slice takes about 150 ms (Avram et al., 2016). With the currently used TR = 4 ms, a multislice acquisition would result in 26 slices. Whole-brain coverage generally requires 12 cm in the superior–inferior direction (without cerebellum), which could be achieved with 26 slices and a 4.6 mm slice thickness. Because in vivo relaxation times are longer, the required TR would have to be on the order of 10 s, which would lead to 66 slices and a 1.8 mm slice thickness. Field of view (FOV) requirements for the human brain are generally 21 cm, and therefore the common matrix of sizes is 128 × 128 or 96×96 with 2 to 3 mm in-plane resolution. EPI readouts use an echo spacing of 0.8 ms, and therefore to avoid long echo time, EPI is done with parallel imaging, which can lead to a minimal echo time of about 32 ms (without diffusion weighting). If no diffusion weighting is used, this duration can be reduced using segmented EPI.
The minimum echo time in DW EPI scans depends strongly on the maximal b-value and the gradient system. For current state-of-the-art whole-body gradients (80 mT/m), b-values of 1500 and 6000 s/mm2 will result in echo times of about 60 and 79 ms, respectively (Avram et al., 2016). Reducing the echo time for diffusion scans can be achieved by using a stimulated echo diffusion EPI acquisition (Avram et al., 2010), or spiral-out trajectories (which start from the center of k-space) (Avram et al., 2014). In the latter case, the readout does not add to the echo time.
The REDCO spectra and nervous system component images in this study were generated by using 88 acquisitions in the T1–T2-D parameter space (instead of the commonly used 1000 to 2000 with conventional methods). This number of acquisitions was translated to a total scan time of 88 min with the currently used pulse sequence on our preclincal scanner. With the above mentioned clinical scanner experimental parameters, 88 acquisitions would take about 15 min, which is well-within the clinically acceptable range.
In this work we encoded D, T2, and T1 in separate, independent acquisitions, without availing ourselves of multichannel coils for parallel imaging, multiband, and other accelerated acquisition methods. Other more advanced MRI pulse sequences allow for more efficient image acquisition, which can result in significant acceleration. For instance, multiecho (Mädler et al., 2008) and modified Look-Locker (Messroghli et al., 2004) acquisitions, which are routinely used in clinical applications, yield multiple T2 and T1 images, respectively, in one shot. Using these standard pulse sequences would considerably reduce the total acquisition time we reported here to well below the clinically accepted threshold.
While T1- and T2-weighted experiments do not have a directional preference, dMRI acquisitions are acquired with diffusion gradients applied along a certain direction, thus encoding diffusivity in that direction. Since spinal cord WM is mainly comprised of relatively well-aligned axons, optimal diffusion contrast was achieved in the present study by setting the diffusion direction perpendicular to the main axis of the spinal cord. In other brain regions, where the fiber orientation is unknown, an isotropic DW sequence (Szczepankiewicz et al., 2015) or an orientationally averaged acquisition scheme over multiple well-distributed directions (Avram et al., 2017) could be used. In the latter study whole-brain human isotropic acquisitions with a maximal b-value of 6000 s/mm2 resulted in a 1D diffusion spectrum, which consistently contained two to three separable components (intracellular, extracellular, and CSF). However, these strategies would not help to distinguish between dispersed axons or dendrites that exhibit identical diffusion profiles as a heterogeneous distribution of isotropic tissue components (Mitra, 1995). The difference between such cases can be fully captured by estimating the 2D correlation of isotropic and directional diffusion (de Almeida Martins and Topgaard, 2016). Although still limited to NMR applications, this method may be used in conjunction with the MADCO framework to significantly reduce the number of acquisitions in the densely sampled 2D parameter space, thereby permitting measurements within the time frame of clinical MRI.
An additional practical consideration is the extent of dynamic migration of water from one domain to another, referred to as molecular exchange. If the exchange times between the microenvironments are shorter than the nominal acquisition times, then the demonstrated separation of the REDCO peaks will decline. In particular, the absence of a myelin sheath layer on neuronal and glial soma should increase the water exchange rate to and from them. Although our findings suggest that, indeed, the cell membrane is sufficient to induce a relatively low diffusivity and, in addition, the intraneuronal and intraglial peaks were well-resolved, we cannot exclude the effects of fast exchange in these two cases. The impact of exchange is expected to increase with in vivo applications because of the elevated temperature, the presence of active water and ion channels (Zhang et al., 2011), and the longer diffusion times necessary when using clinical systems. This issue may be addressed by direct measurement of the exchange rate spectrum, either via relaxation exchange spectroscopy (REXSY) (Lee et al., 1993) or via diffusion exchange spectroscopy (DEXSY) (Callaghan and Fur’o, 2004). Spatially resolved, accelerated, and efficient REXSY and DEXSY experiments were recently demonstrated by using the MADCO framework (Bai et al. (2016) and Benjamini et al. (2017), respectively), and could be integrated with MRMI, as a complementary measurement. Alternatively, filter-exchange imaging may be used to obtain a single global apparent exchange rate value (Nilsson et al., 2013), assuming two exchanging compartments.
4. Conclusions
Using MRMI, we identified specific tissue components on the basis of their multispectral signature within individual imaging voxels and in a clinically acceptable time range. The spatially resolved images obtained by using the MADCO framework with REDCO spectroscopic imaging allowed us, for the first time, to detect and distinguish between different intracellular components: axons, neuronal soma, and what is hypothesized to be glial soma. Interstitial spaces and myelin associated macromolecules within gray and white matter were also disentangled, identified, and imaged. These seven cellular, interstitial, and extracellular components may be present in any single MRMI spinal cord voxel. These have the potential to become a new family of microdynamic and physiological biomarkers for neurodegenerative diseases, neuroinflammation, and characterization of traumatic brain injury, as well as signatures of normal and abnormal development. MRMI delivers unprecedented spatially resolved information, which could have only been obtained by using laborious histological procedures on a fixed specimen. MRMI is clearly not limited to applications within the CNS; it can be used on any type of tissue or material in which relaxation, diffusion, and transport properties can be measured, providing exciting opportunities for investigators in a range of disciplines.
Acknowledgments
This work was supported by funds provided by the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (grant number ZIAHD000266). The authors thank FD Neurotechnologies Inc. for the histopathological staining and service, Dr. Alexandru V. Avram and Dr. Elizabeth B. Hutchinson for providing meaningful clinical insight, and Ms. Liz Salak for editing the manuscript.
Appendix A. MRI data processing
Appendix A.1. 1D relaxometry and diffusometry
Depending on the type of 1D relaxometry/diffusometry experiment, the signal attenuation, M, can be described by the following discrete sum (Menon and Allen, 1991):
| (A.1) |
where ε(β) is the experimental noise, which is assumed to be Gaussian. βi are experimental parameters determined by the data acquisition scheme, ω is the measured relaxation/diffusion parameter, which is distributed according to F(ω) with N discrete components, and K(β,ω) relates β and ω, and is called the kernel.
The applied MRI pulse sequence determines the experimental contrast (i.e., weighting), and subsequently the expression for the kernel. The respective kernels of the three present MRI contrasts, diffusion, T1, and T2, are
| (A.2a) |
| (A.2b) |
| (A.2c) |
while it is worth noting that KT1 is in fact a modified version of the conventional T1 kernel, obtained by subtracting the fully recovered data from the data set, and is done to eliminate any signal offset. In addition, a constant that accounts for a possible signal offset was added to Eq. A.1 in the case of the diffusion and T2 kernels, and therefore in those cases F(ω) contains N+1 components.
For each contrast, 1D encoding can be done by sampling the corresponding experimental parameter Nβ timess. In this case, Eq. A.1 can be written in matrix form as
| (A.3) |
where M and ε are Nβ ×1 vectors, F is an N ×1 vector, and K is an Nβ × N matrix (or (N + 1) × 1 vector and Nβ × (N + 1) matrix in the cases of diffusion or T2 encoding). Eq. A.3 represents an ill-posed problem, i.e., a small change in M may result in large variations in F. A standard approach to solving ill-conditioned problems is to regularize them. When the distribution is expected to be smooth, ℓ2 regularization is appropriate (Fordham et al., 1995), and therefore the regularized problem considered in this study was
| (A.4) |
where || · · · || is the ℓ2 norm. The regularization term is a measure of the desired smoothness in F(ω), and although it makes the inversion less ill-conditioned, it may cause a bias. Choosing the suitable value of α is still an open research question, with several approaches having been proposed (for a comprehensive review, please refer to Mitchell et al. (2012)). The regularization parameter in this study was chosen by means of the L-curve method (Hansen, 1992). Note that since F(ω) is a probability density function, nonnegativity constraints are imposed. Acquired 1D data using diffusion-, T1-, and T2-weighted experiments are then used to solve Eq. A.4 with the appropriate kernels from Eq. A.2, resulting in the 1D (marginal) distributions, F(D), F(T1), and F(T2).
Appendix A.2. 2D relaxation–diffusion correlation (REDCO)
In the above described cases (i.e., diffusion-, T1-, and T2-weighted experiments), the experimental parameters b, τ1, and τ2 are independent variables with respect to each other. Two-dimensional experiments that combine two contrast mechanisms can also be used. Eq. A.1 can be extended to the following general expression (English et al., 1991), which describes the signal attenuation from 2D experiments with separable kernels:
| (A.5) |
where the notation in Eq. A.1 is kept, only expanded to the 2D case. Eq. A.5 can be written as
| (A.6) |
and Eq. A.4 as
| (A.7) |
Here, a robust and widely used algorithm developed by Venkataramanan et al. (Venkataramanan et al., 2002; Song et al., 2002) was used to solve Eq. A.7.
Appendix A.3. MADCO framework implementation
It is generally accepted that if Nβ1 measurements are required to estimate the 1D distribution, F(ω1), then to reconstruct the 2D distribution, F(ω1, ω2), would require an order of Nβ1 × Nβ2 acquisitions, which is not feasible in clinical and biological applications. In this work we apply MADCO (Benjamini and Basser, 2016), a robust framework to stabilize the solution of Eq. A.7, while significantly reducing the number of required acquisitions and improving accuracy. Since the 2D distribution, F(ω1, ω2) is, in fact, the joint distribution of ω1 and ω2, it is related to the 1D marginal distributions F(ω1) and F(ω2) by
| (A.8a) |
| (A.8b) |
As described above, these marginal distributions can be separately estimated from 1D experiments, which is the main principle of the MADCO experimental design and reconstruction framework. Instead of sampling the entire experimental parameters space, (β1, β2), and directly estimating the 2D distribution F(ω1, ω2), using MADCO would only require sampling along β1 and β2 axes (i.e., 1D data), complemented with a small number of acquisitions in the 2D space (Fig. 1a). The framework therefore has two steps: (1) estimate F(ω1) and F(ω2) from 1D experiments using 𝒪(2Nβ) 1D measurements, and (2) use F(ω1) and F(ω2) as additional constrains (Eq. A.8) when solving Eq. A.7 with very few 2D measurements.
These equality constraints are correct in an idealized system; however, expected errors in the 1D estimations of F(ω1) and F(ω2) require a relaxed version of Eq. A.8,
| (A.9a) |
| (A.9b) |
In this work we set σ1,2 to be the standard deviation of the noise (as determined after complete signal decay) normalized by the unattenuated signal and N1,2. Similar to the standard nonnegativity constraints, the inequality constraints in Eq. A.9 also represent physical conditions that must be fulfilled (“conservation of mass” of the 2D probability distribution projected onto one of its axes) and can be applied in a similar manner.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander DC, Hubbard PL, Hall MG, Moore EA, Ptito M, Parker GJM, Dyrby TB. Orientationally invariant indices of axon diameter and density from diffusion MRI. NeuroImage. 2010;52(4):1374–89. doi: 10.1016/j.neuroimage.2010.05.043. [DOI] [PubMed] [Google Scholar]
- Assaf Y, Basser PJ. Composite hindered and restricted model of diffusion (CHARMED) MR imaging of the human brain. NeuroImage. 2005;27(1):48–58. doi: 10.1016/j.neuroimage.2005.03.042. [DOI] [PubMed] [Google Scholar]
- Avram AV, Guidon A, Song AW. Myelin water weighted diffusion tensor imaging. NeuroImage. 2010;53(1):132–138. doi: 10.1016/j.neuroimage.2010.06.019. [DOI] [PubMed] [Google Scholar]
- Avram AV, Guidon A, Truong TK, Liu C, Song AW. Dynamic and inherent B 0 correction for DTI using stimulated echo spiral imaging. Magnetic Resonance in Medicine. 2014;71(3):1044–1053. doi: 10.1002/mrm.24767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avram AV, Sarlls J, Hutchinson EB, Basser PJ. Isotropic Diffusion Relaxometry Imaging (IDRI). Proceedings of the 25th annual International Society of Magnetic Resonance in Medicine (ISMRM) Conference; Honolulu, HI, USA. 2017. [Google Scholar]
- Avram AV, Sarlls JE, Barnett AS, Özarslan E, Thomas C, Irfanoglu MO, Hutchinson E, Pierpaoli C, Basser PJ. Clinical feasibility of using mean apparent propagator (MAP) MRI to characterize brain tissue microstructure. NeuroImage. 2016;127:422–434. doi: 10.1016/j.neuroimage.2015.11.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azevedo FA, Carvalho LR, Grinberg LT, Farfel JM, Ferretti RE, Leite RE, Filho WJ, Lent R, Herculano-Houzel S. Equal numbers of neuronal and nonneuronal cells make the human brain an iso-metrically scaled-up primate brain. The Journal of Comparative Neurology. 2009;513(5):532–541. doi: 10.1002/cne.21974. [DOI] [PubMed] [Google Scholar]
- Bai R, Benjamini D, Cheng J, Basser PJ. Fast, accurate 2D-MR relaxation exchange spectroscopy ( REXSY ): Beyond compressed sensing. The Journal of Chemical Physics. 2016;145:154202. doi: 10.1063/1.4964144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bai R, Cloninger A, Czaja W, Basser PJ. Efficient 2D MRI relaxometry using compressed sensing. Journal of Magnetic Resonance. 2015;255:88–99. doi: 10.1016/j.jmr.2015.04.002. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Mattiello J, LeBihan D. MR diffusion tensor spectroscopy and imaging. Biophysical Journal. 1994;66(1):259–67. doi: 10.1016/S0006-3495(94)80775-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Magnetic Resonance in Medicine. 2000;44(4):625–32. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Baumann N, Pham-Dinh D. Biology of oligodendrocyte and myelin in the mammalian central nervous system. Physiological Reviews. 2001;81(2):871–927. doi: 10.1152/physrev.2001.81.2.871. [DOI] [PubMed] [Google Scholar]
- Beaulieu C, Fenrich FR, Allen PS. Multicomponent water proton transverse relaxation and T2-discriminated water diffusion in myelinated and nonmyelinated nerve. Magnetic Resonance Imaging. 1998;16(10):1201–10. doi: 10.1016/s0730-725x(98)00151-9. [DOI] [PubMed] [Google Scholar]
- Benjamini D, Basser PJ. Joint radius-length distribution as a measure of anisotropic pore eccentricity: An experimental and analytical framework. The Journal of Chemical Physics. 2014;141(21):214202. doi: 10.1063/1.4901134. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini D, Basser PJ. Use of marginal distributions constrained optimization (MADCO) for accelerated 2D MRI relaxometry and diffusometry. Journal of Magnetic Resonance. 2016;271:40–45. doi: 10.1016/j.jmr.2016.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini D, Basser PJ. Towards clinically feasible relaxation-diffusion correlation MRI using MADCO. Microporous and Mesoporous Materials. 2017 doi: 10.1016/j.micromeso.2017.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini D, Komlosh ME, Basser PJ. Imaging Local Diffusive Dynamics Using Diffusion Exchange Spectroscopy MRI. Physical Review Letters. 2017;118(15):158003. doi: 10.1103/PhysRevLett.118.158003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benjamini D, Komlosh ME, Holtzclaw LA, Nevo U, Basser PJ. White matter microstructure from nonparametric axon diameter distribution mapping. NeuroImage. 2016;135:333–344. doi: 10.1016/j.neuroimage.2016.04.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernin D, Topgaard D. NMR diffusion and relaxation correlation methods: New insights in heterogeneous materials. Current Opinion in Colloid & Interface Science. 2013;18(3):166–172. [Google Scholar]
- Bjarnason T, Vavasour I, Chia C, MacKay A. Characterization of the NMR behavior of white matter in bovine brain. Magnetic Resonance in Medicine. 2005;54(5):1072–1081. doi: 10.1002/mrm.20680. [DOI] [PubMed] [Google Scholar]
- Burcaw LM, Fieremans E, Novikov DS. Mesoscopic structure of neuronal tracts from time-dependent diffusion. NeuroImage. 2015;114:18–37. doi: 10.1016/j.neuroimage.2015.03.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Callaghan PT, Furó I. Diffusion-diffusion correlation and exchange as a signature for local order and dynamics. The Journal of Chemical Physics. 2004;120(8):4032. doi: 10.1063/1.1642604. [DOI] [PubMed] [Google Scholar]
- CVX Research. CVX: Matlab Software for Disciplined Convex Programming, version 2.0. 2012 URL http://cvxr.com/cvx.
- de Almeida Martins JP, Topgaard D. Two-Dimensional Correlation of Isotropic and Directional Diffusion Using NMR. Physical Review Letters. 2016;116(8):087601. doi: 10.1103/PhysRevLett.116.087601. [DOI] [PubMed] [Google Scholar]
- Does MD, Gore JC. Compartmental study of T1 and T2 in rat brain and trigeminal nerve in vivo. Magnetic Resonance in Medicine. 2002;47(2):274–283. doi: 10.1002/mrm.10060. [DOI] [PubMed] [Google Scholar]
- Dortch RD, Apker GA, Valentine WM, Lai B, Does MD. Compartment-specific enhancement of white matter and nerve ex vivo using chromium. Magnetic Resonance in Medicine. 2010;64(3):688–97. doi: 10.1002/mrm.22460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- English AE, Whittall KP, Joy MLG, Henkelman RM. Quantitative Two-Dimensional time Correlation Relaxometry. Magnetic Resonance in Medicine. 1991;22(2):425–434. doi: 10.1002/mrm.1910220250. [DOI] [PubMed] [Google Scholar]
- Fawcett JK, Scott JE. A rapid and precise method for the determination of urea. Journal of Clinical Pathology. 1960;13:156–9. doi: 10.1136/jcp.13.2.156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flint JJ, Hansen B, Portnoy S, Lee CH, King MA, Fey M, Vincent F, Stanisz GJ, Vestergaard-Poulsen P, Blackband SJ. Magnetic resonance microscopy of human and porcine neurons and cellular processes. NeuroImage. 2012;60(2):1404–1411. doi: 10.1016/j.neuroimage.2012.01.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fordham E, Sezginer A, Hall L. Imaging Multiexponential Relaxation in the (y, LogeT1) Plane, with Application to Clay Filtration in Rock Cores. Journal of Magnetic Resonance, Series A. 1995;113(2):139–150. [Google Scholar]
- Frisch R, Waugh FV. Partial Time Regressions as Compared with Individual Trends. Econometrica. 1933 Oct;1(4):387. [Google Scholar]
- Galvosas P, Callaghan PT. Multi-dimensional inverse Laplace spectroscopy in the NMR of porous media. Comptes Rendus Physique. 2010;11(2):172–180. [Google Scholar]
- Gochberg DF, Gore JC. Quantitative magnetization transfer imaging via selective inversion recovery with short repetition times. Magnetic Resonance in Medicine. 2007;57(2):437–41. doi: 10.1002/mrm.21143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant MC, Boyd SP. Recent Advances in Learning and Control. Springer London; London: 2008. Graph Implementations for Nonsmooth Convex Programs; pp. 95–110. [Google Scholar]
- Gusnard D, Kirschner RH. Cell and organelle shrinkage during preparation for scanning electron microscopy: effects of fixation, dehydration and critical point drying. Journal of Microscopy. 1977;110(1):51–57. doi: 10.1111/j.1365-2818.1977.tb00012.x. [DOI] [PubMed] [Google Scholar]
- Hansen PC. Analysis of Discrete Ill-Posed Problems by Means of the L-Curve. SIAM Review. 1992;34(4):561–580. [Google Scholar]
- Harrison R, Bronskill MJ, Mark Henkelman R. Magnetization Transfer and T2 Relaxation Components in Tissue. Magnetic Resonance in Medicine. 1995;33(4):490–496. doi: 10.1002/mrm.1910330406. [DOI] [PubMed] [Google Scholar]
- Henkelman RM, Huang X, Xiang QS, Stanisz GJ, Swanson SD, Bronskill MJ. Quantitative interpretation of magnetization transfer. Magnetic Resonance in Medicine. 1993;29(6):759–766. doi: 10.1002/mrm.1910290607. [DOI] [PubMed] [Google Scholar]
- Johansen-Berg H, Behrens TE, editors. Diffusion MRI: From Quantitative Measurement to In vivo Neuroanatomy. 2. Academic Press; London, UK: 2013. [Google Scholar]
- Kim D, Doyle EK, Wisnowski JL, Kim JH, Haldar JP. Diffusion-Relaxation Correlation Spectroscopic Imaging: A Multi-dimensional Approach for Probing Microstructure. Magnetic Resonance in Medicine. 2017 doi: 10.1002/mrm.26629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleinberg R, Horsfield M. Transverse relaxation processes in porous sedimentary rock. Journal of Magnetic Resonance (1969) 1990;88(1):9–19. [Google Scholar]
- Lee JH, Labadie C, Springer CS, Harbison GS. Two-dimensional inverse Laplace transform NMR: altered relaxation times allow detection of exchange correlation. Journal of the American Chemical Society. 1993;115(17):7761–7764. [Google Scholar]
- Lovell MC. Seasonal Adjustment of Economic Time Series and Multiple Regression Analysis. Journal of the American Statistical Association. 1963;58(304):993–1010. [Google Scholar]
- MacKay A, Laule C, Vavasour I, Bjarnason T, Kolind S, Mädler B. Insights into brain microstructure from the T2 distribution. Magnetic Resonance Imaging. 2006;24(4):515–525. doi: 10.1016/j.mri.2005.12.037. [DOI] [PubMed] [Google Scholar]
- Mackay A, Whittall K, Adler J, Li D, Paty D, Graeb D. In vivo visualization of myelin water in brain by magnetic resonance. Magnetic Resonance in Medicine. 1994;31(6):673–677. doi: 10.1002/mrm.1910310614. [DOI] [PubMed] [Google Scholar]
- Mädler B, Drabycz SA, Kolind SH, Whittall KP, MacKay AL. Is diffusion anisotropy an accurate monitor of myelination? Magnetic Resonance Imaging. 2008;26(7):874–888. doi: 10.1016/j.mri.2008.01.047. [DOI] [PubMed] [Google Scholar]
- McWhirter JG, Pike ER. On the numerical inversion of the Laplace transform and similar Fredholm integral equations of the first kind. Journal of Physics A: Mathematical and General. 1978;11(9):1729–1745. [Google Scholar]
- Menon RS, Allen PS. Application of continuous relaxation time distributions to the fitting of data from model systmes and excised tissue. Magnetic Resonance in Medicine. 1991;20(2):214–227. doi: 10.1002/mrm.1910200205. [DOI] [PubMed] [Google Scholar]
- Messroghli DR, Radjenovic A, Kozerke S, Higgins DM, Sivananthan MU, Ridgway JP. Modified Look-Locker inversion recovery (MOLLI) for high-resolution T1 mapping of the heart. Magnetic Resonance in Medicine. 2004;52(1):141–6. doi: 10.1002/mrm.20110. [DOI] [PubMed] [Google Scholar]
- Mitchell J, Chandrasekera TC, Gladden LF. Numerical estimation of relaxation and diffusion distributions in two dimensions. Progress in Nuclear Magnetic Resonance Spectroscopy. 2012;64:34–50. doi: 10.1016/j.pnmrs.2011.07.002. [DOI] [PubMed] [Google Scholar]
- Mitra P. Multiple wave-vector extensions of the NMR pulsed-field-gradient spin-echo diffusion measurement. Physical Review B. 1995;51(21):15074–15078. doi: 10.1103/physrevb.51.15074. [DOI] [PubMed] [Google Scholar]
- Mulkern RV, Zengingonul HP, Robertson RL, Bogner P, Zou KH, Gudbjartsson H, Guttmann CR, Holtzman D, Kyriakos W, Jolesz FA, Maier SE. Multi-component apparent diffusion coefficients in human brain: relationship to spin-lattice relaxation. Magnetic Resonance in Medicine. 2000;44(2):292–300. doi: 10.1002/1522-2594(200008)44:2<292::aid-mrm17>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- Nicholson C, Syková E. Extracellular space structure revealed by diffusion analysis. Trends in Neurosciences. 1998;21(5):207–215. doi: 10.1016/s0166-2236(98)01261-2. [DOI] [PubMed] [Google Scholar]
- Niendorf T, Dijkhuizen RM, Norris DG, van Lookeren Campagne M, Nicolay K. Biexponential diffusion attenuation in various states of brain tissue: Implications for diffusion-weighted imaging. Magnetic Resonance in Medicine. 1996;36(6):847–857. doi: 10.1002/mrm.1910360607. [DOI] [PubMed] [Google Scholar]
- Nilsson M, Lätt J, van Westen D, Brockstedt S, Lasič S, Ståhlberg F, Topgaard D. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magnetic Resonance in Medicine. 2013;69(6):1573–81. doi: 10.1002/mrm.24395. [DOI] [PubMed] [Google Scholar]
- Peled S, Cory DG, Raymond SA, Kirschner DA, Jolesz FA. Water diffusion, T(2), and compartmentation in frog sciatic nerve. Magnetic Resonance in Medicine. 1999;42(5):911–8. doi: 10.1002/(sici)1522-2594(199911)42:5<911::aid-mrm11>3.0.co;2-j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prange M, Song YQ. Quantifying uncertainty in NMR T2 spectra using Monte Carlo inversion. Journal of Magnetic Resonance. 2009;196:54–60. doi: 10.1016/j.jmr.2008.10.008. [DOI] [PubMed] [Google Scholar]
- Prantner AM, Bretthorst GL, Neil JJ, Garbow JR, Ackerman JJ. Magnetization transfer induced biexponential longitudinal relaxation. Magnetic Resonance in Medicine. 2008;60(3):555–563. doi: 10.1002/mrm.21671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Price W. NMR Studies of Translational Motion. Cambridge University Press; Cambridge: 2009. [Google Scholar]
- Provencher SW. A constrained regularization method for inverting data represented by linear algebraic or integral equations. Computer Physics Communications. 1982;27(3):213–227. [Google Scholar]
- Quenouille MH. Problems in Plane Sampling. The Annals of Mathematical Statistics. 1949;20(3):355–375. [Google Scholar]
- Rajkowska G, Miguel-Hidalgo JJ, Wei J, Dilley G, Pittman SD, Meltzer HY, Overholser JC, Roth BL, Stockmeier CA. Morphometric evidence for neuronal and glial prefrontal cell pathology in major depression. Biological Psychiatry. 1999;45(9):1085–98. doi: 10.1016/s0006-3223(99)00041-4. [DOI] [PubMed] [Google Scholar]
- Rajkowska G, Selemon LD, Goldman-Rakic PS. Neuronal and Glial Somal Size in the Prefrontal Cortex. Archives of General Psychiatry. 1998;55(3):215. doi: 10.1001/archpsyc.55.3.215. [DOI] [PubMed] [Google Scholar]
- Ramos-Vara JA. Technical aspects of immunohistochemistry. Veterinary Pathology. 2005;42(4):405–26. doi: 10.1354/vp.42-4-405. [DOI] [PubMed] [Google Scholar]
- Ronen I, Moeller S, Ugurbil K, Kim DS. Analysis of the distribution of diffusion coefficients in cat brain at 9.4 T using the inverse Laplace transformation. Magnetic Resonance Imaging. 2006;24(1):61–68. doi: 10.1016/j.mri.2005.10.023. [DOI] [PubMed] [Google Scholar]
- Silva MD, Helmer KG, Lee JH, Han SS, Springer CS, Sotak CH. Deconvolution of Compartmental Water Diffusion Coefficients in Yeast-Cell Suspensions Using Combined T1 and Diffusion Measurements. Journal of Magnetic Resonance. 2002;156(1):52–63. doi: 10.1006/jmre.2002.2527. [DOI] [PubMed] [Google Scholar]
- Snell RS. Clinical Neuroanatomy. 7. Lippincott Williams & Wilkins; Philadelphia, PA: 2009. [Google Scholar]
- Song YQ, Venkataramanan L, Hürlimann M, Flaum M, Frulla P, Straley C. T1–T2 Correlation Spectra Obtained Using a Fast Two-Dimensional Laplace Inversion. Journal of Magnetic Resonance. 2002;154(2):261–268. doi: 10.1006/jmre.2001.2474. [DOI] [PubMed] [Google Scholar]
- Song Y-Q, Venkataramanan L, Kausik R, Heaton N. Two-dimensional NMR of Diffusion and Relaxation. In: Valiullin R, editor. Diffusion NMR of Confined Systems : Fluid Transport in Porous Solids and Heterogeneous Materials. Royal Society of Chemistry; Cambridge, UK: 2016. pp. 111–155. [Google Scholar]
- Standring S. Gray’s Anatomy: The Anatomical Basis of Clinical Practice. 41. Elsevier; 2015. [Google Scholar]
- Stejskal E, Tanner J. Spin diffusion measurements: Spin echoes in the presence of a time-dependent field gradient. Journal of Chemical Physics. 1965;42(1):288–292. [Google Scholar]
- Strausfeld NJ. Functional Neuroanatomy. Springer-Verlag; Berlin: 1983. [Google Scholar]
- Sundaram M, McGuire MH, Schajowicz F. Soft-tissue masses: histologic basis for decreased signal (short T2) on T2-weighted MR images. American Journal of Roentgenology. 1987;148(6):1247–50. doi: 10.2214/ajr.148.6.1247. [DOI] [PubMed] [Google Scholar]
- Syková E, Nicholson C. Diffusion in brain extracellular space. Physiological Reviews. 2008;88(4):1277–340. doi: 10.1152/physrev.00027.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczepankiewicz F, Lasič S, van Westen D, Sundgren PC, Englund E, Westin CF, Ståhlberg F, Lätt J, Topgaard D, Nilsson M. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: Applications in healthy volunteers and in brain tumors. NeuroImage. 2015;104:241–252. doi: 10.1016/j.neuroimage.2014.09.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tax CM, Rudrapatna US, Witzel T, Jones DK. Disentangling in two dimensions in the living human brain: Feasbilty of relaxometry-diffusometry using ultra-strong gradients. Proceedings of the 25th annual International Society of Magnetic Resonance in Medicine (ISMRM) Conference; Honolulu, HI, USA. 2017. [Google Scholar]
- van Gelderen P, de Zwart JA, Lee J, Sati P, Reich DS, Duyn JH. Nonexponential T2* decay in white matter. Magnetic Resonance in Medicine. 2012;67(1):110–117. doi: 10.1002/mrm.22990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venkataramanan L, Song Yi-Qiao, Hurlimann M. Solving Fredholm integrals of the first kind with tensor product structure in 2 and 2.5 dimensions. IEEE Transactions on Signal Processing. 2002;50(5):1017–1026. [Google Scholar]
- Wachowicz K, Snyder RE. Assignment of theT2 components of amphibian peripheral nerve to their microanatomical compartments. Magnetic Resonance in Medicine. 2002;47(2):239–245. doi: 10.1002/mrm.10053. [DOI] [PubMed] [Google Scholar]
- Walhovd K, Johansen-Berg H, Káradóttir R. Unraveling the secrets of white matter ? Bridging the gap between cellular, animal and human imaging studies. Neuroscience. 2014;276:2–13. doi: 10.1016/j.neuroscience.2014.06.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittall KP, MacKay AL. Quantitative interpretation of NMR relaxation data. Journal of Magnetic Resonance (1969) 1989;84(1):134–152. [Google Scholar]
- Zhang H, Schneider T, Wheeler-Kingshott CA, Alexander DC. NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain. NeuroImage. 2012;61(4):1000–16. doi: 10.1016/j.neuroimage.2012.03.072. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Blümich B. Spatially resolved D?T2 correlation NMR of porous media. Journal of Magnetic Resonance. 2014;242:41–48. doi: 10.1016/j.jmr.2014.01.017. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Poirier-Quinot M, Springer CS, Balschi JA. Active Trans-Plasma Membrane Water Cycling in Yeast Is Revealed by NMR. Biophysical Journal. 2011;101(11):2833–2842. doi: 10.1016/j.bpj.2011.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]