Beyond Discrimination: a Comparison of Calibration Methods and Clinical Usefulness of Predictive Models of Readmission Risk

Abstract

Background

Prior to implementing predictive models in novel settings, analyses of calibration and clinical usefulness remain as important as discrimination, but they are not frequently discussed. Calibration is a model’s reflection of actual outcome prevalence in its predictions. Clinical usefulness refers to the utilities, costs, and harms of using a predictive model in practice. A decision analytic approach to calibrating and selecting an optimal intervention threshold may help maximize the impact of readmission risk and other preventive interventions.

Objectives

To select a pragmatic means of calibrating predictive models that requires a minimum amount of validation data and that performs well in practice. To evaluate the impact of miscalibration on utility and cost via clinical usefulness analyses.

Materials and Methods

Observational, retrospective cohort study with electronic health record data from 120,000 inpatient admissions at an urban, academic center in Manhattan. The primary outcome was thirty-day readmission for three causes: all-cause, congestive heart failure, and chronic coronary atherosclerotic disease. Predictive modeling was performed via L1-regularized logistic regression. Calibration methods were compared including Platt Scaling, Logistic Calibration, and Prevalence Adjustment. Performance of predictive modeling and calibration was assessed via discrimination (c-statistic), calibration (Spiegelhalter Z-statistic, Root Mean Square Error [RMSE] of binned predictions, Sanders and Murphy Resolutions of the Brier Score, Calibration Slope and Intercept), and clinical usefulness (utility terms represented as costs). The amount of validation data necessary to apply each calibration algorithm was also assessed.

Results

C-statistics by diagnosis ranged from 0.7 for all-cause readmission to 0.86 (0.78–0.93) for congestive heart failure. Logistic Calibration and Platt Scaling performed best and this difference required analyzing multiple metrics of calibration simultaneously, in particular Calibration Slopes and Intercepts. Clinical usefulness analyses provided optimal risk thresholds, which varied by reason for readmission, outcome prevalence, and calibration algorithm. Utility analyses also suggested maximum tolerable intervention costs, e.g. $1,720 for all-cause readmissions based on a published cost of readmission of $11,000.

Conclusions

Choice of calibration method depends on availability of validation data and on performance. Improperly calibrated models may contribute to higher costs of intervention as measured via clinical usefulness. Decision-makers must understand underlying utilities or costs inherent in the use-case at hand to assess usefulness and will obtain the optimal risk threshold to trigger intervention and intervention cost limits as a result.

Graphical abstract

Assessing the Calibration and Clinical Usefulness of Readmission Risk Prediction

$$U_{\mathit{\text{Pred}}(s)}=P\ast {\mathit{\text{TPR}}}_s\ast U_{(\mathit{\text{treat}},\mathit{\text{dz}})}+P\ast (1-{\mathit{\text{TPR}}}_s)\ast U_{(\neg \mathit{\text{treat}},\mathit{\text{dz}})}+(1-P)\ast {\mathit{\text{FPR}}}_s\ast U_{(\mathit{\text{treat}},\neg \mathit{\text{dz}})}+(1-P)\ast (1-{\mathit{\text{FPR}}}_s)\ast U_{(\neg \mathit{\text{treat}},\neg \mathit{\text{dz}})}+U_{\mathit{\text{test}}}$$

A Utility-Based Framework may help:

1. Estimate Cost Savings or Loss

2. Choose the Right Model to Implement and the Right Threshold at which to Intervene

BACKGROUND AND SIGNIFICANCE

The bulk of the literature on clinical predictive modeling focuses on feature selection, choice of algorithm, and evaluation as defined by discriminatory performance. Calibration may be mentioned via broad goodness of fit tests such as the Hosmer Lemeshow test or not mentioned at all.[1],[2] The informatics community has demonstrated significant interest in calibration of predictive models at national symposia; the need for practical assessments of approaches to calibration has been highlighted.[3] Moreover, increasing attention is being paid to the importance of either providing a continuous prediction to clinicians or to provide a binary recommendation (e.g., “order a test”, “do not order a test”) based on a prior risk threshold. The myriad of published regression models to predict binary outcomes like hospital readmissions all qualify for this consideration. Clinical usefulness is a means to assess model performance across possible risk thresholds and – critically – to incorporate underlying utility, cost, or harm data into the decision analysis.[1,4,5]

The Centers for Medicare and Medicaid Services (CMS) initiated the Hospital Readmissions Reduction Program to incentivize hospitals across the country to limit rates of thirty-day hospital readmission for common diagnoses like congestive heart failure, myocardial infarction, and pneumonia.[6] Numerous predictive models typically based in logistic regression have been described.[7–19] A systematic review of models of hospital readmission in 2011 outlined dozens of published attempts to predict readmission at that time.[11] One widely accepted metric to compare discrimination between models is the area under the receiver-operating characteristic curve (AUROC) or c-statistic. The advantage of the AUROC is that it includes all combinations of sensitivity and specificity throughout the probability space in its calculation. An accompanying Receiver Operating Characteristic (ROC) Plot, if provided, permits selection of sensitivity and specificity combinations at various thresholds.

Discrimination is the ability of a predictive model to separate data into classes. Calibration, however, is a measure of the closeness of model probability to the underlying probability of the population under study.[20,21] A predictive model is well-calibrated if, for example, it produces a predicted probability of 40% risk of readmission for one patient, and similar patients would truly be readmitted 2 out of 5 times.[22] It remains critical because it captures accurate estimation of risk, not simply whether two individuals can be risk-stratified from each other. Calibration can be impacted by temporal variation (new patients over time), geographic variation (patients in a new hospital), and domain validation (predicting heart attack risk in an emergency room setting instead of a primary care outpatient clinic). Failure to account for such variation leads to risk estimates that may be incorrect – the predicted risk of heart attack may be 10%, not 1%, if heart attacks are notably more common in a new setting. With inaccurate risk estimation, clinical decision-making may be compromised. A number of methods to calibrate predictive models have been described. Recent work by Jiang et al, for example, considered methods that calibrate and in some cases extend models to achieve better calibration.[23]

Because there are many readmission risk predictive models available, a reliable measure of calibration is necessary, just as the c-statistic has been chosen as the de facto measure of discrimination in the literature (though it is not without its limitations, as well). Commonly published metrics include goodness-of-fit tests like the Hosmer-Lemeshow test, which has been noted to have technical and practical limitations including detection of overfitting, applicability in small samples, and “poor power to Beyond Discrimination: a Comparison of Calibration Methods and Clinical Usefulness of Predictive Models of Readmission Risk detect miscalibration in the common form of systematic differences between outcomes in the new data and the model development data”.[20] Calibration-in-the-large plots and calibration slope are both useful means of illustrating model calibration, but these graphical summaries may not be interpreted consistently.[2,24,25]

The Brier score, based on the mean square error of predictions, has also been used to measure calibration, but it has been shown to measure a composite of discrimination and calibration in work by Spiegelhalter, Sanders, Murphy, and others.[26,27] Rufibach illustrates succinctly that in some situations the Brier score may be lower for a model that is in fact less well-calibrated than another.[28] Root mean square error (RMSE), is also commonly applied as a binned estimator in the evaluation of predictive models.[29]

Spiegelhalter’s Z-statistic results from a decomposition of the Brier score by Spiegelhalter in 1986.[26] It is represented as

$$Z(p,x)=\frac{{\sum }_{i=1}^n(x_i-p_i)(1-2p_i)}{\sqrt{{\sum }_{i=1}^n{(1-2p_i)}^2\ast p_i\ast (1-p_i)}}$$ (1)

where x=(x₁, … x_n) is the set of outcomes in a sample of n predictive probabilities represented by p = (p₁, …, p_n).[26,28] The equation derives from expanding the square of the Brier score and replacing x_i² with x_i (given x_i is 0 or 1). The numerator represents “lack of calibration”, as Steyerberg noted, in that its expected value is zero in the case of perfect calibration. The denominator represents “lack of spread”, specifically the p_i(1-p_i) term. It has not to date been used widely in the domain of hospital readmission risk prediction to compare different models.

The resolutions of the Brier Score described by Sanders and Murphy yield additional information to describe both the outcome distribution in the underlying data as well as the impact of the predictions or forecasts for the model at hand. Relying on binning risk predictions, p, into a finite number, J, of forecasts, f, Sanders and subsequently Yates decompose the mean Brier Score, B, or Mean Probability Score for N events with outcomes, x, into:

$$\overline{B}=\frac{1}{N}{\sum }_{j=1}^J{\sum }_{i=1}^N{(f_j-x_{\mathit{\text{ij}}})}^2=\frac{1}{N}{\sum }_{j=1}^J{N}_j{\overline{d}}_j(1-{\overline{d}}_j)+\frac{1}{N}{\sum }_{j=1}^J{N}_j{(f_j-{\overline{d}}_j)}^2$$ (2)

Of note, d_j, is the frequency of outcomes of interest over the N_j events in each bin corresponding to the forecast for that bin. The term: $\frac{1}{N}{\sum }_{j=1}^J{N}_j{\overline{d}}_j(1-{\overline{d}}_j)$ denotes the resolution and the term $\frac{1}{N}{\sum }_{j=1}^J{N}_j{(f_j-{\overline{d}}_j)}^2$ denotes the reliability or “reliability-in-the-small” of the Mean Probability Score.[30] The resolution depends on the distribution of outcome events inherent to the data but also on the order in which the outcome events are binned based on the forecasts of the model at hand. Thus, the resolution term is maximized if every event receives an identical prediction and minimized if identical forecasts are never assigned to two different data points. Reliability-in-the-small captures whether binned forecasts match the relative frequencies of their corresponding categories, with the classic example being that it rains 40 out of 100 days which are assigned a 40% predicted probability of rain.[30] Repeating this success at every discrete forecast category yields good calibration-in-the-small.

Work by Steyerberg and colleagues extends the evaluation of clinical predictive models to incorporate the concept of clinical usefulness in model validation.[1,21] Rooted in decision science and similar to the approach of “net benefit”, clinical usefulness incorporates two critical aspects of the application of any clinical predictive model to guide treatment decisions: 1) the selection of a risk threshold; 2) an understanding of the utilities, costs, and harms for the given use-case.[1,31] Clinical utility/benefit or harm terms may be included in usefulness analyses. In the case of hospital readmission risk prediction, one primary driver is that of cost.

Billings et al, 2006, demonstrated that a business case modeled around a readmission risk score algorithm can illustrate the potential costs and impact of an intervention to reduce readmission.[32] That work used a single prediction algorithm and risk score to demonstrate the impact of an intervention to reduce readmission risk. The state of the art today incorporates multiple algorithms predicting multiple reasons for readmission; each algorithm has its own optimal threshold. Readmission risk prediction is intended to guide interventions to minimize rates of readmission and thereby to minimize financial disincentives, i.e. costs of readmission, to a given hospital or center; estimates of hospital penalties for 2014 have been as high as $375,000.[33] Individual readmission cost data are rare, but one study listed a mean cost of a single readmission for recurrent DVT as $11,862.[34]

The first objective of this work is to identify the calibration method that provides acceptable performance with the least amount of requisite validation data. Because calibration performance is a relative quantity, those methods that minimize miscalibration as measured by minimum Brier score, for example, are preferred. The second objective is to apply clinical usefulness to evaluate the potential costs of miscalibration. Usefulness analysis necessitates an understanding of the utilities inherent to the use-case, suggests an optimal risk threshold to guide treatment decisions, and may even indicate possible utility gains or cost savings if the model is put into practice.

METHODS

This predictive modeling study derived an observational cohort from retrospective electronic health record data of all inpatient admissions at an urban, academic medical center – Columbia University Medical Center – from 2005–2009. Readmission risk prediction models were developed and validated internally and then calibrated across temporal variant data from subsequent years. Clinical usefulness was then applied to the resultant models, calibrated and not, with attention to both costs and utilities. Each component of this work will be described in detail.

Model Training

The dataset for model training. The data were modeled at the level of the admission (duplicate medical record numbers permitted in training). Baseline patient characteristics are shown (Table 1).

Table 1.

Demographics and Utilization History Characteristics of Training Dataset (2005–2008)

Training Data Characteristics (Total Number of Patients=92,530)	Number of Patients	Percentage of Total Number of Patients
Age
18–45	26,239	28.4
45–65	32,144	34.7
>65	34,147	36.9
Sex
Male	43,964	47.5
Female	48,566	52.5
Insurance Status
Medicaid	12,152	13.1
Medicare	12,477	13.5
Admission Service Type
Internal Medicine	45,697	49.4
Surgery	13,887	15.0
Psychiatry	5,391	5.8
Neurology	4,380	4.7
Other	23,175	25.0
Discharge Status
To Home	72,749	78.6
To Skilled Nursing Facility	5,950	6.4
With Home Care Services	5,507	6.0
Other	8,324	9.0
Utilization Statistics
Number of ER Visits in Year Preceding Index Admission
0	69,778	75.4
1–4	20,861	22.5
>5	1,891	2.0
Number of Inpatient Visits in Year Preceding Index Admission
0	77,999	84.3
1–4	13,981	15.1
>5	550	0.6
Number of Outpatient Visits in Year Preceding Index Admission
0	57,592	62.2
1–4	19,629	21.2
5–10	7,559	8.2
>10	7,750	8.4

Three common readmission diagnoses were selected for modeling – two single-cause readmission models for comparisons of calibration and one all-cause readmission model to evaluate clinical usefulness and costs (Table 2). The single-cause models, congestive heart failure and chronic coronary atherosclerotic disease, were chosen because they are both included in the readmissions reduction penalty program and because they have both been subject to numerous attempts at risk prediction.

Table 2.

Included Readmissions Diagnoses

Readmission Diagnosis	ICD9 Code (ICD.xx)	Case prevalence (%) 2005–2008
Chronic Coronary Atherosclerotic Disease	414.xx	0.5
Congestive Heart Failure	428.xx	0.6
All-Cause Readmission	N/A	13.4

Data were separated into training data, all admissions and readmissions during 2005–2008, and testing data, all admissions and readmissions during 2009. Each readmission model was trained with 20% prevalence sampling, so the full training dataset was used as the validation set for calibration discussed below. No testing data (2009) were used in calibration of the models. The overall method used here has been described.(27)

Feature selection occurred in two steps. Firstly, clinical domain knowledge and the literature guided selection of features from five types of data – demographic; utilization/clinical visit history; laboratory testing; ICD9 visit codes; and keywords from clinical narrative. Secondly, the regression algorithm described below performed final feature selection for model inclusion.

Models were constructed only with data that would be available within the first 24 hours of each index admission to reflect the use-case of a “Day of Admission Risk Calculation”. For example, laboratory values for the first 24 hours were averaged, and only ICD9 codes assigned to prior admissions before index admissions were included since claims codes are assigned only after discharge. Demographics included age, gender, race, and insurance status. Utilization history data included the number of clinic, inpatient, and emergency room visits in the preceding year. Laboratory testing included basic metabolic panels, and blood counts, among other common laboratory tests. The full feature set used in modeling is recorded in the Appendix. Patients were not clustered at the level of center (a single center was used) or treating physician though there is evidence that accounting for clusters, when possible, may improve resultant predictions.[35]

L1-regularized logistic regression (LASSO estimator) was used to create predictive models of thirty-day hospital readmission risk for each of the four diagnoses shown in Table 1.[36] The lambda hyperparameter was obtained through 10-fold cross validation on training data. The model was then trained at that lambda using 20% prevalence sampling of cases versus randomly selected controls, which were patient records that either did not result in readmission or those that resulted in readmission for another reason than that being predicted. This method had been shown to improve discriminatory performance compared to other proportions of sampled cases.[37] It has also been compared to nonparametric algorithms such as support vector machines and was shown to be no different in terms of discriminatory performance.[37]

Methods of Calibration

Four classes of model training and/or calibration were compared based on those identified in textbooks and the literature.[20] These methods could be divided into four general classes: 1) standard method – logistic regression trained on all available data; 2) model training to optimize discrimination; 3) model recalibration; 4) model extension (Table 3). Regularized and unregularized regression have been shown to have varying performance in the domain of readmission risk prediction and, similarly, model training with prevalence sampling (under- or over-sampling) has been shown to outperform training on all available data in cases of outcome rarity.[37] Hence, class #2 – model training to optimize discrimination – was included in this comparison and these models were then recalibrated by the methods of class #3 – recalibration. As stated above, while models were developed via 20% prevalence sampling from training data (subsampled admissions, 2005–2008), the entire available training dataset (all admissions, 2005–2008) was used for calibration to reflect underlying prevalence of the respective outcomes in the population.

Table 3.

Methods of Model Training with and without Calibration

Standard Method Without Additional Calibration
Method [Key]	Prerequisites	Description
Regularized logistic regression at unsampled outcome prevalence [LASSO (all data)][38]	Derivation set, validation set	L1-regularized logistic regression
Model Training to Optimize Discrimination
Method [Key]	Prerequisites	Description
Regularized logistic regression trained via 20% prevalence sampling [LASSO (subsampled)]	Derivation set, validation set	L1-regularized logistic regression
Unregularized logistic regression trained via 20% prevalence sampling [Unregularized LR (subsampled)]	Derivation set, validation set	Logistic regression without regularization
Recalibration
Method [Key]	Prerequisites	Description
Logistic Calibration[39,40]	Derivation set, validation set	Update intercept and calibration slope by fitting logistic regression model in validation sample with linear predictor of uncalibrated model as only covariate.
Platt Scaling[41]	Derivation set, validation set	Fit logistic regression model as in logistic calibration but scale binary outcome (0,1) to $(\frac{1}{N_{-}+2},\frac{N_{+}+1}{N_{+}+2})$ where N− is the number of controls and N+ is the number of cases.
Prevalence Adjustment [Prevalence Adjustment][42]	Outcome prevalence of validation (x) and derivation (y) sets. Uncalibrated predictions (z). Outputs calibrated predictions, z′	$\text{Log odds ratio }(\text{LOR})=\text{ln }\left(\frac{\frac{x}{1-x}}{\frac{y}{1-y}}\right)z\prime =1+\frac{1}{(\frac{1}{z}-1)\ast e^{-\mathit{\text{LOR}}}}$
Model Extension
Method [Key]	Prerequisites	Description
Model Extension of Unregularized Logistic Regression Using Weight Vector for Cases, Controls [Model Extension][20]	Derivation set, validation set	Logistic regression without regularization with an additional feature vector of weights where cases, controls are assigned weights of $\frac{p_1}{r_1}$ and $\frac{1-p_1}{1-r_1}$, respectively (p1 is outcome prevalence in the validation set and r1 is outcome prevalence in the derivation set).

All methods were compared for discriminatory performance using AUROC and for calibration using Spiegelhalter’s Z-statistic. An empiric estimator for RMSE was devised through binning.[29] Ten bins are used here but numbers of bins may vary. Variance was estimated via the bootstrap (25 samples). We included both Sanders and Murphy resolutions of the Brier Score. Finally, calibration slope and intercept were both aggregated across bootstraps to avoid over-reliance on metrics rooted in Mean Square Error and to capture one aspect of the value of graphical methods of assessing calibration.

Performance of calibration methods was compared with metrics outlined above as well as for impact of each method of calibration on clinical usefulness. A final important attribute was the amount of data necessary to achieve calibration – pragmatically and clinically, methods are preferred that require the minimum amount of new data to properly calibrate any predictive model in a new setting

Methods of Clinical Usefulness

At a given threshold probability, all patients who receive a prediction above threshold will be “positives” and this will be a mix of those who would be readmitted (“True Positives”) and those who would not (“False Positives”). Similarly, those patients receiving predictions below threshold would be combined of true and false negatives. The proportion of each of these four categories will vary based on model discrimination and on threshold. Clinical usefulness analysis extends this concept beyond sensitivity and specificity to add utilities or harms to achieve a weighted sum of classifications.[5] A benefit of these analyses is that they are independent of specific modeling or regression strategies employed and can be applied to a broad number of predictive and machine learning algorithms.

A general approach to calculating the utility of a predictive model at a given threshold can be represented by:

$$U_{\mathit{\text{pred}}(s)}=P\ast {\mathit{\text{TPR}}}_s\ast U_{(\mathit{\text{treat}},\mathit{\text{dz}})}+P\ast (1-{\mathit{\text{TPR}}}_s)\ast U_{(\neg \mathit{\text{treat}},\mathit{\text{dz}})}+(1-P)\ast {\mathit{\text{FPR}}}_s\ast U_{(\mathit{\text{treat}},\neg \mathit{\text{dz}})}+(1-P)(1-{\mathit{\text{FPR}}}_s)\ast U_{(\neg \mathit{\text{treat}},\neg \mathit{\text{dz}})}+U_{\mathit{\text{test}}}$$ (3)

Where U_Pred(s) is utility at cutpoint s, P is the probability of a disease or outcome, TPR and FPR are True Positive Rate and False Positive Rate at cutpoint s, respectively.[5] The Utility terms indicate relative utility of treating or not treating a patient who does or does not have the disease (e.g., U_{(treat, ¬dz)} is the utility of treating a patient that does not have the disease). U_test is the utility, costs, or harms of conducting the diagnostic test (e.g., a blood draw or biopsy).

Utility can be replaced by costs or harms depending on the use-case and, in the case of readmissions, costs are most relevant: 1) Cost of Intervention (C_Int) – the per capita cost of performing the intervention; 2) Cost of Readmission (C_Readmit) – the per capita cost of the subsequent hospital readmission if not prevented, this cost may include both costs of providing care and any associated penalties. The utility terms become:

$$U_{(\mathit{\text{treat}},\mathit{\text{dz}})}=C_{\mathit{\text{Int}}}-C_{\mathit{\text{Readmit}}}$$ (4)

$$U_{(\neg \mathit{\text{treat}},\mathit{\text{dz}})}=C_{\mathit{\text{Readmit}}}$$

$$U_{(\mathit{\text{treat}},\neg \mathit{\text{dz}})}=C_{\mathit{\text{Int}}}$$

$$U_{(\neg \mathit{\text{treat}},\neg \mathit{\text{dz}})}=0$$

$$U_{\mathit{\text{test}}}=0$$

There are no costs associated with true negatives, and the expense of computing an individual risk from the predictive model is assumed to be negligible.

The cost of a single readmission was $11,862 in this study, based on one of the few published costs in this area.[34] The modeled cost of an intervention was $1,100 based on a published intervention cost to prevent readmissions for CHF.[43] Intervention costs can range over $10,000 per capita in some studies – intuition holds that an intervention that costs almost as much as a hypothetical readmission cost of $11,862 may not be worthwhile and so such high costs were not included in our simulation.

Optimal Readmission Intervention Costs

A corollary analysis enabled by the utility model above may determine the optimal ratio of costs – intervention costs and readmission costs – that inform a hypothetical intervention. With a critical threshold at zero utility (U_Pred(s)=0), the utility model can be rearranged to:

$$\frac{C_{\mathit{\text{Int}}}}{C_{\mathit{\text{Readmit}}}}=\frac{2\ast P(\mathit{\text{TPR}}-1)}{P(\mathit{\text{TPR}}-\mathit{\text{FPR}})+\mathit{\text{FPR}}}$$ (5)

This ideal cost ratio can be used with real-world values of readmission costs to inform maximum tolerable costs of intervention. And if the cost of a readmission is a known quantity as it often would be in practice, the C_Readmit term can be used to calculate the limits on intervention costs.

Experimental Setup

Data were preprocessed from the clinical data warehouse in Python. Statistical analyses were conducted in R.[44] The LASSO implementation relied on the glmnet and caret packages.[45,46] Spiegelhalter’s Z-statistic was conducted using code written by the authors (CW) but was checked against results obtained in the package, RMS.[47] Plots were built using the R package, ggplot2.[48]

This study was approved by the Institutional Review Board at Columbia University Medical Center.

RESULTS

Discrimination and Calibration

Performance is shown including confidence intervals (aggregated via normal intervals) for the single-cause readmissions risk models including methods of model calibration and model extension (Table 4).[49] Multiple means of calibration – logistic calibration, Platt Scaling, Prevalence Adjustment – performed similarly based on RMSE and its resolutions. However, inclusion of calibration slope and intercept indicates Prevalence Adjustment of Individual Predictions was more poorly calibrated than Logistic Calibration and Platt Scaling based methods. Prevalence adjustment compresses all predictions based on outcome prevalence and this results in a predicted probability distribution that is notably narrower than the other methods of calibration (and clustered around outcome prevalence). As a result, the calibration slope and intercept for this method are affected as predictions – while still discriminating well – are further from an ideal calibration plot with slope of 0 and an intercept of 1. Hence, RMSE remains low while calibration slope and intercept are relatively high compared to other methods of calibration. Spiegelhalter Z-statistics varied more significantly between methods that were similar in RMSE and AUROC though only in combination with slope and intercept are the performances fully differentiable.

Table 4.

Performance characteristics of models of readmission risk across multiple diagnoses and methods of calibration

Readmission ICD9	Model	C-statistic (AUC)	RMSE	Spiegelhalter Z-statistic (95% CI)	Spiegelhalter p-value
428.xx	Lasso (subsampled, uncalibrated)	0.90 (0.84,0.96)	0.21 (0.19,0.23)	−38.13 (−48.59, −27.68)	<2e-16
428.xx	Lasso (unsampled)	0.89 (0.67,1.10)	0.04 (0.03,0.04)	−4.46 (−7.01, −1.90)	8.3e-06
428.xx	Model Extension	0.82 (0.67,0.96)	0.15 (0.09,0.21)	56.01 (9.83,102.20)	<2e-16
428.xx	Logistic Calibration	0.90 (0.84,0.96)	0.04 (0.03,0.04)	−2.14 (−3.73, −0.55)	3.3e-02
428.xx	Platt Scaling	0.90 (0.84,0.96)	0.04 (0.03,0.04)	−2.13 (−3.72, −0.55)	3.3e-02
428.xx	Prevalence Adjustment	0.90 (0.84,0.96)	0.04 (0.03,0.04)	1.88 (−0.47, 4.23)	6.0e-02
414.xx	Lasso (subsampled, uncalibrated)	0.85 (0.80,0.91)	0.23 (0.22,0.24)	−50.80 (−56.08, −45.53)	<2e-16
414.xx	Lasso (unsampled)	0.85 (0.78,0.92)	0.05 (0.05,0.06)	−4.53 (−6.65, −2.42)	5.9e-06
414.xx	Model Extension	0.82 (0.73,0.91)	0.09 (0.06,0.12)	7.31 (−5.01, 19.63)	2.6e-13
414.xx	Logistic Calibration	0.85 (0.80,0.91)	0.05 (0.05,0.06)	−1.63 (−4.34, 1.09)	1.0e-01
414.xx	Platt Scaling	0.85 (0.80,0.91)	0.05 (0.05,0.06)	−1.63 (−4.34, 1.08)	1.0e-01
414.xx	Prevalence Adjustment	0.85 (0.80,0.91)	0.05 (0.05,0.06)	1.90 (−0.90, 4.70)	5.8e-02

Readmission ICD9	Model	Calibration Slope	Calibration Intercept	Sanders Resolution	Murphy Resolution
428.xx	Lasso (subsampled, uncalibrated)	0.19 (0.16,0.22)	−6.25 (−6.59, −5.92)	0.12	0.00
428.xx	Lasso (unsampled)	0.92 (0.15,1.69)	−1.09 (−5.00, 2.82)	0.00	0.00
428.xx	Model Extension	0.07 (−0.07,0.21)	−6.06 (−6.96, −5.15)	0.03	0.00
428.xx	Logistic Calibration	1.02 (0.88,1.17)	−0.24 (−1.08, 0.61)	0.00	0.00
428.xx	Platt Scaling	1.02 (0.88,1.17)	−0.23 (−1.08, 0.62)	0.00	0.00
428.xx	Prevalence Adjustment	2.09 (1.23,2.96)	6.75 (1.89,11.62)	0.00	0.00
414.xx	Lasso (subsampled, uncalibrated)	0.20 (−0.10,0.51)	−5.41 (−5.91, −4.91)	0.14	0.02
414.xx	Lasso (unsampled)	0.66 (−0.08,1.39)	−2.12 (−5.61, 1.38)	0.00	0.02
414.xx	Model Extension	0.09 (−0.05,0.24)	−5.21 (−6.18, −4.24)	0.01	0.02
414.xx	Logistic Calibration	0.92 (0.47,1.37)	−0.66 (−3.02, 1.71)	0.00	0.02
414.xx	Platt Scaling	0.92 (0.48,1.37)	−0.64 (−3.01, 1.72)	0.00	0.02
414.xx	Prevalence Adjustment	1.81 (1.10,2.51)	4.62 (0.89, 8.36)	0.00	0.02

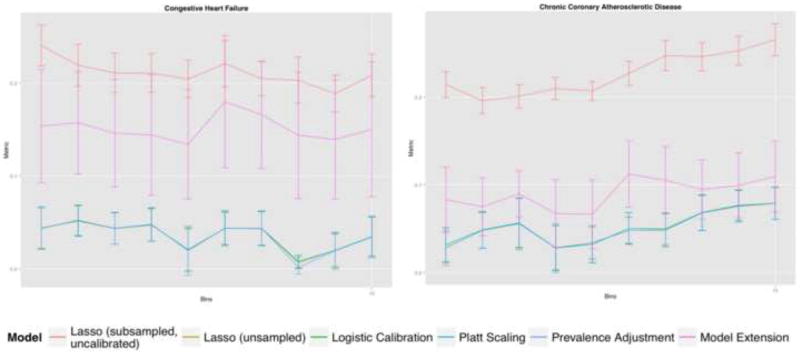
Variation across bins in RMSE with confidence intervals is shown (Figure 1). In general, uncalibrated Lasso was poorly calibrated as was expected. Prevalence adjustment tended toward poorer calibration compared to other methods of calibration but this effect was less apparent than seen with calibration slope/intercept.

Figure 1.

RMSE Estimator with 95% confidence interval error bars for each single-cause readmission diagnosis (bins)

Of note, prevalence adjustment can be run on single predictions or an entire dataset and requires solely knowledge of the outcome prevalence within the validation sample. The remaining methods require all of the predictions within the validation set. Such practical ease must be counterbalanced against the reduction in calibration performance.

Clinical Usefulness

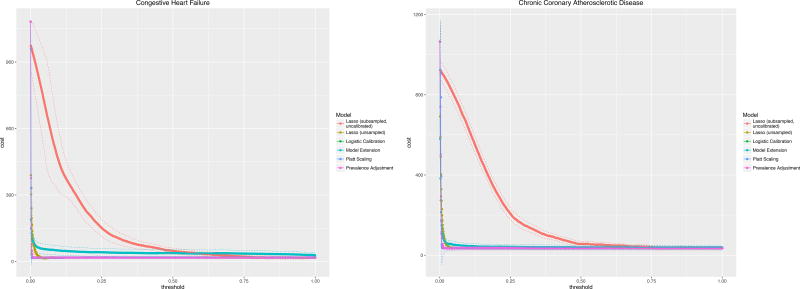
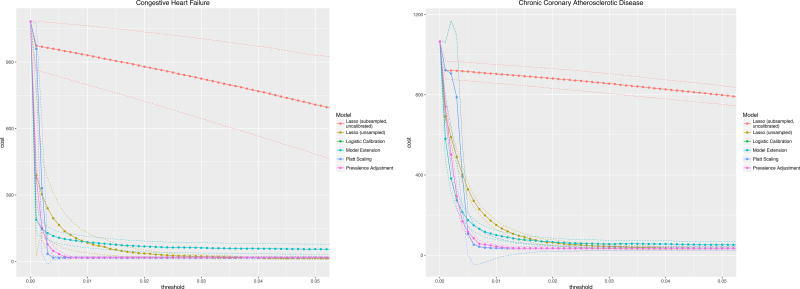
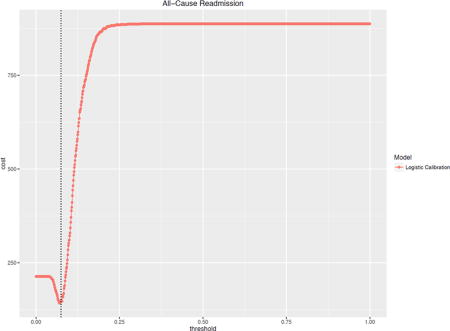
The costs of a hypothetical readmission varied by the risk threshold used to trigger an intervention are illustrated for a Cost of Readmission of $11,862 and Cost of Intervention $1,100 (Figure 2). In practice, choosing a risk threshold for intervention associated with the cost minimum will yield the greatest cost savings. Failing to calibrate properly will lead to lost savings (and lower utility of doing an intervention). The uncalibrated LASSO curve illustrates this effect as its minimum cost occurs at a risk threshold near 0.5 or 50% whereas, when properly calibrated, the optimal cost savings occur at significantly lower thresholds – much closer to the outcome prevalences of less than 1% for these diagnoses.

Figure 2.

Clinical usefulness curves for two readmission diagnoses across all methods of calibration with assumptions: Cost of readmission, $11,862; Cost of intervention $1,100.

Figure 2 shows that both optimal risk thresholds as well as minimum costs vary across different methods of calibration though the optima do not differ significantly based on the established confidence intervals.

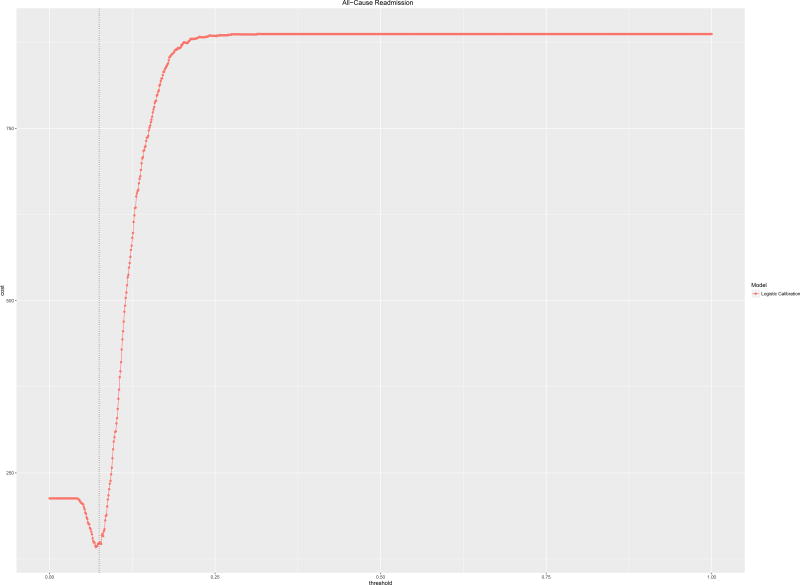
Repeating this analysis for a single algorithm and a higher prevalence outcome, All-Cause Readmissions, AUROC 0.7, the utility function shows different behavior. There is a clear optimum close to the outcome prevalence of 13.4% and cost increases and subsequently plateaus (Figure 3).

Figure 3.

Clinical usefulness curves for all-cause readmission calibrated via logistic calibration with assumptions: Cost of readmission, $11,862; Cost of intervention $1,100.

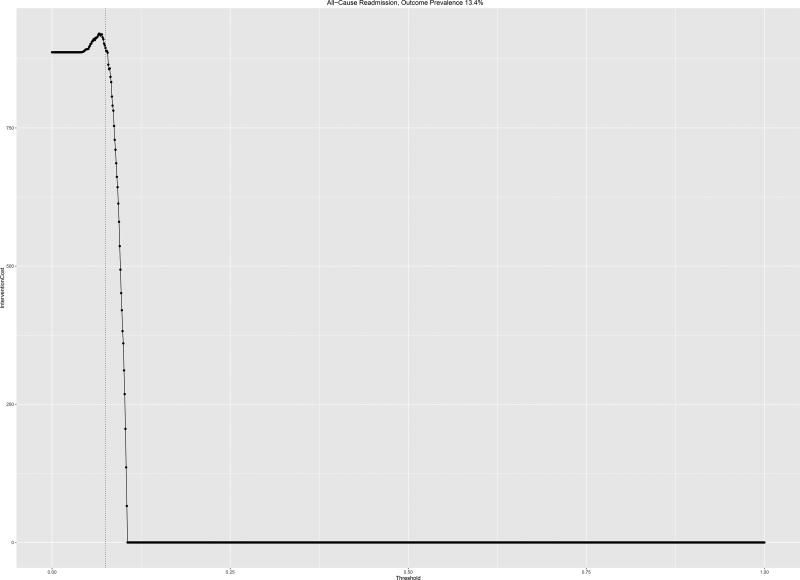
The optimal cost ratio was processed for the readmissions risk model predicting All-Cause Readmissions. Using a readmissions cost of $11,862, the maximum tolerable intervention cost was $1,720 which occurred at an intervention trigger threshold of 8%, compared to a readmission prevalence in this cohort of 13.4%. This analysis for a single-cause readmissions model is associated with much lower tolerable intervention costs at a low threshold of intervention given the concomitantly low outcome prevalence.

DISCUSSION

The principal findings of this work outline an approach to evaluate predictive models beyond discrimination and basic goodness-of-fit calibration metrics. In addition to measuring discrimination via metrics like the AUROC, calibration performance was measured with a combination of RMSE of binned predictions, the Spiegelhalter Z-statistic, Brier Score and its corresponding resolutions, and calibration slope and intercept. Methods like Platt Scaling and Logistic Calibration were associated with lower Spiegelhalter Z-statistics implying a tendency to better calibration, but the RMSE of binned predictions was similar to that of Prevalence Adjustment. Neither Sanders nor Murphy resolutions varied by method of calibration. The method requiring the least additional information to apply, Prevalence Adjustment, appeared to yield comparable performance with other means of calibration until graphical metrics were considered. Inclusion of multiple calibration metrics in parallel not only clarified the limitations of these methods of calibration but also informed and were informed by clinical usefulness analyses.

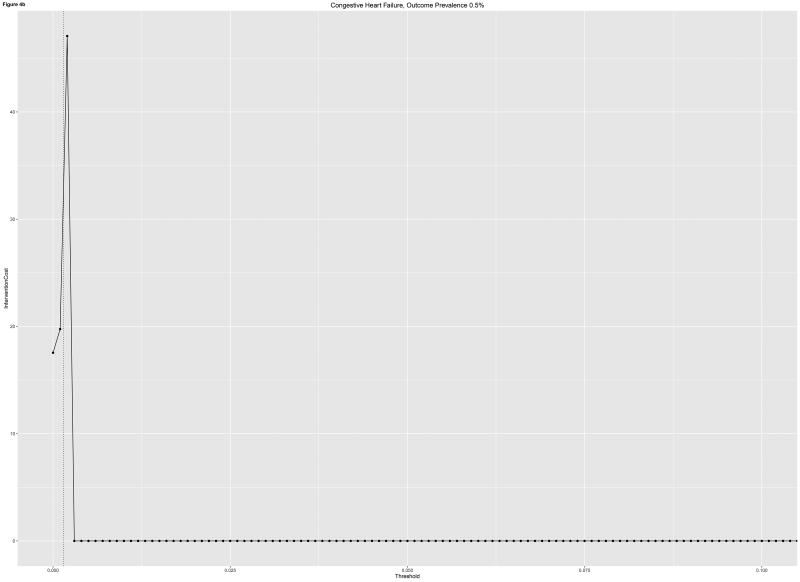
Clinical usefulness analyses differentiated a number of important concerns prior to implementing readmissions risk models into practice. Rare outcomes such as readmission for CHF in our data were associated with lower overall utilities of intervention as well as lower tolerable intervention costs. These findings underline the importance of capturing the utility of readmissions risk intervention holistically. The all-cause readmissions model, while lower performing in terms of discrimination, was associated with higher tolerable intervention costs before usefulness worsened.

We propose an empiric framework in which discrimination, calibration, and clinical usefulness are evaluated via multiple metrics for each category of performance. Because there are threshold-dependent and threshold-independent metrics of discrimination and clinical usefulness, this computation can be performed simultaneously. The additional advantage of this framework is that it requires an a priori designation of the underlying utilities inherent to the use-case and discourages its status as a post hoc analysis or, worse, its omission. Equation (3) represents a generic example for utilities in prevention of hospital readmission. Calibration analyses then inform subsequent iteration.

The suggested approach builds on the work of others by encouraging usefulness analyses in parallel with, not subsequent to, discrimination. It also discourages presentation of threshold-independent metrics such as AUROC as the sole discrimination metric presented in model dissemination. While the statistical literature has espoused all aspects of this framework for some time, practical examples of studies that adhere in full to the triad of discrimination, calibration, and usefulness remain rare compared to those biased to the first over the second or third.

If methods of calibration are indicated, they can be applied and the resultant calibrated output evaluated via discrimination and utility once again. The optimal combination of metrics of discrimination and calibration with maximal potential benefit and minimal harm permits the selection of a modeling approach as well as a potential threshold of intervention. Because predictive models are being disseminated at increasingly rapid rates in the literature and in clinical operations, such an empiric framework will be critical to providers, decision-makers, and data scientists alike.

One consideration is to merge readmissions approaches within this utility framework in which overall risk stratification begins with all-cause readmissions risk prediction on a large population and then single-cause risk predictions are calculated on those same patients to inform the nature of individual risk. Thus, a readmissions intervention program may be couched in the all-cause utility model. The single-cause readmissions risk predictions can be calculated at scale at marginal increased cost; these single-cause risks may then inform the larger intervention in which it becomes more clear not just who is at risk of readmission but why they may be at risk.

We treat as given that predictive modeling methods such as those broadly described in readmission risk require close attention to calibration. In other domains, like acute kidney injury prediction, for example, calibration has been shown to worsen over time.[50] Event rate shift alone was a primary reason for such drift, so practical frameworks incorporating these shifts in program evaluation are important. Our findings underline the cross-sectional impacts of event rate differences not only in calibration but in usefulness and expected utility analyses.

Our investigation relied on the few published costs of both readmissions and interventions at the individual level.[34,43] While one of the first major publications in readmissions risk prediction by Billings in 2006 was grounded in a business case, very few subsequent risk prediction efforts have incorporated utility analyses in their evaluations.[32] Zhou et al. reviewed unplanned readmission risk models in detail in 2016.[51] The review emphasized classification of predictors and performance attributes of the 73 published models across 60 studies, and discrimination (AUROC) and calibration (Hosmer Lemeshow – only if reported) were compared. The state of the literature leaves a significant gap for more frequent inclusion of usefulness analyses as the decision-analytic framework prior to changing clinical workflow requires them. We demonstrated how high discrimination and calibration alone cannot be the sole measures of whether a model may be implemented in practice at tolerable cost.

Over- or under-sampling of data in cases of rare events has been associated with higher discrimination in the past. These results suggest some advantage in discrimination to sampling data for model training and then calibrating rather than training initially on unsampled data. External validation on novel data prior to application of models in practice remains a critical step regardless of this decision.

We represented readmission risk prediction as a binary regression but note that readmission for a single cause may be represented as a trinary regression. The control comparison may be two possible events – no readmission or readmission for another cause. We adhere to binary regression in this study, and it reflects the mode in published readmission risk prediction analyses. But the implications of multinomial regression or multi-class classification to represent this distinction merit further investigation.

Clinical usefulness analysis in this example domain, that of hospital readmission risk prediction, demonstrated both optimal risk thresholds vary across models, across diagnoses, and across underlying utility or cost assumptions. The decision to discretize continuous predictions into a decision to diagnose, to intervene, or to treat is not a trivial one. Clinical usefulness requires the generation of utility assumptions around a given use-case. An added benefit is that the analysis in this case also suggested a cost savings that would form the basis of subsequent prospective evaluation.

The strengths of this work include a large, rich dataset of clinical data and robust statistical methods in regularized regression. The clinical usefulness analysis used here reflects some of the real concerns affecting decision-makers and providers attempting to combat hospital readmissions. It also underlines the importance of capturing cost (more generally, understanding utilities), and integrating it not just into retrospective analysis but also into the decision-making process to initiate an intervention based on risk predictions in the first place. In practice, use of clinical usefulness should include unique utility, cost, or harm terms for each readmission diagnosis as they are clinically unique scenarios.

Limitations of this work include the single-center nature of the study and the heuristic, domain-knowledge approach to feature selection in modeling reported prior. Cost data used in clinical usefulness analysis were based in the sparse literature that includes real-world readmission cost data but did not reflect specific readmission diagnoses. The group of potential calibration methods used here was not comprehensive but our analysis could be readily applied to any number of comparable methods.

CONCLUSIONS

An empiric framework incorporating multiple metrics of discrimination, calibration, and clinical usefulness permits selection of optimal readmission risk modeling strategy including method of calibration to achieve target performance with a minimum of validation data. The simplest means of calibration, Prevalence Adjustment of Individual Predictions, performed well in MSE-based metrics but under-performed Logistic Calibration and Platt Scaling in graphical calibration metrics. Assessing calibration should include evaluation of multiple metrics simultaneously including graphical means. A clinical usefulness framework accomplished two important tasks in applying predictive models: 1) estimated financial impact was derived based on model attributes, outcome prevalences, and cost assumptions alone; 2) an analytic approach to estimating optimal tolerable readmission risk intervention costs was tested. Clinical usefulness is the final third of the triad along with discrimination and calibration that provides a more holistic understanding of candidate predictive models. It requires decision-makers to understand the underlying utility, cost, or harm inherent in the use-case at hand, and it can be used to select optimal risk thresholds at which to intervene and maximum acceptable costs of an intervention.

Figure 4.

a,b: Intervention costs for two models at which utility is zero based on readmission cost of $11,862 per capita for a) All-Cause Readmissions and b) Congestive Heart Failure. Outcome prevalence shown (dotted vertical line)

Highlights.

• A decision-analytic utility framework incorporating multiple metrics of calibration is proposed

• Relying on single measures of discrimination and calibration may be misleading

• Clinical usefulness permits stakeholders to estimate impact and potential cost savings in readmissions risk prevention before implementation